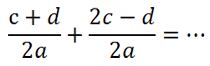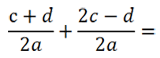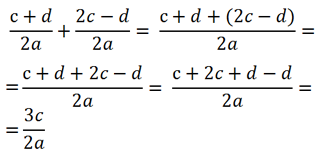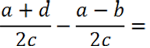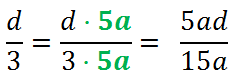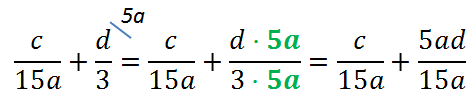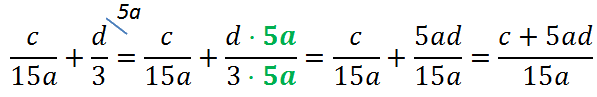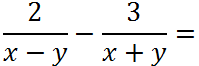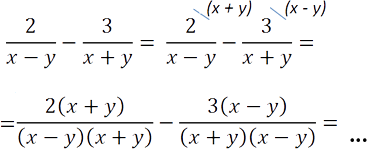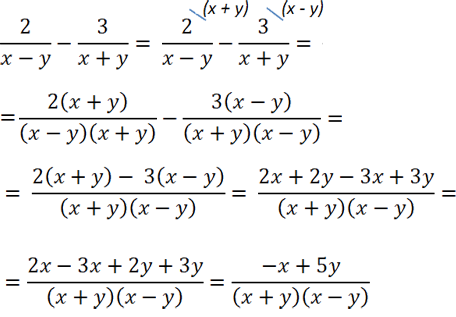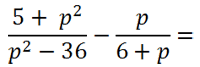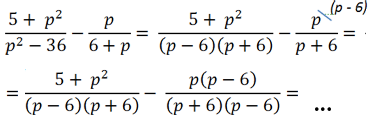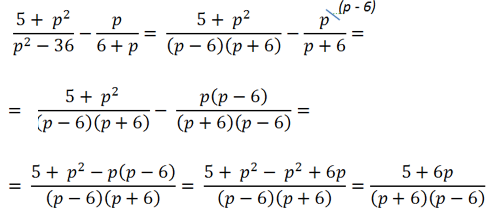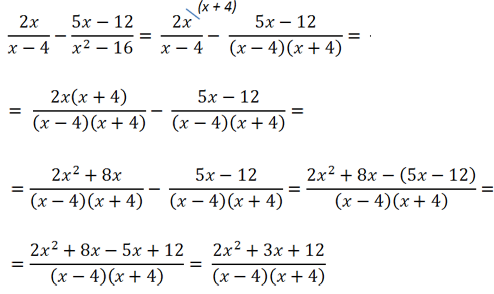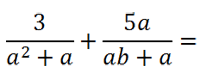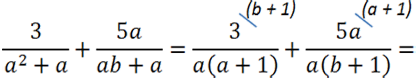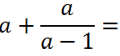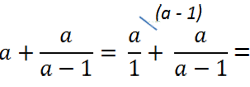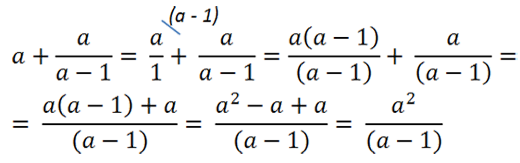Как найти разность дробей с разными знаками

Математика

6 класс

Урок № 44

Обобщение и систематизация знаний по теме «Действия с дробями с разными знаками»

Перечень рассматриваемых вопросов:

– обобщение знаний по теме «Действия с дробями с разными знаками»;

– систематизация знаний по теме «Действия с дробями с разными знаками».

Тезаурус

Отрицательной дробью называют такое число, которое получится, если перед положительной дробью поставить знак «минус». Знак «минус» показывает, что это число на координатной оси изображается точкой, которая находится слева от нуля.

Рациональные числа – множество целых чисел, множество дробей (положительных и отрицательных) и ноль.

Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.

Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.

Список литературы

Обязательная литература:

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.

Дополнительная литература:

1. Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.

Теоретический материал для самостоятельного изучения

На протяжении нескольких уроков мы изучали понятия, правила, законы и свойства сложения и вычитания, умножения и деления положительных и отрицательных дробей. Сегодня мы обобщим и закрепим пройденный материал.

Отрицательная дробь

Если пред положительной дробью поставить знак «–», то получим новое число, которое называется отрицательным дробным числом или отрицательной дробью.

Числа, которые отличаются только знаками, называют противоположными.

Модулем отрицательной дроби называют противоположную ей дробь.

Модули противоположных чисел равны.

Основное свойство дроби

Если числитель и знаменатель дроби умножить на одно и то же целое, не равное нулю число, то получится равная ей дробь.

Это равенство означает, что если числитель и знаменатель дроби имеют общий множитель n (целое, не равное нулю число), то дробь можно сократить на n. При этом получается дробь, равная данной.

Правила сравнения дробей

Две дроби с общим знаменателем и равными числителями равны.

Из двух дробей с общим положительным знаменателем больше та, у которой числитель больше.

Чтобы сравнить две дроби с разными знаменателями, надо привести их к общему знаменателю и сравнить полученные дроби.

Сложение дробей

Сумма дробей с одинаковыми положительными знаменателями есть дробь с тем же знаменателем и суммой их числителей.

Чтобы сложить две дроби с разными знаменателями необходимо сначала привести их к общему знаменателю, а потом сложить числители полученных дробей.

Сумма противоположных дробей равна нулю.

Разность дробей

Разностью двух дробей называют такую дробь, которая в сумме с вычитаемым даёт уменьшаемое.

Чтобы вычислить разность дробей с разными знаменателями, нужно сначала привести их к общему положительному знаменателю.

Произведение дробей

Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей.

Чтобы умножить два числа с одинаковыми знаками, надо поставить знак «плюс» и умножить модули этих чисел.

Чтобы умножить два числа с разными знаками, надо поставить знак «минус» и умножить модули этих чисел.

Свойства умножения

Степенью числа a с натуральным показателем n (n > 1) называют произведение n множителей, каждый из которых равен a.

Частное дробей

Частное двух дробей есть дробь, числитель которой равен произведению числителя первой дроби и знаменателя второй, а знаменатель – произведению знаменателя первой дроби и числителя второй дроби.

Чтобы одну дробь разделить на другую, отличную от нуля, можно делимое умножить на дробь, обратную делителю.

Частным двух дробей с одинаковыми знаками является положительная дробь, модуль которой равен частному модулей этих дробей.

Частное дробей с разными знаками есть отрицательная дробь, модуль которой равен частному модулей делимого и делителя.

Законы сложения и умножения

Переместительный закон сложения

От перестановки мест слагаемых сумма не меняется.

a + b = b + a

Сочетательный закон сложения

Чтобы к сумме двух чисел прибавить третье, можно к первому числу прибавить сумму второго и третьего чисел.

(a + b) + c = a + (b + c) = a + b + c

Распределительный закон

Чтобы число умножить на сумму двух других чисел, нужно это число умножить на каждое слагаемое, а результаты сложить.

a ∙ (b + c) = a ∙ b + a ∙ c

Переместительный закон умножения

От перестановки множителей произведение не изменится.

a ∙ b = b ∙ a

Сочетательный закон умножения

Чтобы произведение двух чисел умножить на третье, можно первое число умножить на произведение второго и третьего чисел.

(a ∙ b) ∙ c = a ∙ (b ∙ c) = а ∙ b ∙ c

Дополнительный материал

Исторические сведения

Завершая тему «Действия с дробями с разными знаками», хотелось бы вспомнить немного истории о дробях.

Дроби всегда считались одним из самых сложных разделов математики. История дробей насчитывает много тысячелетий. Учёные Вавилона и Древнего Египта умели делить целое на части. Со временем действия, которые можно выполнять с дробями, становились сложнее. В каждом древнем государстве были свои понятия, связанные с дробями.

Современное обозначение дробей было введено в Древней Индии. Сама же дробная черта появилась около 300 лет назад. А название «числитель» и «знаменатель» ввёл византийский учёный Максим Плануд примерно 700 лет назад.

Разбор заданий тренировочного модуля

Тип 1. Разместите нужные подписи под изображениями.

Какие законы сложения и умножения изображены?

(a ∙ b) ∙ c = a ∙ (b ∙ c) = а ∙ b ∙ c

(a + b) + c = a + (b + c) = a + b + c

a ∙ (b + c) = a ∙ b + a ∙ c

Варианты ответов:

распределительный закон

сочетательный закон сложения

сочетательный закон умножения

Для ответа на вопрос задания обратимся к теоретическому материалу урока.

Правильный ответ

(a ∙ b) ∙ c = a ∙ (b ∙ c) = а ∙ b ∙ c

сочетательный закон умножения

(a + b) + c = a + (b + c) = a + b + c

сочетательный закон сложения

a ∙ (b + c) = a ∙ b + a ∙ c

распределительный закон

Тип 2. Вставьте в текст нужные слова.

Если перед _____ дробью поставить знак «–», то получим новое число, которое называется _____ дробным _____ или отрицательной _____.

Варианты слов для вставки:

отрицательным

положительной

отрицательной

числом

дробью

Для ответа на вопрос задания обратимся к теоретическому материалу урока.

Правильный ответ:

Если пред положительной дробью поставить знак «–», то получим новое число, которое называется отрицательным дробным числом или отрицательной дробью.

Данная статья начинает изучение действий с алгебраическими дробями: рассмотрим подробно такие действия как сложение и вычитание алгебраических дробей. Разберем схему сложения и вычитания алгебраических дробей как с одинаковыми знаменателями, так и с разными. Изучим, как сложить алгебраическую дробь с многочленом и как произвести их вычитание. На конкретных примерах поясним каждый шаг поиска решения задач.

Действия сложения и вычитания при одинаковых знаменателях

Схема сложения обыкновенных дробей применима и для алгебраических. Мы знаем, что при сложении или вычитании обыкновенных дробей с одинаковыми знаменателями необходимо сложить или вычесть их числители, а знаменатель остается исходным.

К примеру: 37+27=3+27=57 и 511-411=5-411=111.

Соответственно аналогичным образом записывается правило сложения и вычитания алгебраических дробей с одинаковыми знаменателями:

Чтобы осуществить сложение или вычитание алгебраических дробей с одинаковыми знаменателями, нужно соответственно сложить или вычесть числители исходных дробей, а знаменатель записать без изменений.

Данное правило дает возможность сделать вывод, что результат сложения или вычитания алгебраических дробей – новая алгебраическая дробь (в частном случае: многочлен, одночлен или число).

Укажем пример применения сформулированного правила.

Результатом сложения или вычитания может стать сократимая дробь, в этом случае оптимально ее сократить.

По такому же принципу складываются или вычитаются три и более алгебраических дробей при одинаковых знаменателях. К примеру:

1×5+2·x3-1+3·x-x4x5+2·x3-1-x2x5+2·x3-1-2·x3x5+2·x3-1=1+3·x-x4-x2-2·x3x5+2·x3-1

Действия сложения и вычитания при разных знаменателях

Вновь обратимся к схеме действий с обыкновенными дробями: чтобы выполнить сложение или вычитание обыкновенных дробей с разными знаменателями, необходимо привести их к общему знаменателю, а затем сложить полученные дроби с одинаковыми знаменателями.

К примеру, 25+13=615+515=1115 или 12-37=714-614=114.

Так же по аналогии сформулируем правило сложения и вычитания алгебраических дробей с разными знаменателями:

Очевидно, что ключевым здесь будет навык приведения алгебраических дробей к общему знаменателю. Разберем подробнее.

Приведение алгебраических дробей к общему знаменателю

Чтобы привести алгебраические дроби к общему знаменателю, необходимо осуществить тождественное преобразование заданных дробей, в результате которого знаменатели исходных дробей становятся одинаковыми. Здесь оптимально действовать по следующему алгоритму приведения алгебраических дробей к общему знаменателю:

• сначала определяем общий знаменатель алгебраических дробей;
• затем находим дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели исходных дробей;
• последним действием числители и знаменатели заданных алгебраических дробей умножаются на соответствующие дополнительные множители.

Так, мы привели исходные дроби к общему знаменателю. В случае необходимости далее можно преобразовать полученный результат в вид алгебраических дробей, осуществив умножение многочленов и одночленов в числителях и знаменателях.

Уточним также такой момент: найденный общий знаменатель оптимально оставлять в виде произведения на случай необходимости сократить конечную дробь.

Мы рассмотрели подробно схему приведения исходных алгебраических дробей к общему знаменателю, теперь можем приступить к разбору примеров на сложение и вычитание дробей с разными знаменателями.

Обратите внимание еще на такую деталь: перед тем, как алгебраические дроби сложить или вычесть, при наличии возможности их желательно преобразовать с целью упрощения.

Сложение и вычитание алгебраической дроби и многочлена

Данное действие сводится также к сложению или вычитанию алгебраических дробей: необходимо представить исходный многочлен как дробь со знаменателем 1.

Алгебраические дроби складывают и вычитают по
правилам сложения и вычитания
обыкновенных дробей.

Сложение алгебраических дробей

Нельзя складывать дроби без преобразований

Можно складывать дроби

При сложении алгебраических дробей с одинаковыми знаменателями:

1. числитель первой дроби складывается с числителем второй дроби;
2. знаменатель остаётся прежним.

Рассмотрим пример сложения алгебраических дробей.

Так как знаменатель у обеих дробей «2а», значит, дроби можно сложить.

Сложим числитель первой дроби с числителем второй дроби, а знаменатель оставим прежним.
При сложении дробей в полученном числителе
приведем подобные.

Вычитание алгебраических дробей

При вычитании алгебраических дробей с одинаковыми знаменателями:

1. из числителя первой дроби вычитается числитель второй дроби.
2. знаменатель остаётся прежним.

Рассмотрим пример вычитания алгебраических дробей.

Так как у обеих алгебраических дробей знаменатель «2с», значит, эти дроби можно вычитать.

Вычтем из числителя первой дроби «(a + d)» числитель второй дроби
«(a − b)».
Не забудем заключить числитель вычитаемой дроби в скобки. При раскрытии скобок используем
правило раскрытия скобок.

Приведение алгебраических дробей к общему знаменателю

Рассмотрим другой пример. Требуется сложить алгебраические дроби.

В таком виде сложить дроби нельзя, так как у них разные знаменатели.

Прежде чем складывать алгебраические дроби их необходимо привести к общему знаменателю.

Правила приведения алгебраических дробей к общему знаменателю очень похожи на
правила приведения к общему знаменателю
обыкновенных дробей.
.

В итоге мы должны получить многочлен, который без остатка разделится на каждый прежний знаменатель дробей.

Чтобы привести алгебраические дроби к общему знаменателю необходимо сделать следующее.

1. Работаем с числовыми коэффициентами. Определяем
   НОК
   (наименьшее общее кратное) для всех числовых коэффициентов.
2. Работаем с многочленами. Определяем все различные многочлены в наибольших степенях.
3. Произведение числового коэффициента и всех различных многочленов в наибольших степенях и будет общим знаменателем.
4. Определяем, на что нужно умножить каждую алгебраическую дробь, чтобы получить общий знаменатель.

Вернемся к нашему примеру.

Рассмотрим знаменатели «15a» и «3» обеих дробей и найдем для них общий знаменатель.

1. Работаем с числовыми коэффициентами. Находим НОК (наименьшее общее кратное — это число, которое без остатка
   делится на каждый числовый коэффициент).
   Для «15» и «3» — это «15».
2. Работаем с многочленами. Необходимо перечислить все многочлены в наибольших степенях.
   В знаменателях «15a» и «5» есть только
   один одночлен — «а».
3. Перемножим НОК из п.1 «15» и одночлен «а» из п.2. У нас получится «15a». Это и будет общим знаменателем.
4. Для каждой дроби зададим себе вопрос: «На что нужно умножить знаменатель этой дроби, чтобы получить «15a»?».

Рассмотрим первую дробь. В этой дроби и так знаменатель «15a», значит, ее не требуется ни на что умножать.

Рассмотрим вторую дробь. Зададим вопрос: «На что нужно умножить «3», чтобы получить «15a»?»
Ответ — на «5a».

При приведении к общему знаменателю дроби умножаем на «5a»
и числитель, и знаменатель.

Сокращенную запись приведения алгебраической дроби к общему знаменателю можно записать через
«домики».

Для этого держим в уме общий знаменатель. Над каждой дробью сверху «в домике» пишем, на что умножаем каждую из дробей.

Теперь, когда у дробей одинаковые знаменатели, дроби можно сложить.

---

Рассмотрим пример вычитания дробей с разными знаменателями.

В таком виде вычитать дроби нельзя, так как у них разные знаменатели. Чтобы вычесть дроби, необходимо привести их к общему знаменателю.

Рассмотрим знаменатели «(x − y)» и «(x + y)» обеих дробей и найдем для них общий знаменатель.

1. Работаем с числовыми коэффициентами. Числовых коэффициентов в знаменателях нет, поэтому переходим к многочленам.
2. Работаем с многочленами. Находим все различные многочлены из знаменателей в наибольших степенях и перемножаем их.

   Важно!
   

   Многочлены необходимо рассматривать целиком!
   Для удобства заключайте целый многочлен в скобки.

У нас есть два различных многочлена в знаменателях «(x − y)» и «(x + y)».
Их произведение будет общим знаменателем, т.е. «(x − y)(x + y)» — общий знаменатель.

Теперь дроби можно вычитать, т.к. у них одинаковый знаменатель.

Сложение и вычитание алгебраических дробей с помощью формул сокращенного умножения

В некоторых примерах, чтобы привести алгебраические дроби к общему знаменателю, нужно использовать
формулы сокращенного умножения.

Рассмотрим пример сложения алгебраических дробей, где нам потребуется использовать формулу разности квадратов.

В первой алгебраической дроби знаменатель «(p² − 36)». Очевидно, что к нему можно
применить формулу разности квадратов.

После разложения многочлена «(p² − 36)» на произведение
многочленов
«(p + 6)(p − 6)»
видно, что в дробях повторяется многочлен «(p + 6)».
Значит, общим знаменателем дробей будет произведение многочленов «(p + 6)(p − 6)».

Примеры сложения и вычитания дробей с разными знаменателями с использованием формул сокращенного умножения.

Сложение и вычитание алгебраических дробей с вынесением общего множителя за скобки

На первый взгляд одинаковых многочленов в обеих дробях нет.

Вынесем общий множитель
«а» за скобки в обоих знаменателях.

После вынесения общего множителя «а» за скобки, в
обоих знаменателях появился одинаковый одночлен «а».
Значит, общий знаменатель для обеих дробей будет выглядеть так: «а(а + 1)(b + 1)».

Сложение алгебраической дроби с одночленом или числом

Рассмотрим пример. Требуется сложить алгебраическую дробь с одночленом (буквой).

Чтобы сложить одночлен или число с алгебраической дробью,
нужно представить одночлен в виде дроби со знаменателем «1».

Представим одночлен «а» как алгебраическую дробь со знаменателем «1».

Подобное действие можно сделать, так как при делении на единицу получается тот же самый одночлен.

Теперь приведем алгебраические дроби к общему знаменателю «(а − 1)» и решим пример.

---

Ваши комментарии

Оставить комментарий:

---

Технологическая
карта урока.

Предмет: Математика

ФИО (полностью)учителя	Быкова Галина Николаевна
Место работы	МБОУ Горская СОШ
Должность	Учитель математики
Предмет	Математика
Класс	6
Тема и номер урока в теме	Сложение и вычитание обыкновенных дробей с разными знаками (первый урок из пяти по данной теме).
Базовый учебник	С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин. Математика: Учебник для 6 класса общеобразовательных учреждений 4-е изд.,  – М.: Просвещение, 2014

Тип урока: Урок
открытия новых знаний

Форма проведения
урока: Урок проблемного изложения материала.

Время
проведения: 21 декабря 2017 года.

Участники: 6
класс

Оборудование.

Школьная доска,
экран, проектор, компьютер, презентация, карточки-задания на урок, карточки с
дробями, карточки с алгоритмом сложения (вычитания) дробей .

Цель
урока: Сформулировать
правила сложения и вычитания дробей с разными знаками и научиться их применять.

Задачи:

Для
учителя:

1.
Образовательные:

– вывести с
учащимися алгоритм сложения и вычитания дробей с разными знаками;

– сформировать у
учащихся умения и навыки сложения и вычитания дробей с разными знаками.

2.
Развивающие:

– развивать у
учащихся умения анализировать, сравнивать, обобщать, делать выводы;

– развивать у
учащихся умение самостоятельно находить способы решения;

– развивать
критическое мышление;

– развивать
слуховую и зрительную память;

– развивать
внимание;

– развивать
грамотную математическую речь.

3.
Воспитательные:

– воспитывать волю
и настойчивость для достижения конечного результата;

– формировать у
учащихся интерес к предмету;

– воспитывать
доброжелательные, уважительные отношения друг к другу;

– воспитывать
умение объективно оценивать свой труд.

Для
учащихся:

–освоить
знания о том , как происходит сложения и вычитания дробей с
разными знаками;

-выработать умения
сложения и вычитания дробей с разными знаками;

-освоить алгоритм
сложения и вычитания дробей с разными знаками и понять логику его построения;

-выработать умения
применять алгоритм сложения и вычитания дробей с разными знаками;

-развивать умения
самостоятельно определять цели учебной деятельности, планировать пути
достижения целей, контролировать и оценивать учебную деятельность по
результатам.

Планируемый
результат обучения, в том числе и формирование УУД:

к концу
урока учащиеся

– знают алгоритм
сложения и вычитания дробей с разными знаками;

– умеют выполнять
сложения и вычитания дробей с разными знаками.

Познавательные
УУД: развивать
у учащихся умение самостоятельно находить способы решения, развивать
критическое мышление.

Коммуникативные
УУД: воспитывать
доброжелательные, уважительные отношения друг к другу;

Регулятивные
УУД: развивать
у учащихся умения анализировать, сравнивать, обобщать, делать выводы;

Личностные
УУД: воспитывать
волю и настойчивость для достижения конечного результата, умение объективно
оценивать свой труд, развивать слуховую и зрительную память, грамотную
математическую речь .

Основные
понятия:
сложения и вычитания дробей с разными знаками

Интернет –
ресурсы: http://school-collection.edu.ru

Технологическая
карта урока

Этапы урока	Содержание учебного материала. Деятельность учителя	Деятельность обучающихся	ФОУД	Формирование УУД	Комментарий, примечание
1.Организационный этап. (2мин)	Добрый день! Я очень рада вас видеть. -А вы знаете, что ничего не стоит, но очень дорого ценится? (выслушивает варианты ответов) -Это улыбка. Давайте подарим друг другу этот бесценный подарок. Сегодня наш урок будет посвящен одной « особе». Чтобы догадаться , о чем пойдет речь, послушайте загадку: Она бывает барабанная или пальцами, а ещё бывает охотничья (дробь) -Откройте свои тетради, запишите число, классная работа. Наш урок я хотела бы начать с высказывания Л.Н.Толстого Слайд «Человек подобен дроби: в знаменателе – то, что он о себе думает, в числителе – то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь»           Л.Н.Толстой – Как вы понимаете это высказывание? Предлагаю вам выполнить задание « Продолжи фразу…»	Ученики приветствуют учителя стоя. Садятся. Записывают в тетрадь. Отвечают на вопросы.	Фронтальная Индивидуальная	Установление контакта с учащимися
2.Актуализа-ция и фиксиро -вание затруд-нения в проб-ном действи. (6 мин)	Слайд« Продолжи фразу…» 1.Из двух дробей с одинаковыми знаменателями больше та,….. 2.Если числитель и знаменатель дроби умножить или разделить на одно и то же число, отличное от нуля,то… 3.Чтобы сравнить (сложить, вычесть)дроби с разными знаменателями, нужно…. 4.Дробь называется правильной, если…. 5.Сократить дробь, это значит ( Каждый правильный ответ приносит балл, поставьте количество баллов на полях тетради карандашом) Следующее задание выполняем устно,  « Опрос-игра» . 1.К доске вызываются 5 человек, ребятам учитель дает карточки с дробями. Задание  учащимся . -3/8;-1/8;1/2;5/8;7/8. -Построиться в порядке возрастания (молодцы) 2.Сложите четвертую и пятую дробь: 5/8+7/8=12/8 3.Вычтите из пятой четвертую. 7/8-5/8=2/8=1/4 4. Сложите вторую с четвертой. -1/8+5/8  ?	1.Привести их к общему знаменателю, а потом сравнить(сложить, вычесть) 2.Если сумма противоположных чисел равна нулю. 3.У которой числитель больше. 4.Разделить и числитель и знаменатель на одно и тоже число. 5.Получиться равная ей дробь. 6.Числитель меньше знаменателя Учащиеся отвечают на блиц опрос Решают, записывают в карточках Проверяют. Высказывают свои предположения. Сталкиваются с тем, что	Фронтальная	Постановка вопросов Умение с достаточной полнотой и точностью выражать свои мысли	Идёт повторение и закрепление ранее изученного материала Актуализация знаний, необхо-димых для даль-нейшего восп-риятия нового материала. Развитие матема –тической речи.
3. Постановка проблемы, целей урока. (2мин)	-Почему у вас не получилось? -Умеете ли вы складывать и вычитать  дроби с разными знаками? Какая же тема нашего урока? -Ответить на этот вопрос поможет еловые букетики на ваших столах, что вы видите на них вместо игрушек. -Запишем тему урока в тетрадях: « Сложение и вычитание дробей с разными знаками» -Как вы думаете, чему мы будем учиться на сегодня на уроке? -А вам нравиться добиваться побед в учебе? -Что же для этого необходимо? (сила воли, упорство, смекалка, трудолюбие, настойчивость, вера в свои силы, слушать , думать, анализировать). -Ребята, я думаю что все что вы перечислили можно отнести к задачам сегодняшнего урока.	объяснить не могут. -Нет. – Сложение и вычитание дробей с разными знаменателями. Записывают в тетрадь тему урока –освоить знания о том, как происходит сложения и вычитания дробей с разными знаменателями; –выработать умения сложения и вычитания дробей с разными знаменателями; –освоить алгоритм сложения и вычитания дробей с разными знаменателями и понять логику его построения; –выработать умения применять алгоритм сложения и вычитания дробей с разными знаменателями;	Фронтальная	-Смыслообра-зование -познаватель-ная инициа-тива -выдвижение гипотиз и их обоснование -построение логической цепи рассуждений	Учащиеся фор-мулируют цели предстоящей уч-ебной деятель-ности по ана-логии с целями изучения преды-дущих приёмов учебной работы
5. Первичное изучение нового материала ( 4 мин.)	-Давайте вспомним какие правила мы с вами знаем при сложении целых чисел. (правила на стр. 52-53) -Какие обыкновенные дроби мы умеем складывать и вычитать? –Откройте страницы 97-98 учебника прочитайте правило и дополните известный алгоритм шагом или шагами, чтобы можно было по нему выполнить сложение и вычитание дробей с разными знаками. Учитель предлагает из заготовленных карточек восстановить алгоритм, расставляя правильно последовательность шагов ранее изученного алгоритма сложения и вычитания дробей Работа в группах. Учащиеся получают примеры каждая группа свой пример и составляют алгоритм решения своего примера.  1 ряд               2 ряд               3 ряд +(-)       –+(-)         – – После составления алгоритма разместить его на доске с помощью магнитов.	Учащиеся в заготовленных карточках расставляют правильно последовательность алгоритма на сложение и вычитание дробей с разными знаками. Читают учебник стр. 97-98 и выделяют алгоритм сложения (вычитания) дробей с разными знаменателями. В результате работы с учебником ребята составляют алгоритм сложения (вычитания) дробей с разными знаменателями. Алгоритм сложения (вычитания) обыкновенных дробей с разными знаками. 1)Суммой( или разностью)дробей является дробь. 2) Если дроби имеют разные знаменатели, то нужно привести данные дроби к наименьшему общему знаменателю. 3) При сложении дробей с одинаковыми знаменателями и  с разными знаками, нужно из числителя с большим модулем, вычесть числитель с  меньшим модулем, а знаменатель оставить без изменения.  4) При сложении отрицательных дробей с одинаковыми знаменателями , нужно сложить модули числителей, перед суммой поставить знак минус, а знаменатель оставить без изменения. 5)При вычитании дробей, разность заменяем на сложение уменьшаемого и числа, противоположного вычитаемому.  6)Если возможно сократить полученную дробь и выделить из нее целую часть.	Групповая в парах	Логические универсаль-ные действия – выбор оснований и критериев для сравнения
6. Этап первичной проверки понимания изученного. ( 5 мин)	– Ребята, мы достигли цели нашего урока? – Почему? Поэтому наша задача: не только хорошо знать алгоритм, но и уметь его применять. Открываем учебник и выполняем на доске и в тетрадях №503,504(абв),506(абв), 508( по времени)	-Нет -Необходимо научиться применять в решении составленный алгоритм Один ученик у доски (с записью на доске)с проговариванием всех шагов алгоритма выполняет задание с презентации остальные в тетрадях -После каждого этапа проверяем ответы	Индивидуальная Фронтальная	Контроль, коррекция, оценка действий партнёра.
7.Физминутка ( 2 мин)	Ну-ка в сторону карандаши, Ни тетрадей ни ручек, ни мела. Вы устали, ребята, сейчас отдохнем, Чтобы дальше идти нам смело. У вас на столах у каждого лежит дробь. Встаньте, показывая дробь, те у кого дробь: -неправильная; -правильная; -сократимая; -несократимая; -больше нуля; -меньше нуля. Молодцы!	Учащиеся выполняют упражнения. Отдыхают, развивают память и внимание	Фронтальная		Переключение с одного вида деятельности на другой, отдых.
8. Этап закрепления изученного ( 11 мин)	-На столах у вас лежат листочки с алгоритмом, возьмите его, прочитайте ещё раз этот алгоритм каждый про себя. -А теперь давайте алгоритм повторим вслух. -Вы снова полны сил, заряжены энергией, направим её на отработку умения как складывать (или вычитать) дроби с разными знаками? Работа в парах: Решаем примеры с компьютера.      1 ряд                     2 ряд                  3 ряд – + (-)             –+ (-)           – + (-) + (-)               + (-)          + (-) – +              – +                – +      –                   –                   –   – –                   –  –              – – -Найти ответы, которые записаны на шарах ( на еловых ветках) Проверка через компьютер. Ответы: 1 ряд:  – ;  – ;  ;  – ;  – . 2 ряд:  – ;  – ;  ;  – ; – . 3 ряд:  – ; – ; ;  – ; – . -Каждый правильный ответ балл, оценки поставьте на полях карандашом. -Ребята, а знаете, что еще до нашей эры древнекитайские ученые умели складывать и вычитать отрицательные числа. А знаки + и – ввел математик Ян Кидман в 15 веке. Давайте отгадаем Загадку Математики Древнего Египта вместо знаков  «+» и «-» использовали знаки «»  и « »  (“идущие ноги”). Вы сейчас сможете узнать, какое действие обозначали каждый из этих знаков. Среди равенств: а)       в)   б)         г) одно неверное, остальные верные. Какое действие обозначено знаком    ?  Знаком   ?    (– «+»;– «-»; б) – неверно) Предлагаю вам выполнить тест по теме  « Сложение и вычитание дробей с разными знаками». (карточки у каждого) 1 вариант 1)      – ;  а) 11/17;  б) 6/17;   в)-6/17   г)-11/17 2)       –  ; а) -3/5;   б)3/5;    в) 9/5;    г)-9/5           3) –  ; а) 7/30;  б)11/30;  в)-7/30  г)-11/30 4)      –  +(- ); а) -9/15;   б) 9/15;    в) 7/15;   г)-7/15          5)  –  + .; а) 2/14;  б)  5/24;  в) -5/24;  г) 4/16 2 вариант 1)      – ;  а)14/19;  б) -14/19;  в) -12/19; г) 12/19 2)      ; а) 4/31;  б) -4/31;  в) 21/62; г)21/31 3)      – ; а) 4/23;   б) -4/23;   в) 21/23;  г)-21/23 4)      – +(- ); а) -5/8;   б)5/8;   в) 1/8;   г)-1/8     5) –  + а) 4/25;  б) -7/30;    в)7/30  г) 2/5 Ответы:       Взаимопроверка 1 вариант: б) а) в) а) б) 2 вариант: в)  а) г) а) в)	Читают про себя. Говорят вслух (один ученик – один пункт алгоритма). Самостоятельно выполняют указанные номера в парах. Проверяют. Выставляют отмеки.	Фронтальная В парах	Коррекция Контроль Оценка Коррекция Оценка Логические универсальные действия	Активизация внимания. Настрой на работу. Развитие умения применять алгоритм в стандартной ситуации. Развитие внимания. Воспитание уверенности в себе, доброжелательного отношения друг к другу. Обратная связь. Дифференцируемый подход. Вырабатывается умение решать задачи по изучаемой теме.
9. Рефлексия ( 4 мин)	Организация учебного процесса: – Какую цель мы ставили в начале урока? – Наша цель теперь достигнута? – Что нам помогло справиться с затруднением? – Какие знания нам пригодились при выполнении заданий на уроке? – Молодцы, ребята, вы очень хорошо поработали на сегодняшнем уроке и, несомненно, добились побед, больших и маленьких. -Поднимите руки, кто понял, как складывать и вычитать дроби с разными знаками.. Не расстраивайтесь те, у кого сегодня на уроке не всё получилось. На следующем уроке мы продолжим изучение этой темы. Ребята за окном зима, но к сожалению снег постоянно тает ,а как хочется слепить снеговика. Вот и сейчас  к завершению нашего урока предлагаю вам выполнить аппликации снеговиков в соответствии своих отметок на уроке. -Наклейте круги на листе , чтобы получился снеговик, каждый  цвет круга соответствует оценки. –Ребятам которые активно работали на уроке дополнительно дается ведерко для снеговика. При выходе из класса  прикрепите лист на доску магнитом.	Обучающиеся отвечают на вопросы учителя Оценивают собственную деятельность на уроке. -Наносят результаты на горизонтальные шкалы ( на заранее подготовленных листочках)	Индивидуальная	Оценивание усваиваемого содержания Выделение и осознание обучающимися того, что уже усвоено и что ещё нужно усвоить, осознание качества и уровня усвоения; оценка результатов работы. Рефлексия. Обратная связь. Воспитание уважения друг к другу и к учителю.	Обобщение и систематизация полученных на уроке знаний. Установка на последующие уроки.
11 Домашнее задание (2мин)	А теперь внимание, домашнее задание П.3.4 (выучить алгоритм),№510,511.  Творческое задание  по желанию Используя дроби 2 и 3,придумать Истории о дробях. Слайд. «Человек подобен дроби: в знаменателе – то, что он о себе , в числителе – то, что он есть на самом деле. Чем больше знаменатель, тем меньше дробь.» Л.Н.Толстой. Пусть ваша дробь всегда будет неправильной! А идеально – равной единице.	Пишут в дневник: П.3.4 (выучить алгоритм), №360 (а-е), №339. Творческое задание: Используя дроби 2 и 3 ,придумать Истории о дробях	Фронтальная	Осмысление задания	Закрепление умений и навыков.
Подведение итогов (2 мин)	Вот и закончился урок, Подведем сейчас итог Кто же лучше всех трудился На уроке отличился Учащиеся прикрепляют снеговиков на доску. Спасибо за урок!