Как найти разность двух чисел определение - Сайт, где вы сможете решить свои вопросы

Вычита́ние (убавление) — одна из вспомогательных бинарных математических операций (арифметических действий) двух аргументов (уменьшаемого и вычитаемого), результатом которой является новое число (разность)^[1], получаемое уменьшением значения первого аргумента на значение второго аргумента. На письме обычно обозначается с помощью знака «минус»: . Вычитание — операция обратная сложению.

В общем виде можно записать: , где ain A и bin A . То есть каждой паре элементов (a,b) из множества ставится в соответствие элемент , называемый разностью и .
Вычитание возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).

При наличии отрицательных чисел, вычитание удобно рассматривать (и определять) как разновидность сложения — сложение с отрицательным числом^[2]. К примеру, 5-2=3 можно рассматривать как сложение: .

На множестве вещественных чисел область значений функции сложения графически имеет вид плоскости проходящей через начало координат и наклоненной к осям на 45° угловых градусов.

У вычитания есть несколько важных свойств (например для ):

Антикоммутативность:

{displaystyle a-b=-(b-a),quad forall a,bin A.}

Неассоциативность:

{displaystyle (a-b)-cneq a-(b-c),quad exists a,b,cin A.}

Дистрибутивность:

{displaystyle xcdot (a-b)=(xcdot a)-(xcdot b),quad forall a,bin A.}

Вычитание

(нулевого элемента) даёт число равное исходному:

{displaystyle x-0=x,quad forall xin A,quad exists 0in A.}

В качестве примера, на картинке справа запись 5-2=3 обозначает пять яблок вычесть два яблока, что в результате дает три яблока. Заметим, что нельзя вычесть например из 5 яблок 2 груши. Помимо счета яблок, вычитание также может представлять разность других физических и абстрактных величин, таких как: отрицательные числа, дробные числа, векторы, функции, и другие.

Формы записи и терминология[править | править код]

Вычитание записывается с использованием символа «минус»: «» между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте символ «минус» является бинарным оператором. Результат записывается с использованием знака равенства «», например:

;

(«шесть минус три равно три») ;

(«шестьдесят четыре минус тридцать пять равно двадцать девять») .

На письме символ «минус» очень похож на другие письменные символы «дефис», «тире» и другие. Следует внимательнее разбирать выражение, чтобы не возникло ошибочного истолкования символа.

Свойства[править | править код]

Операция вычитание на числовых множествах имеет следующие основные свойства:

Вычитание антикоммутативно — от перемены мест аргументов разность изменяется:

Антикоммутативность:

{displaystyle a-bneq b-a,quad forall a,bin A.}

Вычитание антиассоциативно — при последовательном выполнении вычитания трёх или более чисел последовательность выполнения операций имеет значение, результат изменится:

Антиассоциативность:

{displaystyle (a-b)-cneq a-(b-c),quad forall a,b,cin A.}

Вычитание дистрибутивно, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве, также известно, как распределительный закон^[4] .

Дистрибутивность:

Относительно вычитания в множестве существует единственный нейтральный элемент, вычитание из числа нулевого (или нейтрального элемента) даёт число равное исходному:

Нулевой элемент:

Вычитание нуля идемпотентно — повторное применение операции к объекту даёт тот же результат, что и одинарное:

Идемпотентность:

{displaystyle x=x-0=(x-0)-0=((x-0)-0)-...-0,quad forall xin A,quad exists 0in A}

;

Вычитание противоположного элемента даёт удвоенное число:

{displaystyle a-(-a)=a+a=2a,quad forall ain A,quad exists -ain A.}

Результат вычитания не всегда является определённым для множества натуральных чисел : чтобы получить натуральное число в результате вычитания, уменьшаемое должно быть больше вычитаемого. Невозможно в рамках натуральных чисел вычесть из меньшего числа большее.

Операция вычитания чисел определённых на множествах даёт число (разность) принадлежащее этому же множеству, следовательно операция вычитание относится к замкнутым операциям (операциям, не выводящим результат из данного множества чисел), то есть множества чисел образуют кольца относительно операции вычитания.

Выполнение вычитания[править | править код]

Операцию вычитания можно представить, как некий «черный ящик» с уменьшаемым и вычитаемым на входе и одним выходом — разностью:

При практическом решении задачи вычитания двух чисел необходимо свести её к последовательности более простых операций: «простое вычитание», заём, сравнение и др. Для этого разработаны различные методы вычитания, например для чисел, дробей, векторов и др. На множестве натуральных чисел в настоящее время используется алгоритм поразрядного вычитания. При этом следует рассматривать вычитание как процедуру (в отличие от операции).

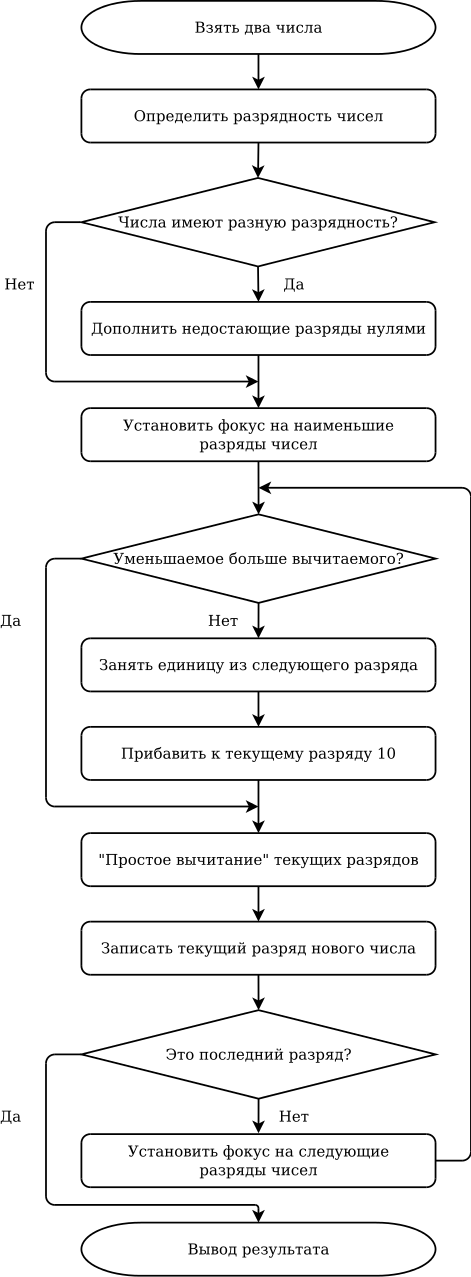
Примерный алгоритм процедуры поразрядного вычитания двух чисел

Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при вычитании больших чисел может занять продолжительное время.

Пример пошагового вычитания из числа 6 числа 4 на числовой прямой.

«Простое вычитание» — в данном контексте обозначает операцию вычитания чисел меньше двадцати, которая может быть легко сведена к декрементированию. Является гипероператором декрементирования:

${displaystyle a-b=operatorname {hyper-1} (a,b)=operatorname {hyper} (a,-1,b)=a^{(-1)}b.}$

${displaystyle a{^{(-1)}}b=a-b=underbrace {1+1+dots +1} _{a}underbrace {-1-1-dots -1} _{b}.}$

где: — последовательность операций инкрементирования, выполненная раз;
— последовательность операция декрементирования, выполненная раз.

Чтобы упростить и ускорить процесс вычитания используют табличный метод «простого вычитания», для этого заранее вычисляют все комбинации разностей чисел от 18 до 0 и берут готовый результат из этой таблицы ^[5]:

таблица для вычитания в десятичной системе счисления

–	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18
0	0	1	2	3	4	5	6	7	8	9
1		0	1	2	3	4	5	6	7	8	9
2			0	1	2	3	4	5	6	7	8	9
3				0	1	2	3	4	5	6	7	8	9
4					0	1	2	3	4	5	6	7	8	9
5						0	1	2	3	4	5	6	7	8	9
6							0	1	2	3	4	5	6	7	8	9
7								0	1	2	3	4	5	6	7	8	9
8									0	1	2	3	4	5	6	7	8	9
9										0	1	2	3	4	5	6	7	8	9

Данная процедура применима к вычитанию натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.

Вычитание чисел[править | править код]

Натуральные числа[править | править код]

Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Обозначим классы эквивалентности конечных множеств порождённых биекциями, с помощью скобок: . Тогда арифметическая операция «вычитание» определяется следующим образом:

где — разность множеств. Данная операция на классах введена корректно, то есть не зависит от выбора элементов классов, и совпадает с индуктивным определением.

Взаимно однозначное отображение конечного множества на отрезок ${displaystyle N_{a}}$ можно понимать как нумерацию элементов множества ${displaystyle A:quad Asim N_{a}}$ . Этот процесс нумерации называют «СЧЕТОМ». Таким образом, «счет» — это установление взаимно однозначного соответствия между элементами множества и отрезком натурального ряда чисел.

Для вычитания натуральных чисел в позиционной системе обозначения чисел применяется поразрядный алгоритм вычитания. Если даны два натуральных числа и такие, что:

${displaystyle a=a_{n-1}a_{n-2}dots a_{0},quad b=b_{n-1}b_{n-2}dots b_{0},quad forall a_{k},b_{k}in {P},quad forall a_{n-1},b_{n-1}neq 0,quad ageqslant b,quad exists 0in mathbb {N} ;}$

где ${displaystyle a_{0dots n-1}=a_{k}P^{k},quad b_{0dots n-1}=b_{k}P^{k}}$ ; — количество цифр в числе ; — порядковый номером разряда (позиции), ; — основание системы счисления; множество числовых знаков (цифр), конкретной системы счисления: ${displaystyle {P_{2}}={0,1}}$ , ${displaystyle {P_{10}}={0,1,2,3,4,5,6,7,8,9}}$ , ${displaystyle {P_{16}}={0,1,2,3,4,5,6,7,8,9,A,B,C,D,F}}$ ; тогда:

${displaystyle c=a-b;quad c_{n-1}c_{n-2}dots c_{0}=a_{n-1}a_{n-2}dots a_{0}-b_{n-1}b_{n-2}dots b_{0};}$

вычитая поразрядно, получаем:

${displaystyle c_{0}={begin{cases}a_{0}-b_{0},quad &{text{if }}a_{0}geqslant b_{0}{text{ }}\a_{0}+P-b_{0},quad a_{1}=a_{1}-1&{text{if }}a_{0}<b_{0}{text{ }}end{cases}}}$
${displaystyle c_{1}={begin{cases}a_{1}-b_{1},quad &{text{if }}a_{1}geqslant b_{1}{text{ }}\a_{1}+P-b_{1},quad a_{2}=a_{2}-1&{text{if }}a_{1}<b_{1}{text{ }}end{cases}}}$
${displaystyle c_{n-1}={begin{cases}a_{n-1}-b_{n-1},quad &{text{if }}a_{n-1}geqslant b_{n-1}{text{ }}\a_{n-1}+P-b_{n-1},quad a_{n}=a_{n}-1&{text{if }}a_{n-1}<b_{n-1}{text{ }}end{cases}}}$

Таким образом операция вычитания сводится к процедуре последовательного простого вычитания натуральных чисел ${displaystyle a_{k}-b_{k}}$ , с формированием заёма при необходимости, которое производится либо табличным методом, либо декрементированием (счетом).

Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно пользоваться таблицей вычитания, соответствующей данному основанию системы счисления.

Пример вычитания натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления, для удобства числа записываются друг под другом соответственно разрядам, знак заёма пишется сверху, недостающие разряды дополняются нулями:

${displaystyle {begin{array}{ccccccccc}&.&.&_{10}&&.&_{10}\&1&1&0&1&1&0\-&0&1&1&1&0&1\hline &&1&1&0&0&1end{array}};quad quad {begin{array}{ccccccc}&.&_{10}&\&8&4&5&6&7\-&3&7&5&4&1\hline &4&7&0&2&6end{array}};quad quad {begin{array}{ccccccc}&.&_{10}&&&_{.}&_{10}\&C&5&6&D&E&4\-&0&F&2&A&1&F\hline &B&6&4&3&C&5end{array}}.}$

Целые числа[править | править код]

Множество целых чисел — расширение множества натуральных чисел , получаемое добавлением отрицательных чисел ^[6] вида . Множество целых чисел обозначается Арифметические операции над целыми числами определяются как непрерывное продолжение соответствующих операций над натуральными числами.

Положительное и отрицательное числа на числовой прямой.

Наличие отрицательных чисел позволяет рассматривать (и определять) «вычитание» как разновидность «сложения» — сложение с отрицательным числом. Однако рассмотрим в рамках данной статьи «вычитание», как операцию определённую на множестве целых чисел, это также относится и к следующим числовым множествам. Отличие от натуральных чисел состоит в том, что отрицательные числа на числовой прямой направлены в противоположную сторону, это несколько меняет процедуру вычитания. Необходимо учитывать взаимное направление чисел, здесь возможны несколько случаев:

Здесь и далее также используется алгоритм поразрядного вычитания (сложения). Например, рассмотрим выражение: ; так как у чисел и разные знаки, то выносим минус за скобки: , вычисляя далее получим ответ: .

Рациональные числа[править | править код]

Множество рациональных чисел обозначается (от англ. quotient «частное») и может быть записано в таком виде: ${mathbb {Q}}=left{{frac {m}{n}}mid min {mathbb {Z}},nin {mathbb {N}}right}.$

Для вычитания рациональных чисел в виде обыкновенных (или простых) дробей вида: $pm {frac {m}{n}}$ , их следует преобразовать (привести) к общему (одинаковому) знаменателю. Например, взять произведение знаменателей, числители при этом умножаются на соответствующие знаменатели. Затем вычесть полученные числители, а произведение знаменателей станет общим.

Если даны два рациональных числа и такие, что: ${displaystyle a={frac {m_{a}}{n_{a}}},b={frac {m_{b}}{n_{b}}}quad forall m_{a},n_{a},m_{b},n_{b}in mathbb {N} quad forall {n_{a}},{n_{b}}neq 0}$ (дроби не сокращаемые), тогда:

${displaystyle c=a-b={frac {m_{a}}{n_{a}}}-{frac {m_{b}}{n_{b}}}={frac {m_{a}cdot n_{b}}{n_{a}cdot n_{b}}}-{frac {n_{a}cdot m_{b}}{n_{a}cdot n_{b}}}={frac {m_{a}cdot n_{b}-m_{b}cdot n_{a}}{n_{a}cdot n_{b}}}.}$ ^[7]

Либо можно найти наименьшее общее кратное (НОК) знаменателей. Порядок действий:

Находим наименьшее общее кратное знаменателей: ${displaystyle M=[n_{a},n_{b}]}$ .
Умножаем числитель и знаменатель первой дроби на ${displaystyle {frac {M}{n_{a}}}}$ .
Умножаем числитель и знаменатель второй дроби на ${displaystyle {frac {M}{n_{b}}}}$ .

После этого знаменатели обеих дробей совпадают (равны ). В ряде простых случаев это упрощает вычисления, но в случае больших чисел расчёты значительно усложняются. Можно взять в качестве любое другое общее кратное.

Пример вычитания:

${displaystyle {frac {2}{3}}-{frac {1}{5}}={frac {2cdot 5}{3cdot 5}}-{frac {3cdot 1}{3cdot 5}}={frac {2cdot 5-3cdot 1}{3cdot 5}}={frac {10-3}{15}}={frac {7}{15}}.}$

Если знаменатели обеих дробей совпадают, то:

${displaystyle {frac {1}{4}}-{frac {2}{4}}={frac {1-2}{4}}=-{frac {1}{4}}.}$

Если знаменатели кратны какому-либо числу, то преобразуем только одну дробь:

${displaystyle {frac {3}{8}}-{frac {1}{4}}={frac {3}{8}}-{frac {1cdot 2}{4cdot 2}}={frac {3-1cdot 2}{8}}={frac {1}{8}}.}$

Арифметическая операция «вычитание» над рациональными числами относится к замкнутым операциям.

Вещественные числа[править | править код]

Арифметические операции над вещественными числами представимых бесконечными десятичными дробями определяются как непрерывное продолжение^[8] соответствующих операций над рациональными числами.

Если даны два вещественных числа, представимые бесконечными десятичными дробями:

${displaystyle alpha =pm a_{0},a_{1}a_{2}ldots a_{n}ldots ={a_{n}}}$ ,
${displaystyle beta =pm b_{0},b_{1}b_{2}ldots b_{n}ldots ={b_{n}}}$

определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: $alpha =[a_{n}]$ и $beta =[b_{n}]$ , то их разностью называют число ${displaystyle gamma =[c_{n}]}$ , определённое разностью последовательностей ${a_{n}}$ и ${b_{n}}$ :

${displaystyle gamma =alpha -beta {overset {text{def}}{=}}[a_{n}]-[b_{n}]=[a_{n}-b_{n}]}$ ;

вещественное число , удовлетворяет следующему условию:

Таким образом разностью двух вещественных чисел alpha и beta является такое вещественное число gamma которое содержится между всеми разностями вида с одной стороны и всеми разностями вида с другой стороны^[9].

На практике для того, чтобы вычесть два числа alpha и beta , необходимо заменить их с требуемой точностью приближёнными рациональными числами и . За приближенное значение разности чисел берут разность указанных рациональных чисел a-b . При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают alpha и beta . Сложение производится по алгоритму поразрядного сложения.

При вычитании приближённых чисел их абсолютные погрешности складываются , абсолютная погрешность числа принимается равной половине последнего знака этого числа. Относительная погрешность разности заключена между наибольшим и наименьшим значениями относительных погрешностей аргументов; на практике принимается наибольшее значение . Полученный результат округляют до первой верной значащей цифры, значащая цифра приближенного числа является верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.

Пример вычитания , с точностью до 3-го знака после запятой:

График[править | править код]

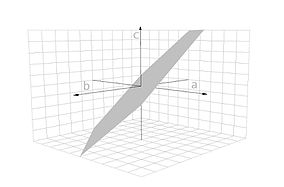
На множестве вещественных чисел область значений функции вычитания графически имеет вид плоскости проходящей через начало координат и наклоненной к осям на 45° угловых градусов.

Так как , то и для этих множеств область значений функции вычитания будет принадлежать этой плоскости.

Комплексные числа[править | править код]

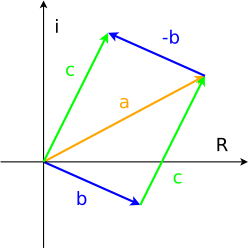
Вычитание двух комплексных c=a-b чисел может быть представлено геометрически через построение треугольника.

Множество комплексных чисел с арифметическими операциями является полем и обычно обозначается символом .

Комплексные числа вычитаются друг с другом путём вычитания действительных и мнимых частей^[10]. Это значит, что:

{displaystyle c+fi=(a+di)-(b+ei)=(a-b)+(d-e)i, }

Где: , — мнимая единица. Используя представление комплексных чисел как векторов на комплексной плоскости, можно дать вычитанию комплексных чисел следующую геометрическую интерпретацию: разностью комплексных чисел и , представленных векторами на комплексной плоскости, будет вектор, соединяющий концы уменьшаемого вектора и вычитаемого вектора и направленный от вычитаемого к уменьшаемому, он является разностью векторов и соответственно разностью комплексных чисел (аналогично будет если к уменьшаемому вектору прибавить вектор обратный вычитаемому вектору).

Аналогично для комплексных чисел n-ой размерности: ${displaystyle A=a_{1}1+a_{2}i_{2}+dots +a_{n}i_{n},~~~B=b_{1}1+b_{2}i_{2}+dots +b_{n}i_{n};}$
${displaystyle C=A-B=(a_{1}1+a_{2}i_{2}+dots +a_{n}i_{n})-(b_{1}1+b_{2}i_{2}+dots +b_{n}i_{n})=}$ ${displaystyle =(a_{1}-b_{1})1+(a_{2}-b_{2})i_{2}+dots +(a_{n}-b_{n})i_{n}=c_{1}1+c_{2}i_{2}+dots +c_{n}i_{n}.}$

Экспоненциальная запись[править | править код]

В экспоненциальной записи числа записываются в виде ${displaystyle a=pm xcdot P^{pm n}}$ , где — мантисса, ${displaystyle P^{n}}$ — характеристика числа, — основание системы счисления. Для вычитания двух чисел, которые записаны в экспоненциальной форме, требуется, чтобы у них были одинаковые характеристики: ${displaystyle acdot P^{n}-bcdot P^{n}=(a-b)cdot P^{n},}$ согласно свойству дистрибутивности.

Например:

${displaystyle 2.3cdot 10^{-5}-5.67cdot 10^{-6}=2.34cdot 10^{-5}-0.567cdot 10^{-5}=(2.34-0.567)cdot 10^{-5}=1.773cdot 10^{-5}}$

Вычитание произвольных чисел[править | править код]

При вычитании чисел принадлежащих разным множествам необходимо произвести расширение числа из множества с меньшей мощностью в сторону числа из множества с большей мощностью, либо оба числа расширить до уравнивания множеств, если существует такая возможность. Например, если нужно вычесть из рационального числа натуральное число , то воспользовавшись тем, что натуральные числа являются подмножеством рациональных, расширяем натуральное число до рационального числа и вычитаем два рациональных числа . Аналогично, пользуясь тем, что: можно вычитать числа из различных множеств между собой.

Особенности обучения вычитанию школьников[править | править код]

Практика показывает, что школьников легче научить вычислять разность чисел, чем научить их принимать решение о применимости операции вычитания в той или иной задаче. Это связано с тем, что вычитание, в отличие, например, от сложения, — некоммутативная операция, её аргументы играют разные роли, и ситуации задач на вычитание, которые должен разрешить ученик, существенно разнообразней, чем при сложении. В связи с этим детям, решившим задачу на вычитание одного вида, может быть затруднительно решить задачу на вычитание другого вида, даже с такими же числовыми данными. Педагог, работающий с ребёнком, должен убедиться, что его ученик уверенно чувствует себя и находит решение задач на вычитание следующих видов:

Виды задач	Примеры задач
Задачи на нахождение результата действия или процесса, приводящих к уменьшению (расходу) начального количества	У Васи было 5 яблок, 3 из них он раздал друзьям. Сколько яблок у него осталось?
Задачи на сравнение чисел и величин, нахождение разницы, превышения, избытка	На участке дороги максимальная разрешённая скорость — 60 км/ч. Автомобиль едет по ней со скоростью 85 км/ч. На сколько водитель превышает допустимую скорость?
Задачи на измерение интервалов — временных и пространственных (как особый cлучай предыдущего вида задач)	В школе уроки заканчиваются в 13 часов 05 минут. Сейчас 10 часов 42 минуты. Сколько ещё ждать до конца уроков?
Задачи на нахождение неизвестной части совокупности (объёма) как дополнения к известной части.	В классе 25 учеников. У двоих из них — рыжий цвет волос, у восьми — каштановый, шестеро — блондинов, остальные — брюнеты. Сколько в классе брюнетов?
Задачи на обращение операции сложения. Восстановление первого операнда	Маша положила в копилку 25 рублей и всего у неё стало 583 рубля. Сколько денег было у Маши до этого?
Задачи на обращение операции сложения. Восстановление второго операнда	Одна ручка стоит 20 рублей, а ручка и блокнот стоят 50 рублей. Сколько стоит блокнот?
Задачи на обращение операции вычитания. Восстановление второго операнда (вычитаемого)	На дереве сидело 16 ворон. Несколько ворон улетело, а осталось 5. Сколько ворон улетело?

См. также[править | править код]

Сумма
Сложение
Умножение
Деление

Примечания[править | править код]

↑ Вычитание // Математическая энциклопедия. М.: Советская энциклопедия, 1977—1985.
↑ Subtraction (англ.) на сайте PlanetMath.
↑ Лебедев, 2003, с. 97.
↑ Так эти свойства называются в учебниках для младших классов
↑ Истомина, 2005, с. 165.
↑ Выгодский, 2003.
↑ Гусев, 1988, с. 20.
↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида
↑ Ильин, 1985, с. 46.
↑ Конвей, 1986, с. 107.

Литература[править | править код]

Ильин В.А. и др. Математический анализ. Начальный курс. (неопр.). — МГУ, 1985. — Т. 1. — 662 с.
Эндертон Г. Элементы теории множеств = Elements of Set Theory. — Gulf Professional Publishing, 1977. — 279 с. — ISBN 0-12-238440-7.
Барсуков А.Н. Алгебра. Учебник для 6-8 классов. (неопр.). — Просвещение, 1966. — 296 с.
Гусев В.А., Мордкович А.Г. Математика. Справочные материалы, книга для учащихся. (неопр.). — Просвещение, 1988. — 416 с.
Истомина Н.Б. Методика обучения математике в начальной школе: Развивающее обучение. (неопр.). — Ассоциация XXI век, 2005. — 272 с. — ISBN 5-89308-193-5.
Выгодский М. Я. Справочник по элементарной математике (неопр.). — М.: АСТ, 2003. — ISBN 5-17-009554-6.
В.И. Игошин. КУРС ЧИСЛОВЫХ СИСТЕМ ДЛЯ ПЕДАГОГИЧЕСКОГО ВУЗА (рус.) : статья. — Саратовский государственный университет имени Н.Г. Чернышевского, 2010.
Кононюк А.Е. Обобщенная теория моделирования. (неопр.). — Освіта України, 2012. — Т. 2. — 548 с. — ISBN 978-966-7599-50-8.
Тире, минус и дефис, или Черты русской типографики : [арх. 24 августа 2011] // Ководство / Артемий Лебедев. — 2003. — § 97 (15 января).
Conway, John B. Функция одной комплексной переменной = Functions of One Complex Variable I. — Springer Science, 1986. — 322 с. — ISBN 0-387-90328-3.

Источник

Разность чисел как определить?

Ирина Эргашева

17 октября 2018 · 87,3 K

Разность – это число, составляющее остаток в вычитании.

То есть, разность чисел определяется вычитанием одного числа из другого. Например: 10-7=3. В этом примере “10” – уменьшаемое, “7” – вычитаемое, а “3” – разность.

22,9 K

Разность – это число, обладающее свойством: в сумме с вычитаемым давать уменьшаемое.
Странно, но в учебнике этого… Читать дальше

Комментировать ответ…Комментировать…

Любитель книг, кошек, увлекаюсь написанием рецензий · 21 нояб 2018

Разность получается путем вычитания одного числа (вычитаемого) из другого (уменьшаемого). То есть, чтобы определить разность, нужно просто вычесть из большего числа меньшее. Например, числа 15 и 10.

15-10=5

5 и будет разность этих чисел

61,3 K

Комментировать ответ…Комментировать…

Источник

Слово «разность» может употребляться во многих значениях. Это может означать и разницу чего-либо, например, мнений, взглядов, интересов. В некоторых научных, медицинских и других профессиональных сферах этим термином обозначают разные показатели, к примеру, уровня сахара в крови, атмосферного давления, погодных условий. Понятие «разность», как математический термин тоже существует.

…

Оглавление:

Арифметические действия с числами

Разность в математике

Видео: Математика 6 Делимость суммы и разности чисел

Как найти разницу величин

Математические действия с разностью чисел

Видео: Математика 2 класс. Разность двухзначных чисел

Простые примеры

Более сложные примеры

Математика для блондинок

Видео: Разность двух отрицательных целых чисел. Математика 6 класс.

Арифметические действия с числами

Основными арифметическими действиями в математике являются:

сложение;
вычитание;
умножение;
деление.

Каждый результат этих действий также имеет своё название:

сумма — результат, получившийся при сложении чисел;
разность — результат, получившийся при вычитании чисел;
произведение — результат умножения чисел;
частное — результат деления.

Это интересно: что такое модуль числа?

Более простым языком объясняя понятия суммы, разности, произведения и частного в математике, можно упрощённо записать их лишь как словосочетания:

сумма — прибавить;
разность — отнять;
произведение — умножить;
частное — разделить.

Разность в математике

Рассматривая определения, что же такое разность чисел в математике, можно обозначить это понятие несколькими способами:

Разность чисел означает, насколько одно из них больше другого.
Разностью в математике называется итог, получившийся при отнимании друг от друга двух и более чисел.
Это вычитание одного числа из другого.
Это цифра, составляющая остаток при минусовании двух величин.
Это величина, являющаяся результатом вычитания двух значений.
Разность показывает количественное различие между двумя цифрами.
Это результат одного из четырёх арифметических действий, которым является вычитание.
Это то, что получится, если из уменьшаемого отнять вычитаемое.

Видео: Математика 6 Делимость суммы и разности чисел

И все эти определения являются верными.

Как найти разницу величин

Возьмём за основу то обозначение разности, которое нам предлагает школьная программа:

Разностью называется результат вычитания одного числа из другого. Первое из этих чисел, из которого осуществляется вычитание, называется уменьшаемым, а второе, которое вычитают из первого, называется вычитаемым.

Ещё раз прибегнув к школьной программе, мы находим правило, как найти разность:

Чтобы найти разность, надо от уменьшаемого отнять вычитаемое.

Всё понятно. Но при этом мы получили ещё несколько математических терминов. Что они значат?

Уменьшаемое — это математическое число, от которого отнимают и оно уменьшается (становится меньше).
Вычитаемое — это математическое число, которое вычитают из уменьшаемого.

Теперь понятно, что разность состоит из двух чисел, которые для её вычисления должны быть известны. А как их найти тоже воспользуемся определениями:

Чтобы найти уменьшаемое, надо к вычитаемому прибавить разность.
Чтобы найти вычитаемое, нужно из уменьшаемого вычесть разность.

Математические действия с разностью чисел

Опираясь на выведенные правила, можно рассмотреть наглядные примеры. Математика, интереснейшая наука. Мы здесь возьмём для решения лишь самые простые цифры. Научившись вычитать их, вы научитесь решать и более сложные значения, трёхзначные, четырёхзначные, целые, дробные, в степенях, корнях, другие.

Видео: Математика 2 класс. Разность двухзначных чисел

Простые примеры

Пример 1. Найти разницу двух величин.

Дано:

20 — уменьшаемое значение,

15 — вычитаемое.

Решение: 20 — 15 = 5

Ответ: 5 — разница величин.

Пример 2. Найти уменьшаемое.

Дано:

48 — разность,

32 — вычитаемое значение.

Решение: 32 + 48 = 80

Ответ: 80.

Пример 3. Найти вычитаемое значение.

Дано:

7 — разность,

17 — уменьшаемая величина.

Решение: 17 — 7 = 10

Ответ: вычитаемое значение 10.

Более сложные примеры

На примерах 1—3 рассмотрены действия с простыми целыми числами. Но в математике разницу вычисляют с применением не только двух, но и нескольких чисел, а также целых, дробных, рациональных, иррациональных, др.

Пример 4. Найти разницу трёх значений.

Даны целые значения: 56, 12, 4.

56 — уменьшаемое значение,

12 и 4 — вычитаемые значения.

Решение можно выполнить двумя способами.

1 способ (последовательное отнимание вычитаемых значений):

1) 56 — 12 = 44 (здесь 44 — получившаяся разница двух первых величин, которая во втором действии будет уменьшаемым);

2) 44 — 4 = 40.

2 способ (отнимание из уменьшаемого суммы двух вычитаемых, которые в таком случае называются слагаемыми):

1) 12 + 4 = 16 (где 16 — сумма двух слагаемых, которая в следующем действии будет вычитаемым);

2) 56 — 16 = 40.

Ответ: 40 — разница трёх значений.

Пример 5. Найти разницу рациональных дробных чисел.

Даны дроби с одинаковыми знаменателями, где

4/5 — уменьшаемая дробь,

3/5 — вычитаемая.

Чтобы выполнить решение, нужно повторить действия с дробями. То есть, надо знать как отнимать дроби с одинаковым знаменателем. Как обращаться с дробями, имеющими разные знаменатели. Их надо уметь привести к общему знаменателю.

Решение: 4/5 — 3/5 = (4 — 3)/5 = 1/5

Ответ: 1/5.

Пример 6. Утроить разницу чисел.

А как выполнить такой пример, когда требуется удвоить или утроить разницу?

Вновь прибегнем к правилам:

Удвоенное число — это величина, умноженная на два.
Утроенное число — это величина, умноженная на три.
Удвоенная разность — это разница величин, умноженная на два.
Утроенная разность — это разница величин, умноженная на три.

Дано:

7 — уменьшаемая величина,

5 — вычитаемая величина.

Решение:

1) 7 — 5 = 2;

2) 2 * 3 = 6. Ответ: 6 — разница чисел 7 и 5.

Пример 7. Найти разницу величин 7 и 18.

Дано:

7 — уменьшаемая величина;

18 — вычитаемая.

Вроде всё понятно. Стоп! Вычитаемое больше уменьшаемого?

И опять есть применяемое для конкретного случая правило:

Если вычитаемое больше уменьшаемого, разница окажется отрицательной.

Решение:

7 — 18 = — 11

Ответ: — 11. Это отрицательное значение и есть разница двух величин, при условии, что вычитаемая величина больше уменьшаемой.

Математика для блондинок

Во Всемирной паутине можно найти массу тематических сайтов, которые ответят на любой вопрос. Точно так же в любых математических расчётах вам помогут онлайн-калькуляторы на любой вкус. Все расчёты, производимые на них, прекрасное подспорье для торопливых, нелюбознательных, ленивых. Математика для блондинок — один из таких ресурсов. Причём прибегаем к нему мы все, независимо от цвета волос, пола и возраста.

В школе подобные действия с математическими величинами нас учили вычислять в столбик, а позднее — на калькуляторе. Калькулятор — это также удобное подспорье. Но, для развития мышления, интеллекта, кругозора и других жизненных качеств, советуем производить арифметические действия на бумаге или даже в уме. Красота человеческого тела — это великое достижение современного фитнес-плана. Но мозг — это тоже мышца, которая требует иногда её качать. А значит, не откладывая, начинайте думать.

И пусть в начале пути вычисления сводятся к примитивным примерам, всё у вас впереди. А освоить придётся немало. Мы видим, что действий с разными величинами в математике множество. Поэтому кроме разницы необходимо изучить, как вычислить и остальные результаты арифметических действий:

сумму — сложением слагаемых;
произведение — умножением множителей;
частное — делением делимого на делитель.

Вот такая интересная арифметика.

Видео: Разность двух отрицательных целых чисел. Математика 6 класс.

Источник

Вычесть значит отнять одно число от другого. Вычитание есть такое действие, в котором отнимают меньшее число от большего. При вычитании целых чисел большее число уменьшается на столько единиц, сколько их содержится в меньшем.

Вычесть одно число из другого значит убавить одно число другим, поэтому вычитание есть действие обратное сложению.

Вычитание

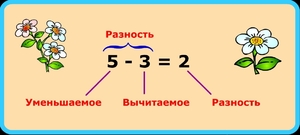
В вычитании два данных числа называются уменьшаемым и вычитаемым, а искомое — разностью.

Уменьшаемым называют большее число, от которого отнимают другое. Оно уменьшается от вычитания.

Вычитаемым называют меньшее число, которое отнимают от большего.

Разностью называют вывод, полученный от вычитания. Разность определяет, чем одно число больше другого или показывает разницу между двумя числами.

Знак вычитания. Действие вычитания обозначается знаком — (минус).

Вычитание однозначных чисел

Чтобы обозначить, что из 9 нужно вычесть 6, пишут эти числа рядом, отделяя их знаком — (минус):

9 — 6.

Разность между этими числами будет 3, и ход вычисления выражают словесно:

девять без шести равно трем.

Письменно:

9 — 6 = 3.

Большее число 9 будет уменьшаемым, меньшее 6 вычитаемым, число 3 остатком.

Способы вычитания

Можно двумя способами вычесть одно число из другого:

или можно отнять от большего числа столько единиц, сколько их содержится в меньшем. Так, из 9 вычесть 6 значит от 9 отнять 6. Число 3 будет искомый остаток;
или можно к меньшему числу прибавлять по единице до тех пор, пока не получим большее число. Так, вычитая 6 из 9, мы к 6 прибавляем 3 единицы.

Число единиц, которое нужно прибавить к меньшему числу, чтобы уравнять его с большим, определяет разность.

Меньшее число с разностью должно равняться большему числу, следовательно, меньшее число и разность суть слагаемые, а большее — их сумма. На этом основано другое определение вычитания:

Вычитание есть такое действие, в котором по данной сумме и одному слагаемому отыскивается другое слагаемое.

В этом случае данная сумма есть уменьшаемое, данное слагаемое — вычитаемое, а искомаяразность — другое слагаемое.

Вычитание многозначных чисел

Вычитание многозначных чисел основывается на том свойстве чисел, по которому вычесть число все-равно, что вычесть все его части. Из этого свойства видно, что вычесть какое-нибудь число все-равно, что вычесть последовательно все его единицы, десятки, сотни и т. д. Чтобы обозначить, что из числа 7228 нужно вычесть 3517, пишут:

7228 — 3517 и вычитают отдельно единицы из единиц, десятки из десятков и т. д.

Чтобы облегчить вычитание, подписывают меньшее число под большим так, чтобы единицы одинаковых порядков находились в одном вертикальном столбце, проводят черту, слева ставят знак вычитания — и под чертою подписывают разность.

Ход вычисления выражают словесно:

Начинаем вычитание с простых единиц: 8 без 7 составляют 1; подписывают под единицами 1.
Вычитаем десятки: 2 без 1 дают 1, подписываем под десятками 1.
Вычитаем сотни. Пять нельзя вычесть из 2, поэтому занимаем у следующего высшего порядка (тысяч) единицу, что и обозначаем тем, что над 7 ставим точку. Единица каждого порядка содержит 10 единиц следующего меньшего порядка. Присоединяя эти 10 единиц к 2, получим 12; 12 без 5 составляют 7, подписываем под сотнями 7. Когда занимают единицу у высшего порядка, обозначают это тем, что ставят точку над порядком, у которого занимают.
Вычитаем тысячи. Тысяч осталось вместо 7 только 6, ибо одна была взята. 6 без 3 составляют 3; подписываем под тысячами 3.

Ход вычисления выражают письменно:

Пример. Из 17004 вычесть 6025.

Из 4 нельзя вычесть 5. Занимаем единицу у десятков, следующего высшего порядка, но в этом порядке единиц нет; занимаем у сотен, — и сотен нет; занимаем у тысяч и обозначаем это точкой над цифрой 7.

Единица четвертого имеет 10 единиц третьего порядка. Взяв из них одну для десятков, оставляем их в сотнях только 9. Присоединив 10 к 4, имеем 14.

Производя вычитание, получим:

для единиц 14 — 5 = 9
для десятков 9 — 2 = 7
для сотен 9 — 0 = 9
для тысяч 6 — 6 = 0

Для десятков тысяч имеем 1, ибо эту цифру уменьшаемого переносим в разность без изменения.

Ход вычисления выразится письменно:

Из предыдущих примеров выводим правила вычитания:

Чтобы сделать вычитание целых чисел, нужно вычитаемое подписать под уменьшаемым так, чтобы единицы одинаковых порядков стояли в одном вертикальном столбце, провести черту, под которою и подписать разность.
Вычитание нужно начинать с простых единиц, то есть с первого столбца, и затем, переходя к следующим столбцам от правой руки к левой, вычитают десятки из десятков, сотни из сотен и т. д.
Если цифра вычитаемого меньше цифры уменьшаемого, разность подписывают в том же столбце; если цифры равны, разность будет нуль.
Если же цифра вычитаемого больше соответствующей цифры уменьшаемого, занимают единицу у следующего порядка уменьшаемого, отмечая это точкой, поставленной над цифрой, у которой занимают, прикладывают 10 к цифре уменьшаемого и производят вычитание. Цифру же с точкой считают на единицу меньше.
Если при вычитании цифра уменьшаемого, у которого занимают, будет 0, за которым в уменьшаемом следуют тоже нули, то занимают у первой значащей цифры, ставя над нею и всеми промежуточными нулями точки. Цифру с точкой считают на единицу меньше, а нули с точкой считают за 9.
Вычитание продолжают до тех пор, пока не получат полной разности.
Лишние цифры уменьшаемого переносят в разность.

Зависимость между данными и искомыми вычитания

Из примера 9 — 6 = 3 видно, что

Уменьшаемое равно вычитаемому, сложенному с разностью: 9 = 6 + 3.
Вычитаемое равно уменьшаемому без разности: 6 = 9 — 3.
Разность равна уменьшаемому без вычитаемого: 3 = 9 — 6.

Арифметическое дополнение. Разность между числом и ближайшей большей единицей называется арифметическим дополнением. Так, арифметическими дополнениями чисел 7, 79, 983 будут числа:

10 — 7 = 3
100 — 79 = 21
1000 — 983 = 17

Арифметическим дополнением иногда пользуются для облегчения арифметических вычислений.

Источник: https://maths-public.ru/arithmetic/subtraction

Вычитание чисел

Вычитание – это арифметическое действие обратное сложению, посредством которого из одного числа вычитают (отнимают) столько единиц, сколько их содержится в другом числе.

Число, из которого вычитают, называется уменьшаемым, число, которое указывает сколько единиц будет вычтено из первого числа, называется вычитаемым. Число, получаемое в результате вычитания, называется разностью (или остатком).

Рассмотрим вычитание на примере. На столе лежит 9 конфет, если съесть 5 конфет, то их останется 4. Число 9 является уменьшаемым, 5 – вычитаемым, а 4 – остатком (разностью):

Для записи вычитания используется знак — (минус). Он ставится между уменьшаемым и вычитаемым, при этом уменьшаемое записывается слева от знака минус, а вычитаемое – справа. Например, запись 9 — 5 означает, что из числа 9 вычитается число 5. Справа от записи вычитания ставят знак = (равно), после которого записывают результат вычитания. Таким образом, полная запись вычитания выглядит так:

Эта запись читается так: разность девяти и пяти равняется четырём или девять минус пять равно четыре.

Чтобы в результате вычитания получить натуральное число или 0, уменьшаемое должно быть больше вычитаемого или равно ему.

Рассмотрим, как, используя натуральный ряд, можно выполнить вычитание и найти разность двух натуральных чисел. Например, нам необходимо вычислить разность чисел 9 и 6, отметим в натуральном ряду число 9 и отсчитаем от него влево 6 чисел. Получим число 3:

9 — 6 = 3

Вычитание также можно использовать для сравнения двух чисел. Желая сравнить между собой два числа, мы задаёмся вопросом, на сколько единиц одно число больше или меньше другого.

Чтобы узнать это, надо из большего числа вычесть меньшее. Например, чтобы узнать, на сколько 10 меньше 25 (или на сколько 25 больше 10), надо из 25 вычесть 10.

Тогда найдём, что 10 меньше 25 (или 25 больше 10) на 15 единиц.

Проверка вычитания

Рассмотрим выражение

15 — 7 = 8

где 15 – это уменьшаемое, 7 – это вычитаемое, а 8 – разность. Чтобы узнать правильно ли было выполнено вычитание, можно:

вычитаемое сложить с разностью, если получится уменьшаемое, то вычитание было выполнено верно:7 + 8 = 15
от уменьшаемого отнять разность, если получится вычитаемое, то вычитание было выполнено верно:15 — 8 = 7

Источник: https://naobumium.info/arifmetika/vychitanie.php

Что такое разность чисел в математике?

Для многих точные науки, вроде математики, воспринимаются как нечто более простое, чем сферы, требующие рассуждений, предполагающие большую вариативность. Однако все предметы имеют свои сложности, в том числе и технические.

Вычитание

Для того, чтобы понять, чем является разность, необходимо разобраться в ряде математической терминологии. В первую очередь, нужно выяснить, чем является вычитание.

По-другому это понятие называют убавлением, и по такому названию понять смысл процесса несколько проще. По своей сути вычитание является одной из математических операций.

Что же это за операции? Как правило, под ними понимают определенные арифметические или логические действия. Встает логичный вопрос – в чем же суть арифметических действий?

Понятие арифметики появилось достаточно давно. Оно зародилось в древнегреческом языке, где переводилось как «число». Сегодня это раздел математики, который изучает числа, их отношения друг к другу, а также свойства.

Итак, вычитание – это операции с числами, относящиеся к бинарным. Суть бинарных операций в том, что в них используются два аргумента (параметра), и получается один результат.

Стоит рассмотреть, как найти разность какого-то числа. В первую очередь, необходимы два аргумента, то есть два числа. Затем необходимо уменьшить значение первого числа на значение второго.

Когда данная операция выражается письменно, используется знак «минус». Это выглядит так: а – б = с, где а является первым числовым значением, б – вторым, а с – разностью чисел.

Как правило, у учеников возникает гораздо больше проблем именно с вычитанием, нежели со сложением. Отчасти это связано со свойствами данных математических операций.

Всем известно, что от перемены мест слагаемых значение суммы не меняется. В вычитании же всё гораздо сложней. Если поменять числа местами, получится совершенно другой результат.

Схожим свойством в прибавлении и убавлении является то, что нулевой элемент не меняет исходное число.

В вычитании всё относительно просто, если первое число больше второго, однако в школе будут рассматриваться и противоположные примеры. В этом случае возникает понятие отрицательного числа.

Например, если нужно вычесть из 5 число 2, то всё несложно. 5-2=3, таким образом разность числа составит 3. Однако, что делать, если необходимо посчитать, сколько будет два минус пять?

В выражении 2-5 разность уйдет в минус, то есть в отрицательное значение. Из двойки легко можно вычесть двойку, получив таким образом ноль, однако от пятерки остается ещё три. Таким образом, результатом данного выражения будет отрицательное число три. То есть, 2-5=-3.

Источник: https://topkin.ru/voprosy/nauka-voprosy/chto-takoe-raznost-chisel-v-matematike/

Что такое разность чисел: уменьшаемое, вычитаемое, разность — правило

Статья познакомит читателя с понятиями «разность чисел», «вычитаемое» и «уменьшаемое».

В арифметике существует всего четыре основных действия, которые мы называем сложением, умножением, вычитанием и делением.

Такие действия являются основой всей математики – они позволяют нам осуществлять все вычисления: как простые, так и самые сложные.

Самыми простыми действиями считаются сложение и вычитание, которые противоположны друг другу. Правда, слово «сложение» мы также используем и в обычной жизни.

Мы можем встретить фразу «сложить усилия, например, когда нам нужно сделать какую-нибудь работу всем вместе. Но вот с термином «вычитание» дело обстоит немного сложнее, и в разговоре оно встречается реже.

Мы редко услышим такие выражения, как «уменьшаемое», «вычитаемое», «разность». Но в сегодняшней статье мы подробно поговорим о них с точки зрения математики.

Что значит число уменьшаемое, число вычитаемое и разность чисел?

Что значит число уменьшаемое, число вычитаемое и разность чисел? Как известно, многие научные термины и выражения взяты из других языков, чаще греческого и латинского. Но те слова, которые будут рассмотрены ниже, имеют русское происхождение, потому нам будет проще их разобрать.

Например, что можно сказать о разности чисел? Если мы обратим внимание на корень слова «разность», то нам представится, например, его однокоренное слово «разница».

А если речь идет о математике, то тут и думать нечего – слово «разность» означает разницу между какими-то цифрами, а точнее, двумя числами.

Разница нам показывает, насколько одна величина больше другой или, наоборот, вторая меньше первой. Строго в математике это выглядит как результат вычитания.

Сразу же приведем пример. Допустим, буфетчица несет на подносе восемь пирожков. Пять из них она раздала посетителям. Сколько пирожков останется у буфетчицы на подносе? Если из 8 вычесть 5, то получится — 3. Теперь запишем это математически:

То есть разница между восемью и пятью – это три. Теперь нам понятно, что такое термин «разница».

Внимание: Если два числа равны друг другу, то разницы между ними не существует, она равна нулю (8 – 8 = 0).

Теперь нам следует выяснить, что такое вычитаемое и уменьшаемое. Снова представим значение слов по их смыслу. Чем может являться число уменьшаемое? Уменьшаемое – это то число, которое уменьшается при вычитании. От этого числа отнимают другое число. А что такое вычитаемое? Вычитаемым как раз и является том числом, которые мы отнимаем от уменьшаемого.

Вернемся к примеру с буфетчицей. Мы помним, как от восьми отнимали пять, и у нас получилось три. Мы выяснили, что тройка является разницей между двумя этими числами. Теперь нам уже не сложно понять, что 8 – это число уменьшаемое, а 5 – это число вычитаемое.

Как найти уменьшаемое и вычитаемое число?

Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:

Y – 10 = 18, где Y – число уменьшаемое
Значит, Y = 18 + 10
18 + 10 = 28
Y = 28

Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:

28 – B = 10, где B – число вычитаемое
Значит, B = 28 – 10
28 – 10 = 18
B = 18

Источник: https://heaclub.ru/chto-takoe-raznost-chisel-umenshaemoe-vychitaemoe-raznost-pravilo

Что такое разность чисел в математике и как найти разность чисел

В этой статье мы рассмотрим, что такое разность чисел в математике, и как человеку, интересующемуся этой наукой, найти разность чисел.

Что такое разность чисел в математике

Вычитание является одной из 4 арифметических операций. Для его обозначения служит математический знак «−» (минус). Вычитание противоположно по смыслу операции сложения.

Операция вычитания в общем случае записывается следующим образом:

A − B = C

Число Математическое название

A	Уменьшаемое
B	Вычитаемое
C	Разность чисел

Пример: 6 − 2 =4

Здесь разностью чисел будет являться число 4. Следовательно, разность между любыми числами A и B это такое число C, которое при прибавлении к B даст в сумме A (4 при прибавлении к 2 дает 6 — значит, 4 это разность 6 и 2).

Как найти разность чисел

Уже из самого определения следует, как вычислить разность между двумя числами. При небольших числах можно делать это в уме. Детей в начальной школе учат следующим образом. Представьте, что у Вас есть 5 яблок, и 3 из них забрали. Сколько у Вас осталось? Правильно — 2 яблока. Постепенно Вы доведете вычисления до автоматизма и будете сразу выдавать ответ.

Однако для чисел выше 50 такое наглядное представление перестает работать. Большое количество предметов тяжело представить в уме, поэтому здесь на помощь приходит другой способ:

Вычисление разности в столбик

Школьники изучают этот способ в рамках курса математики, обычно во втором или третьем классе. Взрослые люди, пользующиеся калькулятором, зачастую забывают, как считать в столбик. Однако калькулятор не всегда бывает под рукой. Освежите в памяти школьные знания, посмотрев это видео.

Вычисление разности в столбик – видео

Этот способ применим и тогда, когда Вам нужно вычесть большее число из меньшего. В реальной жизни такое обычно не требуется, но может пригодиться при решении математических задач.

Допустим, в примере «A − B = C» B больше, чем A. Тогда C будет отрицательным. Чтобы вычислить разность, «разверните» пример: посчитайте значение B − A.

Когда Вы закончите считать эту разность, у вас получится число C, только с противоположным знаком: оно будет больше нуля. Чтобы завершить вычисления, припишите к нему спереди знак минус.

Источник: https://www.chto-kak-skolko.ru/index.php/nauki/matematika/chto-takoe-raznost-chisel-v-matematike-i-kak-najti-raznost-chisel

Источник

Что такое разность чисел и как ее найти

Добавлено: 22 марта 2022 в 10:52

К слову «разность» можно подобрать однокоренные слова, такие как, различный, разный.

То есть, разность имеет значение того, что между объектами имеются какие-либо отличия, что они не одинаковые. В математике данный термин является часто используемым. Изучение отличия чисел начинается с первого класса. Это основной, базовый процесс, который должен знать каждый.

По мимо математики, без определения разницы не обходится ни одна точная наука. Разность определяется и в быту, ежедневно. Например, при походе в магазин, необходимо из числа, которое является номиналом купюры, вычесть стоимость продукта. То, что останется (сдача), будет называться разностью.

Таким образом, отличия чисел — это результат математического действия, вычитания.

Виды математических действий и их результаты

Вычитание (результат — разность).
Сложение (результат — сумма).
Деление (частное).
Умножение (произведение).

Данные действия являются основополагающими в вычислительных процессах. Они не взаимозаменяемы. Это индивидуальные виды вычислений, которые не следует путать.

Как найти разность чисел

Чтобы найти разность чисел, необходимо выполнить процесс вычитания. А именно, из уменьшаемого вычесть (или отнять) вычитаемое. В результате получится разница.

Пример: 7 — 2 = 5,

В данном случае, разность равна 5. Уменьшаемое 7, его мы уменьшаем, делаем меньше. Вычитаемое 2, это число мы вычитаем (отнимаем).

Данную процедуру можно записать и в буквенном выражении.

Пример: С — А = В,

В — разность; С — уменьшаемое; А — вычитаемое.

В младших классах ученикам объясняют то, чтобы найти разность чисел, нужно из большего числа вычесть меньшее. Это наиболее часто встречающееся правило. Но, при более глубоком изучении математики становится ясно, что и из меньшего числа можно вычесть большее. Тогда получится результат со знаком «-«.

Пример: 5 — 7 = — 2,

Но дело в том, что разность показывает:

— чем отличаются числа,

— на сколько они отличаются,

— на сколько одно число больше другого,

— на сколько одно число меньше другого,

— отличаются ли числа, или они равны.

Следовательно, разность не может выражаться со знаком «-«. Иначе, она не будет иметь логического смысла. Поэтому, в ситуациях, когда из меньшего вычитается большее, берется модуль разницы, то есть число без минуса «-«.

Знак «модуля» в математике обозначается двумя вертикальными линиями, между которыми пишется число. Модуль всегда положительный.

Математика включает себя бесконечное количество различных чисел, не только целых, но и дробных. Разность дробей находится аналогичным способом.

Пример: 1 — 1/4 = 3/4,

Разность 3/4, уменьшаемое 1, вычитаемое 1/4.

То же самое можно проводить с процентами, буквенными и числовыми выражениями в скобках.

Как проверить, верно ли найдена разность

В математических вычислениях большую роль играет проверка. Когда решен пример по поиску избытка, чтобы проверить его правильность, нужно совершить обратное действие.

Пример: 8 — 5 = 3, (разность 3),

Чтобы совершить проверку, сделаем известное уменьшаемое неизвестным. Чтобы найти уменьшаемое, нужно к разнице прибавить вычитаемое.

Тогда получим: 5 + 3 = 8 (получилось 8, как и было, следовательно, пример решен верно).

Второй способ проверки: 8 — 3 = 5 (тоже верно). Чтобы найти вычитаемое, из уменьшаемого отнимают разницу.

То есть, чтобы уметь проверять правильность решения, важно знать не только, как найти разность, но и как вычисляются уменьшаемое и вычитаемое.

А — С = В,

А — В = С,

С + В = А.

Бывают примеры, когда разность равна нулю (0). Это означает, что уменьшаемое и вычитаемое равны между собой. Нет между ними различия.

Сложные примеры с разностью

В математике помимо стандартного нахождения отличий существует множество усложненных вычислений, которые можно решать не в одно действие.

Пример: Из уменьшаемого 40 нужно отнять два вычитаемых 10 и 15.

Данный пример можно вычислить одним действием или двумя.

Решение в одно действие: 40 — 10 — 15 = 15,

Решение в два действия:

Сначала находим сумму: 10 + 15 = 25,

40 — 25 = 15.

Главное, чтобы ответы совпали в обоих способах.

Также, может вызвать затруднение пример: Утройте разность. В данном случае нужно будет найти отличия чисел и умножить ее на 3.

Навык нахождения разности бесспорно важен. Но не более и не менее, чем навыки нахождения суммы, произведения, частного. В математике все взаимосвязано и без одних знаний невозможно получить другие. Не зря говорят, что математика является «царицей наук», и ее азы используются повсеместно.

Поэтому, для достижения успеха в математике одной лишь школьной программы будет не достаточно.

Для достижения максимальных результатов в изучении этого предмета мы рекомендуем начать посещать курсы по математике для школьников в Москве. Обучение на этих курсах проходит по запатентованной методологии в малых группах. Это увеличивает эффективность занятий в несколько раз.

Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Эксперт по подготовке к ЕГЭ, ОГЭ и ВПР

Задать вопрос

Закончил Московский физико-технический институт (Физтех) по специальности прикладная физика и математика. Магистр физико-математических наук. Преподавательский стаж более 13 лет. Соучредитель курсов ЕГЭ и ОГЭ в паре TwoStu.

Формы записи и терминология[править | править код]

Свойства[править | править код]

Выполнение вычитания[править | править код]

Вычитание чисел[править | править код]

Натуральные числа[править | править код]

Целые числа[править | править код]

Рациональные числа[править | править код]

Вещественные числа[править | править код]

График[править | править код]

Комплексные числа[править | править код]

Экспоненциальная запись[править | править код]

Вычитание произвольных чисел[править | править код]

Особенности обучения вычитанию школьников[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Разность чисел как определить?

Арифметические действия с числами

Разность в математике

Видео: Математика 6 Делимость суммы и разности чисел

Как найти разницу величин

Математические действия с разностью чисел

Видео: Математика 2 класс. Разность двухзначных чисел

Простые примеры

Более сложные примеры

Математика для блондинок

Видео: Разность двух отрицательных целых чисел. Математика 6 класс.

Вычитание

Вычитание однозначных чисел

Способы вычитания

Вычитание многозначных чисел

Зависимость между данными и искомыми вычитания

Вычитание чисел

Проверка вычитания

Что такое разность чисел в математике?

Вычитание

Что такое разность чисел: уменьшаемое, вычитаемое, разность — правило

Что значит число уменьшаемое, число вычитаемое и разность чисел?

Как найти уменьшаемое и вычитаемое число?

Что такое разность чисел в математике и как найти разность чисел

Что такое разность чисел в математике

Как найти разность чисел

Вычисление разности в столбик

Вычисление разности в столбик – видео

Что такое разность чисел и как ее найти

Виды математических действий и их результаты

Как найти разность чисел

Как проверить, верно ли найдена разность

Сложные примеры с разностью

Занимайтесь на курсах ЕГЭ и ОГЭ в паре TwoStu и получите максимум баллов на экзамене:

Читайте также:

Вам также может понравиться

Как найти интернет магазин по параметрам

Как исправить мятую купюру

Как найти певца алексеев

Добавить комментарий Отменить ответ