Вычитание рациональных чисел
План урока
- Вычитание рациональных чисел
Цели урока
- Знать правило вычитания рациональных чисел.
- Уметь находить разность рациональных чисел.
Разминка
- Как сложить два отрицательных числа?
- Как сложить числа с разными знаками?
- Чему равна сумма противоположных чисел?
Вычитание рациональных чисел
Разность рациональных чисел определяют так же, как и разность натуральных чисел.
Разностью рациональных чисел a и b называют такое число c, которое в сумме с числом b дает число a.
a – b = c, если c + b = a.
Так как – 7,2 + (– 8,8) = – 16, то – 16 – (– 8,8) = – 7,2.
Такой же результат получим, если к числу –16 прибавим число, противоположное числу – 8,8, то есть число 8,8.
Поэтому разность – 16 – (– 8,8) можно заменить суммой – 16 + 8,8, у которой к уменьшаемому прибавляется число, противоположное вычитаемому:
– 16 – (– 8,8) = – 16 + 8,8 = – 7,2.
Чтобы найти разность двух рациональных чисел, можно к уменьшаемому прибавить число, противоположное вычитаемому.
a – b = a + (– b),
Любое выражение, содержащее действия сложения и вычитания, можно заменить на выражение, которое содержит только действие сложения.
3,6 – 6 + 1,1 – 9,4 – 12 = 3,6 + (– 6) + 1,1 +(– 9,4) + (– 12)
Обратите внимание, в 5 классе мы не могли из меньшего числа вычесть большее, теперь, зная отрицательные числа, мы можем выполнить такое действие.
5 – 8 = 5 + (– 8) = – 3
При вычитании из большего числа меньшего, разность — положительное число.
При вычитании из меньшего числа большего, разность — отрицательное число.
Пусть a – b = c. Тогда если a > b, то c > 0, если a < b, то c < 0.
1. Выполните вычитание:
1. 16,7-(-8,9);
2. 7,2-8,9;
3. 0-5,7;
4. -13,6-14,4;
5. -14,8-(-8,12);
6. 0 -(-19,3);
7. -724-(-1736);
8. 29-13;
9. 315-(-417).
2. Найдите значение выражения – 5,7 – с, если:
1) с = – 4,3; 2) с = 3,8; 3) с = 516.
1. Как найти разность двух рациональных чисел?
2. Можно ли вычитание заменить сложением?
3. В каком случае разность двух чисел отрицательна?
4. Какое число получится (положительное или отрицательное), если из большего числа вычесть меньшее?
5. Получится ли нуль в результате разности двух противоположных чисел?
Ответы
1. 1) 25,6; 2) – 1,7; 3) – 5,7; 4) – 28;
5) – 6,68; 6) 19,3; 7) 1372; 8) -19; 9) 71235.
2. 1) – 1,4; 2) – 9,5; 3) -101315.
Вычитание рациональных чисел – это обратное действие сложению рациональных чисел. Пользуясь простым алгоритмом действий, вы легко разберетесь в уроке математике: “Вычитание рациональных чисел”.
Урок: понятие вычитания рациональных чисел.
Вспомним, что такое сумма рациональных чисел. Рассмотрим формулу суммы рациональных чисел.
a+b=c
где a и b – слагаемые, c – сумма.
Если нам не известно одно из слагаемых мы его будем искать по такой формуле:
c-a=b или с-b=a
Чтобы найти неизвестное слагаемое надо от суммы отнять известное слагаемое. Отсюда мы получаем вычитание рациональных чисел.
Пример:
Рассмотрим смысл вычитания рациональных числе.
(begin{align}frac{1}{5}+frac{2}{5}=frac{1+2}{5}=frac{3}{5}\\ end{align})
Если нам одно из слагаемых не известно, то мы воспользуемся вычитанием.
(begin{align}frac{3}{5}-frac{1}{5}=frac{3-1}{5}=frac{2}{5}\\ end{align})
Вычитание рациональных чисел с одинаковым знаменателем.
Чтобы выполнить вычитание рациональных чисел, применяем следующее правило:
Так как у дробей одинаковый знаменатель, переписываем знаменатель в итоговую дробь и выполняем вычитание числителей по правилам вычитания целых чисел.
Пример:
Выполните вычитание рациональных чисел с одинаковыми знаменателями (frac{5}{13}-frac{2}{13}).
Решение:
У дробей знаменатели одинаковые, поэтому считаем числители.
(begin{align}frac{5}{13}-frac{2}{13}=frac{5-2}{13}=frac{3}{13}\\ end{align})
Вычитание рациональных чисел с разными знаменателями.
Правила вычитания рациональных чисел с разными знаменателями:
- Найти общий знаменатель дробей.
- После того как нашли общий знаменатель, вычислить числители.
- Если возможно, то сократить итоговую дробь.
Пример:
Выполните вычитание рациональных чисел с разными знаменателями: а) (frac{11}{18}-frac{1}{12}) б) (-frac{4}{7}-(-frac{5}{14})) в) (-frac{6}{15}-frac{1}{10})
Решение:
а) Нужно найти общий знаменатель дробей (frac{11}{18}) и (frac{1}{12}), она равен 36. Первую дробь (frac{11}{18}) умножаем на дополнительный множитель 2, а вторую дробь (frac{1}{12}) на 3 .
(begin{align}frac{11}{18}-frac{1}{12}=frac{11 times 2}{18 times 2}-frac{1 times 3}{12 times 3}=frac{22}{36}-frac{6}{36}=frac{22-6}{36}=frac{16}{36}=frac{4 times 4}{9 times 4}=frac{4}{9}\\ end{align})
б) Сначала находим общий знаменатель, он равен 14, а потом вычисляем числитель. Числитель считаем по правилам вычитания целых отрицательных чисел.
(begin{align}-frac{4}{7}-(-frac{5}{14})=-frac{4 times 2}{7 times 2}-(-frac{5}{14})=-frac{8}{14}-(-frac{5}{14})=frac{-8-(-5)}{14}=frac{-8+5}{14}=-frac{3}{14}\\ end{align})
в) Находим общий знаменатель, он равен 30. Потом считаем числитель по правилу вычитания целых чисел.
(begin{align}-frac{6}{15}-frac{1}{10}=-frac{6 times 2}{15 times 2}-frac{1 times 3}{10 times 3}=-frac{12}{30}-frac{3}{30}=frac{-12-(+3)}{30}=-frac{15}{30}=-frac{1 times 15}{2 times 15}=-frac{1}{2}\\ end{align})
Представим
себе такую историю…
–
Паша, что ты читаешь? – спросил у друга Саша.
–
Я читаю энциклопедию, которую мне подарили родители, – ответил Паша.
–
И что нового ты узнал? – снова задал вопрос Саша.
–
В ней очень много интересной и полезной информации. Вот, например, я узнал, что
Эверест – это самая высокая гора в мире. Она возвышается на 8848,43
метра над уровнем моря. А самое глубокое место на Земле – Марианская впадина. Она
находится в Тихом океане, и её глубина равна 11 034 метрам
ниже уровня моря, – начал рассказывать Паша.
–
Интересно, если бы Марианская впадина располагалась под горой Эверест, то какое
расстояние пришлось бы пролететь камню с вершины горы до дна впадины? – задумался
Саша.
–
Давай представим, что над Марианской впадиной расположен Эверест. Отметим
высоту нашей горы и глубину впадины, – начал рассуждать Паша.
–
А разве перед 11 034 не надо ставить знак «»?
– обратил внимание друга Саша. – Ведь Марианская впадина находится ниже уровня
моря.
–
Точно! Ты прав, – сказал Паша. – Тогда, чтобы найти расстояние, которое
пришлось бы лететь камню, мы должны от 8848,43 отнять
.
–
А как из положительного числа мы вычтем отрицательное число? – спросил Саша.
–
Я не знаю, – немного растерянно ответил Паша и тут же предложил, – давай
попросим Мудряша нам помочь.
–
Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и
выполним устные задания, – предложил Мудряш.
–
Теперь сверимся! – сказал Мудряш. –
Посмотрите, что у вас должно было получиться!
–
А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, у вас возник
вопрос, как найти разность положительного и отрицательного чисел. Мы с вами
знаем, что в случае с натуральными числами, если нам известны сумма и одно из
слагаемых, неизвестное слагаемое находят вычитанием из суммы известного
слагаемого. Это будет справедливо и для рациональных чисел.
Запомните!
Разностью рациональных чисел a
и
b называют такое рациональное число x,
которое в сумме с числом b
даёт число a. То есть ,
если .
Обозначим
.
Тогда воспользовавшись только что сформулированным правилом, можем записать,
что .
Теперь, чтобы найти неизвестное слагаемое ,
мы с вами прибавим к левой и правой части нашего равенства ,
то есть число, противоположное известному слагаемому.
Сумма
противоположных чисел в левой части выражения равна 0,
тогда получаем, что .
Обратите
внимание, что в равенстве у
нас равен
разности положительного и отрицательного чисел. В равенстве у
нас равен
сумме уменьшаемого и числа, противоположного вычитаемому. А мы с вами умеем
складывать рациональные числа.
Таким
образом, вычитание рациональных чисел мы заменили сложением.
Сформулируем
правило. Запомните! Чтобы найти разность двух чисел, можно к
уменьшаемому прибавить число, противоположное вычитаемому. То есть для любых
рациональных чисел a
и b справедливо
равенство: .
–
Давайте решим несколько примеров: ;
;
;
– предложил мальчишкам Мудряш. – Для этого воспользуемся уже известным нам
равенством: .
Итак,
в первом примере мы
к уменьшаемому, то есть к ,
прибавим число, противоположное вычитаемому, то есть .
Вычислим сумму и
получим 18.
Во
втором примере мы
к прибавим
число, противоположное ,
то есть .
Теперь найдём сумму чисел с разными знаками: .
,
а значит, сумма будет отрицательной. Запишем разность большего
и меньшего модулей со знаком «»:
.
Выполним вычисления и получим .
И
в третьем примере мы
разность заменим суммой: .
Чтобы вычислить эту сумму, запишем сумму модулей слагаемых со знаком «»:
.
Выполним сложение в скобках и получим .
–
Получается, что теперь мы можем из меньшего числа вычесть большее, – заметил
Саша.
–
Верно! – сказал Мудряш. – Это стало возможным, так как мы с вами уже с вами
знаем отрицательные числа. И обратите внимание, что в первом примере мы
вычитали из большего числа меньшее и получили положительную разность. А во
втором и третьем примерах мы вычитали из меньшего числа большее и получили
отрицательные разности.
Запомните!
Если
разность отрицательна,
то ;
если разность положительна,
то .
Ребята,
теперь мы можем любое выражение, которое содержит действия сложения и
вычитания, заменить на выражение, содержащее только действие сложения.
Например, выражение можем
заменить на выражение .
–
Давайте для закрепления нового материала выполним несколько заданий, –
предложил Мудряш.
Задание
первое: Выполните вычитание:
а)
;
б) ;
в) ;
г) ;
д) ;
е) .
Решение: Чтобы
решить данные примеры, воспользуемся равенством: .
Первый
пример: . Заменим
вычитание сложением. Для этого к прибавим
число, противоположное ,
то есть . Выполним
сложение и
получим .
Второй
пример:. Также
заменим вычитание сложением. Прибавим к число,
противоположное ,
то есть .
Сумма будет
отрицательной, так как .
Запишем разность модулей со знаком «»:
. Выполним вычисления и
получим .
В
третьем примере мы
к прибавим
число, противоположное ,
то есть .
Получили сумму противоположных чисел: . Она
равна 0.
В
следующем примере снова
заменим вычитание сложением. Прибавим к число,
противоположное ,
то есть .
Сумма равна
.
Ещё
один пример:. Заменим
разность дробей суммой. К прибавим
дробь, противоположную ,
то есть .
Запишем сумму модулей этих слагаемых и
со
знаком «»:
.
Дроби в скобках приведём к общему знаменателю – 9.
Дополнительным множителем к первой дроби будет 1,
ко второй дроби – 3. Умножим дроби на их
дополнительные множители: .
Вычислим сумму в скобках и в результате получим .
И
последний пример:.
Прибавим
к число,
противоположное ,
то есть .
Найдём сумму .
Сложим целые и дробные части смешанных чисел: .
Сумма 5
и 1
равна 6.
Чтобы найти сумму дробей ,
приведём их к общему знаменателю – 14.
Дополнительным множителем к первой дроби будет 7,
ко второй дроби – 2. Умножим дроби на их
дополнительные множители и получим .
Сложим дроби с одинаковыми знаменателями и получим .
Теперь прибавим к
6.
В результате имеем .
Второе
задание: Решите уравнения:
а)
;
б) ;
в) ;
г) .
Решение: в
первом уравнении нам
неизвестно слагаемое x.
Мы знаем, чтобы найти неизвестное слагаемое, надо из суммы вычесть известное
слагаемое. Тогда можем записать, что .
Заменим вычитание в правой части уравнения сложением, прибавив к 5
число, противоположное 11, то есть .
Сумма будет
у нас отрицательной, так как .
Запишем разность модулей со знаком «»:
.
Выполнив вычисления, получим, что .
Во
втором уравнении нам
неизвестно вычитаемое. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого
вычесть разность. Тогда запишем: .
Заменим разность суммой, прибавив к число,
противоположное ,
то есть .
Сумма будет
отрицательной, так как .
Запишем разность модулей со знаком «»:
.
Выполним вычисления и в результате получим, что .
В
следующем уравнении также
неизвестно вычитаемое. Тогда .
Заменим разность суммой уменьшаемого и
числа, противоположного вычитаемому, то есть .
Теперь найдём сумму .
Для этого запишем сумму модулей слагаемых со знаком «»:
.
Выполним вычисления и получим, что .
И
последнее уравнение .
Здесь нам неизвестно уменьшаемое .
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Тогда получаем, что .
Полученная сумма будет положительной, так как .
Вычтем из большего модуля меньший, то есть .
В результате получим, что .
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Рациональные числа
- Вычитание рациональных чисел
Например:
12
18 = 6, так как 6 + 18 = 12;
25(8) = 33, так как 33 +(8) = 25;
4313 = 56, так как 56 + 13 = 43;
34(15) = 19, так как 19 + (15) = 34.
Рассмотрев полученные разности, мы можем заметить, что:
1218 = 6, но и 12 + (18) = 6;
25(8) = 33, но и 25 + 8 = 33;
4313 = 56, но и 43 + (13) = 56;
34(15) = 19, но и 34 + 15 = 19.
То есть вычитание рациональных чисел можно заменить сложением:
При этом любое выражение, в котором содержатся только знаки сложения и вычитания, можно рассматривать как сумму.
Например:
172,5 + 3,746 + 115
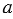= 17 + (2,5) + 3,7 + (46) + 115 + ().
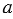Если уменьшаемое больше вычитаемого, то разность положительна:
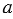
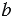
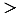0, если .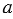
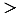
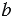Если уменьшаемое меньше вычитаемого, то разность отрицательна:
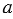
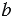
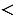0, если .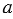
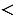
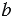Если уменьшаемое равно вычитаемому, то разность равна нулю:
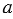
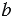= 0, если = .
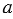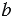Мы знаем, что если на координатной прямой заданы, например, две точки А(-12) и В(5), то длина отрезка АВ покажет на сколько единичных отрезков необходимо переместить вправо точку А, чтобы она перешла в точку В. Или другими словами сколько надо прибавить к числу -12, чтобы получить число 5. Пусть АВ =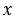 
, тогда запишем -12 + 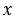= 5, найдем неизвестное слагаемое и получим, что 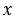= 5 – (-12) или 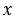= 17. То есть мы получили, что АВ = 17 единичных отрезков. Из данного примера мы можем сделать вывод:
Советуем посмотреть:
Положительные и отрицательные числа. Координаты на прямой
Модуль числа
Рациональные числа
Сравнение рациональных чисел
Сложение рациональных чисел
Умножение рациональных чисел
Деление рациональных чисел
Свойства действий с рациональными числами
Раскрытие скобок
Решение уравнений
Рациональные числа
Правило встречается в следующих упражнениях:
6 класс
Номер 1004,
Мерзляк, Полонский, Якир, Учебник
Номер 1009,
Мерзляк, Полонский, Якир, Учебник
Номер 1082,
Мерзляк, Полонский, Якир, Учебник
Номер 1093,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Задание 1127,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1322,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1324,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1377,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1416,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 49,
Мерзляк, Полонский, Якир, Учебник
Номер 53,
Мерзляк, Полонский, Якир, Учебник
Номер 182,
Мерзляк, Полонский, Якир, Учебник
Номер 362,
Мерзляк, Полонский, Якир, Учебник
Номер 374,
Мерзляк, Полонский, Якир, Учебник
Номер 485,
Мерзляк, Полонский, Якир, Учебник
Номер 739,
Мерзляк, Полонский, Якир, Учебник
Номер 1040,
Мерзляк, Полонский, Якир, Учебник
Номер 1,
Мерзляк, Полонский, Якир, Учебник
Номер 3,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 70,
Мерзляк, Полонский, Якир, Учебник
Номер 102,
Мерзляк, Полонский, Якир, Учебник
Номер 104,
Мерзляк, Полонский, Якир, Учебник
Номер 105,
Мерзляк, Полонский, Якир, Учебник
Номер 134,
Мерзляк, Полонский, Якир, Учебник
Номер 198,
Мерзляк, Полонский, Якир, Учебник
Номер 226,
Мерзляк, Полонский, Якир, Учебник
Номер 389,
Мерзляк, Полонский, Якир, Учебник
Номер 397,
Мерзляк, Полонский, Якир, Учебник
Номер 419,
Мерзляк, Полонский, Якир, Учебник
Действия с рациональными числами
- Сложение
- Вычитание
- Умножение
- Деление
Сложение
При сложении двух рациональных чисел с одинаковым знаком складываются их модули и перед суммой ставится их общий знак.
Пример 1. Найти сумму рациональных чисел 2,5 и 3,2.
Решение: Так как модуль положительного числа равен самому числу, то в данном примере числа можно просто сложить:
2,5 + 3,2 = 5,7.
Пример 2. Найти сумму отрицательных чисел (-2,5) и (-3,2).
Решение: Сначала надо сложить модули слагаемых:
2,5 + 3,2 = 5,7.
Так как сумма двух отрицательных чисел должна быть отрицательным числом, то решение будет выглядеть так:
(-2,5) + (-3,2) = -5,7.
Из данных примеров следует, что в результате сложения двух положительных чисел получится положительное число, а в результате сложения двух отрицательных чисел – отрицательное число.
При сложении двух рациональных чисел с разными знаками нужно взять их модули и из большего вычесть меньший. В результате ставится знак того числа, у которого модуль больше.
Другими словами, можно просто, не обращая внимания на знаки, вычесть из большего числа меньшее и у получившегося результата поставить знак большего числа:
Примеры:
(-4,7) + (+12) = 7,3, так как 12 – 4,7 = 7,3;
9 + (-15) = -6, так как 15 – 9 = 6.
Из данных примеров следует, что в результате сложения двух чисел с разными знаками, может получится как положительное, так и отрицательное число.
Сумма двух противоположных чисел равна нулю.
Примеры:
125 + (-125) = 0;
-34 + (+34) = 0.
Вычитание
Вычитание одного рационального числа из другого можно заменить сложением. При этом уменьшаемое берётся со своим знаком, а вычитаемое – с противоположным.
Примеры:
(+10) – (+3,4) = (+10) + (-3,4) = 6,6;
(+10) – (-3,4) = (+10) + (+3,4) = 13,4;
(-10) – (-3,4) = (-10) + (+3,4) = -6,6;
(-10) – (+3,4) = (-10) + (-3,4) = -13,4.
Из данных примеров следует, что чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.
Умножение
При умножении двух рациональных чисел умножаются их модули. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные.
Примеры:
3 · 5 = 15;
3 · (-5) = -15;
-3 · 5 = -15;
-3 · (-5) = 15.
Ниже представлена схема (правило знаков при умножении):
| + | · | + | = | + |
| + | · | – | = | – |
| – | · | + | = | – |
| – | · | – | = | + |
Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.
При умножении любого числа на -1 получится число, противоположное данному.
Примеры:
-1,5 · (-1) = 1,5;
2,5 · (-1) = -2,5.
Деление
При делении одного рационального числа на другое делят модуль первого числа на модуль второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.
Примеры:
15 : 5 = 3;
15 : (-5) = -3;
-15 : 5 = -3;
-15 : (-5) = 3.
При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):
| + | : | + | = | + |
| + | : | – | = | – |
| – | : | + | = | – |
| – | : | – | = | + |
Из данных примеров следует, что частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.
При делении любого числа на -1 получится число, противоположное данному.
Примеры:
-1,5 : (-1) = 1,5;
2,5 : (-1) = -2,5.
