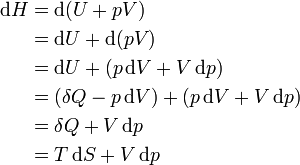Как найти разность энтальпий

Энтальпия
— это энергосодержание системы,
включающее внутреннюю энергию и работу

Энтальпи́я,
также тепловая
функция
и теплосодержание —
термодинамический
потенциал,
характеризующий состояние системы в
термодинамическом равновесии при
выборе в качестве независимых переменных
давления,
энтропии
и числа частиц. Если термомеханическую
систему рассматривать как состоящую
из макротела (газа)
и поршня с грузом весом Р
= p S,
уравновешивающего давление газа р
внутри сосуда, то такая система называется
расширенной.

Энтальпия
или энергия расширенной системы Е
равна сумме внутренней энергии газа U
и потенциальной энергии поршня с грузом
E_пот
= pSx
= pV

H
= E
= U
+ pV

Таким
образом, энтальпия в данном состоянии
представляет собой сумму внутренней
энергии тела и работы, которую необходимо
затратить, чтобы тело объёмом V
ввести в окружающую среду, имеющую
давление р
и находящуюся с телом в равновесном
состоянии. Энтальпия системы H —
аналогично внутренней
энергии
и другим термодинамическим потенциалам
 — имеет вполне определенное значение
для каждого состояния, т. е. является
функцией состояния. Следовательно, в
процессе изменения состояния

ΔH
= H₂
− H₁

Изменение
энтальпии не зависит от пути процесса,
определяясь только начальным и конечным
состоянием системы. Если система
каким-либо путём возвращается в исходное
состояние (круговой процесс), то изменение
любого её параметра, являющегося
функцией состояния, равно нулю, отсюда
ΔH
= 0, или же

Дифференциал
энтальпии, выраженный в собственных
переменных — через энтропию
S и давление
p:

Поскольку
в квазиравновесных
процессах
 — количество теплоты, подведенной
к системе, отсюда вытекает физический
смысл введения понятия энтальпии: ее
изменение — это тепло, подведенное
к системе в изобарическом
процессе
(при постоянном давлении). Практическое
применение этой функции основано на
том, что множество химических процессов
в реальных или лабораторных условиях
реализуются именно при постоянном
(атмосферном) давлении, когда резервуар
открыт. Так, энтальпия
образования —
количество энергии, которое выделяется
или поглощается при образовании сложного
вещества из простых веществ.

Все
химические реакции сопровождаются
выделением (экзотермические) или
поглощением (эндотермические) тепла.
Мерой теплоты реакции служит изменение
энтальпии ΔН, которая соответствует
теплообмену при постоянном давлении.
В случае экзотермических реакций
система теряет тепло и ΔН — величина
отрицательная. В случае эндотермических
реакций система поглощает тепло и ΔН —
величина положительная.

Энтальпией
системы удобно пользоваться в тех
случаях, когда в качестве независимых
переменных, определяющих состояние
системы, выбирают давление р
и температуру Т
H
= H(p,T)
В этом случае изменение энтальпии в
изобарическом процессе практически
удобно рассчитывать, зная теплоемкость
при постоянном давлении C_p(T):

Энтальпия —
величина
аддитивная
(экстенсивная),
т. е. для сложной системы равна сумме
энтальпий её независимых частей

.
Подобно другим термодинамическим
потенциалам, энтальпия определяется
с точностью до постоянного слагаемого,
которому в термодинамике часто придают
произвольные значения (например, при
расчете и построении тепловых диаграмм).
При наличии немеханических сил величина
энтальпии системы равна

где
X_i —
обобщённая сила; y_i —
обобщённая
координата.

Таким
образом, энтальпия — сложная математическая
функция, оп: ределяющая энергию,
необходимую для приведения системы в
данное состояние, и учитывающая изменение
внутренней энергии и совершаемую
работу.

На рис. 83 приведены кривые
зависимости энтальпии -от температуры
для газов, используемых как
плазмообразователи в плазмотронах.

Для исследования процессов,
происходящих в материальных системах,
мы пользуемся не абсолютными значениями
энтальпий, а их изменением (разностью)
между .начальным и конечным состояниями
системы. Разности энтальпий мы можем
измерять с любой степенью точности,
отсчитывая энтальпии не от абсолютного
нуля, а от любого, но всегда одного и
того же уровня (рис. 84). За такой уровень
приняты стандартные условия: Г = 298,15 К,
р = 1,013-105 Па.

Кроме того, для
термохимических расчетов приняты
следующие два условия:

1. Разность
энтальпий простых веществ (ДЯ°) в
состоянии, устойчивом при стандартных
условиях, .принимается равной нулю.
Например: ДЯН, =0, но Д#П>0 (так как для
образования атомарного водорода при
стандартных условиях надо затратить
энергию диссоциации, равную 217,9 кДж/моль).

2. Разность энтальпий сложного
вещества обратна по знаку и равна
тепловому эффекту при постоянном
давлении (—реакции его образования из
простых веществ в состоянии, устойчивом
при стандартных условиях, т. е. энтальпии
образования. Например:

В
настоящее время стандартные разности
энтальпий (А#°) и их зависимости от
температуры (#° — #§98,15) можно найти в
справочной литературе для очень большого
числа неорганических и органических
соединений (некоторые данные см. в
приложении) .

Термохимические расчеты
с использованием табличных данных
значительно упростились. Рассмотрим
пример расчета разности энтальпий
химической реакции в общем виде для
уравнения

где А, В, С, V —- символы
реагирующих веществ: а, Ь, с, а1 —
сте-хиометрические коэффициенты.

Исходные вещества (аА+ЬВ) соответствуют
начальному состоянию системы, и сумма
их энтальпий вычитается, так как они в
результате процесса исчезают, конечные
продукты (сС-МО), составляющие конечную
систему, появляются в процессе, и их
энтальпии входят со знаком плюс. Если
данное вещество в уравнение химической
реакции входит с коэффициентом, отличным
от единицы, то при суммировании энтальпий
эти коэффициенты надо взять как
множители.

Во избежание возможных
ошибок надо суммирование энтальпий
производить непосредственно под
уравнением химической реакции

д/-/»з0
= _241,8 кДж/моль; АЯ|

ыо == +90,37 кДж/моль.

аА + 6В = сС + еПЭ

аА~НВ = сС-г-?Ш

143

Л/Сак,,,.,. = ~а/Н1 – ЬАНк + сАНЬ + с.1АН1

Подставляя значения энтальпий из
справочной литературы, находим
Д#?еа.шн…

Допустим, нужно определить
разность энтальпий реакции восстановления
ТЮ4 металлическим магнием:

т;С14(ж)
+2Мё(кр) =2МёС12(кр) + ‘П(кр) д/уо = -(-800)- 0 +
2(—641,38) + 0.

Стандартные энтальпии
магния и титана равны нулю, так как
магний и титан находятся в кристаллическом
состоянии, устойчивом при стандартных
условиях. Разность энтальпий реакции
ДЯ° = = 800 — 1282,76 = —482,76 кДж, т.е. разность
энтальпий меньше нуля (ДЯ<0), следовательно,
реакция экзотермическая.

Однако
общий процесс получения титана
вытеснением его магнием из тетрахлорида
титана — процесс эндотермический. Он
осуществляется по стадиям: сначала
диоксид титана переводится в тетрахлорид:

ТЮ2(кр) +2С(т) + 2С12(г) = ‘ПС14(ж) +2СО(г) ДА/»
= —(—942,6) — 0 -0 + (-800) + 2(—110,5)=-78,4 кДж.

Свободный хлор для первой реакции
и свободный магний для второй реакции
можно получить электролитическим
разложением:

2Л^С18 = 2Мд + 2С12 АН[| =
-2(-641,38) + 0 + 0= 1282,76 кДж.

Таким образом,
общее изменение энтальпии системы
составит Л#° = ЬНЧ + А//§ + АН°3 = -482,76 – 78,4
+ 1282,76 = +721,6 кДж.

Следовательно, для
получения 1 моль Т1 необходимо затратить
721,6 кДж энергии (не считая потерь энергии
на нагревание до необходимых температур
и т.д.).

Все расчеты можно значительно
упростить, если предварительно проследить
по стадиям процесс восстановления
титана, суммировать все стадии и провести
расчет по окончательному уравнению:

ТЮ2 + 2С + 2С1,, = ИС14 + 2СО Т!С14 + 2Ме =
Т1+2М^С12 2М?С12 = 2М? + 2С12

. ТЮ2 + 2С = Т! + 2СО

Однако по этой схеме процесс реально
не пойдет, так как отдельные стадии
требуют для своего развития различных
условий (Т, р).

Определив разность
энтальпий результирующей реакции, мы
получим тот же самый результат:

ТЮ2
+ 2С = Т- + 2СО А//0 = _(_942,6) + о + 0 + 2( -110,5) = +
721,6 кДж.

144

Приведенный расчет
еще раз подтверждает закон Г. И. Гесса
о независимости энергоизменения от
последовательности и характера отдельных
стадий процесса.

Чтобы получить
разность энтальпий реакций для более
высоких температур, чем стандартные,
используют зависимость разности
энтальпий от температуры и учитывают
при этом изменения энергии, потребной
для нагрева данных веществ и для
изменения их фазовых состояний:

г

ДЯ/=Д/-/°+ 5 6>1Т + АА/,М. (tt.ll)

.2118,1!)

Для многих веществ эти функции
рассчитаны и приведены в справочных
таблицах (А#г — Я0).

Если абсолютное
значение разности энтальпий реакций
достаточно велико (300—400 кДж), то в первом
приближении температурной зависимостью
можно пренебречь, так как теплоемкости
измеряются в Дж/(моль-К), а разности
энтальпий — в кДж/моль, т.е. на 3 порядка
выше.

Для органических соединений
в справочных таблицах часто приводится
разность энтальпий горения этих веществ,
рассчитанная для случая образования
жидкой воды, так как обычно определения
производятся в калориметрических
бомбах, охлаждаемых по окончании опыта
до комнатной температуры.

Зная
разность энтальпий сгорания, легко
определить разность энтальпий образования
органического вещества. Схема расчета
приведена для общего случая горения
органического вещества:

с л-1,А + (х+1
-1-) о2=А-со2+1иао

ЛЯ!?,.,,,, = -ЛЯЦбра:, +
хДЯ&и, (г) + УгЛЯГш.ж, •

Отсюда

Л/СР1К1 = АС,,, + хАН?;0; (г) + “/аЛМ’ц.с,
,ж..

Атомы других элементов (О, N. 8 и
т.д.), входящие в состав органической
молекулы, при горении выделяются в
молекулярном виде или в виде устойчивых
оксидов (502, Р205), так как горение происходит
в атмосфере кислорода (3-105Па).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Энтальпия. Этому элементу I–d диаграммы я посвятил отдельную тему, потому как для меня этот элемент являлся наименее понятным среди остальных (температуры, влагосодержания и относительной влажности) и требующим разбора других попутных понятий.
Продублирую рисунок из прошлой статьи http://mrcynognathus.livejournal.com/7641.html:

    Стандартная теплота реакции определяется как разность энтальпий продуктов и исходных веществ. Говоря точнее, это — энтальпия реакции, или теплота реакции при постоянном давлении. Помимо агрегатных состояний веществ, при определении стандартной теплоты реакции должны быть указаны стехнометрические коэффициенты. Например, уравнение [c.41]

    Тепловой эффект изобарной реакции можно рассчитать на основе закона Гесса как разность энтальпий продуктов и исходных веществ (табл. VI- ). Кроме того, тепловой эффект реакции можно определить, суммируя сторонами уравнения и тепловые эффекты разных реакций (например, сгорания) так, чтобы получить в результате интересующее нас уравнение (табл. У1-2). [c.144]

    Согласно этим уравнениям, разности количеств встречных на одном уровне потоков паров и флегмы и содержащегося в них произвольного компонента системы, а также разности полных энтальпий встречных паровых и жидких потоков сохраняют неизменные значения по всей высоте укрепляющей колонны. Следовательно, сами эти параметры могут меняться лишь в одну сторону и на одну и ту же величину, чтобы их разности сохранялись постоянными. [c.150]

    Здесь Ко — коэффициент, учитывающий наличие люков, не используемой тарелками части колонны (Ко=1.18) Цк —стоимость материала колонны, тыс. руб,/т Рп —плотность пара, кг/м нип — допустимая скорость пара в свободном сечении колонны, м/с т) — к. п. д. тарелки g — масса тарелки, отнесенная к 1 м ее поверхности, т/м р — плотность материала корпуса колонны, т/м Я — расстояние между тарелками, м г — удельная теплота испарения дистиллята. кДж/т 0 — продолжительность работы установки, ч/год Ц,- —цена теплоносителя, используемого при эксплуатации кипятильника и цена хладоагента в дефлегматоре, тыс./руб. т Дй,- — изменение энтальпии теплоносителя и хладоагента, МДж/т К1 — коэффициент теплопередачи в кипятильнике и дефлегматоре, МВт/(м -К) А ср — средняя разность температур при теплопередаче, С. [c.104]

    Из этих уравнений непосредственно следует, что разности чисел кмолей встречных на одном уровне потоков флегмы и паров, разности количеств содержащегося в этих потоках произвольного компонента и, наконец, разности их полных энтальпий сохраняют постоянные значения по всей высоте колонны. Следовательно, сами эти параметры могут меняться только в одну сторону и на одну и ту же величину, чтобы их разности оставались постоянными. [c.137]

    Для сопоставления можно вычислить характеристику градирни методом среднелогарифмической разности энтальпий. Разность энтальпий по кривым Hs и На составляет на выходе АЯ — 278 — 191,7 -= 86,3 кдж кг на входе АЯ = 115 — 89,7 = 25,3 кдж кг. Найденная по рис. 15.11 для конечной температуры воды 29,5 С и для ширины зоны охлаждения 19,4 С поправка к энтальпии ah равна 10 кдж кг. Уточненное значение среднелогарифмической разности энтальпий (с учетом поправки) будет [c.307]

    Изменение стандартной энтропии в химической реакции (298 К) определяется, как и изменение энтальпии, разностью суммарной энтропии продуктов реакции и суммарной энтропии исходных веществ  [c.128]

    Разность ДЯ = Нр т- — Нрт представляет собой приращение мольной энтальпии газовой фазы при ее изотермическом расширении от данного давления до практически нулевого, при кото- [c.62]

    В процессе непрерывной ректификации неизменность во времени составов и температур жидких и паровых потоков, пересекающих один и тот же горизонтальный уровень, позволяет сделать принципиально важный вывод о постоянстве разности масс и энтальпий встречных разноименных потоков на любом уровне по высоте укрепляющей колонны. Однако для условий периодической ректификации, когда поступающие в колонну пары непрерывно утяжеляются, этот вывод уже не является справедливым. В самом деле, количества вещества и тепла, поступающие в течение определенного конечного промежутка времени в произвольно выбранный объем периодически действующей укрепляющей колонны, не будут равны количествам вещества и тепла, покидающим этот же объем колонны в течение другого промежутка времени равной продолжительности. Это и является основной причиной того, что, несмотря на наличие строго разработанной теории непрерывной ректификации, до сих пор не предложено столь же убедительной теории для периодического процесса. Однако при ближайшем рассмотрении этой проблемы можно установить некоторые особенности, позволяющие привлечь к анализу периодической ректификации принципиальные положения, оказавшиеся плодотворными при изучении процесса непрерывной ректификации. [c.221]

    Эта гипотеза не исключает указанного выше свойства рассматриваемых разностей масс встречных потоков паров и флегмы и их энтальпий меняться во времени, но подчеркивает ту особенность непрерывно изменяющейся картины процесса, согласно которой, несмотря на такой переменный характер, можно считать, что в каждый данный момент разности масс и энтальпий встречных паровых и жидких потоков имеют одни и те же значения для всех межтарелочных отделений колонны. В каждый следующий момент эти разности будут иметь уже другие абсолютные значения, но по-прежнему одни и те же для всех уровней колонны [c.221]

    Отсюда разность энтальпий встречных на одном уровне потоков флеГмы и паров, постоянная по всей высоте рассматриваемой верхней секции второй колонны, будет равна [c.286]

    Если изучать энтальпию в виде разности величин 2 — / (Аг) при отсчете от 0°К или от 0°С, то изменение энтальпии выразится в первом случае  [c.73]

    Зная зависимость Ср = / (7 ) для какого-либо вещества в интервале температур от О до Т° К, можно вычислить также его энтальпию в этом интервале температур. Поскольку энтальпия тела или системы при абсолютном нуле не равна нулю, то всегда измеряют разность величин — 0, а именно [c.73]

    При увеличении рециркуляционного потока непрерывно уменьшается разность энтальпий, а следовательно, и разность температур между точками входа и выхода из элемента процесса. При полной рециркуляции обе разности становятся равными нулю. [c.286]

    Разность энтальпий и разность энтропий в конце и начале процесса сжатия для идеального газа [8]  [c.58]

    Разность энтальпий торможения в начале и конце процесса определяется выражением [c.78]

    После этого КПД можно представить в зависимости от приведенной разности энтальпий торможения  [c.78]

    Чтобы установить, находится ли искомая точка А в области перегретого пара, здесь же с помощью процедуры 1РТ(Р1,Т1,Э) [см. (1.61)1 определяют энтальпию сухого насыщенного пара в точке Б. Если заданная энтальпия меньше энтальпии насыщенного пара, то искомая точка соответствует или влажному пару (точка В), или жидкости (точки Г и Д). и управление передается оператору с меткой М1. В противном случае искомая точка А лежит в области перегретого пара или (предельный вариант) на правой пограничной кривой и совпадает с точкой Б. Тогда управление передается оператору с меткой МО и поиск решения далее ведется шаговым методом, который заключается в следующем. С помощью процедуры 1РТ(Р1,Т1,Э) [см. (1.61)1 при заданном давлении р и начальной температуре Ту находят текущее значение энтальпии вещества 1 и разность = г — (ОЭ) между ее заданным и текущим значениями. Если эта разность [c.105]

    Так как при использовании уравнения Боголюбова—Майера S = / (р. Т) и t = / (р, Т), то в качестве величины при итерациях принята температура Т (рис. 3.7). Ее начальное значение Ti задается минимально возможным, а начальное значение шага DT (DT) выбрано равным одной трети разности критической и начальной температур DT = (Т р — Ti)/3. Поиск решения ведется шаговым методом. Сначала по известным температуре Ti и энтропии S определяется энтальпия в точке 1. Если она оказывается меньше заданной энтальпии i (точка А на рис. 3.7), то температура [c.110]

    Числа в скобках означают энтальпии 1 кг углеводородов при соответствующих температурах, а для водорода—разность температур. [c.278]

    Вообще для технологических расчетов требуется лишь величина изменения энтальпии, т. е. количества тепла, необходимого для нагревания (охлаждения) определенного количества вещества от одной температуры до другой. Такие вычисления очень просты изменение энтальпии равно разности энтальпии вещества в конечных состояниях, так как пулевая энтальпия, являющаяся постоянной интегрирования, при этом сокращается. [c.199]

    Площадь T1AA2T2 соответствует изменению внутренней энергии газа при нагревании от Ti до Гг, а площадь Т1ВВ2Т2 — изменению энтальпии. Разность АН—AU будет представлена площадью АВВ2А2, численно равной / (Гг—Ti)=p(Vi—V )—pAV, т. е. работе расширения газа при нагревании от Г] до Гг при постоянном давлении. [c.23]

    Разности плотностей 0,9—0,85 = 0,05 отвечает разность энтальпии 237,3— —230,6 = 6,7, а разности 0,89—0,85 = 0,04 разгюсть х  [c.21]

    Изменение энтальпии ДЯ реакции находится как разность энтальппи продуктов реакции и исходных веществ  [c.65]

    Разность между энтальпией моля чистого химического соединения и суммарной энтальпией хилшческпх элементов, пз которых оно состоит, называется теплотой образования вещества (АЯ ). Эта величина определяет изменение энергии, происходящее при соединении атомов в молекулу. Значение теилоты образования следует давать с указанием температуры, давления и агрегатного состояния веществ, которым оно соответствует. Давление 1 атм и темпе- [c.40]

    В действительности реакция может не идти при 1 атм и 25° С с заметной скоростью тем не менее очень важно знать стандартную теплоту образования вен1 ества. Закон Гесса утверждает, что разность энтальпий начального и конечного состояний не зависит от пути перехода между ними. Если поднять температуру и давление, провести реакцию, а затем сконденсировать образовавшуюся воду, то по возвращении к стандартным условиям мы получим то же самое изменение энтальпии. [c.41]

    Исходным принципиальным положением является следующая рабочая гипотеза. В каждый данный момент времени мгновенное значение разностей масс паровых и жидких потоков, пересекающих одно и то же произвольное м жтарелочное отделение укрепляющей колонны, равно как и мгновенное значение разности их полных энтальпий, сохраняет постоянное значение по всей высоте колонны. [c.221]

    Если для углеводородных смесс п пренебречь теплотой MOiiie-ния, то разность энтальпий встречных бинарных паров и флегмы можно представпть следующим образом  [c.144]

    Выражение в фигургилх скобках мало сравпителыго с двумя друт ими членами, и если приближенно принять, что разность энтальпий встречных потоков равна скрытой теплоте исиарения одного моля пара  [c.144]

    Таким образом, холодопроизводительность дроссельного цикла равна разности энтальпии газа до и после изотеэмического [c.123]

    Рассмотрим адиабатны 1 процесс сжатия с потерями. В адиабатно-изолированной машине вся потерянная работа подводится к газу в виде теплоты лн-к- Такой процесс можно условно представить как обратимый политропный, в котором подведенная теплота подв = Ят-к 1461. Полная работа сжатия равна разности энтальпий в конце и начале процесса  [c.57]

    Доля потерянной работы в полной работе, переданной сжимаемому веществу в рабочем колесе, в значительной степени зависит от перепада энтальпий в колесе или, что то же самое, от разности кинетических энергий потока при выходе из колеса и входе в него, которые определяются его геометрией и режимом работы. Перепад энтальпий 1-2 — i l зависит от коэффициента реактивности колеса Qi o- Для большинства типов рабочих колес = 0,6-f-0,8. [c.64]

    Установим связь между политропным КПД и коэффициентом изоэнтропности диффузора. Из уравнения (2.17) видно, что разность кинетических энергий при входе в диффузор и выходе из него равна перепаду энтальпий. Кинетическая энергия при входе в диффузор С]/2. Подставив эти значения в выражения (2.25) и (2.26), найдем зависимости  [c.67]

    Если условиться, что под перепадами энтальпии, энтротш и любых других термодинамических параметров будем понимать разности их значении в конце и начале процесса с учетом знака, т. е. [c.77]

    Реакции в газовой фазе обычно проводят в реакторах непрерывт ного действия. У капельных жидкостей разность между энтальпией и внутренней энергией настолько незначительна, что баланс энтальпии остается справедливым даже для жидкофазных реакций при постоянном объеме. Следовательно, для подавляющего большинства важнейших промышленных реакций запись первого закона термодинамики в форме AH=q достаточна в качестве полного выражения всех энергетических соотношений реагирующих систем. [c.91]

---

Химия (1986) — [

c.142

]

Химия (1975) — [

c.122

]

---

Разность – энтальпие – реакция

Cтраница 1

Разности энтальпий реакции и члены, содержащие разности энтропии, умноженные на температуру, сократятся при вычитании, а также исчезнет и ЛОравнов, равное нулю.
 [1]

Разность энтальпий реакции нейтрализации для всех сильных кислот и сильных оснований одинаковая: – 56 5 кДж / моль ЬЬО.
 [2]

Разность энтальпий реакции нейтрализации для всех кислот и оснований одинаковая 56 5 кдж / экв.
 [3]

Определить разность энтальпий реакции диссоциации водорода при Г1000 К, используя данные табл. 6.1 и уравнения температурной зависимости теплоемкостей.
 [5]

Зависимость разности энтальпий реакции от температуры можно найти легко, зная зависимости от температуры энтальпий отдельных веществ, уравнения которых (6.26), (6.27), (6.28) приведены на стр.
 [6]

Так как разность энтальпий реакции находится через интегралы в пределах, то, для обобщения задачи, можно, подставив уравнения зависимости теплоемкостей от температуры, преобразовать решение и получить его в виде непрерывной температурной функции, удобной для исследования.
 [7]

Таким образом, разность энтальпий реакции еще не определяет возможности ее протекания в данных конкретных физических условиях.
 [9]

Согласно уравнению (10.7), разность энтальпий реакций, идущих от одинаковых начальных состояний к двум различным конечным состояниям, равна энтальпии перехода от одного конечного состояния к другому. Энтальпия простых веществ ( элементов) при стандартных условиях ( р – 101 325 кПа, Т – 298 15 К) принята равной нулю.
 [10]

Используется и другое следствие закона Гесса: разность энтальпий реакций, идущих от различных начальных состояний к одному конечному, равна энтальпии перехода от одного начального состояния к другому.
 [11]

В этом случае так же образуется дихлоркарбен и термодинамически устойчивый тетрахлоргерман, хотя разность энтальпий реакций для ( о -) и ( 5) направлений ( 3 2 ккал / моль) невелика и лаже свидетельствует в пользу ( S) процесса.
 [12]

Стандартные энтальпии магния и титана равны нулю, так как магний и титан находятся в кристаллическом состоянии, устойчивом при стандартных условиях. Разность энтальпий реакции Д / / 800 – 1282 76 – 482 76 кДж, т.е. разность энтальпий меньше нуля ( Д / / 0), следовательно, реакция экзотермическая.
 [13]

Так, например, водород и кислород, соединяясь со взрывом при обычных температурах и образуя воду, при высоких температурах реагируют обратимо, а при температуре выше 4000 К существование водяного пара практически невозможно. Таким образом, разность энтальпий реакции еще не определяет возможности ее протекания в данных конкретных физических условиях.
 [15]

Страницы:  

   1

Тепловой эффект химической реакции — изменение внутренней энергии или энтальпии системы вследствие протекания химической реакции и превращения исходных веществ (реактантов) в продукты реакции в количествах, соответствующих уравнению химической реакции (стехиометрии реакции^[1]) при следующих условиях:

• единственно возможной работой при этом является работа против внешнего давления,
• как исходные вещества, так и продукты реакции имеют одинаковую температуру^[2][3].

Теплота термохимического процесса и тепловой эффект химической реакции[править | править код]

Поясним приведённое выше определение теплового эффекта химической реакции^{[K 1]}. Для этого запишем фундаментальные уравнения Гиббса для внутренней энергии и энтальпии простой^[10] открытой однородной термодинамической системы^[11][12]:

(Фундаментальное уравнение Гиббса для внутренней энергии)

(Фундаментальное уравнение Гиббса для энтальпии)

Здесь  — абсолютная температура,  — энтропия,  — давление,  — объём,  — количество (или масса) -го составляющего систему вещества,  — химический потенциал этого вещества (см. Энтропия открытой системы).

Для бесконечно малого^[13] квазистатического изохорного процесса ()

(Изменение внутренней энергии в бесконечно малом квазистатическом изохорном процессе)

для бесконечно малого квазистатического изобарного процесса ()

(Изменение энтальпии в бесконечно малом квазистатическом изобарном процессе)

Важно понимать, что представление о теплоте химической реакции при сохранении исторически сложившегося названия (восходящего ко временам, когда любое изменение температуры связывали с поглощением или выделением теплоты) уже не имеет прямого отношения к общефизическому понятию количества теплоты. Действительно, при химической реакции в изолированной системе (например, инициируемом электрической искрой взрыве гремучего газа в герметически закрытом термосе) может иметь место изменение температуры (за счёт выделения теплоты), но не происходит обмена с окружающей средой(так как попросту это термос — изолированная система), ни изменения внутренней энергии системы. Наконец, традиционная трактовка теплоты, основанная на представлении об адиабатической изоляции системы от окружающей среды^[14] (см. Неоднозначность понятий «теплота» и «работа») к открытым системам не применима, и для них теплоту бесконечно малого квазистатического процесса полагают равной^[15][16]

(Дефиниция теплоты для любого бесконечно малого квазистатического процесса)

Таким образом, теплота бесконечно малого квазистатического изохорного процесса равна

(Теплота бесконечно малого квазистатического изохорного процесса)

а теплота бесконечно малого квазистатического изобарного процесса равна

(Теплота бесконечно малого квазистатического изобарного процесса)

Для закрытых систем изменение энергии системы за счёт изменения масс составляющих систему веществ (химическую работу^{[17][18][19][20][21]}, работу перераспределения масс составляющих систему веществ^[22]) учитывать не требуется^[23][24], и выражения для теплот ещё более упрощаются:

(Теплота бесконечно малого квазистатического изохорного процесса в простой закрытой системе)

(Теплота бесконечно малого квазистатического изобарного процесса в простой закрытой системе)

Из сказанного ясно, почему в дефиниции теплового эффекта химической реакции фигурируют внутренняя энергия, энтальпия и запрет на любые виды работ в системе, кроме работы расширения/сжатия. Уточним, что в понятии «химическая работа» термин «работа» не имеет отношения к понятию «термодинамическая работа» и использован просто как синоним словосочетания «изменение энергии». Наконец, подчеркнём, что когда речь идёт о тепловом эффекте химической реакции, то, как и во многих других случаях, касающихся термохимии, подразумевается, что речь идёт о закрытой системе и полномасштабное применение мощного, но громоздкого математического аппарата термодинамики систем переменного состава не требуется^[23][24][25].

Энергетический эффект химической реакции всегда рассматривают применительно к конкретному термохимическому уравнению, которое может не иметь отношения к реальному химическому процессу. Термохимическое уравнение лишь показывает, какие наборы начальных и конечных индивидуальных веществ, находящихся в определённых состояниях и количественных соотношениях, исчезают и образуются. В начальном состоянии должны присутствовать только исходные вещества (реактанты), а в конечном — только продукты химической реакции. Единственным условием при записи термохимического уравнения является соблюдение материального и зарядового баланса. Вещества в растворённом или адсорбированном состоянии тоже считаются индивидуальными соединениями; если растворитель или адсорбент не участвует непосредственно в химической реакции и не реагирует с растворённым веществом, то он рассматривается просто как фактор, влияющий на термодинамические свойства рассматриваемого вещества. Наконец, в термохимическом уравнении могут фигурировать частицы, не способные к самостоятельному существованию (электроны, протоны, ионы, радикалы, атомарные простые вещества)^[26].

Энергетический эффект реального процесса с химической реакцией зависит от условий проведения процесса и не может служить стандартной характеристикой конкретной химической реакции^[3]. Химическая же термодинамика нуждается в показателе, связанном с энергетикой химической реакции, но не зависящем от условий её проведения. Покажем, как может быть получен интересующий нас показатель. Для этого рассмотрим следующий мысленный эксперимент. Возьмем чистые индивидуальные исходные вещества в мольных количествах, соответствующих стехиометрическим коэффициентам интересующего нас термохимического уравнения, и находящиеся при определённых температуре и давлении. Если привести эти вещества в контакт, то энтальпия образовавшейся неравновесной системы в начальный момент времени будет равна сумме энтальпий исходных веществ. Теперь рассмотрим конечное состояние изучаемой системы в предположении, что реактанты прореагировали полностью^[27] и продукты реакции находятся при той же температуре и том же давлении, что и реактанты. Энтальпия системы (в общем случае неравновесной) из продуктов химической реакции будет равна сумме энтальпий этих веществ. Поскольку энтальпия — функция состояния, то разность энтальпий системы в конце и начале рассмотренного мысленного эксперимента не зависит от условий проведения химической реакции. Эту разность энтальпий и называют изобарным тепловым эффектом (термохимической теплотой) химической реакции, соответствующей определённому термохимическому уравнению^[28][29]. Важно, что реальная осуществимость рассмотренного мысленного эксперимента, гипотетические условия его проведения и неравновесность исходного и конечного состояний термохимической системы не сказываются на дефиниции теплового эффекта химической реакции.

Часто тепловой эффект химической реакции относят к 1 молю одного из продуктов реакции^[30].

Резюмируем сказанное: теплота процесса, связанного с фактическим протеканием химической реакции, и энергетический эффект химической реакции отнюдь не одно и то же, а дефиниция теплового эффекта химической реакции вообще не предполагает действительного осуществления реакции, соответствующей рассматриваемому термохимическому уравнению^[31].

И внутренняя энергия, и энтальпия представляют собой функции состояния, поэтому тепловой эффект химической реакции зависит от природы и состояния исходных веществ и конечных продуктов, но не зависит от пути реакции, то есть от числа и характера промежуточных стадий (закон Гесса)^{[32][33][34][35]}.

Тепловой эффект химической реакции, протекающей при постоянном давлении, и равный изменению энтальпии системы в процессе, соответствующем термохимическому уравнению, называется изобарным тепловым эффектом или энтальпией химической реакции. Тепловой эффект химической реакции, протекающей при постоянном объёме, и равный изменению внутренней энергии системы в процессе, соответствующем термохимическому уравнению, называют изохорным тепловым эффектом^[2].

Для отдельных типов химических реакций вместо общего термина «тепловой эффект химической реакции» используют специальные (сокращённые) термины: теплота образования, теплота сгорания и т. п.^[1]

Дефиниции тепловых эффектов должны быть дополнены указанием на начальные точки отсчёта значений энергии и энтальпии. Для сравнения тепловых эффектов и упрощения термодинамических расчётов все величины тепловых эффектов реакций относят к стандартным условиям (все вещества находятся в стандартных состояниях)^[1]. Если реакцию — реально или гипотетически — проводят при стандартных условиях (T = 298,15 К = 25 °С и P = 1 бар = 100 кПа)^[36], то тепловой эффект называют стандартным тепловым эффектом реакции или стандартной энтальпией реакции ΔHo
r.

Химические реакции, сопровождающиеся повышением температуры, называют экзотермическими, понижением температуры — эндотермическими. В термодинамической системе знаков тепловой эффект экзотермической реакции ( или ) считают отрицательным, эндотермической ( или ) — положительным. В устаревшей и не рекомендуемой к употреблению термохимической системе знаков положительным, наоборот, считается тепловой эффект экзотермической реакции, а отрицательным — эндотермической^[37].

Тепловые эффекты химических реакций важны для теоретической химии и необходимы при расчётах равновесных составов смесей, выхода продуктов реакций, удельной тяги топлив реактивных двигателей и для решения многих других прикладных задач^[1].

Изучение тепловых эффектов химических реакций составляет важнейшую задачу термохимии^[3]. Для расчёта стандартных тепловых эффектов химических реакций используют таблицы стандартных теплот образования или сгорания^[37].

Стандартная энтальпия образования (стандартная теплота образования)[править | править код]

Под стандартной теплотой образования понимают тепловой эффект реакции образования одного моля вещества из простых веществ, его составляющих, находящихся в устойчивых стандартных состояниях.

Например, стандартная энтальпия образования 1 моля метана из углерода и водорода равна тепловому эффекту реакции:

С(тв) + 2H₂(г) = CH₄(г) + 74,9 кДж/моль.

Стандартная энтальпия образования обозначается ΔHo
f. Здесь индекс f означает formation (образование), а знак «O» в верхнем индексе указывает, что величина относится к стандартному состоянию вещества: один моль индивидуального химического соединения, взятого в чистом виде при стандартных условиях в том агрегатном состоянии, которое устойчиво в этих условиях (если нет специальной оговорки)^[38]. Иногда для обозначения стандартного состояния используют перечёркнутый символ «O» в верхнем индексе; согласно рекомендациям ИЮПАК по использованию обозначений в физической химии^[39], перечёркнутый и неперечёркнутый символ «O», используемые для обозначения стандартного состояния, одинаково приемлемы. В литературе часто встречается другое обозначение стандартной энтальпии — ΔHo
298,15, где знак «O» указывает на равенство давления одной атмосфере^[40] (или, несколько более точно, на стандартные условия^[41]), а 298,15 — температура. Иногда индекс «O» используют для величин, относящихся к чистому веществу, оговаривая, что обозначать им стандартные термодинамические величины можно только тогда, когда в качестве стандартного состояния выбрано именно чистое вещество^[42]. Стандартным также может быть принято, например, состояние вещества в предельно разбавленном растворе.

Энтальпия образования простых веществ принимается равной нулю, причем нулевое значение энтальпии образования относится к агрегатному состоянию, устойчивому при T = 298,15 K. Например, для иода в кристаллическом состоянии ΔH^o(I₂, тв) = 0 кДж/моль, а для жидкого иода ΔH^o(I₂, ж) = 22 кДж/моль. Энтальпии образования простых веществ при стандартных условиях являются их основными энергетическими характеристиками.

Тепловой эффект любой реакции находится как разность между суммой теплот образования всех продуктов и суммой теплот образования всех реагентов в данной реакции (следствие закона Гесса):

ΔH^o_{реакции} = ΣΔHo
f (продукты) — ΣΔHo
f (реагенты).

Термохимические эффекты можно включать в химические реакции. Химические уравнения в которых указано количество выделившейся или поглощенной теплоты, называются термохимическими уравнениями. Реакции, сопровождающиеся выделением тепла в окружающую среду имеют отрицательный тепловой эффект и называются экзотермическими. Реакции, сопровождающиеся поглощением тепла имеют положительный тепловой эффект и называются эндотермическими. Тепловой эффект обычно относится к одному молю прореагировавшего исходного вещества, стехиометрический коэффициент которого максимален.

Температурная зависимость теплового эффекта (энтальпии) реакции[править | править код]

Чтобы рассчитать температурную зависимость энтальпии реакции, необходимо знать мольные теплоемкости веществ, участвующих в реакции. Изменение энтальпии реакции при увеличении температуры от Т₁ до Т₂ рассчитывают по закону Кирхгофа (предполагается, что в данном интервале температур мольные теплоемкости не зависят от температуры и нет фазовых превращений):

Если в данном интервале температур происходят фазовые превращения, то при расчёте необходимо учесть теплоты соответствующих превращений, а также изменение температурной зависимости теплоемкости веществ, претерпевших такие превращения:

где ΔC_p(T₁, T_φ) — изменение теплоемкости в интервале температур от Т₁ до температуры фазового перехода;  — тепловой эффект фазового перехода; ΔC_p(T_φ, T₂) — изменение теплоемкости в интервале температур от температуры фазового перехода до конечной температуры, и T_φ — температура фазового перехода.

Стандартная энтальпия сгорания[править | править код]

Стандартная энтальпия сгорания — ΔHо
гор., тепловой эффект реакции сгорания одного моля вещества в кислороде до образования оксидов в высшей степени окисления. Теплота сгорания негорючих веществ принимается равной нулю.

Стандартная энтальпия растворения[править | править код]

Стандартная энтальпия растворения — ΔHо
раств., тепловой эффект процесса растворения 1 моля вещества в бесконечно большом количестве растворителя. Складывается из теплоты разрушения кристаллической решётки и теплоты гидратации (или теплоты сольватации для неводных растворов), выделяющейся в результате взаимодействия молекул растворителя с молекулами или ионами растворяемого вещества с образованием соединений переменного состава — гидратов (сольватов). Разрушение кристаллической решетки, как правило, эндотермический процесс — ΔH_реш. > 0, а гидратация ионов — экзотермический, ΔH_гидр. < 0. В зависимости от соотношения значений ΔH_реш. и ΔH_гидр. энтальпия растворения может иметь как положительное, так и отрицательное значение. Так растворение кристаллического гидроксида калия сопровождается выделением тепла:

ΔHо
раств.KOH = ΔHо
реш. + ΔHо
гидр.К⁺ + ΔHо
гидр.OH⁻ = −59 кДж/моль.

Под энтальпией гидратации ΔH_гидр. понимается теплота, которая выделяется при переходе 1 моля ионов из вакуума в раствор.

Стандартная энтальпия нейтрализации[править | править код]

Стандартная энтальпия нейтрализации ΔHо
нейтр. — энтальпия реакции взаимодействия сильных кислот и оснований с образованием 1 моля воды при стандартных условиях:

HCl + NaOH = NaCl + H₂O

H⁺ + OH⁻ = H₂O, ΔHо
нейтр. = −55,9 кДж/моль

Стандартная энтальпия нейтрализации для концентрированных растворов сильных электролитов зависит от концентрации ионов, вследствие изменения значения ΔHо
гидратации ионов при разбавлении.

См. также[править | править код]

• Термохимия
• Химическая термодинамика

Комментарии[править | править код]

Примечания[править | править код]

Литература[править | править код]

• Callen H. B. Thermodynamics and an Introduction to Thermostatistics. — 2nd ed. — N. Y. e. a.: John Wiley, 1985. — XVI + 493 p. — ISBN 0471862568, 9780471862567.
• Lebon G., Jou D., Casas-Vázquez J. Understanding Non-equilibrium Thermodynamics: Foundations, Applications, Frontiers. — Berlin — Heidelberg: Springer, 2008. — XIII + 325 p. — ISBN 978-3-540-74251-7, 978-3-540-74252-4. — doi:10.1007/978-3-540-74252-4.
• Александров Н. Е., Богданов А. И., Костин К. И. и др. Основы теории тепловых процессов и машин. Часть II / Под ред. Н. И. Прокопенко. — 5-е изд. (электронное). — М.: Бином. Лаборатория знаний, 2015. — 572 с. — ISBN 978-5-9963-2613-6. (недоступная ссылка)
• Базаров И. П. Термодинамика. — 5-е изд. — СПб.—М.—Краснодар: Лань, 2010. — 384 с. — (Учебники для вузов. Специальная литература). — ISBN 978-5-8114-1003-3.
• Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: Советская Энциклопедия, 1976. — Т. 25: Струнино — Тихорецк. — 600 с. Архивная копия от 5 августа 2017 на Wayback Machine
• Борщевский А. Я. Физическая химия. Том 1 online. Общая и химическая термодинамика. — М.: Инфра-М, 2017. — 868 с. — ISBN 978-5-16-104227-4.
• Бурдаков В. П., Дзюбенко Б. В., Меснянкин С. Ю., Михайлова Т. В. Термодинамика. Часть 2. Специальный курс. — М.: Дрофа, 2009. — 362 с. — (Высшее образование. Современный учебник). — ISBN 978-5-358-06140-8.
• Жариков В. А. Основы физической геохимии. — М.: Наука; Изд-во МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
• Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
• Карякин Н. В. Основы химической термодинамики. — М.: Академия, 2003. — 463 с. — (Высшее профессиональное образование). — ISBN 5-7695-1596-1. (недоступная ссылка)
• Кнорре Д. Г., Крылова Л. Ф., Музыкантов В. С. Физическая химия. — 2. — М.: Высшая школа, 1990. — 416 с. — ISBN 5-06-000655-7.
• Кубо Р. Термодинамика. — М.: Мир, 1970. — 304 с.
• Ляшков В. И. Теоретические основы теплотехники. — М.: Курс; Инфра-М, 2015. — 328 с. — ISBN 978-5-905554-85-8, 978-5-16-0І0639-7.
• Морачевский А. Г., Кохацкая М. С. Прикладная химическая термодинамика. — СПб.: Изд-во Политехн. ун-та, 2008. — 254 с. — ISBN 978-5-7422-2006-0.
• Морачевский А. Г., Фирсова Е. Г. Физическая химия. Термодинамика химических реакций. — 2-е изд., испр. — СПб.: Лань, 2015. — 101 с. — (Учебники

для вузов. Специальная литература). — ISBN 978-5-8114-1858-9. (недоступная ссылка)

• Мюнстер А. Химическая термодинамика / Пер. с нем. под. ред. чл.-корр. АН СССР Я. И. Герасимова. — М.: Мир, 1971. — 296 с.
• Нараев В. Н. Физическая химия. Часть 1. Химическая термодинамика. Фазовые равновесия и учение о растворах. Электрохимия. — СПб.: Санкт-Петербургский государственный технологический институт (Технический университет), 2007. — 262 с. (недоступная ссылка)
• Никольский Б. П., Смирнова Н. А., Панов М. Ю. и др. Физическая химия. Теоретическое и практическое руководство / Под ред. Б. П. Никольского. — 2-е изд., перераб. и доп. — Л.: Химия, 1987. — 880 с. — (Для высшей школы).
• Путилов К. А. Термодинамика / Отв. ред. М. Х. Карапетьянц. — М.: Наука, 1971. — 376 с.
• Степановских Е. И., Брусницына Л. А., Маскаева Л. Н. Химическая термодинамика в вопросах и ответах. — Екатеринбург: УИПЦ, 2014. — 221 с. — ISBN 978-5-4430-0061-9.
• Сычёв В. В. Сложные термодинамические системы. — 5-е изд., перераб. и доп. — М.: Издательский дом МЭИ, 2009. — 296 с. — ISBN 978-5-383-00418-0.
• Тамм М. Е., Третьяков Ю. Д. Неорганическая химия. Том 1. Физико-химические основы неорганической химии / Под. ред. акад. Ю. Д. Третьякова. — М.: Академия, 2004. — 240 с. — (Высшее профессиональное образование). — ISBN 5-7695-1446-9.
• Термодинамика. Основные понятия. Терминология. Буквенные обозначения величин / Отв. ред. И. И. Новиков. — АН СССР. Комитет научно-технической терминологии. Сборник определений. Вып. 103. — М.: Наука, 1984. — 40 с.
• Химическая энциклопедия / Гл. ред. Н. С. Зефиров. — М.: Большая Российская энциклопедия, 1995. — Т. 4: Пол — Три. — 640 с. — ISBN 5-85270-092-4.
• Химический энциклопедический словарь / Гл. ред. И. Л. Кнунянц. — М.: Советская энциклопедия, 1983. — 792 с.
• Шмидт Э. Введение в техническую термодинамику / Пер. с нем. — М.—Л.: Энергия, 1965. — 392 с.
• Эткинс П. Физическая химия. — М.: Мир, 1980.