Как найти разность фаз в звуке

Условие задачи:

Найти разность фаз колебаний между двумя точками звуковой волны, отстоящими друг от друга на 25 см, если частота колебаний 680 Гц. Скорость звука 340 м/с.

Задача №9.6.13 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(Delta l=25) см, (nu=680) Гц, (upsilon=340) м/с, (Delta varphi-?)

Решение задачи:

Если точки, находящиеся на расстоянии (Delta l), колеблются с разностью фаз (Delta varphi), а точки, находящиеся на расстоянии (lambda) – c разностью фаз (2pi), то справедливо записать следующее соотношение:

[frac{{Delta l}}{{Delta varphi }} = frac{lambda }{{2pi }}]

Выразим отсюда разность фаз (Delta varphi):

[Delta varphi = frac{{2pi Delta l}}{lambda };;;;(1)]

Скорость распространения колебаний (upsilon) можно определить через длину волны (lambda) и частоту колебаний (nu) следующим образом:

[upsilon = lambda nu ]

Откуда длина волны (lambda) равна:

[lambda = frac{upsilon }{nu };;;;(2)]

Подставим выражение (2) в формулу (1), тогда получим:

[Delta varphi = frac{{2pi Delta lnu }}{upsilon }]

Задача решена в общем виде, подставим данные задачи в полученную формулу и посчитаем численный ответ:

[Delta varphi = frac{{2 cdot 3,14 cdot 0,25 cdot 680}}{{340}} = 3,14 ;рад = 180^circ]

Ответ: 180°.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

9.6.12 Определить расстояние между двумя ближайшими точками бегущей волны
9.6.14 Длина волны 60 см. На каком расстоянии друг от друга находятся точки волны
9.6.15 Вдоль резинового шнура распространяется волны со скоростью 3 м/с при частоте 2 Гц

Предполагаемое время на прочтение: 7 минут(ы)

Фазовый сдвиг – что это? А фаза звукового сигнала? Попробуем немного разобраться в этом вопросе. Не факт, что смогу ясно разъяснить этот вопрос, но примерное понятие должно получиться.

Пролог

Музыканты, меломаны, а так же, любители “хай-эндовского” звука, в разговорах между собой, часто используют, вроде бы всем понятные термины – спектр, фаза, частота, меандр, глубина и локализация сцены, и прочие узкозначимые слова. Но зачастую, даже некоторые из “знатоков”, до конца не могут понять, что же это на самом деле такое.

Такие понятия как – “Фазовый сдвиг” очень часто упоминаются при проектировании кроссоверов для акустики. Подробно про кроссоверы мы уже поговорили чуть ранее.

При наличии интернета выяснить тот или иной вопрос не составляет проблем. В отсутствии такового – можно сходить в библиотеку, найти пару реально научных книжек и почитать саму теорию. Но все нынче стали на столько занятые, что даже выуживать информацию из интернета – времени нет. Попробуем найти простое объяснение – что же такое “фазовый сдвиг”?

Что означают эти термины на самом деле? Можно ли “пощупать” их истинное значение? Да, однозначно, можно. Сейчас мы попробуем разобраться в вопросе – “Что такое – фазовый сдвиг?”

Фаза сигнала

Для начала порассуждаем, что такое – “фаза сигнала”. Фаза сигнала никогда не существует сама по себе. Это виртуальное понятие. Вообще, можно сказать так: Фаза – это уровень сигнала в текущий момент времени, или иначе, – это уровень звукового давления в текущий момент времени в измеряемой точке пространства (к примеру, это место, где находится слушатель).

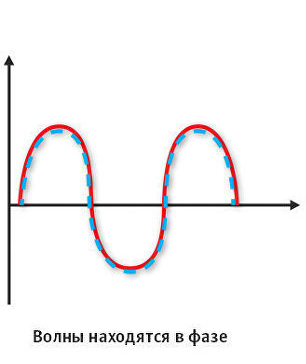
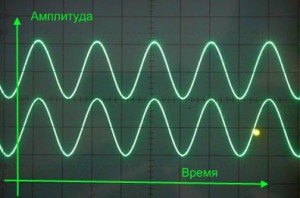
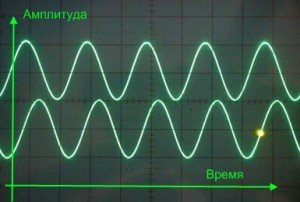
Вот картинка, изображающая звуковые волны в фазе. К примеру, звуковые сигналы двух каналов нашей акустики совпадают. В этом случае, музыка звучит чётко, без каких либо искажений. В музыкальном произведении можно услышать все задействованные инструменты, которые звукорежиссер слышал при записи. Имеется некая область звукового давления, где ощущается “эффект присутствия” – это то, о чем спорят меломаны и аудиофилы. Иными словами – получаем ожидаемый звук и впечатления.

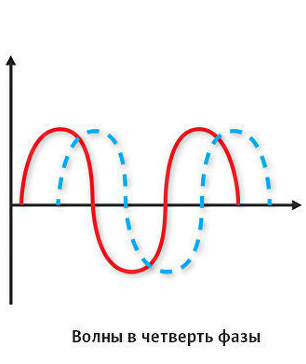
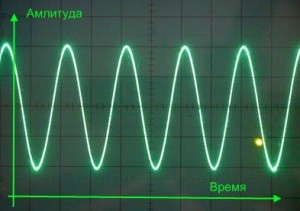
На следующей картинке ниже, фаза смещена на 90 градусов, или на четверть фазы. Этот эффект можно услышать в виде небольшого эха. Это может и не связано с оборудованием самой комнаты. Эффект звуковой задержки с небольшим смещением фазы вносит некую сумятицу в музыку, теряется “картинка”, исполнители “уходят в разные стороны”, появляется ощущение, что находишься в огромном зале с каменными стенами. Звуки становятся не естественными, искаженными.

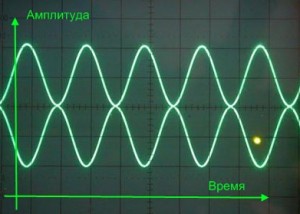
Далее, мы наблюдаем смещение фаз на 180 градусов. То есть, акустика в этом случае играет в противофазе. Чуть ниже подробно об этом. В данном случае, общая “звуковая картина” на столько становится не понятной, что слушать музыку становится просто не интересно и противно. Звуки становятся “ватные”, многие часты просто могут отсутствовать, хотя они и воспроизводятся колонками. Может сложиться такое впечатление, что слушаешь музыку в завязанной шапке-ушанке.

Далее, немного теории без научных выкладок.

К примеру, слушая, сидя у себя дома, свои акустические системы, мы слышим, как они порождают в районе дивана те или иные переменные звуковые давления. Звуковые волны складываются друг с другом. Эти волны имеют разные частоты и амплитуду. Они то нарастают, то убывают.

Противофаза

А теперь предположим, что давления от обоих колонок (звуковые волны) изменяются одинаково, но имеют противоположную направленность. То есть, одна колонка излучает “плюсовые” волны, а другая колонка – “минусовые”. Это может случиться, когда слушатель, случайно, перепутал клеммы подключения одного из каналов (левый канал например).

Немного проще. Динамики правой колонки играют вперёд, а динамики в левой колонке играют назад, одновременно пытаясь воспроизводить одну и туже частоту. Одна колонка создаёт давление, скажем, 1 Паскаль, а другая – минус 1 Паскаль. Такой эффект называется – противофаза.

Общая громкость звука в том месте, где находится слушатель, теоретически, должна стремится к нулю, но это не означает, что какой либо звук вообще будет не слышно. В этом случае, может сильно поломаться “звуковая сцена”, “картинка” музыкального произведения, а в каком либо месте помещения звук реально будет затухать, но не совсем. Звук станет “смазанным” и исчезнут некоторые частотные составляющие из общего звукового сигнала.

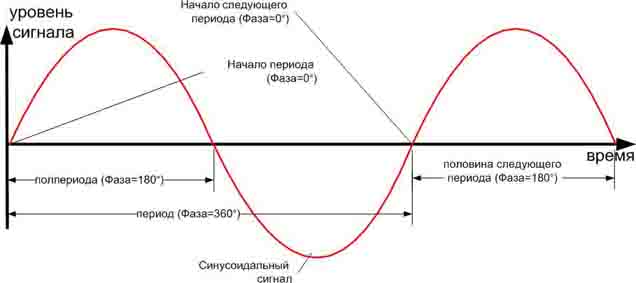
Не будем вдаваться в непростую научную формулировку, приводя формулы. Можно сказать так, что из второй колонки звук доходит к слушателю, но с задержкой по времени (не забываем, что сигнал на колонки подаётся одинаковый!). И задержка в этом случае получается именно 180 градусов. Почему так? Попробуем разобраться на картинке, нагляднее – понятнее.

360 градусов – длина периода сигнала (Фаза), 180 градусов – половина периода сигнала.

Фазовый сдвиг

А теперь, мы дошли до момента, когда можно уже разобрать вопрос – “Что такое – фазовый сдвиг?”

Фаза — это временная связь двух сигналов. И в течении периода колебания меняется от 0 до 360 градусов. Потом опять – от 0 до 360, и так далее. Можно сказать, что это мгновенный уровень сигнала в определенной точке времени внутри периода. Саму фазу мы не слышим, но слышим фазовый сдвиг одного сигнала относительно другого.

Вики про это говорит так: Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.

Фазовый сдвиг является безмерной величиной и измеряется в градусах или долях периода.

Вывод

Предположим, вы подключили два динамика к выходу усилителя (пусть физически это будут ваши акустические системы). Один динамик как положено – плюс на плюс, минус на минус. А второй, перепутали и он получился подключенным плюс на минус и минус на плюс. Включив усилитель, что мы услышим? Вероятнее всего – жалкое подобие звука. Один динамик будет как-бы гасить сигнал другого своими звуковыми волнами.

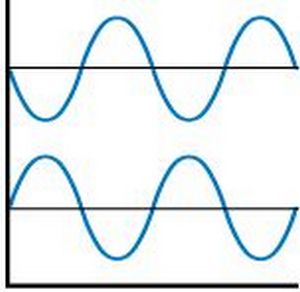
На картинках ниже будет нагляднее. Представим, что это мы видим на экране осциллографа, который измеряет сигналы левого и правого каналов вашего усилителя.

На первой картинке левый и правый канал – в фазе. Сигнал одинаков в обоих каналах. Линии идеально повторяют сигнал. У них синхронная амплитуда на всем протяжении. Тут можно сказать, что сигналы находятся «в фазе». Если практически, то суммирующий уровень сигнала будет усиливаться сигналами левого и правого каналов.

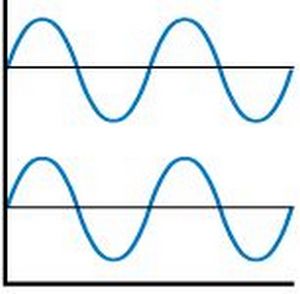
Вторая картинка демонстрирует осциллограмму полного не совпадения. “Горб” левого канала по времени совпадает с “ямой” правого. Чисто по школьной физике – в результате сложения таких колебаний, в идеале, получится ноль. Эти сигналы будут взаимно подавлять друг друга. Сигналы в противофазе.

Фазовый сдвиг подразумевает запаздывание первого сигнала по времени относительно второго.

При двух гармонических колебаниях одной частоты результатом сдвига фаз будет частичное ослабление сигнала. Степень ослабления результирующего сигнала будет зависеть как раз от этого самого сдвига фаз. В предельном случае (в противофазе), на выходе получится абсолютный ноль.

Все эти картинки и рассуждения, о физических свойствах звуковых волн, отдаленно относятся к практике, к реальности. Звуки любого музыкального инструмента нельзя назвать – “одночастотным сигналом” (как осциллограмма на картинках). Частичный сдвиг фаз может ослаблять одни частоты по сравнению с другими. А иногда, усиливать некоторые из них.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Прочитай то что тут написано. Тут много, но ничего сложного. Всё на пальцах.

Если записать уравнение гармонического колебания, то в произвольном виде это будет:
А*sin(wt+Ф0)
A – амплитуда, w – круговая частота, t – время, Ф0 – начальная фаза.

А вообще фаза Ф – это то, что стоит под знаком синуса (или косинуса).

Очевидно фаза может принимать любые значения, но поскольку синус и косинус периодические функции – принято считать фазу в каком-то интервале длиной в 360 градусов или в 2*пи радиан. Т.е. Ф принадлежит [0,2*pi] или [-pi,pi]

Физически это вообще что значит. Вот есть волна. Она в принципе бесконечна. Координата (или другая величина, которая изменяется по гармоническому закону) то увеличивается, то уменьшается. Вот её положение в, так сказать, измерении – это и есть фаза колебания.

Ясное дело, что практически важно рассматривать не абсолютное значение фазы, а фазовый сдвиг между двумя колебаниями или разность фаз одной волны в разных точках.

Итак фаза меняется по закону Ф= wt+Ф0
Поскольку интересует разность фаз за промежуток времени – Ф0 всё равно сократится, так что можно сразу положить его равным нулю.

Формулы нужны.
длина – насколько я понял дана длина волны L
скорость – насколько я понял дана скорость звука s
Тогда частота f = s/L
f – линейная частота – измеряется в Гц = 1/сек Т.е. количество колебаний в секунду.
1/f = T – период колебаний. Т.е. время, за которое совершается одно колебание.
w – круговая частота. w = 2*pi*f . Она измеряется в рад/сек, т.е. это количество радиан, на которые изменяется фаза за секунду.

Таким образом можно выразить w через то что задано:
w = 2*pi*s/L
Тогда Ф(t) = 2*pi*s/L * t
А разность фаз, т.е. изменение фазы: dФ = 2*pi*s/L * dt, где dt это то время, за которое волна распространяется.

Далее есть разность фаз получается больше чем 2пи, можно (при необходимости) привести её к интервалу [0,2пи] или [-пи,пи] путём вычитания целого количества 2пи из полученного числа. Но это уже от задачи зависит – надо или не надо.

Доброго всем времени суток!

Сегодня отчего-то захотелось поговорить о такой немаловажной штуке, как фаза аудио-сигнала. Так, освежим школьный курс физики применительно к нашим гитарным и, вообще, звуковым делам.

Если вспомнить школьный курс физики, а именно раздел, посвященный гармоническим колебаниям, то из глубин памяти можно выудить, что фаза – это аргумент периодической функции, который отвечает за то, какая будет амплитуда сигнала в определенный момент времени.

Что нам это дает с музыкальной точки зрения? И где же стоит искать проблемы с этой пресловутой фазой?

Допустим, мы записываем гитару, снимая звук с комбика двумя микрофонами, сигнал с которых микшируем, затем в один канал. Вот тут, при суммировании двух сигналов и могут возникнуть проблемы с фазой.

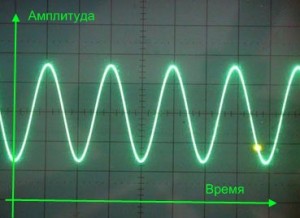
Вариант первый. Сигналы приходят в фазе.

На экране осциллографа это будет выглядеть примерно так.

Видно, что сигналы идеально повторяют друг друга, т.е. «пики и впадины» амплитуд двух сигналов идут синхронно во времени. Это и означает, что сигналы «в фазе». С практической точки зрения это будет означать, что сигналы будут усиливать друг друга. И в идеальном случае амплитуда результирующего сигнала будет представлять собой сумму амплитуд каждого из них.

Такой случай нам, собственно, ничем не грозит, а даже наоборот – это то, к чему стоит стремиться в большинстве случаев.

Вариант второй. Сигналы в противофазе.

Этот случай прямо противоположенный первому.

Видно, что там, где «пик» первого сигнала, там же и «впадина» у второго. Не трудно догадаться, что результатом сложения таких колебаний в идеальном случае будет полный ноль, т.е. взаимное подавление обоих сигналов.

Случай, надо сказать, самый поганый, и которого, стоит избегать.

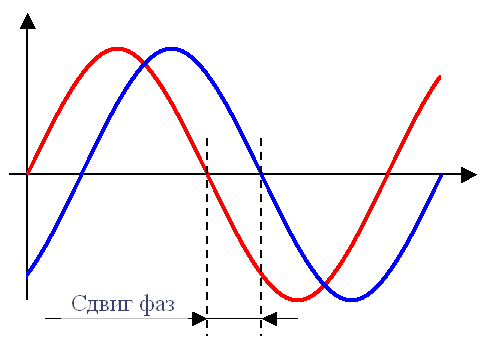
Вариант третий. Фазовый сдвиг.

Так говорят, когда первый сигнал запаздывает по времени относительно второго.

Еще говорят, что сигналы «частично не в фазе». В случае двух гармонических колебаний одной частоты (на практике, это примерно, как сферический конь в вакууме), сдвиг фаз будет приводить к частичному ослаблению сигнала. А то, насколько ослабится результирующий сигнал, как раз будет зависеть от этого самого сдвига фаз. В предельном случае (см. Вариант 2), на выходе будет полный ноль.

Все эти картинки имеют лишь отдаленное отношение к практике, т.к. обычно мы имеем дело не с одночастотным сигналом. В звуке гитары (да и любого другого инструмента) довольно много гармоник (читай частот) и обертонов (тоже читай частот). Поэтому при частичном сдвиге фаз некоторые частоты будут ослабляться больше, чем другие, а иные могут быть даже усилены. Как не трудно догадаться все зависит от сдвига фаз (разности фаз) между конкретными гармониками.

Кстати, именно на этом принципе – усиление одних частот и ослабление других, основан всем нам известный гитарный эффект – фэйзер (phaser). Конечно, схему сдабривают частотными фильтрами, цепями обратной связи и смешиванием обработанного и не обработанного сигнала, но основной принцип именно тот – сдвиг фаз.

Вообще, фазовые дела могут доставить довольно много неприятностей. Это хорошо если у вас всего два микрофона, в этом случае можно просто поиграть расстоянием от источника звука до миков и найти те положения при которых сигналы от них приходят в фазе. А представьте, что вам надо подзвучить сцену? Или барабаны на реп. точке?

Кстати, на многих преампах для микрофонов есть переключатель полярности сигналов. По физическим принципам к фазе это никакого отношения не имеет, но вот эффект может дать точно такой же, как в вариантах 1 и 2. Только совпадение или несовпадение «пиков» и «впадин» сигналов будет зависеть не от их разности фаз, а от полярности сигналов. Однако, раз эффект это дает такой же, поэтому инвертирование сигналов можно использовать при проблемах с фазой. Другое дело, что это может помочь, а может и не помочь.

Еще одним решением проблемы может стать коррекция фазы уже записанного сигнала в любимой программе звукозаписи, благо сейчас цифровая обработка позволяет творить чудеса.

На слух фазовое несовпадение сигналов можно определить по характерной потере яркости звука, его «истощению». Если чувствуете, что со звуком твориться что-то не то и симптому совпадают с вышеперечисленными, то можно попробовать поиграть с фазой.

Фазовые проблемы могут возникнуть не только при снятии звука микрофонами. Вот человек включает фэйзер в параллельный разрыв на комбике и что? Судя по симптомам, имеет фазовые проблемы, т.к. фэйзер сам по себе сдвигает фазу исходного сигнала, а потом смешивает ее с необработанным, плюс еще параллельная петля… Итог закономерен – звучит хреново.

Надеюсь, что доступно объяснил, что такое фаза сигнала и, с чем ее едят? =)