Как найти разность хода двух лучей

Оптическая разность хода.

Вместо разности фаз

интерферирующих волн удобно ввести в
рассмотрение пропорциональную ей
величину

– оптическую разность хода, которая
отличается множителем

,
где

– длина световой волны.

Изменению
разности фаз на

соответствует изменение разности хода
на

.

В
вакууме оптическая разность хода в
отличие от разности фаз имеет наглядную
и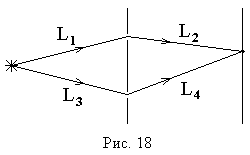
нтерпретацию.
Если две интерферирующие волны испускаются
одним источником света, то разность
хода – это геометрическая разность длин
путей, по которым два интерферирующих
луча от одной точки источника достигли
одной точки экрана.

Например,
в оптической схеме опыта Юнга, изображенной
на рис. 18, разность хода для точки P на
экране находится по формуле:

.

В
изотропной среде скорость света в n
раз меньше, чем в вакууме, здесь n
– показатель преломления среды. Частота
света в среде и в вакууме одинакова,
поэтому длина волны в среде в n
раз меньше. В соответствии с соотношением

вместо реального уменьшения длины волны

можно рассматривать неизменную

и соответствующее увеличение длины
пути луча. С этой целью вводится понятие
оптической длины пути, которая в n
раз больше геометрической длины. Далее,
употребляя термин “разность хода”,
всегда будем иметь в виду оптическую
разность хода.

Заменяя
разность фаз интерферирующих волн
оптической разностью хода, получаем
следующее выражение для интенсивности
интерференционной картины:

.

Приемники
света в оптическом диапазоне реагируют
на интенсивность света, а не на
напряженность электрического или
магнитного полей. Поэтому измеряемые
в опыте величины, ширина полос и видность,
также могут быть выражены через
интенсивность, а значит и через оптическую
разность хода. Следовательно, понятие
оптической разности хода позволяет
свести оптическую задачу по интерференции
к геометрической задаче отыскания
разности хода.

Отметим,
что разность хода лучей можно отсчитывать
не только как разность длин путей от
источника до точки наблюдения, но и как
разность длин путей от двух точек любой
поверхности равной фазы волны до точки
наблюдения. При этом, конечно, две точки
на поверхности равной фазы – не произвольные
точки, а должны быть точками, через
которые реально проходят лучи, попадающие
в точку наблюдения. Так на рис. 18

,
поэтому две щели находятся на поверхности
равной фазы, и, следовательно, разность
хода можно найти по упрощенной формуле

.
Этот прием часто используется при
решении задач.

18.1.2.1. Условия максимума и минимума на разность фаз δ

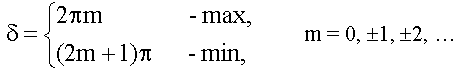
18.1.2.2. Оптическая разность хода

Пусть
для простоты, начальные фазы α₁
и α₂
интерферирующих волн равны нулю, тогда:

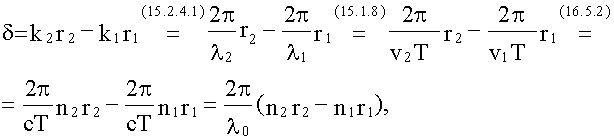
здесь
λ₀ = cT
– длина световой волны в вакууме.

Оптической
разностью хода называют величину:

.

Тогда:

.

18.1.2.3. Условия максимума и минимума на оптическую разность хода

Из
(18.1.2.1.)
и (18.1.2.2.):

П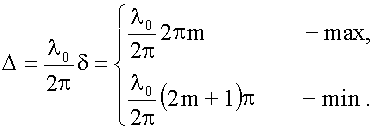
осле
сокращения получим условия на Δ:

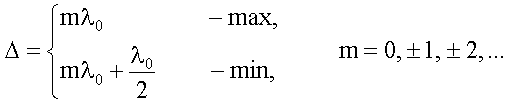
30. Интерференция при отражении от тонких пленок. Пример расчета интерференционной картины для плоскопараллельной пластинки.

Интерференция
– физическое явление, наблюдаемое при
сложении волн (световых, звуковых и т.
п.), усиление волн в одних точках
пространства и ослабление в других (или
сложение двух или более
волн, при котором амплитуда результирующей
волны зависит от разности фаз исходных
волн в данной точке пространства)

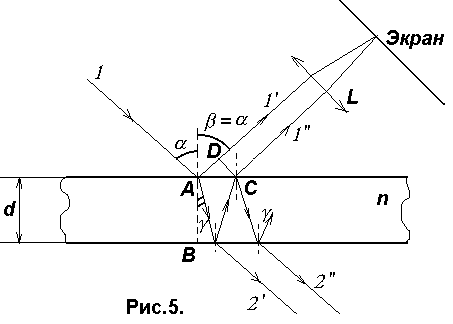
Пусть
на плоскопараллельную прозрачную пленку
(пластинку) с показателем преломления
n и толщиной d под углом 
падает плоская монохроматическая волна
(для простоты рассмотрим один луч).

На
поверхности пленки в точке А волна
частично отражается (луч 1- ) и частично
преломляется (луч АВ). В точке В волна
также частично отражается (луч ВС) и
частично преломляется (луч 2- ). То же
самое происходит в точке С.

Причем
преломленная волна (луч 1″ ) накладывается
на волну непосредственно отраженную
от верхней поверхности (луч 1- ). Эти две
волны когерентны, если оптическая
разность хода

меньше
длины когерентности l_ког, и в этом
случае они интерферируют.

Оптическая
разность хода двух волн =(AB+BC)n-(AD-/2),

где
/2 – потеря полуволны
при отражении луча 1- в точке А. Используя
закон преломления n₁sin
= n₂sin и учитывая,
что в рассматриваемом случае n₁=1,
n₂=n, можно показать, что

.(17)

В
точке наблюдения на экране будет
максимум, если m
и минимум, если (2m+1)/2[см.(15),(16)].

Возможность
уменьшения вредного отражения света
вследствие интерференции в тонких
пленках широко используется в современных
оптических приборах. Для этого на
передние поверхности линз, призм наносят
тонкие пленки с показателем преломления
n=

и толщиной d, которая определяется из
условия минимума при интерференции
волн, отраженных от границ раздела сред
с n₁ и n и n и n₂


2dn=(2m+1)/2,
m=0,1,2-(18)

Минимальная
толщина пленки соответствует m=0

d=/(4n)

Такая
оптика получила название просветленной
оптики.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Волновая оптика: оптическая разность хода

В задачах, представляемых вашему вниманию, появляются призмы и плоскопараллельные пластинки, необходимо определить оптическую разность хода, а также мы начинаем рассмотрение интерференции света.

Задача 1.

Найти разность фаз   в двух точках светового луча, если расстояние между ними ; , где -целое число.
Если расстояние между точками – целое число длин волн, то разность фаз будет равна

Во втором случае

Ответ: , .

Задача 2.

На пути одного из параллельных световых лучей поместили, нормально ему, плоскопараллельную стеклянную пластинку толщиной мм. Какую оптическую разность хода лучей вносит пластинка?
Оптическая разность хода определяется выражением , где – показатель преломления пластинки, – показатель преломления воздуха. – толщина пластинки, так как в данном случае лучи преодолевают одно и то же расстояние.

Ответ: м.

Задача 3.

Два параллельных монохроматических луча  падают на стеклянную призму () и выходят из нее. Расстояние между падающими лучами см. Преломляющий угол призмы . Определить разность хода лучей при выходе из призмы.

Рассмотрим треугольники и . Они подобны, поэтому можем записать отношение сходственных сторон:

В задаче известен преломляющий угол призмы. Его тангенс равен

Перепишем (1), воспользовавшись свойством пропорции:

Тогда

Теперь определяем разность хода:

Ответ: .

Задача 4.

Два когерентных световых луча достигают некоторой точки с разностью хода мкм. Что произойдет в этой точке усиление или ослабление света – если свет: a) красного цвета ( нм); б) желтого цвета ( нм); в) фиолетового цвета ( нм)?
Усиление света происходит, если выполняется условие – в разность хода укладывается четное число полуволн:

Определим количество полуволн  в разности хода для света каждого цвета:

В первом и втором случае число полуволн нечетно, следовательно, произойдет ослабление света. В последнем случае (число полуволн четно) свет усилится.

Задача 5.

Оптическая разность хода волн от двух когерентных источников в некоторой точке пространства мкм. Каков будет результат интерференции в этой точке, если длина волны будет: а) ( нм); б) ( нм)?

Определим количество полуволн  в разности хода для каждой длины волны:

В первом случае число полуволн нечетно, следовательно, произойдет ослабление света. Во втором случае (число полуволн четно) свет усилится.

Явление интерференции света

Волны, как и колебания, могут складываться. Сложение волн может быть интерференционным и неинтерференционным. Интерференцией называется сложение когерентных волн, при котором в разных точках пространства получается усиление или ослабление амплитуды результирующей волны, не изменяющееся с течением времени. Интерференция наблюдается только от когерентных источников. Когерентность — значит согласованность. Когерентными источниками называются такие источники, которые дают волны одинаковой частоты, и для фиксированной точки пространства разность фаз колебаний остается постоянной.

Независимые источники света не могут быть когерентными, так как в каждом из них свет испускается множеством атомов, излучающих несогласованно. Разность фаз колебаний, испускаемых совокупностью атомов таких источников, быстро и беспорядочно меняется во времени. Когерентность можно обеспечить, разделив волну от одного источника на две части и затем сведя их вместе. Две части одной волны когерентны между собой и при наложении будут интерферировать.

Существуют различные методы получения когерентных световых источников. Самый простой из них — метод Юнга, в котором световая волна делится на две части с помощью экрана с двумя узкими параллельными щелями.

Условия максимума и минимума интенсивности
при интерференции

Найдем условия максимума и минимума интенсивности при интерференции. Пусть S₁ и S₂ — два когерентных источника, совершающих колебания в одинаковой фазе. До точки наблюдения М волны проходят разное расстояние.

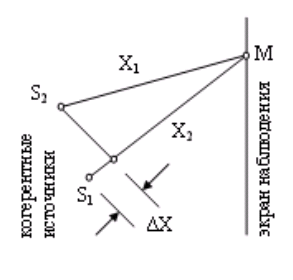
Запишем для них уравнения волн

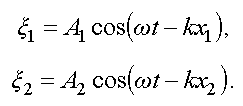
Найдем разность фаз складываемых волн

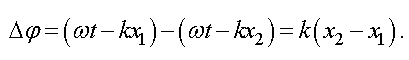
Обозначим через Δx — разность хода. Волновое число равно

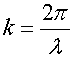
тогда связь между разностью хода и разностью фаз дается уравнением

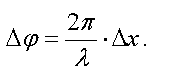
Амплитуда результирующего колебания в точке наблюдения определяется уравнением

Так как интенсивность пропорциональна среднему значению квадрата амплитуды, то получим выражение для результирующей интенсивности

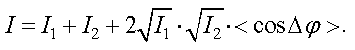
Если источники некогерентные, то 

 , т. е. интерференция не наблюдается. Для когерентных источников разность фаз  и среднее значение косинуса равно косинусу разности фаз

При наложении двух когерентных световых волн происходит пространственное перераспределение световой энергии, в результате чего в одних местах возникают максимумы, а в других — минимумы интенсивности, т. е. появляется интерференционная картина.

Максимумы интенсивности появляются там, где

 т. е. при

 где m = 0, 1, 2, … Следовательно,

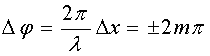
 Отсюда получим условие максимума интенсивности при интерференции

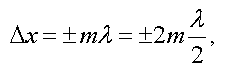
где m — порядок интерференционного максимума.

Условие максимума интенсивности при интерференции читается следующим образом.

Если разность хода равна целому числу длин волн или четному числу полуволн, то будет наблюдаться максимум интенсивности при интерференции.

Аналогично найдем условие минимума. Если

 , то

 , где m = 0, 1, 2, …

Тогда

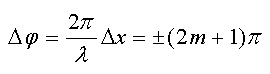
и

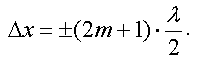
Условие минимума интенсивности при интерференции читается следующим образом.

Если разность хода равна нечетному числу полуволн, то в данной точке экрана будет наблюдаться минимум интенсивности при интерференции.

Кольца Ньютона

Установка для наблюдения колец Ньютона состоит из плоско-параллельной пластины и плосковыпуклой линзы большого радиуса кривизны. Свет на установку падает вертикально.

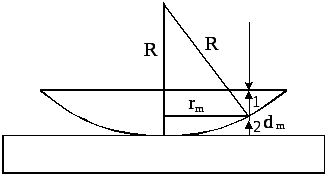
Тонкая пленка образуется между линзой и пластинкой. Это воздушная пленка или жидкая. Пленка имеет вид клина. Поэтому возникают полосы равной толщины. Из-за симметрии они имеют вид окружностей.

Рассмотрим ход одного из лучей. Поскольку угол клина мал, можно считать, что угол падения везде ноль. Когерентными являются лучи, отразившиеся в точках 1 и 2. В точке 1 они накладываются. Найдем радиус m-ого кольца r_m.

Оптическая разность хода между лучами 1 и 2 равна: 

В нашем случае α = 0, поэтому

Предположим, что кольцо темное, тогда 

Отсюда выражаем толщину клина в точке m кольца d_m:

Из рис. следует, что 

Пренебрегая членом d_m², получаем:

Приравнивая оба выражения для d_m, получаем:

Отсюда выражаем радиус m-ого темного кольца:

Для воздушной пленки (n = 1), это выражение принимает вид:

Найдем радиусы светлых колец. Оптическая разность хода в этом случае равна 

Отсюда

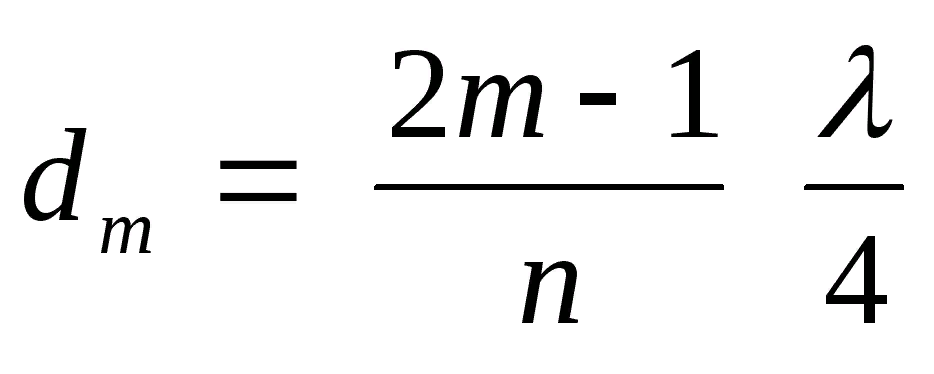
Приравнивая с предыдущим выражением d_m, получим:

Радиусы колец зависят от длины волны λ, поэтому, если свет немонохроматический, то кольца будут окрашены.

Явление дифракции. Принцип Гюйгенса — Френеля

Дифракцией называется огибание волнами препятствий. Дифракция наблюдается для волн различной природы (звуковых, световых, волн на воде и т. д.) Явление дифракции проявляется сильнее, если размеры препятствий соизмеримы с длиной волны.

Объяснить дифракционные явления можно с помощью принципа Гюйгенса — Френеля, согласно которому каждая точка фронта волны является источником вторичных волн, которые когерентны. Амплитуда и фаза волны в любой точке пространства — есть результат интерференции волн, излучаемых вторичными источниками.

На рис. изображено препятствие П в форме щели шириной b, размеры которого соизмеримы с длиной волны λ. На щель падает плоская монохроматическая волна. Любая точка фронта волны S₁ становится источником вторичных волн, которые являются сферическими и огибающая которых S₂ дает положение фронта волны в следующий момент времени.

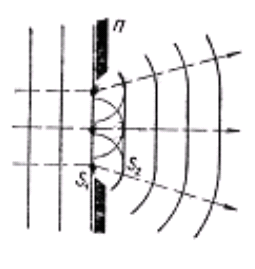
Проходя через щель, волны отклоняются от прямолинейного распространения (дифрагируют). Если на их пути поставить экран, то на нем будет наблюдаться дифракционная картина, причем интенсивность в любой точке экрана наблюдения будет определяться результатом интерференции вторичных волн, пришедших в точку наблюдения.

Зоны Френеля. Дифракция света на одной щели

Объяснить и рассчитать распределение интенсивности света в дифракционной картине можно, применив вспомогательный прием — метод зон Френеля. Зоны Френеля — это участки волновой поверхности, построенные таким образом, что расстояние от краев соседних зон до точки наблюдения различается на половину волны (на λ/2 ). Известно, что разность хода и разность фаз связаны соотношением

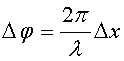
Следовательно, если Δx = λ/2 , то  Δ φ = π, т. е. колебания, создаваемые соседними зонами Френеля находятся в противофазе и попарно гасят друг друга. Тогда, если отверстие щели открывает четное число зон Френеля, то в точке наблюдения находится минимум интенсивности, а, если нечетное, то — максимум.

Применим метод зон Френеля к рассмотрению дифракции света на одной щели.

Пусть на щель шириной b нормально падает плоская монохроматическая волна. Все точки волновой поверхности, открытые щелью, являются источниками вторичных волн, которые когерентны и распространяются по всем направлениям. Поставим между щелью и экраном наблюдения линзу, которая собирает параллельные лучи в одну точку. Дифракция в параллельных лучах называется дифракцией Фраунгофера. В результате интерференции вторичных волн на экране получится дифракционная картина. Распределение интенсивности вдоль экрана изображено в нижней части (кривая с максимумами и минимумами).

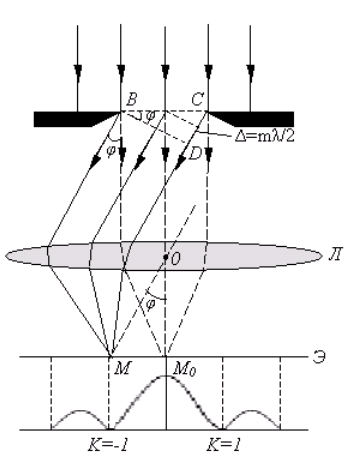
В центре дифракционной картины будет светлая полоса — центральный максимум, так как при φ = 0 все волны придут на экран в точку М₀ в одинаковой фазе и усилят друг друга. Чтобы определить результат интерференции вторичных волн при φ ≠ 0, разобьем открытый участок волновой поверхности на ряд зон Френеля. В данном случае они будут представлять собой узкие полоски, параллельные краям щели. Чтобы найти число зон Френеля m₁, нужно разность хода крайних лучей  Δ = b sin φ поделить на λ/2

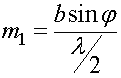
, тогда  

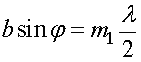
При четном числе зон Френеля m₁= 2k будет наблюдаться минимум интенсивности, при нечетном m₁= 2k +1 — максимум. Условие дифракционного минимума для одной щели имеет вид

где k = 1, 2, 3, …

«Плюс-минус» показывает, что картина симметрична относительно центрального максимума.

Условие дифракционного максимума от щели имеет следующий вид

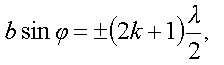
k  называется порядком максимума или минимума, k = 1, 2, 3, …

Дифракция Фраунгофера на дифракционной решетке

Дифракционной решеткой называется совокупность большого числа одинаковых щелей, расположенных на одинаковом расстоянии друг от друга.

Величина d = a + b называется постоянной (или периодом) дифракционной решетки, где b — ширина щели, a — ширина непрозрачного промежутка.

Рассмотрим дифракцию плоской монохроматической волны, падающей нормально на дифракционную решетку. Для наблюдения дифракции Фраунгофера поставим между решеткой и экраном собирающую линзу.

Каждая из щелей посылает свет по всем направлениям, кроме тех, которые удовлетворяют условию дифракционного минимума. Следовательно, условие минимума для дифракции от одной щели является условием минимума для решетки. Распределение интенсивности за счет дифракции света на всех щелях будет подобно распределению, представленному на рисунке, но результирующая амплитуда будет в N раз, а интенсивность в N² раз больше, чем от одной щели, где N — число щелей.

При определении характера дифракционной картины необходимо учесть не только дифракцию света на каждой из щелей, но и интерференцию лучей, приходящих в данную точку экрана от разных щелей.

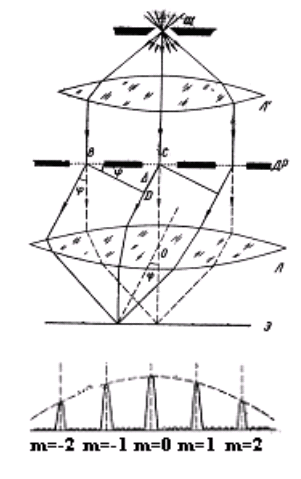
В нижней части рисунка изображено распределение интенсивности света вдоль экрана при дифракции на дифракционной решетке. Пунктирная кривая построена с учетом дифракции света на всех щелях, сплошная кривая учитывает также интерференцию волн от различных щелей. Разность хода лучей, идущих от двух соседних щелей под углом φ будет равна

Положение главных максимумов определяется условием:

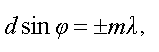
где m = 1, 2, 3, … — порядок главного максимума, φ   — угол дифракции.

Условие максимума при интерференции, согласно которому разность хода лучей, идущих от соседних щелей , должна быть равна четному числу полуволн. Из условия главных максимумов для дифракционной решетки следует, что, если освещать решетку белым светом, то все максимумы, кроме центрального, представляют собой спектры (так как при любом m ≠ 0 чем больше λ, тем больше φ ). Таким образом, дифракционная решетка разлагает сложный свет в спектр и поэтому применяется в спектральных приборах.

Поляризация света

Согласно современным представлениям, свет представляет собой совокупность электромагнитных волн, которые излучаются отдельными атомами в виде порций (или квантов). Поскольку акты излучения отдельных атомов никак не связаны между собой, то свет от естественных источников представляет собой совокупность электромагнитных волн, световой вектор  которых колеблется беспорядочно во всех направлениях перпендикулярно лучу, причем все направления равновероятны. Такой свет называется неполяризованным (или естественным).

Поляризованным светом называется свет, в котором колебания светового вектора каким-то образом упорядочены. Если колебания светового вектора  происходят в одной плоскости, то такой свет называется плоскополяризованным. Плоскость, в которой колеблется вектор , называется плоскостью поляризации. Если имеется преимущественное (но не единственное) направление светового вектора , то такой свет называется частично поляризованным.

Возможные случаи колебаний вектора  в плоскости, перпендикулярной лучу, представлены на рис.

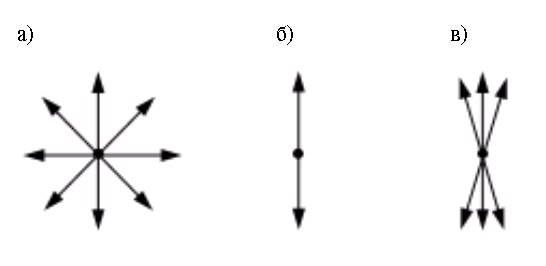
а) естественный свет; б) плоскополяризованный свет;
в) частично поляризованный свет

Подчеркнем, что луч перпендикулярен чертежу.

Свет естественных источников может приобрести частичную или полную поляризацию при взаимодействии с веществом. Поляризация состоит в выделении из светового пучка колебаний определенного направления. Для этой цели используют специальные устройства, например, призму Николя, пластинку турмалина, поляроид и т. д. Устройства, создающие поляризованный свет, называются поляризаторами. Глаз человека не отличает поляризованный свет от ествественного. Для анализа поляризованного света используется такое же, как поляризатор, устройство, которое называется анализатором.

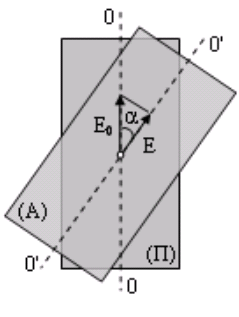
Если плоскополяризованный свет, прошедший через поляризатор (П), падает на анализатор (А) (луч перпендикулярен чертежу, то через него будет пропущена составляющая

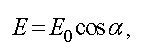
где E₀ — амплитуда света, прошедшего через поляризатор, E — амплитуда света, прошедшего через анализатор, α — угол между плоскостями пропускания колебаний поляризатора и анализатора.

Возведем в квадрат обе части уравнения. Так как интенсивность пропорциональна квадрату амплитуды, то получим:

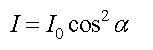
Это уравнение представляет собой закон Малюса.

Интенсивность света, прошедшего поляризатор и анализатор, равна интенсивности света, прошедшего через поляризатор, умноженной на квадрат косинуса угла между плоскостями пропускания колебаний поляризатора и анализатора.

Если на поляризатор падает естественный свет, то интенсивность света уменьшается наполовину

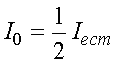
При повороте анализатора вокруг луча можно найти его положение, при котором свет совсем не проходит. При

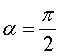
  («скрещенные» поляризатор и анализатор) — I = 0. Это надежный способ убедиться в том, что свет полностью поляризован.

Задачи:

1. В установке для наблюдения колец Ньютона используется плосковыпуклая линза с радиусом кривизны 8,6 м. При освещении установки монохроматическим светом, падающим нормально на плоскую поверхность линзы, радиус четвертого темного кольца был равен 4,5 мм. Определить длину волны света, если наблюдение велось в отраженном свете.
2. Почему при наблюдении на экране интерференционной картины от тонкой мыльной пленки, полученной на вертикально расположенном каркасе, в отраженном монохроматическом свете расстояние между интерференционными полосами в верхней части меньше, чем в нижней?
3. Две когерентные световые волны приходят в некоторую точку пространства с разностью хода 2,25 мкм. Каков результат интерференции в этой точке, если свет: а) красный ( λ = 750 нм); б) зеленый ( λ = 500 нм)?
4. Дифракционная решетка содержит 120 штрихов на 1 мм. Найти длину волны монохроматического света, падающего на решетку, если угол между двумя спектрами первого порядка равен 8°.
5. Определить угол отклонения лучей зеленого света ( λ = 0,55 мкм) в спектре первого порядка, полученном с помощью дифракционной решетки, период которой равен 0,02 мм.
6. Линия с длиной волны λ₁ = 426 нм, полученная при помощи дифракционной решетки в спектре второго порядка, видна под углом φ₁ = 4,9º. Найти, под каким углом φ₂. видна линия с длиной волны λ₂ = 713 нм в спектре первого порядка.

Задания и вопросы для самоконтроля

1. Что называется интерференцией?
2. Какие источники называются когерентными? В чем заключается общий принцип получения когерентных световых волн?
3. Сформулируйте условия максимума и минимума интенсивности света при интерференции.
4. В чем состоит явление дифракции? Сформулируйте принцип Гюйгенса — Френеля.
5. Какой свет называется плоскополяризованным?
6. Сформулируйте закон Малюса.