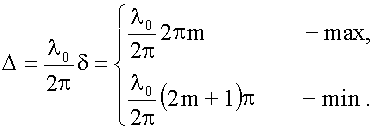IV. Оптика
Тестирование онлайн
Интерференция
Интерференция – сложение в пространстве двух (или нескольких) волн, при котором в разных его точках получается усиление или ослабление амплитуды результирующей волны. Явление характерно для волн любой природы: звуковых волн, волн на поверхности воды, электромагнитных волн и др.
Устойчивую интерференционную картину дают только когерентные волны, т.е. волны, имеющие одинаковые частоты и постоянную во времени разность фаз колебаний.
Пусть в точку А пришли две волны одинаковой частоты, прошедшие перед этим различные расстояния l1 и l2 от своих источников.
Амплитуда результирующего колебания зависит от величины, называемой разностью хода волн.
Если разность хода равна целому числу волн, то волны приходят в точку синфазно. Складываясь, волны усиливают друг друга и дают колебание с удвоенной амплитудой.
Если разность хода равна нечетному числу полуволн, то волны приходят в точку А в противофазе. В этом случае они гасят друг друга, амплитуда результирующего колебания равна нулю.
В других точках пространства наблюдается частичное усиление или ослабление результирующей волны.
Опыт Юнга
В 1802 г. английский ученый Томас Юнг поставил опыт, в котором наблюдал интерференцию света. Свет из узкой щели S, падал на экран с двумя близко расположенными щелями S1 и S2. Проходя через каждую из щелей, световой пучок расширялся, и на белом экране световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.
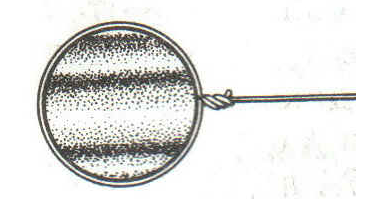
Ход луча в мыльной пленке
На рисунке изображена в разрезе сильно увеличенная по толщине мыльная пленка. Пусть в точке А пленки попадает световая волна. Часть света отражается от этой поверхности, а часть – преломляется, проходит внутрь пленки и отражается от ее поверхности в точке В. Эти два отраженных пучка света имеют одинаковую частоту, поскольку исходят от одного источника. Складываясь, они образуют интерференционную картину.

С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен, рисунки на крыльях некоторых бабочек и жуков и др.
Оптическая разность хода.
Вместо разности фаз
интерферирующих волн удобно ввести в
рассмотрение пропорциональную ей
величину
– оптическую разность хода, которая
отличается множителем
,
где
– длина световой волны.
Изменению
разности фаз на
соответствует изменение разности хода
на
.
В
вакууме оптическая разность хода в
отличие от разности фаз имеет наглядную
и
нтерпретацию.
Если две интерферирующие волны испускаются
одним источником света, то разность
хода – это геометрическая разность длин
путей, по которым два интерферирующих
луча от одной точки источника достигли
одной точки экрана.
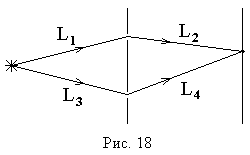
Например,
в оптической схеме опыта Юнга, изображенной
на рис. 18, разность хода для точки P на
экране находится по формуле:
.
В
изотропной среде скорость света в n
раз меньше, чем в вакууме, здесь n
– показатель преломления среды. Частота
света в среде и в вакууме одинакова,
поэтому длина волны в среде в n
раз меньше. В соответствии с соотношением
вместо реального уменьшения длины волны
можно рассматривать неизменную
и соответствующее увеличение длины
пути луча. С этой целью вводится понятие
оптической длины пути, которая в n
раз больше геометрической длины. Далее,
употребляя термин “разность хода”,
всегда будем иметь в виду оптическую
разность хода.
Заменяя
разность фаз интерферирующих волн
оптической разностью хода, получаем
следующее выражение для интенсивности
интерференционной картины:
.
Приемники
света в оптическом диапазоне реагируют
на интенсивность света, а не на
напряженность электрического или
магнитного полей. Поэтому измеряемые
в опыте величины, ширина полос и видность,
также могут быть выражены через
интенсивность, а значит и через оптическую
разность хода. Следовательно, понятие
оптической разности хода позволяет
свести оптическую задачу по интерференции
к геометрической задаче отыскания
разности хода.
Отметим,
что разность хода лучей можно отсчитывать
не только как разность длин путей от
источника до точки наблюдения, но и как
разность длин путей от двух точек любой
поверхности равной фазы волны до точки
наблюдения. При этом, конечно, две точки
на поверхности равной фазы – не произвольные
точки, а должны быть точками, через
которые реально проходят лучи, попадающие
в точку наблюдения. Так на рис. 18
,
поэтому две щели находятся на поверхности
равной фазы, и, следовательно, разность
хода можно найти по упрощенной формуле
.
Этот прием часто используется при
решении задач.
18.1.2.1. Условия максимума и минимума на разность фаз δ
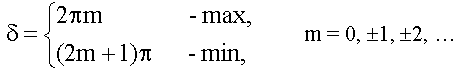
18.1.2.2. Оптическая разность хода
Пусть
для простоты, начальные фазы α1
и α2
интерферирующих волн равны нулю, тогда:
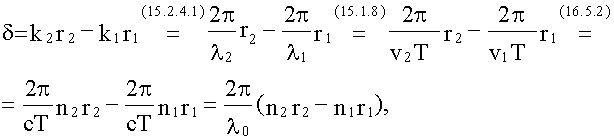
здесь
λ0 = cT
– длина световой волны в вакууме.
Оптической
разностью хода называют величину:
.
Тогда:
.
18.1.2.3. Условия максимума и минимума на оптическую разность хода
Из
(18.1.2.1.)
и (18.1.2.2.):
П
осле
сокращения получим условия на Δ:
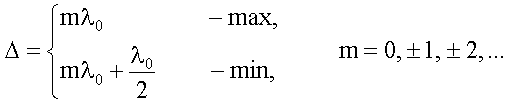
30. Интерференция при отражении от тонких пленок. Пример расчета интерференционной картины для плоскопараллельной пластинки.
Интерференция
– физическое явление, наблюдаемое при
сложении волн (световых, звуковых и т.
п.), усиление волн в одних точках
пространства и ослабление в других (или
сложение двух или более
волн, при котором амплитуда результирующей
волны зависит от разности фаз исходных
волн в данной точке пространства)
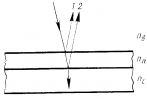
Пусть
на плоскопараллельную прозрачную пленку
(пластинку) с показателем преломления
n и толщиной d под углом
падает плоская монохроматическая волна
(для простоты рассмотрим один луч).
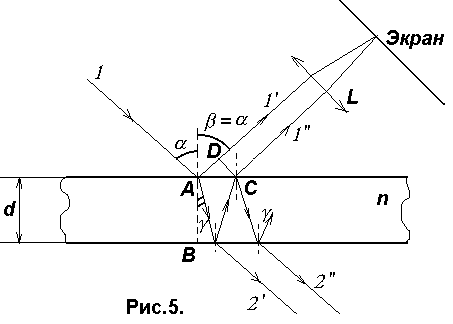
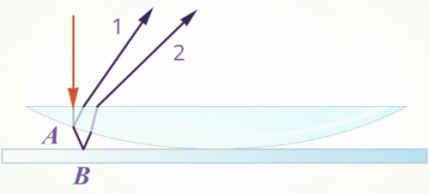
На
поверхности пленки в точке А волна
частично отражается (луч 1- ) и частично
преломляется (луч АВ). В точке В волна
также частично отражается (луч ВС) и
частично преломляется (луч 2- ). То же
самое происходит в точке С.
Причем
преломленная волна (луч 1″ ) накладывается
на волну непосредственно отраженную
от верхней поверхности (луч 1- ). Эти две
волны когерентны, если оптическая
разность хода
меньше
длины когерентности lког, и в этом
случае они интерферируют.
Оптическая
разность хода двух волн =(AB+BC)n-(AD-/2),
где
/2 – потеря полуволны
при отражении луча 1- в точке А. Используя
закон преломления n1sin
= n2sin и учитывая,
что в рассматриваемом случае n1=1,
n2=n, можно показать, что
.(17)
В
точке наблюдения на экране будет
максимум, если m
и минимум, если (2m+1)/2[см.(15),(16)].
Возможность
уменьшения вредного отражения света
вследствие интерференции в тонких
пленках широко используется в современных
оптических приборах. Для этого на
передние поверхности линз, призм наносят
тонкие пленки с показателем преломления
n=
и толщиной d, которая определяется из
условия минимума при интерференции
волн, отраженных от границ раздела сред
с n1 и n и n и n2
2dn=(2m+1)/2,
m=0,1,2-(18)
Минимальная
толщина пленки соответствует m=0
d=/(4n)
Такая
оптика получила название просветленной
оптики.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для всех волн характерны явления интерференции и дифракции. Если свет — это волна, то для него также должны быть присущи эти явления. Так рассуждали ученые, которые считали, что свет имеет волновую природу. Первым привел экспериментальные доказательства интерференции и дифракции света Томас Юнг в 1801 году.
Это интересно! Явление интерференции света было описано и объяснено в 1801 году, но само понятие «интерференция света» было введено немного позже — в 1803 году.
Интерференция механических волн
Чтобы лучше понять явление интерференции, сначала объясним его на примере механических волн, за которыми удобней наблюдать. Часто случается, что в среде одновременно распространяется несколько различных волн. К примеру, когда в комнате может одновременно находиться несколько источников звука. Что же происходит, когда волны пересекают друг друга? Объясним это на примере волн, образуемых на поверхности воды.
Если бросить в воду два камешка, образуются две круговые волны. Если наблюдать за их распространением, мы увидим, что каждая волна проходит сквозь другую. Причем она ведет себя так, как будто другой волны не существовало. Точно так же любое количество звуковых волн может одновременно распространяться в воздухе. И они не будут друг другу мешать. Множество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, которые улавливаются нами одновременно. При этом звуки не сливаются в шум: наши органы слуха способны легко отличить один звук от другого.
Теперь рассмотрим более подробно процесс, когда волны накладываются одна на другую. Для этого будем наблюдать волны на поверхности воды от двух брошенных в воду камней. При этом мы заметим, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если два гребня двух волн встречаются в одном месте, то в этом месте возмущение поверхности воды становится более сильным. Если же гребень одной волны встречается с впадиной другой, то поверхность воды в этом месте остается спокойной. Получается, что в каждой точке среды колебания, вызванные двумя волнами, складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.
Интерференция — сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды.
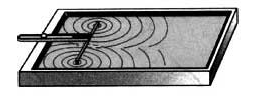
Чтобы выяснить, при каких условиях наблюдается интерференция волн, одновременно возбудим две круговые волны в ванночке с помощью двух шариков, прикрепленных к стержням, колеблющимся по гармоническому закону.
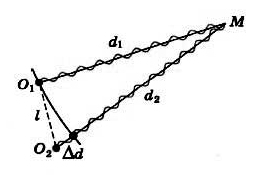
Теперь представим явление интерференции схематически. В любой точке М на поверхности воды будут складываться колебания, вызванные двумя волнами от источников O1 и O2 (см. рисунок ниже). Амплитуды колебаний, вызванных в точке М обеими волнами, будут различаться, если волны проходят различные пути d1 и d2. Но если расстояние l между источниками много меньше этих путей, то обе амплитуды можно считать приближенно одинаковыми.
Результат сложения волн, приходящих в точку М зависит от разности фаз между ними. Пройдя различные расстояния d1 и d2, волны имеют разность хода, определяемую формулой:
Δd = d2 − d1
Когда разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой на один период. Так как за период волна проходит путь, равный ее длине волны, то в точке встречи двух волн фазы совпадают. Если в этой точке волны имеют гребни, то совпадают гребни, если впадины — совпадают впадины.
Условие минимумов и максимумов
Когда гребни волн на поверхности волны складываются в одной точке, их амплитуда резко возрастает. В этом случае говорят, что в этой точке образуется интерференционный максимум. Когда впадины волн на поверхности волны складываются в одной точке, их амплитуда резко уменьшается. В этом случае говорят, что в этой точке образуется интерференционный минимум. Интерференционные минимумы и максимумы образуются при соблюдении определенных условий.
Если разность хода волн равна нечетному числу полуволн, то в точке наложения этих волн образуется интерференционный минимум. Амплитуда колебаний в данной точке минимальна.
Δd=(2k+1)λ2
k = 0, 1, 2, … .
Если разность хода волн равна целому числу волн, то в точке наложения этих волн образуется интерференционный максимум. Амплитуда колебаний в данной точке максимальна.
Δd=kλ
Если разность хода ∆d принимает промежуточное значение между λ и λ/2, амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важной примечательностью является то, что амплитуда колебаний в любой точке с течением времени не меняется. Поэтому на поверхности воды возникает определенное, постоянное во времени распределение амплитуд колебаний, которое называют интерференционной картиной.
Для формирования устойчивой интерференционной картины важно, чтобы источники волн имели одинаковую частоту, и разность фаз их колебаний не менялась с течением времени. Такие источники волн называют когерентными.
Когерентные волны — это волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
Только когерентные волны при сложении формируют устойчивую интерференционную картину. Если же источники волн некогерентные, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет с течением времени изменяться. Поэтому амплитуда результирующих колебаний также будет непрерывно изменяться. В результате максимумы и минимумы в пространстве будут иметь неопределенное положение. Поэтому интерференционная картина получается размытой.
Распределение энергии при интерференции
Любая волна переносит энергию без переноса вещества. Но что же с этой энергией происходит при интерференции волн? Если волны встречаются друг с другом, энергия никуда не исчезает и не превращается в другие формы энергии. Она лишь перераспределяется таким образом, что в минимумах он не поступает совсем, поскольку концентрируется в максимумах.
Интерференция света
Ели свет — это поток волн, то должно наблюдаться явление интерференции. Однако получить интерференционную картину, при которой чередуются минимумы и максимумы с помощью двух независимых источников света (к примеру, двух ламп), невозможно. Включение второй лампы лишь увеличивает освещенность поверхности, но не создает картины из минимумов и максимумов. Это объясняется несогласованностью волн друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные, то есть когерентные световые волны. Они должны иметь одинаковые длины волн и постоянную во времени разность фаз в любой точке пространства.
Однако наблюдать интерференцию света все же можно. Вы ее наблюдали, когда пускали мыльные пузыри или рассматривали пленку нефти на поверхности воды.
Томас Юнг — первый из ученых, который предложил объяснить изменение цветов тонких пленок сложением волн. Согласно его предположению, одна волна отражается от наружной поверхности плёнки, а другая — от внутренней. При этом возникает явление, называемой интерференцией световых волн.
Усиление света происходит в том случае, если преломлённая волна запаздывает по сравнению с отражённой волной на целое число длин волн. Здесь действует условие максимумов, о котором мы говорили выше:
Δd=kλ
Если вторая волна запаздывает по сравнению с первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света. Здесь действует условие минимумов, о котором мы также уже говорили:
Δd=(2k+1)λ2
Четкая интерференционная картина получается потому, что волны, отраженные от внутренней и внешней оболочки тонкой пленки, являются когерентными. Когерентность этих волн объясняется тем, что они являются частями одного и того же светового луча.
Юнг сделал вывод, что многообразие цветов на мыльной пленке связано с разницей в длине волны. Если плёнка имеет неоднородную толщину, то при освещении её белым светом появляются различные цвета.
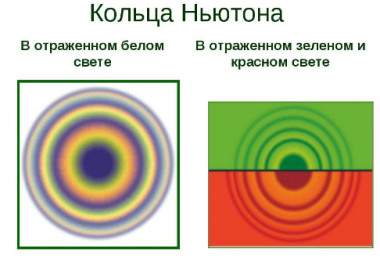
Простую интерференционную картину также можно получить, если положить на стеклянную поверхность плоско-выпуклую линзу, сферическая поверхность которой имеет большой радиус кривизны. Интерференционная картина, полученная таким способом, носит название колец Ньютона.
Исаак Ньютон исследовал интерференционную картину, получаемую в тонкой прослойке воздуха между стеклом и линзой, не только в белом свете, но и при освещении линзы монохроматическими лучами. Так он установил, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному. Так, красные кольца имеют максимальный радиус. Расстояние между соседними кольцами уменьшаются с увеличением их радиусов.
Ньютону удалось получить кольца, но их появление он объяснить не смог. Но это удалось сделать Юнгу. Проведенный им опыт показал, что волна определённой длины падает на плосковыпуклую линзу почти перпендикулярно. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе сред стекло-воздух, а волна 2 — в результате отражения от пластины на границе сред воздуха- стекло.
Если вторая волна запаздывает по сравнению с первой на целое число длин волн, то при сложении волны усиливают друг друга. Если вторая волна запаздывает по сравнению с первой на нечётное число полуволн, то колебания в точке сложения будут совпадать в противоположных фазах. При этом волны погасят друг друга.
В результате проделанного эксперимента Юнг смог получить картину, которая состоит из чередующихся параллельных полос (темных и светлых)
Интерференция света – это явление сложения двух и более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующегося максимумом и минимумом интенсивности.
Это интересно! Измеряя радиусы колец Ньютона, можно вычислить длины волн. В ходе измерений было установлено, что для красного света λкр = 8∙10–7 м, а для фиолетового — λa = 4∙ 10–7 м.
Пример №1. Будет ли наблюдаться интерференционная картина при освещении мыльной пленки монохроматическим светом? Какой она будет?
Поскольку источник света один и тот же, то отраженные от обеих поверхностей мыльной пленки волны будут когерентными. Поэтому интерференционная картина наблюдаться будет. Она примет вид чередующихся цветных и темных полос. Цвет полос определяется цветом световой волны, который зависит от ее длины волны.
Задание EF17533
На поверхность тонкой прозрачной плёнки падает по нормали пучок белого света. В отражённом свете плёнка окрашена в зелёный цвет. При использовании плёнки такой же толщины, но с несколько меньшим показателем преломления, её окраска будет
Ответ:
а) только зелёной
б) находиться ближе к красной области спектра
в) находиться ближе к синей области спектра
г) только полностью чёрной
Алгоритм решения
1.Описать наблюдаемое явление.
2.Записать условие наблюдения интерференционного максимума.
3.Выполнить решение в общем виде.
4.Установить, в какой цвет будет окрашена пленка.
Решение
При освещении тонкой плёнки можно наблюдать интерференцию световых волн, отражённых от передней и задней поверхностей плёнки. Условием интерференционного максимума для излучения с длиной волны λ является:
kλ=2dn+Δ
Δ — либо 0, либо λ2 (это зависит от соотношения показателей преломления на границе двуз сред). Тогда при малом изменении значения показателя преломления в меньшую сторону и сохранении порядка k (как в нашем случае и есть), длина волны света будет уменьшаться. Это значит, что из зеленой части спектра она сдвинется в синюю часть.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
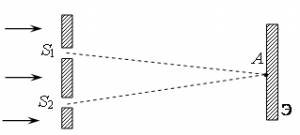
Задание EF17707
Ответ:
а) S2А – S1А = 2k⋅λ/2, где k– любое целое число
б) S2А – S1А = (2k + 1) ⋅λ/2, где k– любое целое число
в) S2А – S1А = λ/3k, где k– любое целое число
г) S2А – S1А = λ/(2k+1), где k– любое целое число
Алгоритм решения
1.Записать условие наблюдения интерференционного минимума.
2.Выбрать выражение, удовлетворяющее этому условию.
Решение
В точке А будет наблюдаться темное пятно, если волны, достигающие этой точки, будут гасить друг друга. Это возможно при соблюдении условия минимума:
Δd=(2k+1)λ2
Разность хода в данном случае равна:
Δd=S2A−S1A
Следовательно:
S2A−S1A=(2k+1)λ2
где k — целое число.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17972
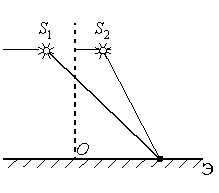
Ответ:
а) каждое своей лампочкой накаливания
б) каждое своей горящей свечой
в) одно зелёным лазером, другое красным
г) светом одной лампочки накаливания
Алгоритм решения
- Записать условие наблюдения интерференционной картины.
- Проанализировать источники и выбрать подходящий под условие.
Решение
Четкая интерференционная картина наблюдается только при освещении щелей когерентными лучами света, имеющими постоянную разность фаз. Когерентные — значит волнами одной частоты. Поэтому лазер зеленый и красный сразу не подходят — они имеют разные частоты.
Одна и та же частота и постоянная разность фаз будет только при условии, что щели освещаются одним источником света. В данном случае — одной и той же лампой накаливания.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.6k
Интерференция света
Явление интерференции свидетельствует о том, что свет — это волна.
Интерференцией световых волн называется сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.
Условия интерференции
Волны должны быть когерентны. Когерентность – согласованность. В простейшем случае когерентными являются волны одинаковой длины, между которыми существует постоянная разность фаз.
Все источники света, кроме лазера, некогерентны, однако Т. Юнг впервые пронаблюдал (1802) явление интерференции, разделив волну на две с помощью двойной щели.
Свет от точечного монохроматического источника S падал на два небольших отверстия на экране. Эти отверстия действуют как два когерентных источника света S1 и S2.
Волны от них интерферируют в области перекрытия, проходя разные пути: ℓ1 и ℓ2.
На экране наблюдается чередование светлых и темных полос.
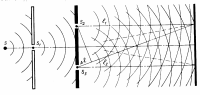
Условие максимума.
Пусть разность хода между двумя точками ,
тогда условие максимума:
т. е. на разности хода волн укладывается четное число полуволн (k= 1, 2, 3, …).
или
Условие минимума
Пусть разность хода между двумя точками ,
тогда условие минимума: ,
т. е. на разности хода волн укладывается нечетное число полуволн (k= 1, 2, 3, …).
Интерференция света в тонких пленках
Различные цвета тонких пленок — результат интерференции двух волн, отражающихся от нижней и верхней поверхностей пленки. При отражении от верхней поверхности пленки происходит потеря полуволны. Следовательно, оптическая разность хода .
Тогда условие максимального усиления интерферирующих лучей в отраженном свете следующее: .
Если потерю полуволны не учитывать, то .
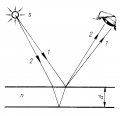
Кольца Ньютона
Интерференционная картина в тонкой прослойке воздуха между стеклянными пластинами — кольца Ньютона.
Волна 1 — результат отражения ее от точки А (граница стекло —воздух). Волна 2 — отражение от плоской пластины (точка В, граница воздух — стекло). Волны когерентны: возникает интерференционная картина в прослойке воздуха между точками А и В в виде-концентрических колец. Зная радиусы колец, можно вычислить длину волны, используя формулу , где r – радиус кольца, R — радиус кривизны выпуклой поверхности линзы.
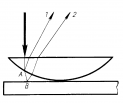
Использование интерференции в технике
Проверка качества обработки поверхности до одной десятой длины волны. Несовершенство обработки определяют но искривлению интерференционных полос, образующихся при отражении света от проверяемой поверхности. Интерферометры служат для точного измерения показателя преломления газов и других веществ, длин световых волн.
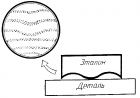
Просветление оптики. Объективы фотоаппаратов и кинопроекторов, перископы подводных лодок и другие оптические устройства состоят из большого числа оптических стекол, линз, призм. Каждая отполированная поверхность стекла отражает около 5% падающего на нее света. Чтобы уменьшить долю отражаемой энергии, используется явление интерференции света.
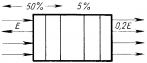
На поверхность оптического стекла наносят тонкую пленку. Для того чтобы волны 1 и 2 ослабляли друг друга, должно выполняться условие минимума. В отраженном свете разность хода волн равна: . Потеря полуволны происходит при отражении как от пленки, так и от стекла (показатель преломления стекла больше, чем пленки), поэтому, эту потерю можно не учитывать. Следовательно,
, где n – показатель преломления пленки; h — толщина пленки. Минимальная толщина пленки будет при k=0. Поэтому
. При равенстве амплитуд гашение света будет полным. Толщину пленки подбирают так, чтобы полное гашение при нормальном падении имело место для длин волн средней части спектра (для зеленого цвета):
.
Чтобы рассчитать толщину пленки в этой формуле необходимо взять длину волны и показатель преломления зеленого света.
Лучи красного и фиолетового цвета ослабляются незначительно.поэтому объективы оптических приборов в отраженном свете имеют сиреневые оттенки
Интерференция волн.
-
Сложение колебаний.
-
Когерентные источники.
-
Условие максимума и минимума.
-
Интерференционная картина.
-
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: интерференция света.
В предыдущем листке, посвящённом принципу Гюйгенса, мы говорили о том, что общая картина волнового процесса создаётся наложением вторичных волн. Но что это значит – “наложением”? В чём состоит конкретный физический смысл наложения волн? Что вообще происходит, когда в пространстве одновременно распространяются несколько волн? Этим вопросам и посвящён данный листок.
к оглавлению ▴
Сложение колебаний.
Сейчас мы будем рассматривать взаимодействие двух волн. Природа волновых процессов роли не играет – это могут быть механические волны в упругой среде или электромагнитные волны (в частности, свет) в прозрачной среде или в вакууме.
Опыт показывает, что волны складываются друг с другом в следующем смысле.
Принцип суперпозиции. Если две волны накладываются друг на друга в определённой области пространства, то они порождают новый волновой процесс. При этом значение колеблющейся величины в любой точке данной области равно сумме соответствующих колеблющихся величин в каждой из волн по отдельности.
Например, при наложении двух механических волн перемещение частицы упругой среды равно сумме перемещений, создаваемых в отдельности каждой волной. При наложении двух электромагнитных волн напряжённость электрического поля в данной точке равна сумме напряжённостей в каждой волне (и то же самое для индукции магнитного поля).
Разумеется, принцип суперпозиции справедлив не только для двух, но и вообще для любого количества накладывающихся волн. Результирующее колебание в данной точке всегда равно сумме колебаний, создаваемых каждой волной по отдельности.
Мы ограничимся рассмотрением наложения двух волн одинаковой амплитуды и частоты. Этот случай наиболее часто встречается в физике и, в частности, в оптике.
Оказывается, на амплитуду результирующего колебания сильно влияет разность фаз складывающихся колебаний. В зависимости от разности фаз в данной точке пространства две волны могут как усиливать друг друга, так и полностью гасить!
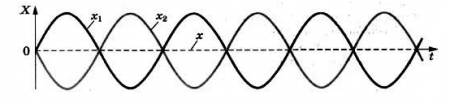
Предположим, например, что в некоторой точке фазы колебаний в накладывающихся волнах совпадают (рис. 1).
 |
| Рис. 1. Волны в фазе: усиление колебаний |
Мы видим, что максимумы красной волны приходятся в точности на максимумы синей волны, минимумы красной волны – на минимумы синей (левая часть рис. 1). Складываясь в фазе, красная и синяя волны усиливают друг друга, порождая колебания удвоенной амплитуды (справа на рис. 1).
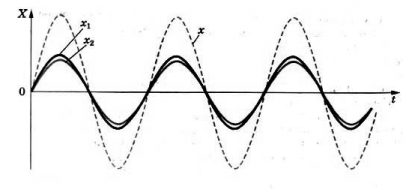
Теперь сдвинем синюю синусоиду относительно красной на половину длины волны. Тогда максимумы синей волны будут совпадать с минимумами красной и наоборот – минимумы синей волны совпадут с максимумами красной (рис. 2, слева).
 |
| Рис. 2. Волны в противофазе: гашение колебаний |
Колебания, создаваемые этими волнами, будут происходить, как говорят, в противофазе – разность фаз колебаний станет равна . Результирующее колебание окажется равным нулю, т. е. красная и синяя волны попросту уничтожат друг друга (рис. 2, справа).
к оглавлению ▴
Когерентные источники.
Пусть имеются два точечных источника, создающие волны в окружающем пространстве. Мы полагаем, что эти источники согласованы друг с другом в следующем смысле.
Когерентность. Два источника называются когерентными, если они имеют одинаковую частоту и постоянную, не зависящую от времени разность фаз. Волны, возбуждаемые такими источниками, также называются когерентными.
Итак, рассматриваем два когерентных источника и
. Для простоты считаем, что источники излучают волны одинаковой амплитуды, а разность фаз между источниками равна нулю. В общем, эти источники являются “точными копиями” друг друга (в оптике, например, источник
служит изображением источника
в какой-либо оптической системе).
Наложение волн, излучённых данными источниками, наблюдается в некоторой точке . Вообще говоря, амплитуды этих волн в точке
не будут равны друг другу – ведь, как мы помним, амплитуда сферической волны обратно пропорциональна расстоянию до источника, и при разных расстояниях
и
амплитуды пришедших волн окажутся различными. Но во многих случаях точка
расположена достаточно далеко от источников – на расстоянии гораздо большем, чем расстояние между самими источниками. В такой ситуации различие в расстояниях
и
не приводит к существенному отличию в амплитудах приходящих волн. Следовательно, мы можем считать, что амплитуды волн в точке
также совпадают.
к оглавлению ▴
Условие максимума и минимума.
Однако величина , называемая разностью хода, имеет важнейшее значение. От неё самым решительным образом зависит то, какой результат сложения приходящих волн мы увидим в точке
.
 |
| Рис. 3. Усиление колебаний в точке P |
В ситуации на рис. 3 разность хода равна длине волны . Действительно, на отрезке
укладываются три полных волны, а на отрезке
– четыре (это, конечно, лишь иллюстрация; в оптике, например, длина таких отрезков составляет порядка миллиона длин волн). Легко видеть, что волны в точке
складываются в фазе и создают колебания удвоенной амплитуды – наблюдается, как говорят, интерференционный максимум.
Ясно, что аналогичная ситуация возникнет при разности хода, равной не только длине волны, но и любому целому числу длин волн.
Условие максимума. При наложении когерентных волн колебания в данной точке будут иметь максимальную амплитуду, если разность хода равна целому числу длин волн:
(1)
Теперь посмотрим на рис. 4. На отрезке укладываются две с половиной волны, а на отрезке
-три волны. Разность хода составляет половину длины волны (d=lambda /2[/math]).
 |
| Рис. 4. Гашение колебаний в точке P |
Теперь нетрудно видеть, что волны в точке складываются в противофазе и гасят друг друга – наблюдается интерференционный минимум. То же самое будет, если разность хода окажется равна половине длины волны плюс любое целое число длин волн.
Условие минимума.
Когерентные волны, складываясь, гасят друг друга, если разность хода равна полуцелому числу длин волн:
(2)
Равенство (2) можно переписать следующим образом:
.
Поэтому условие минимума формулируют ещё так: разность хода должна быть равна нечётному числу длин полуволн.
к оглавлению ▴
Интерференционная картина.
А что, если разность хода принимает какое-то иное значение, не равное целому или полуцелому числу длин волн? Тогда волны, приходящие в данную точку, создают в ней колебания с некоторой промежуточной амплитудой, расположенной между нулём и удвоенным значением 2A амплитуды одной волны. Эта промежуточная амплитуда может принимать все значения от 0 до 2A по мере того, как разность хода меняется от полуцелого до целого числа длин волн.
Таким образом, в той области пространства, где происходит наложение волн когерентных источников и
, наблюдается устойчивая интерференционная картина – фиксированное не зависящее от времени распределение амплитуд колебаний. А именно, в каждой точке
данной области амплитуда колебаний принимает своё значение, определяемое разностью хода
приходящих сюда волн, и это значение амплитуды не меняется со временем.
Такая стационарность интерференционной картины обеспечивается когерентностью источников. Если, например, разность фаз источников будет постоянно меняться, то никакой устойчивой интерференционной картины уже не возникнет.
Теперь, наконец, мы можем сказать, что такое интерференция.
Интерференция – это взаимодействие волн, в результате которого возникает устойчивая интерференционная картина, то есть не зависящее от времени распределение амплитуд результирующих колебаний в точках области, где волны накладываются друг на друга.
Если волны, перекрываясь, образуют устойчивую интерференционную картину, то говорят попросту, что волны интерферируют. Как мы выяснили выше, интерферировать могут только когерентные волны. Когда, например, разговаривают два человека, то мы не замечаем вокруг них чередований максимумов и минимумов громкости; интерференции нет, поскольку в данном случае источники некогерентны.
На первый взгляд может показаться, явление интерференции противоречит закону сохранения энергии – например, куда девается энергия, когда волны полностью гасят друг друга? Но никакого нарушения закона сохранения энергии, конечно же, нет: энергия просто перераспределяется между различными участками интерференционной картины. Наибольшее количество энергии концентрируется в интерференционных максимумах, а в точки интерференционных минимумов энергия не поступает совсем.
На рис. 5 показана интерференционная картина, созданная наложением волн двух точечных источников и
. Картина построена в предположении, что область наблюдения интерференции находится достаточно далеко от источников. Пунктиром отмечена ось симметрии интерференционной картины.
 |
| Рис. 5. Интерференция волн двух точечных источников |
Цвета точек интерференционной картины на этом рисунке меняются от чёрного до белого через промежуточные оттенки серого. Чёрный цвет – интерференционные минимумы, белый цвет – интерференционные максимумы; серый цвет – промежуточное значение амплитуды, и чем больше амплитуда в данной точке, тем светлее сама точка.
Обратите внимание на прямую белую полосу, которая идёт вдоль оси симметрии картины. Здесь расположены так называемые центральные максимумы. Действительно, любая точка данной оси равноудалена от источников (разность хода равна нулю), так что в этой точке будет наблюдаться является интерференционный максимум.
Остальные белые полосы и все чёрные полосы слегка искривлены; можно показать, что они являются ветвями гипербол. Однако в области, расположенной на большом расстоянии от источников, кривизна белых и чёрных полос мало заметна, и выглядят эти полосы почти прямыми.
к оглавлению ▴
Интерференционный опыт, изображённый на рис. 5, вместе с соответствующим методом расчёта интерференционной картины называется схемой Юнга. Эта схема лежит в основе знаменитного
опыта Юнга (речь о котором пойдёт в теме Дифракция света). Многие эксперименты по интерференции света так или иначе сводятся к схеме Юнга.
В оптике интерференционную картину обычно наблюдают на экране. Давайте ещё раз посмотрим на рис. 5 и представим себе экран, поставленный перпендикулярно пунктирной оси.
На этом экране мы увидим чередование светлых и тёмных интерференционных полос.
На рис. 6 синусоида показывает распределение освещённости вдоль экрана. В точке O, расположенной на оси симметрии, находится центральный максимум. Первый максимум в верхней части экрана, соседний с центральным, находится в точке A. Выше идут второй, третий (и такдалее) максимумы.
 |
| Рис. 6. Интерференционная картина на экране |
Расстояние , равное расстоянию между любыми двумя соседними максимумами или минимумами, называется шириной интерференционной полосы. Сейчас мы займёмся нахождением этой величины.
Пусть источники находятся на расстоянии друг от друга, а экран расположен на расстоянии
от источников (рис. 7 ). Экран заменён осью
; начало отсчёта
, как и выше, отвечает центральному максимуму.
 |
| Рис. 7. Вычисление координат максимумов |
Точки и
служат проекциями точек
и
на ось
и расположены симметрично относительно точки
. Имеем:
.
Точка наблюдения может находиться на оси
(на экране) где угодно. Координату точки
мы обозначим
. Нас интересует, при каких значениях
в точке
будет наблюдаться интерференционный максимум.
Волна, излучённая источником , проходит расстояние:
. (3)
Теперь вспомним, что расстояние между источниками много меньше расстояния от источников до экрана: . Кроме того, в подобных интерференционных опытах координата
точки наблюдения также гораздо меньше
. Это означает, что второе слагаемое под корнем в выражении (3) много меньше единицы:
.
Раз так, можно использовать приближённую формулу:
(4)
Применяя её к выражению (4), получим:
(5)
Точно так же вычисляем расстояние, которое проходит волна от источника до точки наблюдения:
. (6)
Применяя к выражению (6) приближённую формулу (4), получаем:
. (7)
Вычитая выражения (7) и (5), находим разность хода:
. (8)
Пусть – длина волны, излучаемой источниками. Согласно условию (1), в точке
будет наблюдаться интерференционный максимум, если разность хода равна целому числу длин волн:
Отсюда получаем координаты максимумов в верхней части экрана (в нижней части максимумы идут симметрично):
При получаем, разумеется,
(центральный максимум). Первый максимум рядом с центральным соответствует значению
и имеет координату
.Такой же будет и ширина интерференционной полосы:
.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Интерференция волн.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
07.05.2023