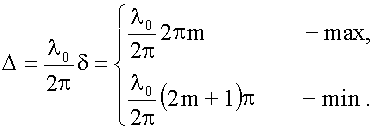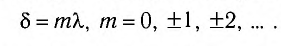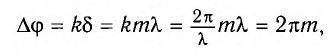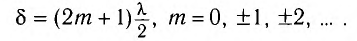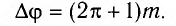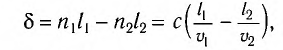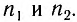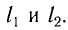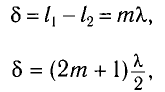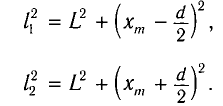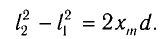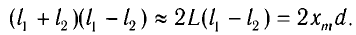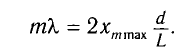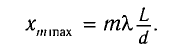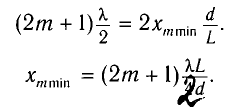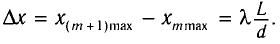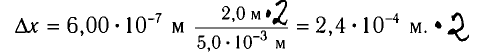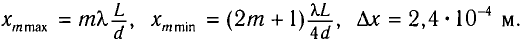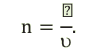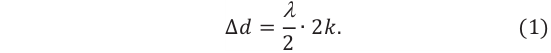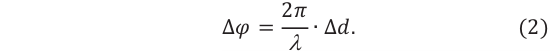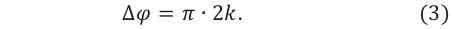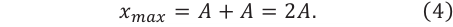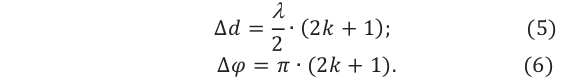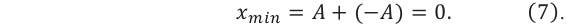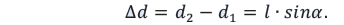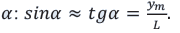Оптическая разность хода.
Вместо разности фаз
интерферирующих волн удобно ввести в
рассмотрение пропорциональную ей
величину
– оптическую разность хода, которая
отличается множителем
,
где
– длина световой волны.
Изменению
разности фаз на
соответствует изменение разности хода
на
.
В
вакууме оптическая разность хода в
отличие от разности фаз имеет наглядную
и
нтерпретацию.
Если две интерферирующие волны испускаются
одним источником света, то разность
хода – это геометрическая разность длин
путей, по которым два интерферирующих
луча от одной точки источника достигли
одной точки экрана.
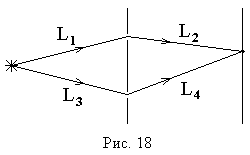
Например,
в оптической схеме опыта Юнга, изображенной
на рис. 18, разность хода для точки P на
экране находится по формуле:
.
В
изотропной среде скорость света в n
раз меньше, чем в вакууме, здесь n
– показатель преломления среды. Частота
света в среде и в вакууме одинакова,
поэтому длина волны в среде в n
раз меньше. В соответствии с соотношением
вместо реального уменьшения длины волны
можно рассматривать неизменную
и соответствующее увеличение длины
пути луча. С этой целью вводится понятие
оптической длины пути, которая в n
раз больше геометрической длины. Далее,
употребляя термин “разность хода”,
всегда будем иметь в виду оптическую
разность хода.
Заменяя
разность фаз интерферирующих волн
оптической разностью хода, получаем
следующее выражение для интенсивности
интерференционной картины:
.
Приемники
света в оптическом диапазоне реагируют
на интенсивность света, а не на
напряженность электрического или
магнитного полей. Поэтому измеряемые
в опыте величины, ширина полос и видность,
также могут быть выражены через
интенсивность, а значит и через оптическую
разность хода. Следовательно, понятие
оптической разности хода позволяет
свести оптическую задачу по интерференции
к геометрической задаче отыскания
разности хода.
Отметим,
что разность хода лучей можно отсчитывать
не только как разность длин путей от
источника до точки наблюдения, но и как
разность длин путей от двух точек любой
поверхности равной фазы волны до точки
наблюдения. При этом, конечно, две точки
на поверхности равной фазы – не произвольные
точки, а должны быть точками, через
которые реально проходят лучи, попадающие
в точку наблюдения. Так на рис. 18
,
поэтому две щели находятся на поверхности
равной фазы, и, следовательно, разность
хода можно найти по упрощенной формуле
.
Этот прием часто используется при
решении задач.
18.1.2.1. Условия максимума и минимума на разность фаз δ
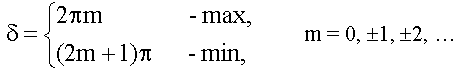
18.1.2.2. Оптическая разность хода
Пусть
для простоты, начальные фазы α1
и α2
интерферирующих волн равны нулю, тогда:
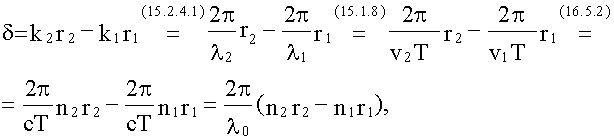
здесь
λ0 = cT
– длина световой волны в вакууме.
Оптической
разностью хода называют величину:
.
Тогда:
.
18.1.2.3. Условия максимума и минимума на оптическую разность хода
Из
(18.1.2.1.)
и (18.1.2.2.):
П
осле
сокращения получим условия на Δ:
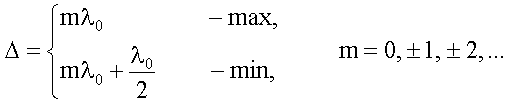
30. Интерференция при отражении от тонких пленок. Пример расчета интерференционной картины для плоскопараллельной пластинки.
Интерференция
– физическое явление, наблюдаемое при
сложении волн (световых, звуковых и т.
п.), усиление волн в одних точках
пространства и ослабление в других (или
сложение двух или более
волн, при котором амплитуда результирующей
волны зависит от разности фаз исходных
волн в данной точке пространства)
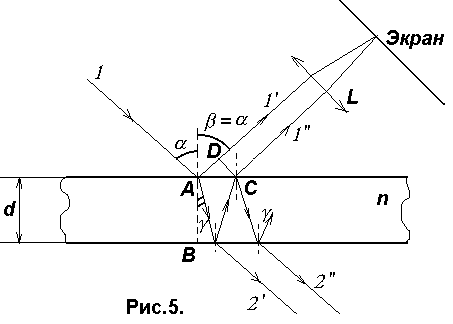
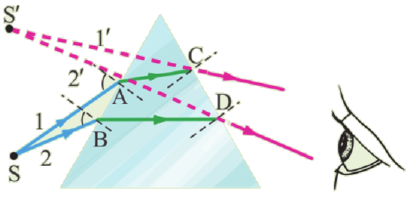
Пусть
на плоскопараллельную прозрачную пленку
(пластинку) с показателем преломления
n и толщиной d под углом
падает плоская монохроматическая волна
(для простоты рассмотрим один луч).
На
поверхности пленки в точке А волна
частично отражается (луч 1- ) и частично
преломляется (луч АВ). В точке В волна
также частично отражается (луч ВС) и
частично преломляется (луч 2- ). То же
самое происходит в точке С.
Причем
преломленная волна (луч 1″ ) накладывается
на волну непосредственно отраженную
от верхней поверхности (луч 1- ). Эти две
волны когерентны, если оптическая
разность хода
меньше
длины когерентности lког, и в этом
случае они интерферируют.
Оптическая
разность хода двух волн =(AB+BC)n-(AD-/2),
где
/2 – потеря полуволны
при отражении луча 1- в точке А. Используя
закон преломления n1sin
= n2sin и учитывая,
что в рассматриваемом случае n1=1,
n2=n, можно показать, что
.(17)
В
точке наблюдения на экране будет
максимум, если m
и минимум, если (2m+1)/2[см.(15),(16)].
Возможность
уменьшения вредного отражения света
вследствие интерференции в тонких
пленках широко используется в современных
оптических приборах. Для этого на
передние поверхности линз, призм наносят
тонкие пленки с показателем преломления
n=
и толщиной d, которая определяется из
условия минимума при интерференции
волн, отраженных от границ раздела сред
с n1 и n и n и n2
2dn=(2m+1)/2,
m=0,1,2-(18)
Минимальная
толщина пленки соответствует m=0
d=/(4n)
Такая
оптика получила название просветленной
оптики.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 сентября 2015 года; проверки требуют 5 правок.
Оптическая длина пути между двумя точками среды — расстояние, на которое свет (оптическое излучение) распространился бы в вакууме за время его прохождения между этими точками[1].
Оптическая длина пути 



В случае неоднородной среды путь, пройденный светом, необходимо предварительно разбить на столь малые элементарные промежутки 
Соответственно, полная оптическая длина пути, пройденного светом между некоторыми точками А и В среды, будет результатом интегрирования по всей траектории луча света:
Оптическая разность хода[править | править код]
Если два световых луча имеют общие начальную и конечные точки, то разность оптических длин путей таких лучей называют оптической разностью хода[2][3].
Примечания[править | править код]
- ↑ Оптическая длина пути // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 431. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Сивухин Д. В. Общий курс физики. — 3-е изд., стереот. — М.: Физматлит, МФТИ, 2005. — Т. IV. Оптика. — С. 205. — 792 с. — ISBN 5-9221-0228-1.
- ↑ ГОСТ 7601-78. Физическая оптика. Термины, буквенные обозначения и определения основных величин. Дата обращения: 19 сентября 2015. Архивировано 30 ноября 2021 года.
Волновая оптика: оптическая разность хода
В задачах, представляемых вашему вниманию, появляются призмы и плоскопараллельные пластинки, необходимо определить оптическую разность хода, а также мы начинаем рассмотрение интерференции света.
Задача 1.
Найти разность фаз в двух точках светового луча, если расстояние между ними
;
, где
-целое число.
Если расстояние между точками – целое число длин волн, то разность фаз будет равна
Во втором случае
Ответ: ,
.
Задача 2.
На пути одного из параллельных световых лучей поместили, нормально ему, плоскопараллельную стеклянную пластинку толщиной мм. Какую оптическую разность хода лучей вносит пластинка?
Оптическая разность хода определяется выражением , где
– показатель преломления пластинки,
– показатель преломления воздуха.
– толщина пластинки, так как в данном случае лучи преодолевают одно и то же расстояние.
Ответ: м.
К задаче 3
Задача 3.
Два параллельных монохроматических луча падают на стеклянную призму () и выходят из нее. Расстояние между падающими лучами
см. Преломляющий угол призмы
. Определить разность хода лучей при выходе из призмы.
Рассмотрим треугольники и
. Они подобны, поэтому можем записать отношение сходственных сторон:
В задаче известен преломляющий угол призмы. Его тангенс равен
Перепишем (1), воспользовавшись свойством пропорции:
Тогда
Теперь определяем разность хода:
Ответ: .
Задача 4.
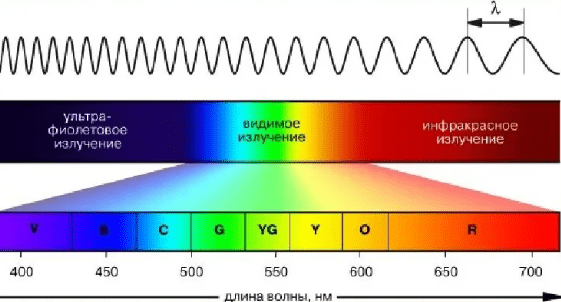
Два когерентных световых луча достигают некоторой точки с разностью хода мкм. Что произойдет в этой точке усиление или ослабление света – если свет: a) красного цвета (
нм); б) желтого цвета (
нм); в) фиолетового цвета (
нм)?
Усиление света происходит, если выполняется условие – в разность хода укладывается четное число полуволн:
Определим количество полуволн в разности хода для света каждого цвета:
В первом и втором случае число полуволн нечетно, следовательно, произойдет ослабление света. В последнем случае (число полуволн четно) свет усилится.
Задача 5.
Оптическая разность хода волн от двух когерентных источников в некоторой точке пространства мкм. Каков будет результат интерференции в этой точке, если длина волны будет: а) (
нм); б) (
нм)?
Определим количество полуволн в разности хода для каждой длины волны:
В первом случае число полуволн нечетно, следовательно, произойдет ослабление света. Во втором случае (число полуволн четно) свет усилится.
Содержание:
Интерференция света:
Фаза — аргумент периодической функции, определяющий значение физической величины в любой момент времени t. Она определяет состояние колебательной системы (координаты, скорости, ускорения) в любой момент времени при заданной амплитуде. Монохроматической волной называется электромагнитное излучение постоянной частоты.
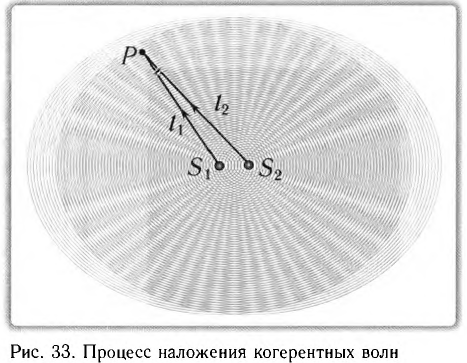
Рассмотрим процесс наложения волн длиной
Монохроматические волны одной и той же частоты, приходящие от этих источников в некоторую точку пространства Р, возбуждают в ней гармонические колебания той же частоты.
В силу этого, разность фаз колебаний, возбуждаемых рассматриваемыми источниками в точке Р, остается постоянной с течением времени, даже если начальные фазы этих колебаний различны.
Волны называются когерентными, если разность фаз колебаний, возбуждаемых ими, не изменяется с течением времени. Соответственно, свойство, характеризующее согласованность протекания в пространстве и времени нескольких колебательных или волновых процессов, называется когерентностью (от латинского слова cohaerens — связанный, сцепленный).
Опыт показывает, что амплитуда результирующего колебания в точке Р, создаваемого двумя одинаковыми источниками, зависит от геометрической разности хода волн до рассматриваемой точки:
Если разность хода волн 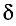
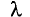
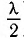
Действительно, разность фаз колебаний в рассматриваемой точке в этом случае
т. е. кратна 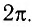
В случае, когда разность хода волн равна нечетному числу полуволн, волны приходят в точку Р в противофазе и ослабляют друг друга. Это соответствует выполнению условия минимума:
Убедитесь самостоятельно, что разность фаз колебаний в этом случае
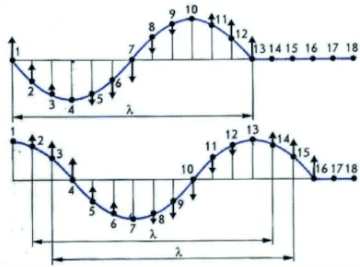
Таким образом, в результате сложения колебаний, возбуждаемых когерентными волнами на поверхности воды, образуется устойчивая картина распределения минимумов и максимумов результирующего колебания (рис. 34). Это означает, что когерентные волны интерферируют друг с другом.
Интерференция (от латинских слов inter — взаимно, между собой и fеrio — ударяю, поражаю) — явление сложения двух или более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующихся максимумов и минимумов амплитуд результирующего колебания.
Пространственная картина устойчивого во времени распределения амплитуд результирующего колебания при интерференции называется интерференционной картиной.
Вследствие того, что энергия волны пропорциональна квадрату амплитуды, энергия результирующего колебания в общем случае не равна сумме энергий складываемых колебаний, так как 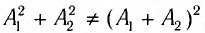
Отметим, что если бы в точке Р складывались две некогерентные волны с одинаковыми амплитудами, то энергия результирующего колебания была бы равна сумме энергий отдельных волн, независимо от положения точки Р относительно источника. Это означало бы просто удвоение энергии, принесенной одной из волн в данную точку.
Закономерности интерференции волн носят универсальный характер, т. е. справедливы для волн любой природы.
При рассмотрении интерференции света (электромагнитных волн) следует учесть, что длина волны света в веществе изменяется в зависимости от показателя преломления вещества. Это эквивалентно замене геометрической разности хода на оптическую разность хода
т. е. разность расстояний, пройденных волнами, с учетом различных скоростей 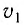
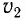
В вакууме (с = 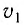
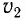
Распространенные бытовые источники света (лампы накаливания, лампы дневного света, свечи и т. д.) не являются когерентными, т. е. не позволяют наблюдать явление интерференции.
Изобретение и распространение когерентных источников излучения — лазеров — сделало демонстрацию явления интерференции достаточно простой.
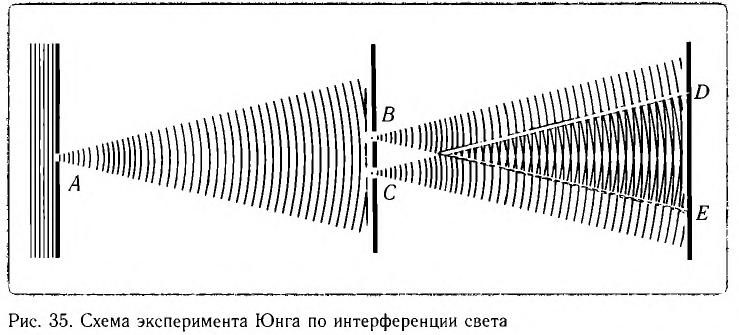
Для получения интерференционной картины при отсутствии лазеров пользуются классической интерференционной схемой (схемой Юнга), где пучок света разделяется на два пучка с помощью отверстий В и С в ширме (рис. 35). Поскольку эти пучки созданы одним и тем же источником, они являются когерентными. На экране в области DE наблюдается интерференционная картина.
Классический эксперимент по наблюдению интерференции Томас Юнг провел в 1801 г. Это позволило измерить длину световой волны и убедительно подтвердить волновую природу света.
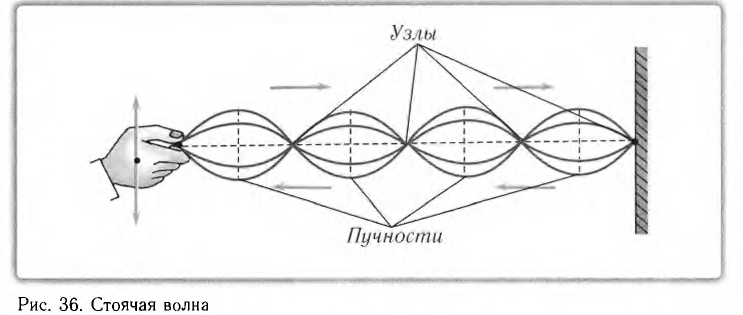
Рассмотрим еще один распространенный случай интерференции — сложение волн с одинаковыми частотами, распространяющихся в противоположных направлениях (например, падающей и отраженной волны), приводящее к образованию в пространстве устойчивой картины чередования максимумов амплитуды колебаний (пучностей) и минимумов (узлов).
Волна, возникающая в результате сложения двух волн одинаковой частоты, распространяющихся в противоположных направлениях, называется стоячей волной (рис. 36).
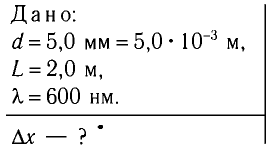
Пример решения задачи:
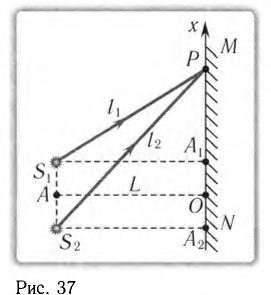
Рассчитайте положения максимумов и минимумов интерференционной картины на экране MN, находящемся на расстоянии L = АО = 2,0 м от двух одинаковых когерентных источников света 
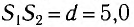
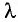
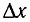
Решение
До некоторой точки Р на экране волны проходят пути
Максимумы интенсивности будут наблюдаться при условии
а минимумы при условии –
где m = 0, ±1, ±2…..
По теореме Пифагора из треугольников 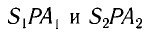
Откуда
С учетом того, что 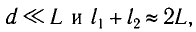
С учетом условия максимумов получаем
Откуда расстояние от центра экрана до т-й светлой полосы находится из соотношения
Из условия минимумов находим положение темных полос:
Откуда
Расстояние между соседними максимумами
Из полученной формулы видно, что ширина интерференционных полос увеличивается при уменьшении расстояния d между когерентными источниками.
Ответ:
Волновая природа света и дисперсия света
Показатель преломления среды относительно вакуума называется абсолютным показателем преломления этой среды. Абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше скорости света в вакууме:
Луч света, падающий на боковую грань треугольной призмы, отклоняется к основанию призмы.
Природа света
Несколько веков имели место два разных представления о природе света: корпускулярная и волновая природа света.
Основоположником представлений о корпускулярной природе света является И. Ньютон. Он считал, что свет является потоком частиц (корпускул). Прямолинейное распространение света и его отражение легко объяснялись согласно этому представлению.
Основоположником представлений о волновой природе света является голландский ученый Христиан Гюйгенс (1629-1695). Основной причиной возникновения этих представлений является прохождение световых лучей сквозь друг друга при распространении подобно волнам. В XIX веке английский ученый Томас Юнг (1773-1829) провел эксперименты, в которых обнаружил многочисленные факты, подтверждающие волновую природу света. Основоположник теории электромагнитного поля Дж. Максвелл теоретически обосновал электромагнитную волновую природу света. Согласно современным представлениям свет и другие электромагнитные волны обладают двойной – корпускулярной и волновой природой.
- Заказать решение задач по физике
Дисперсия света
Одним из явлений, доказывающих волновую природу света, является дисперсия света.
Дисперсия света — это зависимость показателя преломления среды от частоты (длины волны) падающего света.
Впервые это явление исследовал Исаак Ньютон. Он поместил прозрачную стеклянную треугольную призму на пути тонкого пучка солнечного света, попадающего в затемненную комнату через маленькое отверстие в ставнях. Пройдя призму, солнечный луч разделился на спектр из семи составных цветных лучей. Последовательность цветов составных частей в дисперсионном спектре всегда одинакова: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый.
Среди монохроматических (содержащих свет одного цвета) лучей наиболее сильно преломляются фиолетовые лучи, а меньше других – красные (см: а). Причина явления объясняется на основе волновых представлений о свете. Так, абсолютный показатель преломления среды показывает, во сколько раз скорость света в этой среде меньше, чем в вакууме:
Здесь 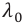
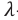
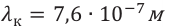
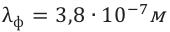
Результат. Таким образом, явление дисперсии показало, что белый свет обладает сложным строением – состоит из монохроматических световых лучей разного цвета. Каждый монохроматический луч света обладает собственной частотой и длиной волны. Поэтому при прохождении монохроматического луча через стеклянную призму он, только преломляясь, изменяет своё направление (не разлагается на составные, не меняет окраски). Если разложенный призмой свет, состоящий из монохроматических составляющих, направить на вторую перевернутую призму, то на выходе из второй призмы опять получится белый свет.
Согласно физике цвета, ни один из трех основных цветов – красный, зеленый и синий, не могут получиться при смешивании двух других. Однако смешиванием основных цветов можно получить все остальные цвета и их оттенки.
Многоцветное восприятие нами окружающего мира объясняется явлениями поглощения, преломления и отражения света. Например, лист бумаги воспринимается нашим зрением белым потому, что он отражает падающий на него белый свет полностью. Если тело полностью поглощает падающий на него свет, то он воспринимается как черный, например, сажа.
Интерференция волн и интерференция света
• Самые часто встречаемые колебания в природе являются колебаниями в связанных системах. В связанных колебательных системах колебания передаются от одного звена системы другой. Например, бросив в воду камень, можно наблюдать распространение концентрических водных кругов из точки падения камня. Нам кажется, что происходит распространение воды в виде выпуклостей и впадин.
Какая связанная система создает волну в воде?
Какие явления происходят в среде при распространении волны?
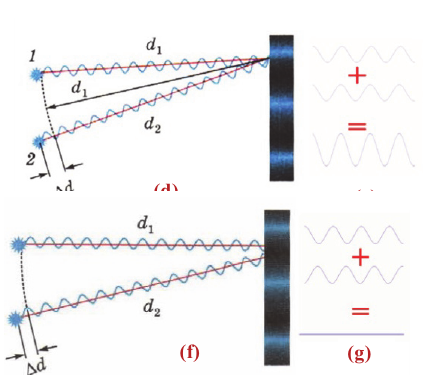
Обратите внимание на картину, образованную на неподвижной поверхности воды поплавками удочек рыболовов (а). При встрече волн друг с другом происходит их сложение. В результате в определенных точках пространства они усиливают друг друга (а, 1), а в других ослабляют (а, 2).
Интерференция волн
В исследовании вы наблюдали результат сложения когерентных волн, созданных на поверхности воды гармоническими колебаниями шариков генератора с одинаковой частотой.
Когерентные волны — это волны, созданные различными источниками колебания, имеющими одинаковую частоту колебаний и постоянную разность фаз, не зависящую от времени.
Результирующие колебания, образованные сложением когерентных волн, в зависимости от разности между расстояниями от источника колебаний до точки их встречи или усиливаются, или ослабляются – происходит интерференция волн.
Интерференция волн -усиление или ослабление амплитуды колебаний результирующей волны в результате сложения когерентных волн (лат. “интер” взаимно, “ферио” – ударю).
Усиление или ослабление амплитуды результирующей волны определяется условиями максимума и минимума интерференции.
Условие максимума интерференции
Максимум интерференции наблюдается в точках пространства (поверхности), в которых максимумы слагаемых волн накладываются друг на друга. Это зависит от разницы пройденных волнами путей от источника колебаний до этой точки.
Интерференционный максимум результирующей волны образуется в точках, в которых разность хода складываемых волн равна нулю или четному числу полудлин волн (разность фаз равна нулю или четному количеству 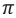
Здесь 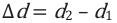
Учитывая выражение (1) в формуле (2), для разницы фаз максимума интерференции получим:
В этом случае при равенстве амплитуд складываемых волн амплитуда результирующего колебания будет равна сумме амплитуд исходных волн (е):
Условие минимума интерференции
Минимумы интерференции наблюдаются в тех точках пространства, в которые волны доходят в противофазе. При этом максимум одной волны совпадает с минимумом другой. В результате волны ослабляют друг друга.
Минимум интерференции наблюдается в точках, в которых разность хода слагаемых волн равна нечетному числу полудлин волн (разность фаз равна нечетному количеству 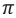
Если при этом амплитуды складываемых волн равны, то в точке минимума интерференции амплитуда результирующей волны уменьшается до нуля (g):
Интерференция света
Интерференция – характерное свойство всех видов волн, в том числе и световых. Так, две световые волны при сложении в пространстве могут усиливать или ослаблять друг друга, даже может случиться и такой вариант: свет + свет = темнота.
Интерференция света – явление увеличения или уменьшения амплитуды результирующих световых колебаний в разных точках пространства вследствие сложения двух когерентных световых волн.
Долгие годы не могли найти способ получения когерентных световых волн, поэтому невозможно было доказать способность световых волн интерферировать.
Только в начале XIX века с помощью несложного устройства Томас Юнг смог наблюдать интерференцию света (h).
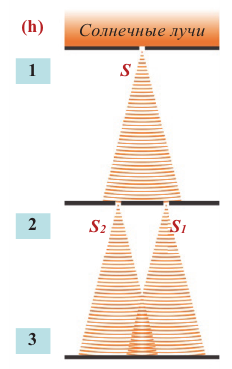
Классический опыт по наблюдению интерференции света состоит в следующем: солнечный свет освещает непрозрачный экран 1 и, пройдя через малое отверстие S в этом экране (проделанное булавкой), попадает на экран 2. Световые лучи, вышедшие из малых отверстий S1 и S2 на втором экране, являются когерентными. В результате интерференции этих волн на экране 3 появляются интерференционные полосы. В центральной части экрана наблюдаются чередующиеся цветные и темные полосы. По мере удаления от центра интерференционная картина ослабевает. Используя условие максимумов в этих опытах, Юнг смог на основе формулы (1) измерить длины световых волн для разных цветов. Как ни странно, первый опыт по интерференции света был проведен отрицающим его волновую природу Исааком Ньютоном. Поместив на стеклянной пластине плоско-выпуклую стеклянную линзу выпуклой стороной вниз, он осветил её сверху (i, 1). Посмотрев на линзу сверху, Ньютон увидел чередующиеся светлые и темные концентрические круги (i, 2), которые впоследствии стали называть кольцами Ньютона. Но ни Ньютон, ни повторявшие этот интересный опыт в течение более чем 100 лет ученые не смогли объяснить причину возникновения этих колец. И только в 1802 году Юнгу удалось объяснить происхождение колец Ньютона. Он объяснил кольца Ньютона таким образом: когда пучок света падает на плоскую поверхность линзы, то он, проходя сквозь нее, частично отражается от нижней сферической поверхности линзы (см. i-З, луч 1), а частично – от поверхности стеклянной пластинки, на которой лежит линза (см. i-З, луч 2). Вследствие такого многократного отражения образуются два когерентных луча. Эти лучи, складываясь, в соответствии с максимумами и минимумами интерференции создают интерференционную картину чередующихся темных и светлых концентрических кольца.
Определение длины световой волны
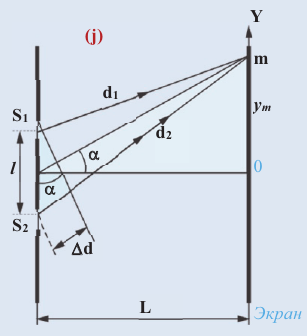
Представим, что расстояние между источниками когерентных волн S1 и S2 намного меньше расстояния от источников до экрана (j): 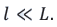
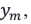
Вследствие малости угла
Условие интерференционного максимума в этом случае будет:
Отсюда можно найти длину волны:
- Дифракция света
- Принцип Гюйгенса — Френеля
- Прохождение света через плоскопараллельные пластинки и призмы
- Поляризация света
- Преломление света
- Полное отражение
- Дисперсия света
- Электромагнитная природа света
- ГЛАВНАЯ >
- ПРЕДМЕТЫ >
- ОПТИКА >
- ОПТИЧЕСКАЯ ДЛИНА ПУТИ. ОПТИЧЕСКАЯ РАЗНОСТЬ ХОДА. СВЯЗЬ МЕЖДУ РАЗНОСТЬЮ ФАЗ И ОПТИЧЕСКОЙ РАЗНОСТЬЮ ХОДА СВЕТОВЫХ ВОЛН
Оптическая длина пути. Оптическая разность хода. Связь между разностью фаз и оптической разностью хода световых волн
Без воды — краткий вариант ответа,
легко понять и
запомнить
Оптическая длина пути между двумя точками среды — расстояние, на которое свет (оптическое излучение) распространился бы в вакууме за время его прохождения между этими точками.
Оптическая длина пути световой волны в однородной среде
где — геометрическая длина пути световой волны.
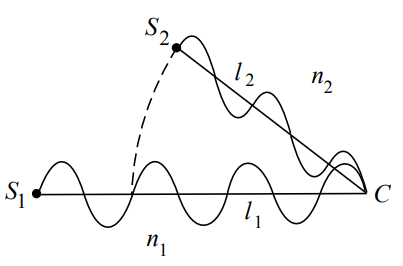
Оптическая разность хода — это разность оптических длин путей, проходимых волнами (рис. 1.1).
Оптическая разность хода двух световых волн
где , — показатели преломления первой и второй сред; и — геометрические длины путей волн в первой и второй средах.
рис. 1.1
Связь между разностью фаз и оптической разностью хода световых волн
где — длина волны света в вакууме (воздухе).
Длина волны — наименьшее расстояние между двумя точками волны, в которых колебания происходят в одинаковых фазах.
Теперь на ZNZN можно делать свои конспекты
Легко создавать, делиться и просматривать с устройств
Доступно в ПК-версии сайта