Оптическая разность хода.
Вместо разности фаз
![]()
интерферирующих волн удобно ввести в
рассмотрение пропорциональную ей
величину
![]()
– оптическую разность хода, которая
отличается множителем
![]()
,
где
![]()
– длина световой волны.
![]()
Изменению
разности фаз на
![]()
соответствует изменение разности хода
на
.
В
вакууме оптическая разность хода в
отличие от разности фаз имеет наглядную
и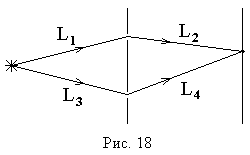
нтерпретацию.
Если две интерферирующие волны испускаются
одним источником света, то разность
хода – это геометрическая разность длин
путей, по которым два интерферирующих
луча от одной точки источника достигли
одной точки экрана.
Например,
в оптической схеме опыта Юнга, изображенной
на рис. 18, разность хода для точки P на
экране находится по формуле:
.![]()
В
изотропной среде скорость света в n
раз меньше, чем в вакууме, здесь n
– показатель преломления среды. Частота
света в среде и в вакууме одинакова,
поэтому длина волны в среде в n
раз меньше. В соответствии с соотношением
вместо реального уменьшения длины волны
можно рассматривать неизменную
и соответствующее увеличение длины
пути луча. С этой целью вводится понятие
оптической длины пути, которая в n
раз больше геометрической длины. Далее,
употребляя термин “разность хода”,
всегда будем иметь в виду оптическую
разность хода.
Заменяя
разность фаз интерферирующих волн
оптической разностью хода, получаем
следующее выражение для интенсивности
интерференционной картины:
.
![]()
Приемники
света в оптическом диапазоне реагируют
на интенсивность света, а не на
напряженность электрического или
магнитного полей. Поэтому измеряемые
в опыте величины, ширина полос и видность,
также могут быть выражены через
интенсивность, а значит и через оптическую
разность хода. Следовательно, понятие
оптической разности хода позволяет
свести оптическую задачу по интерференции
к геометрической задаче отыскания
разности хода.
Отметим,
что разность хода лучей можно отсчитывать
не только как разность длин путей от
источника до точки наблюдения, но и как
разность длин путей от двух точек любой
поверхности равной фазы волны до точки
наблюдения. При этом, конечно, две точки
на поверхности равной фазы – не произвольные
точки, а должны быть точками, через
которые реально проходят лучи, попадающие
в точку наблюдения. Так на рис. 18
![]()
,
поэтому две щели находятся на поверхности
равной фазы, и, следовательно, разность
хода можно найти по упрощенной формуле
![]()
.
Этот прием часто используется при
решении задач.
18.1.2.1. Условия максимума и минимума на разность фаз δ
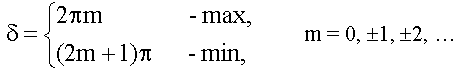
18.1.2.2. Оптическая разность хода
Пусть
для простоты, начальные фазы α1
и α2
интерферирующих волн равны нулю, тогда:
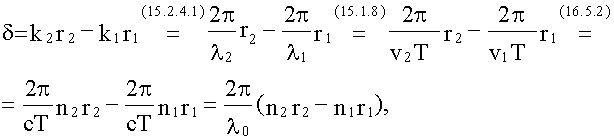
здесь
λ0 = cT
– длина световой волны в вакууме.
Оптической
разностью хода называют величину:
![]()
.
Тогда:

.
18.1.2.3. Условия максимума и минимума на оптическую разность хода
Из
(18.1.2.1.)
и (18.1.2.2.):
П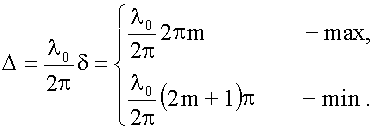
осле
сокращения получим условия на Δ:
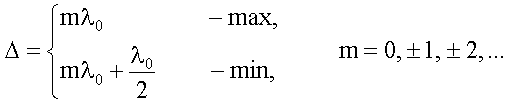
30. Интерференция при отражении от тонких пленок. Пример расчета интерференционной картины для плоскопараллельной пластинки.
Интерференция
– физическое явление, наблюдаемое при
сложении волн (световых, звуковых и т.
п.), усиление волн в одних точках
пространства и ослабление в других (или
сложение двух или более
волн, при котором амплитуда результирующей
волны зависит от разности фаз исходных
волн в данной точке пространства)
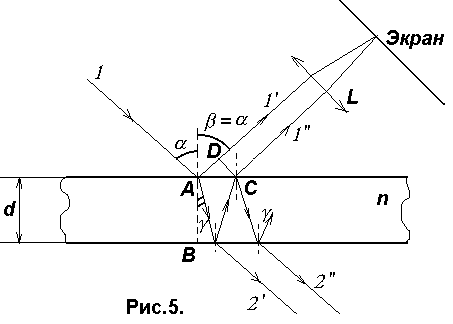
Пусть
на плоскопараллельную прозрачную пленку
(пластинку) с показателем преломления
n и толщиной d под углом
падает плоская монохроматическая волна
(для простоты рассмотрим один луч).
На
поверхности пленки в точке А волна
частично отражается (луч 1- ) и частично
преломляется (луч АВ). В точке В волна
также частично отражается (луч ВС) и
частично преломляется (луч 2- ). То же
самое происходит в точке С.
Причем
преломленная волна (луч 1″ ) накладывается
на волну непосредственно отраженную
от верхней поверхности (луч 1- ). Эти две
волны когерентны, если оптическая
разность хода
![]()
меньше
длины когерентности lког, и в этом
случае они интерферируют.
Оптическая
разность хода двух волн =(AB+BC)n-(AD-/2),
где
/2 – потеря полуволны
при отражении луча 1- в точке А. Используя
закон преломления n1sin
= n2sin и учитывая,
что в рассматриваемом случае n1=1,
n2=n, можно показать, что
![]()
.(17)
В
точке наблюдения на экране будет
максимум, если m
и минимум, если (2m+1)/2[см.(15),(16)].
Возможность
уменьшения вредного отражения света
вследствие интерференции в тонких
пленках широко используется в современных
оптических приборах. Для этого на
передние поверхности линз, призм наносят
тонкие пленки с показателем преломления
n=![]()
и толщиной d, которая определяется из
условия минимума при интерференции
волн, отраженных от границ раздела сред
с n1 и n и n и n2

2dn=(2m+1)/2,
m=0,1,2-(18)
Минимальная
толщина пленки соответствует m=0
d=/(4n)
Такая
оптика получила название просветленной
оптики.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- ГЛАВНАЯ >
- ПРЕДМЕТЫ >
- ОПТИКА >
- ОПТИЧЕСКАЯ ДЛИНА ПУТИ. ОПТИЧЕСКАЯ РАЗНОСТЬ ХОДА. СВЯЗЬ МЕЖДУ РАЗНОСТЬЮ ФАЗ И ОПТИЧЕСКОЙ РАЗНОСТЬЮ ХОДА СВЕТОВЫХ ВОЛН
Оптическая длина пути. Оптическая разность хода. Связь между разностью фаз и оптической разностью хода световых волн
Без воды — краткий вариант ответа,
легко понять и
запомнить
Оптическая длина пути между двумя точками среды — расстояние, на которое свет (оптическое излучение) распространился бы в вакууме за время его прохождения между этими точками.
Оптическая длина пути световой волны в однородной среде
где — геометрическая длина пути световой волны.
Оптическая разность хода — это разность оптических длин путей, проходимых волнами (рис. 1.1).
Оптическая разность хода двух световых волн
где , — показатели преломления первой и второй сред; и — геометрические длины путей волн в первой и второй средах.
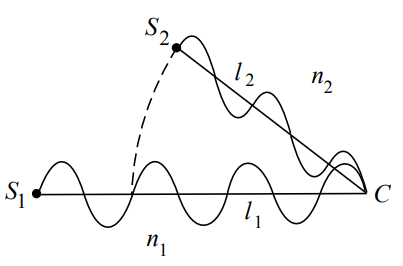
рис. 1.1
Связь между разностью фаз и оптической разностью хода световых волн
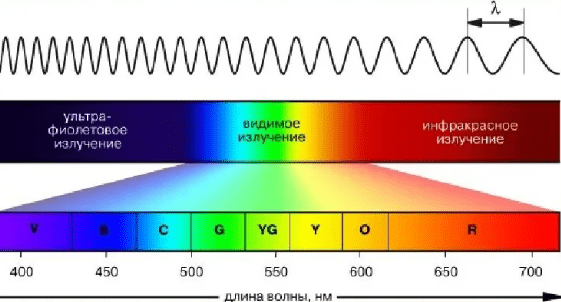
где — длина волны света в вакууме (воздухе).
Длина волны — наименьшее расстояние между двумя точками волны, в которых колебания происходят в одинаковых фазах.
Теперь на ZNZN можно делать свои конспекты
Легко создавать, делиться и просматривать с устройств
Доступно в ПК-версии сайта

Интерференция света – явление ослабления или усиления интенсивности света в зависимости от соотношения фаз складываемых световых когерентных волн, линейно поляризованных в одной плоскости. Для уровня школьной физики данное определение является излишним. По умолчанию, световые волны являются когерентными и линейно поляризованными.
Таким образом, для нас в задачах на интерференцию важно наличие нескольких (чаще всего двух) волн и разности фаз (разности хода) между ними.
В школьных задачах на интерференцию основным вопросом является результат интерференции в наблюдаемой точке (усиление или ослабление света).
Для математического описания явления интерференции вводят оптическую длину пути () — произведение показателя преломления среды, по которой проходит свет, на геометрическую длину пути, которую прошёл луч. Тогда для двух лучей (рис. 1):
(1)
- где

Рис. 1. Интерференция
Пусть от точечного источника системой зеркал два луча развели по двум областям с различными показателями преломления ( и
). Пути лучей в этих системах
и
соответственно. Затем, вышедшие из областей, лучи обратно свели в точку
. За счёт того, что в средах с различным показателем преломления луч от одного и того же источника движется с разной скоростью, к одной и той же точке они приходят с ненулевой разностью хода (1).
Тогда результат интерференции (усиление или ослабление света) диктуется соотношениями:
- максимум интерференции (максимальное усиление):
(2)
(3)
Тогда для ответа на вопрос об усилении и ослаблении света можно анализировать приведённое уравнение (2):
(4)
Тогда, если полученное целое или ближе к целому, то в точке
наблюдается усиление света, в случае, если
полуцелое или близко к полуцелому, в точке
— темнота.
Вывод: фактически задачи на интерференцию сводятся к анализу уравнения (4) и поиску оптической длины пути для (1).
Пример: Оптическая разность хода волн от двух когерентных источников в некоторой точке пространства мкм. Каков будет результат интерференции в этой точке, если длина волны будет:
нм,
нм.
Исходя из аналитической формулы (4):
(5)
(6)
Таким образом, получившийся параметр получился целым числом, это говорит о том, что при данных параметрах в точке соединения лучей будет наблюдаться усиление света. Параметр
оказался ближе к полуцелому, таким образом, в исследуемой точке будет наблюдаться ослабление света.
Для всех волн характерны явления интерференции и дифракции. Если свет — это волна, то для него также должны быть присущи эти явления. Так рассуждали ученые, которые считали, что свет имеет волновую природу. Первым привел экспериментальные доказательства интерференции и дифракции света Томас Юнг в 1801 году.
Это интересно! Явление интерференции света было описано и объяснено в 1801 году, но само понятие «интерференция света» было введено немного позже — в 1803 году.
Интерференция механических волн
Чтобы лучше понять явление интерференции, сначала объясним его на примере механических волн, за которыми удобней наблюдать. Часто случается, что в среде одновременно распространяется несколько различных волн. К примеру, когда в комнате может одновременно находиться несколько источников звука. Что же происходит, когда волны пересекают друг друга? Объясним это на примере волн, образуемых на поверхности воды.
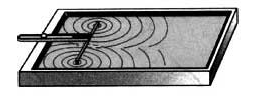
Если бросить в воду два камешка, образуются две круговые волны. Если наблюдать за их распространением, мы увидим, что каждая волна проходит сквозь другую. Причем она ведет себя так, как будто другой волны не существовало. Точно так же любое количество звуковых волн может одновременно распространяться в воздухе. И они не будут друг другу мешать. Множество музыкальных инструментов в оркестре или голосов в хоре создает звуковые волны, которые улавливаются нами одновременно. При этом звуки не сливаются в шум: наши органы слуха способны легко отличить один звук от другого.

Теперь рассмотрим более подробно процесс, когда волны накладываются одна на другую. Для этого будем наблюдать волны на поверхности воды от двух брошенных в воду камней. При этом мы заметим, что некоторые участки поверхности не возмущены, в других же местах возмущение усилилось. Если два гребня двух волн встречаются в одном месте, то в этом месте возмущение поверхности воды становится более сильным. Если же гребень одной волны встречается с впадиной другой, то поверхность воды в этом месте остается спокойной. Получается, что в каждой точке среды колебания, вызванные двумя волнами, складываются. Результирующее смещение любой частицы среды представляет собой алгебраическую сумму смещений, которые происходили бы при распространении одной из волн в отсутствие другой.
Интерференция — сложение в пространстве волн, при котором образуется постоянное во времени распределение амплитуд результирующих колебаний частиц среды.
Чтобы выяснить, при каких условиях наблюдается интерференция волн, одновременно возбудим две круговые волны в ванночке с помощью двух шариков, прикрепленных к стержням, колеблющимся по гармоническому закону.
Теперь представим явление интерференции схематически. В любой точке М на поверхности воды будут складываться колебания, вызванные двумя волнами от источников O1 и O2 (см. рисунок ниже). Амплитуды колебаний, вызванных в точке М обеими волнами, будут различаться, если волны проходят различные пути d1 и d2. Но если расстояние l между источниками много меньше этих путей, то обе амплитуды можно считать приближенно одинаковыми.
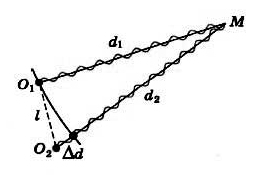
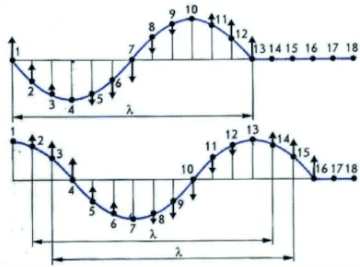
Результат сложения волн, приходящих в точку М зависит от разности фаз между ними. Пройдя различные расстояния d1 и d2, волны имеют разность хода, определяемую формулой:
Δd = d2 − d1
Когда разность хода равна длине волны λ, то вторая волна запаздывает по сравнению с первой на один период. Так как за период волна проходит путь, равный ее длине волны, то в точке встречи двух волн фазы совпадают. Если в этой точке волны имеют гребни, то совпадают гребни, если впадины — совпадают впадины.
Условие минимумов и максимумов
Когда гребни волн на поверхности волны складываются в одной точке, их амплитуда резко возрастает. В этом случае говорят, что в этой точке образуется интерференционный максимум. Когда впадины волн на поверхности волны складываются в одной точке, их амплитуда резко уменьшается. В этом случае говорят, что в этой точке образуется интерференционный минимум. Интерференционные минимумы и максимумы образуются при соблюдении определенных условий.
Если разность хода волн равна нечетному числу полуволн, то в точке наложения этих волн образуется интерференционный минимум. Амплитуда колебаний в данной точке минимальна.
Δd=(2k+1)λ2
k = 0, 1, 2, … .
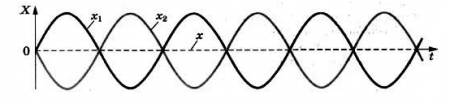
Если разность хода волн равна целому числу волн, то в точке наложения этих волн образуется интерференционный максимум. Амплитуда колебаний в данной точке максимальна.
Δd=kλ
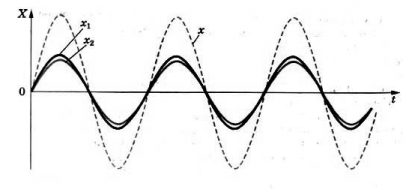
Если разность хода ∆d принимает промежуточное значение между λ и λ/2, амплитуда результирующих колебаний принимает некоторое промежуточное значение между удвоенной амплитудой и нулем. Но важной примечательностью является то, что амплитуда колебаний в любой точке с течением времени не меняется. Поэтому на поверхности воды возникает определенное, постоянное во времени распределение амплитуд колебаний, которое называют интерференционной картиной.

Для формирования устойчивой интерференционной картины важно, чтобы источники волн имели одинаковую частоту, и разность фаз их колебаний не менялась с течением времени. Такие источники волн называют когерентными.
Когерентные волны — это волны, имеющие одинаковые частоты, постоянную разность фаз, а колебания происходят в одной плоскости.
Только когерентные волны при сложении формируют устойчивую интерференционную картину. Если же источники волн некогерентные, то в любой точке среды разность фаз колебаний, возбуждаемых двумя волнами, будет с течением времени изменяться. Поэтому амплитуда результирующих колебаний также будет непрерывно изменяться. В результате максимумы и минимумы в пространстве будут иметь неопределенное положение. Поэтому интерференционная картина получается размытой.
Распределение энергии при интерференции
Любая волна переносит энергию без переноса вещества. Но что же с этой энергией происходит при интерференции волн? Если волны встречаются друг с другом, энергия никуда не исчезает и не превращается в другие формы энергии. Она лишь перераспределяется таким образом, что в минимумах он не поступает совсем, поскольку концентрируется в максимумах.
Интерференция света
Ели свет — это поток волн, то должно наблюдаться явление интерференции. Однако получить интерференционную картину, при которой чередуются минимумы и максимумы с помощью двух независимых источников света (к примеру, двух ламп), невозможно. Включение второй лампы лишь увеличивает освещенность поверхности, но не создает картины из минимумов и максимумов. Это объясняется несогласованностью волн друг с другом. Для получения же устойчивой интерференционной картины нужны согласованные, то есть когерентные световые волны. Они должны иметь одинаковые длины волн и постоянную во времени разность фаз в любой точке пространства.
Однако наблюдать интерференцию света все же можно. Вы ее наблюдали, когда пускали мыльные пузыри или рассматривали пленку нефти на поверхности воды.

Томас Юнг — первый из ученых, который предложил объяснить изменение цветов тонких пленок сложением волн. Согласно его предположению, одна волна отражается от наружной поверхности плёнки, а другая — от внутренней. При этом возникает явление, называемой интерференцией световых волн.
Усиление света происходит в том случае, если преломлённая волна запаздывает по сравнению с отражённой волной на целое число длин волн. Здесь действует условие максимумов, о котором мы говорили выше:
Δd=kλ
Если вторая волна запаздывает по сравнению с первой на половину длины волны или на нечетное число полуволн, то произойдет ослабление света. Здесь действует условие минимумов, о котором мы также уже говорили:
Δd=(2k+1)λ2
Четкая интерференционная картина получается потому, что волны, отраженные от внутренней и внешней оболочки тонкой пленки, являются когерентными. Когерентность этих волн объясняется тем, что они являются частями одного и того же светового луча.
Юнг сделал вывод, что многообразие цветов на мыльной пленке связано с разницей в длине волны. Если плёнка имеет неоднородную толщину, то при освещении её белым светом появляются различные цвета.
Простую интерференционную картину также можно получить, если положить на стеклянную поверхность плоско-выпуклую линзу, сферическая поверхность которой имеет большой радиус кривизны. Интерференционная картина, полученная таким способом, носит название колец Ньютона.
Исаак Ньютон исследовал интерференционную картину, получаемую в тонкой прослойке воздуха между стеклом и линзой, не только в белом свете, но и при освещении линзы монохроматическими лучами. Так он установил, что радиусы колец одного и того же порядкового номера увеличиваются при переходе от фиолетового конца спектра к красному. Так, красные кольца имеют максимальный радиус. Расстояние между соседними кольцами уменьшаются с увеличением их радиусов.
Ньютону удалось получить кольца, но их появление он объяснить не смог. Но это удалось сделать Юнгу. Проведенный им опыт показал, что волна определённой длины падает на плосковыпуклую линзу почти перпендикулярно. Волна 1 появляется в результате отражения от выпуклой поверхности линзы на границе сред стекло-воздух, а волна 2 — в результате отражения от пластины на границе сред воздуха- стекло.
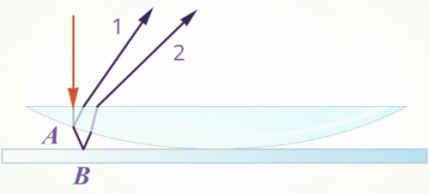
Если вторая волна запаздывает по сравнению с первой на целое число длин волн, то при сложении волны усиливают друг друга. Если вторая волна запаздывает по сравнению с первой на нечётное число полуволн, то колебания в точке сложения будут совпадать в противоположных фазах. При этом волны погасят друг друга.
В результате проделанного эксперимента Юнг смог получить картину, которая состоит из чередующихся параллельных полос (темных и светлых)
Интерференция света – это явление сложения двух и более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующегося максимумом и минимумом интенсивности.
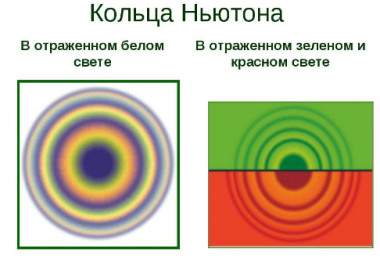
Это интересно! Измеряя радиусы колец Ньютона, можно вычислить длины волн. В ходе измерений было установлено, что для красного света λкр = 8∙10–7 м, а для фиолетового — λa = 4∙ 10–7 м.
Пример №1. Будет ли наблюдаться интерференционная картина при освещении мыльной пленки монохроматическим светом? Какой она будет?
Поскольку источник света один и тот же, то отраженные от обеих поверхностей мыльной пленки волны будут когерентными. Поэтому интерференционная картина наблюдаться будет. Она примет вид чередующихся цветных и темных полос. Цвет полос определяется цветом световой волны, который зависит от ее длины волны.
Задание EF17533
На поверхность тонкой прозрачной плёнки падает по нормали пучок белого света. В отражённом свете плёнка окрашена в зелёный цвет. При использовании плёнки такой же толщины, но с несколько меньшим показателем преломления, её окраска будет
Ответ:
а) только зелёной
б) находиться ближе к красной области спектра
в) находиться ближе к синей области спектра
г) только полностью чёрной
Алгоритм решения
1.Описать наблюдаемое явление.
2.Записать условие наблюдения интерференционного максимума.
3.Выполнить решение в общем виде.
4.Установить, в какой цвет будет окрашена пленка.
Решение
При освещении тонкой плёнки можно наблюдать интерференцию световых волн, отражённых от передней и задней поверхностей плёнки. Условием интерференционного максимума для излучения с длиной волны λ является:
kλ=2dn+Δ
Δ — либо 0, либо λ2 (это зависит от соотношения показателей преломления на границе двуз сред). Тогда при малом изменении значения показателя преломления в меньшую сторону и сохранении порядка k (как в нашем случае и есть), длина волны света будет уменьшаться. Это значит, что из зеленой части спектра она сдвинется в синюю часть.
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17707
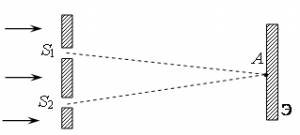 На две щели в экране слева падает плоская монохроматическая световая волна перпендикулярно экрану. Длина световой волны λ. Свет от щелей S1 и S2, которые можно считать когерентными синфазными источниками, достигает экрана Э. На нём наблюдается интерференционная картина. Тёмная полоса в точке А наблюдается, если
На две щели в экране слева падает плоская монохроматическая световая волна перпендикулярно экрану. Длина световой волны λ. Свет от щелей S1 и S2, которые можно считать когерентными синфазными источниками, достигает экрана Э. На нём наблюдается интерференционная картина. Тёмная полоса в точке А наблюдается, если
Ответ:
а) S2А – S1А = 2k⋅λ/2, где k– любое целое число
б) S2А – S1А = (2k + 1) ⋅λ/2, где k– любое целое число
в) S2А – S1А = λ/3k, где k– любое целое число
г) S2А – S1А = λ/(2k+1), где k– любое целое число
Алгоритм решения
1.Записать условие наблюдения интерференционного минимума.
2.Выбрать выражение, удовлетворяющее этому условию.
Решение
В точке А будет наблюдаться темное пятно, если волны, достигающие этой точки, будут гасить друг друга. Это возможно при соблюдении условия минимума:
Δd=(2k+1)λ2
Разность хода в данном случае равна:
Δd=S2A−S1A
Следовательно:
S2A−S1A=(2k+1)λ2
где k — целое число.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17972
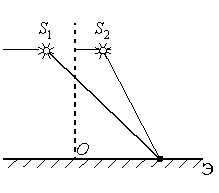 Точечные источники света S1 и S2 находятся близко друг от друга и создают на удалённом экране Э устойчивую интерференционную картину (см. рисунок). Это возможно, если S1 и S2 – малые отверстия в непрозрачном экране, освещённые
Точечные источники света S1 и S2 находятся близко друг от друга и создают на удалённом экране Э устойчивую интерференционную картину (см. рисунок). Это возможно, если S1 и S2 – малые отверстия в непрозрачном экране, освещённые
Ответ:
а) каждое своей лампочкой накаливания
б) каждое своей горящей свечой
в) одно зелёным лазером, другое красным
г) светом одной лампочки накаливания
Алгоритм решения
- Записать условие наблюдения интерференционной картины.
- Проанализировать источники и выбрать подходящий под условие.
Решение
Четкая интерференционная картина наблюдается только при освещении щелей когерентными лучами света, имеющими постоянную разность фаз. Когерентные — значит волнами одной частоты. Поэтому лазер зеленый и красный сразу не подходят — они имеют разные частоты.
Одна и та же частота и постоянная разность фаз будет только при условии, что щели освещаются одним источником света. В данном случае — одной и той же лампой накаливания.
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.7k
IV. Оптика
Тестирование онлайн
Интерференция
Интерференция – сложение в пространстве двух (или нескольких) волн, при котором в разных его точках получается усиление или ослабление амплитуды результирующей волны. Явление характерно для волн любой природы: звуковых волн, волн на поверхности воды, электромагнитных волн и др.
Устойчивую интерференционную картину дают только когерентные волны, т.е. волны, имеющие одинаковые частоты и постоянную во времени разность фаз колебаний.
Пусть в точку А пришли две волны одинаковой частоты, прошедшие перед этим различные расстояния l1 и l2 от своих источников.

Амплитуда результирующего колебания зависит от величины, называемой разностью хода волн.


Если разность хода равна целому числу волн, то волны приходят в точку синфазно. Складываясь, волны усиливают друг друга и дают колебание с удвоенной амплитудой.


Если разность хода равна нечетному числу полуволн, то волны приходят в точку А в противофазе. В этом случае они гасят друг друга, амплитуда результирующего колебания равна нулю.


В других точках пространства наблюдается частичное усиление или ослабление результирующей волны.
Опыт Юнга
В 1802 г. английский ученый Томас Юнг поставил опыт, в котором наблюдал интерференцию света. Свет из узкой щели S, падал на экран с двумя близко расположенными щелями S1 и S2. Проходя через каждую из щелей, световой пучок расширялся, и на белом экране световые пучки, прошедшие через щели S1 и S2, перекрывались. В области перекрытия световых пучков наблюдалась интерференционная картина в виде чередующихся светлых и темных полос.

Ход луча в мыльной пленке
На рисунке изображена в разрезе сильно увеличенная по толщине мыльная пленка. Пусть в точке А пленки попадает световая волна. Часть света отражается от этой поверхности, а часть – преломляется, проходит внутрь пленки и отражается от ее поверхности в точке В. Эти два отраженных пучка света имеют одинаковую частоту, поскольку исходят от одного источника. Складываясь, они образуют интерференционную картину.


С интерференционными явлениями мы сталкиваемся довольно часто: цвета масляных пятен, рисунки на крыльях некоторых бабочек и жуков и др.
