Диаграммы Эйлера-Венна
Содержание:
-
Что такое диаграммы Эйлера-Венна
- Принцип построения
- Дополнение множества
- Объединение множеств
- Пересечение множеств
- Симметричная разность множеств
- Разность множеств
- Использование диаграмм Эйлера-Венна для доказательства логических равенств
- Примеры задач с решением
Что такое диаграммы Эйлера-Венна
Определение
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принцип построения
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
- В первую очередь необходимо начертить диаграмму, заштриховав все множества, находящиеся в левой части равенства.
- Следующим шагом будет начертание другой диаграммы и штриховка всех множеств, которые находятся в правой части равенства.
- В случае, когда на диаграммах заштрихована одна и та же область, торжество истинно.
Дополнение множества
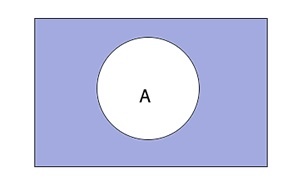
Дополнением к множеству A является множество (overline A), которое состоит из элементов, не входящих в А.
(overline A;=;left{x;vert;x;notin;Aright})
При этом не все элементы, не являющиеся элементами А, могут быть включены в (overline A.) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение overline A определяется следующим образом:
(overline A;=;U;backslash;A)
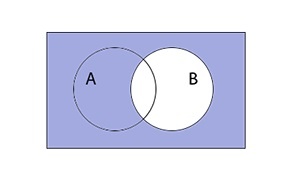
Таким образом выглядит дополнение (overline A) графически:
Объединение множеств
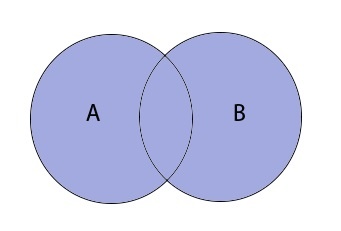
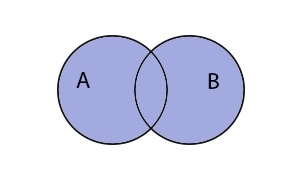
Объединением множеств A и B называют множество (A;cup;B), которое состоит из элементов, принадлежащих хотя бы одному из множеств.
Объединение записывается следующим образом:
(A;cup;B;=;left{x;vert;x;in;A;или;x;in:Bright})
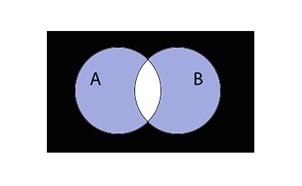
Таким образом объединение множеств выглядит графически:
Пересечение множеств
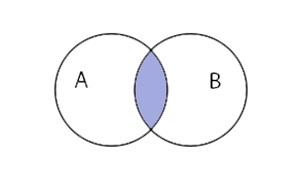
Пересечением множеств A и B является множество (A;cap;B), которое состоит из элементов, входящих в оба множества.
Пересечение множеств записывается следующим образом:
(A;cap;B;=;left{x;vert;x;in;A;и;x;in;Bright})
Таким образом пересечение множеств выглядит графически:
Симметричная разность множеств
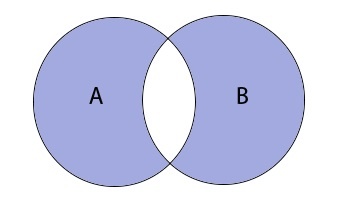
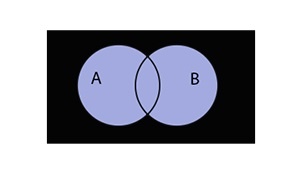
Симметричная разность A B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество
Разность множеств записывается следующим образом:
(Abigtriangleup B=(Abackslash B)cup(Bbackslash A))
Таким образом разность выглядит графически:
Разность множеств
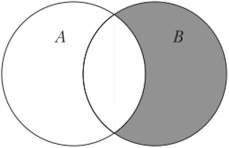
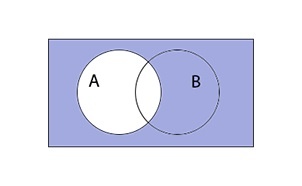
Разностью A B является множество элементов A, не входящих в B.
Разность множеств записывается следующим образом:
(A;backslash;B;=;left{x;vert;x;in;A;и;x;notin;Bright})
Таким образом разность выглядит графически:
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
Предположим, что перед нами конъюнкция множеств (A;wedge;B)
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.
Теперь отобразим инверсию, заштриховав область за пределами множеств.
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.
Проведем аналогичную операцию с множеством B.
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
Задача
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
(n(U);=;100\n(Р);=;28,;n(Ф);=;42,;n(К);=;30\n;(Р;cap;Ф);=;10,;n(Р;cap;К);=;8,;n;(Ф;cap;К);=;5\n;(Р;cap;Ф;cap;К);=;3)
Необходимо найти (n(Р;cup;Ф;cup;К);=;n;(U;backslash;(Р;cap;Ф;cap:К)))
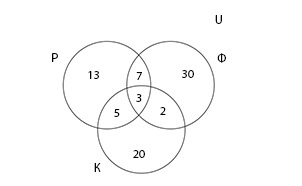
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в (Р;cap;Ф;cap:К) три элемента, а в множестве (Р;cap;Ф) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
(n(Р;cup;Ф;cup;К);=;13;+;7;+;30;+5;+;3;+;2:+;20;=;80)
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
(n(U;backslash;(Р;cup;Ф;cup;К));=;100;-;80;=;20)
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
- множество задач по алгебре («А»);
- множество задач по геометрии («Г»);
- множество задач по тригонометрии («Т»).
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
Теперь используя диаграмму, обозначим область, которую необходимо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
- Область А = 0, Г = 0, Т = 1: школьников нет.
- Область А = 0, Г = 1, Т = 0: школьников нет.
- Область А = 0, Г = 1, Т = 1: 100 школьников.
- Область А = 1, Г = 0, Т = 0: школьников нет.
- Область А = 1, Г = 0, Т = 1: 200 школьников.
- Область А = 1, Г = 1, Т = 0: 300 школьников.
- Область А = 1, Г = 1, Т = 1: 300 школьников.
Теперь внесем значения всех областей в диаграмму:
Определим x:
(x;=;U;-;(A;cup;Г;cup;Т);)
При U — универсум
U = 1000
((A;cup;Г;cup;Т);=; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900)
x = 1000 – 900 = 100
Ответ: 100 школьников не решило ни одной задачи.
Лекция 4. Вычитание
множеств, дополнение подмножества.
Определение. Разностью множеств
А и В называется множество, содержащее те и только те элементы, которые
принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А В. Таким образом, по определению
разности А В = { х | х ∈
А и х ∉В}.
Например, если А = { a , c , k , m , n }
и В = { a , b , c , d , e }, то
А В = { k , m , n }.
Если
изобразить А и В при помощи кругов Эйлера-Венна, то разность данных множеств
является заштрихованная область (рис. 5).
Определение. Пусть В является подмножеством
множества А. В этом случае разность множеств А и В называют дополнением подмножества
В до множества А и обозначают В’А. Дополнение можно изобразить
как показано на рис. 5. Если В – подмножество универсального множества U, то
дополнение подмножества В до U обозначают В’.
Например, если В – множество однозначных
натуральных чисел, то В’– множество неоднозначных натуральных чисел, если С –
множество равнобедренных треугольников, то С’ – множество треугольников, у
которых все стороны имеют разную длину.
Разность множеств и дополнение к подмножеству
обладают рядом свойств.
1) (А В) С = (А С)
В.
2) (А∪В)
С = (А С) ∪ (В С).
3) (А В) ∩ С = (А ∩С)
(В ∩ С).
4) (А ∪
В)’ = А’ ∩ В’.
5) (А ∩ В)’ = А’ ∪В’.
Задания для самостоятельной работы по теме:
1.
Найдите разность множеств А и В, если
а) А = {1,2, 3,4,
5, 6}, В = {2, 4, 6, 8, 10};
б) А =
{1,2,3,4,5,6},В={1,3,5};
в) А =
{1,2,3,4,5,6},В={6,2,3,4,5,1}.
2. В
каких случаях, выполняя упражнение 1, вы находили дополнение множества В до
множества А?
3.
Из каких чисел состоит дополнение:
а) множества натуральных
чисел до множества целых;
б) множества целых чисел
до множества рациональных;
в) множества рациональных
чисел до множества действительных.
Вновь
возьмём множества Х
=
{0, 1, 3, 5} и
Y
= {1, 2, 3, 4} и наряду с ними рассмотрим
множество {0, 1, 2, 3, 4, 5}. Это множество
содержит все элементы множества Х
и
все элементы множества Y
и
не содержит никаких других элементов.
Множество,
состоящее из всех элементов, принадлежащих
или множеству А
или
множеству
В, называется
объединением
множеств А
и
В, обозначается
А U
В. А U
В = { х
А или
х
В }
Итак,
{0,
1, 3, 5}
{1, 2, 3, 4} = {0, 1, 2, 3, 4, 5}.
Если
изобразить множества А
и
В при
помощи кругов Эйлера, то объединение
данных множеств изобразится заштрихованной
областью.
А U
В
Если множества не
имеют общих элементов, то их объединение
выглядит так:
А U
В
Е
одно из множеств является подмножеством
другого, то их объединение будет выглядеть
так:
А U
В
Часто
приходится рассматривать объединение
и пересечение трёх и более множеств.
Объединение множеств А,
В и
С
есть множество, каждый элемент которого
принадлежит хотя бы одному из множеств
А, В или
С; пересечение
множеств А,
В и
С есть
множество всех элементов, принадлежащих
и множеству А,
и множеству В,
и множеству С.
А U
В U С

∩ В ∩ С
Например, объединение
множеств остроугольных, тупоугольных
и прямоугольных треугольников есть
множество всех треугольников.
Еще
операции над множествами можно показать
с помощью детского анекдота: Однажды
лев, царь зверей, собрал зверей на поляне
и повелел им разделиться на умных и
красивых. После того, как пыль улеглась,
лев увидел на поляне две большие группы
зверей и мартышку, прыгающую между ними.
На вопрос: почему она прыгает туда, сюда,
мартышка ответила: «Что мне, разорваться,
что ли?». Так вот, мартышка из анекдота
– это пример пересечения умных
зверей и красивых.
А объединением умных и красивых зверей
является все множество зверей.
Объединение и
пересечение множеств обладают многими
свойствами, аналогичными свойствам
суммы и произведения чисел:
|
№ п/п |
Свойство |
Свойство |
Название |
|
1 |
|
a + b = |
Коммутативность |
|
2 |
|
|
|
|
3 |
|
(а+b)+c |
Ассоциативность |
|
4 |
|
|
|
|
5 |
|
|
Дистрибутивность |
Однако эта аналогия
не всегда имеет место. Например, для
множеств справедливы равенства:
6.
(А U
С)
∩ (В
U
С) = (A
∩
B)
U
С.
7.
А U
А = А.
8.
А ∩
А
= А.
Соответствующие
равенства для чисел верны не всегда.
Заметим, что, если
в выражении есть знаки пересечения и
объединения множеств, и нет скобок, то
сначала выполняют пересечение, так как
считают, что пересечение более «сильная»
операция, чем объединение.
1.3.3 Вычитание множеств
Если заданы два
множества, то можно не только найти их
пересечение и объединение, но и вычесть
из одного множества другое. Результат
вычитания называют разностью и определяют
следующим образом.
Разностью
множеств
А и
В называется
множество, содержащее все элементы,
которые принадлежат множеству А
и не
принадлежат множеству В,
обозначается А
В. А
В = {х
А и х
В}.
Х
Y
= {0, 1, 3, 5} {1, 2, 3, 4} = {0, 5}.
Если мы найдем разность множеств Y
и Х, то результат будет выглядеть так:
Y
X
= {2; 4}. Таким
образом, разность множеств не обладает
переместительным (коммутативным)
свойством.
Е
изобразить множестваА
и
В при
помощи кругов Эйлера, то разность данных
множеств изобразится заштрихованной
областью.
А
В
Если множества не
имеют общих элементов, то их разность
будет изображаться так:
В
А
А
В
Если одно из
множеств является подмножеством другого,
то их разность будет изображаться так:
А
В
В
Пересечение
– более «сильная» операция, чем вычитание.
Поэтому порядок выполнения действий в
выражении А
В
∩ С
такой: сначала
находят пересечение множеств В
и С,
а затем полученное множество вычитают
из множества А.
Что касается
объединения и вычитания множеств, то
их считают равноправными. Например, в
выражении А В U С надо сначала выполнить
вычитание (из А вычесть В), а затем
полученное множество объединить с
множеством С.
Вычитание множеств
обладает рядом свойств:
-
(А В) С = (А С)
В. -
(А U В) С = (А С) U
(В С). -
(А В) ∩ С = (А ∩ С)
(В ∩С). -
А (В U С) = (А В) ∩
(А С). -
А (В ∩ С) = (А В)
U (А С).
Соседние файлы в папке теория 1 курс
- #
- #
- #
- #
- #
- #
Пересечение, объединение и разность множеств
- Пересечение множеств
- Объединение множеств
- Универсум и отрицание
- Свойства операций пересечения и объединения
- Разность множеств
- Формулы включений и исключений
- Примеры
Пересечение множеств
Пересечением множеств A и B называют множество, содержащее те и только те элементы, которые входят одновременно как в множество A, так и в множество B:
$$ A cap B = {x|x in Bbb A и x in Bbb B } $$
Если множества не пересекаются, то $A cap B = varnothing $ – пустое множество в пересечении. Если $B subseteq A$ – подмножество, то $A cap B = B$ – пересечением будет меньшее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A cap B$ = {3;5}.
Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A cap B$ = {f|f-квадрат}.
Если A = ${n|n⋮3, n in Bbb N }$ – натуральные числа, кратные 3, B = ${n|n⋮5, n in Bbb N }$ – натуральные числа, кратные 5, то $A cap B = {n|n⋮15, n in Bbb N}$ – натуральные числа, кратные 15.
Если A = {a│a-слон}, B = {a|a-птица}, то $A cap B = varnothing$.
Объединение множеств
Объединением – множеств A и B называют множество, содержащее те и только те элементы, которые входят хотя бы в одно из множеств, A или B:
$$ A cup B = { x|x in Bbb A или x in Bbb B } $$
Если $B subseteq A$ – подмножество, то $A cap B = A$ – объединением будет большее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A cup B$ = {1;3;5;7;9;11}.
Если $A = {x|x^2-4 = 0, x in Bbb R}, B = {x|x+3 = 2, x in Bbb R }, то A cup$ B = {-2;-1;2}
Если $A = {n│n in Bbb Z }$- все целые числа, $B = {x|x = frac{a}{b}, a in Bbb Z, b in Bbb N }$ – все дроби, то $A cup B = {x│x in Bbb Q}$ – множество рациональных чисел. Заметим, что в данном случае $A subset B$.
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:
Примеры универсумов:
При рассмотрении целочисленных задач, универсум – это множество целых чисел.
При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Отрицание (абсолютное дополнение) множества A – множество всех элементов универсума, не принадлежащих A:
$$ bar{A} = {x|x notin A } $$
Читается «не A».
У отрицания есть любопытное свойство: $bar{bar{Α}} = Α $(два раза «нет» – это «да»).
Например:
Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $bar{A} = {1;2;6;7}$
Если U = ${x|x in Bbb R}$ – все действительные числа, A = ${x|x gt 0, x in Bbb R }$ – все положительные действительные числа, то $ bar{A} = {x|x le 0, x in Bbb R}$.
Свойства операций пересечения и объединения
$A cap B = B cap A$
$ A cup B = B cup A $
$(A cap B) cap C = A cap (B cap C)$
$ (A cup B) cup C = A cup ( B cup C) $
$(A cup B) cap C = (A cap C) cup (B cap C)$
$ (A cap B) cup C = (A cup C) cap (B cup C) $
$A cap A = A$
$ A cup A = 0 $
Взаимодействие с отрицанием, пустым множеством и универсумом
$A cap bar{A} = varnothing $
$A cap U = A$
$A cap varnothing = varnothing$
$A cup bar{A} = U $
$A cup U = U$
$A cup varnothing = A$
$ overline{(A cap B)} = bar{A} cup bar{B} $
$ overline{(A cup B)} = bar{A} cap bar{B} $
$ (A cup B) cap A = A $
$ (A cap B) cup A = A $
Разность множеств
Разностью двух множеств A и B называют множество, в которое входят все элементы из множества A, не принадлежащие множеству B:
$$ AB = {x|x in Bbb A , x notin B} $$
Читается «A без B».
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:
Получается, что отрицание – частный случай разности: $ bar{A} = {x|x in Bbb U, x notin A } $= UA
«Не A» – это «универсум без A».
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A cap B)$.
Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A cup B)$?
Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A cup B) = n(A)+ n(B)-n(A cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.
Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.е. отнять сумму $(n(A cap B)+n(A cap C)+n(B cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A cap B cap C)$; значит, его нужно «вернуть».
Получаем:
$$ n(A cup B cup C) = n(A)+ n(B)+n(C)- $$
$$ -(n(A cap B)+n(A cap C)+n(B cap C) )+n(A cap B cap C) $$
Примеры
Пример 1. Найдите пересечение данных множеств:
а) A = {0;5;8;10},
B = {3;6;8;9}
$A cap B$ = {8}
$б) A = {x|x lt 3, x in Bbb R}, $
$ B = {x|x gt 1, x in Bbb R} $
$A cap B = {x|1 lt x lt 3, x in Bbb R}$ – отрезок
$в) A = {x|x lt 3, x in Bbb R}, $
$ B = {x|x gt 1, x in Bbb N} $
$A cap B = {x|1 lt x lt 3, x in Bbb N } или A cap B = {2}$ – одна точка
г) A = {f|f-правильный многоугольник},
B = {f|f-четырехугольник}
$A cap B = {f|f-квадрат}$
Пример 2. Найдите объединение данных множеств:
а) A = {0;5;8;10}, B = {3;6;8;9}
$A cup B$ = {0;3;5;6;8;9;10}
б) A = {1;2}, B = {1;2;3;4}
$A subset B$ – строгое подмножество
$A cup B $ = B = {1;2;3;4}
$в) A = {x|x lt 1, x in Bbb R}, B = {x|x gt 1,x in Bbb R} $
$A cup B = {x|x neq 1, x in Bbb R }$
$г) A = {n│n⋮3, n in Bbb Z}, B = {n|n⋮9,n in Bbb N} $
$B subset A$ – строгое подмножество
$ A cup B = A = {n│n⋮3, n in Bbb Z} $
Пример 3. Найдите отрицание данного множества на данном универсуме:
а) U = {1;2;3;4;5}, A = {2;3}
$ bar{A} = {1;4;5}$
б) U = ${x│x in Bbb Q }$, A = ${ frac{4}{5}, frac{7}{8} }$
$ bar{A} = {x|x neq frac{4}{5}, x neq frac{7}{8}, x in Bbb Q} $
$в) U = {x│x in Bbb R}, A = {x|x ge 2, x in Bbb R} $
$bar{A} = {x|x lt 2, x in Bbb R}$
г) U = { 0;1}, A = { 0}
$ bar{A} = {1}$
Пример 4. Найдите обе разности данных множеств:
а) A = {0;1;2;3;4}, B = {2;4}
AB = {0;1;3}, $BA = {∅}$
б) A = {0;1;3}, B = {2;4;6}
AB = {0;1;3}, BA = {2;4;6}
$в) A = {x|x gt 1, x in Bbb R}, $
$ B = {x|x lt 3, x in Bbb R} $
AB $ = {x|x ge 3, x in Bbb R}$
BA $ = {x|x le 1,x in Bbb R} $
$ г*) A = {(x,y)|x gt 0, x in Bbb R, y in Bbb R} $
$ B = {(x,y)|x le 5, x in Bbb R, y in Bbb R} $
AB $ = {(x,y)|x gt 5, x in Bbb R, y in Bbb R} $
BA $ = {(x,y)|x le 0, x in Bbb R, y in Bbb R} $
Пример 5. Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?
n(U) = 100
n(A) = 28, n(B) = 30, n(C) = 42
$ n(A cap B) = 8, n(B cap C) = 5, n(A cap C) = 10 $
$n(A cap B cap C) = 3$
Всего программистов:
$ n(A cup B cup C) = n(A)+n(B)+n(C)- $
$ (n(A cap B)+n(B cap C)+n(A cap C) )+n(A cap B cap C) $
$n(A cup B cup C) = 28+30+42-(8+5+10)+3 = 100-23+3 = 80$
Число не умеющих программировать:
$n(U)-n(A cup B cup C) = 100-80 = 20$
Ответ: 20 человек
Симметрическая разность множеств
Симметрическую разность можно описать двумя способами:
Например, если А=<1,2,3,4>, B=<3,4,5,6>, то А Δ В = (А В) ∪ (В А) = <1,2>∪ <5,6>=
Онлайн калькулятор позволяет найти симметрическую разность множеств A и B (А Δ B).
Также доступны следующие операции над множествами: объединение, пересечение, разность.
Онлайн калькуляторы
Calculatorium.ru — это бесплатные онлайн калькуляторы для самых разнообразных целей: математические калькуляторы, калькуляторы даты и времени, здоровья, финансов. Инструменты для работы с текстом. Конвертеры. Удобное решение различных задач — в учебе, работе, быту.
Актуальная информация
Помимо онлайн калькуляторов, сайт также предоставляет актуальную информацию по курсам валют и криптовалют, заторах на дорогах, праздниках и значимых событиях, случившихся в этот день. Информация из официальных источников, постоянное обновление.
1.1.4 Операции над множествами
В результате операций над множествами из одних множеств могут получаться другие множества. Основные из этих операций – объединение, пересечение и дополнение множеств. Кроме того, часто применяются операции разности и симметрической разности множеств.
Объединение множеств. Пусть заданы множества A и В. Объединение этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат или множеству A, или множеству B (т.е. хотя бы одному из них). Объединение двух множеств обозначают как 
Аналогично определяется объединение нескольких множеств. Пусть даны множества 


Пересечение множеств. Пусть заданы множества A и В. Пересечение этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат и множеству A, и множеству B (т.е. обоим множествам сразу). Пересечение двух множеств обозначают как 
Аналогично определяется пересечение нескольких множеств. Пусть даны множества 


Дополнение множества. Пусть задано множество A. Дополнение этого множества – множество, состоящее из всех тех и только тех элементов, которые не принадлежат множеству A. Дополнение множества обозначают как 
Разность множеств. Пусть заданы множества A и В. Разность этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству A, но не принадлежат множеству B. Разность множеств обозначают как S = A B.
Симметрическая разность множеств. Пусть заданы множества A и В. Симметрическая разность этих множеств – множество, состоящее из всех тех и только тех элементов, которые принадлежат или множеству A, или множеству B, но не им обоим сразу. Симметрическую разность множеств обозначают как S = A B.
Следует обратить внимание, что операции пересечения и объединения выполняются с несколькими множествами (двумя или более), а операция дополнения – с одним множеством. Операции разности и симметрической разности выполняются с двумя множествами.
Операции разности и симметрической разности можно выразить через операции пересечения, объединения и дополнения:

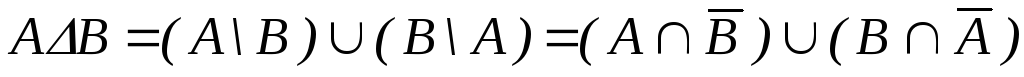
Эти равенства можно доказать на основе определений операций над множествами.
Пример 1.1 – Даны множества: A = <2, 7, 9, 12>, B = <3, 6, 7, 12, 15>. Выполнить над этими множествами операции, рассмотренные выше.
Чтобы найти дополнения множеств A и B, необходимо уточнить, что в данной задаче имеется в виду под универсальным множеством. Пусть под ним имеется в виду все множество целых чисел (обозначим его как Z). Тогда дополнение множества A можно записать как 

1Числа во множествах записаны по возрастанию только для удобства. На самом деле, порядок элементов во множествах безразличен. Поэтому, например, пересечение множествAиBможно записать и как <7, 12>, и как <12, 7>.
2Следует обратить внимание, что в операциях пересечения, объединения, а также симметрической разности порядок множеств, с которыми выполняется операция, безразличен:

Пример 1.2 – Даны множества: A = <a | 5 a < 20>, B = <b | b 17>, C = <c | 10 < c 12>. Приведем некоторые примеры операций над этими множествами:
X = C A =
X = 
X = 
Диаграммы Эйлера-Венна
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принцип построения
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
- В первую очередь необходимо начертить диаграмму, заштриховав все множества, находящиеся в левой части равенства.
- Следующим шагом будет начертание другой диаграммы и штриховка всех множеств, которые находятся в правой части равенства.
- В случае, когда на диаграммах заштрихована одна и та же область, торжество истинно.
Дополнение множества
Дополнением к множеству A является множество (overline A) , которое состоит из элементов, не входящих в А.
При этом не все элементы, не являющиеся элементами А, могут быть включены в (overline A.) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение overline A определяется следующим образом:
Таким образом выглядит дополнение (overline A) графически:
Объединение множеств
Объединением множеств A и B называют множество (A;cup;B) , которое состоит из элементов, принадлежащих хотя бы одному из множеств.
Объединение записывается следующим образом:
Таким образом объединение множеств выглядит графически:
Пересечение множеств
Пересечением множеств A и B является множество (A;cap;B) , которое состоит из элементов, входящих в оба множества.
Пересечение множеств записывается следующим образом:
Таким образом пересечение множеств выглядит графически:
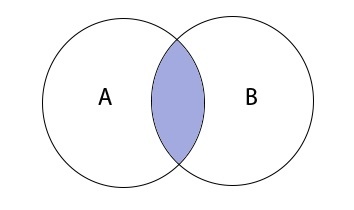
Симметричная разность множеств
Симметричная разность A B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество
Разность множеств записывается следующим образом:
(Abigtriangleup B=(Abackslash B)cup(Bbackslash A))
Таким образом разность выглядит графически:
Разность множеств
Разностью A B является множество элементов A, не входящих в B.
Разность множеств записывается следующим образом:
Таким образом разность выглядит графически:
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
Предположим, что перед нами конъюнкция множеств (A;wedge;B)
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.
Теперь отобразим инверсию, заштриховав область за пределами множеств.
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.
Проведем аналогичную операцию с множеством B.
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
Задача
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
Необходимо найти (n(Р;cup;Ф;cup;К);=;n;(U;backslash;(Р;cap;Ф;cap:К)))
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в (Р;cap;Ф;cap:К) три элемента, а в множестве (Р;cap;Ф) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
- множество задач по алгебре («А»);
- множество задач по геометрии («Г»);
- множество задач по тригонометрии («Т»).
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
Бинарные операции над упорядоченными множествами
В предыдущей статье я писал о бинарных операциях над неупорядоченными множествами. В этой статье мы рассмотрим алгоритмы с меньшей сложностью выполнения, для упорядоченных множеств. 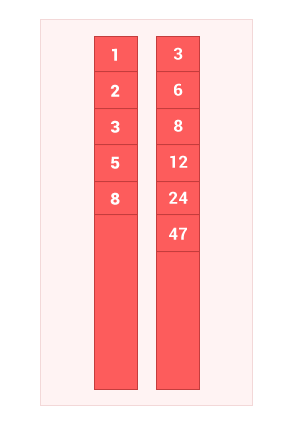
I. Пересечение упорядоченных множеств
Пересечение двух упорядоченных множеств A и B — это множество только с теми элементами A и B, которые одновременно принадлежат обоим множествам, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных множеств A и B соответственно.
Сделал небольшую анимацию, чтобы показать как работает алгоритм.
Пример реализации на javascript:
Обращение к функции:
II. Разность упорядоченных множеств
Разность двух упорядоченных множеств A и B — это множество с элементами A, не совпадающими с элементами B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
III. Объединение упорядоченных множеств
Объединение двух упорядоченных множеств A и B — это множество с элементами A и элементы множества B, без дублей. Сложность алгоритма O(m+n), где m и n — длины входных упорядоченных множеств A и B соответственно.
IV. Симметрическая разность упорядоченных множеств
Симметрическая разность двух упорядоченных множеств A и B — это такое множество, куда входят все те элементы первого упорядоченного множества, которые не входят во второе упорядоченное множество, а также те элементы второго упорядоченного множества, которые не входят в первое упорядоченное множество. Сложность алгоритма O(2(m+n)), где m и n — длины входных упорядоченных множеств A и B соответственно.
По сути это вычитание множеств, сначала A из B, затем B из A.