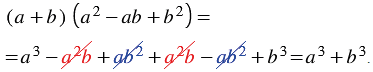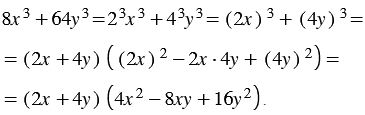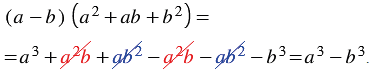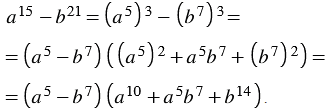Формула суммы кубов
Возьмём формулу куба суммы (см. §23 данного справочника):
$$ (a+b)^3 = a^3+3a^2 b+3ab^2+b^3 $$
и найдём из неё сумму двух кубов:
$$ a^3+b^3 = (a+b)^3-3a^2 b-3ab^2 = (a+b)^3-3ab(a+b) = $$
$$= (a+b)((a+b)^2-3ab) = (a+b)(a^2+2ab+b^2-3ab) =$$
$$ = (a+b)(a^2-ab+b^2 ) $$
Скобка $(a^2-ab+b^2 )$ называется неполным квадратом разности.
Полный квадрат разности – это $ (a^2-2ab+b^2 ) = (a-b)^2 $
Мы получили формулу для разложения суммы двух кубов на множители:
$$ a^3+b^3 = (a+b)(a^2-ab+b^2 ) $$
Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности.
$$ a^3+b^3 = (a+b)(a^2-ab+b^2 )$$
Формула разности кубов
Возьмём формулу куба разности (см. §23 данного справочника):
$$ (a-b)^3 = a^3-3a^2 b+3ab^2-b^3 $$
и найдём из неё разность двух кубов:
$$ a^3-b^3 = (a-b)^3+3a^2 b-3ab^2 = (a-b)^3+3ab(a-b) = $$
$$ = (a-b)((a-b)^2+3ab) = (a-b)(a^2-2ab+b^2+3ab) = $$
$$ = (a-b)(a^2+ab+b^2 ) $$
Скобка $(a^2+ab+b^2 )$ называется неполным квадратом суммы.
Полный квадрат суммы – это $(a^2+2ab+b^2 ) = (a+b)^2$
Мы получили формулу для разложения разности двух кубов на множители:
$$ a^3-b^3 = (a-b)(a^2+ab+b^2 ) $$
Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат их суммы.
$$ a^3-b^3 = (a-b)(a^2+ab+b^2 ) $$
Примеры
Пример 1. Разложите на множители:
а) $ x^3+y^3 = (x+y)(x^2-xy+y^2 )$
б) $ m^3-n^3 = (m-n)(m^2+mn+n^2 ) $
в) $ 8a^3+1 = (2a)^3+1^3 = (2a+1)(4a^2-2a+1) $
г) $125-64y^3 = 5^3-(4y)^3 = (5-4y)(25+20y+16y^2 )$
д) $ frac{1}{8} k^6-8 = ( frac{1}{2} k^2 )^3-2^3=(frac{1}{2} k^2-2)(frac{1}{4} k^4+k^2+4) $
е) $27+ frac{m^3}{125} = 3^3+(frac{m}{5})^3 = (3+frac{m}{5})(9-frac{3m}{5}+frac{m^2}{25})$
Пример 2. Докажите что выражения $19^3-11^3$ кратно 8
$$ frac{19^3-11^3}{8} = frac{(19-11)(19^2+19cdot11+11^2 )}{8} = frac{8(19^2+19cdot11+11^2 )}{8} = $$
$ = 19 ^2+19cdot11+11^2 $
Что и требовалось доказать.
Пример 3*. Дайте геометрическое объяснение формуле суммы кубов (аналогичная задача – см. Пример 5 §23 данного справочника).
Рассмотрим куб со стороной (a+b), в противоположные углы которого вписаны кубы со сторонами a и b.
Объемы кубов: $V_{a+b} = (a+b)^3, V_a = a^3, V_b = b^3$
Объём фигуры, закрашенной оранжевым: $V_{ор} = a(a+b)^2-V_a = a(a^2+2ab+b^2 )-a^3$ $= 2a^2 b+ab^2$
Объём фигуры, закрашенной синим: $V_{син} = b(a+b)^2-V_b = b(a^2+2ab+b^2 )-b^3$ $= a^2 b+2ab^2$
Общий объём:
$$ V_{a+b} = V_a+V_b+V_{ор}+V_{син} $$
$$ (a+b)^3 = a^3+b^3+2a^2 b+ab^2+a^2 b+2ab^2 $$
$$ a^3+b^3 = (a+b)^3-3a^2 b-3ab^2 = (a+b)^3-3ab(a+b) = $$
$$ = (a+b)((a+b)^2-3ab) = (a+b)(a^2+2ab+b^2-3ab) = $$
$$ = (a+b)(a^2-ab+b^2 )$$
Мы получили формулу суммы кубов.
В данной публикации мы рассмотрим одну из формул сокращенного умножения, а именно, разложение разности кубов на множители. Также разберем примеры решения задач для закрепления представленного материала.
-
Формула разности кубов
- Доказательство формулы
- Примеры задач
Формула разности кубов
Разность кубов чисел/выражений равняется произведению их разности на неполный квадрат их суммы.
a3 – b3 = (a – b)(a2 + ab + b2)
Полный квадрат суммы выглядит следующим образом: (a + b)2 = a2 + 2ab + b2. В нашем случае во второй скобке напротив второго слагаемого нет множителя 2, поэтому выражение является неполным.
Формула верна и в обратную сторону:
(a – b)(a2 + ab + b2) = a3 – b3
Примечание: a3 – b3 ≠ (a – b)3
Доказательство формулы
Достаточно просто умножить скобку (a – b) на (a2 + ab + b2), чтобы убедиться в том, что выражение верно, т.е. пойти от обратного:
(a – b)(a2 + ab + b2) = a3 + a2b + ab2 – a2b – ab2 – b3 = a3 – b3.
Примеры задач
Задание 1
Представьте в виде произведения множителей выражение: (7x)3 – 53.
Решение
(7x)3 – 53 = (7x – 5)((7x)2 + 7x ⋅ 5 + 52) = (7x – 5)(49x2 + 35x + 25)
Задание 2
Представьте выражение 512x3 – 27y3 в виде разности кубов и разложите его на множители.
Решение
512x3 – 27y3 = ((8x)3 – (3y)3) = (8x – 3y)((8x)2 + 8x ⋅ 3y + (3y)2) = (8x – 3y)(64x2 + 24xy + 9y2)
Алгебра
7 класс
Урок № 30
Сумма кубов. Разность кубов
Перечень вопросов, рассматриваемых в теме:
- Формулы сокращённого умножения.
- Сумма кубов, разность кубов.
- Разложение многочлена на множители.
- Тождественные преобразования.
- Вычисление значения числовых выражений.
Тезаурус:
Формулы сокращённого умножения.
(a + b)2 = a2 + 2ab + b2
(a – b)2 = a2 – 2ab + b2
(a + b)(a – b) = a2 – b2
a3 + b3= (a + b)(a 2– ab + b2)
a3 – b3= (a – b)(a2 + ab + b2)
Применение:
- упрощение умножения многочленов;
- разложение многочлена на множители;
- вычисление значения числового выражения;
- тождественные преобразования.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Формула суммы кубов.
Рассмотрим произведение;
(a + b)(a2 – ab + b2).
Применив правило умножения многочленов, и приведя подобные члены, получим:
(a + b)(a2 – ab + b2) = a3 – a2b + ab2 + ba2 – ab2 +b3 = a3 + b3
a3 + b3 = (a + b)(a2 – ab + b2)
Равенство называют формулой суммы кубов.
Читается так: «сумма кубов двух чисел равна произведению суммы этих чисел и неполного квадрата их разности».
Формула разности кубов.
Аналогично докажем формулу разности кубов.
(a – b)(a2 + ab + b2) = a3 + a2b + ab2 – ba2 – ab2 – b3= a3 – b3
Читается так: «разность кубов двух чисел равна произведению разности этих чисел и неполного квадрата их суммы».
a3 – b3= (a – b)(a2+ ab + b2)
Выражения (a2+ ab + b2) и (a2– ab + b2) называют неполным квадратом суммы или разности.
Формула задаёт разложение многочленов:
a3 + b3 и a3 – b3 на два множителя:
(a + b)(a2 – a b+ b2) и (a – b)(a2+ ab + b2).
Формулы суммы и разности кубов используют для упрощения вычислений.
Разбор решения заданий тренировочного модуля.
Задача 1.
Выполните умножение многочленов:
- ( x + 3)(x2 –3x +9) = x3 + 33 = x3 + 27.
- (2x – 3y)(4x2 +6xy + 9y2) = (2x)3 – (3y)3 = 8x3 –27y3.
Задача 2.
Разложите многочлен на множители:
- x3 – 8 y3 = x3 – (2y)3 = (x – 2y) (x2 +2xy + 4y2 )
- 64 a3 – 27c3 = (4a)3 – (3c)3 = (4a – 3c)(16a2 +12 ac + 9c2).
Задача 3.
Упростите выражение:
(x +2)(x2 – 2x +4) – x(x–3)(x+3).
Решение:
x3 + 23 – x(x2 – 9) = x3 + 8 – x3 + 9x = 8 + 9x.
Ответ: 8 + 9x.
Задача 4.
Доказать, что выражение 1233 + 273 кратно 50.
Используем формулу:
a3 + b3 = (a + b)(a2 – ab + b2),
получим: (123 + 27)(1232 –123 · 27 + 272) =150 · (1232 –123 · 27 + 272).
Произведение делится на 50, так как первый множитель делится на 50: (150 : 50 = 3). Нет необходимости считать значение выражения в скобках. Утверждение доказано.
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Алгебра
- Формулы сокращенного умножения
- Сумма и разность кубов двух выражений
Сумма кубов двух выражений
Найдем произведение двучлена 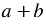
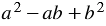
Итак, мы получили тождество:
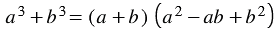
Многочлен 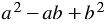
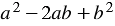
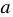
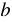
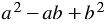
Правило:
Сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.
Пример:
Разложите на множители многочлен 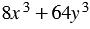
Решение:
Используя свойства степени, представляем данный многочлен в виде суммы кубов двух выражений, получаем:
Разность кубов двух выражений
Найдем произведение двучлена 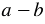
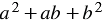
Итак, мы получили тождество:
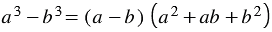
Многочлен 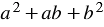
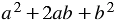
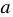
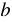
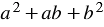
Правило:
Разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.
Пример:
Разложите на множители многочлен 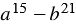
Решение:
Используя свойства степени, представляем данный многочлен в виде разности кубов двух выражений, получаем:
Советуем посмотреть:
Произведение разности и суммы двух выражений. Разность квадратов двух выражений.
Квадрат суммы и квадрат разности двух выражений
Введение в алгебру
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
Тождественно равные выражения. Тождества
Степень с натуральным показателем
Свойства степени с натуральным показателем
Одночлены
Многочлены
Сложение и вычитание многочленов
Умножение одночлена на многочлен
Умножение многочлена на многочлен
Разложение многочленов на множители
Формулы сокращенного умножения
Функции
Системы линейных уравнений с двумя переменными
Алгебра
Правило встречается в следующих упражнениях:
7 класс
Номер 681,
Мерзляк, Полонский, Якир, Учебник
Номер 682,
Мерзляк, Полонский, Якир, Учебник
Номер 690,
Мерзляк, Полонский, Якир, Учебник
Номер 691,
Мерзляк, Полонский, Якир, Учебник
Номер 696,
Мерзляк, Полонский, Якир, Учебник
Номер 714,
Мерзляк, Полонский, Якир, Учебник
Номер 721,
Мерзляк, Полонский, Якир, Учебник
Номер 730,
Мерзляк, Полонский, Якир, Учебник
Номер 785,
Мерзляк, Полонский, Якир, Учебник
Номер 2,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 24,
Мерзляк, Полонский, Якир, Учебник
Номер 36,
Мерзляк, Полонский, Якир, Учебник
Номер 38,
Мерзляк, Полонский, Якир, Учебник
Номер 76,
Мерзляк, Полонский, Якир, Учебник
Номер 121,
Мерзляк, Полонский, Якир, Учебник
Номер 123,
Мерзляк, Полонский, Якир, Учебник
Номер 159,
Мерзляк, Полонский, Якир, Учебник
Номер 180,
Мерзляк, Полонский, Якир, Учебник
Номер 189,
Мерзляк, Полонский, Якир, Учебник
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Онлайн калькулятор поможет найти разность кубов двух выражений, которая равна произведению разности этих выражений на неполных квадрат их суммы.
Формула разность кубов: a3 – b3 = (a – b)(a2 + ab + b2)
Разность кубов двух выражений |
| a = |
| b = |
|
|
Разделитель групп разрядов
Округлить до
Число прописью
Скачать калькулятор
Рейтинг: 2.5 (Голосов 37)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Формулы сокращенного умножения | Квадрат суммы | Квадрат разности | Разность квадратов |
| Куб суммы | Куб разности | Сумма кубов | Разность кубов |