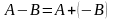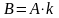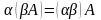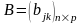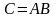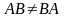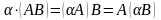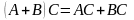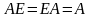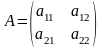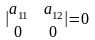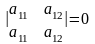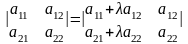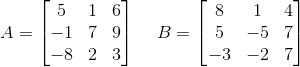Мы уже знакомы с темой «Сложение матриц». Вычитание матриц аналогично их сложению. Данное действие требует от студентов лишь арифметических знаний и внимательности. Перед изучением новой темы рекомендуем повторить, что такое матрица. Особое внимание следует уделить ее размеру.
Онлайн-калькулятор
Приступим к рассмотрению действия над матрицами, которое называется вычитанием.
Как и при сложении, вычитать будем те матрицы, которые имеют одинаковый размер. Вычесть из матрицы «шесть на восемь» можно только матрицу «шесть на восемь», а из матрицы «два на четыре» только матрицу «два на четыре».
При вычитании матриц справедливо равенство Amn−Bmn=CmnA_{mn}-B_{mn}=C_{mn}. Оно означает, что вычитая из матрицы AA порядка m×nmtimes n матрицу BB порядка m×nmtimes n, получим матрицу CC такого же порядка.
Правило вычитания матриц
Разность матриц PP и KK получается вычитанием их соответствующих элементов. Первый элемент новой матрицы получается вычитанием из первого элемента матрицы PP первого элемента матрицы KK, второй элемент новой матрицы — вычитанием из второго элемента матрицы PP второго элемента матрицы KK. Также поступаем с остальными элементами.
Найдем разность A=(a11a12…a1na21a22…a2n…………am1am2…amn)A=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{m1}&a_{m2}&…&a_{mn}end{pmatrix} и B=(b11b12…b1nb21b22…b2n…………bm1bm2…bmn)B=begin{pmatrix}b_{11}&b_{12}&…&b_{1n}\b_{21}&b_{22}&…&b_{2n}\…&…&…&…\b_{m1}&b_{m2}&…&b_{mn}end{pmatrix}.
A−B=(a11a12…a1na21a22…a2n…………am1am2…amn)−(b11b12…b1nb21b22…b2n…………bm1bm2…bmn)A-B=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{m1}&a_{m2}&…&a_{mn}end{pmatrix}-begin{pmatrix}b_{11}&b_{12}&…&b_{1n}\b_{21}&b_{22}&…&b_{2n}\…&…&…&…\b_{m1}&b_{m2}&…&b_{mn}end{pmatrix}=
=(a11−b11a12−b12…a1n−b1na21−b21a22−b22…a2n−b2n…………am1−bm1am2−bm2…amn−bmn)= begin{pmatrix}a_{11}-b_{11}&a_{12}-b_{12}&…&a_{1n}-b_{1n}\a_{21}-b_{21}&a_{22}-b_{22}&…&a_{2n}-b_{2n}\…&…&…&…\a_{m1}-b_{m1}&a_{m2}-b_{m2}&…&a_{mn}-b_{mn}end{pmatrix}.
Алгоритм выполнения вычитания:
- определяем размеры матриц;
- если матрицы имеют одинаковый размер, выполняем вычитание (в противном случае найти разность невозможно).
Пример 1
Найти разность матриц GG и HH, если G=(39214321925171534)G=begin{pmatrix}39&21&4\32&19&25\17&15&34end{pmatrix} и H=(451915161833241610)H=begin{pmatrix}45&19&15\16&18&33\24&16&10end{pmatrix}.
Матрицы имеют размер 3×33times 3. Для нахождения разности G−HG-H из соответствующих элементов матрицы GG нужно вычесть соответствующие элементы матрицы HH:
G−H=(39214321925171534)−(451915161833241610)=(39−4521−194−1532−1619−1825−3317−2415−1634−10)=G-H=begin{pmatrix}39&21&4\32&19&25\17&15&34end{pmatrix}-begin{pmatrix}45&19&15\16&18&33\24&16&10end{pmatrix}=begin{pmatrix}39-45&21-19&4-15\32-16&19-18&25-33\17-24&15-16&34-10end{pmatrix}=
=(−62−11161−8−7−124)=begin{pmatrix}-6&2&-11\16&1&-8\-7&-1&24end{pmatrix}
Пример 2
Найти разность матриц TT и FF, если T=(243716152433461168571324)T=begin{pmatrix}24&37&16\15&24&33\46&11&68\57&13&24end{pmatrix} и F=(3954295119313491843515)F=begin{pmatrix}39&54&29\51&19&31\34&9&18\43&5&15end{pmatrix}.
Матрицы имеют размер 4×34times 3. Для нахождения разности T−FT-F из соответствующих элементов матрицы TT нужно вычесть соответствующие элементы матрицы FF:
T−F=(243716152433461168571324)−(3954295119313491843515)=(24−3937−5416−2915−5124−1933−3146−3411−968−1857−4313−524−15)=T-F=begin{pmatrix}24&37&16\15&24&33\46&11&68\57&13&24end{pmatrix}-begin{pmatrix}39&54&29\51&19&31\34&9&18\43&5&15end{pmatrix}=begin{pmatrix}24-39&37-54&16-29\15-51&24-19&33-31\46-34&11-9&68-18\57-43&13-5&24-15end{pmatrix}=
=(−15−17−13−3652122501489)=begin{pmatrix}-15&-17&-13\-36&5&2\12&2&50\14&8&9end{pmatrix}
Как видно из примеров, вычитание является таким же простым действием, как и сложение. Продолжайте изучение темы «матрицы» с нами, и тогда данная тема покажется вам очень простой.
Помощь с выполнением задач онлайн от экспертов на бирже Студворк!
Тест по теме «Вычитание матриц»
Разность матриц
Определение:
Разностью двух матриц называется
матрица той же размерности, что и
исходные, каждый элемент которой
определяется как разность соответствующих
элементов матриц.
Пусть
и
.
Тогда
,
где
,
,
.
Разность матриц
А и В обозначается символом
.
Замечание 1.
А, В, С
– матрицы одинаковых размеров.
Замечание 2.
Разность матриц
можно определить также следующим
образом:
,
где
– матрица, противоположная матрице В.
Произведение матрицы на число
В результате
умножения матрицы на число получается
матрица такой же размерности, что и
исходная, каждый элемент которой является
результатом произведения соответствующего
элемента исходной матрицы на число.
Пусть
,
k – число. Тогда
такая, что
(17) (
,
).
Обозначения:
или
.
Пример
3.
Найти матрицу
3А-2В, если
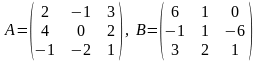
Решение
Имеем
,
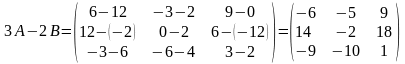
Справедливы
следующие свойства
А,
В – матрицы.
,
– числа.
Произведение матриц
Определение:
Пусть
,
.
Тогда
,
такая, что
,
,
,
.
Произведение
матрицы А на матрицу В обозначают
.
Следует
запомнить, что операция умножения
двух матриц вводится только для случая,
когда число столбцов первой матрицы
равно числу строк второй матрицы.
Следует
запомнить.
Из определения
произведения матриц следует, что элемент
матрицы АВ, стоящий в i-й
строке и k-м столбце, равен сумме
произведений элементов i-й строки
матрицы А на соответствующие элементы
k–го столбца матрицы
В.
Замечание 1.
Если матрицы А
и В квадратные одного размера, то
произведения АВ и ВА всегда
существуют.
Замечание 2.
Если матрицу А
можно умножить на матрицу В, а В
можно умножить на А, то, вообще
говоря,
.
Пример
4.
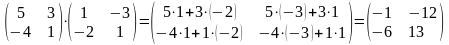
Пример
5.
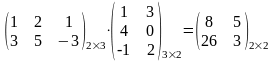
Пример
6.
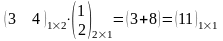
Справедливы
следующие свойства умножения матриц:
-
-
-
-
,
А – квадратная матрица, Е –
единичная матрица того же порядка.
Лекция № 2. § 2. Определители. Определитель второго порядка
Определение:
Определителем 2-го порядка называют
число, которое получается из элементов
квадратной матрицы
по указанному правилу.
Определитель
второго порядка:
.
Обозначение
определителя:
.
Определитель матрицы А также называют
ее детерминантом.
Замечание
Вычислить
определитель 2-го порядка означает найти
разность из произведения элементов,
стоящих на главной диагонали матрицы
(идущей из левого верхнего в правый
нижний угол) и произведения элементов,
находящихся на побочной, диагонали.
Пример
1.
Вычислить:

Свойства определителя второго порядка
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В данной публикации мы рассмотрим, как можно сложить две матрицы или вычесть одну из другой. Также приведем примеры для лучшего понимания изложенного материала.
-
Сумма матриц
- Свойства сложения матриц
- Разность матриц
- Примеры задач
Сумма матриц
Если сложить матрицы A и B одинакового размера, то получится матрица C того же размера, элементы которой равны сумме соответствующих элементов исходных матриц.
Am x n + Bm x n = Cm x n
Примечание: найти можно только сумму матриц одинакового размера.
Свойства сложения матриц
1. Переместительный закон
A + B = B + A
2. Асоциативный закон
(A + B) + C = A + (B + C)
3. Если к матрице прибавить нулевую матрицу, она не изменится.
A + Θ = A, где Θ – нулевая матрица.
4. Если из матрицы вычесть ее же, получится нулевая матрица.
A – A = Θ
Разность матриц
Разность матриц можно представить в виде сложения или умножения матрицы на число.
С = A – B = A + (-B) = A + (-1) ⋅ B
На деле это означает, что мы просто находим разность соответствующих элементов матриц.
Примечание: вычитать также, как и складывать, можно только матрицы одинакового размера.
Примеры задач
Задание 1
Найдем сумму матриц A и B, представленных ниже.
Решение:
Задание 2
Вычислим разность матриц A и B.
Решение:
Вычитание матриц
Вычитание матриц – это операция нахождения разности двух матриц одного и того же размера,
которая определяется через сложение матриц и через умножение матрицы на число.
Разность матриц А и В – это матрица С = А – В такого же размера
как исходные матрицы, получаемая из исходных путем прибавления к матрице А матрицы В,
умноженной на -1.
Таким образом, разность матриц выглядит так:
Аm×n – Вm×n = Аm×n + (-1) × Вm×n = Аm×n + (-Вm×n) = Сm×n
Фактически при вычитании матриц от элементов aij матрицы А отнимают соответствующие
элементы bij матрицы В:
aij – bij = aij + (-1) × bij = aij + (-bij) = сij
где i принимает значение от 1 до m, j имеет значения от 1 до n.
Рассмотрим пример вычитания матриц равного размера 3×3.
Даны две матрицы:
Найти разность матриц А и В.
Решение:
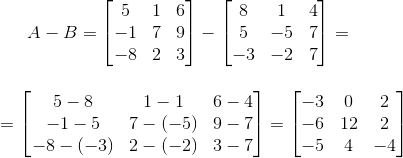
Вы также можете
в качестве элементов матрицы вводить целые и дробные числа, а также выражения с переменной x
(например, в ячейку матрицы можно ввести 2x, или sin(x), или даже ((x+2)^2)/lg(x)).
Полный список доступных функций можно найти в справке.
Содержание:
- Сумма матриц
- Разность матриц
- Свойства сложения и вычитания матриц:
Сложение и вычитание матриц, допускаются только для матриц одинакового размера.
Сумма матриц
Определение
Суммой матриц $A$ и $B$
одного размера называется матрица $C = A+B$ такого же
размера, получаемая из исходных путем сложения соответствующих элементов:
$$ A_{m times n}+B_{m times n}=C_{m times n} ; c_{i j}=a_{i j}+b_{i j}, i=overline{1 ; m}, j=overline{1 ; n} $$
Замечание
Складывать можно только матрицы одинакового размера.
Пример
Задание. Найти $A+B$, если
$ A=left( begin{array}{ll}{1} & {4} \ {2} & {3}end{array}right) $ ,
$ B=left( begin{array}{ll}{4} & {4} \ {5} & {2}end{array}right) $
Решение. $ C=A+B=left( begin{array}{cc}{1} & {4} \ {2} & {3}end{array}right)_{2 times 2}+left( begin{array}{ll}{4} & {4} \ {5} & {2}end{array}right)_{2 times 2}= $
$ =left( begin{array}{cc}{1+4} & {4+4} \ {2+5} & {3+2}end{array}right)=left( begin{array}{ll}{5} & {8} \ {7} & {5}end{array}right) $
Ответ. $ A+B=left( begin{array}{ll}{5} & {8} \ {7} & {5}end{array}right) $
Свойства сложения и вычитания матриц:
- Ассоциативность $ (A+B)+C=A+(B+C) $
- $ A+Theta=Theta+A $, где $Theta$ –
нулевая матрица соответствующего размера. - $ A-A=Theta $
- Коммутативность $ A+B=B+A $
Разность матриц
Разность двух матриц одинакового размера можно определить через операцию сложения матриц и через
умножение матрицы на число.
Вычитание матриц вводится следующим образом: $ A-B=A+(-1) cdot B $
То есть к матрице $A$ прибавляется матрица $B$, умноженная на (-1).
Определение
Разностью матриц $A$ и $B$ одного и того же размера называется матрица $C = A-B$ такого же размера,
получаемая из исходных путем прибавления к матрице $A$ матрицы $B$, умноженной на (-1).
На практике же от элементов матрицы $A$ попросту отнимают соответствующие
элементы матрицы $B$ при условии, что заданные матрицы одного размера.
Замечание
Вычитать можно только матрицы одинакового размера.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти матрицу $ C=A-3 B $,
если $ A=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right) $ ,
$ B=left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right) $
Решение. $ C=A-3 B=left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-3 cdot left( begin{array}{rr}{-1} & {1} \ {1} & {2} \ {0} & {0}end{array}right)= $
$ left( begin{array}{rr}{1} & {2} \ {2} & {-1} \ {3} & {0}end{array}right)-left( begin{array}{rr}{-3} & {3} \ {3} & {6} \ {0} & {0}end{array}right)=left( begin{array}{rr}{1-(-3)} & {2-3} \ {2-3} & {-1-6} \ {3-0} & {0-0}end{array}right)=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right) $
Ответ. $ C=left( begin{array}{rr}{4} & {-1} \ {-1} & {-7} \ {3} & {0}end{array}right) $
Читать дальше: умножение матриц.