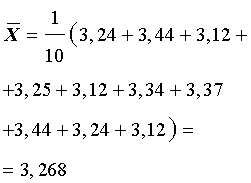Как найти разность моды ряда данных

Как найти разность моды ряда данных

Среднее арифметическое, размах, мода и медиана

  1. Алгебра
  2. Среднее арифметическое, размах, мода и медиана
Статистические характеристики

количество чисел

Калькулятор вычислит среднее арифметическое чисел, а также размах ряда чисел, моду ряда
чисел, медиану ряда. Для вычисления укажите количество чисел, добавьте числа и нажмите
рассчитать.

Среднее арифметическое, размах, мода и медиана

Средним арифметическим ряда чисел называется частное от деления суммы этих
чисел на число слагаемых.

Для ряда a1,a1,..,an среднее арифметическое вычисляется по
формуле:

begin{align}
& overline{a}=frac{a_1+a_2+…+a_n}{n}\
end{align}

Найдем среднее арифметическое для чисел 5,24, 6,97, 8,56, 7,32 и 6,23.

begin{align}
& overline{a}=frac{5,24+6,97+8,56+7,32+6,23}{5}=6.864\
end{align}

Размахом ряда чисел называется разность между наибольшим и наименьшим из
этих чисел.

Размах ряда 5,24, 6,97, 8,56, 7,32, 6,23 равен 8,56-5,24=3.32

Модой ряда чисел называется число, которое встречается в данном ряду чаще
других.

Ряд чисел может иметь более одной моды, а может не иметь моды совсем.

Модой ряда 32, 26, 18, 26, 15, 21, 26 является число 26, встречается 3 раза.

В ряду чисел 5,24, 6,97, 8,56, 7,32 и 6,23 моды нет.

Ряд 1, 1, 2, 2, 3 содержит 2 моды: 1 и 2.

Медианой упорядоченного ряда чисел с нечётным числом членов называется
число, записанное посередине, а медианой упорядоченного ряда чисел с чётным
числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного
ряда.

Медиана ряда 4, 1, 2, 3, 3, 1 равна 2.5.

Примеры

Рассмотрим примеры нахождения среднего арифметического чисел, а также размаха, медианы и моды
ряда.

  1. Среднее арифметическое чисел 30, 5, 23, 5, 28, 30

    begin{align}
    & overline{a}=frac{30+5+23+5+28+30}{6}=20frac{1}{6}\
    end{align}

    Размах ряда: 30-5=25

    Моды ряда: 5 и 30

    Медиана ряда: 25.5

  2. Среднее арифметическое чисел 40, 35, 30, 25, 30, 35

    begin{align}
    & overline{a}=frac{40+35+30+25+30+35}{6}=32frac{1}{2}\
    end{align}

    Размах ряда: 40-25=15

    Моды ряда: 30, 35

    Медиана ряда: 32.5

  3. Среднее арифметическое чисел 21, 18,5, 25,3, 18,5, 17,9

    begin{align}
    & overline{a}=frac{21+18,5+25,3+18,5+17,9}{5}=20,24\
    end{align}

    Размах ряда: 25,3-17,9=7,4

    Мода ряда: 18,5

    Медиана ряда: 18,5

Примеры

Примеры нахождения среднего арифметического отрицательных и вещественных чисел.

  1. Среднее арифметическое чисел 67,1, 68,2, 67,1, 70,4, 68,2

    begin{align}
    & overline{a}=frac{67,1+68,2+67,1+70,4+68,2}{5}=68,2\
    end{align}

    Размах ряда: 70,4-67,1=3,3

    Моды ряда: 67.1, 68.2

    Медиана ряда: 68.2

  2. Среднее арифметическое чисел 0,6, 0,8, 0,5, 0,9, 1,1

    begin{align}
    & overline{a}=frac{0,6+0,8+0,5+0,9+1,1}{5}=0.78\
    end{align}

    Размах ряда: 1,1-0,5=0.6

    Ряд не имеет моды

    Медиана ряда: 0.8

  3. Среднее арифметическое чисел -21, -33, -35, -19, -20, -22

    begin{align}
    & overline{a}=frac{(-21)+(-33)+(-35)+(-19)+(-20)+(-22)}{6}=-25\
    end{align}

    Размах ряда: (-19)-(-35)=16

    Ряд не имеет моды

    Медиана ряда: -21,5

  4. Среднее арифметическое чисел -4, -6, 0, -4, 0, 6, 8, -12

    begin{align}
    & overline{a}=frac{(-4)+(-6)+0+(-4)+0+6+8+(-12)}{8}=-1,5\
    end{align}

    Размах ряда: 8-(-12)=20

    Моды ряда: -4, 0

    Медиана ряда: -2

  5. Среднее арифметическое чисел 275, 286, 250, 290, 296, 315, 325

    begin{align}
    & overline{a}=frac{275+286+250+290+296+315+325}{7}=291\
    end{align}

    Размах ряда: 325-250=75

    Ряд не имеет моды

    Медиана ряда: 290

  6. Среднее арифметическое чисел 38, 42, 36, 45, 48, 45, 45, 42, 40, 47, 39

    begin{align}
    & overline{a}=frac{38+42+36+45+48+45+45+42+40+47+39}{11}=42frac{6}{11}\
    end{align}

    Размах ряда: 48-36=12

    Мода ряда: 45

    Медиана ряда: 42

  7. Среднее арифметическое чисел 3,8, 7,2, 6,4, 6,8, 7,2

    begin{align}
    & overline{a}=frac{3,8+7,2+6,4+6,8+7,2}{5}=6,28\
    end{align}

    Размах ряда: 7,2-3,8=3,4

    Мода ряда: 7,2

    Медиана ряда: 6,8

  8. Среднее арифметическое чисел 21,6, 37,3, 16,4, 12,6

    begin{align}
    & overline{a}=frac{21,6+37,3+16,4+12,6}{4}=21,025\
    end{align}

    Размах ряда: 37,3-12,6=24,7

    Мода ряда: 12,6

    Медиана ряда: 17,1

Источник

Среднее арифметическое нескольких величин – это отношение суммы величин к их количеству.

Правило. Чтобы вычислить среднее арифметическое нескольких чисел, нужно взять сумму этих чисел и разделить все на количество слагаемых. Частное и будет средним арифметическим этих чисел.

Например: найдем среднее арифметическое чисел 2; 6; 9; 15.

У нас четыре числа, значит надо их сумму разделить на четыре. Это и будет среднее арифметическое данных чисел: (2 + 6 + 9 + 15) : 4 = 8.

Размах ряда чисел – это разность между наибольшим и наименьшим из этих чисел.

Например: найдем размах чисел 2; 5; 8; 12; 33.

Наибольшее число здесь – 33, наименьшее – 2. Значит, размах составляет 31, т. е.: 33 – 2 = 31.

Мода ряда чисел – это число, которое встречается в данном ряду чаще других.

Например: найдем моду ряда чисел 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 8.

Чаще всего в этом ряде чисел встречается число 7 (3 раза). Оно и является модой данного ряда чисел.

Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине, а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел, записанных посередине.

Медианой произвольного ряда чисел называется медиана соответствующего упорядоченного ряда.

Например: в ряде чисел 2; 5; 9; 15; 21 медианой является число 9, находящееся посередине.

Найдем медиану в ряде чисел 4; 5; 7; 11; 13; 19.

Здесь четное количество чисел (6). Поэтому ищем не одно, а два числа, записанных посередине. Это числа 7 и 11. Находим среднее арифметическое этих чисел: (7 + 11) : 2 = 9. Число 9 является медианой данного ряда чисел.

  1. В институте сдавали зачет по высшей математике. В группе было 10 человек, и они получили соответствующие оценки: 3; 5; 5; 4; 4; 4; 3; 2; 4; 5.

    Какую оценку получали чаще всего? Каков средний балл сдавшей зачет группы?

  2. Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

    Найдите медиану и размах ряда.

  3. Дан ряд чисел: 175; 172; 179; 171; 174; 170; 172; 169.

    Найдите моду ряда и среднее арифметическое ряда.

  4. Имеются следующие данные о месячной заработной плате пяти рабочих (тг): 126000; 138000; 132000; 141000; 150000.

    Найдите среднюю заработную плату.

  5. Магазин продает 8 видов булочек по следующим ценам: 31; 22; 24; 27; 30; 36; 19; 27.

    Найдите разность среднего арифметического и медианы этого набора.

  6. Найдите объем и медиану числового ряда.

    9; 7; 1; 1; 11; 5; 1.

  7. Товарные запасы хлопчатобумажных тканей в магазине за первое полугодие составили (тыс. тг) на начало каждого месяца:

    I II III IV V VI VII
    37 34 35 32 36 33 38

    Определите средний товарный запас хлопчатобумажных тканей за первое полугодие.

  8. Провели несколько измерений случайной величины: 2,5; 2,2; 2; 2,4; 2,9; 1,8.

    Найдите среднее арифметическое этого набора чисел.

  9. Провели несколько измерений случайной величины: 6; 18; 17; 14; 4; 22.

    Найдите медиану этого набора чисел.

  10. Провели несколько измерений случайной величины:

    800; 3200; 2000; 2600; 2900; 2000. Найдите моду этого набора чисел.

  11. Магазин продает 8 видов хлеба по следующим ценам: 60, 75, 80, 85, 90, 100, 110, 120 тенге.

    Найдите разность среднего арифметического и медианы этого набора.

  12. Дан числовой ряд: 1; 7; 3; 8; 7; 12; 22; 7; 11; 22; 7,8.

    Найдите среднее арифметическое, размах и моду.

Источник

Статистические исследования числовых рядов. Статистические характеристики числовых рядов

Очень часто из-за дороговизны или слишком большого числа наблюдений невозможно получить полной информации об объектах, событиях или наблюдениях. По этой причине информацию получают на основе анализа части всего множества объектов, событий или наблюдений, называемой рядом числовых данных, рядом выборочных данных или, просто, выборкой.

Выборка представляет собой конечный ряд чисел (выборочных данных), количество чисел в котором называют объемом выборки

Для обеспечения достоверности информации об объектах, событиях или наблюдениях, полученных на основе статистических исследований числовых рядов (анализа выборочных данных), отбор выборочных данных должен носить случайный характер и иметь достаточно большой объем, то есть выборка должны быть репрезентативной (представительной).

Статистические исследования числовых рядов (рядов чисел, рядов выборочных данных) удобно проводить в соответствии со следующей схемой, которую мы изложим на примере следующей выборки   X :

X = {3,24;   3,44;   3,12;   3,25;   3,12;   3,34;   3,37;   3,44;   3,24;   3,12} (1)

  1. Определяем объем выборки (число чисел в числовом ряде).

    В числовом ряде (1) десять чисел, поэтому объем выборки равен   10.

  2. Вычисляем среднее арифметическое числового ряда   X   (среднее выборочное значение), которое обозначают статистическое исследование выборка ряд числовых данных выборочные данные объем выборки репрезентативная выборка среднее выборочное значение медиана выборки мода выборки размах выборки статистические характеристики числовых рядов таблица частот числового ряда.

    Для числового ряда (1)

    статистическое исследование выборка ряд числовых данных выборочные данные объем выборки репрезентативная выборка среднее выборочное значение медиана выборки мода выборки размах выборки статистические характеристики числовых рядов таблица частот числового ряда

    статистическое исследование выборка ряд числовых данных выборочные данные объем выборки репрезентативная выборка среднее выборочное значение медиана выборки мода выборки размах выборки статистические характеристики числовых рядов таблица частот числового ряда

    статистическое исследование выборка ряд числовых данных выборочные данные объем выборки репрезентативная выборка среднее выборочное значение медиана выборки мода выборки размах выборки статистические характеристики числовых рядов таблица частот числового ряда

  3. Производим упорядочение числового ряда по возрастанию (ранжирование числовых данных). Полученный числовой ряд, который обозначим   X1 ,   называют вариационным рядом.

    Для числового ряда   X   вариационный ряд   X1   имеет следующий вид:

    X1 = {3,12;   3,12;   3,12;   3,24;   3,24;   3,25;   3,34;   3,37;   3,44;   3,44}

  4. Вычисляем размах числового ряда   X ,   то есть разность между наибольшим числом из числового ряда и наименьшим числом из числового ряда.

    В числовом ряде   X ,  как и в вариационном ряде   X1 ,   число   3,44   является наибольшим числом, а число   3,12   является наименьшим числом. Поэтому размах числового ряда   X   равен

    3,44 – 3,12 = 0,32

  5. Вычисляем медиану числового ряда.

    В случае, когда объем выборки (число членов числового ряда) – чётное число, медианой числового ряда является число, равное половине суммы двух чисел, стоящих в середине вариационного ряда.

    Число членов ряда   X   равно чётному числу   10 ,   а в середине вариационного ряда   X1  стоят числа   3,24   и   3,25 .   Поэтому медиана числового ряда, которую обычно обозначают символом   Me ,   равна

    статистическое исследование выборка ряд числовых данных выборочные данные объем выборки репрезентативная выборка среднее выборочное значение медиана выборки мода выборки размах выборки статистические характеристики числовых рядов таблица частот числового ряда

    В случае, когда объем выборки (число членов числового ряда) –нечётное число, медианой числового ряда является число, стоящее в середине вариационного ряда.

    Например, медианой числового ряда

    {2;   3;   7;   9;   15}

    является число   7 .

  6. Составляем таблицу частот числового ряда.

    Если взглянуть на числа (выборочные данные), составляющие вариационный ряд   X1 ,   то можно заметить, некоторые числа повторяются, а другие встречаются лишь по одному разу. Это наблюдение приводит к следующему определению.

    ОПРЕДЕЛЕНИЕ 1. Если выборочное данное встречается в вариационном ряде   m   раз, то число   m   называют частотой (абсолютной частотой) этого выборочного данного.

    Воспользовавшись определением 1, сформируем для числового ряда   X   таблицу, содержащую две строки, которую называют таблицей частот (абсолютных частот) числового ряда. Для этого в первой строке таблицы запишем числа, составляющие вариационный ряд   X1 ,   причем запишем числа в порядке возрастания и без повторений. Во второй строке таблицы запишем частоты (абсолютные частоты), соответствующие числам из первой строки таблицы.

    ТАБЛИЦА ЧАСТОТ ЧИСЛОВОГО РЯДА

    Числа, составляющие вариационный ряд (без повторений) 3,12 3,24 3,25 3,34 3,37 3,44
    Частоты 3 2 1 1 1 2
    Числа, составляющие вариационный ряд (без повторений) Частоты
    3,12 3
    3,24 2
    3,25 1
    3,34 1
    3,37 1
    3,44 2

    ЗАМЕЧАНИЕ. Сумма частот, то есть сумма чисел, записанных во второй строке таблицы частот числового ряда, равна объему выборки (числу чисел в числовом ряде). В рассматриваемом случае это число   10 .

  7. Составляем таблицу относительных частот (в процентах).

    ОПРЕДЕЛЕНИЕ 2. Относительной частотой (в процентах) выборочного данного называют число процентов, которое составляет частота этого выборочного данного от всего объема выборки (количества членов числового ряда).

    Для того, чтобы сформировать таблицу относительных частот числового ряда, заменим частоты, записанные во второй строке таблицы частот числового ряда, на соответствующие им относительные частоты. В результате получим следующую таблицу.

    ТАБЛИЦА ОТНОСИТЕЛЬНЫХ ЧАСТОТ (В ПРОЦЕНТАХ)

    Числа, составляющие вариационный ряд (без повторений) 3,12 3,24 3,25 3,34 3,37 3,44
    Относительные частоты (%) 30% 20% 10% 10% 10% 20%
    Числа, составляющие вариационный ряд (без повторений) Относительные частоты (%)
    3,12 30%
    3,24 20%
    3,25 10%
    3,34 10%
    3,37 10%
    3,44 20%

  8. Находим моду числового ряда.

    ОПРЕДЕЛЕНИЕ 3. Модой числового ряда называют выборочное данное с наибольшей частотой.

    Из таблицы частот числового ряда видно, что модой числового ряда   X   является число   3,12 ,   поскольку его частота   3   является наибольшей. Очевидно, что и относительная частота этого выборочного данного является самой большой   (30%) .

    ЗАМЕЧАНИЕ. Объем выборки, среднее выборочное значение, размах, медиана и мода числового ряда являются одними из статистических характеристик числовых рядов.

Источник

ПЕРМСКИЙ КРАЙ

ОРДИНСКИЙ МУНИЦИПАЛЬНЫЙ РАЙОН

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«КАРЬЕВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»

Статистические характеристики числового ряда

(урок алгебры, 7 класс)

Автор:

Минсадирова Фамира Закрулловна,
учитель информатики и математики

Методическая разработка
урока алгебры в 7 классе

Тема
урока: «Статистические характеристики числового ряда»

Цели и
задачи:

  • Познакомить
    с понятиями     «статистика», «среднее
    арифметическое числового набора    », «медиана
    как статистическая характеристика    », «размах» и «мода».
  • Научить
    решать статистические задачи, используя различные способы и методы.
  • Развивать
    исследовательские и коммуникативные навыки учащихся.
  • Формировать
    умение обучаться в сотрудничестве.

Оборудование:
Ноутбук,
проектор, экран.

Ход урока:

1.    
Этап самоопре­деления к деятельности.

(Слайд №1 – пустой)

– Здравствуйте, ребята! Сегодня мне
хотелось бы поговорить с вами о нашем будущем. А вначале урока я хочу
рассказать вам одну известную притчу. Давным-давно в
старинном городе жил Мудрец, окружённый учениками. Самый способный из них
однажды задумался: «А есть ли вопрос, на который наш Мудрец не смог бы дать
ответа?» Он пошёл на цветущий луг, поймал самую красивую бабочку и спрятал её
между ладонями. Бабочка цеплялась лапками за его руки, и ученику было щекотно.
Улыбаясь, он подошёл к Мудрецу и спросил:

– Скажите, Мудрец, какая бабочка у меня в
руках: живая или мёртвая?

Мудрец посмотрел на него и подумал
(если я скажу что бабочка живая, он сомкнет ладони и придавит ее, а если я
скажу – что мертвая, он откроет ладони и она улетит).

Ученик крепко держал бабочку в
сомкнутых ладонях и был готов в любое мгновение сжать их ради своей истины.
Мудрец, наконец, ответил:

– Всё в твоих руках.

–  И наше
будущее, ребята, оно тоже в наших руках. И оно начинается сегодня. А что для
вас будущее?

–  Семья, дом,
работа, карьера, …

–  Каждый из нас со
школы мечтает о своей будущей профессии. Вы мечтаете о своей будущей профессии?

–  Кто-то хочет,
наверно, стать менеджером, водителем, инженером, продавцом и т.д.

–  Представим, что вы
выросли, получили образование по какой-то специальности и ищете работу? Какую
работу вы бы выбрали?

–  Высокооплачиваемую,
интересную, …

– Замечательно. (Слайд №2) Вот
4 компании рекламируют себя и приглашают вас на работу к себе в компанию. В
какую  компанию вы бы пошли работать?

–  Чем привлекают Вас
те или иные компании? Куда бы Вы устроились на работу?

2.
Этап актуализации знаний и фиксации затруднения в индивидуальной деятельности. Открытие нового понятия. Этап построения проекта
выхода из затруднения.

– Я выделила в рекламах каждой
компании по одному слову (Слайд №3): мода, средняя, размах, медиана.

–  Какие из этих слов
вам понятны?

–  Средняя.

–  А что, значит,
средняя?

–  С этим
понятием вы знакомы с 5 класса. Какое понятие начинается со слова среднее….
(среднее арифметическое числового ряда).

–  (Нажимаем на слово – Средняя – Слайд №5)

–  (Нажимаем на кнопку  – Слайд №3)

– А с чем
ассоциируется у вас слово «мода»? Как вы понимаете это слово?

–  (Нажимаем на слово – Мода – Слайд №4)

–  Модой ряда
чисел называется число, наиболее часто встречающееся в данном ряду.

–
Посмотрите первый числовой ряд? И попробуйте найти моду данного ряда? (18). Это
самое модное число.

–
Обратите внимание на второй числовой ряд и определите моду?

–
Какой вывод можно сделать по моде числового ряда? Любой
ли ряд чисел имеет моду? (Ряд чисел может иметь более одной моды, а может
не иметь моды.)

–  (Нажимаем на кнопку  – Слайд №3)

–  Третье понятие «размах». А с этим словом вы 
встречались? Например: размах крыльев. (Нажимаем на слово – Размах – Слайд №6)

–   (Размахом
ряда чисел называется разность между наибольшим и наименьшим из этих чисел).

–  (Нажимаем на кнопку  – Слайд №3)

–
Последнее понятие – медиана. С этим понятием вы тоже знакомы. Что она
обозначает? Медиану выразите одним словом. – Середина. (Нажимаем
на слово – Медиана – Слайд №7) Обратите внимание на
числовой ряд.  Как записаны числа? Чтобы найти середину
этого ряда надо записать числа в порядке возрастания.

–
Мы с вами познакомились с понятиями: мода, среднее арифметическое, медиана и
размах. Что нам дают эти понятия о числовом ряде? (статистику, данные,
характеристику) (Слайды №8, №9)

–  Сегодняшняя
наша тема урока (Слайд №10) «Статистические
характеристики числового ряда». Мы с вами определили понятия мода, размах,
медиана, среднее арифметическое. И какова будет задача нашего урока?

–  Научиться
решать статистические задачи.

3. Первичное закрепление во внешней речи.

Задача (Слайд №11).
В одной солидной компании работают 12 человек.

Заработная плата
персонала:

Директор – 60
тысяч руб,

заместитель
директора – 35 тысяч руб,

главный бухгалтер
– 30 тысяч руб,

рекламодатель – 20
тысяч руб,

кассир – 22 тысячи
руб,

менеджер – 25
тысяч руб,

сотрудник по
внешней связи – 18 тысяч руб,

сотрудник (стаж
работы – 1 год) – 15 тысяч руб,

сотрудник (стаж
работы – 2 года) – 16 тысяч руб,

сотрудник (стаж
работы – 3 года) – 17 тысяч руб,

секретарь-делопроизводитель
– 18 тысяч руб,

водитель – 12
тысяч руб.

– Давайте, попробуем найти медиану, моду, размах заработной платы и
среднюю заработную плату в данной компании.

Медиана – 19

Мода – 18

Размах – 48

Средняя заработная плата – 24 (Слайд №12)

–
А теперь, давайте, вернемся на рекламы компаний (Слайд №13), с которыми
мы познакомились в начале урока.

–
Что можно сказать, читая эти рекламы?

Ответы
учащихся, обсуждение реклам.

4. Этап самостоятельной работы и включения в
систему знаний и повторения.

– Ребята, я вам предлагаю 3 задачи (Слайд №14)
для самостоятельной работы:

1. Записан возраст (в годах) семи сотрудников 25, 37,
42, 24, 33, 50, 27. Определите средний возраст сотрудников. На
сколько отличается среднее арифметическое этого набора чисел от его медианы?

2.      
Каждые
полчаса гидролог замеряет температуру воды в водоеме и получает следующий ряд
значений: 12,8; 13,1; 12,7; 13,2; 12,7; 13,3; 12,6; 12,9; 12,7; 13; 12,7.
Найдите медиану этого ряда.

3. В аттестате о среднем образовании у
четырех друзей – выпускников школы – оказались следующие оценки:

Ильин:
4, 4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 4, 5, 4, 4;

Семенов:
3, 4, 3, 3, 3, 3, 4, 3, 3, 3, 3, 4, 4, 5, 4;

Попов:
5, 5, 5, 5, 5, 4, 4, 5, 5, 5, 5, 5, 4, 4, 4;

Романов:
3, 3, 4, 4, 4, 4, 4, 3, 4, 4, 4, 5, 3, 4, 4.

С каким средним баллом окончил школу
каждый из этих выпускников? Укажите наиболее типичную для каждого из них оценку
в аттестате. Какие статистические характеристики вы использовали при ответе?

Взаимопроверка, выставление оценок.

5.    
Этап рефлексии деятельности.

– Итак, ребята, давайте подведем итог
нашего урока. Что собой представляет среднее арифметическое ряда чисел? (Слайд
№15)

– Среднее арифметическое представляет
собой то значение величины, которое получается, когда сумма всех наблюдаемых
значений мысленно распределяется поровну между единицами наблюдения. Иногда
вычисление среднего арифметического не дает полезной информации.

– 
Когда находят размах и моду ряда?

–             
Размах ряда находят, когда хотят
определить, как велик разброс данных в ряду. Моду ряда данных обычно находят,
когда хотят выявить некоторый типичный показатель. Например, если изучаются
данные о размерах мужских сорочек, проданных в определенный день в универмаге,
то удобно воспользоваться таким показателем, как мода, который характеризует
размер, пользующийся наибольшим спросом. Среднее арифметическое в этом случае
не дает полезной информации.

–             
Проведя опрос учащихся, можно получить ряд
данных, показывающих, каким видом спорта они предпочитают заниматься, какую из
развлекательных телевизионных программ они считают наиболее интересной. Как вы
думаете, какой характеристикой будут служить ответы, которые встречаются чаще
всего? Этим и объясняется само название «мода».

– Я очень довольна, ребята, вашей работой
на уроке. Все вы были очень активны, давали хорошие ответы. Надеюсь, что каждый
из вас в будущем хорошо окончит школу, университеты, колледжи и устроится на
высокооплачиваемую работу. «Все
в ваших руках!» Спасибо за работу.
До свидания!

Приложение

Раздаточный материал

Задача.
В одной солидной компании работают 12 человек.

Заработная плата
персонала:

Директор
– 60 тысяч руб,

заместитель
директора – 35 тысяч руб,

главный
бухгалтер – 30 тысяч руб,

рекламодатель
– 20 тысяч руб,

кассир
– 22 тысяч руб,

менеджер
– 25 тысяч руб,

сотрудник
по внешней связи –18 тысяч руб,

сотрудник
(стаж работы – 1 год) – 15 тысяч руб,

сотрудник
(стаж работы – 2 года) – 16 тысяч руб,

сотрудник
(стаж работы – 3 года) – 17 тысяч руб,

секретарь-делопроизводитель
– 18 тысяч руб,

водитель
– 12 тысяч руб.

Найти медиану,
моду, размах заработной платы и среднюю заработную плату данной компании.

Самостоятельная работа

1.      
Записан
возраст (в годах) семи сотрудников 25, 37, 42, 24, 33, 50, 27. Определите
средний возраст сотрудников. На сколько отличается среднее арифметическое этого
набора чисел от его медианы?

2.      
Каждые
полчаса гидролог замеряет температуру воды в водоеме и получает следующий ряд
значений: 12,8; 13,1; 12,7; 13,2; 12,7; 13,3; 12,6; 12,9; 12,7; 13; 12,7.
Найдите медиану этого ряда.

3.      
В аттестате о среднем образовании у четырех друзей – выпускников
школы – оказались следующие оценки:

Ильин:
4, 4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 4, 5, 4, 4;

Семенов:
3, 4, 3, 3, 3, 3, 4, 3, 3, 3, 3, 4, 4, 5, 4;

Попов:
5, 5, 5, 5, 5, 4, 4, 5, 5, 5, 5, 5, 4, 4, 4;

Романов:
3, 3, 4, 4, 4, 4, 4, 3, 4, 4, 4, 5, 3, 4, 4.

С каким средним баллом окончил школу каждый из этих
выпускников? Укажите наиболее типичную для каждого из них оценку в аттестате.
Какие статистические характеристики вы использовали при ответе?

Список
литературы

1. Алгебра. 7 класс: учеб. для общеобразоват.
учреждений / [Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова]; под
ред. С.А. Теляковского. – М.: Просвещение, 2010.

Источник

8.4. МОДА и МЕДИАНА (структурные средние)

 Мода и медиана наиболее часто используемые в экономической практике структурные средние.

Мода – это величина признака (варианта), который наиболее часто встречается  в данной совокупности, т.e. это варианта, имеющая наибольшую частоту.

В дискретном ряду мода определяется в соответствии с определением, т.е. это одна из вариант признака, которая в ряду распределения имеет наибольшую частоту.

Для интервального ряда моду находим по формуле (8.16), сначала по наибольшей частоте определив модальный интервал:

Статистика Формула Мода для интервального ряда

(8.16 – формула Моды)

где хо – начальная (нижняя) граница модального интервала;

h – величина интервала;

fМо – частота модального интервала;

fМо-1 – частота интервала, предшествующая модальному;

fМо+1– частота интервала следующая за модальным.

Медианой  называется такое значение признака, которое приходится на середину ранжированного ряда, т.е. в ранжированном ряду распределения одна половина ряда имеет значение признака больше медианы, другая – меньше медианы.

В дискретном ряду медиана находится  непосредственно по накопленной частоте, соответствующей номеру медианы.

В случае интервального вариационного ряда медиану определяют по формуле:

Статистика Формула Медиана для интервального ряда                                           (8.17 – формула Медианы)

где хо – нижняя граница медианного интервала;

NМе– порядковый номер медианы (Σf/2);

S Me-1 – накопленная частота до медианного интервала;

fМе –  частота медианного интервала.

Пример вычисления Моды.

Рассчитаем моду и медиану по данным табл. 8.4.

Таблица 8.4 – Распределение семей города N  по размеру среднедушевого дохода в январе 2018 г. руб.(цифры условные)

Группы семей по размеру дохода, руб. Число

семей

 Накоп-

ленные частоты

в % к итогу
До 5000 600 600 6
5000-6000 700 1300

(600+700)

 13
6000-7000 1700 (fМо-1) 3000 (S Me-1 )

(1300+1700)

 30
7000-8000

 (хо)

 2500

(fМо)

(fМе)

 5500 (S Me) 55
8000-9000 2200 (fМо+1) 7700 77
9000-10000 1500 9200 92
Свыше 10000 800 10000 100
Итого 10000 – –

Пример вычисления Моды. Найдем моду по формуле (8.16) см. обозначения в таблице, а h = 8000-7000=1000, т.е. получаем:

Статистика. Пример расчета Моды (структурные средние)

Пример вычисления Моды

Пример вычисления Медианы интервального вариационного ряда. Рассчитаем медиану по формуле (8.17):

1) сначала находим  порядковый  номер медианы: NМе = Σfi/2= 5000.

2) по накопленным частотам в соответствии с номером медианы определяем, что 5000 находится в интервале (7000 – 8000), далее  значение медианы  определим по формуле (8.17):

Статистика. Пример Медиана

Пример вычисления Медианы

Вывод: по моде – наиболее часто встречается среднедушевой доход в размере 7730 руб., по медиане – что половина семей города имеет среднедушевой доход ниже 7800 руб., остальные семьи – более 7800 руб.

Пример .СРЕДНИЙ, МЕДИАННЫЙ И МОДАЛЬНЫЙ УРОВЕНЬ ДЕНЕЖНЫХ ДОХОДОВ НАСЕЛЕНИЯ  ЦЕЛОМ ПО РОССИИ И ПО СУБЪЕКТАМ РОССИЙСКОЙ ФЕДЕРАЦИИ ЗА 2013 год см. по ссылке. Источник: оценка на основании данных выборочного обследования бюджетов домашних хозяйств и макроэкономического показателя денежных доходов населения

Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию.

Если Мо<Ме<Х – имеет место правосторонняя асимметрия.

При Х<Ме<Мо следует сделать вы­вод о левосторонней асимметрии ряда.

Средние величины (арифметическая, гармоническая, геометрическая, квадратическая) см. по ссылке

Оценка статьи:

Загрузка…

Источник

Добавить комментарий