Способы отображения разницы на линейном графике
На чтение 3 мин Опубликовано 11.01.2016
В двух словах: Бывает очень непросто увидеть разницу между двумя линиями на линейном графике. В этой статье я покажу несколько способов, как можно указать разницу на графике в Microsoft Excel.
Уровень сложности: Новичок.
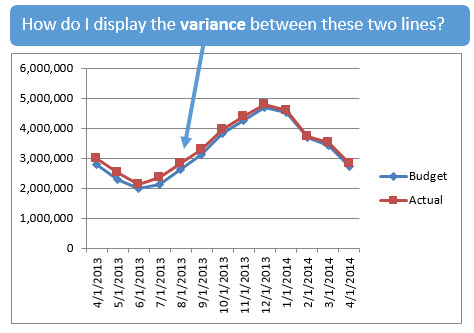
У моего друга возник интересный вопрос. Имеется диаграмма с двумя линейными графиками на ней. Требуется показать на диаграмме разницу между этими линиями.
Разница между двумя рядами данных в некоторые месяцы очень велика (более $200000). Но на графике не удаётся показать эту разницу достаточно наглядно. А все потому, что масштаб вертикальной оси также очень велик – $6000000.
Как же сделать, чтобы разница была видна более ясно?
Содержание
- Решение №1: Отображаем на графике разницу в процентах
- Решение №2: Показываем разницу как отдельный график
- Как это делаете Вы?
Решение №1: Отображаем на графике разницу в процентах
Одно из возможных решений – добавить значения разницы в процентах рядом с линией графика.
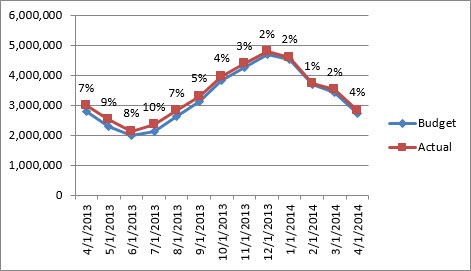
Сделать это было бы достаточно сложно, если бы не некоторые новые возможности Excel 2013, которые значительно упрощают задачу. На панели Формат в разделе Формат подписей данных (Format Data Labels) есть параметр Значения из ячеек (Value From Cells).
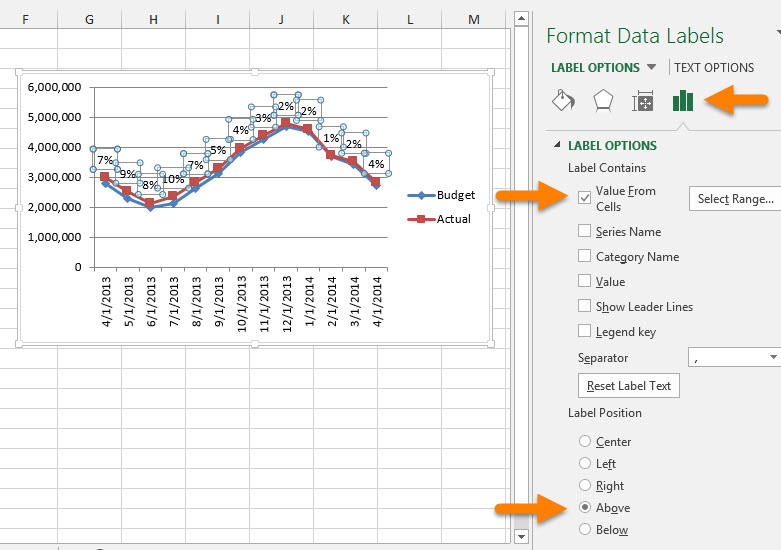
Этот параметр позволяет выбрать диапазон ячеек, значения которых будут добавлены в подписи данных. Для примера я вычислил разницу в отдельном столбце и добавил этот столбец в подписи данных диаграммы.
Решение №2: Показываем разницу как отдельный график
Часто мы ловим себя на том, что пытаемся уместить слишком много данных в одной диаграмме. Полагаю, это связано с размещением диаграмм на слайдах в PowerPoint, когда желательно расположить все данные на одном слайде.
Я же сторонник того, чтобы для отображения различных данных создавать отдельные диаграммы. Так значительно проще увидеть тренд, понять и сделать соответствующие выводы из имеющихся данных.
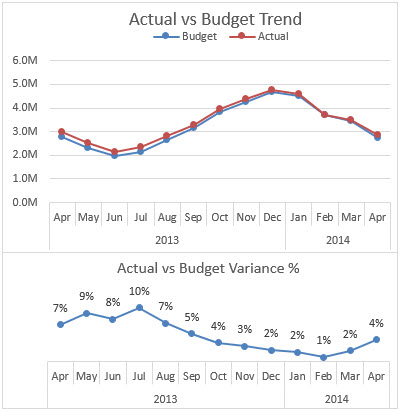
На рисунке выше я вывел разницу на отдельном графике и поместил его под исходную диаграмму. Так пользователь может ясно видеть тренд в значениях разницы – с июля по февраль разница каждый месяц уменьшается, в то время как объём продаж увеличивается.
Диаграммы, представленные ниже, показывают еще один способ отобразить разницу – на панели диаграмм. Панель диаграмм – это просто несколько диаграмм, объединённых в группу.
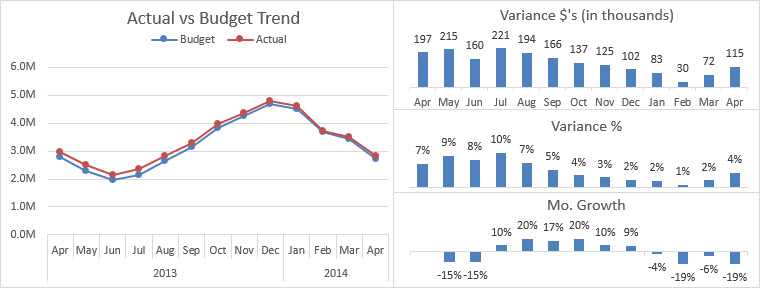
На показанной выше панели я добавил диаграмму (нижняя справа), которая отображает ежемесячный прирост по ряду Actual. Согласитесь, видеть эти значения в цифрах очень удобно.
Как это делаете Вы?
Очень хотелось бы услышать Ваше мнение на эту тему. Как бы Вы показали разницу между линейными графиками?
Существует множество путей решения этой задачи, и было бы интересно узнать каждый из них. Расскажите о своём варианте решения в комментариях под статьёй.
Спасибо!
Оцените качество статьи. Нам важно ваше мнение:
Задание 2. ЕГЭ. Определите разность между наибольшей и наименьшей среднемесячными температурами
Задание. На диаграмме показана среднемесячная температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали – температура в градусах Цельсия. Определите по приведенной диаграмме разность между наибольшей и наименьшей среднемесячными температурами. Ответ дайте в градусах Цельсия.

Решение:
Наибольшая среднемесячная температура наблюдалась в августе и была равна 240С, наименьшая среднемесячная температура наблюдалась в феврале и была равна 40С. Следовательно, разность между наибольшей и наименьшей среднемесячными температурами равна: 24 – 4 = 200С.

Ответ: 20
Оставить комментарий
Рубрики
- Демоверсия ЕГЭ по информатике
- Демоверсия ЕГЭ по математике
- Демоверсия ОГЭ по информатике
- Демоверсия ОГЭ по математике
- Материалы по аттестации
- Решаем ЕГЭ по математике
- Задание 1
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
- Решаем ОГЭ по математике
- Задание 21
- Задание 22
- Задание 24
- Скачать экзаменационные варианты по информатике
- ЕГЭ по информатике
- ОГЭ по информатике
- Скачать экзаменационные варианты по математике
- ЕГЭ по математике
- ОГЭ по математике
- Тематическое планирование
Диаграммы Эйлера-Венна
Содержание:
-
Что такое диаграммы Эйлера-Венна
- Принцип построения
- Дополнение множества
- Объединение множеств
- Пересечение множеств
- Симметричная разность множеств
- Разность множеств
- Использование диаграмм Эйлера-Венна для доказательства логических равенств
- Примеры задач с решением
Что такое диаграммы Эйлера-Венна
Определение
Диаграмма Эйлера-Венна — геометрическая схема, которая используется для моделирования множеств и для схематичного изображения и отношений между ними.Диаграмма позволяет наглядно отразить различные утверждения о множествах. При использовании этого метода универсальное множество изображается в виде прямоугольника, подмножества изображают кругами. Диаграммы нашли свое применение в математике, логике, менеджменте и других прикладных направлениях.
Для отражения отношений между множествами математики Джон Венн и Леонард Эйлер использовали для способа. Если Венн использовал для обозначения множеств замкнутые фигуры, то Эйлер использовал круги.
Диаграммы Эйлера-Венна являются важным частным случаем кругов Эйлера. Диаграммы изображают все 2^n комбинаций n свойств, что является конечной булевой алгеброй. В случае n = 3 диаграмма Эйлера-Венна обычно состоит из трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приближенно равным длине стороны треугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Принцип построения
Построение диаграммы Эйлера-Венна — это изображение большого прямоугольника, который представляет универсальное множество U. Внутри прямоугольника изображаются замкнутые фигуры, обозначающие множества. Если множеств не более 3, то изображаются круги, и эллипсы, если множеств 4. Фигуры пересекаются в наиболее общем случае, требуемом задачей, что обозначается соответствующим образом.
Предположим, что на диаграмме изображен круг, представляющий множество А. Область в середине круга множества А отражает истинность выражения А, в то время как область вне круга обозначает ложь. Логическая операция будет отображаться на диаграмме при помощи штриховки тех областей, в которых ее значения истинны. В соответствии с алгеброй логики, конъюнкция множеств А и B будет истинна только тогда, когда истинны оба множества. Тогда на диаграмме будет отмечена область пересечения множеств.
С помощью диаграмм Эйлера-Венна можно доказать все законы алгебры, представляя их графически. Это возможно через выполнение следующего алгоритма:
- В первую очередь необходимо начертить диаграмму, заштриховав все множества, находящиеся в левой части равенства.
- Следующим шагом будет начертание другой диаграммы и штриховка всех множеств, которые находятся в правой части равенства.
- В случае, когда на диаграммах заштрихована одна и та же область, торжество истинно.
Дополнение множества
Дополнением к множеству A является множество (overline A), которое состоит из элементов, не входящих в А.
(overline A;=;left{x;vert;x;notin;Aright})
При этом не все элементы, не являющиеся элементами А, могут быть включены в (overline A.) Принято считать, что все множества, которые участвуют в решении задачи, являются подмножествами некоторого общего универсального множества U. Учитывая это, дополнение overline A определяется следующим образом:
(overline A;=;U;backslash;A)
Таким образом выглядит дополнение (overline A) графически:
Объединение множеств
Объединением множеств A и B называют множество (A;cup;B), которое состоит из элементов, принадлежащих хотя бы одному из множеств.
Объединение записывается следующим образом:
(A;cup;B;=;left{x;vert;x;in;A;или;x;in:Bright})
Таким образом объединение множеств выглядит графически:
Пересечение множеств
Пересечением множеств A и B является множество (A;cap;B), которое состоит из элементов, входящих в оба множества.
Пересечение множеств записывается следующим образом:
(A;cap;B;=;left{x;vert;x;in;A;и;x;in;Bright})
Таким образом пересечение множеств выглядит графически:
Симметричная разность множеств
Симметричная разность A B — это такое множество, куда входят все те элементы первого множества, которые не входят во второе множество, а, также те элементы второго множества, которые не входят в первое множество
Разность множеств записывается следующим образом:
(Abigtriangleup B=(Abackslash B)cup(Bbackslash A))
Таким образом разность выглядит графически:
Разность множеств
Разностью A B является множество элементов A, не входящих в B.
Разность множеств записывается следующим образом:
(A;backslash;B;=;left{x;vert;x;in;A;и;x;notin;Bright})
Таким образом разность выглядит графически:
Использование диаграмм Эйлера-Венна для доказательства логических равенств
Рассмотрим, как диаграммы Эйлера-Венна применяются для доказательства логических равенств.
Предположим, что перед нами конъюнкция множеств (A;wedge;B)
В первую очередь обратим внимание на левую часть равенства. Построим диаграмму для множеств А и B. Графически отметим дизъюнкцию, заштриховав оба круга цветом.
Теперь отобразим инверсию, заштриховав область за пределами множеств.
Обратим внимание на правую часть равенства. В первую очередь отобразим инверсию A штриховкой область за пределами круга множества A цветом.
Проведем аналогичную операцию с множеством B.
Теперь штриховкой черным цветом всех областей пересечения отобразим конъюнкцию инверсий множеств А и B.
При сравнении области для отображения правой и левой частей, становится очевидно, что они равны. Справедливость логического равенства доказана с помощью диаграммы Эйлера-Венна.
Примеры задач с решением
Задача
Группа туристов из 100 человек пробыла в городе N три дня. За это время в ресторане питались 28 туристов, фастфуде — 42, кофейне — 30. И в ресторане, и в фастфуде побывало 10 человек; в ресторане и кофейне — 8; в фастфуде и кофейне — 5. Все во всех трех местах побывали три человека. Сколько туристов питалось в других местах и не посетило ни одного из перечисленных?
Решение
В условии задачи три множества — Р, Ф и К. Туристы, которые пытались в ресторане, фастфуде и кофейне, соответственно. Универсальное множество U — это множество всех туристов группы. Запишем условие задачи, где n(X) — количество элементов множества X.
(n(U);=;100\n(Р);=;28,;n(Ф);=;42,;n(К);=;30\n;(Р;cap;Ф);=;10,;n(Р;cap;К);=;8,;n;(Ф;cap;К);=;5\n;(Р;cap;Ф;cap;К);=;3)
Необходимо найти (n(Р;cup;Ф;cup;К);=;n;(U;backslash;(Р;cap;Ф;cap:К)))
В решении задачи поможет представление данных графически с помощью диаграммы Эйлера-Венна. Составляя ее, важно помнить, что если в (Р;cap;Ф;cap:К) три элемента, а в множестве (Р;cap;Ф) — 10 элементов, то в диаграмме в месте пересечений множеств Р и Ф мы проставляем 7 элементов, так как 3 элемента уже учтено.
Теперь, когда на диаграмме все элементы учтены по одному разу, можно вычислить количество туристов, которые побывали хотя бы одном из заведений.
(n(Р;cup;Ф;cup;К);=;13;+;7;+;30;+5;+;3;+;2:+;20;=;80)
Тогда, количество туристов, которые не побывали ни в ресторане, ни в фастфуде, ни в кофейне можно вычислить следующим образом:
(n(U;backslash;(Р;cup;Ф;cup;К));=;100;-;80;=;20)
Ответ: 20 туристов не побывали ни в одном из указанных заведений.
Задача
На олимпиаде по математике школьникам предложили решить три задачи: одну по алгебре, одну по геометрии, одну по тригонометрии. В олимпиаде участвовало 1000 школьников. Результаты олимпиады были следующие: задачу по алгебре решили 800 участников, по геометрии — 700, по тригонометрии — 600. 600 школьников решили задачи по алгебре и геометрии, 500 — по алгебре и тригонометрии, 400 — по геометрии и тригонометрии. 300 человек решили задачи по алгебре, геометрии и тригонометрии. Сколько школьников не решило ни одной задачи?
Решение
Начнем с определения множеств и введения обозначений. В данном случае, их три:
- множество задач по алгебре («А»);
- множество задач по геометрии («Г»);
- множество задач по тригонометрии («Т»).
Используя диаграмму Эйлера-Венна графически изобразим информацию, данную в условии задачи.
Теперь используя диаграмму, обозначим область, которую необходимо найти:
Определим количество школьников для всех возможных областей.
Обозначим искомую область А = 0, Г = 0, Т = 0 как «х».
Найдем остальные области:
- Область А = 0, Г = 0, Т = 1: школьников нет.
- Область А = 0, Г = 1, Т = 0: школьников нет.
- Область А = 0, Г = 1, Т = 1: 100 школьников.
- Область А = 1, Г = 0, Т = 0: школьников нет.
- Область А = 1, Г = 0, Т = 1: 200 школьников.
- Область А = 1, Г = 1, Т = 0: 300 школьников.
- Область А = 1, Г = 1, Т = 1: 300 школьников.
Теперь внесем значения всех областей в диаграмму:
Определим x:
(x;=;U;-;(A;cup;Г;cup;Т);)
При U — универсум
U = 1000
((A;cup;Г;cup;Т);=; 0 + 0 + 0 + 300 + 300 + 200 + 100 = 900)
x = 1000 – 900 = 100
Ответ: 100 школьников не решило ни одной задачи.
Методы графического сложения, вычитания
Чтобы построить график функции y = f(x) + g(x) ,
надо построить на одном чертеже графики y = f(x)
и y = g(x) ,
потом при каждом x сложить ординаты двух графиков.
Если необходимо построить график разности двух функций
y = f(x) – g(x) ,
то этот случай сводится к построению суммы:
y = f(x) + ( – g(x)) .
Причем, график функции y = – g(x)
получается из графика функции y = g(x)
симметричным отражением относительно оси OX .
В случае, когда вторая функция – константа, то графическое сложение означает сдвиг графика первой функции по вертикали
на эту константу, причем, если константа положительная, то сдвиг осуществляется вверх, а если отрицательная, то вниз.
Методы графического умножения, деления
Чтобы построить график функции y=f(x)·g(x) , надо построить на одном чертеже графики y=f(x) и
y=g(x) , потом при каждом x перемножить ординаты двух графиков.
Графическое деление выполняется аналогично произведению.
В частном случае при построении графика функции y=A·f(x) ,
где A – константа надо график функции y=f(x) растянуть в |A|
раз по вертикали, при условии |A|≥1 , или сжать в
![]() раз по вертикали, если |A|<1
раз по вертикали, если |A|<1
, и затем полученный график отобразить симметрично относительно оси OX, если A<0 .
В данном параграфе рассмотрены следующие примеры:
![]()
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н · м. Скорость автомобиля (в км/ч) приближенно выражается формулой υ = 0,036n, где n — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 120 Н · м? Ответ дайте в километрах в час.
2
На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурой воздуха 15 июля. Ответ дайте в градусах Цельсия.
3
На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.
4
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме разность между наибольшей и наименьшей среднемесячными температурами в 1973 году. Ответ дайте в градусах Цельсия.
5
В ходе химической реакции количество исходного вещества (реагента), которое еще не вступило в реакцию, со временем постепенно уменьшается. На рисунке эта зависимость представлена графиком. По горизонтали откладывается время в минутах, прошедшее с момента начала реакции, по вертикали — масса оставшегося реагента, который еще не вступил в реакцию (в граммах). Определите по графику, сколько граммов реагента вступило в реакцию за три минуты?
Пройти тестирование по этим заданиям
