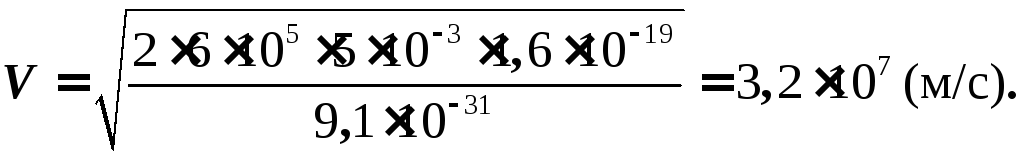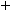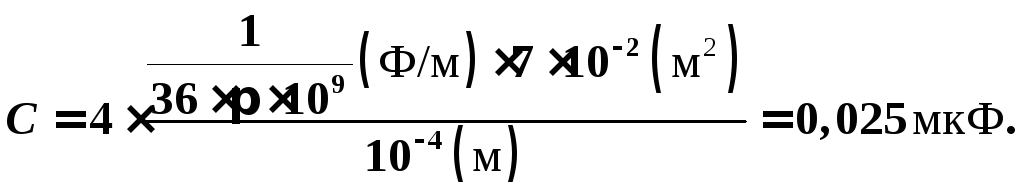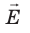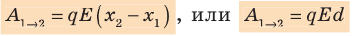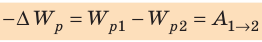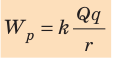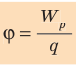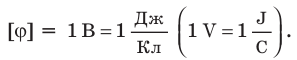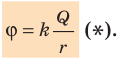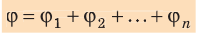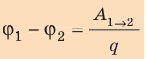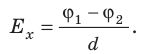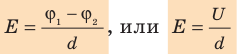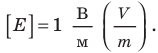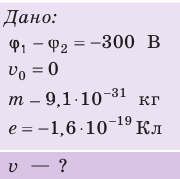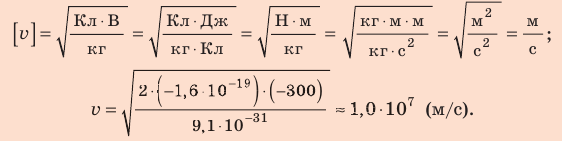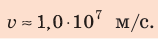Как найти разность потенциалов если есть скорость

m = 9,1 * 10^-31 кг.

q = 1,6 * 10^-19 Кл.

V1 = 1000 км/с = 10⁶ м/с.

V2 = 3000 км/с = 3 * 10⁶ м/с.

φ2 – φ1 – ?

Так как электрон обладает элементарным зарядом q = 1,6 * 10^-19 Кл, то электрическое поле выполняет работу А по разгону электрона, значения которой выразим формулой: А = q * (φ2 – φ1).

Согласно закону сохранения энергии, работа электростатического поля А идёт на увеличение кинетической энергии электрона: А = ΔЕк.

Движущийся электрон обладает кинетической энергией: Ек = m * V² / 2, где m – его масса, V – скорость его движения.

Увеличение кинетической энергии электрона ΔЕк выразим формулой: ΔЕк = m * V2² / 2 – m * V1² / 2 = m * (V2² – V1²) / 2.

q * (φ2 – φ1) = m * (V2² – V1²) / 2.

φ2 – φ1 = m * (V2² – V1²) / 2 * q.

φ2 – φ1 = 9,1 * 10^-31 кг * ((3 * 10⁶ м/с) ² – (1 * 10⁶ м/с) ²) / 2 * 1,6 * 10^-19 Кл = 22,75 В.

Ответ: электрон в элктрическом поле прошёл ускоряющую разность потенциалов в φ2 – φ1 = 22,75 В.

m = 9,1 *10^-31 кг.

q = 1,6 *10^-19 Кл.

V1 = 1000 км/с = 10⁶ м/с.

V2 = 3000 км/с = 3 *10⁶ м/с.

φ2  – φ1 – ?

Так как электрон обладает элементарным зарядом q = 1,6 *10^-19 Кл, то электрическое поле выполняет работу А по разгону электрона, значения которой выразим формулой: А = q  * (φ2  – φ1).

Согласно закону сохранения энергии, работа электростатического поля А идёт на увеличение кинетической энергии электрона: А = ΔЕк.

Движущийся электрон обладает кинетической энергией: Ек = m * V² /2, где m – его масса, V – скорость его движения.

Увеличение кинетической энергии электрона ΔЕк выразим формулой: ΔЕк  = m * V2² / 2 – m * V1² / 2 = m * (V2² –  V1² ) / 2.

q  * (φ2  – φ1) = m * (V2² –  V1² ) / 2.

φ2  – φ1 = m * (V2² –  V1² ) / 2 * q.

φ2  – φ1 = 9,1 *10^-31 кг * ((3 *10⁶ м/с )² – (1 *10⁶ м/с)² ) / 2 * 1,6 *10^-19 Кл  = 22,75 В.

Ответ: электрон в элктрическом поле прошёл ускоряющую разность потенциалов в φ2  – φ1 =  22,75 В.

Задача
5. Электрон переместился в ускоряющем
поле из точки с потенциалом 200В в точку
с потенциалом 300В. Найти кинетическую
энергию электрона, изменение потенциальной
энергии взаимодействия с полем и
приобретенную скорость. Начальная
скорость электрона равна нулю.

РЕШЕНИЕ

При
перемещении электрона с зарядом е
силами электростатического поля
совершается работа:

A
= –e
(φ₁
– φ_2).

Эта работа численно
равна изменению потенциальной энергии
заряда в электрическом поле, взятому с
противоположным знаком:

A
= –ΔW_p
или ΔW_p
= e
(φ₁
– φ₂)_.

По
теореме о кинетической энергии работа
сил электрического поля численно
равна
приобретенной электроном кинетической
энергии W_K:

A
= W_K
или –
e
(φ₁
– φ₂)
=.

Отсюда
скорость электрона,
прошедшего
разность потенциалов
φ₁
– φ_2:



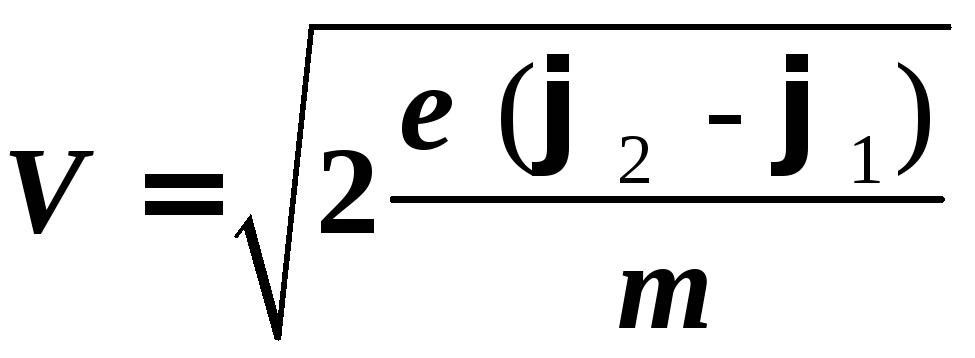
где
е
= 1,610^-19
Кл, m
= 9,110^-31кг
— заряд и масса
электрона.

Вычисления:
W_Р
= -1,610^-19
(300 – 200) = -1,610^-17
Дж.

Потенциальная
энергия электрона уменьшилась.

W_K
= 1,610^-17
Дж.

Кинетическая
энергия электрона увеличилась.

.

4.Движенне заряженных частиц в электростатическом поле

Задача
6.

Какова
максимальная
сила взаимодействия между двумя
про­тонами, каждый с энергией
10⁶
эВ,
летящих во
встречных
пучках?

РЕШЕНИЕ

Выберем
систему отсчета связанную с одним из
протонов, тогда скорость второго протона
увеличиться в два раза, а его кинетическая
энергия — в четыре раза.По
мере сближения протонов кинетическая
энергия движущегося протона уменьшается,
переходя в потенциальную энергию W_P
взаимодействия
двух протонов. Условие остановки
протонов:

W_К
= W_P.

Учитывая,
что Wp
= q
φ
получаем:

W_К
= q
φ

(1)

где
q
— заряд движущегося протона и

(2)

— потенциал
поля неподвижного протона, r
— расстояние
между протонами.
Из формул (1-2)
находим расстояние r,
на которое сблизятся протоны:

.
(3)

Зная
расстояние r
, найдем максимальную силу F
взаимодействия протонов. По закону
Кулона:

С
учетом (3):
.

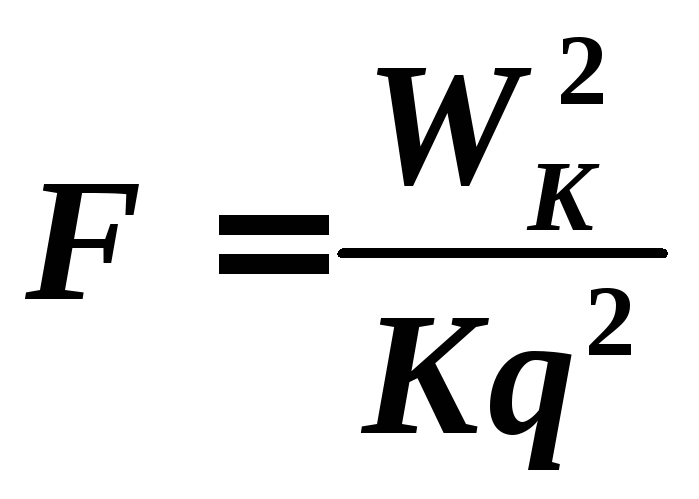
Проверка
размерности:
.

q
= 1,610^-19
Кл,

W_K
= 410
⁶ 1,610^-19
= 6,410^-13
Дж.

.

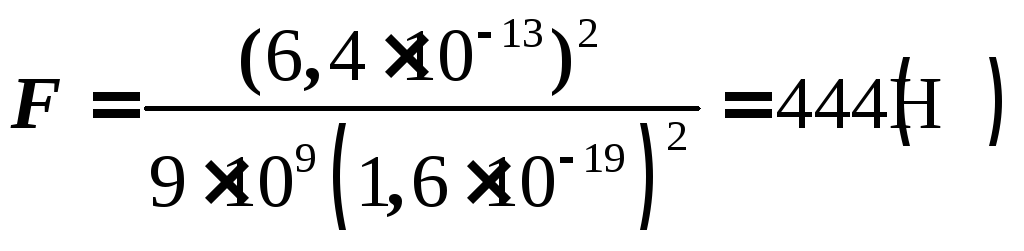
Задача
7. Электрон
испускается верхней пластиной конденсатора
с нулевой скоростью. Напряженность поля
между пластинами 6 10⁵
В/м, расстояние
─
5 мм. Найти: 1)
силу, действующую на электрон; 2) ускорение
электрона;
3) скорость,
с которой электрон подлетает
ко второй пластине; 4) плотность заряда
на пластинах.

ДАНО:
E
= 6 10⁵
В/м, V₀
= 0, d
= 0,05 м.

О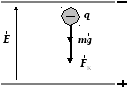ПРЕДЕЛИТЬ:F_К
,
a
, V,
.

РЕШЕНИЕ

1. На
   частицу с зарядом q
   в
   электрическом поле горизонтально
   расположенного конденсатора действуют
   две силы:
   mg
   — сила тяжести
   и F_К
   = q
   E
   —
   кулоновская сила со стороны поля.

Рис.
5

Результирующая
этих сил равна:
F
= mg
+ q
E.

1. Из
   второго закона Ньютона, определяем
   ускорение электрона:

.

1. Движение
   электрона —
   равноускоренное
   с ускорением а
   и начальной скоростью,
   равной нулю.
   Поэтому:

,

где
d
— расстояние между пластинами.

1. Плотность
   заряда на пластине конденсатора найдем
   из формулы напряженности поля плоского
   конденсатора:

Вычисления:
Силой тяжести mg
вследствие её малости можно пренебречь.

F
=
1,610^-19610⁵
= 9,610^-14
(Н).

Задана
8. В
пространство между двумя параллельными
заряженными пластинами, помещенными в
вакуум, параллельно им влетает электрон
со скоростью V₀
. На расстоянии L
скорость электрона отклоняется на угол
α
от первоначального
направления. Найти напряженность поля
конденсатора.

РЕШЕНИЕ

На
заряд действует сила Кулона

F
= q
E,

поэтому
электрон приобретает ускорение вдоль
оси OY
:

.

(1)

Рис.6

Рис.6

Скорость
электрона вдоль оси Y
:

.

(2)

Вдоль
оси X
электрон движется с постоянной скоростью
V₀.
Время t
, за которое электрон пройдет расстояние
L:

.

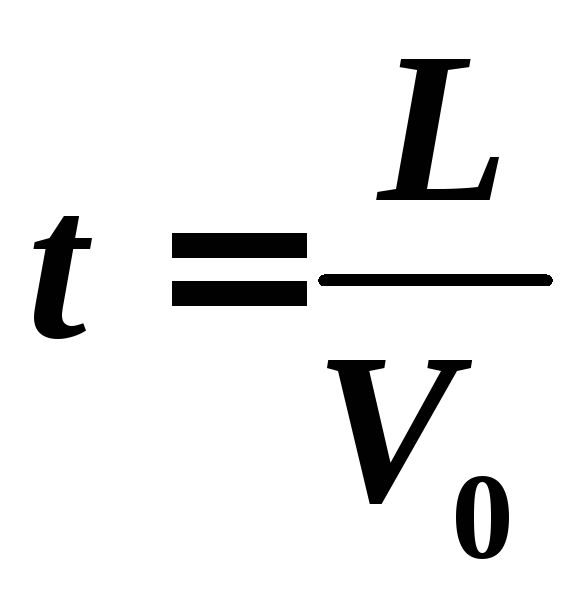
(3)

Подставив
(3) в (2),
получим:

.

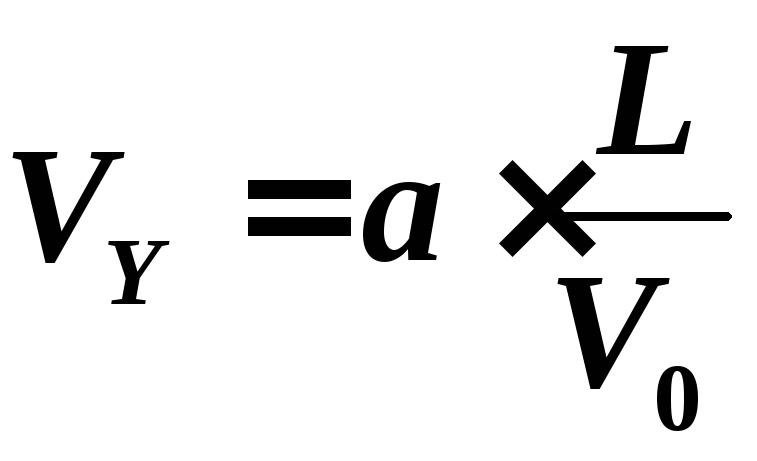
(4)

С
другой стороны,

можно выразить из треугольника скоростей
(см. рис.6):

.


(5)

Из формул (4) и (5) находим:

.
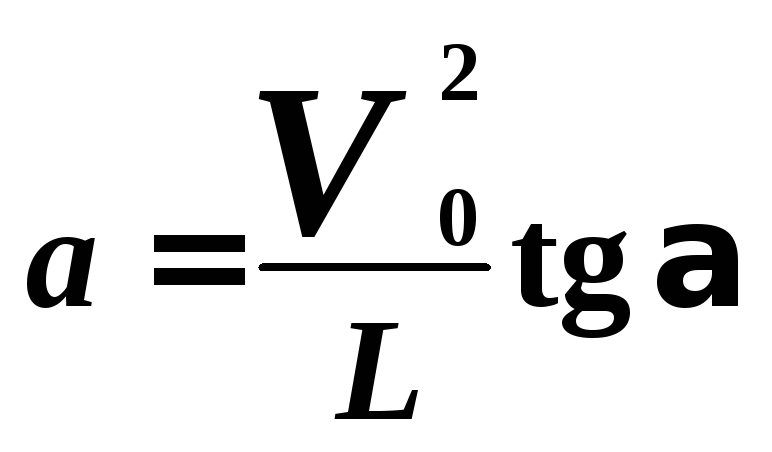
(6)

Напряженность
электростатического поля конденсатора
E
выразим из соотношения (1) с учетом (6):

.

Проверка
размерности:
:

1. Электроемкость

Задача
9.
Тысяча одинаковых наэлектризованных
капель сливаются в одну, причем их общий
заряд сохраняется. Как изменится общая
электрическая энергия капель, если
считать, что капли сферические и маленькие
капли находились на большом расстоянии
друг от друга?

РЕШЕНИЕ:

Обозначим
через
радиус, емкость, энергию и заряд одной
капли до слияния;
радиус, емкость,
энергию и заряд большой капли. Приравняем
объем капель после и до слияния:

,

откуда

,

где
n
— число маленьких капель,
— емкость шара.

Электрическая
энергия одной капли до слияния
.

Энергия
n
капель в n
раз больше и равна
.

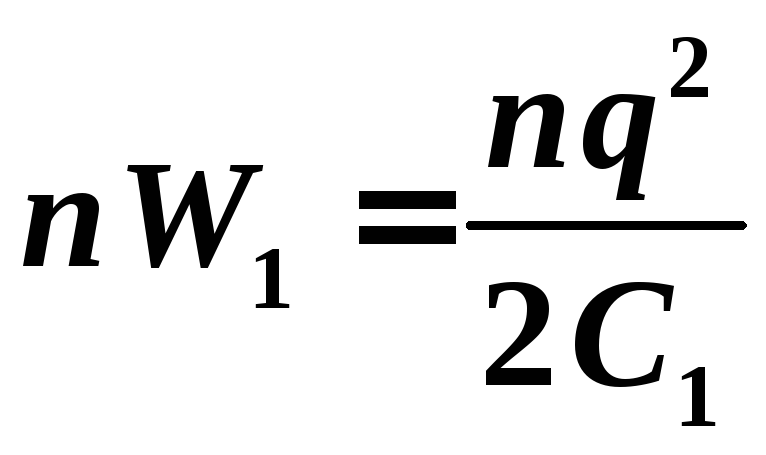
Энергия
капели после слияния равна
.

Отношение

.

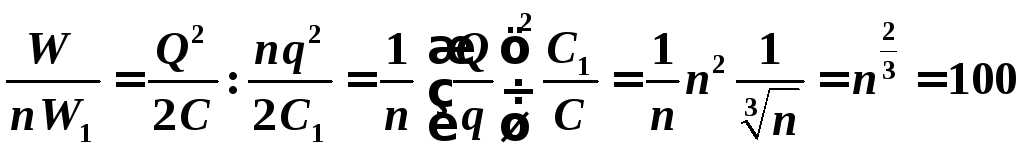
Энергия
увеличилась в 100 раз.

Задача
10.
Батарея
конденсаторов сделана из четырех
слюдяных пласти­нок толщиной d
= 0,1 мм и площадью
S
= 100 см²
каждая из
пластинок станиоля (проводник). Сколько
понадобилось пластинок станиоля (n)
при
параллельном
соединении батареи? Начертить схему
соединения. Опре­делить емкость
батареи. Определить запас электрической
энергии, если
батарея
подключена к источнику на­пряжения
U
= 220 В.
Диэлектрическая
проницаемость слюды ε
= 7.

Станиоль

Рис.
7

РЕШЕНИЕ

При
параллельном соединении конденсаторов
между собой соединяются все положительные
и все отрицательно заряженные пластинки
станиоля. Каждая пластинка станиоля
может служить обкладкой двух соседних
конденсаторов, как показано на втором
рисунке. Количество пластинок станиоля
n
= 5.
Общая
емкость C
= nC₁
, где C₁
— емкость одного конденсатора:
.
Общая емкость.

Энергия
батареи конденсаторов:

Соседние файлы в папке 1 семестр ФИЗИКА

• #
• #
• #
• #
• #
• #

Содержание:

Работа по перемещению заряда в электростатическом поле:

В повседневной жизни мы довольно часто, особенно в сухую погоду, встречаемся с ситуацией, когда, коснувшись какого-либо тела, чувствуем неприятный удар. Как показывает опыт, таких сюрпризов можно ожидать от тел, имеющих высокий потенциал.

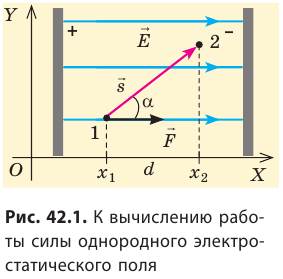
Работа по перемещению заряда в однородном электростатическом поле

Если электростатическое поле действует с некоторой силой на электрически заряженные тела, то оно способно совершить работу по перемещению этих тел.

Пусть в однородном электростатическом поле напряженностью

Вычислим работу А, которую совершает сила 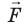, действующая на заряд со стороны электростатического поля. По определению работы: A=Fscosα.

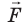
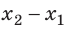
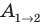
Поле однородное, поэтому сила постоянна, ее модуль равен: F=qE, а scosα=d=является проекцией вектора перемещения на направление силовых линий поля. Следовательно, работа сил однородного электростатического поля по перемещению электрического заряда q из точки 1 в точку 2 ( ) равна:

Обратите внимание! Если бы в данном случае заряд перемещался не из точки 1 в точку 2, а наоборот, то знак работы изменился бы на противоположный, то есть работа совершалась бы против сил поля.

Обратите внимание! Формула 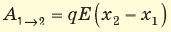будет справедлива в случаях движения заряда по любой траектории. То есть однородное электростатическое поле является потенциальным.

Потенциальным является любое электростатическое поле: работа электростатических (кулоновских) сил (как и работа гравитационных сил) не зависит от формы траектории, по которой перемещается заряд, а определяется начальным и конечным положениями заряда. Если траектория движения заряда замкнута, работа сил поля равна нулю.

Потенциальная энергия заряженного тела в поле, созданном точечным зарядом

Заряженное тело, помещенное в электростатическое поле, как и тело, находящееся в гравитационном поле Земли, обладает потенциальной энергией. Потенциальную энергию заряда, находящегося в электрическом поле, обычно обозначают символом . Согласно теореме о потенциальной энергии изменение потенциальной энергии заряда, взятое с противоположным знаком, равно работе, которую совершает электростатическое поле по перемещению заряда из точки 1 в точку 2 поля:

Потенциальную энергию взаимодействия двух точечных зарядов Q и q, расположенных на расстоянии r друг от друга, определяют по формуле:

Обратите внимание: 1) потенциальная энергия взаимодействия зарядов положительна ( > 0), если заряды одноименные, и отрицательна ( < 0), если заряды разноименные; 2) если заряды бесконечно отдалить друг от друга (r → ∞), то = 0 (заряды не будут взаимодействовать). Таким образом, потенциальная энергия взаимодействия двух точечных зарядов равна работе, которую должно совершить электростатическое поле для увеличения расстояния между этими зарядами от r до бесконечности.

Что называют потенциалом электростатического поля

Потенциал 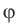электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии электрического заряда, помещенного в данную точку поля, к значению q этого заряда:

Единица потенциала в Си — вольт:

Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле:

Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.

Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов 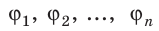полей, созданных каждым зарядом:

Как определяют разность потенциалов

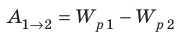
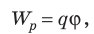
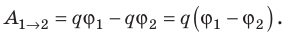
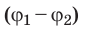
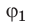
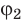
Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком: . Поскольку то Выражение называют разностью потенциалов, где — значение потенциала в начальной точке траектории движения заряда, — значение потенциала в ее конечной точке.

Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:

Единица разности потенциалов в Си — вольт: 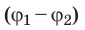= 1 В (V).

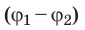
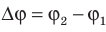
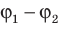
Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов − также называют напряжением (U). Важно не путать изменение потенциала и разность потенциалов (напряжение) .

Как связаны напряженность однородного электростатического поля и разность потенциалов

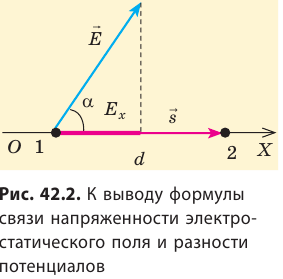
Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).

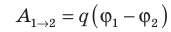
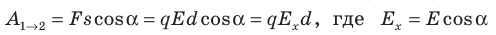
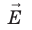
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2:; 2) через напряженность поля: — проекция вектора на ось Ох, проведенную через точки 1 и 2.

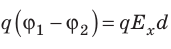
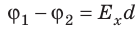
Приравняв оба выражения для работы, получим: , откуда: , или

Если заряд перемещается в направлении напряженности электрического поля () , последняя формула примет вид:

Из последней формулы следует единица напряженности в Си — вольт на метр:

Какие поверхности называют эквипотенциальными

Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.

Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.

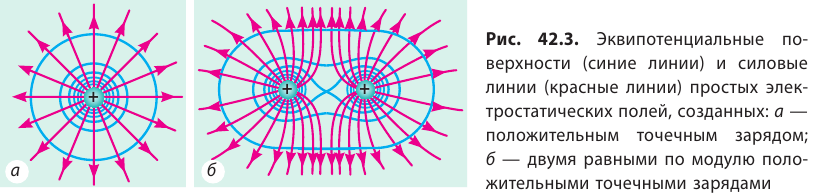
Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).

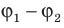
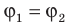
Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q ( ), а на эквипотенциальной поверхности .

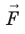
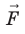
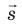
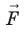
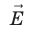
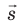
Работу электростатического поля также можно представить через силу , действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами и . Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы , а следовательно, и вектор напряженности поля в любой точке перпендикулярны вектору перемещения .

Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).

Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.

• Заказать решение задач по физике

Пример решения задачи

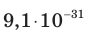
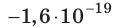
Электрон, начав движение из состояния покоя, прошел ускоряющую разность потенциалов –300 В. Какую скорость приобрел электрон? Масса электрона кг, заряд Кл.

Заряд электрона — отрицательный, его начальная скорость 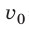= 0, поэтому под действием сил поля электрон будет двигаться в направлении, противоположном направлению силовых линий поля, то есть в направлении увеличения потенциала. Поле будет совершать положительную работу, в результате кинетическая энергия электрона и его скорость будут возрастать.

Решение:

Поиск математической модели, решение Согласно теореме о кинетической энергии:

— работа сил поля.

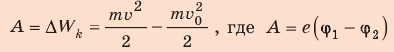
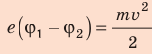
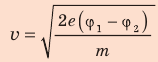
Таким образом, , отсюда .

Проверим единицу, найдем значение искомой величины:

Ответ:

Выводы: