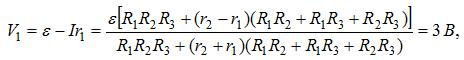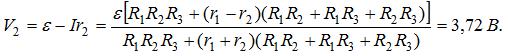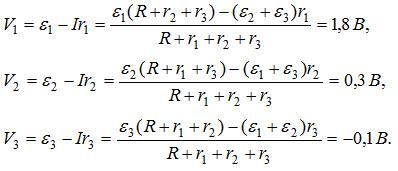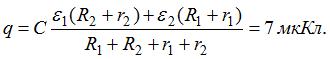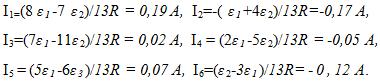Правило Кирхгофа
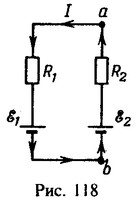
1 Найти разность потенциалов между точками а и b в схеме, изображенной на рис. 118. Э. д. с. источников тока ε1= 1 В и ε1 =1,3 В, сопротивления резисторов R1 = 10 Ом и R2 = 5 Ом.
Решение:
Поскольку ε2>ε1 то ток I будет идти в направлении, указанном на рис. 118, при этом разность потенциалов между точками а и b
2 Два элемента с э. д. с. ε1 = 1,5 B и ε2 = 2 В и внутренними сопротивлениями r1=0,6 Ом и r2 = 0,4 Ом соединены по схеме, изображенной на рис. 119. Какую разность потенциалов между точками а и b покажет вольтметр, если сопротивление вольтметра велико по сравнению с внутренними сопротивлениями элементов?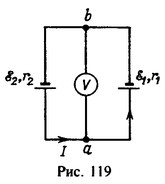
Решение:
Поскольку ε2>ε1, то ток I будет идти в направлении, указанном на рис. 119. Током через вольтметр пренебрегаем ввиду
того, что его сопротивление велико по сравнению с внутренними сопротивлениями элементов. Падение напряжения на внутренних сопротивлениях элементов должно равняться разности э. д. с. элементов, так как они включены навстречу друг другу: 
отсюда
Разность потенциалов между точками а и b (показание вольтметра)
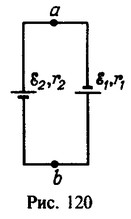
3 Два элемента с э. д. с. ε1=1.4B и ε2 = 1,1 В и внутренними сопротивлениями r =0,3 Ом и r2 = 0,2 Ом замкнуты разноименными полюсами (рис. 120). Найти напряжение на зажимах элементов. При каких условиях разность потенциалов между точками а и b равна нулю?
Решение:
4 Два источника тока с одинаковыми э. д. с. ε = 2 В и внутренними сопротивлениями r1 =0,4 Ом и r2 = 0,2 Ом соединены последовательно. При каком внешнем сопротивлении цепи R напряжение на зажимах одного из источников будет равным нулю?
Решение: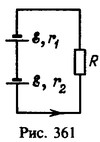
Ток в цепи
(рис.361). Напряжения на зажимах источников тока
Решая первые два уравнения при условии V1=0, получим
Условие V2=0 неосуществимо, так как совместное решение первого и третьего уравнений приводит к значению R<0.
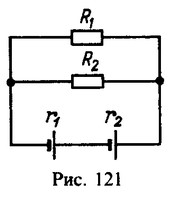
5 Найти внутреннее сопротивление r1 первого элемента в схеме, изображенной на рис. 121, если напряжение на его зажимах равно нулю. Сопротивления резисторов R1 = 3 Ом, R2 = 6 0м, внутреннее сопротивление второго элемента r2 = 0,4 Ом, э. д. с. элементов одинаковы.
Решение:
Ток в общей цепи
где внешнее сопротивление цепи
По условию задачи напряжение на зажимах первого элемента
отсюда
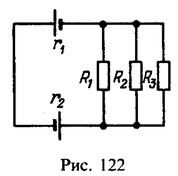
6 При каком соотношении между сопротивлениями резисторов R1, R2, R3 и внутренними сопротивлениями элементов r1, r2 (рис. 122) напряжение на зажимах одного из элементов будет равно нулю? Э. д. с. элементов одинаковы.
Решение:
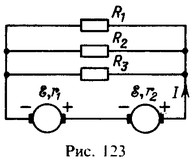
7 Два генератора с одинаковыми э. д. с. ε = 6 В и внутренними сопротивлениями r1 =0,5 Ом и r2 = 0,38 Ом включены по схеме, изображенной на рис. 123. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 7 Ом. Найти напряжения V1 и V2 на зажимах генераторов.
Решение:
Ток в общей цепи
где внешнее сопротивление цепи
Напряжения на зажимах первого и второго генератора
напряжение на зажимах второго генератора
8 Три элемента с э. д. с. ε1 = 2,2 В, ε2 = 1,1 В и ε3 = 0,9 В и внутренними сопротивлениями r1 = 0,2 Ом, r2 = 0,4 Ом и r3 = 0,5 Ом включены в цепь последовательно. Внешнее сопротивление цепи R=1 Ом. Найти напряжение на зажимах каждого элемента.
Решение:
По закону Ома для полной цепи ток
Напряжение на зажимах каждого элемента равно разности э. д. с. и падения напряжения на внутреннем сопротивлении элемента:
Напряжение на зажимах батареи элементов равно падению напряжения на внешнем сопротивлении цепи:
Напряжение на зажимах третьего элемента оказалось отрицательным, так как ток определяется всеми сопротивлениями цепи и суммарной э.д.с, а падение напряжения на внутреннем сопротивлении r3 больше, чем э.д.с. ε3.
9 Батарея из четырех последовательно включенных в цепь элементов с э. д. с. ε = 1,25 В и внутренним сопротивлением r = 0,1 Ом питает два параллельно соединенных проводника с сопротивлениями R1 = 50 Ом и R2 = 200 Ом. Найти напряжение на зажимах батареи.
Решение:
10 Сколько одинаковых аккумуляторов с э. д. с. ε = 1,25B и внутренним сопротивлением r = 0,004 Ом нужно взять, чтобы составить батарею, которая давала бы на зажимах напряжение V=115 В при токе I=25 А?
Решение:
Напряжение на зажимах батареи
Следовательно,
11 Батарея из n= 40 последовательно включенных в цепь аккумуляторов с э. д. с. ε = 2,5 В и внутренним сопротивлением r = 0,2 Ом заряжается от сети с напряжением V=121 В. Найти зарядный ток, если последовательно в цепь введен проводник с сопротивлением R = 2 Ом.
Решение:
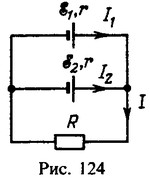
12 Два элемента с э. д. с. ε1 = 1,25 В и ε2 = 1,5 В и одинаковыми внутренними сопротивлениями r = 0,4 Ом соединены параллельно (рис. 124). Сопротивление резистора R= 10 Ом. Найти токи, текущие через резистор и каждый элемент.
Решение:
Падение напряжения на резисторе, если токи текут в направлениях, указанных на рис. 124,
Учитывая, что I=I1+I2, находим
Заметим, что I1<0. Это значит, что направление тока противоположно указанному на рис. 124.
13 Два элемента с э. д. с. ε1 =6 В и ε2 = 5 В и внутренними сопротивлениями r1 = 1 Ом и r2 = 20м соединены по схеме, изображенной на рис. 125. Найти ток, текущий через резистор с сопротивлением R= 10 Ом.
Решение: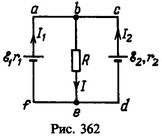
Выбрав направления токов, указанные на рис. 362, составим уравнения Кирхгофа. Для узла b имеем I1+I2-I=0; для контура abef (обход по часовой стрелке)
и для контура bcde (обход против часовой стрелки)
Из этих уравнений найдем
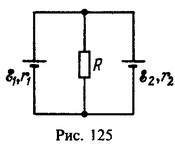
14 Три одинаковых элемента с э. д. с. ε = 1,6 В и внутренним сопротивлением r=0,8 Ом включены в цепь по схеме, изображенной на рис. 126. Миллиамперметр показывает ток I=100 мА. Сопротивления резисторов R1 = 10Ом и R2 = 15 0м, сопротивление резистора R неизвестно. Какое напряжение V показывает вольтметр? Сопротивление вольтметра очень велико, сопротивление миллиамперметра пренебрежимо мало.
Решение:
Внутреннее сопротивление элементов
Сопротивление параллельно включенных резисторов
Общая э. д. с. элементов e0=2e Согласно закону Ома для полной цепи
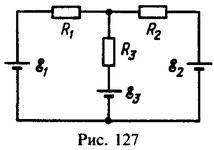
15 Сопротивления резисторов R1 и R2 и э. д. с. ε1 и ε2 источников тока в схеме, изображенной на рис. 127, известны. При какой э.д.с. ε3 третьего источника ток через резистор R3 не течет?
Решение: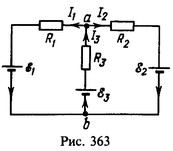
Выберем направления токов I1, I2 и I3 через резисторы R1, R2 и R3, указанные на рис. 363. Тогда I3=I1+I2. Разность потенциалов между точками а и b будет равна
Если
Исключая I1 находим
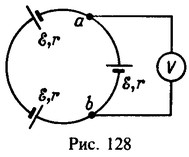
16 Цепь из трех одинаковых последовательно соединенных элементов с э.д.с. ε и внутренним сопротивлением r замкнута накоротко (рис. 128). Какое напряжение покажет вольтметр, подключенный к зажимам одного из элементов?
Решение: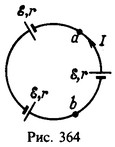
Рассмотрим ту же схему без вольтметра (рис. 364). Из закона Ома для полной цепи находим
Из закона Ома для участка цепи между точками а и b получим
Подключение вольтметра к точкам, разность потенциалов между которыми равна нулю, ничего не может изменить в цепи. Поэтому вольтметр будет показывать напряжение, равное нулю.
17 Источник тока с э.д.с. ε0 включен в схему, параметры которой даны на рис. 129. Найти э.д.с. ε источника тока и направление его подключения к выводам а и b, при которых ток через резистор с сопротивлением R2 не идет.
Решение: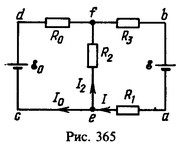
Подключим источник тока к выводам а и b и выберем направления токов, указанные на рис. 365. Для узла е имеем I=I0+I2. При обходе контуров aefb и ecdf по часовой стрелке получим
Используя условие I2 = 0, находим
Знак минус показывает, что полюсы источника тока на рис. 365 нужно поменять местами.
18 Два элемента с одинаковыми э.д.с. ε включены в цепь последовательно. Внешнее сопротивление цепи R = 5 Ом. Отношение напряжения на зажимах первого элемента к напряжению на зажимах второго элемента равно 2/3. Найти внутренние сопротивления элементов r1 и r2, если r1=2r2.
Решение:
19 Два одинаковых элемента с э.д.с. ε=1,5 В и внутренним сопротивлением r = 0,2 Ом замкнуты на резистор, сопротивление которого составляет в одном случае R1=0,2 Oм, В другом — R2 = 20 Ом. Как нужно соединить элементы (последовательно или параллельно) в первом и во втором случаях, чтобы получить наибольший ток в цепи?
Решение:
При параллельном соединении двух элементов внутреннее сопротивление и э.д.с. равны r/2 и ε при последовательном соединении они равны 2r и 2ε. Через резистор R при этом текут токи
Отсюда видно, что I2>I1, если R/2+r<R+r/2, т. е. если r1=r; следовательно, токи при параллельном и последовательном соединениях одинаковы. Во втором случае R2>r.Поэтому ток больше при последовательном соединении.
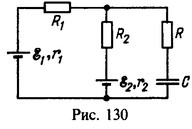
20 Два элемента с э.д.с. ε1=4В и ε2 = 2В и внутренними сопротивлениями r1 = 0,25 Ом и r2 = 0,75 Ом включены в схему, изображенную на рис. 130. Сопротивления резисторов R1 = 1 Ом и R2 = 3 Ом, емкость конденсатора С=2 мкФ. Найти заряд на конденсаторе.
Решение:
21 К батарее из двух параллельно включенных элементов с э.д.с. ε1 и ε2 и внутренними сопротивлениями r1 и r2 подключен резистор с сопротивлением R. Найти ток I, текущий через резистор R, и токи I1 и I2 в первом и втором элементах. При каких условиях токи в отдельных цепях могут быть равными нулю или изменять свое направление на обратное?
Решение: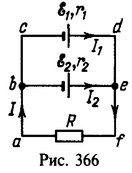
Выберем направления токов, указанные на рис. 366. Для узла b имеем I-I1-I2=0. При обходе контуров abef и bcde по часовой стрелке получим
Из этих уравнений находим
Ток I=0 тогда, когда изменена полярность включения одного из элементов и, кроме того, выполнено условие
Ток I1=0 при
а ток I2 = 0 при
Токи I1 и I2 имеют направления, указанные на рис.366, если
Они меняют свое направление при
22 Батарея из n одинаковых аккумуляторов, соединенных в одном случае последовательно, в другом— параллельно, замыкается на резистор с сопротивлением R. При каких условиях ток, текущий через резистор, в обоих случаях будет один и тот же?
Решение:
При n(R-r) = R-r. Если R=r, то число элементов произвольно; если R№r, задача не имеет решения (n=1).
23 Батарея из n = 4 одинаковых элементов с внутренним сопротивлением r=2 Ом, соединенных в одном случае последовательно, в другом — параллельно, замыкается на резистор с сопротивлением R=10Ом. Во сколько раз показание вольтметра н одном случае отличается от показания вольтметра в другом случае? Сопротивление вольтметра велико по сравнению с R и r.
Решение:
где V1 — показание вольтметра при последовательном соединении элементов, V2-при параллельном.
24 Как изменится ток, текущий через резистор с сопротивлением R = 2 Ом, если n =10 одинаковых элементов, соединенных последовательно с этим резистором, включить параллельно ему? Э.д.с. элемента ε = 2 В, его внутреннее сопротивление r = 0,2 Ом.
Решение:
25 Батарея составлена из N=600 одинаковых элементов так, что n групп соединены последовательно и в каждой из них содержится т элементов, соединенных параллельно. Э.д.с. каждого элемента ε = 2 В, его внутреннее сопротивление r = 0,4 Ом. При каких значениях n и m батарея, будучи замкнута на внешнее сопротивление R = 0,6 Ом, отдаст во внешнюю цепь максимальную мощность? Найти при этом ток, текущий через сопротивление R.
Решение: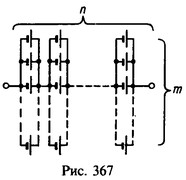
Общее число элементов N=nm (рис. 367). Ток во внешней цепи
где r/m— внутреннее сопротивление группы из т параллельно соединенных элементов, а nr/m — внутреннее сопротивление n групп, соединенных последовательно. Максимальная мощность отдается во внешнюю цепь при равенстве сопротивления R внутреннему сопротивлению батареи элементов nr/m, т. е. 
При этом через сопротивление R течет точек I=46 А.
26 Емкость аккумулятора Qo=80А⋅ч. Найти емкость батареи из n = 3 таких аккумуляторов, включенных последовательно и параллельно.
Решение:
При последовательном соединении через все аккумуляторы батареи течет один и тот же ток, поэтому все они разрядятся в течение одного и того же времени. Следовательно, емкость батареи будет равна емкости каждого аккумулятора: 
При параллельном соединении n аккумуляторов через каждый из них течет 1/n часть общего тока; поэтому при том же разрядном токе в общей цепи батареи будет разряжаться в n раз дольше, чем один аккумулятор, т. е. емкость батареи в п раз больше емкости отдельного аккумулятора:
Заметим, однако, что энергия
отдаваемая батареей в цепь, и при последовательном и при параллельном соединении n аккумуляторов в n раз больше энергии, отдаваемой одним аккумулятором. Это происходит потому, что при последовательном соединении э. д. с. батареи в n раз больше э. д. с. одного аккумулятора, а при параллельном соединении э.д.с. батареи остается той же, что и для каждого аккумулятора, но Q увеличивается в n раз.
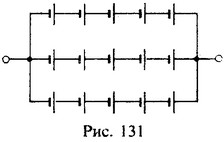
27 Найти емкость батареи аккумуляторов, включенных по схеме, изображенной на рис.131. Емкость каждого аккумулятора Q0=64 А⋅ч.
Решение:
Каждая группа из пяти аккумуляторов, включенных последовательно, имеет емкость
Три параллельно включенные группы дают общую емкость батареи
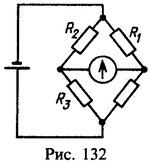
28 Мост для измерения сопротивлений сбалансирован так, что ток через гальванометр не идет (рис. 132). Ток в правой ветви I=0,2 А. Найти напряжение V на зажимах источника тока. Сопротивления резисторов R1 = 2 Ом, R2 = 4 Ом, R3 = 1 Ом.
Решение:
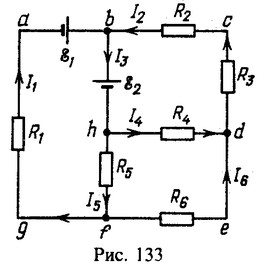
29 Найти токи, протекающие в каждой ветви цепи, изображенной на рис. 133. Э.д.с. источников тока ε1 = 6,5 В и ε2 = 3,9 В. Сопротивления резисторов R1=R2=R3=R4=R5=R6=R=10 Ом.
Решение:
Составляем уравнения Кирхгофа в соответствии с направлениями токов, указанными на рис. 133: I1 + I2 — I3 = 0 для узла b;
I3 — I4 — I5 =0 для узла h; I5 — I1 — I6 = 0 для узла f: при этом
Для контура abfg (обход по часовой стрелке),
Для контура bcdh (обход против часовой стрелки) и
для контура hdef (обход по часовой стрелке). Решая эту систему уравнений с учетом, что все сопротивления одинаковы и равны R=10 Ом, получим
Отрицательные значения токов I2, I4 и I6 показывают, что при данных э.д.с. источников и сопротивлениях резисторов эти токи текут в стороны, противоположные указанным на рис. 133.
Постоянный ток: источники тока 2
Расчет падений напряжений между различными точками, определение токов и напряжений в цепи в том числе с использованием законов Кирхгофа – вот что нас ждет в этой статье.
Задача 1.
В батарее, изображенной на рисунке, 
В, Ом, В‚ Ом‚ В, Ом; Ом‚ Ом. Найти ЭДС и внутреннее сопротивление этой батареи.
К задаче 1
Внутренние сопротивления просто сложим (соединены последовательно):
Чтобы найти ЭДС, обратим внимание, что источники включены «неправильно», поэтому ЭДС будет равна
Ответ: Ом, В.
Задача 2.
Вычислить ЭДС и внутреннее сопротивление батареи, состоящей из трех источников ЭДС (рис.), если ЭДС источников соответственно 10 В, 20 В, 30 В, а их внутренние сопротивления одинаковы и равны 1 Ом.
При параллельном соединении источников их можно пересчитать в один по следующим формулам:
К задаче 2
Тогда
Теперь пересчитаем последовательное соединение двух источников:
Ответ: Ом, В.
Задача 3.
В некоторой цепи имеется участок, изображенный на рисунке, Ом, Ом‚ Ом, В, В‚ В. Найти силу тока в каждом сопротивлении и потенциал .
К задаче 3
По первому закону Кирхгофа .
Пусть
Тогда:
Тогда сила тока в ветвях:
Задача 4.
Определить разность потенциалов между клеммами в схеме, изображенной на рисунке, если В, Ом, Ом.
К задаче 4
Сопротивления ветвей равны
Так как сопротивления ветвей равны, то общее сопротивление обеих ветвей
А ток в неразветвленной части цепи равен
Этот ток разделится ровно пополам в точке – опять же по причине равенства сопротивлений ветвей. Таким образом, токи в ветвях равны 1 A.
Эти токи создадут падения напряжений В, В.
Из рисунка можем записать по второму закону Кирхгофа:
Ответ: В.
Задача 5.
Найти разность потенциалов на зажимах каждого источника тока, если Ом, Ом, Ом, В.
К задаче 5
Определим ток в цепи, для этого сначала определим суммарную ЭДС:
Ток в цепи равен:
Такой ток создаст падение напряжения на :
На :
Тогда на зажимах первого источника
На зажимах второго источника
Ответ: B, B.
Задача 6.
В цепь включены три источника ЭДС и два резистора (рис.) Определить ЭДС и внутреннее сопротивление эквивалентного источника‚ действующего в цепи, а также разность потенциалов между точками А и В, если В, В, В, Ом, Ом, Ом, Ом, Ом.
К задаче 6
Вcе сопротивления просто сложим (соединены последовательно):
Чтобы найти ЭДС, обратим внимание, что источники включены «неправильно», поэтому ЭДС будет равна
Ток в цепи будет равен:
Такой ток создаст падения напряжений:
По второму закону Кирхгофа запишем:
Ответ: В.
Задача 7.
В схему включены три батареи (рис. 12.62) В, В, В, Ом, Ом, Ом. Найти напряжение на зажимах первой батареи.
К задаче 7
Вcе сопротивления просто сложим (соединены последовательно):
Чтобы найти ЭДС, обратим внимание, что источники включены «неправильно», поэтому ЭДС будет равна
Ток в цепи будет равен:
Такой ток создаст падение напряжения:
Искомое напряжение равно
Ответ: В.
Для школьников.
При прохождении тока через нагрузку электрическая энергия превращается в другие виды энергии :тепловую (в электроплитке); в тепло и свет (в электрической лампе); в механическую энергию (в электродвигателе).
Превращение энергии из одного вида в другой всегда связано с работой.
Согласно закону сохранения энергии, для замкнутой электрической цепи можно записать:
Здесь
есть полная или затраченная работа, совершаемая сторонними силами, существующими внутри источника, по переносу заряда по цепи.
В гальваническом элементе сторонними силами являются силы химической реакции.
– это полезная работа, совершаемая электрическим полем при прохождении тока через нагрузку;
это работа, совершаемая внутри источника, по преодолению его внутреннего сопротивления.
Так как работа, совершённая за единицу времени, есть мощность, то из уравнения (1) получим выражение для мощности:
Здесь
есть полная или затраченная мощность, это мощность развиваемая источником тока.
это мощность выделяемая внутри источника тока
это полезная мощность, создаваемая во внешней части цепи (на нагрузке).
Здесь U – напряжение на зажимах источника при замкнутой цепи (при разомкнутой цепи оно равно ЭДС источника).
Так как для однородного участка цепи напряжение равно произведению тока на сопротивление, то полезную мощность можно найти ещё по следующей формуле:
Ток в замкнутой цепи
тогда формулу для полезной мощности можно записать так:
Проанализируем зависимость полезной мощности от сопротивления нагрузки.
При коротком замыкании вся развиваемая источником мощность выделяется на его внутреннем сопротивлении в виде теплоты.
Таким образом, полезная мощность, развиваемая во внешней цепи, достигает максимального значения тогда, когда сопротивление нагрузки равно внутреннему сопротивлению источника.
На следующем рисунке показан график зависимости полезной мощности от сопротивления нагрузки.
Получена формула для нахождения максимальной полезной мощности
При этом ток в цепи в два раза меньше тока короткого замыкания:
Но чему при этом будет равно КПД источника?
Из графика видно, что при равенстве сопротивления нагрузки и внутреннего сопротивления источника тока КПД источника равен 50%.
Коэффициент полезного действия (КПД) источника показывает, какая часть затраченной (полной) работы источника пошла на пользу или КПД есть отношение полезной работы к затраченной:
Задачи (теория дана в предыдущей записи)
1. ЭДС аккумулятора 2 В, его внутреннее сопротивление 0,4 Ом, сопротивление внешней цепи 1 Ом. Найти разность потенциалов на зажимах аккумулятора и КПД его работы.
Напряжение на зажимах аккумулятора:
Ток в цепи:
КПД аккумулятора:
Ответ: 1,43 В; 71 %.
2. Какую максимальную полезную мощность может выделить аккумулятор с ЭДС 10 В и внутренним сопротивлением 1 Ом? Каково при этом сопротивление внешней цепи?
Максимальная полезная мощность:
Полезная мощность достигает максимального значения при
Ответ: 25 Вт; 1 Ом.
3. КПД источника тока, замкнутого на внешнее сопротивление R, равно 60%. Каков будет КПД источника, если внешнее сопротивление увеличить в 6 раз?
Внутреннее сопротивление источника величина постоянная, его можно выразить из первого уравнения через R, затем найти второе значение КПД:
Ответ: 90%.
На приборах часто отмечается потребляемая ими мощность – мощность, необходимая для нормальной работы этого прибора.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Зарядка и разрядка конденсатора.
Следующая запись: Занятие 59. Электрический ток в электролитах.
Ссылки на занятия до электростатики даны в Занятии 1.
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45.
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.
как определить разность потенциалов на зажимах батареи?
Знаток
(287),
закрыт
9 лет назад
Валентина Вавилова(Серкова)
Гений
(62183)
9 лет назад
Вычислим внешнее сопротивление
1 / R= 1 / R1 + 1 / R2. ( так как соединение параллельное)
1 / R=1 / 2 + 1 / 8=5 / 8.
R=8 / 5=1,6 Ом. Теперь по закону Ома для полной цепи вычислим силу тока.
I=ЭДС / ( R+r ). ( r -внутреннее сопротивление)
I=6 / (1,6 +1,4 )=2A. падение напряжения U=I*R.
U=2*1,6=3,2B.
КПД=R / (R+r ) либо КПД=U / ЭДС.
КПД=1,6 / 3=0,53… ( КПД=3,2 / 6=0,53….) (53%).
Зеркало
Оракул
(76390)
9 лет назад
Для начала нарисовать цепь, потом вспомнить закон Ома, правило делителя напряжений, формулу для мощности электрической цепи, что такое КПД и тупо решить.
Тимер
Знаток
(471)
9 лет назад
сначало расчитаем общее сопротивление двух паралельно подключенных резисторов по формуле Rоб=R1*R2/(R1+R2) = 1.6 Ома. потом Применяя закон Ома для полной цепи находим ток в цепи. I=e/(R+r) = 2А. Разность потенциалов на зажимах применяем закон ома для участка цепи U=R*I=2.8В. на резисторах напряжение известно, можно также этим законом найти токи резисторов. КПД= 46,6%.
Физический смысл закона
Потребители электрического тока вместе с источником тока образуют замкнутую электрическую цепь. Ток, проходящий через потребитель, проходит и через источник тока, а значит, току кроме сопротивления проводника оказывается сопротивление самого источника. Таким образом, общее сопротивление замкнутой цепи будет складываться из сопротивления потребителя и сопротивления источника.
Физический смысл зависимости тока от ЭДС источника и сопротивления цепи заключается в том, что чем больше ЭДС, тем больше энергия носителей зарядов, а значит больше скорость их упорядоченного движения. При увеличении сопротивления цепи энергия и скорость движения носителей зарядов, следовательно, и величина тока уменьшаются.
Зависимость можно показать на опыте. Рассмотрим цепь, состоящую из источника, реостата и амперметра. После включения в цепи идет ток, наблюдаемый по амперметру, двигая ползунок реостата, увидим, что при изменении внешнего сопротивления ток будет меняться.
Что такое напряжение
Электрическое напряжение (обозначается как U) – это физическая величина, которая отражает количественную характеристику работы электрического поля по переносу заряда из точки А в точку В. Соответственно напряжение может быть между двумя точками цепи, но в отличии от ЭДС оно может быть между двумя выводами какого-то из элементов цепи. Напомним, что ЭДС характеризует работу, выполненную сторонними силами, то есть работу самого источника тока или ЭДС по переносу заряда через всю цепь, а не на конкретном элементе.
Это определение можно выразить простым языком. Напряжение источников постоянного тока – это сила, которая перемещает свободные электроны от одного атома к другому в определенном направлении.
Для переменного тока используют следующие понятия:
- мгновенное напряжение — это разность потенциалов между точками в данный промежуток времени;
- амплитудное значение – представляет максимальную величину по модулю мгновенного значения напряжения за промежуток времени;
- среднее значение – постоянная составляющая напряжения;
- среднеквадратичное и средневыпрямленное.
Напряжение участка цепи зависит от материала проводника, сопротивления нагрузки и температуры. Так же как и электродвижущая сила измеряется в Вольтах.
Часто для понимания физического смысла напряжения, его сравнивают с водонапорной башней. Столб воды отождествляют с напряжением, а поток с током.
При этом столб воды в башне постепенно уменьшается, что характеризует понижение напряжения и уменьшения силы тока.
Постоянный ток: источники тока 2
Расчет падений напряжений между различными точками, определение токов и напряжений в цепи в том числе с использованием законов Кирхгофа – вот что нас ждет в этой статье.
Задача 1. В батарее, изображенной на рисунке, В, Ом, В‚ Ом‚ В, Ом; Ом‚ Ом. Найти ЭДС и внутреннее сопротивление этой батареи.
Внутренние сопротивления просто сложим (соединены последовательно):
Чтобы найти ЭДС, обратим внимание, что источники включены «неправильно», поэтому ЭДС будет равна
Ответ: Ом, В.
Задача 2. Вычислить ЭДС и внутреннее сопротивление батареи, состоящей из трех источников ЭДС (рис.), если ЭДС источников соответственно 10 В, 20 В, 30 В, а их внутренние сопротивления одинаковы и равны 1 Ом. При параллельном соединении источников их можно пересчитать в один по следующим формулам:
К задаче 2
Тогда
Теперь пересчитаем последовательное соединение двух источников:
Ответ: Ом, В. Задача 3. В некоторой цепи имеется участок, изображенный на рисунке, Ом, Ом‚ Ом, В, В‚ В. Найти силу тока в каждом сопротивлении и потенциал .
По первому закону Кирхгофа .
Пусть
Тогда:
Тогда сила тока в ветвях:
Задача 4. Определить разность потенциалов между клеммами в схеме, изображенной на рисунке, если В, Ом, Ом.
Сопротивления ветвей равны
Так как сопротивления ветвей равны, то общее сопротивление обеих ветвей
А ток в неразветвленной части цепи равен
Этот ток разделится ровно пополам в точке – опять же по причине равенства сопротивлений ветвей. Таким образом, токи в ветвях равны 1 A.
Эти токи создадут падения напряжений В, В.
Из рисунка можем записать по второму закону Кирхгофа:
Ответ: В.
Задача 5. Найти разность потенциалов на зажимах каждого источника тока, если Ом, Ом, Ом, В.
К задаче 5
Определим ток в цепи, для этого сначала определим суммарную ЭДС:
Ток в цепи равен:
Такой ток создаст падение напряжения на :
На :
Тогда на зажимах первого источника
На зажимах второго источника
Ответ: B, B.
Задача 6. В цепь включены три источника ЭДС и два резистора (рис.) Определить ЭДС и внутреннее сопротивление эквивалентного источника‚ действующего в цепи, а также разность потенциалов между точками А и В, если В, В, В, Ом, Ом, Ом, Ом, Ом.
Вcе сопротивления просто сложим (соединены последовательно):
Чтобы найти ЭДС, обратим внимание, что источники включены «неправильно», поэтому ЭДС будет равна
Ток в цепи будет равен:
Такой ток создаст падения напряжений:
По второму закону Кирхгофа запишем:
Ответ: В.
Задача 7. В схему включены три батареи (рис. 12.62) В, В, В, Ом, Ом, Ом. Найти напряжение на зажимах первой батареи.
К задаче 7
Вcе сопротивления просто сложим (соединены последовательно):
Чтобы найти ЭДС, обратим внимание, что источники включены «неправильно», поэтому ЭДС будет равна
Ток в цепи будет равен:
Такой ток создаст падение напряжения:
Искомое напряжение равно
Ответ: В.
Примеры задач на применение закона Ома для замкнутой цепи
К источнику ЭДС 10 В и внутренним сопротивлением 1 Ом подключен реостат, сопротивление которого 4 Ом. Найти силу тока в цепи и напряжение на зажимах источника.
| Дано: | Решение: |
|
|
При подключении к батарее гальванических элементов резистора сопротивлением 20 Ом сила тока в цепи была 1 А, а при подключении резистора сопротивлением 10 Ом сила тока стала 1,5 А. Найти ЭДС и внутреннее сопротивление батареи.
§ 5. Электродвижущая сила и напряжение источника электрической энергии
При соединении проводником двух разноименно заряженных тел а и б (рис. 11, а), т. е. таких тел, между которыми действует некоторая разность потенциалов, свободные электроны в этих телах и в соединительном проводнике придут в движение и возникнет электрический ток. Этот ток будет протекать по проводнику до тех пор, пока потенциалы обоих тел не станут равными.
Можно, однако, обеспечить и непрерывное движение электронов по проводнику, соединяющему два разноименно заряженных тела, т.е. непрерывное прохождение электрического тока. Для этого надо каким-то образом возвращать электроны обратно на отрицательно заряженное тело, другими словами, поддерживать постоянными заряды этих тел. Это означает, что для прохождения постоянного тока по металлическому проводнику необходимо все время обеспечивать на его концах разность потенциалов, или напряжение. Для этого проводник надо подключить к источнику электрической энергии и создать замкнутую электрическую цепь (рис. 11, б). В проводнике положительные заряды движутся от точек с более высоким потенциалом к точкам с более низким потенциалом, т. е. от положительного зажима источника электрической энергии к отрицательному. Но внутри источника эти заряды должны перемещаться от отрицательного зажима к положительному, т. е. от точки с низшим потенциалом к точке с высшим потенциалом. Такое перемещение зарядов внутри источника совершается благо-
даря электродвижущей силе (э. д. с), которая возбуждается в источнике. Э. д. с. поддерживает разность потенциалов на зажимах источника электрической энергии, обеспечивая прохождение тока по электрической цепи. Эта разность потенциалов определяет собой напряжение источника электрической энергии. Э. д. с. обозначается буквой Е (е) и численно равна работе, которую нужно затратить на перемещение единицы положительного заряда от одного зажима источника к другому. Э. д. с. и напряжение источника тесно связаны друг с другом. Если в источнике не возбуждается э. д. с, то будет отсутствовать и напряжение на его зажимах.
Следует отметить, что э. д. с. и напряжение источника могут существовать независимо от наличия тока в цепи. Если электрическая цепь постоянного тока разомкнута, то ток по цепи не проходит, но при работающем генераторе или аккумуляторе в них возбуждается э. д. с. и между их зажимами действует напряжение.
За единицу э. д. с, также как и напряжения, принят вольт. В разных источниках электрической энергии э. д. с. возникает по различным физическим причинам. Например, в электрических генераторах э. д. с. получается в результате электромагнитной индукции, в химических источниках тока (аккумуляторах, гальванических элементах) — вследствие электрохимических реакций.
Количественная разница между э. д. с. и напряжением источника будет рассмотрена в § 9.
