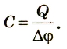Конденсатор служит для накопления электрического заряда. Он представляет собой два проводника, разделенных слоем диэлектрика.
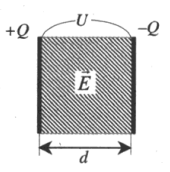
Плоский конденсатор — система двух разноименно заряженных пластин.
Разность потенциалов U (В) между обкладками конденсатора (напряжение между пластинами), определяется произведением напряженности создаваемого ими электрического поля на расстояние между ними:
U=Ed
Электроемкость конденсатора
Определение
Электрическая емкость — характеристика проводника, мера его способности накапливать электрический заряд.
Электроемкость обозначается как C. Единица измерения электрической емкости — Фарад (Ф).
Электроемкость конденсатора определяется формулой:
C=ε0εSd
- ε0 — диэлектрическая постоянная, равная 8,85∙10–12 Кл2/(Н∙м2);
- ε — диэлектрическая проницаемость среды;
- S (м2) — площадь каждой пластины.
Внимание! У воздушного конденсатора диэлектрическая проницаемость среды равна 1.
Связь между электроемкостью конденсатора, зарядом и напряжением определяется формулами:
C=QU=qU
Важно! Электроемкость конденсатора зависит только от площади его пластин, расстояния между ними и диэлектрической проницаемости среды. От заряда и напряжения эта величина не зависит.
Энергия конденсатора
Формула энергии конденсатора
Энергия конденсатора связана с его электроемкостью и вычисляется по следующим формулам:
Wэ=q22C=CU22
Подсказки к задачам
| Конденсатор отключен от источника | q = q′ |
| Конденсатор подключен к источнику | U = U′ |
| Количество теплоты и энергия конденсатора | Q = ∆Wэ |
Пример №1. Вычислить электроемкость плоского воздушного конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от друга. Ответ округлить до десятых.
10 см = 0,1 м
1 мм = 0,001 м
Так как между обкладками конденсатора находится воздух, примем диэлектрическую проницаемость среды за единицу.
Площадь квадратной пластины равна квадрату ее стороны:
S = a2
Соединения конденсаторов
| Последовательное соединение | Параллельное соединение | |
| Схема | 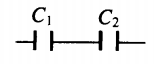 |
 |
| Напряжение |
U=U1+U2 |
U=U1=U2 |
| Заряд |
q=q1=q2 |
q=q1+q2 |
| Электроемкость |
1C=1C1+1C2 |
C=C1+C2 |
Подсказки к задачам
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов одноименными полюсами. | Схема соединения конденсаторов одноименными полюсами:
Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
| Два конденсатора, электроемкости которых C1 и C2, заряжены до напряжения U1 и U2. Найдите разность потенциалов после соединения конденсаторов разноименными полюсами. |
Схема соединения конденсаторов разноименными полюсами:
Заряд системы после соединения: q′ Электрическая емкость системы: C′ Напряжение: U′ |
Пример №2. К конденсатору, электрическая емкость которого C = 16 пФ, подключают два одинаковых конденсатора емкостью X: один параллельно, а второй — последовательно (см. рисунок). Емкость образовавшейся батареи конденсаторов равна емкости C. Какова емкость X? Ответ округлите до десятых.
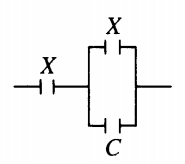
Электрическая емкость параллельного соединения равна:
Cпарал=X+C
Электроемкость последовательного соединения:
1Cпослед=1Cпарал+1X=1X+C+1X
Учтем, что суммарная электроемкость равна C:
1C=1X+C+1X
Преобразуем, умножим выражение на CX(X+C):
X(X+C)=CX+C(X+C)
Раскроем скобки:
X2+XC=CX+CX+C2
X2−CX−C2=0
Решив уравнение, получим: X = 25,9 пФ.
Разбор задач на тему «Заряженная частица в поле конденсатора»
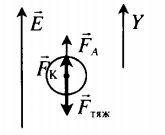
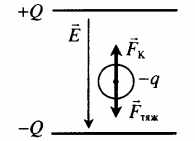
| Шарик, находящийся в масле плотностью ρ, «висит» в поле плоского конденсатора. Плотность вещества шарика ρш > ρ, его радиус r, расстояние между обкладками конденсатора d. Каков заряд шарика, если электрическое поле направлено вверх, а разность потенциалов между обкладками U? | Условие равновесия исходит из второго закона Ньютона:
−Fтяж+−FK+−FA=0 ρш > ρ, поэтому −Fтяж> −FA. В этом случае сила Кулона направлена вверх, а заряд шарика положительный. Схематически это можно отобразить так:
Проекция второго закона Ньютона на ось ОУ: FK+FA=Fтяж Сила тяжести равна произведению объема на плотность шарика и на ускорение свободного падения: Fтяж=ρш43πr3g Архимедова сила равна произведению объема шарика на плотность масла и на ускорение свободного падения: FА=ρ43πr3g Сила Кулона: FK=qUd qUd+ρ43πr3g=ρш43πr3g q=(ρш43πr3g−ρ43πr3g)dU=4πr3gd(ρш−ρ)3U |
| Маленький шарик с зарядом q и массой m, подвешенный на невесомой нити с коэффициентом упругости k, находится между вертикальными пластинами воздушного конденсатора. Расстояние между обкладками конденсатора d. Какова разность потенциалов между обкладками конденсатора U, если удлинение нити ∆l? | 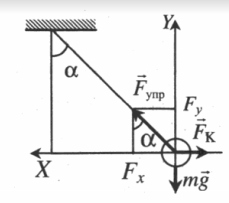
Условие равновесия исходит из второго закона Ньютона: −Fтяж+−FK+−Fупр=0 Проекции на оси ОХ и ОУ соответственно: Fупрsinα−FK=0 Fупрcosα−mg=0 Отсюда: kΔlsinα=qUd kΔlcosα=mg Чтобы избавиться от угла α, возведем уравнения в квадрат и сложим их: (kΔl)2sin2α+(kΔl)2cos2α=(qUd)2+(mg)2 (kΔl)2(sin2α+cos2α)=(qUd)2+(mg)2 sin2α+cos2α=1 (kΔl)2=(qUd)2+(mg)2 U=dq√(kΔl)2−(mg)2 |
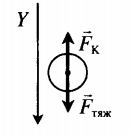
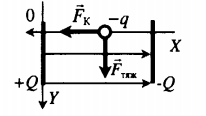
| Пластины плоского конденсатора расположены горизонтально на расстоянии d друг от друга. Напряжение на пластинах конденсатора U. В пространстве между пластинами падает капля жидкости. Масса капли m, ее заряд q. Определите расстояние между пластинами. Влиянием воздуха на движение капли пренебречь. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=0
Проекция на вертикальную ось: Fтяж−FK=0 Fтяж=mg FK=qUd mg=qUd d=qUmg |
| Между двумя параллельными горизонтально расположенными диэлектрическими пластинами создано однородное электрическое поле с напряженностью −E, направленное вертикально вниз. Между пластинами помещен шарик на расстоянии d от верхней пластины и b от нижней. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Через какой промежуток времени t шарик ударится об одну из пластин, если система находится в поле силы тяжести Земли? | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a Согласно условию данной задачи, сила тяжести противоположно направлена силе Кулона. Построим рисунок:
Если Fтяж > FK, то шарик движется с ускорением вниз. Ускорение и перемещение в этом случае равны: a=mg−qEm s=b Если Fтяж < FK, то шарик движется с ускорением верх. Ускорение и перемещение в этом случае равны: a=qE−mgm s=d Начальная скорость шарика равна нулю. Поэтому перемещение также равно: s=at22 Сделаем вычисления для случая Fтяж > FK: at22=b mg−qEmt22=b t=√2bmmg−qE Выполняя вычисления для случая Сделаем вычисления для случая Fтяж < FK, получим: t=√2bmqE−mg |
| Между двумя параллельными, вертикально расположенными диэлектрическими пластинами создано однородное электрическое поле, напряженность которого −E и направлена слева направо. Между пластинами помещен шарик на расстоянии b от левой пластины и d от правой. Заряд шарика –q, масса m. Шарик освобождают, и он начинает двигаться. Найдите смещение шарика по вертикали ∆h до удара об одну из пластин. Пластины имеют достаточно большой размер. | Второй закон Ньютона в векторной форме:
−Fтяж+−FK=m−a
Если сила Кулона направлена вправо, то sx = d. Если сила Кулона направлена вправо, то sx = b. Учитывая, что заряд меньше нуля, а вектор напряженности направлен вправо, делаем вывод, что кулоновская сила направлена влево. Из проекций второго закона Ньютона выразим проекции ускорения на оси ОХ и ОУ соответственно: ax=qEm ay=g Проекции перемещений на эти же оси: sx=axt22 sx=Δh=gt22 axt22=b Или: qEmt22=b Так как время движения шарика по вертикали и горизонтали одинаково: t2=2Δhg=2mbqE Δh=mbgqE |
Задание EF17979
Введите ответ в поле ввода
Плоский конденсатор подключён к гальваническому элементу. Как изменятся при уменьшении зазора между обкладками конденсатора три величины: ёмкость конденсатора, величина заряда на его обкладках, разность потенциалов между ними?
Для каждой величины определите соответствующий характер изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
1.Определить, от чего зависит емкость конденсатора, и как она изменится при уменьшении зазора между его обкладками.
2.Определить, от чего зависит величина заряда конденсатора, и как она изменится после уменьшения зазора между его обкладками.
3.Определить, от чего зависит разность потенциалов между обкладками конденсатора, и как она изменится при уменьшении зазора.
Решение
Емкость конденсатора определяется формулой:
C=ε0εSd
Следовательно, емкость имеет обратно пропорциональную зависимость от расстояния между обкладками. Если расстояние уменьшить, то емкость увеличится.
Вот как взаимосвязана электроемкость и заряд конденсатора:
C=qU
Мы выяснили, что электроемкость увеличивается. Следовательно, увеличится и заряд, так как они имеют прямо пропорциональную зависимость.
С учетом того, что плоский конденсатор подключен к гальваническому элементу, разность потенциалов никак не зависит от расстояния между обкладками. Поэтому величина U остается неизменной.
Ответ: 113
pазбирался: Алиса Никитина | обсудить разбор
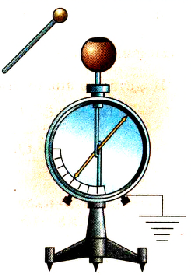
Задание EF18574
Воспользовавшись оборудованием, представленным на рис. 1, учитель собрал модель плоского конденсатора (рис. 2), зарядил нижнюю пластину положительным зарядом, а корпус электрометра заземлил. Соединённая с корпусом электрометра верхняя пластина конденсатора приобрела отрицательный заряд, равный по модулю заряду нижней пластины. После этого учитель сместил одну пластину относительно другой не изменяя расстояния между ними (рис. 3). Как изменились при этом показания электрометра (увеличились, уменьшились, остались прежними)? Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения. Показания электрометра в данном опыте прямо пропорциональны разности потенциалов между пластинами конденсатора.

Алгоритм решения
1.Проанализировать каждый этап эксперимента.
2.Установить, от чего зависит угол отклонения стрелки электрометра.
3.Выяснить, что поменяется при смещении одной пластины конденсатора относительно другой, и что при этом произойдет со стрелкой электрометра.
Решение
На первом рисунке стрелка и стержень электрометра, соединённые с нижней пластиной, но изолированные от корпуса, заряжаются положительно. Поэтому стрелка отклоняется на некоторый угол. В верхней пластине и металлическом корпусе электрометра происходит перераспределение свободных электронов таким образом, что верхняя пластина заряжается отрицательно.
На втором рисунке заряды пластин одинаковы по модулю и противоположны по знаку, пластины образуют конденсатор с ёмкостью:
C=ε0εSd
S — площадь перекрытия пластин, d — расстояние между ними, ε — диэлектрическая проницаемость диэлектрика между пластинами.
Характер изменения угла отклонения стрелки совпадает с изменением разности потенциалов между пластинами: при увеличении разности потенциалов увеличивается угол отклонения, при уменьшении разности потенциалов угол уменьшается.
На рисунке 3 площадь перекрытия пластин уменьшилась. Следовательно, уменьшилась электроемкость, которая имеет обратно пропорциональную зависимость от разности потенциалов:
C=qU
Заряд остается постоянным, поскольку система изолированная — заряду просто некуда деться. Поэтому с уменьшением электроемкость растет разность потенциалов. Поэтому показания электрометра увеличатся.
Ответ: Увеличатся
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18695
Ученик изучает свойства плоского конденсатора. Какую пару конденсаторов (см. рисунок) он должен выбрать, чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками?
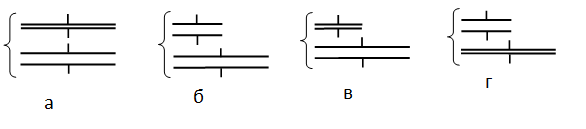
Алгоритм решения
- Установить, какие величины в данном эксперименте должны быть переменными, а какие — постоянными.
- Найти рисунок с парой конденсаторов, удовлетворяющий требованиям, выявленным в шаге 1.
Решение
Чтобы на опыте обнаружить зависимость ёмкости конденсатора от расстояния между его обкладками, нужно сохранить все величины постоянными, кроме самого расстояния. Поэтому площади обкладок должны быть одинаковыми, но расстояние между ними разными, как на рисунке 1.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18703
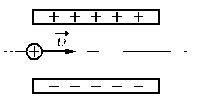 Протон влетает в электрическое поле конденсатора параллельно его пластинам в точке, находящейся посередине между пластинами (см. рисунок). Найдите минимальную скорость υ, с которой протон должен влететь в конденсатор, чтобы затем вылететь из него. Длина пластин конденсатора 5 см, расстояние между пластинами 1 см, напряжённость электрического поля конденсатора 5000 В/м. Поле внутри конденсатора считать однородным, силой тяжести пренебречь.
Протон влетает в электрическое поле конденсатора параллельно его пластинам в точке, находящейся посередине между пластинами (см. рисунок). Найдите минимальную скорость υ, с которой протон должен влететь в конденсатор, чтобы затем вылететь из него. Длина пластин конденсатора 5 см, расстояние между пластинами 1 см, напряжённость электрического поля конденсатора 5000 В/м. Поле внутри конденсатора считать однородным, силой тяжести пренебречь.
Ответ записать в км/с, округлив до десятков.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Выполнить рисунок. Указать направление движения протона и силы, действующие на него.
3.Выяснить, при каком условии протон успеет вылететь из конденсатора.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса протона: m = 1,67∙10–27 кг.
• Заряд протона: q = 1,6∙10–19 Кл.
• Расстояние между обкладками конденсатора: d = 1 см.
• Длина пластин конденсатора: l = 5 см.
• Напряженность однородного поля внутри конденсатора: E = 5000 В/м.
1 см = 0,01 м
5 см = 0,05 м
Сделаем рисунок:
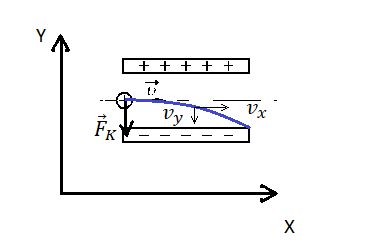
Изначально протон обладает только горизонтальной скоростью v, равной vx. Влетев в однородное электростатическое поле внутри конденсатора, протон обретает вертикальную компоненту скорости, которая растет за счет ускорения, придаваемого кулоновскими силами. Положительно заряженный протон притягивается нижней отрицательно зараженной пластиной конденсатора.
Чтобы протон вылетел из конденсатора, его горизонтальная компонента скорости должна быть достаточной для того, чтобы частица не притянулась к нижней пластине раньше. Время, которое понадобится протону для преодоления длины пластин конденсатора со скоростью vx:
t=lvx=lv
Протон влетел в пространство между обкладками конденсатора на одинаковом расстоянии от них. Следовательно, прежде чем он упадет на нижнюю пластину, по оси OY он переместится на расстояние, равное 0,5d. Так как начальная компонента скорости равна нулю (мы пренебрегаем силой тяжести):
0,5d=at22
Протон вылетит из конденсатора, а не упадет на его пластину, если время горизонтального перемещения до конца пластин будет как минимум равно времени падения. Выразим время падения:
t=√da
Приравняем правые части уравнений времени и получим:
lv=√da
Отсюда скорость равна:
v=√al2d
Ускорение выразим из второго закона Ньютона:
FK=ma=qUd
a=qUmd
Но известно, что:
U=Ed
Поэтому:
a=qEdmd=qEm
Отсюда:
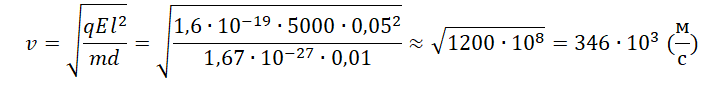
Минимальная скорость, с которой протон должен влететь в конденсатор, составляет 346∙103 м/с. Округлим до десятков и переведем в км/с. Получим 350 км/с.
Ответ: 350
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.9k
Проводники электричества — это вещества и материалы, которые хорошо проводят электричество. Схема из двух проводящих пластин, расположенных параллельно друг другу, называется плоским конденсатором.
Однако конденсаторы — это не только искусственные устройства. Часто в природе мы встречаем системы, которые можно рассматривать как плоские конденсаторы. Примером такого «конденсатора» являются клеточные мембраны внутри вашего тела (рис. 1). Знаете ли вы, какова напряженность электрического поля внутри такой мембраны?

Клеточная мембрана: биологическая мембрана, функция которой заключается в отделении внутренней части клетки от внешней среды. Эта мембрана состоит из двух липидных слоев. Между его стенками существует разность потенциалов. Это позволяет ему реагировать на внешние раздражители.
Что такое плоский конденсатор?
Плоский конденсатор — это расположение двух параллельных друг другу металлических пластин, называемых обкладками конденсатора. Пусть площадь каждой из этих пластин равна S, а расстояние между крышками равно d. На рисунке 2 показана схема заряженного плоского конденсатора.

Линии электрического поля обозначены на рис. 2. В каждой точке вектор напряженности электрического поля одинаков, т.е. поле однородно.
Согласно закону Гаусса, значение напряженности поля от каждой обкладки составляет: E+/- = σ / 2ε0 .
Закон Гаусса (для электричества):
Закон Гаусса (для электричества): уравнение, связывающее электрическое поле и его источник. Оно гласит, что поток ФE напряженности электрического поля Е, проникающий через любую замкнутую поверхность S, равен суммарному заряду q внутри этой поверхности, деленному на диэлектрическую проницаемость вакуума.
Напротив, результирующая напряженность поля от обоих покрытий составляет:
E = E+ + E— = 2 * σ / 2ε0 = σ / ε0 , где
σ — плотность поверхностного заряда, определяемая как отношение заряда q, накопленного на поверхности, к величине площади поверхности S: σ = q / S ,
ε0 — диэлектрическая проницаемость вакуума, ε0 = 8,85 · 10-12 Ф · м−1 .
Таким образом:
E = q / S * ε0
Из приведенной выше формулы мы можем определить единицу напряженности поля — [ В / м ].
Таким образом, единицей напряженности электрического поля, помимо ньютона на кулон, является вольт на метр.
Расчет разности потенциалов между обкладками плоского конденсатора
Итак, мы уже знаем, как выглядит поле между обкладками плоского конденсатора. Теперь рассмотрим, существует ли связь между разностью потенциалов и напряженностью электростатического поля в конденсаторе. В конце концов, и напряженность, и потенциал являются величинами, характеризующими электростатическое поле.
По определению, разность потенциалов ΔV между точками A и B электрического поля равна отношению работы, необходимой для переноса пробного заряда между этими точками (WAB), к величине этого заряда.
ΔV = WAB / q
Единицей измерения потенциала является вольт, который мы обозначаем символом В.
В случае плоского конденсатора, когда мы перемещаем заряд в однородном электрическом поле, работа WAB равна скалярному произведению вектора силы, действующей на образец заряда, и вектора смещения с длиной, равной расстоянию между обкладками d, и возвратом, соответствующим возврату вектора напряженности электрического поля (рис. 3).
WAB = F * d

Из определения напряженности электрического поля следует, что: F = E * q
То есть:
WAB = F * d = E * q * d = q * E * d * cos α
Где α (угол между вектором напряженности электрического поля и вектором смещения) равен 0, т.е. cosα = 1. Поэтому:
WAB = E * d * q
Подставляя приведенную выше формулу для: ΔV = WAB / q = q * E * d / q = E * d
Эта формула определяет связь между разностью потенциалов и напряженностью электрического поля в плоском конденсаторе.
Теперь преобразуем эту формулу, чтобы получить зависимость напряженности поля от разности потенциалов:
E = ΔV / d
Эта формула говорит нам, что величина напряженности поля в плоском конденсаторе равна отношению разности потенциалов между обкладками этого конденсатора к расстоянию между этими обкладками. Таким образом, мы видим, что напряженность поля в плоском конденсаторе E прямо пропорциональна разности потенциалов между его обкладками ∆V. Это означает, что если разность потенциалов между обкладками конденсатора увеличится (например, в два раза), то значение напряженности поля между обкладками также увеличится (также в два раза).
Формула для напряженности поля:
E = q / S * ε0
справедлива для вакуумного конденсатора. Если у нас есть диэлектрик между обкладками конденсатора, мы все равно должны учитывать его относительную электрическую проницаемость εr, которая является безразмерной величиной.
Тогда формула принимает вид:
E = q / S * ε0 * εr
Содержание:
Электроемкость:
Сообщая телу определенный заряд, мы изменяем его потенциал. Это изменение непосредственно связано со значением заряда, сообщаемого телу.
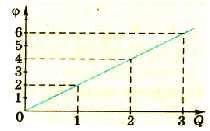
Для исследования зависимости потенциала тела от его заряда проведем опыт с электрометром, корпус которого соединен с поверхностью Земли. ‘Гикая система может измерять потенциал тела относительно Земли. Укрепим на стержне этого электрометра пустотелый металлический шар и будем сообщать ему заряд с помощью маленького металлического шарика на изоляционной ручке. Если коснуться заряженным шариком внутренней поверхности металлического шара, то весь его заряд перейдет на шар, а стрелка электрометра покажет увеличение потенциала шара. Последовательно повторяя опыт с переносом заряда на большой шар, заметим, что каждый раз его потенциал увеличивается (рис. 1.28).
Применяя более точные способы измерения заряда и потенциала, можно установить, что потенциал возрастает пропорционально возрастанию заряда. Потенциал пропорционален заряду шара. Результаты одного из таких опытов отражены на графике (рис 1.29).
Если ни стержне электрометра укрепим шар большего (меньшего) диаметра и продолжим опыты (рис. 1.31), то увидим, что скорость зарядки изменилась, соответственно уменьшилась (увеличилась).
Процесс электризации шара большего диаметра отображен графиком на рисунке 1.32.
Сопоставив графики, которые иллюстрируют процессы зарядки шаров различных диаметров (рис. 1.30 и 1.32), увидим, что графики имеют различный наклон относительно горизонтальной оси. Это свидетельствует о том, что при одинаковых значениях заряда шары разных диаметров будут иметь разные потенциалы. Оказывается, что на князь между зарядом и потенциалом шара существенно влияют геометрические размеры шаров.
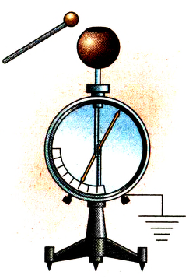
Рис. 130. Электризация шара большего диаметра
Потенциал металлического шара пропорционален его заряду; коэффициент пропорциональности для различных шаров разный.
Анализируя результаты опытов и соответствующие графики, можно сделать выводы:
- потенциал каждого шара пропорционален его заряду:
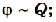
- для тел различных размеров коэффициент пропорциональности разный.
Установлено, что этот коэффициент для каждого тела имеет вполне определенное значение, что отражает способность тела накапливать электрический заряд. Физическая величина, равная отношению электрического заряда, сообщенного телу, к его потенциалу, называется электроемкостью тела.
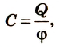
где C – электроемкость проводника; Q – заряд; φ – потенциал.
Для измерения электроемкости в физике применяют единицу, которую называют фарад (Ф).
Тело имеет электроемкость в 1 фарад, если при изменении его заряда на 1 кулон потенциал изменяется па 1 вольт:
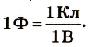
Электроемкость 1 фарад имеют тела, у которых при изменении заряда на 1 кулон потенциал изменяется на 1 вольт.
- 1Ф – довольно большое значение электроемкости. Например, электроемкость Земли, имеющей радиус 6400 км, составляет всего 7 ∙ 104 Ф. Поэтому на практике используют единицу электроемкости, кратную фараду:
- 1 микрофарад = 1 мкФ = 10-5 Ф.
- 1 пикофарад = 1 пФ = 10-12 Ф.
Пример:
Два шара, электроемкости которых 50 мкф и 80 мкФ, а потенциалы 120 В и 50 В соответственно, соединяют проводом. Найти потенциал шаров после соединения.
|
Дано: |
Решение |
| φ-? |
После соединения шаров произойдет перераспределение зарядов между ними так, что их потенциалы станут одинаковыми. Согласно закону сохранения электрических зарядов
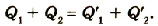
Отсюда
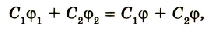
или
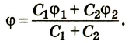
Подставив значения физических величин и произведя расчеты, получим:
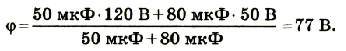
Ответ: после соединения шары будут иметь потенциал 77 В.
Конденсатор
Чтобы экспериментально определить электроемкость проводника, как и его потенциал, нужно создать условия, исключающие влияние всех окружающих тел, которые, влияя па тело, изменяют его потенциал и электроемкость.
Это утверждение можно проверить опытом.
Укрепим на стержне электрометра металлический шар и сообщим ему определенный заряд. Стрелка прибора отклонится от положения равновесия и покажет определенное значение потенциала относительно земли.
Поднесем к шару металлическую пластину, соединенную проводником с землей (рис. 1.32).

Pиc. 132. Заземленная металлическая пластина влияет на электроемкость шара
Показания стрелки электрометра уменьшатся. Поскольку заряд шара в опыте не изменялся, то уменьшение потенциала свидетельствует об увеличении электроемкости шара. Изменение потенциала и соответственно электроемкости шара будет наблюдаться и в случае изменения расстояния между шаром и пластиной.
Таким образом, определяя электроемкость тела, необходимо учитывать также наличие окружающих тел. Поскольку на практике это сделать трудно, то применяют систему из двух или более проводников произвольной формы, разделенных диэлектриком. В этом случае электрические свойства такой системы проводников и диэлектрика не зависят от окружающих тел. Такую систему называют конденсатором. Простейшим для изучения и расчетов является конденсатор из двух металлических пластин, разделенных диэлектриком.
Электроемкость конденсатора, в отличие от обособленного тела, определяется по разности потенциалов между пластинами:
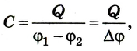
где Q – заряд одной пластины; (φl– φ2) и ∆φ – разность потенциалов между пластинами.
Слово конденсатор обозначает накопитель. В электричестве понимают как «накопитель электрических зарядов».
Пример:
Какую электроемкость имеет конденсатор, если на его обкладках накапливается заряд 50 нКл при разности потенциалов 2,5 кВ?
|
Дано: |
Решение |
| С-? |
Подставим значения физических величин:
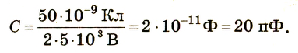
Ответ: электроемкость данного конденсатора 20 пФ.
Первый конденсатор был создан в 1745 г. голландским ученым Питером ван Мушенбруком, профессором Лейденского университета. Проводя опыты по электризации различных тел, он опустил проводник от кондуктора электрической машины в стеклянный графин с водой (рис. 1.33).
 |
Питер ван Мушенбрук (1692-1781) – голландский физик; работы посвящены электричеству, теплоте, оптике; изобрел первый конденсатор – лейденскую банку и провел опыты с ней. |

Pиc. 133. Из истории открытия простейшего конденсатора лейденской банки
Случайно коснувшись пальцем этого проводника, ученый ощутил сильный электрический удар. В дальнейшем жидкость заменили металлическими проводниками, укрепленными на внутренней и внешней поверхностях банки. Такой конденсатор назвали лейденской банкой. В таком первозданном виде она использовалась в лабораториях более 200 лет.
Более совершенные конденсаторы применяются в современной электротехнике и радиоэлектронике. Их можно найти в преобразователях напряжения (адаптерах), питающих постоянным электрическим током электронные приборы, в радиоприемниках и радиопередатчиках как поставные части колебательных контуров. Они применяются практически во всех функциональных узлах электронной аппаратуры. В фотовспышках конденсаторы накапливают большие заряды, необходимые для действия вспышки.
В электротехнике конденсаторы обеспечивают необходимый режим работы электродвигателей, автоматических и релейных приборов, линий электропередач и т. п.
Во многих широкодиапазонных радиоприемниках конденсаторы переменной емкости (рис. 1.34) позволяют плавно изменять собственную частоту колебательного контура н процессе поиска передачи определенной радиостанции.

Рис. 134. Конденсатор переменной емкости с воздушным диэлектриком
Весьма распространены конденсаторы варикапы, электроемкость которых можно изменять электрическим способом. Конструктивно они весьма схожи с полупроводниковыми диодами.
Конденсаторы могут быть плоскими, трубчатыми, дисковыми. В качестве диэлектрика в них используют парафинированную бумагу, слюду, воздух, пластмассы, керамику (рис. 1.35).

Рис. 1.35. Различные типы конденсаторов
Искусственно созданные диэлектрические материалы позволяют создавать конденсаторы больших емкостей при небольших размерах.
Электроемкость плоского конденсатора
Плоским конденсатором обычно называют систему плоских проводящих пластин – обкладок, разделенных диэлектриком. Благодаря простоте конструкции такого конденсатора легко рассчитывать его емкость и получать значения, подтверждаемые опытами. Для этого достаточно знать его геометрические параметры и электрические свойства диэлектрика между его пластинами. Зависимость электроемкости плоского конденсатора от указанных параметров можно исследовать в школьной лаборатории.
Создадим плоский конденсатор из двух плоских пластин. Для этого одну пластину укрепим на стержне электрометра, я другую — па изоляционной подставке, присоединив ее проводником к корпусу электрометра (рис. 1.36.). В такой системе электрометр будет измерять разность потенциалов между пластинами, образующими плоский конденсатор.
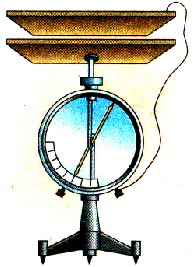
Pиc. 136. Плоский конденсатор, присоединенный к электрометру
Проводя исследования, нужно помнить, что при постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
При постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
Сообщим пластинам некоторый заряд и отметим показания стрелки прибора. Когда начнем сближать пластины, уменьшая расстояние между ними, показания стрелки начнут уменьшаться. Это будет свидетельством того, что при уменьшении расстояния между пластинами электроемкость конденсатора будет увеличиваться. При увеличении расстояния между пластинами показания стрелки будут увеличиваться, что свидетельствует об уменьшении электроемкости.
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
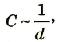
где d – расстояние между обкладками.
Эту, зависимость можно изобразить на графике как обратно пропорциональную зависимость (рис. 1.37).
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
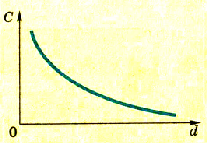
Pиc. 137. График зависимости электроемкости и плоского конденсатора от расстояния между пластинами
Будем смещать одну пластину относительно другой в параллельных плоскостях, не изменяя расстояния между ними. При атом площадь перекрытия между пластинами будет изменяться (рис. 1.38). Изменение разности потенциалов, отмеченное электрометром, засвидетельствует изменение электроемкости.
Pиc. 138. При расчетах электроемкости плоского конденсатора учитывают площадь перекрытия пластин
Увеличение площади перекрытия приведет к увеличению электроемкости, при уменьшении – наоборот.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
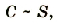
где S – площадь пластин, которые перекрываются.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
Эту зависимость можно изобразить графиком прямой пропорциональной зависимости (рис. 1.39).
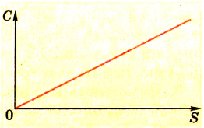
Pиc. 139. График зависимости электроемкости плоского конденсатора от площади его пластин
Возвратив пластины в первоначальное положение, внесем в пространство между обкладками пластину из диэлектрика. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости. Если внести пластину из другого диэлектрика (другая диэлектрическая проницаемость), то изменение электроемкости будет другим.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика между обкладками.
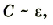
где ε – диэлектрическая проницаемость диэлектрика.
Эта зависимость изображена графиком на рисунке 1.40.
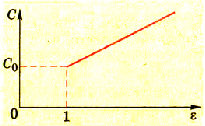
Рис. 1.40. График зависимости электроемкости плоского конденсатора от диэлектрической проницаемости диэлектрика
Результаты описанных выше исследований можно обобщить формулой электроемкости плоского конденсатора
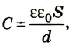
где ε – относительная диэлектрическая проницаемость диэлектрика; ε0– электрическая постоянная; d – расстояние между пластинами; S – площадь пластины.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.
Соединение конденсаторов в батареи
Для получения необходимых значений электроемкости конденсаторы соединяют в батареи. На практике встречается параллельное, последовательное и смешанное соединение конденсаторов.
При параллельном соединении конденсаторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рисунке 1.41 приведена схема такого соединения. При таком соединении каждая группа обкладок имеет одинаковый потенциал.
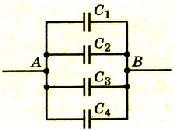
Pиc 1.41. Схема параллельного соединения конденсаторов
Если батарею параллельно соединенных конденсаторов зарядить, то между обкладками каждого конденсатора будет одинаковая разность потенциалов. Общий заряд батареи будет равен сумме зарядов каждого из конденсаторов, входящих в батарею:
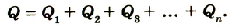
Если учесть, что 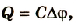 то
то
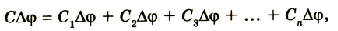
или
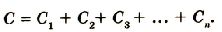
Электроемкость батареи параллельно соединенных конденсаторов равна сумме электроемкостей всех конденсаторов.
При последовательном соединении конденсаторов соединяются между собой только две пластины разных конденсаторов. Если в каждом конденсаторе пластины обозначить буквами А и В, то при последовательном соединении пластина B1 будет соединена с пластиной A2, пластина B2 -с пластиной А3 и т. д. (рис. 1.43).
Если цепочку последовательно соединенных конденсаторов присоединить к источнику тока, то об-
кладка A1 и обкладка B1 будут иметь одинаковые по значению заряды +Q и -Q. Благодаря этому все обкладки внутри цепочки будут иметь такие же, но попарно противоположные по знаку заряды:
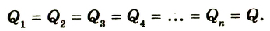
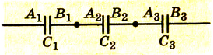
Pиc. 1.42. Последовательное соединение конденсаторов
Вместе с тем общая разность потенциалов на концах цепочки будет равна сумме разностей потенциалов на каждом конденсаторе:
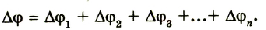
Учитывая, что 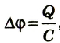 будем иметь
будем иметь
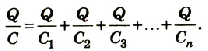
Разделим левую и правую части равенства на Q:
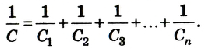
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно с
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
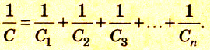
При последовательном соединении конденсаторов разной электроемкости C1, C2, C3, … Сn общая электроемкость С будет меньше электроемкости самого меньшего конденсатора.
Если C1 < C7 < C9 < … < Cn, то C < C1.
Электроемкость
То, что деньги хранят в банках, знает даже первоклассник. А вот где хранят заряды? И зачем вообще хранить заряды?
Что такое электроемкость
Электроемкость характеризует способность проводника или системы проводников накапливать электрический заряд. Различают электроемкость уединенного проводника и электроемкость системы проводников (например, конденсатора). Уединенным называют проводник, расположенный вдали от других тел так, что они не оказывают на этот проводник никакого влияния.
Электроемкость уединенного проводника (C) — физическая величина, характеризующая способность проводника накапливать заряд и равная отношению электрического заряда q проводника к его потенциалу М:
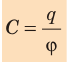
Единица электроемкости в Си — фарад: [C] = 1 Ф (названа в честь М. Фарадея).
1 Ф — это электроемкость такого проводника, потенциал которого равен 1 В при сообщении ему заряда 1 Кл; 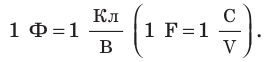
1 Ф — очень большая единица емкости, поэтому используют дольные единицы: 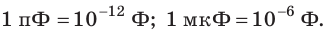
Что такое конденсатор
Конденсатор — устройство, представляющее собой систему из двух проводящих обкладок, разделенных тонким слоем диэлектрика (рис. 44.1).

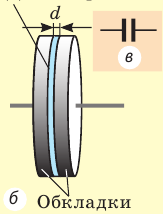
Рис. 44.1. Школьный воздушный конденсатор: а — вид; б — устройство; в — обозначение на схемах
Обкладкам конденсатора передают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов: разноименные заряды притягиваются, а значит, располагаются на внутренних поверхностях обкладок.
Обычно для зарядки конденсатора обе его обкладки соединяют с полюсами батареи аккумуляторов: на обкладках появляются равные по модулю, но противоположные по знаку заряды. Результат не изменится, если соединить с полюсом батареи только одну обкладку, заземлив вторую: вследствие электростатической индукции на заземленной обкладке тоже появится заряд, равный по модулю заряду на другой обкладке, но имеющий противоположный знак.
Зарядом конденсатора называют модуль заряда одной из обкладок. Отношение заряда q данного конденсатора к разности потенциалов (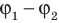 ) между его обкладками не зависит ни от значения q, ни от разности потенциалов (
) между его обкладками не зависит ни от значения q, ни от разности потенциалов (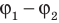 ), а значит, может служить характеристикой конденсатора. Такую характеристику называют электроемкостью (емкостью) конденсатора:
), а значит, может служить характеристикой конденсатора. Такую характеристику называют электроемкостью (емкостью) конденсатора:
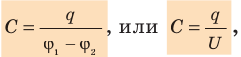
где U — напряжение между обкладками: 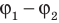 .
.
Как показывают исследования, емкость конденсатора увеличится, если увеличить площадь поверхности обкладок или приблизить обкладки друг к другу. На емкость конденсатора влияет также диэлектрик: чем больше его диэлектрическая проницаемость, тем большую емкость имеет конденсатор.
Конденсатор, состоящий из двух параллельных металлических пластин (обкладок), разделенных слоем диэлектрика, называют плоским (см. рис. 44.1). Электроемкость плоского конденсатора вычисляют по формуле:
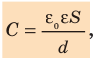
где 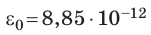 Ф/м — электрическая постоянная; ε — диэлектрическая проницаемость диэлектрика; S — площадь пластины конденсатора; d — расстояние между пластинами.
Ф/м — электрическая постоянная; ε — диэлектрическая проницаемость диэлектрика; S — площадь пластины конденсатора; d — расстояние между пластинами.
Поле между пластинами плоского конденсатора однородно, поэтому напряженность Е поля связана с напряжением U на конденсаторе формулой U=Ed.
Как рассчитывают электроемкость батареи конденсаторов
Конденсаторы характеризуются емкостью и максимальным рабочим напряжением Umax. Если напряжение, поданное на конденсатор, значительно превысит Umax, произойдет пробой — между обкладками возникнет искра, которая разрушит изоляцию.
Чтобы получить необходимую электроемкость при определенном рабочем напряжении, конденсаторы соединяют в батареи, применяя параллельное, последовательное и смешанное соединения. Рассмотрим батарею из трех конденсаторов электроемкостями 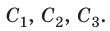
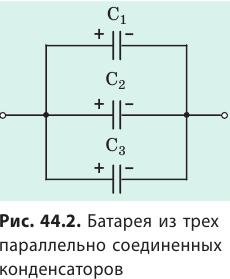
При параллельном соединении конденсаторов положительно заряженные обкладки всех конденсаторов соединяют в один узел, а отрицательно заряженные — в другой узел (рис. 44.2). В таком случае общий заряд q батареи конденсаторов равен алгебраической сумме зарядов отдельных конденсаторов:
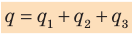
Соединенные в один узел обкладки представляют собой один проводник, поэтому потенциалы обкладок, а следовательно, и разность потенциалов (напряжение) между обкладками всех конденсаторов одинаковы:
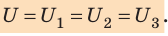
Таким образом, при параллельном соединении конденсаторов допустимое рабочее напряжение батареи определяется рабочим напряжением одного конденсатора.
Поскольку 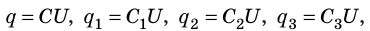 то
то 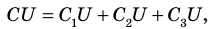 следовательно, электроемкость батареи из трех параллельно соединенных конденсаторов равна:
следовательно, электроемкость батареи из трех параллельно соединенных конденсаторов равна:
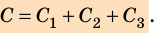
При последовательном соединении конденсаторы соединяют друг с другом разноименно заряженными обкладками (рис. 44.3). В этом случае заряды всех конденсаторов будут одинаковы и равны заряду батареи:
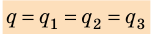
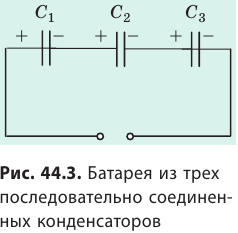
Напряжение на батарее последовательно соединенных конденсаторов равно сумме напряжений на отдельных конденсаторах:
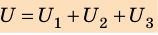
Таким образом, допустимое рабочее напряжение батареи последовательно соединенных конденсаторов больше допустимого рабочего напряжения отдельного конденсатора. Электроемкость батареи последовательно соединенных конденсаторов вычисляют по формуле:
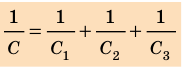
При последовательном соединении конденсаторов емкость батареи меньше, чем емкость конденсатора с минимальной емкостью.
Приведенные соотношения можно обобщить для любого количества конденсаторов.
Обратите внимание!
- Если батарея содержит n параллельно соединенных конденсаторов электроемкостью C′ каждый, то: C=nC′
- Если батарея содержит n последовательно соединенных конденсаторов электроемкостью C′ каждый, то:
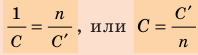
Энергия заряженного конденсатора
Заряженный конденсатор, как и любая другая система заряженных тел, обладает энергией.
Убедимся в этом с помощью простого эксперимента. Присоединим к обкладкам заряженного конденсатора лампочку. Замкнем ключ — лампочка загорится. Теперь измерим напряжение на обкладках конденсатора — оно равно нулю, то есть конденсатор разрядился, а это означает, что заряженный конденсатор обладал энергией, которая частично превратилась в энергию света.
Вычислим энергию заряженного до напряжения 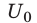 конденсатора емкостью С, на котором накоплен заряд
конденсатора емкостью С, на котором накоплен заряд  . Эту энергию точнее было бы назвать энергией электростатического поля, которое существует между обкладками заряженного конденсатора, поскольку энергия любых заряженных тел сосредоточена в электрическом поле, создаваемом этими телами.
. Эту энергию точнее было бы назвать энергией электростатического поля, которое существует между обкладками заряженного конденсатора, поскольку энергия любых заряженных тел сосредоточена в электрическом поле, создаваемом этими телами.
При разрядке конденсатора напряжение U на его обкладках изменяется прямо пропорционально заряду q конденсатора:  поэтому график зависимости U(q) имеет вид, представленный на рис. 44.4.
поэтому график зависимости U(q) имеет вид, представленный на рис. 44.4.
Рис. 44.4. К определению работы, которую совершает электрическое поле заряженного конденсатора при его разрядке
Мысленно разделим весь заряд конденсатора на маленькие «порции» Dq и будем считать, что при потере каждой такой «порции» напряжение на конденсаторе не изменяется. Таким образом получим ряд полос. Площадь S′ каждой полосы равна произведению двух ее сторон: 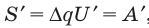 , где U′ — напряжение, при котором конденсатор терял данную «порцию» заряда
, где U′ — напряжение, при котором конденсатор терял данную «порцию» заряда 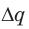 ; A′ — работа, которую совершило поле при потере конденсатором заряда
; A′ — работа, которую совершило поле при потере конденсатором заряда 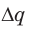 . Полная работа, которую совершило поле при уменьшении заряда конденсатора от
. Полная работа, которую совершило поле при уменьшении заряда конденсатора от 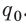 до 0, определяется площадью выделенного на рис. 44.4 треугольника.
до 0, определяется площадью выделенного на рис. 44.4 треугольника.
Следовательно,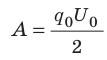 . Учитывая, что
. Учитывая, что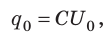 получим:
получим: 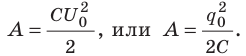 С другой стороны, данная работа равна уменьшению энергии электрического поля конденсатора от
С другой стороны, данная работа равна уменьшению энергии электрического поля конденсатора от 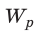 до нуля: A=
до нуля: A=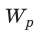 − 0 = W. Таким образом, энергия
− 0 = W. Таким образом, энергия 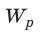 заряженного до напряжения U конденсатора, имеющего электроемкость С и заряд q, равна:
заряженного до напряжения U конденсатора, имеющего электроемкость С и заряд q, равна:
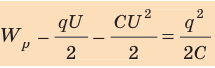
Для чего нужны конденсаторы
В современной технике сложно найти отрасль, где не применялись бы конденсаторы. Без них не обходятся радио и телеаппаратура (настройка колебательных контуров), радиолокационная и лазерная техника (получение мощных импульсов), телефония и телеграфия (разделение цепей переменного и постоянного токов, тушение искр в контактах), электроизмерительная техника (создание образцов емкости). И это далеко не полный перечень.
В современной электроэнергетике конденсаторы тоже имеют широкое применение: они присутствуют в конструкциях люминесцентных светильников, электросварочных аппаратов, устройств защиты от перенапряжений. Конденсаторы применяют и в других, не электротехнических, областях техники и промышленности (в медицине, фототехнике и т. д.).
Разнообразие областей применения обусловливает большое разнообразие конденсаторов. Наряду с миниатюрными конденсаторами, имеющими массу меньше грамма, а размеры порядка нескольких миллиметров, существуют конденсаторы массой несколько тонн и высотой больше человеческого роста. Емкость современных конденсаторов может составлять от долей, а рабочее напряжение может быть в пределах от нескольких вольт до нескольких сотен киловольт. Конденсаторы можно классифицировать по следующим признакам и свойствам:
- по назначению — постоянной и переменной емкости;
- по форме обкладок — плоские, сферические, цилиндрические и др.;
- по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и др.
Выводы:

- Энергию заряженного конденсатора можно вычислить по формулам:
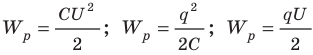
- Конденсаторы классифицируют по назначению (постоянной и переменной емкости); по форме обкладок (плоские, сферические, цилиндрические и др.); по типу диэлектрика (воздушные, бумажные, слюдяные, керамические, электролитические и др.).
- Полупроводники
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Диэлектрики в электрическом поле
- Закон Кулона
Тема: разность потенциалов между пластинами конденсатора (Прочитано 12922 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Одной из пластин плоского конденсатора емкостью С сообщили заряд Q, другой — 4Q. Найти разность потенциалов между пластинами конденсатора.
« Последнее редактирование: 27 Июля 2014, 07:32 от alsak »

Записан
Мы не можем здесь воспользоваться формулой U = C∙q, т.к. заряд пластин не одинаковый.
Разность потенциалов между обкладками конденсатора найдем следующим образом
[varphi _{1} -varphi _{2} =U=Ecdot Delta x,]
где Е — напряженность между пластинами конденсатора, Δx = d — расстояние между пластинами.
Напряженность поля между обкладками плоского конденсатора, согласно принципу суперпозиции (рис. 1), равна
[begin{array}{c} {vec{E}=vec{E}_{1} +vec{E}_{2} ,; ; ; 0X:; ; E_{x} =-E_{1} +E_{2} ,} \ {} \ {E_{1} =frac{left|sigma _{1} right|}{2varepsilon _{0} cdot varepsilon } =frac{left|q_{1} right|}{2varepsilon _{0} cdot varepsilon cdot S} ,; ; E_{2} =frac{left|q_{2} right|}{2varepsilon _{0} cdot varepsilon cdot S} ,} end{array}]
где Е1, Е2 — напряженности электростатических полей, созданных соответственно первой и второй пластинами, q1 = q, q2 = 4q. Площадь S пластин конденсатора найдем следующим образом:
[C=frac{varepsilon cdot varepsilon _{0} cdot S}{d} ,; ; S=frac{Ccdot d}{varepsilon cdot varepsilon _{0} } .]
Тогда
[begin{array}{c} {E_{x} =-frac{left|q_{1} right|}{2varepsilon _{0} cdot varepsilon cdot S} +frac{left|q_{2} right|}{2varepsilon _{0} cdot varepsilon cdot S} =-frac{left|q_{1} right|}{2Ccdot d} +frac{left|q_{2} right|}{2Ccdot d} =frac{-left|q_{1} right|+left|q_{2} right|}{2Ccdot d} =frac{-q+4q}{2Ccdot d} =frac{3q}{2Ccdot d} ,} \ {} \ {varphi _{1} -varphi _{2} , =frac{3q}{2Ccdot d} cdot d=frac{3q}{2C} .; } end{array}]
« Последнее редактирование: 27 Июля 2014, 07:32 от alsak »

Записан
Разность потенциалов
Физическая
величина, равная работе, которую совершат
силы поля, перемещая заряд из одной
точки поля в другую, называется
напряжением
между этими точками поля.
![]()
Рассмотрим
однородное электростатическое поле
(такое поле существует между пластинами
плоского заряженного конденсатора
вдали от его краев):
Во
время перемещения заряда поле совершает
работу:
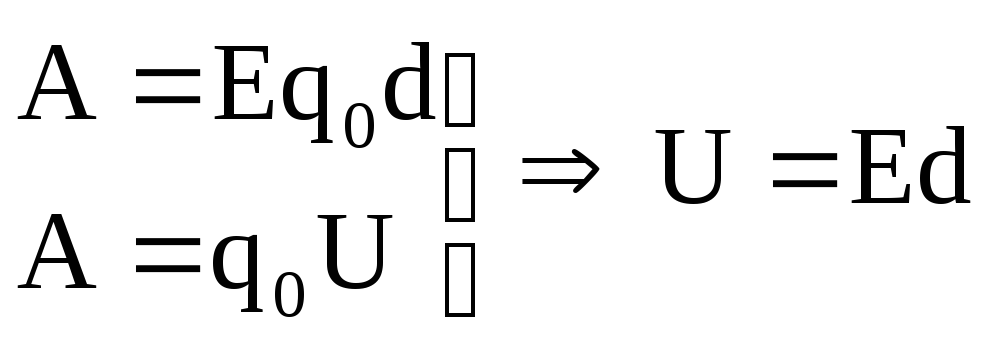
-
Проводник во внешнем электрическом поле (сто происходит, почему индукцируется)
Индукция
электростатическая,
наведение
в проводниках или диэлектриках
электрических зарядов в постоянном
электрическом поле.
В проводникахподвижные заряженные частицы – электроны
– перемещаются под действиемвнешнегоэлектрическогополя.
Перемещение происходит до тех пор, пока
заряд не перераспределится так, что
созданное им электрическоеполевнутрипроводникаполностью скомпенсируетвнешнееполеи
суммарное электрическоеполевнутрипроводникастанет равным нулю. (Если бы этого не
произошло, то внутри проводника,
помещенного в постоянное электрическое
поле, неограниченно долго существовал
бы электрический ток, что противоречило
бы закону сохранения энергии.) В
результате на отдельных участках
поверхности проводника (в целом
нейтрального) образуются равные по
величине наведённые (индуцированные)
заряды противоположного знака.
В диэлектриках,
помещенных в постоянное электрическое
поле, происходит поляризация, которая
состоит либо в небольшом смещении
положительных и отрицательных зарядов
внутри молекул в противоположные
стороны, что приводит к образованию
электрических диполей(с электрическим моментом, пропорциональным
внешнему полю), либо в частичной
ориентации молекул, обладающих
электрическим моментом, в направлении
поля. В том и другом случае электрический
дипольный момент единицы объёма
диэлектрика становится отличным от
нуля. На поверхности диэлектрика
появляются связанные заряды. Если
поляризация неоднородная, то связанные
заряды появляются и внутри диэлектрика.
Поляризованный диэлектрик порождает
электростатическое поле, добавляющееся
к внешнему полю. (См.Диэлектрики.)
-
Электроемкость, конденсатор
Электроемкость
– количественная мера способности
проводника удерживать заряд.
Простейшие
способы разделение разноименных
электрических зарядов – электризация
и электростатическая индукция –
позволяют получить на поверхности тел
не большое количество свободных
электрических зарядов. Для накопления
значительных количеств разноименных
электрических зарядов применяются
конденсаторы.
Конденсатор
– это система из двух проводников
(обкладок), разделенных слоем диэлектрика,
толщина которого мала по сравнению с
размерами проводников. Так, например,
две плоские металлические пластины,
расположенные параллельно и разделенные
слоем диэлектрика, образуют плоский
конденсатор.
Если пластинам плоского конденсатора
сообщить равные по модулю заряды
противоположного знака, то напряженность
электрического поля между пластинами
будет в два раза больше, чем напряженность
поля у одной пластины. Вне пластин
напряженность электрического поля
равна нулю, т. к. равные заряды разного
знака на двух пластинах создают вне
пластин электрические поля, напряженности
которых равны по модулю, но противоположны
по направлению.
Электроемкостью
конденсатора
называется
физическая величина, определяемая
отношением заряда одной из пластин к
напряжению между обкладками конденсатора:
![]()
При
неизменном положении пластин
электроемкость конденсатора является
постоянной величиной при любом заряде
на пластинах.
За
единицу электроемкости в системе СИ
принимают Фарад. 1 Ф – электроемкость
такого конденсатора, напряжение между
обкладками которого равно 1 В при
сообщении обкладкам разноименных
зарядов по 1 Кл.
Электроемкость
плоского конденсатора можно вычислить
по формуле:
![]() ,
,
где
S – площадь обкладок
конденсатора
d – расстояние
между обкладками
![]() –диэлектрическая
–диэлектрическая
проницаемость диэлектрика
Электроемкость
шара можно вычислить по формуле:
![]()
Энергия заряженного
конденсатора.
Если внутри
конденсатора напряженность поля E,
тогда напряженность поля, созданного
зарядом одной из пластин E/2. В однородном
поле одной пластины находится заряд,
распределенный по поверхности другой
пластины. Согласно формуле для
потенциальной энергии заряда в однородном
поле энергия конденсатора равна:
![]()
Используя
формулу электроемкости конденсатора
![]() :
:
![]()