Установленная в
§ 85 связь между напряженностью поля
и потенциалом позволяет по известной
напряженности поля найти разность
потенциалов между двумя произвольными
точками этого поля.
1.
Поле равномерно заряженной бесконечной
плоскости определяется
формулой (82.1): E=/(20),
где
— поверхностная плотность заряда.
Разность потенциалов между точками,
лежащими на расстояниях х1,
и
x2
от
плоскости
140
(используем формулу
(85.1)), равна

2.
Поле двух бесконечных параллельных
разноименно заряженных плоскостей
определяется
формулой (82.2): Е=/0,
где
—
поверхностная плотность заряда.
Разность потенциалов между плоскостями,
расстояние между которыми равно
d
(см. формулу (85.1)), равна

3.
Поле равномерно заряженной сферической
поверхности радиуса
R
с
общим
зарядом Q
вне
сферы
(r>R)
вычисляется
по (82.3):
E=(1/40)Q/r2.
Разность потенциалов между двумя
точками, лежащими на расстояниях r1
и r2
от
центра сферы (r1>R,
r2>R),
равна

Если
принять r1=r
и r2=,
то потенциал поля вне сферической
поверхности, согласно формуле (86.2),
задается выражением

(ср. с формулой
(84.5)). Внутри сферической поверхности
потенциал всюду одинаков и равен
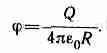
График
зависимости
от r
приведен
на рис. 134.

4.
Поле объемно заряженного шара радиуса
R
с
общим зарядом Q
вне
шара
(r>R)
вычисляется
по формуле (82.3), поэтому разность
потенциалов между двумя точками,
лежащими на расстояниях r1
и
r2
от центра шара (r1>R,
r2>R),
определяется
формулой (86.2). В любой точке, лежащей
внутри
шара
на расстоянии r‘
от
его центра (r'<R),
напряженность
определяется выражением (82.4):
E=(1/40)(Q/R3)r’.
Следовательно,
разность потенциалов между двумя
точками, лежащими на расстояниях r‘1
и
r‘2
от
центра шара (r’1<R,
r’2<R),
равна

5.
Поле равномерно заряженного бесконечного
цилиндра радиуса
К,
заряженного
с линейной плотностью т, вне цилиндра
(r>R)
определяется формулой (82.5):
E=(1/20)(/r).
Следовательно, разность потенциалов
между двумя точками, лежащими на
расстояниях r1
и
r2
от
оси заряженного цилиндра (r1>R,
r2>R),
равна

§ 87. Типы диэлектриков. Поляризация диэлектриков
Диэлектрик
(как и всякое вещество) состоит из
атомов и молекул. Так как положительный
заряд всех ядер молекулы равен
суммарному заряду электронов, то молекула
в целом электрически нейтральна.
Если заменить положительные заряды
ядер молекул суммарным зарядом +Q,
находящемся
в центре «тяжести» положительных
зарядов, а заряд всех электронов —
суммарным отрицательным зарядом –Q,
находящемся
в центре «тяжести» отрицательных
зарядов, то молекулу можно рассматривать
как электрический диполь с электрическим
моментом, определенным формулой (80.3).
Первую
группу диэлектриков (N2,
H2,
О2,
СO2,
СH4,
…) составляют вещества,
141
молекулы
которых имеют симметричное строение,
т. е. центры «тяжести» положительных
и отрицательных зарядов в отсутствие
внешнего электрического поля совпадают
и, следовательно, дипольный момент
молекулы р
равен нулю. Молекулы
таких
диэлектриков называются неполярными.
Под
действием внешнего электрического
поля заряды неполярных молекул смещаются
в противоположные стороны (положительные
по полю, отрицательные против поля) и
молекула приобретает дипольный
момент.
Вторую
группу диэлектриков (H2O,
NH3,
SO2,
CO, …)
составляют вещества, молекулы которых
имеют асимметричное строение, т. е.
центры «тяжести» положительных и
отрицательных зарядов не совпадают.
Таким образом, эти молекулы в отсутствие
внешнего электрического поля обладают
дипольным моментом. Молекулы
таких
диэлектриков называются полярными.
При
отсутствии внешнего поля, однако,
дипольные моменты полярных молекул
вследствие теплового движения
ориентированы в пространстве хаотично
и их результирующий момент равен нулю.
Если такой диэлектрик поместить во
внешнее поле, то силы этого поля будут
стремиться повернуть диполи вдоль поля
и возникает отличный от нуля результирующий
момент.
Третью
группу диэлектриков (NaCl,
КСl,
КВг,…) составляют вещества, молекулы
которых имеют ионное строение. Ионные
кристаллы представляют собой
пространственные решетки с правильным
чередованием ионов разных знаков. В
этих кристаллах нельзя выделить отдельные
молекулы, а рассматривать их можно как
систему двух вдвинутых одна в другую
ионных подрешеток. При наложении на
ионный кристалл электрического поля
происходит некоторая деформация
кристаллической решетки или
относительное смещение подрешеток,
приводящее к возникновению дипольных
моментов.
Таким
образом, внесение всех трех групп
диэлектриков во внешнее электрическое
поле приводит к возникновению отличного
от нуля результирующего электрического
момента диэлектрика, или, иными словами,
к поляризации диэлектрика. Поляризацией
диэлектрика
называется процесс ориентации диполей
или появления под воздействием
электрического поля ориентированных
по полю диполей.
Соответственно
трем группам диэлектриков различают
три вида поляризации:
электронная,
или деформационная, поляризация
диэлектрика
с неполярными молекулами, заключающаяся
в возникновении у атомов индуцированного
дипольного момента за счет деформации
электронных орбит;
ориентационная,
или
дипольная, поляризация диэлектрика
с полярными молекулами, заключающаяся
в ориентации имеющихся дипольных
моментов молекул по полю. Естественно,
что тепловое движение препятствует
полной ориентации молекул, но в результате
совместного действия обоих факторов
(электрическое поле и тепловое
движение) возникает преимущественная
ориентация дипольных моментов молекул
по полю. Эта ориентация тем сильнее, чем
больше напряженность электрического
поля и ниже температура;
ионная
поляризация диэлектриков
с ионными кристаллическими решетками,
заключающаяся в смещении подрешетки
положительных ионов вдоль поля, а
отрицательных — против поля, приводящем
к возникновению дипольных моментов.
Соседние файлы в папке Трофимова Курс физики
- #
16.03.2016155.65 Кб1141.doc
- #
16.03.2016662.53 Кб21010.doc
- #
16.03.2016592.38 Кб25011.doc
- #
- #
16.03.2016181.76 Кб16713.doc
- #
16.03.2016336.38 Кб13614.doc
- #
16.03.2016206.34 Кб14015.doc
- #
16.03.2016169.98 Кб9616.doc
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Каждая точка электрического поля характеризуется векторной величиной – напряженностью поля. Напряженность ![]() поля в данной точке равна силе, действующей на положительный пробный заряд, помещенный в эту точку, и отнесенной к единице заряда. Это – силовая характеристика электрического поля.
поля в данной точке равна силе, действующей на положительный пробный заряд, помещенный в эту точку, и отнесенной к единице заряда. Это – силовая характеристика электрического поля.
При перемещении электрического заряда в поле совершается работа. Электростатическое поле обладает очень важным свойством потенциальностью: работа по перемещению заряда из одной точки поля в другую не зависит от формы траектории. Это позволяет ввести понятие напряжения (или разности потенциалов). Напряжение U между двумя точками поля (*Под словами «пояс», «электрическое поле» здесь и в дальнейшем мы будем понимать электростатическое поле, то есть поле, созданное неподвижными зарядами.) равно работе, совершаемой электрическим полем по перемещению единицы положительного заряда из одной точки в другую.
В отличие от напряженности, определенной в отдельно взятой точке, напряжение характеризует две точки ноля. Если зафиксировать одну точку, выбрав ее за начало отсчета, то любая точка поля будет иметь определенное напряжение по отношению к выбранной точке. Это напряжение называют потенциалом φ. Очевидно, что началу отсчета соответствует нулевой потенциал. Чаще всего нулевой потенциал приписывается точке, бесконечно удаленной от заряда, создающего поле. В этом случае потенциал φ некоторой точки поля равен работе, совершаемой электрическим полем по перемещению единицы положительного заряда из этой точки в бесконечность. Это – энергетическая характеристика электрического поля.
Иногда задавать в каждой точке скалярную величину – потенциал φ – удобнее, чем векторную величину напряженность ![]() . Естественно, что эти две величины должны быть связаны друг с другом.
. Естественно, что эти две величины должны быть связаны друг с другом.
Рассмотрим вначале однородное электрическое поле. Его напряженность ![]() одинакова во всех точках; силовые линии такого поля – параллельные прямые (рис. 1).
одинакова во всех точках; силовые линии такого поля – параллельные прямые (рис. 1).
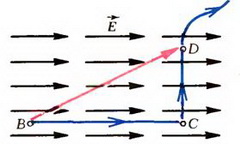
Рис. 1
Найдем разность потенциалов между точками B и D. Потенциал φB точки B равен работе по перемещению единицы заряда из этой точки в бесконечность. Форма траектории при подсчете работы не имеет значения, поэтому будем перемещать заряд сначала по отрезку BC потом по отрезку CD а затем из точки D в бесконечность. Сила, действующая на единицу заряда со стороны электрического поля, равна напряженности. На отрезке ВС работа этой силы равна E·l, где E – проекция вектора напряженности на силовую линию, a l – длина отрезка ВС. На отрезке CD сила работы не совершает, так как она перпендикулярна перемещению. Наконец, работа по перемещению единицы заряда из точки D в бесконечность равна потенциалу φD. Поэтому: 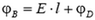 или для разности потенциалов:
или для разности потенциалов:
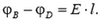 (1)
(1)
Для того чтобы формула (1) давала правильный знак разности потенциалов, величине l надо приписывать определенный знак в зависимости от расположения точек B и C на силовой линии. Будем считать, что l – это проекция вектора BD на направление силовой линии. Тогда знак положителен, если точка C лежит «ниже» по силовой линии, чем точка B и отрицателен в противоположном случае. Для случая, изображенного на рисунке 1, l > 0, и разность потенциалов 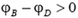 , что соответствует убыванию потенциала вдоль силовой линии
, что соответствует убыванию потенциала вдоль силовой линии 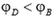 .
.
Итак, в однородном электрическом иоле между напряженностью и разностью потенциалов имеется простая связь, даваемая формулой (1).
Какова связь между потенциалом и напряженностью в случае неоднородного электрического поля? В таком поле напряженность ![]() меняется от точки к точке. Пусть, для простоты рассуждений, изменение напряженности происходит только в одном направлении, которое примем за ось ОХ (рис. 2).
меняется от точки к точке. Пусть, для простоты рассуждений, изменение напряженности происходит только в одном направлении, которое примем за ось ОХ (рис. 2).
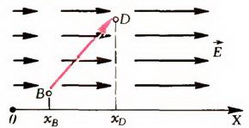
Рис. 2
Тогда напряженность поля ![]() зависит только от координаты x:
зависит только от координаты x: ![]() . Ясно, что в небольших участках пространства напряженность меняется мало, и электрическое поле там можно приближенно считать однородным. Возьмем близкие точки B и D и найдем разность потенциалов между ними. Воспользуемся формулой (1). Потенциал так же, как и напряженность, зависит только от координаты x (*Плоскость x = const эквипотенциальна, так как при перемещении единицы заряда в этой плоскости электрическое поле работы не совершает.):
. Ясно, что в небольших участках пространства напряженность меняется мало, и электрическое поле там можно приближенно считать однородным. Возьмем близкие точки B и D и найдем разность потенциалов между ними. Воспользуемся формулой (1). Потенциал так же, как и напряженность, зависит только от координаты x (*Плоскость x = const эквипотенциальна, так как при перемещении единицы заряда в этой плоскости электрическое поле работы не совершает.):
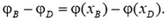
Проекция вектора ![]() на ось ОХ равна разности координат точек D и B:
на ось ОХ равна разности координат точек D и B:
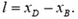
Таким образом, для близких точек B и D получаем:
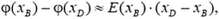
или
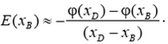 (2)
(2)
Чтобы формула (2) стала точной, надо устремить точку B к точке D и найти предел, к которому стремится правая часть при неограниченном сближении точек:
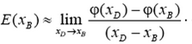 (3)
(3)
Легко увидеть, что правая часть формулы (3) – это производная потенциала, взятая с обратным знаком. Таким образом, в неоднородном электрическом поле связь между потенциалом и напряженностью в каждой точке следующая:
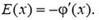 (4)
(4)
Знак минус в формуле (4) означает, что потенциал убывает вдоль силовой линии: поскольку проекция напряженности на силовую линию 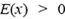
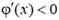 , что и означает убывание потенциала.
, что и означает убывание потенциала.
Если нарисовать график зависимости φ от x, то тангенс угла наклона α касательной к графику в каждой его точке равен производной 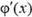 в этой точке (рис. 3). Поэтому можно сказать, что напряженность электрического поля определяет наклон касательной к графику потенциала.
в этой точке (рис. 3). Поэтому можно сказать, что напряженность электрического поля определяет наклон касательной к графику потенциала.

Рис. 3
Рассмотрим теперь несколько конкретных задач.
Задача 1. Сфера радиуса R имеет заряд Q. Найти зависимость напряженности и потенциала от расстояния r от центра сферы. Нарисовать графики.
Найдем вначале напряженность поля. Внутри сферы электрического поля нет: при r < RE = 0. Вне сферы напряженность поля такая же, как у точечного заряда Q помешенного в центр сферы: при r> R проекция напряженности на выбранное направление от центра 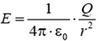 , где ε0 – электрическая постоянная. На поверхности сферы, при r = R электрическое поле испытывает скачок
, где ε0 – электрическая постоянная. На поверхности сферы, при r = R электрическое поле испытывает скачок 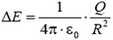 . Зависимость E от r графически показана на рисунке 4, а.
. Зависимость E от r графически показана на рисунке 4, а.
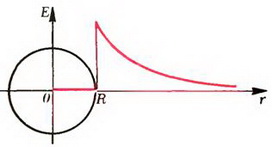
а
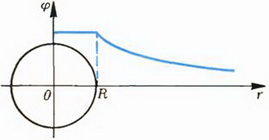
б
Рис. 4
Величину скачка ΔE можно выразить через поверхностную плотность заряда 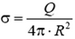 (равную заряду, приходящемуся на единицу площади поверхности сферы):
(равную заряду, приходящемуся на единицу площади поверхности сферы):
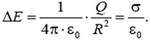
Заметим, что это общее свойство электростатического поля: на заряженной поверхности его проекция на направление нормали всегда испытывает скачок 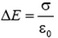 независимо от формы поверхности.
независимо от формы поверхности.
Выясним теперь, как меняется потенциал φ в зависимости от r. Мы уже знаем, что в любой точке тангенс угла наклона касательной к графику потенциала должен совпадать со значением проекции напряженности (взятой с противоположным знаком). При 0 < r < RE = 0, и, следовательно, во всех этих точках касательная к графику потенциала должна быть горизонтальной. Это означает, что на участке 0 < r < R потенциал не меняется: φ = const.
Вне сферы, при r > R производная 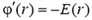 отрицательна и величина ее убывает с расстоянием r. Поэтому и потенциал должен убывать с расстоянием, стремясь к нулю при
отрицательна и величина ее убывает с расстоянием r. Поэтому и потенциал должен убывать с расстоянием, стремясь к нулю при 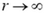 . Действительно, чем дальше расположена точка, в которой мы ищем потенциал, тем меньшую работу надо совершать при перемещении единицы заряда из этой точки в бесконечность. Величина потенциала φ при r > R такая же, как у точечного заряда, помещенного в центр сферы:
. Действительно, чем дальше расположена точка, в которой мы ищем потенциал, тем меньшую работу надо совершать при перемещении единицы заряда из этой точки в бесконечность. Величина потенциала φ при r > R такая же, как у точечного заряда, помещенного в центр сферы:
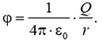
Может ли потенциал испытать скачок на поверхности сферы, то есть при r = R? Очевидно, что нет. Скачок потенциала означал бы, что при перемещении единичного заряда между двумя очень близкими точками 1 и 2 электрическое поле совершало бы конечную работу:
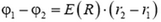
должно оставаться конечным при 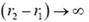 что невозможно. Таким образом, потенциал не испытывает скачков.
что невозможно. Таким образом, потенциал не испытывает скачков.
График зависимости φ от r изображен на рисунке 4, б.
Задача 2. Шар радиуса R равномерно заряжен по всему объему. Полный заряд тара Q. Нарисуйте графики зависимости напряженности и потенциала от расстояния r от центра шара.
Такой шар можно представить себе состоящим из большого числа тонких заряженных сфер, вложенных одна в другую. Каждая сфера внутри себя поля не создает, а вне создает поле такое же, как точечный заряд, помещенный в ее центр. Поэтому вне шара, при r > R напряженность такая же, как напряженность поля точечного заряда Q помещенного в центр шара:
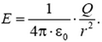
Внутри шара, на расстоянии R поле создают только сферы с радиусами от 0 до r (для сфер большего радиуса рассматриваемая точка находится внутри них). Следовательно, напряженность на расстоянии s от центра шара такая же, как напряженность поля точечного заряда Qr. помещенного в центр шара, где Qr – суммарный заряд всех сфер с радиусами от 0 до r, то есть заряд шара радиуса r. Если на шар радиуса R приходится заряд Q, то на шар радиуса r будет приходиться заряд
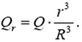
Таким образом, внутри шара напряженность поля 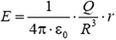 – она линейно растет с расстоянием.
– она линейно растет с расстоянием.
На поверхности шара, в точке r = R напряженность скачка не испытывает. Это находится в соответствии с общим правилом, так как поверхностная плотность заряда в данном случае равна нулю: шар заряжен однородно, и на бесконечно тонкий поверхностный слой приходится бесконечно малый заряд.
График зависимости E от r показан на рисунке 5, a.
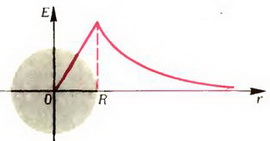
а
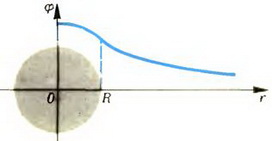
б
Рис. 5
Нарисуем теперь график потенциала. Производная от потенциала
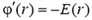
всегда отрицательна (E ≥ 0). Поэтому с увеличением r потенциал должен монотонно убывать. В точке r = 0 производная потенциала равна нулю. Следовательно, касательная к графику в. этой точке горизонтальна: в точке r = 0 потенциал имеет максимум. В точке r = R ни потенциал, ни его производная скачков не испытывают. Первое следует из общего правила для потенциала, о втором мы уже говорили выше. Поэтому кривые, изображающие зависимость потенциала от расстояния при r < R и r > R в точке r = R должны сопрягаться – гладко без излома переходить одна в другую. При 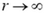 потенциал
потенциал 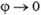 . График зависимости φ от r представлен на рисунке 5, б.
. График зависимости φ от r представлен на рисунке 5, б.
Задача 3. Две плоскости расположены параллельно друг другу на расстоянии d и заряжены с поверхностной плотностью заряда σ1 и σ2 соответственно. Нарисовать графики зависимости напряженности поля и потенциала от координаты x (ось ОХ перпендикулярна пластинам). Рассмотреть случаи одноименных (рис. 6, а) и разноименных (рис. 7, а) зарядов на пластинах.
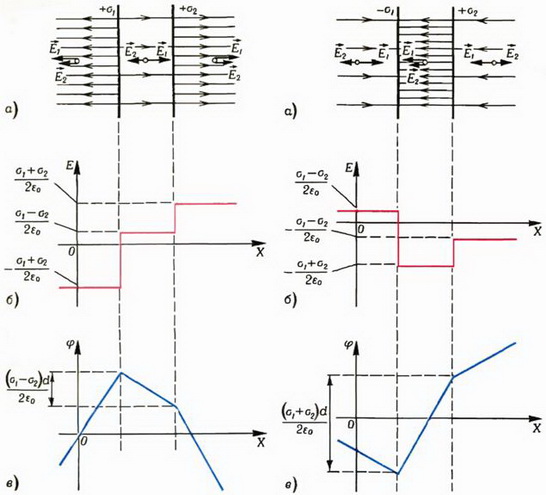
Рис. 6 Рис. 7
Каждая плоскость создает по обе стороны от себя однородное электрическое поле, напряженность которого
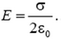
Воспользовавшись принципом суперпозиции, для случая одноименных зарядов приходим к графику, показанному на рисунке 6, б, а для разноименных – к графику на рисунке 7, б. Скачки напряженности опять соответствуют общему правилу:
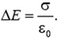
Соответствующие графики для потенциалов показаны на рисунках 6, в и 7, в. На отдельных участках зависимость потенциала от координаты – линейная, так как напряженность поля постоянна. Изломы происходят в тех местах, где напряженность поля испытывает скачок.
Заметим, что в данной задаче потенциал не стремится к нулю при 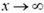 . Это, очевидно, связано с тем, что плоскость бесконечна. В действительности размеры реальных пластин всегда ограничены; это приводит к тому, что потенциал падает с увеличением расстояния от пластин.
. Это, очевидно, связано с тем, что плоскость бесконечна. В действительности размеры реальных пластин всегда ограничены; это приводит к тому, что потенциал падает с увеличением расстояния от пластин.
Задача 4. Две одинаковые параллельные пластины имеют заряды +q и –q. Как меняется разность потенциалов U между пластинами при увеличении расстояния d между ними? Нарисуйте график зависимости U от d.
Пока расстояние между пластинами значительно меньше их размеров, такую систему можно считать плоским конденсатором. Тогда 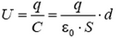 – напряжение линейно растет с расстоянием (начальный участок на рисунке 8).
– напряжение линейно растет с расстоянием (начальный участок на рисунке 8).
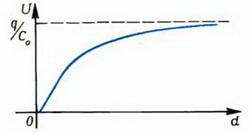
Рис. 8
Это соответствует тому, что напряженность поля 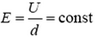 . Как только расстояние между пластинами становится сравнимым с размерами пластин, электрическое поле появляется и вне пространства между пластинами. Тогда становятся существенными так называемые краевые эффекты, и зависимость потенциала от расстояния – довольно сложная. Однако качественно ясно, что, вследствие ослабления поля в области между пластинами, напряжение будет расти медленнее, чем по линейному закону (средний участок на рисунке 8). При дальнейшем увеличении расстояния между пластинами оно станет много больше их размеров. Тогда каждую пластину уже можно считать изолированным телом, и ее потенциал
. Как только расстояние между пластинами становится сравнимым с размерами пластин, электрическое поле появляется и вне пространства между пластинами. Тогда становятся существенными так называемые краевые эффекты, и зависимость потенциала от расстояния – довольно сложная. Однако качественно ясно, что, вследствие ослабления поля в области между пластинами, напряжение будет расти медленнее, чем по линейному закону (средний участок на рисунке 8). При дальнейшем увеличении расстояния между пластинами оно станет много больше их размеров. Тогда каждую пластину уже можно считать изолированным телом, и ее потенциал 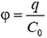 где C0 – емкость уединенной пластины. Таким образом, при очень больших расстояниях разность потенциалов перестает зависеть от расстояния между пластинами (график зависимости U от d. на рисунке 8 имеет горизонтальную асимптоту).
где C0 – емкость уединенной пластины. Таким образом, при очень больших расстояниях разность потенциалов перестает зависеть от расстояния между пластинами (график зависимости U от d. на рисунке 8 имеет горизонтальную асимптоту).
Краевые эффекты часто оказываются существенными при решении электростатических задач, связанных с законом сохранения энергии, рассмотрим, например, такой вариант ускорителя электронов.
Задача 5. В пластинах плоского конденсатора, заряженного до разности потенциалов U сделано сквозное отверстие. Конденсатор помещен в постоянное магнитное поле, направленное перпендикулярно электрическому полю в конденсаторе (рис. 9). Электрон влетает в пространство между пластинами конденсатора, ускоряется, приобретая энергию e·U вылетает через отверстие и. двигаясь в магнитном поле по окружности, возвращается в конденсатор. Затем он снова ускоряется, движется по окружности большего радиуса, опять входит в конденсатор и т.д. На первый взгляд кажется, что таким образом можно разогнать электрон до больших энергий, то есть создать ускоритель. Так ли это?
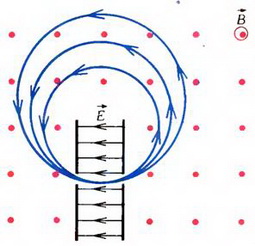
Рис. 9
Оказывается, такой ускоритель работать не будет – не учтен краевой эффект. Вне конденсатора всегда существует слабое электрическое поле, которое тормозит электрон при егодвижении по окружности. Отрицательная работа поля при этом в точности равна положительной работе при разгоне электрона в конденсаторе: работа в электростатическом поле не зависит от формы траектории. Магнитное поле работы не совершает (сила Лоренца перпендикулярна скорости движения электрона). Поэтому полная работа всех сил, действующих на электрон, при его возвращении в начальную точку будет равна нулю, и кинетическая энергия электрона не изменится. Ускоритель работать не будет.
Упражнения
1. Может ли существовать электростатическое поле, у которого силовые линии – параллельные прямые, а абсолютная величина напряженности меняется только в направлении, перпендикулярном силовым линиям (рис. 10)?
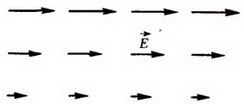
Рис. 10
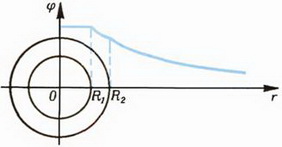
2. Две концентрические металлические сферы радиусов R1 и R2 имеют заряды Q1 и Q2 соответственно. Найдите напряженность и потенциал электрического поля на произвольном расстоянии r от центра сфер. Нарисуйте графики зависимости E от r и φ от r. Рассмотрите случаи одноименных и разноименных зарядов. Как выглядят графики для случая Q1 = –Q2 (сферический конденсатор)?
3. Точечный заряд q окружен металлической сферой радиуса R с зарядом Q. Найдите напряженность поля и потенциал на произвольном расстоянии r от заряда q если он находится в центре сферы; нарисуйте графики зависимости E от r и φ от r. Как изменятся графики, если заряд сместить из центра сферы? Решите ту же задачу для случая, когда металлическая сфера заземлена.
4. Электрон влетает в пространство между пластинами плоского конденсатора так, что его скорость составляет острый угол с направлением силовых линий. Тогда при движении в конденсаторе он будет тормозиться и вылетит с меньшей скоростью; его кинетическая энергии уменьшится. Увеличится ли при этом энергия конденсатора?
5. Два одинаковых конденсатора емкостью C каждый, один из которых заряжен до напряжения U а второй – не заряжен, соединяют параллельно. Найти энергию системы до и после соединения конденсаторов. Почему эти энергии не равны?
6. Точечный заряд q находится вне незаряженной металлической сферы радиуса R на расстоянии d от ее центра. Найти потенциал сферы.
Ответы.
1. Не может, иначе работа по перемещению заряда по замкнутому контуру была бы отлична от нуля.
2. При R1 > r > 0 напряженность E = 0 и 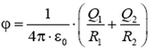 ; при R2 > r > R
; при R2 > r > R 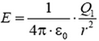 и
и 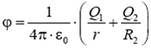 ; при r > R2
; при r > R2 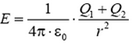 и
и 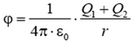 (рис. 11).
(рис. 11).
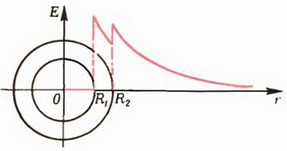
а
б
Рис. 11
3. При R > r > 0 напряженность 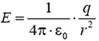 и
и 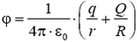 ; при r > R
; при r > R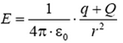 и
и 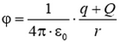 (рис. 12).
(рис. 12).
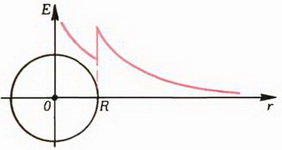
а
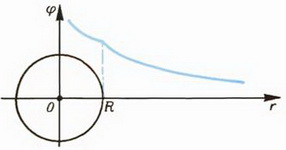
б
Рис. 12
4. Энергия конденсатора не изменяется; изменяется энергия взаимодействия электрона и конденсатора (работа по перемещению электрона в бесконечность из начальной и конечной точек не одна и та же).
5. 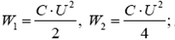 ровно половина энергии перешло в тепло (независимо от сопротивления подводящих проводов).
ровно половина энергии перешло в тепло (независимо от сопротивления подводящих проводов).
6. 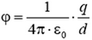 (потенциал сферы такой же, как в ее центре, а там суммарный потенциал поля индуцированных на сфере зарядов равен нулю).
(потенциал сферы такой же, как в ее центре, а там суммарный потенциал поля индуцированных на сфере зарядов равен нулю).
Электростатика: демонстрационный
эксперимент
Продолжение. См. № 17,
18, 19, 20,
21/07
В.В.МАЙЕР,
ГОУ ВПО ГГПИ им. В.Г.Короленко, г. Глазов,
Республика Удмуртия
varaksina_ei@list.ru
Электростатика: демонстрационный
эксперимент
Потенциал относится к самым сложным
понятиям электростатики. Учащиеся выучивают
определение потенциала электростатического
поля, решают многочисленные задачи, но у них нет
ощущения потенциала, они с трудом соотносят
теорию с реальностью. Поэтому роль учебного
эксперимента в формировании понятия потенциала
весьма высока. Нужны такие опыты, которые, с одной
стороны, иллюстрировали бы абстрактные
теоретические представления о потенциале, а с
другой, показывали полную обоснованность
экспериментом введения понятия потенциала.
Стремиться к особой точности количественных
результатов в этих опытах скорее вредно, чем
полезно.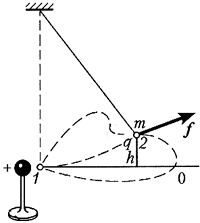
6.1. Потенциальность
электростатического поля
На изолирующей подставке укрепим
проводящее тело и зарядим его. На длинной
изолированной нити подвесим лёгкий проводящий
шарик и сообщим ему пробный заряд, одноимённый с
зарядом тела. Шарик оттолкнётся от тела и из
положения 1 перейдёт в положение 2. Так
как высота шарика в поле тяготения увеличилась
на h, потенциальная энергия его
взаимодействия с Землёй возросла на mgh.
Значит, электрическое поле заряженного тела
совершило над пробным зарядом некоторую работу.
Повторим опыт, но в начальный момент не
просто отпустим пробный шарик, а толкнём его в
произвольном направлении, сообщив ему некоторую
кинетическую энергию. При этом обнаружим, что
двигаясь из положения 1 по сложной
траектории, шарик в конечном итоге остановится в
положении 2. Сообщённая шарику в начальный
момент кинетическая энергия, очевидно,
израсходовалась на преодоление сил трения при
движении шарика, а электрическое поле совершило
над шариком ту же работу, что и в первом случае. В
самом деле, если уберём заряженное тело, то тот же
самый толчок пробного шарика приводит к тому, что
из положения 2 он возвращается в положение 1.
Таким образом, опыт наводит на мысль,
что работа электрического поля над зарядом не
зависит от траектории движения заряда, а
определяется лишь положениями её начальной и
конечной точек. Иными словами, на замкнутой
траектории работа электростатического поля
всегда равна нулю. Поля, обладающие таким
свойством, называются потенциальными.
6.2. Потенциальность центрального
поля
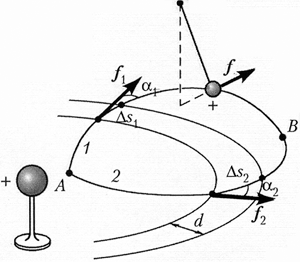
Опыт показывает, что в
электростатическом поле, создаваемом заряженным
проводящим шаром, действующая на пробный заряд
сила всегда направлена от центра заряженного
шара, она монотонно уменьшается с увеличением
расстояния и на равных расстояниях от него имеет
одинаковые значения. Такое поле называется центральным.
Пользуясь рисунком, нетрудно убедиться, что
центральное поле потенциально.
6.3. Потенциальная энергия заряда в
электростатическом поле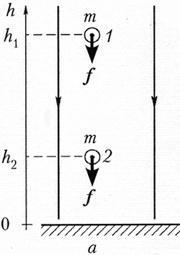
Гравитационное поле, как и
электростатическое, потенциально. Кроме того,
математическая запись закона всемирного
тяготения совпадает с записью закона Кулона.
Поэтому при исследовании электростатического
поля имеет смысл опираться на аналогию между
гравитационным и электростатическим полями.
В небольшой области вблизи
поверхности Земли гравитационное поле можно
считать однородным (рис. а).
На тело массой m в этом поле действует
постоянная по модулю и направлению сила f
= тg. Если предоставленное самому себе
тело падает из положения 1 в положение 2,
то сила тяготения совершает работу A = fs
= mgs = mg (h1 – h2).
Это же самое мы можем сказать иначе.
Когда тело находилось в положении 1, система
Земля–тело обладала потенциальной энергией (т.е.
способностью совершить работу) W1 = mgh1.
Когда тело перешло в положение 2,
рассматриваемая система стала обладать
потенциальной энергией W2 = mgh2.
Совершённая при этом работа равна разности
потенциальных энергий системы в конечном и
начальном состояниях, взятой с обратным знаком: А
= – (W2 – W1). 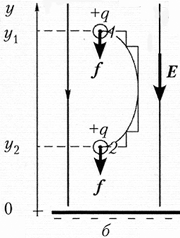
Обратимся теперь к электрическому
полю, которое, напомним, как и гравитационное,
является потенциальным. Представим, что силы
тяжести нет, а вместо поверхности Земли имеется
плоская проводящая пластина, заряженная (для
определённости) отрицательно (рис. б). Введём
координатную ось Y и над пластиной
расположим положительный заряд q. Понятно,
что, поскольку сам по себе заряд не существует,
над пластиной находится какое-то тело
определённой массы, несущее электрический заряд.
Но, поскольку мы считаем поле тяжести
отсутствующим, то и принимать во внимание массу
заряженного тела не будем.
Итак, на положительный заряд q со
стороны отрицательно заряженной плоскости
действует сила притяжения f = qE,
где E – напряжённость
электрического поля. Так как электрическое поле
однородно, то во всех его точках на заряд
действует одна и та же сила. Если заряд
перемещается из положения 1 в положение 2,
то электростатическая сила совершает над ним
работу А = fs = qE s = qE(y1
– y2).
То же самое мы можем выразить другими
словами. В положении 1 находящийся в
электростатическом поле заряд обладал
потенциальной энергией W1 = qEy1,
а в положении 2 – потенциальной энергией W2
= qEy2. При переходе заряда из положения 1
в положение 2 электрическое поле заряженной
плоскости совершило над ним работу А = –(W2
– W1).
Напомним, что потенциальная энергия
определена лишь с точностью до слагаемого: если
нулевое значение потенциальной энергии выбрать
в другом месте оси Y, то в принципе ничего не
изменится.
6.4. Потенциал однородного
электростатического поля
Если потенциальную энергию заряда в
электростатическом поле разделить на величину
этого заряда, то получим энергетическую
характеристику самого поля, которую назвали потенциалом:
![]()
Потенциал в системе СИ выражают в вольтах:
1 В = 1 Дж/1 Кл.
Если в однородном электрическом поле ось Y
направить параллельно вектору напряжённости E,
то потенциал произвольной точки поля будет
пропорционален координате точки: ![]() причём коэффициентом
причём коэффициентом
пропорциональности является напряжённость
электрического поля.
6.5. Разность потенциалов
Потенциальная энергия и потенциал
определяются лишь с точностью до произвольной
постоянной, зависящей от выбора их нулевых
значений. Однако работа поля имеет вполне
определённое значение, поскольку определяется
разностью потенциальных энергий в двух точках
поля:
А = –(W2 – W1) =
–(![]() 2q –
2q – ![]() 1q) = q(
1q) = q(![]() 1 –
1 – ![]() 2).
2).
Работа по перемещению электрического
заряда между двумя точками поля равна
произведению заряда на разность потенциалов
начальной и конечной точек. Разность потенциалов
иначе называют напряжением.
Напряжение между двумя точками равно
отношению работы поля при перемещении заряда из
начальной точки в конечную к этому заряду:
![]()
Напряжение, как и потенциал,
выражается в вольтах.
6.6. Разность потенциалов и
напряжённость
В однородном электрическом поле
напряжённость направлена в сторону убывания
потенциала и, согласно формуле ![]() = Еy, разность потенциалов
= Еy, разность потенциалов
равна U = ![]() 1
1
– ![]() 2= Е(у1
2= Е(у1
– y2). Обозначив разность координат
точек у1 – y2 = d,
получаем U = Ed.
В эксперименте вместо
непосредственного измерения напряжённости
проще определять разность потенциалов и затем
вычислять модуль напряжённости по формуле
![]()
(6.1)
где d – расстояние между двумя
точками поля, близко расположенными в
направлении вектора Е. При этом в
качестве единицы напряжённости используют не
ньютон на кулон, а вольт на метр:
![]()
6.7. Потенциал произвольного
электростатического поля
Опыт показывает, что отношение работы
по перемещению заряда из бесконечности в данную
точку поля к величине этого заряда остаётся
неизменным: ![]() = А/q.
= А/q.
Это отношение принято называть потенциалом
данной точки электростатического поля,
принимая потенциал в бесконечности равным нулю.
6.8. Принцип суперпозиции для
потенциалов
Любое как угодно сложное
электростатическое поле можно представить в
виде суперпозиции полей точечных зарядов. Каждое
такое поле в выбранной точке имеет определённый
потенциал. Поскольку потенциал является
скалярной величиной, результирующий потенциал
поля всех точечных зарядов есть алгебраическая
сумма потенциалов ![]() 1,
1,
![]() 2,
2, ![]() 3, … полей отдельных
3, … полей отдельных
зарядов: ![]() =
= ![]() 1 +
1 + ![]() 2 +
2 + ![]() 3 + … Это соотношение
3 + … Это соотношение
является прямым следствием принципа
суперпозиции электрических полей.
6.9. Потенциал поля точечного
заряда
Обратимся теперь к сферическому
(точечному) заряду. Выше показано, что
напряжённость электрического поля, созданного
равномерно распределённым по сфере зарядом Q,
не зависит от радиуса сферы. Представим, что на
некотором расстоянии r от центра сферы
находится пробный заряд q. Напряжённость
поля в точке, где находится заряд, ![]()
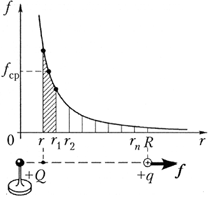
На рисунке изображён график
зависимости силы электростатического
взаимодействия между точечными зарядами от
расстояния между ними. Чтобы найти работу
электрического поля при перемещении пробного
заряда q с расстояния r до расстояния R,
разобьём этот промежуток точками r1, r2,…,
rп на равные отрезки. Средняя сила,
действующая на заряд q в пределах отрезка [rr1],
равна ![]()
Работа этой силы на этом участке:
![]()
Аналогичные выражения для работы
получатся для всех других участков. Поэтому
полная работа:
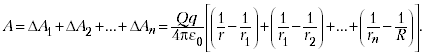
Одинаковые слагаемые с
противоположными знаками уничтожаются, и
окончательно получаем:
– работа поля над зарядом ![]()
– разность потенциалов ![]()
Теперь, чтобы найти потенциал точки
поля относительно бесконечности, устремляем R
к бесконечности и окончательно получаем:
![]()
(6.2)
Итак, потенциал поля точечного заряда
обратно пропорционален расстоянию до заряда.
6.10. Эквипотенциальные поверхности
Поверхность, в каждой точке которой
потенциал электрического поля имеет одно и то же
значение, называется эквипотенциальной.
Эквипотенциальные поверхности поля заряженного
шара нетрудно продемонстрировать подвешенным на
нити пробным зарядом, как это показано на
рисунке.
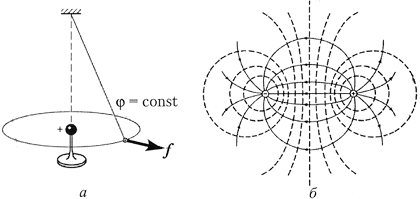
На втором рисунке электростатическое
поле двух разноимённых зарядов представлено
силовыми (сплошные) и эквипотенциальными
(пунктирные) линиями.
Исследование 6.1. Разность
потенциалов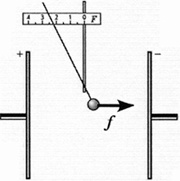
Задание. Разработайте простой
опыт, позволяющий ввести понятие разности
потенциалов, или напряжения.
Вариант выполнения. Два
металлических диска на изолирующих подставках
установите параллельно друг другу на расстоянии
примерно 10 см. Диски зарядите равными по модулю и
противоположными по знаку зарядами. Зарядите
шарик электростатического динамометра зарядом,
например, q = 5 нКл (см. исследование 3.6), и
введите его в область между дисками. При этом
стрелка динамометра покажет определённое
значение силы, действующей на шарик. Зная
параметры динамометра, вычислите значение
модуля силы (см. исследование 3.6). Например, в
одном из наших опытов стрелка динамометра
показала значение х = 2 см, следовательно,
согласно формуле ![]()
модуль силы f = Kх = 17 • 10–5 Н.
Перемещая динамометр, покажите, что во
всех точках поля между заряженными дисками на
пробный заряд действует одна и та же сила.
Перемещая динамометр так, чтобы пробный заряд
прошёл путь s = 5 см в направлении действующей
на него силы, спросите учащихся: какую работу
совершает над зарядом электрическое поле?
Добейтесь понимания, что работа поля над зарядом
по модулю равна
А = fs = 8,5 • 10–6 Дж,
(6.3)
причём она положительна, если заряд
перемещается по направлению напряжённости поля,
и отрицательна, если в противоположном
направлении. Вычислите разность потенциалов
между начальным и конечным положениями шарика
динамометра: U = А/q = 1,7 • 103 В.
С одной стороны напряжённость
электрического поля между пластинами:
![]()
С другой стороны, согласно формуле (6.1),
при d = s:
![]()
Таким образом, опыт показывает, что
напряжённость электрического поля можно
определить двумя способами, которые, разумеется,
приводят к одинаковым результатам.
Исследование 6.2. Градуировка
электрометра по напряжению 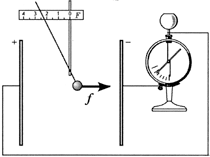
Задание. Разработайте
эксперимент, показывающий, что с помощью
демонстрационного стрелочного электрометра
можно измерять напряжение.
Вариант выполнения.
Экспериментальная установка схематически
изображена на рисунке. Пользуясь
электростатическим динамометром, определите
напряжённость однородного электрического поля и
по формуле U = Еd вычислите разность
потенциалов между проводящими пластинами.
Повторяя эти действия, отградуируйте
электрометр по напряжению так, чтобы получился
электростатический вольтметр.
Исследование 6.3. Потенциал поля
сферического заряда
Задание. Экспериментально
определите работу, которую нужно совершить
против электростатического поля, чтобы
переместить пробный заряд из бесконечности в
некоторую точку поля, созданного заряженной
сферой.
Вариант выполнения. На
изолирующей стойке закрепите шарик из
пенопласта, обёрнутый алюминиевой фольгой.
Зарядите его от пьезоэлектрического или иного
источника (cм. п. 1.10) и одноимённым зарядом
зарядите пробный шарик на стержне
электростатического динамометра. Пробный заряд
находится бесконечно далеко от исследуемого,
если электростатический динамометр не фиксирует
силы электростатического взаимодействия между
зарядами. В эксперименте удобно
электростатический динамометр оставить
неподвижным, а перемещать исследуемый заряд.
Постепенно приближайте заряженный
шарик на изолирующей подставке к шарику
электростатического динамометра. В первую
строку таблицы записывайте значения расстояния r
между зарядами, во вторую строку –
соответствующие им значения силы
электростатического взаимодействия. Удобно
расстояние выражать в сантиметрах, а силу – в
условных единицах, в которых отградуирована
шкала динамометра. По получившимся данным
постройте график зависимости силы от расстояния.
Подобный график вы уже строили, выполняя
исследование 3.5.
Теперь найдите зависимость работы по
перемещению заряда из бесконечности в данную
точку поля. Обратите внимание на то, что в
эксперименте сила взаимодействия зарядов
становится практически равной нулю на
сравнительно небольшом удалении одного заряда
от другого.
Разбейте весь диапазон изменения
расстояния между зарядами на равные участки,
например, по 1 см. Обработку экспериментальных
данных удобнее начинать с конца графика. На
участке от 16 до 12 см среднее значение силы fср
составляет 0,13 усл. ед., поэтому элементарная
работа ![]() А
А
на этом участке равна 0,52 усл. ед. На участке от 12
до 10 см, рассуждая аналогичным образом, получаем
элементарную работу 0,56 усл. ед. Далее удобно
брать участки длиной по 1 см. На каждом из них
найдите среднее значение силы и умножьте его на
длину участка. Полученные значения работы поля ![]() A на всех
A на всех
участках занесите в четвёртую строку таблицы.
Чтобы узнать работу А,
совершённую электрическим полем при перемещении
заряда из бесконечности на данное расстояние,
складывайте соответствующие элементарные
работы и получающиеся значения записывайте в
пятую строку таблицы. В последней строке
запишите значения величины 1/r, обратной
расстоянию между зарядами.

Постройте график зависимости работы
электрического поля от величины, обратной
расстоянию, и убедитесь, что получается прямая
линия (рисунок справа).
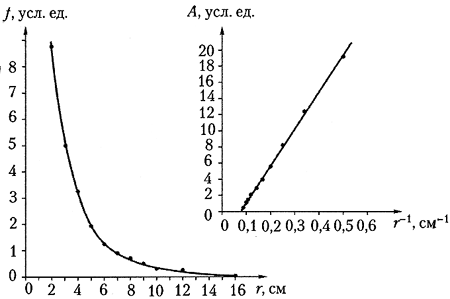
Таким образом, опыт показывает, что
работа электрического поля при перемещении
заряда из бесконечности в данную точку поля
обратно пропорциональна расстоянию от этой
точки до заряда, создающего поле.
Исследование 6.4. Высоковольтный
источник напряжения
Информация. Для школьного
физического эксперимента в настоящее время
промышленность выпускает прекрасные
высоковольтные источники напряжения. Они имеют
две выходные клеммы или два высоковольтных
электрода, разность потенциалов между которыми
плавно регулируется в пределах от 0 до 25 кВ.
Встроенный в прибор стрелочный или цифровой
измеритель напряжения позволяет определять
разность потенциалов между полюсами источника.
Такие приборы повышают уровень учебного
эксперимента по электростатике.
Задание. Разработайте
доказательный учебный эксперимент,
показывающий, что потенциал заряженного шара,
экспериментально определённый в соответствии с
формулой (6.2) для точечного заряда, равен
потенциалу, сообщённому этому шару
высоковольтным источником питания.
Вариант выполнения. Вновь
соберите экспериментальную установку, состоящую
из электростатического динамометра с пробным
шариком и проводящего шара на изолирующей
подставке (см. исследования 3.4 и 6.3). Измерьте
параметры всех элементов установки.
Для определённости укажем, что в одном
из опытов мы использовали электростатический
динамометр, параметры которого указаны в
исследовании 3.4: а = 5 • 10–3 м, b = 55
• 10–3 м, с = 100 • 10–3 м, т = 0,94
• 10–3 кг, причём шарики были одинаковыми и
имели радиус R = 7,5 • 10–3 м.
Для этого динамометра градуировочный
коэффициент K, переводящий условные единицы
силы в ньютоны, даётся формулой ![]() (cм. исследование 3.6).
(cм. исследование 3.6).
График работы по перемещению пробного
заряда из бесконечности в данную точку поля
представлен на рисунке на с. 31. Чтобы в этом
графике от условных единиц работы перейти к
джоулям, нужно в соответствии с формулой ![]() A = fср
A = fср![]() r значения
r значения
расстояния в сантиметрах перевести в метры,
значения силы в усл. ед. (см) перевести в усл. ед. (м)
и умножить на K. Таким образом: ![]() A (Дж) = 10–4 K
A (Дж) = 10–4 K![]() A (уcл. ед.).
A (уcл. ед.). 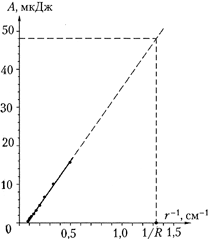
Соответствующий график зависимости
работы от величины, обратной расстоянию,
представлен ниже. Экстраполируя его до R = 7,5
мм, получаем, что работа по перемещению пробного
заряда из бесконечности до поверхности
заряженного шарика А = 57 • 10–4 K = 4,8 • 10–5 Дж.
Так как заряды шариков были одинаковы и
составляли q = 6,6 • 10–9 Кл
(см. исследование 3.6), то искомый потенциал ![]() = А/q = 7300 В.
= А/q = 7300 В.
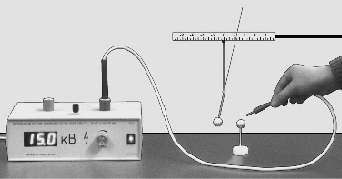
Включите высоковольтный источник и
регулятором установите на нём выходное
напряжение, например, U = 15 кВ. Одним из
электродов поочерёдно прикоснитесь к проводящим
шарикам и выключите источник. При этом каждый из
шариков приобретает относительно Земли
потенциал ![]() =
=
7,5 кВ. Повторите опыт по определению зарядов
шариков методом Кулона (исследование 3.6) и вы
получите значение, близкое к 7 нКл.
Таким образом, в эксперименте двумя
независимыми способами определены заряды шаров.
Первый способ основан на непосредственном
использовании определения потенциала, второй
опирается на сообщение шарикам определённого
потенциала c помощью высоковольтного источника и
последующее измерение их заряда с помощью закона
Кулона. При этом получились совпадающие
результаты.
Конечно, никто из школьников и не
сомневается в том, что современные приборы
правильно измеряют значения физических величин.
Но теперь они убеждены, что правильно измеряются
именно те величины, которые они изучают в
простейших явлениях. Установлена прочная связь
между основами физики и современной техникой,
ликвидирована пропасть между школьными знаниями
и реальной жизнью.
Вопросы и задания для самоконтроля
1. Как экспериментально доказать, что
электростатическое поле потенциально?
2. В чём суть аналогии между
гравитационным и электростатическим полями?
3. Какова связь между напряжённостью и
разностью потенциалов электростатического поля?
4. Предложите опыт, непосредственно
обосновывающий справедливость принципа
суперпозиции для потенциалов.
5. Вычислите потенциал поля точечного
заряда, пользуясь интегральным исчислением.
Сравните сделанный вами вывод формулы с
элементарным выводом, приведённым в лекции.
6. Выясните, почему в опыте по
определению разности потенциалов между двумя
проводящими дисками (исследование 6.1) нельзя
перемещать измеритель напряжённости так, чтобы
его пробный шарик прошёл всё расстояние от
одного диска до другого.
7. Отградуировав электрометр по
напряжению (исследование 6.2), сравните
получившийся результат с теми значениями
чувствительности прибора по напряжению, которые
приводятся в паспортных данных электрометра.
8. Оцените дидактическую эффективность
учебного эксперимента по непосредственному
определению потенциала поля сферического заряда
(исследование 6.3).
9. Детально разработайте методику
формирования в сознании учащихся обоснованной
убеждённости, что введённое при изучении
электростатики понятие потенциала
электрического поля в точности соответствует
тому, которое используется современной наукой и
техникой.
Литература
Бутиков Е.И., Кондратьев А.С.
Физика: Учеб. пособие: В 3 кн. Кн. 2.
Электродинамика. Оптика. – М.: Физматлит, 2004.
Восканян А.Г., Марленский А.Д.,
Шибаев А.Ф. Демонстрация закона Кулона на
основе количественных измерений: В сб. «Учебный
эксперимент по электродинамике», вып. 7. – М.:
Школа-Пресс, 1996.
Касьянов В.А. Физика-10. – М.: Дрофа,
2003.
Мякишев Г.Я., Синяков А.З., Слободсков
Б.А. Физика: Электродинамика. 10–11 кл.: Учеб. для
угл. изучения физики. – М.: Дрофа, 2002.
Учебное оборудование для кабинетов
физики обще- образовательных учреждений: Под ред.
Г.Г.Никифорова. – М.: Дрофа, 2005.
