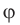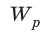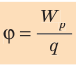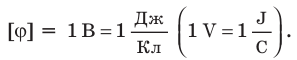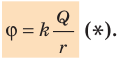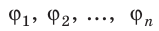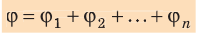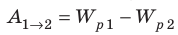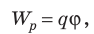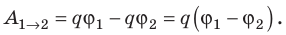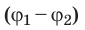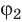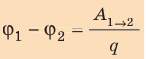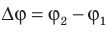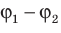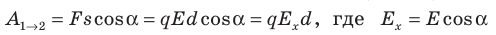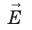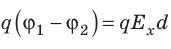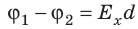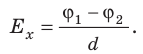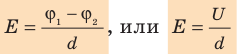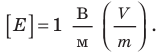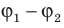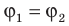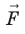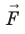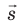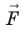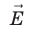Понятие потенциала в физике
Из курса физики известно, что работа некоторых сил, например силы тяжести, не зависит от траектории движения тела, а зависит лишь от величины перемещения.
Такие силы и силовые поля, в которых они действуют, называют потенциальными или консервативными.
Сила, действующая на заряд, помещенный в однородное электростатическое поле, также относится к потенциальным и определяется формулой:
Формула 1
F→=q·E→,
где q — электрический заряд, Кл;
E→ — напряженность электрического поля, В.
В механике работа определяется как произведение силы на расстояние между точками – началом и концом движения и косинусом угла α между векторами силы и скорости. Аналогично выведем формулу для определения работы электростатического поля при перемещении заряда из одного положения в другое.
Формула 2
A=F→·Δr·cosα=q·E→·Δr·cosα=q·E→·(r2-r1)·cosα=(q·E→·r2-q·E→·r1)·cosα.
Величину q·E→·r1 называют потенциальной энергией поля.
Определение 1
Потенциальная энергия является мерой работы, которую совершат силы при перемещении объекта в потенциальном поле.
Работа зависит от разницы потенциальных энергий в начальной и конечной точке. Тогда работу можно представить как:
Формула 3
A=-(W2-W1).
Примечание
Знак «минус» в выражении для работы означает, что если уменьшить потенциальную энергию с помощью силового воздействия, работа поля будет положительной. Если потенциальную энергию увеличить — работа будет отрицательной.
Поместим в некоторую точку неподвижный заряд q, чтобы создать электростатическое поле. Когда заряд q1 попадает в это поле, заряды q и q1 не взаимодействуют друг с другом, на заряд q1 действует само поле. Чтобы ввести новую характеристику поля, не зависящую от помещенных в него зарядов, необходимо поделить потенциальную энергию на заряд q. Полученную величину называют потенциалом.
Определение 2
Потенциал (от слова potentia — сила, возможность) — скалярная величина в физике, равная отношению потенциальной энергии к величине заряда.
В электрике принято следующее обозначение потенциала: φ.
Формула 4
φ=Wq.
Нулевым принято считать потенциал бесконечно удаленной точки (r→∞).
Ток в цепи всегда течет от большего потенциала к меньшему.
Формула для потенциала одного заряда приведена выше. На практике любое заряженное тело можно разделить на несколько элементов, каждый из которых будет иметь свой потенциал. Тогда потенциал системы, состоящей из двух и более зарядов:
Формула 5
φ=φ1+φ2+φ3+…
Понятие разности потенциалов, формула нахождения
Подставим выражение для потенциала в точке в формулу для работы:
Формула 6
A=-(W2-W1)=-(qφ2-qφ1)=-q(φ2-φ1).
Физическую величину, смысл которой заключается в разнице между потенциалами в начальной и конечной точках траектории, называют разностью потенциалов или напряжением (U).
Формула 7
U=φ1-φ2.
В самом простом случае, когда на рассматриваемую цепь или участок цепи действует только электростатическое поле, напряжение можно считать равным разности потенциалов. В иных случаях напряжение в проводнике определяют как сумму разности потенциалов и работу внешних сил (ЭДС), возникающих, например, в результате закона электромагнитной индукции. Тогда напряжение:
Формула 8
U=(φ1-φ2)+ЭДС.
Чтобы понять связь между напряжением и напряженностью, рассмотрим простой конденсатор в виде двух пластин с постоянной емкостью.
Между положительно и отрицательно заряженными пластинами образуется электростатическое поле напряженностью overrightarrow Е. Линии напряженности между обкладками параллельны, а модуль напряженности одинаков.
Если положительный заряд поместить рядом с положительной пластиной, он начнет двигаться в сторону отрицательной пластины, значит, поле совершит некоторую работу. Так как векторы скорости перемещения заряда и напряженности лежат на параллельных прямых, работа:A=F→·S.
Длина перемещения равна расстоянию между обкладками, а сила воздействия поля: F→=q·E→.
Тогда:A=q·E→·SиA=qU.
Приравняем выражения для работы, получим:q·E→·S=q·U.
Напряжение и напряженность связаны формулой:
Формула 9
U=E→·S
Разместим протяженный проводник в электростатическом поле. Будем считать, что линии напряженности расположены горизонтально.
Пусть проводник будет двигаться перпендикулярно линиям напряженности. В этом случае работа по перемещению заряда не совершается, так как косинус угла между векторами силы и скорости движения равен нулю. То есть все точки на поверхности проводника имеют один и тот же потенциал.
Определение 3
Эквипотенциальные поверхности — поверхности, у которых потенциалы в каждой точке одинаковы. Эквипотенциальные поверхности представляют собой плоскость для однородного поля и сферы для поля одиночного заряда.
Единица разности потенциалов
Коробка уравнивания потенциалов
В честь ученого (Алессандро Вольта), впервые доказавшего существование разницы потенциалов, единица измерения названа Вольт. В международной системе единиц напряжение обозначается символами:
- В – в русскоязычной литературе;
- V – в англоязычной литературе.
Кроме этого, существуют кратные обозначения:
- мВ – милливольт (0.001 В);
- кВ – киловольт (1000 В);
- МВ – мегавольт (1000 кВ).
Измерение контактной разности потенциалов
Основная проблема заключатся в том, что контактная разность потенциалов не может быть измерена напрямую, вольтметром, хотя значение ЭДС в цепи с соединением двух различных проводников может составлять от долей до единиц вольт.
Контактная потенциальная разница существенно влияет на вольтамперную характеристику измеряемой цепи. Наглядным примером может служить полупроводниковый диод, где подобное явление возникает на границе соприкосновения полупроводников с разным типом проводимости.
Разность потенциалов на практике
С общепринятой точки зрения, разность потенциалов – это напряжение между двумя выбранными точками цепи. В то же время напряжение между каждой из этих точек и третьей точкой будет отличаться в полном соответствии с определением.
Наглядный пример:
- Точка А в электрической схеме – напряжение 10 В относительно провода заземления;
- В точке В напряжение составляет 25 В относительно того же провода.
Необходимо найти напряжение между точками А и В.
В данном случае искомая разность составляет:
UAB= ϕА-ϕВ=10-25=15 В.
Рассматриваемые понятия важны для минимального объема знаний в области электротехники и электроники, поскольку на них основываются все расчеты и практические решения. Без этих азов невозможно более углубленное изучение электрических дисциплин.
Потенциал. Эквипотенциальные поверхности.
В механике взаимодействие тел характеризует силой или потенциальной энергией. Электрическое поле, которое обеспечивает взаимодействие между электрически заряженными телами, также характеризуют двумя величинами. Напряженность электрического поля — это силовая характеристика. Теперь введем энергетическую характеристику — потенциал. С помощью этой величины можно будет сравнивать между собой любые точки электрического поля. Таким образом, потенциал как характеристика поля должен зависеть от значения заряда, содержащегося в этих точках. Поделим обе части формулы A = W1 — W2 на заряд q, получим
Отношение W/q не зависит от значения заряда и принимается за энергетическую характеристику, которую называют потенциалом поля в данной точке. Обозначают потенциал буквой φ.
Потенциал электрического поля φ — скалярная энергетическая характеристика поля, которая определяется отношением потенциальной энергии W положительного заряда q в данной точке поля к величине этого заряда:
Единица потенциала — вольт:
Подобно потенциальной энергии значения потенциала в данной точке зависит от выбора нулевого уровня для отсчета потенциала. Чаще всего в электродинамике за нулевой уровень берут потенциал точки, лежащей в бесконечности, а в электротехнике — на поверхности Земли.
С введением потенциала формулу для определения работы по перемещению заряда между точками 1 и 2 можно записать в виде
Поскольку при перемещении положительного заряда в направлении вектора напряженности электрическое поле выполняет положительную работу A = q (φ1 — φ2 )> 0, то потенциал φ1 больше чем потенциал φ2 . Таким образом, напряженность электрического поля направлена в сторону уменьшения потенциала.
Если заряд перемещать с определенной точки поля в бесконечность, то работа A = q (φ — φ∞ ). Поскольку φ∞ = 0, то A = qφ. Таким образом, величина потенциала φ определенной точки поля определяется работой, которую выполняет электрическое поле, перемещая единичный положительный заряд из этой точки в бесконечность,
Если электрическое поле создается точечным зарядом q, то в точке, лежащей на расстоянии r от него, потенциал вычисляют по формуле
По этой формуле рассчитывают и потенциал поля заряженного шара. В таком случае r — это расстояние от центра шара до выбранной точки поля. С этой формулы видно, что на одинаковых расстояниях от точечного заряда, который создает поле, потенциал одинаков. Все эти точки лежат на поверхности сферы, описанной радиусом r вокруг точечного заряда. Такую сферу называют эквипотенциальной поверхностью.
Эквипотенциальные поверхности — геометрическое место точек в электрическом поле, которые имеют одинаковый потенциал, — один из методов наглядного изображения электрических полей.
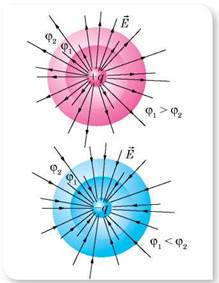
Эквипотенциальные поверхности электрических полей, созданных точечными зарядами разных знаков
Силовые линии всегда перпендикулярны эквипотенциальных поверхностей. Это означает, что работа сил поля по перемещению заряда по эквипотенциальной поверхности равна нулю.
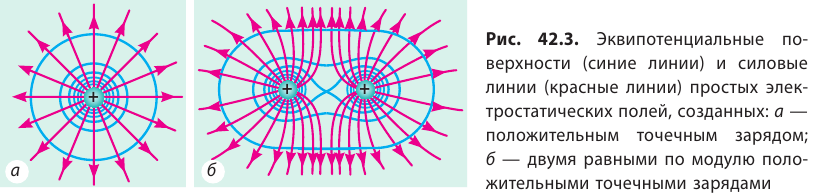
В случае наложения электрических полей, созданных несколькими зарядами, потенциал электрического поля равен алгебраической сумме потенциалов полей, созданных отдельными зарядами, φ = φ1 + φ2 + φ3 . Эквипотенциальные поверхности таких систем имеют сложную форму. Например, для системы из двух одинаковых по значению одноименных зарядов эквипотенциальные поверхности имеют вид, изображенный на рисунке. Эквипотенциальные поверхности однородного поля явлются плоскостями.
Эквипотенциальные поверхности: а — поля двух одинаковых зарядов б — однородного поля
Что называют потенциалом электростатического поля
Потенциал
электростатического поля в данной точке — это скалярная физическая величина, которая характеризует энергетические свойства поля и равна отношению потенциальной энергии
электрического заряда, помещенного в данную точку поля, к значению q этого заряда:
Единица потенциала в Си — вольт:
Из определения потенциала следует, что потенциал ϕ поля, созданного точечным зарядом Q, в точках, которые расположены на расстоянии r от данного заряда, можно рассчитать по формуле:
Из формулы ( *) видно: 1) если поле создано положительным точечным зарядом (Q > 0), то потенциал этого поля в любой точке является положительным ( ϕ > 0); 2) если поле создано отрицательным точечным зарядом (Q < 0), то потенциал этого поля в любой точке является отрицательным (ϕ < 0). Формула ( *) справедлива и для потенциала поля равномерно заряженной сферы (или шара) на расстояниях, которые больше ее радиуса или равны ему.
Если поле создано несколькими произвольно расположенными зарядами, потенциал ϕ поля в любой точке данного поля равен алгебраической сумме потенциалов
полей, созданных каждым зарядом:
Как определяют разность потенциалов
Когда в электростатическом поле заряд движется из точки 1 в точку 2, это поле совершает работу, которая равна изменению потенциальной энергии заряда, взятому с противоположным знаком:
. Поскольку
то
Выражение
называют разностью потенциалов, где
— значение потенциала в начальной точке траектории движения заряда,
— значение потенциала в ее конечной точке.
Разность потенциалов — скалярная физическая величина, равная отношению работы сил электростатического поля по перемещению заряда из начальной точки в конечную к значению этого заряда:
Единица разности потенциалов в Си — вольт:
= 1 В (V).
Разность потенциалов между двумя точками поля равна 1 В, если для перемещения между ними заряда 1 Кл электростатическое поле совершает работу 1 Дж. Обратите внимание: в подобных случаях разность потенциалов
− также называют напряжением (U). Важно не путать изменение потенциала
и разность потенциалов (напряжение)
.
Как связаны напряженность однородного электростатического поля и разность потенциалов
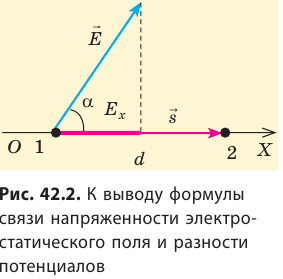
Рассмотрим однородное электростатическое поле на участке между точками 1 и 2, расположенными на расстоянии d друг от друга; пусть из точки 1 в точку 2 под действием поля перемещается заряд q (рис. 42.2).
Совершаемую полем работу можно найти двумя способами: 1) через разность потенциалов между точками 1 и 2: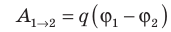
— проекция вектора
на ось Ох, проведенную через точки 1 и 2.
Приравняв оба выражения для работы, получим:
, откуда:
, или
Если заряд перемещается в направлении напряженности электрического поля (
) , последняя формула примет вид:
Из последней формулы следует единица напряженности в Си — вольт на метр:
Какие поверхности называют эквипотенциальными
Для визуализации электростатического поля кроме силовых линий используют также эквипотенциальные поверхности.
Эквипотенциальная поверхность — это поверхность, во всех точках которой потенциал электростатического поля имеет одинаковое значение.
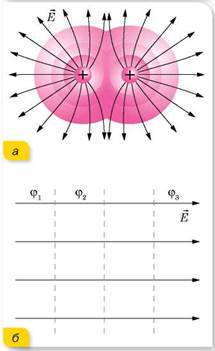
Для наглядности следует рассматривать не одну эквипотенциальную поверхность, а их совокупность. Однако графически изобразить совокупность поверхностей сложно, поэтому обычно изображают только линии пересечения эквипотенциальных поверхностей некоторой плоскостью (рис. 42.3).
Эквипотенциальные поверхности тесно связаны с силовыми линиями электростатического поля. Если электрический заряд перемещается по эквипотенциальной поверхности, то работа поля равна нулю, поскольку A=q (
), а на эквипотенциальной поверхности
Работу электростатического поля также можно представить через силу
действующую на заряд со стороны поля: A F= scosα , где α — угол между векторами
и
Поскольку A = 0, а F ≠ 0 и s ≠ 0, то cosα = 0, то есть α = 90°. Это означает, что при движении заряда вдоль эквипотенциальной поверхности вектор силы
а следовательно, и вектор напряженности
поля в любой точке перпендикулярны вектору перемещения
Таким образом, силовые линии электростатического поля перпендикулярны эквипотенциальным поверхностям (см. рис. 42.3).
Обратите внимание! Симметрия эквипотенциальных поверхностей повторяет симметрию источников поля. Так, поле точечного заряда сферически симметрично, поэтому эквипотенциальными поверхностями поля точечного заряда являются концентрические сферы; при однородном поле эквипотенциальные поверхности — это система параллельных плоскостей.
Для чего нужен потенциометр электрику
Что такое коэффициент мощности
Данный прибор широко применяется в практике для модуляции напряжения. Дело в том, что у многих источников (особенно заточенных под автономное функционирование: аккумуляторные элементы, солнечные батареи и т.д.) константное напряжение, не поддающееся управлению без специальных устройств, что может вызвать проблемы. Чтобы уменьшить исходное напряжение такого элемента, используют устройства-делители, снабженные потенциометрами.
Потенциометр-реостат
Как работает потенциометр? Он представляет собой резистор, имеющий пару выводов и подвижный ползунок с еще одним выводом. Подключаться такое переменное устройство сопротивления может двумя способами:
- По типу реостата, с использованием ползункового вывода и одного из пары других. Сопротивление замеряется движением ползунка по корпусу резистора. Регуляция цепного электротока в таком случае возможна при последовательном подключении такого реостата и источника напряжения.
- Потенциометрическим методом, задействующим каждый вывод из имеющейся у прибора тройки. Два главных вывода включаются параллельно источнику, снятие сниженного напряжения реализуется с ползункового механизма и одного вывода. В этом случае через резисторное устройство течет электроток, создающий спад напряжения между ползунком и боковыми выводами. В такой модели на источник питания ложится большая нагрузка, так как для точности регуляции и отсутствия сбоев необходимо, чтобы резисторное сопротивление в несколько раз уступало нагрузочному.
Потенциометрическое подключение прибора
Таким образом, понятие потенциала используется в разных областях физики: как в механике, так и в изучении электричества. В последнем случае оно выступает в качестве характеристики поля. Непосредственно рассматриваемая величина измерению не поддается, зато можно измерить разность, тогда один заряд берется за точку отсчета.
Понятие потенциала, разности потенциалов
С понятием напряжения электрического тока тесно связано понятие «потенциал» , или «разность потенциалов». Хорошо, обратимся снова к нашей водопроводной аналогии.
Наш резервуар находится на возвышенности что позволяет воде беспрепятственно стекать по трубе вниз. Так как бак с водой на высоте, то и потенциал этой точки будет более высоким или более положительным чем тот что находится на уровне земли. Видите что получается?
У нас появилось две точки имеющие разные потенциалы, точнее разную величину потенциала.
Получается, для того чтобы электрический ток мог бежать по проводу, потенциалы не должны быть равны. Ток бежит от точки с большим потенциалом к точки с меньшим потенциалом.
Помните такое выражение, что ток бежит от плюса к минусу. Так вот это все тоже самое. Плюс это более положительный потенциал а минус более отрицательный.
Кстати а хотите вопрос на засыпку? Что произойдет с током, если величины потенциалов будет периодически меняться местами?
Тогда мы будем наблюдать то как электрический ток меняет свое направление на противоположное каждый раз как потенциалы поменяются. Это получится уже переменный ток. Но его мы пока рассматривать не будем, дабы в голове сформировалось ясное понимание процессов.
Общие сведения
Электрические явления начали интересовать философов ещё со времёнДревней Греции. Существует легенда, согласно которой люди, жившие более двух тысяч лет назад, находили на острове Магнезия камни, притягивающие к себе металлические предметы. Их назвали магнитами. В то же время философ Фалес обнаружил любопытное свойство янтаря. Если его потереть об шерсть, то к нему прилипали лёгкие предметы. Благодаря этим двум явлениям природы и было открыто электричество, ранее называемое янтарностью.
Но на протяжении многих столетий учёные не могли объяснить силы, заставляющие взаимодействовать тела между собой. Существенный вклад в развитие учения внёс Отто Герик, создавший первую электромашину.
Затем Питера ван Мушенбрук смог изготовить источник электричества, названный лейденской банкой. С этого момента начался бум изучения явлений. В своё время их исследовали такие физики, как Гильберт, Кулон, Ампер, Эдисон, Франклин, Вольт, Фарадей.
Благодаря их стараниями стало известно, что электричество и магнетизм — это явления, не существующие друг без друга. Описывать их начали, ведя характеристику, названную электромагнитным полем. Возникновение же последней связано с существованием заряда и возможностью его переноса элементарными частицами. Их условно разделили на два вида:
- отрицательные;
- положительные.
В природе если тело находится в равновесии, то есть на него не оказывается стороннее воздействие, движение частиц происходит хаотично и обусловлено тепловыми процессами.
Но если носители заставить двигаться в одном направлении, возникнет ток. Характеризуется он силой и работой которую необходимо затратить для переноса заряда из одной точки поля в другую.
Затраченную при движении энергию называютэлектродвижущей силой, описывающейся напряжением. Величиной зависящей от изменения потенциала поля в той или иной его точке. В 1827 году Георг Ом опытным путём доказал пропорциональную зависимость силы тока и напряжения. Этот фундаментальный закон был назван его именем, записывается так: I = U / R. Правило установило, что сила электротока зависит от работы, совершаемой полем для переноса заряда из точки A в B.
Предыдущая
РазноеДелаем токопроводящий клей из подручных материалов
Следующая
РазноеЧто такое фаза в электричестве?
Закон Ома назван в честь своего открывателя это ученый Георг Симон Ом. Свои эксперименты в области электричества он начал вдохновляясь опытами Фурье. Ом проводил свои опыты с различными материалами и изучение их электропроводности. Так была разработана знаменитая формула, которая стала краеугольной в современной физике, которая вошла в школьные учебники: I=U/R. Сила тока пропорциональна величине напряжения и имеет обратную пропорциональность сопротивлению.
В статье подробно разобраны области теории и практического применения принципов закона Ома в современной электротехнике. В качестве дополнения, в материале содержатся два обучающих видеоролика и один научный материал на тему статьи.
Закон Ома
Закон Ома показывает отношения между напряжением (U), током (I) и сопротивлением (R). Записано это может быть тремя разными способами:
U = I × R
или
I = V/R
или
R = V/I
Где:
- V – напряжение в вольтах (В);
- I – сила тока в амперах (А);
- R – сопротивление в омах (Ом);
Для большинства схем амперы – слишком большие величины, а омы – слишком маленькие. Поэтому в формулу можно подставлять миллиамперы и килоомы. Если силу тока подставлять в миллиамперах (мА), то сопротивление обязательно должно быть в килоомах (кОм) и наоборот. Напряжение – всегда в вольтах.
Чтобы проще запомнить три разные версии определения Закона Ома, можно воспользоваться «VIR-треугольником».
- Если надо вычислить напряжение, закрываем пальцем V. У нас остаются I и R. Они на одном уровне, значит между ними ставим знак умножения. Получается: V = I × R .
- Если вычисляем ток, закрываем пальцем I. У нас остаётся V над R. Значит напряжение делится на сопротивление: I = V/R .
- Аналогичным образом поступаем при вычислении сопротивления. Закрываем R. Остаётся V над I. Значит: R = V/I .
Закон Ома, определение: Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Есть также частный случай – Закон Ома для участка цепи – сила тока в участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению этого участка.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:
Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Для переменного тока
Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
Для замкнутой цепи
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера применения
Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение. Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1= I2 ;
- U = U1+ U2 ;
- R = R1+ R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения. Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx. Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1+ I2 … ;
- U = U1= U2 … ;
- 1 / R = 1 / R1+ 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение. Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры. Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E. Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.
Друзья, не забывайте подписываться на обновления блога, ведь чем больше читателей подписано на обновления, тем больше я понимаю что делаю что-то важное и полезное и это чертовски мотивирует на новые статьи и материалы.
Понятие электрического потенциала является одним из важных основ теории электростатики и электродинамики. Понимание его сущности является необходимым условием для дальнейшего изучения этих разделов физики.
Содержание
- 1 Что такое электрический потенциал
- 2 Свойства потенциала
- 3 Разность потенциалов
- 4 Эквипотенциальные поверхности
Что такое электрический потенциал
Пусть в поле, создаваемым неподвижным зарядом Q, помещён единичный заряд q, на который действует сила Кулона F=k*Qq/r.
Здесь и далее k=((1/4)*π* ε0* ε), где ε0 — электрическая постоянная (8,85*10-12 Ф/м), а ε – диэлектрическая постоянная среды.
Внесённый заряд под действием этой силы может перемещаться, а сила при этом совершит определенную работу. Это означает, что система из двух зарядов обладает потенциальной энергией, зависящей от величины обоих зарядов и расстояния между ними, причём величина этой потенциальной энергии не зависит от величины заряда q. Здесь и вводится определение электрического потенциала – он равен отношению потенциальной энергии поля к величине заряда:
φ=W/q,
где W – потенциальная энергия поля, создаваемого системой зарядов, а потенциал является энергетической характеристикой поля. Чтобы переместить заряд q в электрическом поле на какое-то расстояние, надо затратить определённую работу на преодоление кулоновских сил. Потенциал точки равен работе, которую надо затратить для перемещения единичного заряда из этой точки в бесконечность. При этом надо отметить, что:
- эта работа будет равна убыли потенциальной энергии заряда (A=W2-W1);
- работа не зависит от траектории перемещения заряда.
В системе СИ единицей измерения потенциала является один Вольт (в русскоязычной литературе обозначается буквой В, в зарубежной – V). 1 В=1Дж/1 Кл, то есть, можно говорить о потенциале точки в 1 вольт, если для перемещения заряда в 1 Кл в бесконечность потребуется совершить работу в 1 Джоуль. Название выбрано в честь итальянского физика Алессандро Вольта, внесшего значительный вклад в развитие электротехники.
Чтобы наглядно представить, что такое потенциал, его можно сравнить с температурой двух тел или температурой, замеренной в разных точках пространства. Температура служит мерой нагрева объектов, а потенциал – мерой электрической заряженности. Говорят, что одно тело нагрето более другого, также можно сказать, что одно тело заряжено более, а другое – менее. Эти тела обладают разным потенциалом.
Значение потенциала зависит от выбора системы координат, поэтому требуется какой-то уровень, который надо принять за ноль. При измерении температуры за базовую границу можно принять, например, температуру тающего льда. Для потенциала за нулевой уровень обычно принимают потенциал бесконечно удаленной точки, но для решения некоторых задач за нулем можно считать, например, потенциал земли или потенциал одной из обкладок конденсатора.
Свойства потенциала
Среди важных свойств потенциала надо отметить следующие:
- если поле создается несколькими зарядами, то потенциал в конкретной точке будет равен алгебраической (с учетом знака заряда) сумме потенциалов, создаваемых каждым из зарядов φ=φ1+φ2+φ3+φ4+φ5+…+φn;
- если расстояния от зарядов таковы, что сами заряды можно считать точечными, то суммарный потенциал считается по формуле φ=k*(q1/r1+q2/r2+q3/r3+…+qn/rn), где r – расстояние от соответствующего заряда то рассматриваемой точки.
Если поле образовано электрическим диполем (двумя связанными зарядами противоположного знака), то потенциал в любой точке, находящейся на расстоянии r от диполя будет равен φ=k*p*cosά/r2, где:
- p – электрическое плечо диполя, равное q*l, где l – расстояние между зарядами;
- r – расстояние до диполя;
- ά – угол между плечом диполя и радиус-вектором r.
Если точка лежит на оси диполя, то cosά=1 и φ=k*p/r2.
Разность потенциалов
Если две точки обладают определённым потенциалом, и если они не равны, то говорят о том, что между двумя точками существует разность потенциалов. Разность потенциалов возникает между точками:
- потенциал которых определяется зарядами разных знаков;
- точкой с потенциалом от заряда любого знака и точкой с нулевым потенциалом;
- точками, имеющими потенциал равного знака, но отличающимися по модулю.
То есть, разность потенциалов не зависит от выбора системы координат. Можно провести аналогию с бассейнами с водой, расположенными на разной высоте относительно нулевой отметки (например, уровня моря).
Вода каждого бассейна имеет определенную потенциальную энергию, но если соединить два любых бассейна трубкой, то в каждой из них возникнет поток воды, расход которой определяется не только размерами трубки, но и разностью потенциальных энергий в гравитационном поле Земли (то есть, разностью высот). Абсолютное значение потенциальных энергий значения в данном случае не имеет.
Точно так же, если соединить проводником две точки с разным потенциалом, по нему потечёт электрический ток, определяемый не только сопротивлением проводника, но и разностью потенциалов (но не их абсолютным значением). Продолжая аналогию с водой, можно сказать, что вода в верхнем бассейне скоро закончится, и если не найдется той силы, которая переместит воду обратно наверх (например, насоса), то и поток очень быстро прекратится.
Так и в электрической цепи – чтобы поддерживать разность потенциалов на определенном уровне, потребуется сила, переносящая заряды (точнее, носители зарядов) к точке с наибольшим потенциалом. Такая сила называется электродвижущей силой и сокращенно обозначается ЭДС. ЭДС может носить различную природу – электрохимическую, электромагнитную и т.п.
На практике имеет значение в основном разность потенциалов между начальной и конечной точками траектории движения носителей зарядов. В этом случае эту разность называют напряжением, и оно в СИ также измеряется в вольтах. О напряжении в 1 Вольт можно говорить, если поле совершает работу в 1 Джоуль при перемещении заряда в 1 Кулон из одной точки в другую, то есть 1В=1Дж/1Кл, и Дж/Кл также может являться единицей измерения разности потенциалов.
Эквипотенциальные поверхности
Если потенциал нескольких точек одинаков, и эти точки образуют поверхность, то такая поверхность называется эквипотенциальной. Таким свойством обладает, например, сфера, описанная вокруг электрического заряда, ведь электрическое поле убывает с расстоянием одинаково во все стороны.
Все точки этой поверхности имеют одинаковую потенциальную энергию, поэтому при перемещении заряда по такой сфере работа затрачиваться не будет. Эквипотенциальные поверхности систем из нескольких зарядов имеют более сложную форму, но у них есть одно интересное свойство – они никогда не пересекаются. Силовые линии электрического поля всегда перпендикулярны поверхностям с одинаковым потенциалом в каждой их точке. Если эквипотенциальную поверхность рассечь плоскостью, получится линия равных потенциалов. Она имеет те же свойства, что и эквипотенциальная поверхность. На практике равный потенциал имеют, например, точки на поверхности проводника, помещенного в электростатическое поле.
Разобравшись с понятием потенциала и разности потенциалов, можно приступать к дальнейшему изучению электрических явлений. Но не ранее, потому что без понимания базовых принципов и понятий углубить знания не получится.
2.2.1..
Неразветвленные и разветвленные
электрические цепи,
Электрические
цепи подразделяют на неразветвленные
и разветвленные.
Схема
простейшей неразветвленной цепи
представлена на рис. 1.1. Очевидно, что
во всех её элементах течет один и тот
же ток.
Простейшая
разветвленная цепь изображена на рис.
2.4, а. В ней имеются три ветви и два узла.
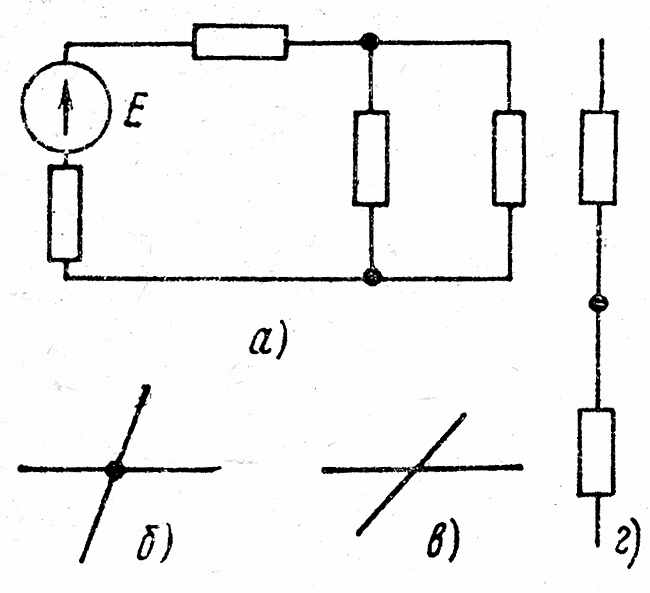
Рис.
2.4.
В
разветвлённой схеме по каждой из ветвей
течет свой ток. Ветвь можно определить
как участок цепи, образованный
последовательно соединенными элементами
(через которые течет одинаковый ток) и
заключенный между двумя узлами. В свою
очередь, узел есть точка цепи, в которой
сходятся не менее трех ветвей.
При
составлении электрических схем всегда
действует следующее правило: если в
месте пересечения двух линий на
электрической схеме поставлена точка
(рис.
2.4, б), то в этом месте есть электрическое
соединение двух линий, в противном
случае (рис. 2.4, в)
его
нет.
Кроме
термина «узел» иногда используют термин
«устранимый узел». Под устранимым узлом
понимают точку, в которой соединены
два последовательных сопротивления
(рис. 2.4, г). При проведении расчетов
такие сопротивления обычно заменяются
одним, величина которого равна сумме
величин реальных сопротивлений.
2.2.2.
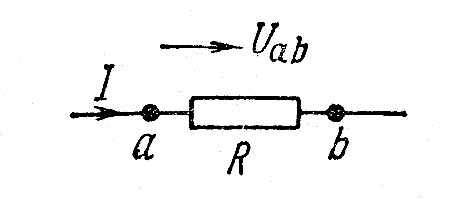
Напряжение на участке цепи.
Под
напряжением
на
некотором участке электрической цепи
понимают разность потенциалов между
крайними точками этого участка.
На
рис. 2.5 изображен участок цепи, крайние
точки которого обозначены буквами а
и
b.
Пусть
ток I
течет от точки а
к
точке b
(от
более высокого потенциала к более
низкому). Очевидно, что потенциал точки
а
(φa)
выше потенциала точки b
(φb)
на значение, равное произведению тока
I
на сопротивление R:
φa
=
φb
+IR.
В соответствии с определением напряжение
между точками а
и
b
Uab
= φa
–
φb
Следовательно,
Uab
=
IR,
т.
е. напряжение на сопротивлении равно
произведению тока, протекающего по
сопротивлению, на значение этого
сопротивления.
Рис
2.5.
В
электротехнике разность потенциалов
на концах сопротивления называют либо
напряжением
на сопротивлении, либо
падением
напряжения. В
дальнейшем разность потенциалов на
концах сопротивления, т. е. произведение
IR
будем именовать падением напряжения.
Положительное
направление падения напряжения на
каком-либо участке (направление отсчета
этого напряжения), указываемое на
рисунках стрелкой, совпадает с
положительным направлением отсчета
тока, протекающего по данному
сопротивлению.
Рассмотрим
теперь вопрос о напряжении на участке
цепи, содержащем не только сопротивление,
но и э.д.c.
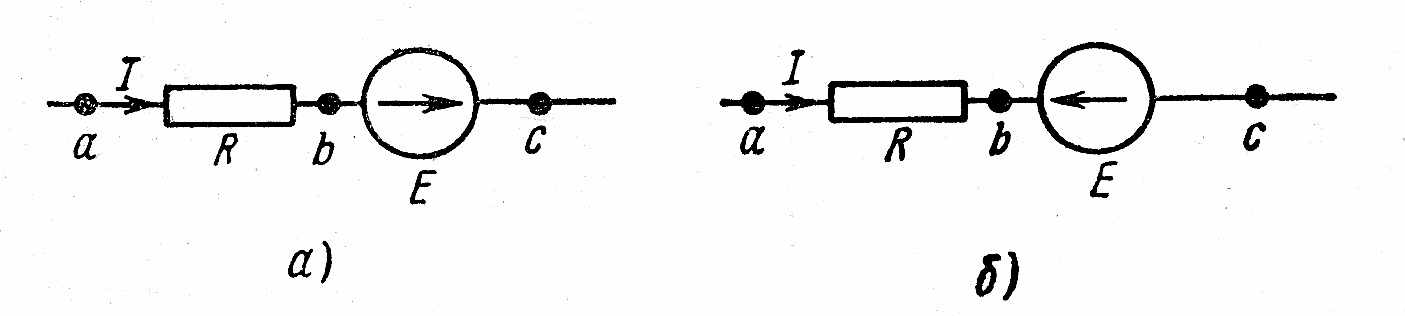
Рис.
2.6.
На
рис. 2.6, а,б
показаны
участки некоторых цепей, по которым
протекает ток I.
Найдем разность потенциалов (напряжение)
между точками а
и
с
для
этих участков. По определению,
Uac
= φa
–
φc
(2.11)
Выразим
потенциал точки а
через
потенциал точки c.
При
перемещении от точки c
к
точке b
встречно направлению э.д.с. Е
(рис.
1.6 а)
потенциал
точки b
оказывается
ниже (меньше), чем потенциал точки c,
на значение э.д.с. Е:
φb
= φc
— Е,
При
перемещении от точки c
к
точке b
согласно
направлению э. д. с. Е
(рис.
2.6,6)
потенциал точки b
оказывается
выше (больше), чем потенциал точки с,
на
значение э. д. с. Е:
φb
= φc
+ Е
Так
как по участку цепи без источника э. д.
с. ток течет от более высокого потенциала
к более низкому, в обеих схемах рис. 2.6
потенциал точки а
выше
потенциала точки b
на значение падения напряжения на
сопротивлении R:
φa
=
φb
+IR.
Таким
образом, для схемы риc.
2.6, а
справедливо
соотношение:
φa
= φc
– Е
+ IR
или
Uac
=
φa
– φc
=
IR –
Е
(2.12)
Для схемы рис.
2.6, б
соответствующие соотношения примут
вид:
φa
= φc
+ Е
+ IR
или
Uac
=
φa
– φc
=
IR +
Е
(2.13)
Положительное
направление напряжения Uac
показывают стрелкой от а
к
с.
Согласно
определению Uca
= φc
–
φa.
Поэтому
Uca
= – Uac,
т. е. изменение чередования
(последовательности) индексов равносильно
изменению знака этого напряжения.
Следовательно, напряжение может быть
и положительной, и отрицательной
величиной.
2.2.3. Закон Ома.
Для
участка цепи, не содержащего источник
э. д. с., закон Ома устанавливает связь
между напряжением и током на этом
участке. Для схемы, изображённой на
рис. 1.8 это соотношение имеет вид:
Uab
=
IR,
или
I
= Uab
/R
= (φa
–
φb)/
R (2.15)
Для
участка цепи, содержащего источник э.
д. с., закон Ома позволяет найти ток
этого участка по известной разности
потенциалов (φa
–
φb)
на концах участка цепи и имеющейся на
этом участке э.д.с. Е.
Так,
из уравнения (2.12) для схемы рис. 2.6, а
следует:
I=
(φa
– φc
+
Е)
/ R=
(Uac+
Е)/
R.
Соответственно
из уравнения (2.13) для схемы рис. 2.6, б
следует:
I=
(φa
– φc
–
Е)
/ R=
(Uac–
Е)/
R.
В общем случае
(2.16)
Уравнение
(2.16) математически выражает закон Ома
для участка цепи, содержащего источник
э. д.с.; знак плюс перед Е
соответствует
рис. 2.6, а,
знак
минус — рис. 2.6, б.
В
частном случае при Е
=
0
уравнение (2.16) переходит в уравнение
(2.15).
Пример
1.
К
зажимам а
и
с
схемы
рис. 2.7 подключен вольтметр, имеющий
очень большое, теоретически бесконечно
большое сопротивление (следовательно,
его подключение или отключение не
влияет на режим работы цепи).
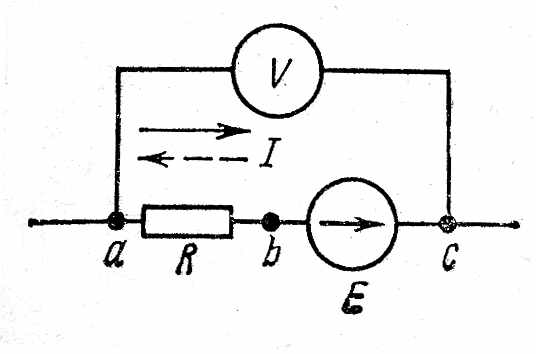
Если
ток I
= 10 А течет от точки а
к
точке с, то показание вольтметра
Uac
=
–
18В;
если этот ток течет от точки с
к
точке а,
то
Uac
=
–
20 В.
Определить сопротивление R
и
э.д.с. Е.
Решение.
В
первом режиме; Uac
=
–
18
= –Е
+
RI
= –Е
+10R
Во
втором режиме:
Űac
=
–
20
= –Е
–
RI
= –Е
–10R
Совместное
решение дает Е
= 19
В, = R
= 0,1
Ом,
2.2.4.
Законы Кирхгофа
Для
расчета электрических цепей наряду с
законом Ома применяются два закона
Кирхгофа, являющиеся следствиями закона
сохранения энергии.
Методы
расчета с применением законов Кирхгофа
позволяют рассчитать электрическую
цепь любой конфигурации и сложности,
т. е. являются основными.
Первый закон
Кирхгофа
Первый
закон Кирхгофа применяется к узлам
электрических цепей и выражает баланс
токов в них: в
узле электрической цепи алгебраическая
сумма токов равна нулю:
(2.17)
В эту
сумму токи входят с разными знаками в
зависимости от направления их по
отношению к узлу. На основании первого
закона Кирхгофа для каждого узла можно
составить уравнение токов.
Так,
например, для точки 3
схемы,
представленной на рис. 2.8, такое уравнение
имеет вид
I1
+ I2
–
I4
–I7
=
0 (2.18)
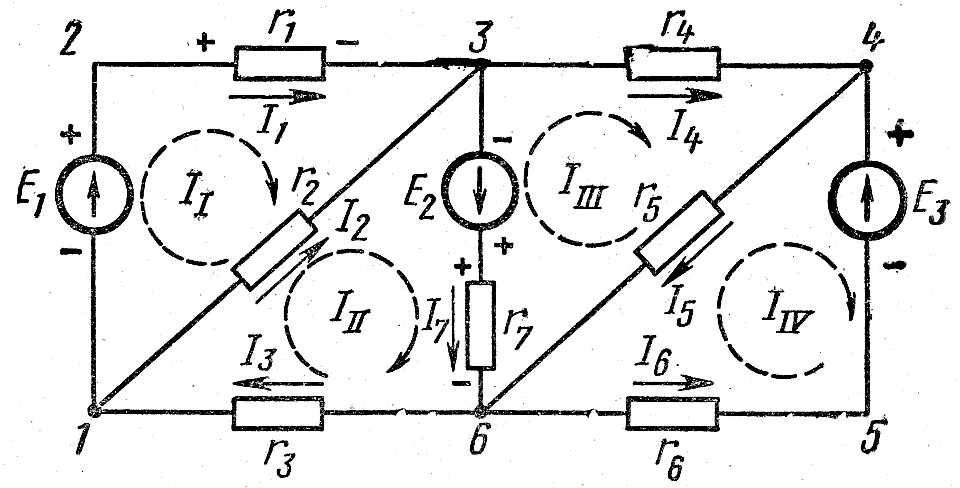
Рис. 2.8
В этом
уравнении токи, направленные к узлу,
условно считаются положительными, а
токи, направленные от узла, —
отрицательными.
Уравнение
(2.18) можно переписать в несколько ином
виде
I1
+ I2
=
I4
+I7
(2.19)
Такая
запись уравнения позволяет дать другую
формулировку первого закона Кирхгофа,
а именно: сумма
токов, направленных к узлу электрической
цепи, равна сумме токов, направленных
от этого узла.
Этот
закон следует из принципа непрерывности
тока. Если допустить преобладание в
узле токов одного направления, то заряд
одного знака должен накапливаться и
потенциал узловой точки должен непрерывно
изменяться, что в реальных цепях не
наблюдается
Второй
закон
Кирхгофа
Второй
закон Кирхгофа применяется к контурам
электрических цепей и выражает баланс
напряжений в них: в контуре
электрической цепи алгебраическая
сумма электродвижущих сил равна
алгебраической сумме падений напряжения
на сопротивлениях, входящих в этот
контур:
ΣE=ΣIR
(2.20)
Для
доказательства второго закона Кирхгофа
определим потенциалы отдельных точек
контура 1—2—3—4—5—6—1
в
схеме,
изображенной на рис. 2.8, обходя контур
в произвольном направлении, например,
по часовой стрелке. Направления токов
в элементах контура взяты также
произвольно.
Обход
контура начнем от точки 1,
потенциал которой φ1.
Потенциал точки 2
φ2
=
φ1
+
E1
и
далее:
φ3
=
φ2
–
I1r1
φ4
=
φ3
–
I4r4
φ5
=
φ4
–
E3
φ6
=
φ5
+
I6r6
φ1
=
φ6
–
I3r3
Как
известно, в потенциальном поле работа,
затрачиваемая на перемещение заряженной
частицы (или частиц) по замкнутому
контуру, всегда равна 0.
Поэтому
и суммарное изменение потенциала по
такому контуру, выражающее эту работу,
также должно быть равно нулю.
Таким
образом, в замкнутом контуре Σφ
=
0,
т.е.
для нашего случая:
φ1
+
φ2
+
φ3
+
φ4
+φ5
+ φ6
=
0,
следовательно
0
= E1
–
I1r1
–
I4r4
–E3
+
I6r6–
I3r3
Перенеся
в левую часть уравнения значения э. д.
с. и поменяв знаки, получим уравнение,
соответствующее второму закону Кирхгофа
в применении к выбранному контуру:
E1
–
E3
=
I1r1
+
I4r4
–
I6r6
+ I3r3
Для
других контуров получаются другие
уравнения. Их нетрудно написать, не
прибегая к определению потенциалов
точек контура. Для этого можно пользоваться
следующим правилом.
В левую часть
уравнения следует записать алгебраическую
сумму э. д. с., встречающихся при обходе
контура, а в правую часть — алгебраическую
сумму падений напряжения в сопротивлениях
контура.
При
этом положительной считается э. д, с.,
направление которой совпадает с
направлением обхода; положительным
считается падение напряжения Ir
на сопротивлении, в котором направление
тока совпадает с направлением обхода.
Согласно
этому правилу, ниже записаны уравнения
для двух других контуров схемы,
представленной на рис.2.8:
контур
1—2—3—6—1
E1
+
E2
=
I1r1
+
I7r7
+ I3r3
контур
3—4—6—3
–E2
=
I4r4
+
I5r5
– I7r7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Что такое разность потенциалов и как её найти
Содержание
- 1 Потенциальная энергия в электрополе
- 2 Что такое потенциал
- 3 При чём тут разность
- 4 Однородное электрополе
- 5 Когда нужна большая разница
- 6 Измерительные приборы
- 7 Видео по теме
Физическая величина, названная потенциалом, является одной из фундаментальных характеристик потенциального поля. Понятие потенциала используется для описания свойств не только электрического, но и других физических полей — гравитационного, акустического, поля упругих деформаций. Для конкретных расчётов используется величина, которую называют разностью потенциалов (РП), поскольку одним из свойств потенциальных полей является зависимость его величины от выбранной системы координат (от точки отсчёта). РП не зависит от этого фактора. Для электрополя дополнительно применяется понятие напряжения, что по сути эквивалентно РП.
Потенциальная энергия в электрополе
Наличие электрического поля E проявляется в его силовом действии на электрические заряды q. Сила F, действующая на электрозаряд, равна F=qE.
При перемещении электрозаряда из одной точки электрополя в другую совершается работа А, которая равна:
В этой формуле Δx — расстояние между двумя точками (начальной и конечной).
Результатом совершённой работы является изменение Δ потенциальной энергии (ПЭ) электрозаряда W:
Электростатическое поле является потенциальным. Его главные признаки:
- Работа, совершаемая полем по перемещению электрозаряда, не зависит от конфигурации пути (траектории). То есть, энергетический результат будет одинаков при перемещении из точки 1 в точку 2 либо четко по прямой, либо по замысловатой кривой.
- Работа поля, совершённая по замкнутой траектории, равна нулю. Результат работы, совершённой на дистанции любой длины, но с возвратом в начальную точку, будет нулевым.
Второе свойство является прямым следствием первого, но его обычно выделяют отдельно, как один из основных признаков потенциальности поля.
Силы потенциальных полей относятся к разряду консервативных. Кроме электрических к таковым относятся:
- Сила гравитации (тяжести).
- Сила упругих деформаций (упругости).
Яркий пример неконсервативной силы — сила трения, на результат работы которой влияет и конфигурация пути, и скорость перемещения.
Что такое потенциал
Многочисленные исследования учёных в ХVIII–XIX в.в. показали, что ПЭ в любых полях (однородных или неоднородных) прямо пропорциональна величине заряда q. На этом основании была введена новая физическая характеристика — потенциал и его обозначение буквой φ.
Как видно из формулы, φ — скалярная величина. Простыми словами можно сказать, что потенциал характеризует энергетические возможности поля в конкретной точке, в то время как напряжённость Е «отвечает» за силовые возможности.
Поскольку W измеряется в джоулях, а q в кулонах, то [φ]=[Дж]/[Кл]. Данная единица измерения получила наименование Вольт в честь итальянского физика, внёсшего огромный вклад в изучение природы электрических явлений. Так же называется и единица измерения электрического напряжения.
При чём тут разность
По аналогии с ПЭ гравитационного поля величина φ в данной точке разнится в зависимости от выбора точки. На практике интерес представляет не абсолютное значение потенциала, а его изменение, которое уже не зависит от точки отсчёта нулевого уровня.
Работа, выполняемая при перемещении электрозаряда q из точки 1 в точку 2, равна:
Таким образом, Δφ — это разность потенциалов, физика которой, четко и корректно описывается данной формулой. На практике для величины Δφ чаще применяют термин напряжение, которое обозначается буквой U, то есть U=Δφ.
Напряжение электросети есть не что иное, как разность потенциалов на концах проводника или участка цепи. Поскольку единица разности потенциалов — вольт, то электронапряжение также измеряется вольтами.
Следует отметить, что в отличие от алгебраической разности, являющейся разностью между конечным и начальным значением некоторой величины, чтобы определить разность электрических потенциалов, надо от начального значения отнять конечное. Если электрозаряд в конечной точке больше, чем в начальной, то разность электропотенциалов будет отрицательной.
Однородное электрополе
В зависимости от системы зарядов возникает суммарное поле распределения электропотенциала, в котором определение его величины может быть весьма непростой задачей. На рисунке ниже показаны некоторые варианты. Системы из двух зарядов (диполя) относятся к неоднородным полям. Вариант в правом нижнем углу — это распределение силовых линий в конденсаторе, между обкладками которого напряжённость Е = const. Разность электрических потенциалов на обкладках плоского конденсатора равна напряжению U, поданному на обкладки.
В однородном электрополе напряженность Е будет одинаковой во всех его точках. Для определения ее величины используется довольно простая формула.
Из этой формулы можно найти единицу измерения напряженности. При φ1-φ2 = 1 В и d = 1 м получим Е=1 В/м.
Когда нужна большая разница
В научных и практических целях в узлах отдельных устройств бывают необходимы электронные блоки, способные быстро ускорять заряженные частицы. Ускоряющая разность потенциалов — это напряжение, разгоняющее электроны до необходимой энергии. На рисунке ниже схематично показана «электронная пушка», используемая в осветительной системе электронного микроскопа.
Чем больше ускоряющее напряжение, тем качественнее получается пространственное разрешение электронного микроскопа. Типичные величины ускоряющих напряжений лежат в диапазоне 10–100 кВ.
Работу ускоряющего напряжения можно определить, исходя из закона сохранения энергии:
Из данной формулы может быть найдено электронапряжение или разность потенциалов:
Измерительные приборы
Измерение разницы электрических потенциалов или напряжения в электроцепях осуществляют с помощью вольтметров, которые бывают:
- Аналоговыми (со стрелкой).
- Цифровыми (со светодиодной индикацией).
Использование вольтметров основывается на принципах электродинамики. Электроток проходит по проволочной рамке прибора, расположенной между полюсами магнитов, и под действием измеряемого электронапряжения создает электромагнитное поле. Под его воздействием рамка отклоняется на некоторый угол. Шкала вольтметра проградуирована пропорционально углу отклонения рамки. Но следует учитывать, что с помощью прибора может быть определен не сам потенциал, а разность потенциалов.
Такое понятие в физике, как потенциал и производная от него разность потенциалов, являются ключевыми характеристиками энергетических возможностей электрополя.