Как найти разность ряда чисел

Вычесть значит отнять одно число от другого. Вычитание есть такое действие, в котором отнимают меньшее число от большего. При вычитании целых чисел большее число уменьшается на столько единиц, сколько их содержится в меньшем.

Вычесть одно число из другого значит убавить одно число другим, поэтому вычитание есть действие обратное сложению.

Вычитание

В вычитании два данных числа называются уменьшаемым и вычитаемым, а искомое — разностью.

Уменьшаемым называют большее число, от которого отнимают другое. Оно уменьшается от вычитания.

Вычитаемым называют меньшее число, которое отнимают от большего.

Разностью называют вывод, полученный от вычитания. Разность определяет, чем одно число больше другого или показывает разницу между двумя числами.

Знак вычитания. Действие вычитания обозначается знаком — (минус).

Вычитание однозначных чисел

Чтобы обозначить, что из 9 нужно вычесть 6, пишут эти числа рядом, отделяя их знаком — (минус):

• 9 — 6.

Разность между этими числами будет 3, и ход вычисления выражают словесно:

девять без шести равно трем.

Письменно:

• 9 — 6 = 3.

Большее число 9 будет уменьшаемым, меньшее 6 вычитаемым, число 3 остатком.

Способы вычитания

Можно двумя способами вычесть одно число из другого:

1. или можно отнять от большего числа столько единиц, сколько их содержится в меньшем. Так, из 9 вычесть 6 значит от 9 отнять 6. Число 3 будет искомый остаток;
2. или можно к меньшему числу прибавлять по единице до тех пор, пока не получим большее число. Так, вычитая 6 из 9, мы к 6 прибавляем 3 единицы.

Число единиц, которое нужно прибавить к меньшему числу, чтобы уравнять его с большим, определяет разность.

Меньшее число с разностью должно равняться большему числу, следовательно, меньшее число и разность суть слагаемые, а большее — их сумма. На этом основано другое определение вычитания:

В этом случае данная сумма есть уменьшаемое, данное слагаемое — вычитаемое, а искомаяразность — другое слагаемое.

Вычитание многозначных чисел

Вычитание многозначных чисел основывается на том свойстве чисел, по которому вычесть число все-равно, что вычесть все его части. Из этого свойства видно, что вычесть какое-нибудь число все-равно, что вычесть последовательно все его единицы, десятки, сотни и т. д. Чтобы обозначить, что из числа 7228 нужно вычесть 3517, пишут:

• 7228 — 3517 и вычитают отдельно единицы из единиц, десятки из десятков и т. д.

Чтобы облегчить вычитание, подписывают меньшее число под большим так, чтобы единицы одинаковых порядков находились в одном вертикальном столбце, проводят черту, слева ставят знак вычитания — и под чертою подписывают разность.

Ход вычисления выражают словесно:

1. Начинаем вычитание с простых единиц: 8 без 7 составляют 1; подписывают под единицами 1.
2. Вычитаем десятки: 2 без 1 дают 1, подписываем под десятками 1.
3. Вычитаем сотни. Пять нельзя вычесть из 2, поэтому занимаем у следующего высшего порядка (тысяч) единицу, что и обозначаем тем, что над 7 ставим точку. Единица каждого порядка содержит 10 единиц следующего меньшего порядка. Присоединяя эти 10 единиц к 2, получим 12; 12 без 5 составляют 7, подписываем под сотнями 7. Когда занимают единицу у высшего порядка, обозначают это тем, что ставят точку над порядком, у которого занимают.
4. Вычитаем тысячи. Тысяч осталось вместо 7 только 6, ибо одна была взята. 6 без 3 составляют 3; подписываем под тысячами 3.

Ход вычисления выражают письменно:

Пример. Из 17004 вычесть 6025.

Из 4 нельзя вычесть 5. Занимаем единицу у десятков, следующего высшего порядка, но в этом порядке единиц нет; занимаем у сотен, — и сотен нет; занимаем у тысяч и обозначаем это точкой над цифрой 7.

Единица четвертого имеет 10 единиц третьего порядка. Взяв из них одну для десятков, оставляем их в сотнях только 9. Присоединив 10 к 4, имеем 14.

Производя вычитание, получим:

• для единиц 14 — 5 = 9
• для десятков 9 — 2 = 7
• для сотен 9 — 0 = 9
• для тысяч 6 — 6 = 0

Для десятков тысяч имеем 1, ибо эту цифру уменьшаемого переносим в разность без изменения.

Ход вычисления выразится письменно:

Из предыдущих примеров выводим правила вычитания:

1. Чтобы сделать вычитание целых чисел, нужно вычитаемое подписать под уменьшаемым так, чтобы единицы одинаковых порядков стояли в одном вертикальном столбце, провести черту, под которою и подписать разность.
2. Вычитание нужно начинать с простых единиц, то есть с первого столбца, и затем, переходя к следующим столбцам от правой руки к левой, вычитают десятки из десятков, сотни из сотен и т. д.
3. Если цифра вычитаемого меньше цифры уменьшаемого, разность подписывают в том же столбце; если цифры равны, разность будет нуль.
4. Если же цифра вычитаемого больше соответствующей цифры уменьшаемого, занимают единицу у следующего порядка уменьшаемого, отмечая это точкой, поставленной над цифрой, у которой занимают, прикладывают 10 к цифре уменьшаемого и производят вычитание. Цифру же с точкой считают на единицу меньше.
5. Если при вычитании цифра уменьшаемого, у которого занимают, будет 0, за которым в уменьшаемом следуют тоже нули, то занимают у первой значащей цифры, ставя над нею и всеми промежуточными нулями точки. Цифру с точкой считают на единицу меньше, а нули с точкой считают за 9.
6. Вычитание продолжают до тех пор, пока не получат полной разности.
7. Лишние цифры уменьшаемого переносят в разность.

Зависимость между данными и искомыми вычитания

Из примера 9 — 6 = 3 видно, что

1. Уменьшаемое равно вычитаемому, сложенному с разностью: 9 = 6 + 3.
2. Вычитаемое равно уменьшаемому без разности: 6 = 9 — 3.
3. Разность равна уменьшаемому без вычитаемого: 3 = 9 — 6.

Арифметическое дополнение. Разность между числом и ближайшей большей единицей называется арифметическим дополнением. Так, арифметическими дополнениями чисел 7, 79, 983 будут числа:

• 10 — 7 = 3
• 100 — 79 = 21
• 1000 — 983 = 17

Арифметическим дополнением иногда пользуются для облегчения арифметических вычислений.

Источник: https://maths-public.ru/arithmetic/subtraction

Вычитание чисел

Вычитание – это арифметическое действие обратное сложению, посредством которого из одного числа вычитают (отнимают) столько единиц, сколько их содержится в другом числе.

Число, из которого вычитают, называется уменьшаемым, число, которое указывает сколько единиц будет вычтено из первого числа, называется вычитаемым. Число, получаемое в результате вычитания, называется разностью (или остатком).

Рассмотрим вычитание на примере. На столе лежит 9 конфет, если съесть 5 конфет, то их останется 4. Число 9 является уменьшаемым, 5 – вычитаемым, а 4 – остатком (разностью):

Для записи вычитания используется знак — (минус). Он ставится между уменьшаемым и вычитаемым, при этом уменьшаемое записывается слева от знака минус, а вычитаемое – справа. Например, запись 9 — 5 означает, что из числа 9 вычитается число 5. Справа от записи вычитания ставят знак = (равно), после которого записывают результат вычитания. Таким образом, полная запись вычитания выглядит так:

Эта запись читается так: разность девяти и пяти равняется четырём или девять минус пять равно четыре.

Чтобы в результате вычитания получить натуральное число или 0, уменьшаемое должно быть больше вычитаемого или равно ему.

Рассмотрим, как, используя натуральный ряд, можно выполнить вычитание и найти разность двух натуральных чисел. Например, нам необходимо вычислить разность чисел 9 и 6, отметим в натуральном ряду число 9 и отсчитаем от него влево 6 чисел. Получим число 3:

9 — 6 = 3

Вычитание также можно использовать для сравнения двух чисел. Желая сравнить между собой два числа, мы задаёмся вопросом, на сколько единиц одно число больше или меньше другого.

Чтобы узнать это, надо из большего числа вычесть меньшее. Например, чтобы узнать, на сколько 10 меньше 25 (или на сколько 25 больше 10), надо из 25 вычесть 10.

Тогда найдём, что 10 меньше 25 (или 25 больше 10) на 15 единиц.

Проверка вычитания

Рассмотрим выражение

15 — 7 = 8

где 15 – это уменьшаемое, 7 – это вычитаемое, а 8 – разность. Чтобы узнать правильно ли было выполнено вычитание, можно:

1. вычитаемое сложить с разностью, если получится уменьшаемое, то вычитание было выполнено верно:7 + 8 = 15
2. от уменьшаемого отнять разность, если получится вычитаемое, то вычитание было выполнено верно:15 — 8 = 7

Источник: https://naobumium.info/arifmetika/vychitanie.php

Что такое разность чисел в математике?

Для многих точные науки, вроде математики, воспринимаются как нечто более простое, чем сферы, требующие рассуждений, предполагающие большую вариативность. Однако все предметы имеют свои сложности, в том числе и технические.

Вычитание

Для того, чтобы понять, чем является разность, необходимо разобраться в ряде математической терминологии. В первую очередь, нужно выяснить, чем является вычитание.

По-другому это понятие называют убавлением, и по такому названию понять смысл процесса несколько проще. По своей сути вычитание является одной из математических операций.

Что же это за операции? Как правило, под ними понимают определенные арифметические или логические действия. Встает логичный вопрос – в чем же суть арифметических действий?

Понятие арифметики появилось достаточно давно. Оно зародилось в древнегреческом языке, где переводилось как «число». Сегодня это раздел математики, который изучает числа, их отношения друг к другу, а также свойства.

Итак, вычитание – это операции с числами, относящиеся к бинарным. Суть бинарных операций в том, что в них используются два аргумента (параметра), и получается один результат.

Стоит рассмотреть, как найти разность какого-то числа. В первую очередь, необходимы два аргумента, то есть два числа. Затем необходимо уменьшить значение первого числа на значение второго.

Когда данная операция выражается письменно, используется знак «минус». Это выглядит так: а – б = с, где а является первым числовым значением, б – вторым, а с – разностью чисел.

Как правило, у учеников возникает гораздо больше проблем именно с вычитанием, нежели со сложением. Отчасти это связано со свойствами данных математических операций.

Всем известно, что от перемены мест слагаемых значение суммы не меняется. В вычитании же всё гораздо сложней. Если поменять числа местами, получится совершенно другой результат.

Схожим свойством в прибавлении и убавлении является то, что нулевой элемент не меняет исходное число.

В вычитании всё относительно просто, если первое число больше второго, однако в школе будут рассматриваться и противоположные примеры. В этом случае возникает понятие отрицательного числа.

Например, если нужно вычесть из 5 число 2, то всё несложно. 5-2=3, таким образом разность числа составит 3. Однако, что делать, если необходимо посчитать, сколько будет два минус пять?

В выражении 2-5 разность уйдет в минус, то есть в отрицательное значение. Из двойки легко можно вычесть двойку, получив таким образом ноль, однако от пятерки остается ещё три. Таким образом, результатом данного выражения будет отрицательное число три. То есть, 2-5=-3.

Источник: https://topkin.ru/voprosy/nauka-voprosy/chto-takoe-raznost-chisel-v-matematike/

Что такое разность чисел: уменьшаемое, вычитаемое, разность — правило

Статья познакомит читателя с понятиями «разность чисел», «вычитаемое» и «уменьшаемое».

В арифметике существует всего четыре основных действия, которые мы называем сложением, умножением, вычитанием и делением.

Такие действия являются основой всей математики – они позволяют нам осуществлять все вычисления: как простые, так и самые сложные.

Самыми простыми действиями считаются сложение и вычитание, которые противоположны друг другу. Правда, слово «сложение» мы также используем и в обычной жизни.

Мы можем встретить фразу «сложить усилия, например, когда нам нужно сделать какую-нибудь работу всем вместе. Но вот с термином «вычитание» дело обстоит немного сложнее, и в разговоре оно встречается реже.

Мы редко услышим такие выражения, как «уменьшаемое», «вычитаемое», «разность». Но в сегодняшней статье мы подробно поговорим о них с точки зрения математики.

Что значит число уменьшаемое, число вычитаемое и разность чисел?

Что значит число уменьшаемое, число вычитаемое и разность чисел? Как известно, многие научные термины и выражения взяты из других языков, чаще греческого и латинского. Но те слова, которые будут рассмотрены ниже, имеют русское происхождение, потому нам будет проще их разобрать.

Например, что можно сказать о разности чисел? Если мы обратим внимание на корень слова «разность», то нам представится, например, его однокоренное слово «разница».

А если речь идет о математике, то тут и думать нечего – слово «разность» означает разницу между какими-то цифрами, а точнее, двумя числами.

Разница нам показывает, насколько одна величина больше другой или, наоборот, вторая меньше первой. Строго в математике это выглядит как результат вычитания.

Сразу же приведем пример. Допустим, буфетчица несет на подносе восемь пирожков. Пять из них она раздала посетителям. Сколько пирожков останется у буфетчицы на подносе? Если из 8 вычесть 5, то получится — 3. Теперь запишем это математически:

То есть разница между восемью и пятью – это три. Теперь нам понятно, что такое термин «разница».

Внимание: Если два числа равны друг другу, то разницы между ними не существует, она равна нулю (8 – 8 = 0).

Теперь нам следует выяснить, что такое вычитаемое и уменьшаемое. Снова представим значение слов по их смыслу. Чем может являться число уменьшаемое? Уменьшаемое – это то число, которое уменьшается при вычитании. От этого числа отнимают другое число. А что такое вычитаемое? Вычитаемым как раз и является том числом, которые мы отнимаем от уменьшаемого.

Вернемся к примеру с буфетчицей. Мы помним, как от восьми отнимали пять, и у нас получилось три. Мы выяснили, что тройка является разницей между двумя этими числами. Теперь нам уже не сложно понять, что 8 – это число уменьшаемое, а 5 – это число вычитаемое.

Как найти уменьшаемое и вычитаемое число?

Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:

• Y – 10 = 18, где Y – число уменьшаемое
• Значит, Y = 18 + 10
• 18 + 10 = 28
• Y = 28

Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:

• 28 – B = 10, где B – число вычитаемое
• Значит, B = 28 – 10
• 28 – 10 = 18
• B = 18

Источник: https://heaclub.ru/chto-takoe-raznost-chisel-umenshaemoe-vychitaemoe-raznost-pravilo

Что такое разность чисел в математике и как найти разность чисел

В этой статье мы рассмотрим, что такое разность чисел в математике, и как человеку, интересующемуся этой наукой, найти разность чисел.

Что такое разность чисел в математике

Вычитание является одной из 4 арифметических операций. Для его обозначения служит математический знак «−» (минус). Вычитание противоположно по смыслу операции сложения.

Операция вычитания в общем случае записывается следующим образом:

A − B = C

Число Математическое название

A	Уменьшаемое
B	Вычитаемое
C	Разность чисел

Пример: 6 − 2 =4

Здесь разностью чисел будет являться число 4. Следовательно, разность между любыми числами A и B это такое число C, которое при прибавлении к B даст в сумме A (4 при прибавлении к 2 дает 6 — значит, 4 это разность 6 и 2).

Как найти разность чисел

Уже из самого определения следует, как вычислить разность между двумя числами. При небольших числах можно делать это в уме. Детей в начальной школе учат следующим образом. Представьте, что у Вас есть 5 яблок, и 3 из них забрали. Сколько у Вас осталось? Правильно — 2 яблока. Постепенно Вы доведете вычисления до автоматизма и будете сразу выдавать ответ.

Однако для чисел выше 50 такое наглядное представление перестает работать. Большое количество предметов тяжело представить в уме, поэтому здесь на помощь приходит другой способ:

Вычисление разности в столбик

Школьники изучают этот способ в рамках курса математики, обычно во втором или третьем классе. Взрослые люди, пользующиеся калькулятором, зачастую забывают, как считать в столбик. Однако калькулятор не всегда бывает под рукой. Освежите в памяти школьные знания, посмотрев это видео.

Вычисление разности в столбик – видео

Этот способ применим и тогда, когда Вам нужно вычесть большее число из меньшего. В реальной жизни такое обычно не требуется, но может пригодиться при решении математических задач.

Допустим, в примере «A − B = C» B больше, чем A. Тогда C будет отрицательным. Чтобы вычислить разность, «разверните» пример: посчитайте значение B − A.

Когда Вы закончите считать эту разность, у вас получится число C, только с противоположным знаком: оно будет больше нуля. Чтобы завершить вычисления, припишите к нему спереди знак минус.

Источник: https://www.chto-kak-skolko.ru/index.php/nauki/matematika/chto-takoe-raznost-chisel-v-matematike-i-kak-najti-raznost-chisel

Вычесть значит отнять одно число от другого. Вычитание есть такое действие, в котором отнимают меньшее число от большего. При вычитании целых чисел большее число уменьшается на столько единиц, сколько их содержится в меньшем.

Вычесть одно число из другого значит убавить одно число другим, поэтому вычитание есть действие обратное сложению.

Вычитание

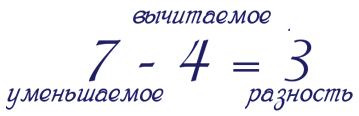
В вычитании два данных числа называются уменьшаемым и вычитаемым, а искомое — разностью.

Уменьшаемым называют большее число, от которого отнимают другое. Оно уменьшается от вычитания.

Вычитаемым называют меньшее число, которое отнимают от большего.

Разностью называют вывод, полученный от вычитания. Разность определяет, чем одно число больше другого или показывает разницу между двумя числами.

Знак вычитания. Действие вычитания обозначается знаком — (минус).

Вычитание однозначных чисел

Чтобы обозначить, что из 9 нужно вычесть 6, пишут эти числа рядом, отделяя их знаком — (минус):

• 9 6.

Разность между этими числами будет 3, и ход вычисления выражают словесно:

девять без шести равно трем.

Письменно:

• 9 6 = 3.

Большее число 9 будет уменьшаемым, меньшее 6 вычитаемым, число 3 остатком.

Способы вычитания

Можно двумя способами вычесть одно число из другого:

1. или можно отнять от большего числа столько единиц, сколько их содержится в меньшем. Так, из 9 вычесть 6 значит от 9 отнять 6. Число 3 будет искомый остаток,
2. или можно к меньшему числу прибавлять по единице до тех пор, пока не получим большее число. Так, вычитая 6 из 9, мы к 6 прибавляем 3 единицы.

Число единиц, которое нужно прибавить к меньшему числу, чтобы уравнять его с большим, определяет разность.

Меньшее число с разностью должно равняться большему числу, следовательно, меньшее число и разность суть слагаемые, а большее — их сумма. На этом основано другое определение вычитания:

• Вычитание есть такое действие, в котором по данной сумме и одному слагаемому отыскивается другое слагаемое.

В этом случае данная сумма есть уменьшаемое, данное слагаемое — вычитаемое, а искомаяразность — другое слагаемое.

Вычитание многозначных чисел

Вычитание многозначных чисел основывается на том свойстве чисел, по которому вычесть число все-равно, что вычесть все его части. Из этого свойства видно, что вычесть какое-нибудь число все-равно, что вычесть последовательно все его единицы, десятки, сотни и т. д. Чтобы обозначить, что из числа 7228 нужно вычесть 3517, пишут:

• 7228 3517 и вычитают отдельно единицы из единиц, десятки из десятков и т. д.

Чтобы облегчить вычитание, подписывают меньшее число под большим так, чтобы единицы одинаковых порядков находились в одном вертикальном столбце, проводят черту, слева ставят знак вычитания и под чертою подписывают разность.

Ход вычисления выражают словесно:

1. Начинаем вычитание с простых единиц: 8 без 7 составляют 1, подписывают под единицами 1.
2. Вычитаем десятки: 2 без 1 дают 1, подписываем под десятками 1.
3. Вычитаем сотни. Пять нельзя вычесть из 2, поэтому занимаем у следующего высшего порядка (тысяч) единицу, что и обозначаем тем, что над 7 ставим точку. Единица каждого порядка содержит 10 единиц следующего меньшего порядка. Присоединяя эти 10 единиц к 2, получим 12, 12 без 5 составляют 7, подписываем под сотнями 7. Когда занимают единицу у высшего порядка, обозначают это тем, что ставят точку над порядком, у которого занимают.
4. Вычитаем тысячи. Тысяч осталось вместо 7 только 6, ибо одна была взята. 6 без 3 составляют 3, подписываем под тысячами 3.

Ход вычисления выражают письменно:

Пример. Из 17004 вычесть 6025.

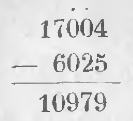
Из 4 нельзя вычесть 5. Занимаем единицу у десятков, следующего высшего порядка, но в этом порядке единиц нет, занимаем у сотен, и сотен нет, занимаем у тысяч и обозначаем это точкой над цифрой 7.

Единица четвертого имеет 10 единиц третьего порядка. Взяв из них одну для десятков, оставляем их в сотнях только 9. Присоединив 10 к 4, имеем 14.

Производя вычитание, получим:

• для единиц 14 5 = 9
• для десятков 9 2 = 7
• для сотен 9 0 = 9
• для тысяч 6 6 = 0

Для десятков тысяч имеем 1, ибо эту цифру уменьшаемого переносим в разность без изменения.

Ход вычисления выразится письменно:

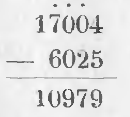
Из предыдущих примеров выводим правила вычитания:

1. Чтобы сделать вычитание целых чисел, нужно вычитаемое подписать под уменьшаемым так, чтобы единицы одинаковых порядков стояли в одном вертикальном столбце, провести черту, под которою и подписать разность.
2. Вычитание нужно начинать с простых единиц, то есть с первого столбца, и затем, переходя к следующим столбцам от правой руки к левой, вычитают десятки из десятков, сотни из сотен и т. д.
3. Если цифра вычитаемого меньше цифры уменьшаемого, разность подписывают в том же столбце, если цифры равны, разность будет нуль.
4. Если же цифра вычитаемого больше соответствующей цифры уменьшаемого, занимают единицу у следующего порядка уменьшаемого, отмечая это точкой, поставленной над цифрой, у которой занимают, прикладывают 10 к цифре уменьшаемого и производят вычитание. Цифру же с точкой считают на единицу меньше.
5. Если при вычитании цифра уменьшаемого, у которого занимают, будет 0, за которым в уменьшаемом следуют тоже нули, то занимают у первой значащей цифры, ставя над нею и всеми промежуточными нулями точки. Цифру с точкой считают на единицу меньше, а нули с точкой считают за 9.
6. Вычитание продолжают до тех пор, пока не получат полной разности.
7. Лишние цифры уменьшаемого переносят в разность.

Зависимость между данными и искомыми вычитания

Из примера 9 6 = 3 видно, что

1. Уменьшаемое равно вычитаемому, сложенному с разностью: 9 = 6 + 3.
2. Вычитаемое равно уменьшаемому без разности: 6 = 9 3.
3. Разность равна уменьшаемому без вычитаемого: 3 = 9 6.

Арифметическое дополнение. Разность между числом и ближайшей большей единицей называется арифметическим дополнением. Так, арифметическими дополнениями чисел 7, 79, 983 будут числа:

• 10 7 = 3
• 100 79 = 21
• 1000 983 = 17

Арифметическим дополнением иногда пользуются для облегчения арифметических вычислений.

Вычитание чисел

Вычитание – это арифметическое действие обратное сложению, посредством которого из одного числа вычитают (отнимают) столько единиц, сколько их содержится в другом числе.

Число, из которого вычитают, называется уменьшаемым, число, которое указывает сколько единиц будет вычтено из первого числа, называется вычитаемым. Число, получаемое в результате вычитания, называется разностью (или остатком).

Рассмотрим вычитание на примере. На столе лежит 9 конфет, если съесть 5 конфет, то их останется 4. Число 9 является уменьшаемым, 5 – вычитаемым, а 4 – остатком (разностью):

Для записи вычитания используется знак (минус). Он ставится между уменьшаемым и вычитаемым, при этом уменьшаемое записывается слева от знака минус, а вычитаемое – справа. Например, запись 9  5 означает, что из числа 9 вычитается число 5. Справа от записи вычитания ставят знак = (равно), после которого записывают результат вычитания. Таким образом, полная запись вычитания выглядит так:

Эта запись читается так: разность девяти и пяти равняется четырём или девять минус пять равно четыре.

Чтобы в результате вычитания получить натуральное число или 0, уменьшаемое должно быть больше вычитаемого или равно ему.

Рассмотрим, как, используя натуральный ряд, можно выполнить вычитание и найти разность двух натуральных чисел. Например, нам необходимо вычислить разность чисел 9 и 6, отметим в натуральном ряду число 9 и отсчитаем от него влево 6 чисел. Получим число 3:

9 6 = 3

Вычитание также можно использовать для сравнения двух чисел. Желая сравнить между собой два числа, мы задаёмся вопросом, на сколько единиц одно число больше или меньше другого.

Чтобы узнать это, надо из большего числа вычесть меньшее. Например, чтобы узнать, на сколько 10 меньше 25 (или на сколько 25 больше 10), надо из 25 вычесть 10.

Тогда найдём, что 10 меньше 25 (или 25 больше 10) на 15 единиц.

Проверка вычитания

Рассмотрим выражение

15 7 = 8

где 15 – это уменьшаемое, 7 – это вычитаемое, а 8 – разность. Чтобы узнать правильно ли было выполнено вычитание, можно:

1. вычитаемое сложить с разностью, если получится уменьшаемое, то вычитание было выполнено верно:7 + 8 = 15
2. от уменьшаемого отнять разность, если получится вычитаемое, то вычитание было выполнено верно:15 8 = 7

Что такое разность чисел в математике?

Для многих точные науки, вроде математики, воспринимаются как нечто более простое, чем сферы, требующие рассуждений, предполагающие большую вариативность. Однако все предметы имеют свои сложности, в том числе и технические.

Вычитание

Для того, чтобы понять, чем является разность, необходимо разобраться в ряде математической терминологии. В первую очередь, нужно выяснить, чем является вычитание.

По-другому это понятие называют убавлением, и по такому названию понять смысл процесса несколько проще. По своей сути вычитание является одной из математических операций.

Что же это за операции? Как правило, под ними понимают определенные арифметические или логические действия. Встает логичный вопрос – в чем же суть арифметических действий?

Понятие арифметики появилось достаточно давно. Оно зародилось в древнегреческом языке, где переводилось как «число». Сегодня это раздел математики, который изучает числа, их отношения друг к другу, а также свойства.

Итак, вычитание – это операции с числами, относящиеся к бинарным. Суть бинарных операций в том, что в них используются два аргумента (параметра), и получается один результат.

Стоит рассмотреть, как найти разность какого-то числа. В первую очередь, необходимы два аргумента, то есть два числа. Затем необходимо уменьшить значение первого числа на значение второго.

Когда данная операция выражается письменно, используется знак «минус». Это выглядит так: а – б = с, где а является первым числовым значением, б – вторым, а с – разностью чисел.

Как правило, у учеников возникает гораздо больше проблем именно с вычитанием, нежели со сложением. Отчасти это связано со свойствами данных математических операций.

Всем известно, что от перемены мест слагаемых значение суммы не меняется. В вычитании же всё гораздо сложней. Если поменять числа местами, получится совершенно другой результат.

Схожим свойством в прибавлении и убавлении является то, что нулевой элемент не меняет исходное число.

В вычитании всё относительно просто, если первое число больше второго, однако в школе будут рассматриваться и противоположные примеры. В этом случае возникает понятие отрицательного числа.

Например, если нужно вычесть из 5 число 2, то всё несложно. 5-2=3, таким образом разность числа составит 3. Однако, что делать, если необходимо посчитать, сколько будет два минус пять?

В выражении 2-5 разность уйдет в минус, то есть в отрицательное значение. Из двойки легко можно вычесть двойку, получив таким образом ноль, однако от пятерки остается ещё три. Таким образом, результатом данного выражения будет отрицательное число три. То есть, 2-5=-3.

Что такое разность чисел: уменьшаемое, вычитаемое, разность — правило

Статья познакомит читателя с понятиями «разность чисел», «вычитаемое» и «уменьшаемое».

В арифметике существует всего четыре основных действия, которые мы называем сложением, умножением, вычитанием и делением.

Такие действия являются основой всей математики – они позволяют нам осуществлять все вычисления: как простые, так и самые сложные.

Самыми простыми действиями считаются сложение и вычитание, которые противоположны друг другу. Правда, слово «сложение» мы также используем и в обычной жизни.

Мы можем встретить фразу «сложить усилия, например, когда нам нужно сделать какую-нибудь работу всем вместе. Но вот с термином «вычитание» дело обстоит немного сложнее, и в разговоре оно встречается реже.

Мы редко услышим такие выражения, как «уменьшаемое», «вычитаемое», «разность». Но в сегодняшней статье мы подробно поговорим о них с точки зрения математики.

Что значит число уменьшаемое, число вычитаемое и разность чисел?

Что значит число уменьшаемое, число вычитаемое и разность чисел? Как известно, многие научные термины и выражения взяты из других языков, чаще греческого и латинского. Но те слова, которые будут рассмотрены ниже, имеют русское происхождение, потому нам будет проще их разобрать.

Например, что можно сказать о разности чисел? Если мы обратим внимание на корень слова «разность», то нам представится, например, его однокоренное слово «разница».

А если речь идет о математике, то тут и думать нечего – слово «разность» означает разницу между какими-то цифрами, а точнее, двумя числами.

Разница нам показывает, насколько одна величина больше другой или, наоборот, вторая меньше первой. Строго в математике это выглядит как результат вычитания.

Сразу же приведем пример. Допустим, буфетчица несет на подносе восемь пирожков. Пять из них она раздала посетителям. Сколько пирожков останется у буфетчицы на подносе? Если из 8 вычесть 5, то получится — 3. Теперь запишем это математически:

То есть разница между восемью и пятью – это три. Теперь нам понятно, что такое термин «разница».

Внимание: Если два числа равны друг другу, то разницы между ними не существует, она равна нулю (8 – 8 = 0).

Теперь нам следует выяснить, что такое вычитаемое и уменьшаемое. Снова представим значение слов по их смыслу. Чем может являться число уменьшаемое? Уменьшаемое – это то число, которое уменьшается при вычитании. От этого числа отнимают другое число. А что такое вычитаемое? Вычитаемым как раз и является том числом, которые мы отнимаем от уменьшаемого.

Вернемся к примеру с буфетчицей. Мы помним, как от восьми отнимали пять, и у нас получилось три. Мы выяснили, что тройка является разницей между двумя этими числами. Теперь нам уже не сложно понять, что 8 – это число уменьшаемое, а 5 – это число вычитаемое.

Как найти уменьшаемое и вычитаемое число?

Как в математике найти разницу чисел мы уже разобрались. Это довольно просто. Но сможем ли мы найти уменьшаемое и вычитаемое число, если одно число неизвестно? Конечно можем, так как нам будут известны два других числа. Например, как мы можем найти уменьшаемое число? Если мы знаем значение разницы и вычитаемого, то сумма этих двух чисел равняется уменьшаемому:

• Y – 10 = 18, где Y – число уменьшаемое
• Значит, Y = 18 + 10
• 18 + 10 = 28
• Y = 28

Вычитаемое находится так же просто. Если мы знаем разницу и уменьшаемое, значит вычитаемое мы получим, отняв от уменьшаемого числа разность:

• 28 – B = 10, где B – число вычитаемое
• Значит, B = 28 – 10
• 28 – 10 = 18
• B = 18

Что такое разность чисел в математике и как найти разность чисел

В этой статье мы рассмотрим, что такое разность чисел в математике, и как человеку, интересующемуся этой наукой, найти разность чисел.

Что такое разность чисел в математике

Вычитание является одной из 4 арифметических операций. Для его обозначения служит математический знак «−» (минус). Вычитание противоположно по смыслу операции сложения.

Операция вычитания в общем случае записывается следующим образом:

A − B = C

Число Математическое название

A	Уменьшаемое
B	Вычитаемое
C	Разность чисел

Пример: 6 − 2 =4

Здесь разностью чисел будет являться число 4. Следовательно, разность между любыми числами A и B это такое число C, которое при прибавлении к B даст в сумме A (4 при прибавлении к 2 дает 6 — значит, 4 это разность 6 и 2).

Как найти разность чисел

Уже из самого определения следует, как вычислить разность между двумя числами. При небольших числах можно делать это в уме. Детей в начальной школе учат следующим образом. Представьте, что у Вас есть 5 яблок, и 3 из них забрали. Сколько у Вас осталось? Правильно — 2 яблока. Постепенно Вы доведете вычисления до автоматизма и будете сразу выдавать ответ.

Однако для чисел выше 50 такое наглядное представление перестает работать. Большое количество предметов тяжело представить в уме, поэтому здесь на помощь приходит другой способ:

Вычисление разности в столбик

Школьники изучают этот способ в рамках курса математики, обычно во втором или третьем классе. Взрослые люди, пользующиеся калькулятором, зачастую забывают, как считать в столбик. Однако калькулятор не всегда бывает под рукой. Освежите в памяти школьные знания, посмотрев это видео.

Вычисление разности в столбик – видео

Этот способ применим и тогда, когда Вам нужно вычесть большее число из меньшего. В реальной жизни такое обычно не требуется, но может пригодиться при решении математических задач.

Допустим, в примере A − B = C B больше, чем A. Тогда C будет отрицательным. Чтобы вычислить разность, «разверните» пример: посчитайте значение B − A.

Когда Вы закончите считать эту разность, у вас получится число C, только с противоположным знаком: оно будет больше нуля. Чтобы завершить вычисления, припишите к нему спереди знак минус.

Многие слышали об арифметической прогрессии, но не все хорошо представляют, что это такое. В данной статье дадим соответствующее определение, а также рассмотрим вопрос, как найти разность прогрессии арифметической, и приведем ряд примеров.

Математическое определение

Итак, если речь идет о прогрессии арифметической или алгебраической (эти понятия определяют одно и то же), то это означает, что имеется некоторый числовой ряд, удовлетворяющий следующему закону: каждые два соседних числа в ряду отличаются на одно и то же значение. Математически это записывается так:

a_{n + 1}-a_n = d

Здесь n означает номер элемента a_n в последовательности, а число d – это разность прогрессии (ее название следует из представленной формулы).

О чем говорит знание разности d? О том, как “далеко” друг от друга отстоят соседние числа. Однако знание d является необходимым, но не достаточным условием для определения (восстановления) всей прогрессии. Необходимо знать еще одно число, которым может быть совершенно любой элемент рассматриваемого ряда, например, a₄, a10, но, как правило, используют первое число, то есть a₁.

Формулы для определения элементов прогрессии

В общем, информации выше уже достаточно, чтобы переходить к решению конкретных задач. Тем не менее до того, как будет дана прогрессия арифметическая, и найти разность ее будет необходимо, приведем пару полезных формул, облегчив тем самым последующий процесс решения задач.

Несложно показать, что любой элемент последовательности с номером n может быть найден следующим образом:

a_n = a₁ + (n – 1) * d

Действительно, проверить эту формулу может каждый простым перебором: если подставить n = 1, то получится первый элемент, если подставить n = 2, тогда выражение выдает сумму первого числа и разности, и так далее.

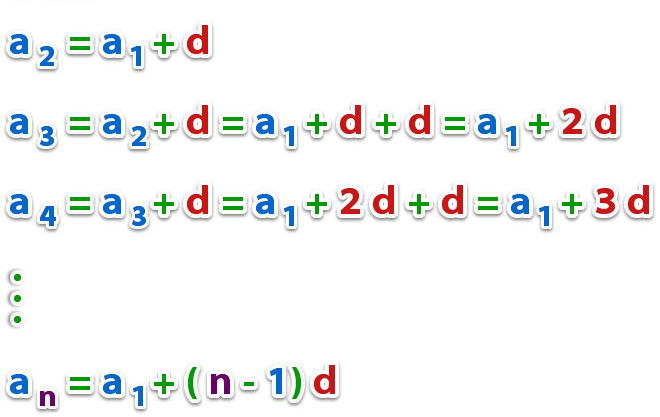
Условия многих задач составляются таким образом, что по известной паре чисел, номера которых в последовательности также даны, необходимо восстановить весь числовой ряд (найти разность и первый элемент). Сейчас мы решим эту задачу в общем виде.

Итак, пусть даны два элемента с номерами n и m. Пользуясь полученной выше формулой, можно составить систему из двух уравнений:

a_n = a₁ + (n – 1) * d;

a_m = a₁ + (m – 1) * d

Для нахождения неизвестных величин воспользуемся известным простым приемом решения такой системы: вычтем попарно левую и правую части, равенство при этом останется справедливым. Имеем:

a_n = a₁ + (n – 1) * d;

a_n – a_m = (n – 1) * d – (m – 1) * d = d * (n – m)

Таким образом, мы исключили одну неизвестную (a₁). Теперь можно записать окончательное выражение для определения d:

d = (a_n – a_m) / (n – m), где n > m

Мы получили очень простую формулу: чтобы вычислить разность d в соответствии с условиями задачи, необходимо лишь взять отношение разностей самих элементов и их порядковых номеров. Следует обратить на один важный момент внимание: разности берутся между “старшим” и “младшим” членами, то есть n > m (“старший” – имеется в виду стоящий дальше от начала последовательности, его абсолютное значение может быть как больше, так и меньше более “младшего” элемента).

Выражение для разности d прогрессии следует подставить в любое из уравнений в начале решения задачи, чтобы получить значение первого члена.

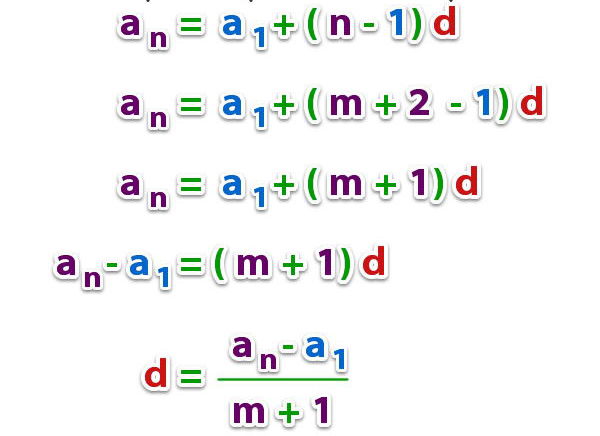
Далее в статье приведем примеры решения задач на вычисления d и на восстановление числового ряда алгебраической прогрессии. Здесь же хотелось бы отметить один важный момент.

В наш век развития компьютерных технологий многие школьники стараются найти решения для своих заданий в Интернете, поэтому часто возникают вопросы такого типа: найти разность арифметической прогрессии онлайн. По подобному запросу поисковик выдаст ряд web-страниц, перейдя на которые, нужно будет ввести известные из условия данные (это могут быть как два члена прогрессии, так и сумма некоторого их числа) и моментально получить ответ. Тем не менее такой подход к решению задачи является непродуктивным в плане развития школьника и понимания сути поставленной перед ним задачи.

Рекомендуется по указанным причинам самостоятельно решать подобные задачи. Кроме того, они не являются сложными.

Решение без использования формул

Решим первую задачу, при этом не будем использовать никакие из приведенных формул. Пусть даны элементы ряда: а6 = 3, а9 = 18. Найти разность прогрессии арифметической.

Известные элементы стоят близко друг к другу в ряду. Сколько раз нужно добавить разность d к наименьшему, чтобы получить наибольшее из них? Три раза (первый раз добавив d, мы получим 7-й элемент, второй раз – восьмой, наконец, третий раз – девятый). Какое число нужно добавить к трем три раза, чтобы получить 18? Это число пять. Действительно:

3 + 5 + 5 + 5 = 18

Таким образом, неизвестная разность d = 5.

Конечно же, решение можно было выполнить с применением соответствующей формулы, но этого не было сделано намеренно. Подробное объяснение решения задачи должно стать понятным и ярким примером, что такое арифметическая прогрессия.

Задача, подобная предыдущей

Теперь решим похожую задачу, но изменим входные данные. Итак, следует найти разность прогрессии арифметической, если а3 = 2, а9 = 19.

Конечно, можно прибегнуть снова к методу решения “в лоб”. Но поскольку даны элементы ряда, которые стоят относительно далеко друг от друга, такой метод станет не совсем удобным. А вот использование полученной формулы быстро приведет нас к ответу:

d = (а₉ – а₃) / (9 – 3) = (19 – 2) / (6) = 17 / 6 ≈ 2,83

Здесь мы округлили конечное число. Насколько это округление привело к ошибке, можно судить, проверив полученный результат:

a₉ = a₃ + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 = 18,98

Этот результат отличается всего на 0,1 % от значения, данного в условии. Поэтому использованное округление до сотых можно считать успешным выбором.

Задачи на применение формулы для an члена

Рассмотрим классический пример задачи на определение неизвестной d: найти разность прогрессии арифметической, если а1 = 12, а5 = 40.

Когда даны два числа неизвестной алгебраической последовательности, причем одним из них является элемент a₁, тогда не нужно долго думать, а следует сразу же применить формулу для a_n члена. В данном случае имеем:

a₅ = a₁ + d * (5 – 1) => d = (a₅ – a₁) / 4 = (40 – 12) / 4 = 7

Мы получили точное число при делении, поэтому нет смысла проверять точность рассчитанного результата, как это было сделано в предыдущем пункте.

Решим еще одну аналогичную задачу: следует найти разность арифметической прогрессии, если а1 = 16, а8 = 37.

Используем аналогичный предыдущему подход и получаем:

a₈ = a₁ + d * (8 – 1) => d = (a₈ – a₁) / 7 = (37 – 16) / 7 = 3

Что еще следует знать о прогрессии арифметической

Помимо задач на нахождение неизвестной разности или отдельных элементов, часто необходимо решать проблемы суммы первых членов последовательности. Рассмотрение этих задач выходит за рамки темы статьи, тем не менее для полноты информации приведем общую формулу для суммы n чисел ряда:

∑ⁿ_{i = 1}(a_i) = n * (a₁ + a_n) / 2

Содержание:

Числовые ряды:

При решении ряда математических задач, в том числе и в приложениях математики в экономике, приходится рассматривать суммы, составленные из бесконечного множества слагаемых. Из теории действительных чисел известно лишь, что означает сумма любого конечного числа чисел. Задача суммирования бесконечного множества слагаемых решается в теории рядов.

Основные понятия. Сходимость ряда

Определение. Числовым рядом называется бесконечная последовательность чисел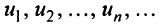

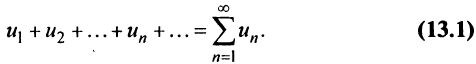
Числа 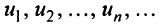называются членами ряда, а член 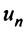— общим или 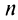-м членом ряда.

Ряд (13.1) считается заданным, если известен его общий член 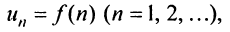т.е. задана функция 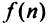натурального аргумента. Например, ряд с общим членом 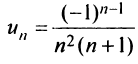имеет вид

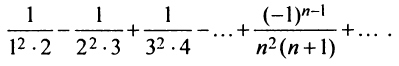
Более сложной является обратная задача: по нескольким первым членам ряда написать общий член. Эта задача имеет бесконечно много решений, но иногда удается найти самое естественное решение.

Пример:

Найти в простейшей форме общий член ряда:

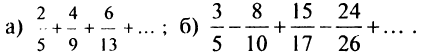
Решение:

Нетрудно убедиться, что для ряда а) общий член 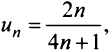а для ряда б)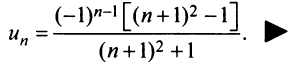

Рассмотрим суммы конечного числа членов ряда:

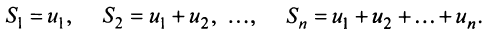
Сумма п первых членов ряда 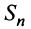называется 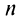-й частичной суммой ряда.

Определение. Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм, т.е.

Число 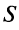называется суммой ряда. В этом смысле можно записать

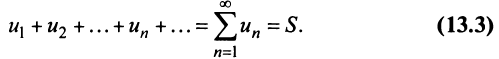
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

Пример:

Исследовать сходимость геометрического ряда, т.е. ряда, составленного из членов геометрической профессии

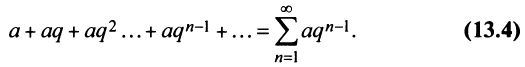
Решение:

Необходимо установить, при каких значениях знаменателя профессии 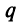ряд (13.4) сходится и при каких — расходится.

Из школьного курса алгебры известно, что сумма 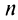первых членов геометрической профессии, т.е. 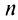-я частичная сумма ряда при 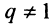равна

Возможно несколько случаев:

1) если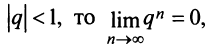

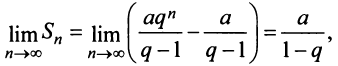т.е. ряд сходится и его сумма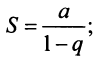

2) если 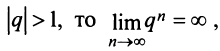следовательно, 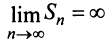и ряд расходится;

3) если 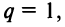то ряд (13.4) примет вид 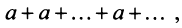его 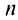-я частичная сумма 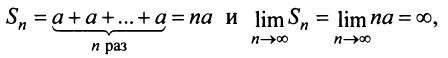т.е. ряд расходится;

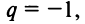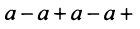
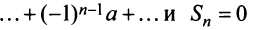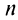4) если то ряд (13.4) примет вид при четном 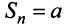и — при 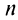нечетном, следовательно, 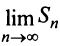не существует, и ряд расходится.

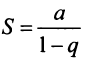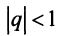Таким образом, геометрический ряд сходится к сумме при и расходится при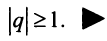

Пример:

Найти сумму ряда

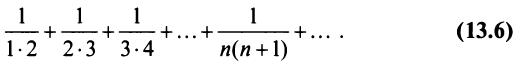
Решение:

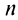-я частичная сумма ряда

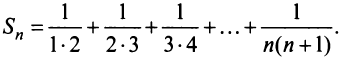Учитывая, что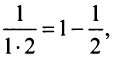

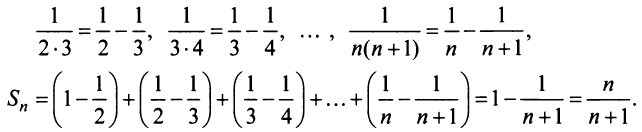Отсюда 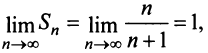т.е. сумма ряда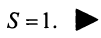

Свойства сходящихся рядов. 1. Если ряд сходится и имеет сумму 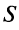, то и ряд 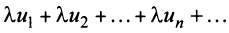(полученный умножением данного ряда на число 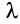) также сходится и имеет сумму .

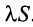2. Если ряды 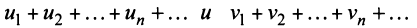сходятся и их суммы соответственно равны 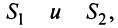то и ряд 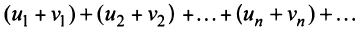(представляющий сумму данных рядов) также сходится, и его сумма равна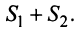

Свойства 1 и 2 непосредственно вытекают из свойств пределов числовых последовательностей.

3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.

Пусть в сходящемся ряде (13.1) отброшены 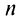членов (в принципе можно отбрасывать члены с любыми номерами, лишь бы их было конечное число). Покажем, что полученный ряд

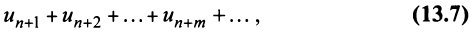
имеющий частичную сумму 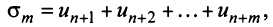также сходится.

Очевидно, что 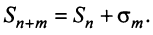Отсюда следует, что при фиксированном 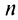конечный предел 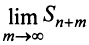существует тогда и только тогда, когда существует конечный предел 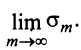. А это и означает, что ряд (13.7) сходится. ■

Ряд (13.7), полученный из данного отбрасыванием его первых 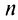членов, называется 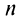-м остатком ряда.

Если сумму 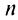-го остатка ряда обозначить через 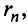т.е.

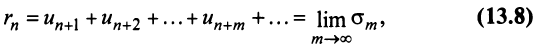
то сумму ряда (13.1) можно представить в виде

В результате мы подошли к свойству 4.

4. Для того чтобы ряд (13.1) сходился, необходимо и достаточно, чтобы при 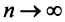остаток ряда стремился к нулю, т.е. чтобы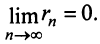

Это свойство вытекает из теоремы о связи бесконечно малых с пределами функций (см. § 6.3).

Установить сходимость (расходимость) ряда путем определения 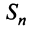и вычисления 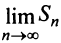(как это сделано в примерах 13.2, 13.3) возможно далеко не всегда из-за принципиальных трудностей при нахождении 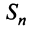(суммировании 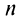членов ряда). Проще это можно сделать на основании признаков сходимости, к изучению которых мы переходим.

Необходимый признак сходимости. Гармонический ряд

Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена 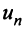при 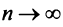равен нулю, т.е.

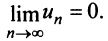
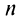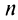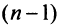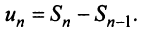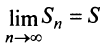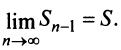Выразим -й член ряда через сумму его и членов, т.е. Так как ряд сходится, то и Поэтому

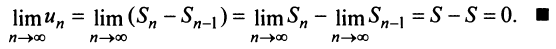
Пример №1

Проверить выполнение необходимого признака для ряда (13.6).

Решение:

Выше было доказано, что ряд (13.6) сходится, и действительно 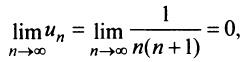т.е. необходимый признак сходимости выполняется. ►

Следствие. Если предел общего члена ряда (13.1) при 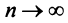не равен нулю, т.е. 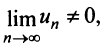то ряд расходится.

Предположим противное, т.е. ряд (13.1) сходится. Но в этом случае из приведенной выше теоремы следует 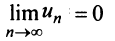, что противоречит условию, заданному в следствии, т.е. ряд (13.1) расходится. ■

Пример №2

Исследовать сходимость ряда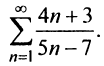

Решение:

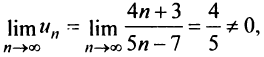т.е. необходимый признак сходимости не выполняется, следовательно, ряд расходится. ►

Замечание. Следует подчеркнуть, что рассмотренная теорема выражает лишь необходимый, но недостаточный признак сходимости ряда. Если 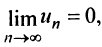то из этого еще не следует, что ряд сходится.

В качестве примера рассмотрим ряд

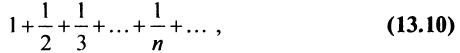
называемый гармоническим.

Необходимый признак сходимости выполнен: 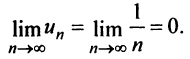Докажем, что, несмотря на это, гармонический ряд расходится.

Вначале получим вспомогательное неравенство. С этой целью запишем сумму первых 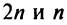членов ряда:

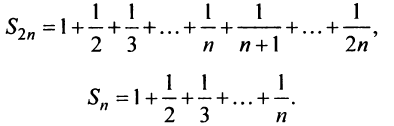
Найдем разность

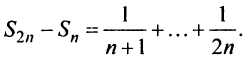
Заменяя в сумме каждое слагаемое наименьшим, равным 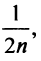придем к вспомогательному неравенству

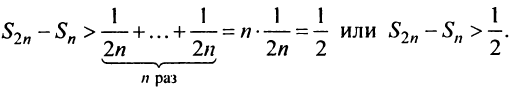
Предположим противное, т.е. что гармонический ряд сходится, тогда 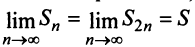и, переходя к пределу в неравенстве (см. § 6.5), получим, что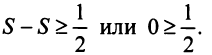

Мы пришли к противоречию, следовательно, наше предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится. ■

В следующих двух параграфах рассмотрим достаточные признаки сходимости.

Ряды с положительными членами

Теорема (признак сравнения). Пусть даны два ряда с положительными членами: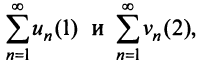 причем члены первого ряда не превосходят членов второго, т.е. при любом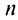

Тогда: а) если сходится ряд 2, то сходится и ряд 1; б) если расходится ряд 1, то расходится и ряд 2.

а) Пусть частичные суммы рядов 1 и 2 соответственно равны 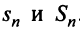. По условию ряд 2 сходится, следовательно, существует 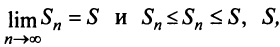так как члены ряда 2 положительны. Рассмотрим последовательность частичных сумм 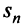ряда 1. Эта последовательность является: возрастающей (так как с ростом 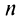увеличивается сумма 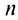положительных слагаемых) и ограниченной (так как 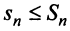в силу условия (13.11), т.е. ).

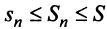Следовательно, на основании признака существования предела (см. § 6.5) последовательность 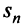имеет предел, т.е. ряд 1 сходится.

б) Применим метод доказательства от противного. Предположим, что ряд 2 сходится. Тогда согласно первой части теоремы сходится и ряд 1, что противоречит предположению; т.е. ряд 2 расходится. ■

Замечание. Так как сходимость ряда не изменяется при отбрасывании конечного числа членов ряда, то условие (13.11) не обязательно должно выполняться с первых членов рядов и только для членов с одинаковыми номерами 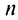. Достаточно, чтобы оно выполнялось, начиная с некоторого номера 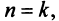или чтобы имело место неравенство 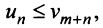где 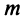— некоторое целое число.

Пример №3

Исследовать сходимость ряда

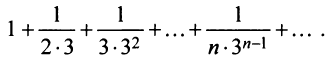
Решение:

Сравним данный ряд со сходящимся геометрическим рядом 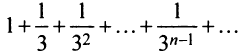(его знаменатель ).

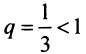Так как члены данного ряда, начиная со второго, меньше членов сходящегося геометрического ряда 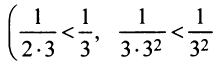и вообще 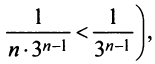то на основании признака сравнения ряд сходится. ►

Пример №4

Исследовать сходимость ряда

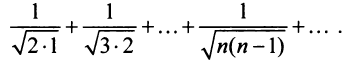
Решение:

Сравним данный ряд с гармоническим 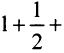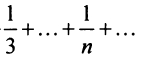, мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на расходимость ряда). Так как 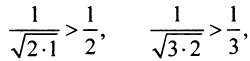и вообще 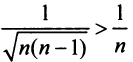(ибо 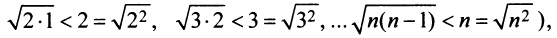т.е. члены данного ряда больше членов расходящегося гармонического ряда, то на основании признака сравнения ряд расходится. ►

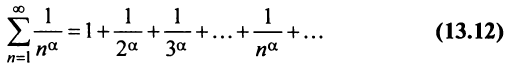
сходится при 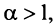расходится при 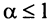здесь же отметим, что при 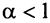расходимость ряда (13.12) следует из признака сравнения, так как в этом случае члены ряда 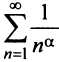больше соответствующих членов гармонического ряда 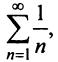а в частном случае при 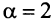сходимость ряда (13.12) может быть доказана сравнением этого ряда со сходящимся (13.6)).

Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (13.11), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т.п.). В ряде случаев более простым оказывается предельный признак сравнения.

Теорема (предельный признак сравнения)

Теорема (предельный признак сравнения). Если 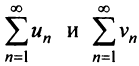— ряды с положительными членами и существует конечный предел отношения их общих членов 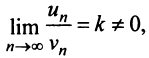то ряды одновременно сходятся либо расходятся.

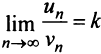Так как , то по определению предела числовой последовательности (см. § 6.1) для любого 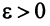существует такой номер 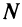, что для всех 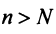выполняется неравенство

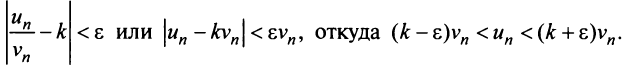
Если ряд 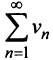сходится, то сходится ряд 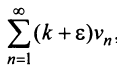и в силу признака сравнения будет сходиться ряд 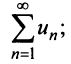аналогично, если сходится ряд 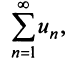сходится ряд 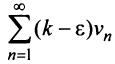и сходится 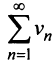. Таким образом, из сходимости одного ряда следует сходимость другого. Утверждение теоремы о расходимости рядов доказывается аналогично. 

Пример №5

Исследовать сходимость ряда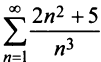

Решение:

Сравним данный ряд с расходящимся гармоническим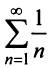 (выбор такого ряда для сравнения может подсказать то, что при больших 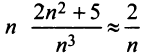). Так как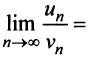 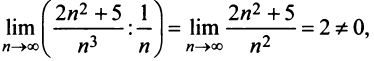то данный ряд, так же как и гармонический, расходится. ►

Весьма удобным на практике является признак Даламбера.

Теорема (признак Даламбера)

Теорема (признак Даламбера). Пусть для ряда 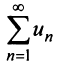с положительными членами существует предел отношения 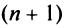-го члена к 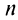-му члену 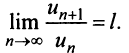Тогда, если 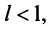то ряд сходится; если 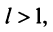то ряд расходится; если 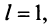то вопрос о сходимости ряда остается нерешенным.

 Из определения предела последовательности следует, что для любого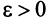 существует такой номер 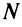, что для всех 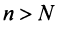выполняется неравенство 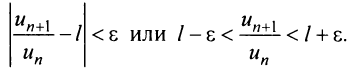1) Пусть 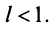Выберем 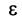настолько малым, что число

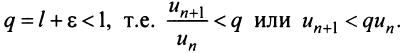
Последнее неравенство будет выполняться для всех 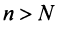, т.е. для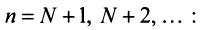

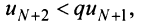
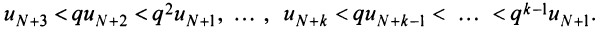
Получили, что члены ряда 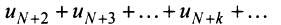меньше соответствующих членов геометрического ряда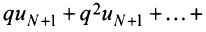 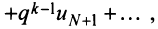сходящегося при 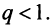Следовательно, на основании признака сравнения этот ряд сходится, а значит, сходится и рассматриваемый ряд 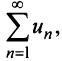отличающийся от полученного на первые 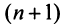членов.

2) Пусть 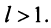Возьмем 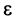настолько малым, что 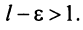Тогда из условия 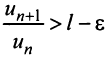следует, что 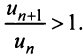Это означает, что члены ряда возрастают, начиная с номера 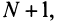поэтому предел общего члена ряда не равен нулю, т.е. не выполнен необходимый признак сходимости, и ряд расходится. ■

Пример №6

Исследовать сходимость рядов:

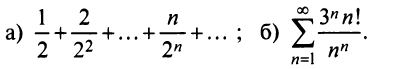
Решение:

а) Так как 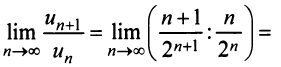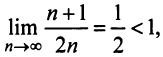то по признаку Даламбера ряд сходится.

б) Так как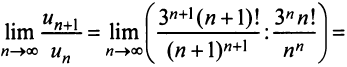

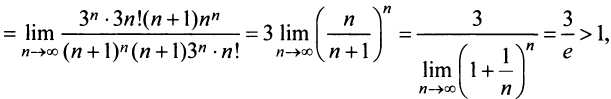то по признаку Даламбера ряд расходится. ►

Замечание 1. Если 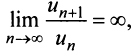то ряд расходится.

Замечание 2. Если 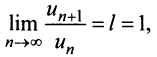то, как отмечалось выше, признак Даламбера ответа о сходимости ряда не дает, и рекомендуется перейти к другим признакам сходимости.

Теорема (интегральный признак сходимости)

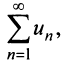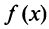Теорема (интегральный признак сходимости). Пусть дан ряд члены которого положительны и не возрастают, т.е.а функция , определенная при 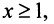непрерывная и невозрастающая и

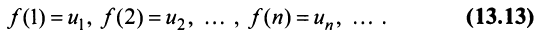
Тогда для сходимости ряда 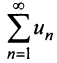необходимо и достаточно, чтобы сходился несобственный интеграл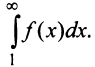

Рассмотрим ряд

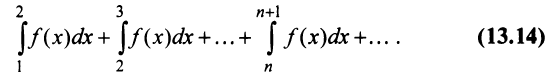
Его 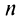-й частичной суммой будет

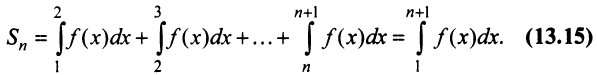
Сходимость ряда (13.14) означает существование предела последовательности его частичных сумм (13.15), т.е. сходимость несобственного интеграла 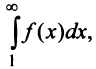поскольку 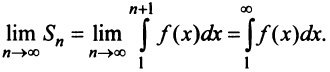В силу монотонности функции 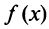на любом отрезке 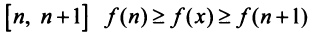или, учитывая (13.13),

Интегрируя (13.16) на отрезке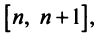 получим

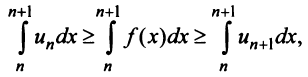
откуда

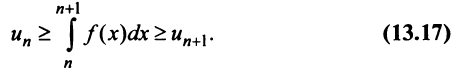
Если ряд 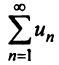сходится, то по признаку сравнения рядов в силу первого неравенства (13.17) должен сходиться ряд (13.14), а значит, и несобственный интеграл 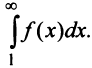Обратно, если сходится J/(jc)c&, т.е. ряд (13.14), то согласно тому же признаку сравнения на основании второго неравенства (13.17) будет сходиться ряд 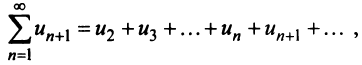а следовательно, и данный ряд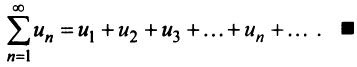

Пример №7

Исследовать сходимость обобщенного гармонического ряда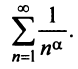

Решение:

Пусть 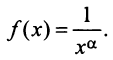Функция 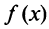при 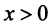(а значит, и при 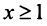) положительная и невозрастающая (точнее убывающая). Поэтому сходимость ряда равносильна сходимости несобственного интеграла 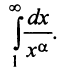Имеем 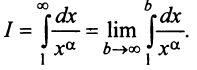Если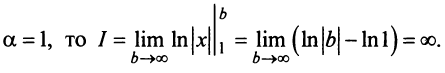

Если 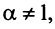то

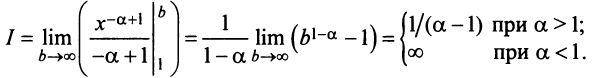Итак, данный ряд сходится при 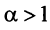и расходится при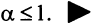

Ряды с членами произвольного знака

Знакочередующиеся ряды. Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны

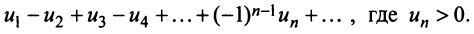
Теорема (признак Лейбница). Если члены знакочередующегося ряда убывают по абсолютной величине 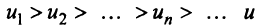и предел его общего члена при 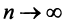равен нулю, т.е.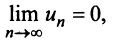то ряд сходится, а его сумма не превосходит первого члена: .

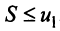 Рассмотрим последовательность частичных сумм четного числа членов при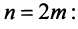

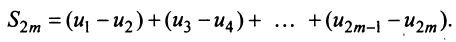
Эта последовательность возрастающая (так как с ростом 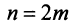увеличивается число положительных слагаемых в скобках) и ограниченная (это видно из того, что 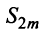можно представить в виде

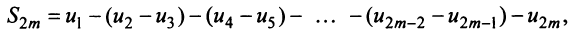
откуда следует, что 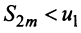). На основании признака существования предела (см. § 6.5) последовательность 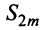имеет предел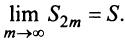

Попутно заметим, что, переходя к пределу в неравенстве 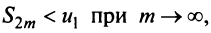получим, что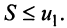

Теперь рассмотрим последовательность частичных сумм нечетного числа членов при 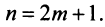Очевидно, что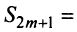 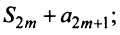поэтому, учитывая необходимый признак сходимости ряда,

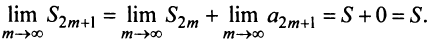
Итак, при любом 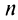(четном или нечетном) 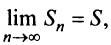т.е. ряд сходится. Рис. 13.1 иллюстрирует сходимость 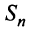к числу 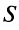слева при четном 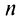и справа при нечетном . ■

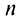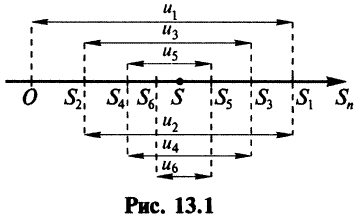
Из рис. 13.1 вытекает еще одна оценка для суммы 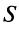сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница: при любом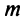

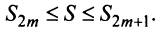
Пример №8

Исследовать сходимость ряда

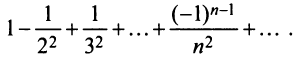
Решение:

Так как члены знакочередующегося ряда убывают по абсолютной величине 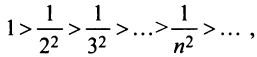и предел общего члена 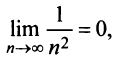то по признаку Лейбница ряд сходится. ►

Замечание. В теореме Лейбница существенно не только условие 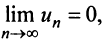но и условие 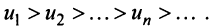Так, например, для ряда ,

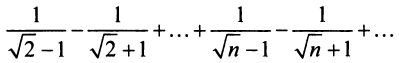второе условие нарушено и, хотя 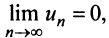ряд расходится. Это видно, если данный ряд представить (после попарного сложения его членов) в виде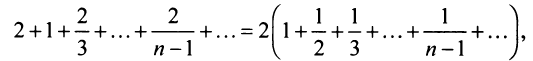

т.е. «удвоенного» гармонического ряда.

Следствие. Погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда, удовлетворяющего условиям теоремы Лейбница, по абсолютной величине не превышает абсолютной величины первого отброшенного члена.

По формуле (13.9) сумму сходящегося ряда можно представить как сумму 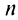членов ряда и суммы 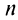-гo остатка ряда, т.е. 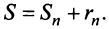Полагая приближенно 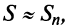мы допускаем погрешность, равную 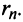Так как при четном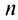 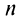-й остаток знакочередующегося ряда 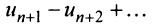представляет ряд, удовлетворяющий условиям теоремы Лейбница, то его сумма 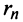не превосходит первого члена 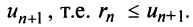Так как при нечетном 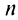для 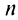-го остатка ряда 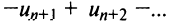его сумма 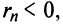то, очевидно, что при любом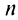

Пример №9

Какое число членов ряда 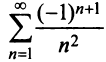надо взять, чтобы вычислить его сумму с точностью до 0,001?

Решение:

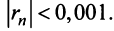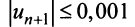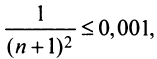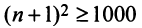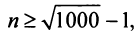По условию Учитывая следствие теоремы Лейбница (13.18), запишем более сильное неравенство или откуда и или 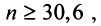т.е. необходимо взять не менее 31 члена ряда. ►

Знакопеременные ряды. Пусть знакопеременный ряд (13.1), в котором любой его член 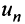может быть как положительным, так и отрицательным.

Теорема (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов данного ряда (13.1)

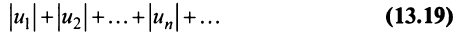
сходится, то сходится и данный ряд.

 Обозначим 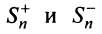суммы абсолютных величин членов данного ряда (13.1), входящих в него со знаком «плюс» и «минус».

Тогда частичная сумма данного ряда 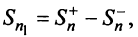а ряда, составленного из абсолютных величин его членов, 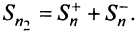По условию ряд (13.19) сходится, следовательно, существует конечный предел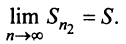

Последовательности 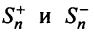являются возрастающими (так как с увеличением 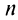увеличиваются 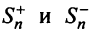) и ограниченными

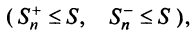значит, существуют пределы 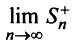и 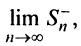и соответственно предел частичной суммы данного ряда

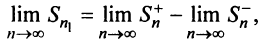т.е. ряд (13.1) сходится. ■

Следует отметить, что обратное утверждение неверно. Ряд (13.19) может расходиться, а ряд (13.1) сходиться. Например, ряд 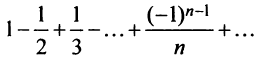сходится по признаку Лейбница, а ряд из абсолютных величин его членов 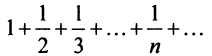(гармонический ряд) расходится.

Поэтому введем следующие определения.

Определение 1. Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.

Определение 2. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Таким образом, рассмотренный выше ряд 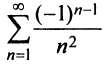— абсолютно сходящийся, а ряд 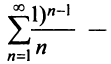условно сходящимся.

Грубо говоря, различие между абсолютно сходящимися и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся — в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.

Свойства абсолютно и условно сходящихся рядов существенно отличаются. Абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы, их можно складывать, перемножать, переставлять местами члены ряда.

Условно сходящиеся ряды такими свойствами не обладают.

Возьмем, например, ряд 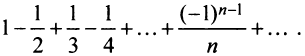Переставим члены местами и сгруппируем их следующим образом:

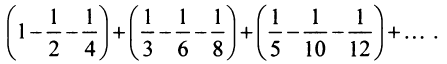
Перепишем ряд в виде:

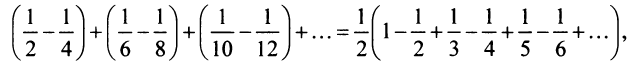
т.е. от перестановки членов ряда сумма его уменьшилась в 2 раза.

Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.

Пример №10

Найти сумму ряда 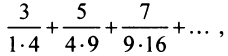доказав его сходимость.

Решение:

Очевидно, что общий член ряда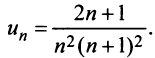

Представим сумму 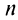членов ряда в виде 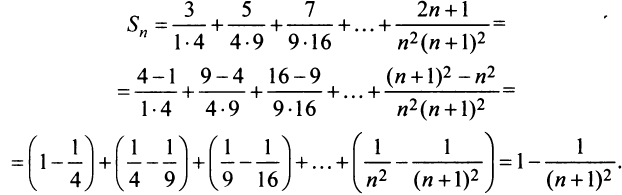Так как при 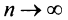последовательность 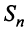имеет конечный предел, то ряд сходится, и его сумма

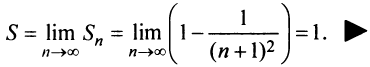
Пример №11

Исследовать сходимость ряда:

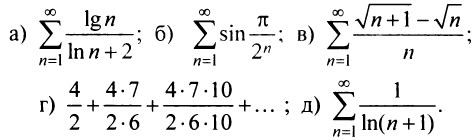
Решение:

а) Проверим выполнение необходимого признака сходимости, найдя предел общего члена:

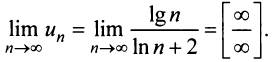
Для вычисления предела отношения двух бесконечно больших функций натурального аргумента правило Лопиталя непосредственно применять нельзя, ибо для таких функций не определено понятие производной. Поэтому применяя теорему о «погружении» дискретного аргумента 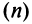в непрерывный 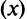, получим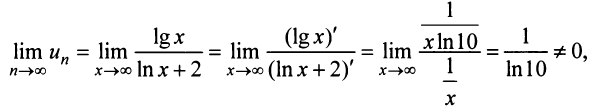

следовательно, ряд расходится.

б) Очевидно, что задан ряд с положительными членами, так как 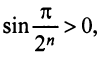ибо аргумент синуса 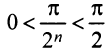при любом 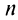. Так как члены данного ряда меньше членов сходящегося геометрического ряда со знаменателем

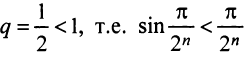(ибо при 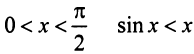), то данный ряд сходится.

в) Представим общий член ряда в виде

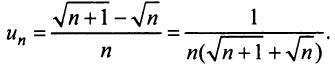Применим предельный признак сравнения, сравнив данный ряд со сходящимся «эталонным» рядом (13.12) при 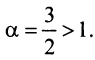Так как предел отношения общих членов двух рядов

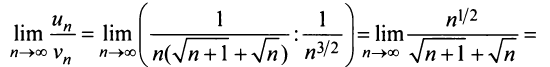
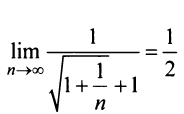
есть конечное число, не равное нулю, то данный ряд, так же как и «эталонный», сходится.

г) Применим признак Даламбера, заметив, что общий член ряда 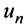имеет вид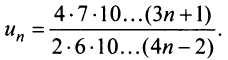

Тогда 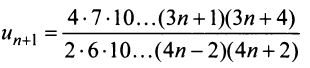и 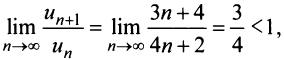т.е. данный ряд сходится.

д) Применим признак Даламбера:

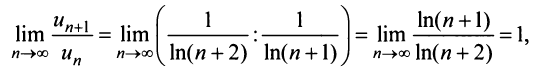
т.е. вопрос о сходимости ряда остается открытым. Проверим выполнение необходимого признака (с этого можно было начать исследование): 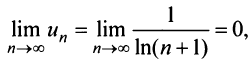т.е. необходимый признак выполнен, но вопрос о сходимости ряда по-прежнему не решен.

Применим признак сравнения в более простой предельной форме. Сравним данный ряд, например, с гармоническим.

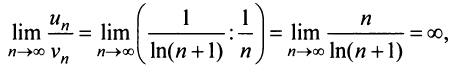т.е. ответа о сходимости ряда нет. Аналогичная картина ( 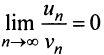или 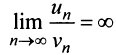) наблюдается и при использовании других «эталонных» рядов (см. § 13.3). Применим, наконец, признак сравнения в обычной форме. Сравним данный ряд с тем же гармоническим рядом, у которого отброшен первый член:

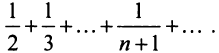Так как члены рассматриваемого ряда больше членов расходящегося гармонического ряда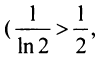 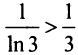и вообще

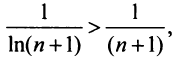что вытекает из очевидного неравенства 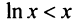), то данный ряд расходится. ►

Пример №12

Исследовать сходимость ряда:

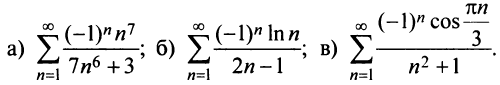
Решение:

а) Предел общего члена ряда 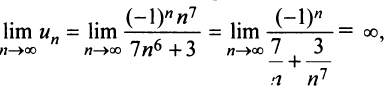так как знаменатель дроби стремится к нулю, а числитель колеблется, принимая значения 1 (при четном 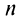) и —1 (при нечетном 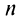). Следовательно, необходимый признак сходимости не выполнен, и ряд расходится.

б) Так как члены знакочередующегося ряда, начиная со второго, убывают по абсолютной величине —

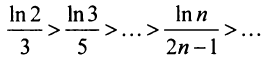
и предел общего члена 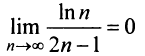(это можно установить, например, с помощью правила Лопиталя), то по признаку Лейбница ряд сходится. Ряд 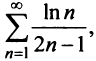составленный из абсолютных величин членов данного ряда, расходится, так как его члены больше членов расходящегося гармонического ряда, умноженного на 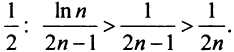Следовательно, данный ряд условно сходящийся.

в) Ряд, составленный из абсолютных величин членов данного ряда, сходится, так как его члены меньше членов сходящегося ряда (13.12) при 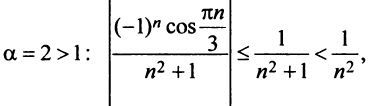следовательно, данный ряд сходится и притом абсолютно. ►

Определение ряда и его сходимость

Пусть

бесконечная последовательность чисел.

Определение 27.1.1. Выражение

называется числовым рядом, а элементы последовательности 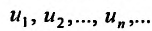членами ряда.

Поскольку выражение (27.1.2) рассматривается как единое целое, то для задания ряда необходимо задать каждый его член 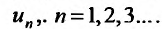Обычно член ряда задается как некоторая функция от своего номера. Аналитическое выражение этой функции называют общим членом ряда. Например, общим членом ряда геометрической прогрессии 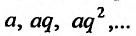является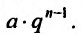

Припишем теперь определенный смысл выражению (27.1.2), т.е. введем определение.

Определение 27.1.2. Сумма n первых членов ряда (27.1.2) 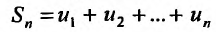называется n-ой частичной суммой этого ряда.

Ясно, что первая, вторая, третья и т.д. частичные суммы ряда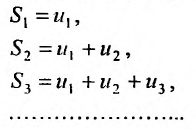

составляют бесконечную последовательность: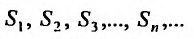

Определение 27.1.3. Ряд (27.1.2) называется сходящимся, если последовательность 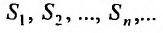его частичных сумм имеет конечный предел: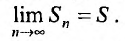

Значение S этого предела называется суммой ряда (27.1.2). Ряд (27.1.2) называется расходящимся, если последовательность его частичных сумм предела не имеет (например, если члены последовательности возрастают по модулю неограниченно).

Содержание теории числовых рядов состоит в установлении сходимости или расходимости тех или иных рядов и в вычислении сумм сходящихся рядов.

В принципе можно доказывать сходимость или расходимость каждого ряда, а также вычислять сумму сходящегося ряда, опираясь непосредственно на определения сходимости и суммы. Для этого в каждом случае составляется аналитическое выражение для n- ой частичной суммы ряда и находится предел этого выражения при возрастании n.

Пример:

Для ряда 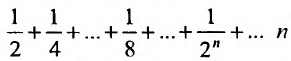-я частичная сумма 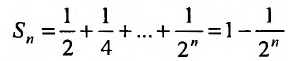, и предел ее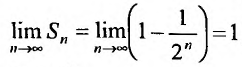, поэтому этот ряд сходится и его сумма равна 1.

Пример:

Последовательность вида

называется геометрической прогрессией, где а – первый член, а

q – её знаменатель; выражение 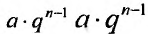называется общим членом геометрической прогрессии.

Числовой ряд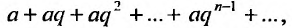 члены которого являются членами геометрической прогрессии, называется геометрическим рядом со знаменателем q .

Если в прогрессии (27.1.3) имеется только конечное число членов, то прогрессия называется конечной; в противном случае, если за каждым членом прогрессии следует ещё хотя бы один член, то прогрессия называется бесконечной.

В случае конечной прогрессии 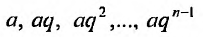можно говорить о сумме всех её членов 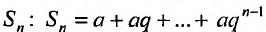, которую можно назвать n- ой частичной суммой геометрического ряда.

Известно, что при 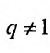, эта сумма равна 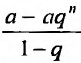. Из определения 27.1.3 следует, что суммой геометрического ряда

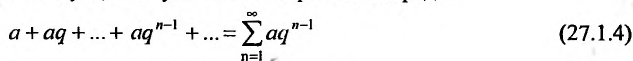
называется предел её частичных сумм 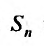при неограниченном возрастании n:

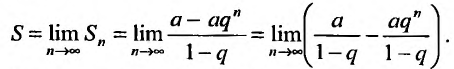
Так как а и q от n не зависят, то последнюю формулу представим в виде:

Если 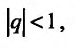то предел 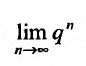равен нулю, и мы получаем

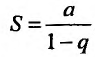, т.е. при 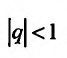прогрессия (27.1.5) сходится. Следователь-

но, сходится и ряд (27.1.4). Если же 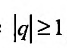, то предел справа в равенстве (27.1.5) не существует и, следовательно, ряд (27.1.4) расходится.

Итак, мы привели примеры, в которых исследование сходимости рядов проводили, применяя определение 27.1.3., т.е. вычисляли частичные суммы и находили предел их последовательностей. Ясно, что в общем случае, составление аналитического выражения для n- ой частичной суммы трудный вопрос. Кроме того, при исследовании рядов нередко значения сумм не представляют интереса, т.к. нужно определить только сходится ряд или нет. Поэтому представляют интерес методы анализа рядов, когда не требуется вычислять суммы рядов. Далее перейдем к изложению таких методов.

Свойства сходящихся рядов

Пусть дан ряд

Определение 27.2.1. Ряд 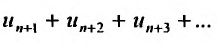называется n-м остатком ряда (27.2.1.)

Очевидно, m- я частичная суммаn -го остатка ряда равна разности 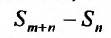частичных сумм самого ряда. Кроме того, 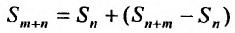, откуда, переходя к пределу по m при 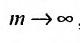, получим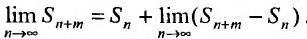

Предел слева есть сумма исходного ряда, а предел справа-сумма его n – го остатка: 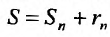. Ясно, что из существования предела в левой части равенства следует существование другого предела в правой части и наоборот. Поэтому если сходится один из остатков ряда, то сходится и сам ряд. Точно так же из сходимости ряда следует сходимость каждого его остатка. Кроме того, справедлива следующая теорема.

Теорема 27.2.1. Если ряд (27.2.1) сходится, то сумма его n-го остатка с ростом n стремится к нулю.

Доказательство. Выше показано, что 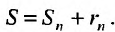. Так как это равенство справедливо для любого n, то мы можем перейти в нем по n к пределу: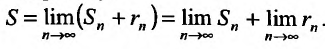

Но для сходящегося ряда 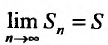, поэтому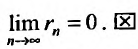

Рассмотрим теперь свойства сходящихся рядов, которые позволяют действовать с ними, как с конечными суммами.

Теорема 27.2.2. Если ряд

имеет сумму S, то ряд

полученный из предыдущего умножением всех членов на одно и тоже число a, имеет сумму aS.

Доказательство. Обозначим последовательность частичных сумм ряда (27.2.2) 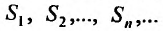Тогда последовательность частичных сумм ряда (27.2.3) очевидно будет иметь вид: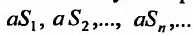. И поэтому 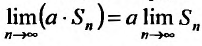. Так как ряд

(27.2.2) сходится, то 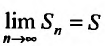существует и, следовательно, существует предел 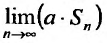ив силу этого же равенства он равен aS.

Теорема 27.2.3. Если ряды

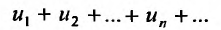и 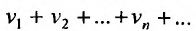сходятся, а их суммы соответственно равны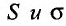, то и ряд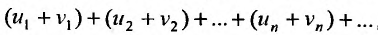называемый суммой данных рядов, также сходится и его сумма равна сумме сумм данных рядов 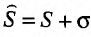, другими словами, сходящиеся ряды можно почленно складывать.

Доказательство. Пусть 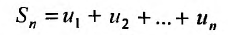и

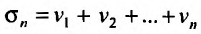. Тогда n -ая частичная сумм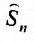а ряда

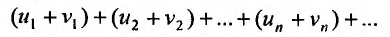будет равна 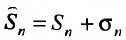и так как 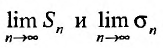существуют, то

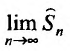существует и равен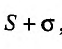, т.е.

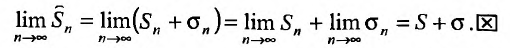
Следствие. Разность двух сходящихся рядов-ряд сходящийся.

Теорема 27.2.4. Свойства сходимости или расходимости ря-,ki не нарушается, если в ряде исключить или приписать к нему любое конечное число членов.

Доказательство. Пусть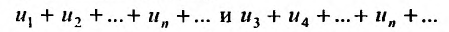 два ряда, причём второй получается из первого исключением первых двух членов. Тогда, если 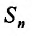– n-я частичная сумма первого ряда, а 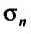– n-я частичная сумма второго ряда, то, очевидно, что

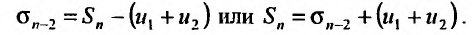
Из этого равенства следует, что, если 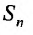имеет предел, то 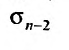также имеет предел. Ясно, что эти пределы будут различны, а, именно 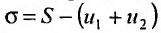Если же 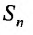не имеет предела, то 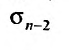также не имеет предела.

Теорема 27.2.5. (Необходимое условие сходимости ряда). Если ряд 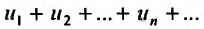сходится, то его общий член стремится к нулю, т.е.

Доказательство. Пусть ряд 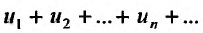сходится и его сумма равна S. Из определения n -ой частичной суммы следует, что общий член ряда можно представить в виде разности и-ой частичной суммы и (n-1)-ой частичной суммы: 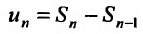. Переходя к пределу в этом равенстве, получим утверждение теоремы:

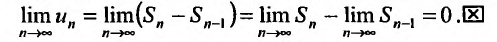
Отметим, что условие (27.2.4) не является достаточным, т.е. общий член может стремиться к нулю, но ряд все же может быть расходящимся. Но если общий член ряда не стремится к нулю, то ряд будет расходящийся.

• Заказать решение задач по высшей математике

Пример №13

Исследуем на сходимость гармонический ряд

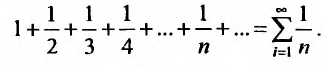
Решение:

Вначале находим предел общего члена: 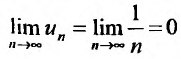. Нетрудно, однако, показать, что сумма n первых членов гармонического ряда беспредельно возрастает. Для этого сгруппируем слагаемые, начиная со второго, в группы из 1, 2, 4, 8,… членов: 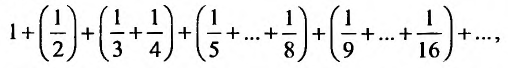так что в k – ой группе будет 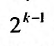членов. Fx л и в каждой групп заменим все члены последним, то получим ряд:

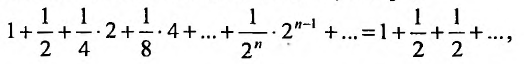сумма n первых членов которого, равна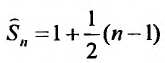, очевидно, стремится к :

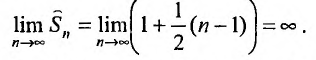Но сумма n первых членов заданного гармонического ряда больше суммы n первых членов преобразованного ряда, т.е. 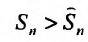. Тогда 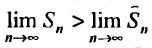, что означает, что 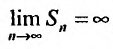следовательно, гармонический ряд расходится.

Пример №14

Найти формулу для общего члена ряда

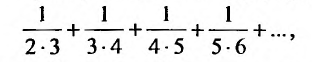
считая, что каждый его последующий член определяется по тому же закону, по которому образованы записанные члены, и найти ею сумму.

Решение:

Каждый член данного ряда представляет собой дробь, числитель которой равен 1, а знаменатель равен произведению двух последовательных натуральных чисел 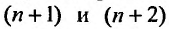. Следовательно, искомая формула общего члена ряда имеет вид:

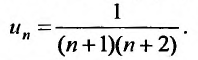
Для вычисления суммы ряда составим n -ую частичную сумму:

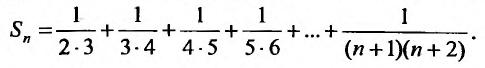
Представим выражение для общего члена в виде разности:

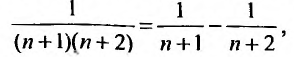
тогда

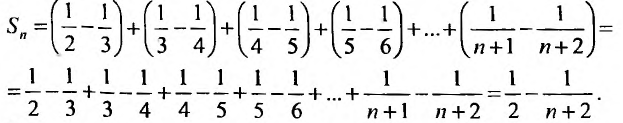
Переходя к пределу, получаем сумму ряда:

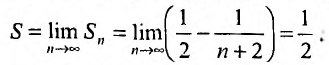
Пример №15

Исследовать сходимость ряда

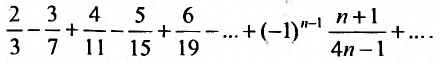
Решение:

Общий член ряда определяется формулой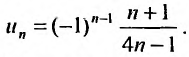

Вычислим предел модуля общего члена: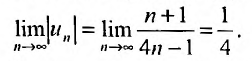

Так как предел общего члена не стремится к нулю, то ряд расходится.

Признаки сходимости числовых знакоположительных рядов

Рассмотрим числовые ряды с положительными членами. Существует много приёмов, называемых признаками сходимости, позволяющих установить сходимость или расходимость числовых рядов Так мы познакомились с методом исследования сходимости ряда на основании выяснения имеет ли предел последовательность частичных сумм. Стремление к нулю члена ряда по мерс роста его номера также является признаком сходимости, хотя только необходимым. Ниже мы приведём ряд достаточных признаков сходимости.

Признаки сравнения

Теорема 27.3.1. (I признак сравнения). Пусть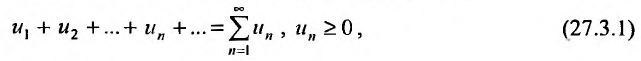

и

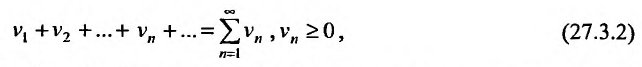
два ряда, причём члены первого ряда, начиная с некоторого номера k , не превосходят соответствующих членов второго

Тогда из сходимости ряда (27.3.2) следует сходимость ряда (27.3.1), а из расходимости ряда (27.3.1) следует расходимость ряда (27.3.2).

Доказательство. Так как исключение конечного числа членов ряда не влияет на его сходимость (теорема 27.2.4.), то достаточно доказать теорему для случая когда неравенства (27.3.3) выполняются для k = 1.

Пусть 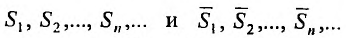последовательности частичных сумм рядов (27.3.1) и (27.3.2) соответственно. Это возрастающие последовательности, так как члены рядов неотрицательные числа. В силу неравенств (27.3.3), имеем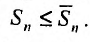

Пусть ряд (27.3.2) сходится. Тогда сходится соответствующая последовательность частичных сумм ряда (27.3.2), т.е.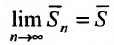

Поскольку выполняются неравенства (27.3.3), то члены последовательности частичных сумм ряда (27.3.1) удовлетворяют неравенству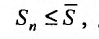 для всех т. Следовательно, последовательность 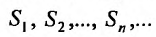возрастает и ограничена: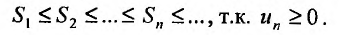

Поэтому, в силу признака Больцано-Всйсрштраса, последовательность частичных сумм ряда (27.3.1) сходится. По определению 27.1.3, сходится и ряд (27.3.1).

Пусть теперь ряд (27.3.1) расходится. Это значит, что его частичные суммы неограниченно возрастают. Но тогда, в силу неравенств (27.3.3), неограниченно возрастают и частичные суммы ряда (27.3.2), что означает, что этот ряд расходится. 

Пример №16

Пусть дан ряд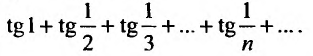

Исследуем его сходимость.

Решение:

Необходимый признак выполняется, т.е.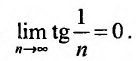

Для исследования сходимости заданного ряда применим 1 признак

сравнения (теорему 27.3.1). Сравним заданный ряд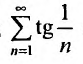с гармоничсским рядом 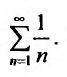. Так как выполняются неравенства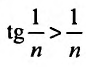то ряд 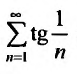расходится, потому что расходится гармонический ряд.

Пример №17

Исследовать сходимость ряда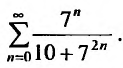

Решение:

Очевидно, что предел общего члена при возрастании т стремится к нулю.

Сравним данный ряд, общий член которого 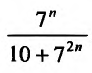с гармоническим рядом 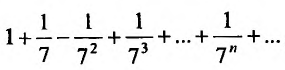который сходится, так как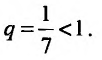

Поскольку 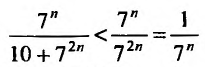для 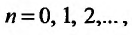т.е. выполняются неравенства (27.3.3), то на основании первого признака сравнения заключаем, что исследуемый ряд также сходится.

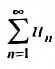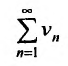Теорема 27.3.2. (II признак сравнения). Если для рядов и отношение общих членов 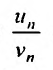стремится к некоторому положительному и конечному пределу:

то ряды 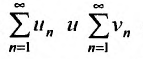сходятся или расходятся одновременно.

Доказательство. Предельное соотношение (27.3.4), в силу определения 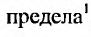означает, что, начиная с некоторою номера N ,

выполняется неравенство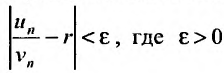. Это неравенство равносильно неравенству:

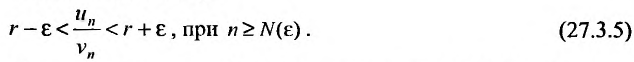
Обозначив 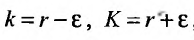, неравенство (27.3.5) запишется в виде:

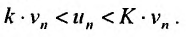
Предположим, что ряд 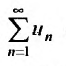сходится. Поскольку выполняется неравенство 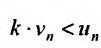то, из первого признака сравнения, следует сходимость ряда 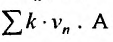в силу теоремы 27.2.2, и ряда 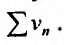. Если же ряд 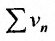расходится, то расходится и ряд 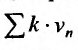по теореме 27.2.2. Тогда, поскольку выполняется неравенство 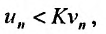, расходится и ряд 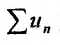в силу I признака сравнения. Аналогично рассуждая можно показать, что из сходимости ряда 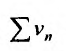следует сходимость ряда 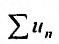по I признаку сравнения с использованием теоремы 27.2.2. 13

Последовательность 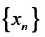называется сходящейся, если существует такое вещественное число а , что для любого положительного числа 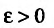найдется номер 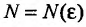такой, что для всех 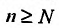выполняется неравенство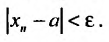

Пример №18

Исследовать сходимость ряда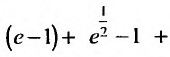

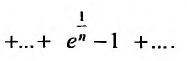
Решение:

Очевидно, что 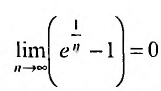. Поэтому, воспользуемся признаком сравнения, сравнив заданный ряд с гармоническим. Найдем предел отношения общих членов исследуемого ряда и гармонического:

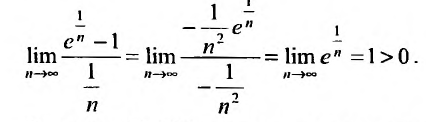
Теорема 27.3.2 выполняется, поэтому из расходимости гармонического ряда 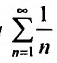следует расходимость исследуемого ряда.

Признаки Д’Аламбсра и Коши

Иногда вместо признаков сравнения оказываются полезными некоторые специальные признаки сходимости ряда. Отметим среди них признаки Д’Аламбсра и Коши, непосредственно получающиеся из признаков сравнения, если в качестве ряда сравнения взять соответствующим образом выбранную геометрическую прогрессию.

Теорема 27.3.3. (признак Д’Аламбера). Если для ряда

с положительными членами существует такой номер 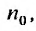, начиная с которого, т.е. при 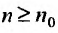, отношение последующего члена к предыдущему удовлетворяет неравенству: 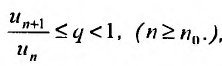, то ряд (27.3.6) сходится. Если же существует номер 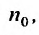, начиная с которого, т.е. при 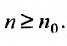отношение последующего члена к предыдущему больше единицы: 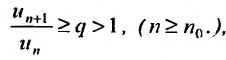то ряд (27.3.6) расходится.

Доказательство. Пусть 0 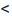q 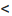1 и пусть существует такой номер , что при 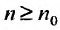. выполняется неравенство: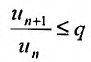Перепишем это неравенство в виде: 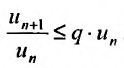. Тогда, начиная с номера 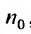буду последовательно выполнятся неравенства:

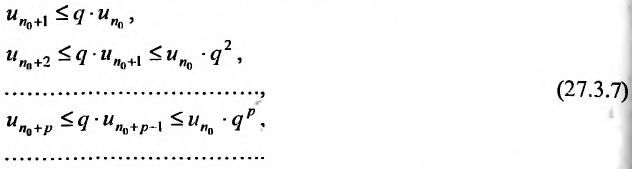
Ряд 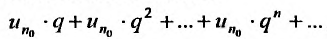, являясь суммой член геометрической прогрессии со знаменателем 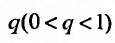, сходите Из неравенств (27.3.7) следует, что по I признаку сравнения, сходится и ряд 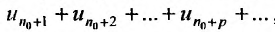значит и весь ряд (27.3.6

т.к. на сходимость ряда не влияет исключение конечного числа е^ членов.

Если же существует такое 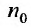, что выполняется неравенств 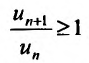для всех 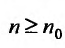, то, переписав его в виде 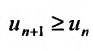, можно для всех 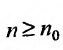, последовательно записать следующие неравенство

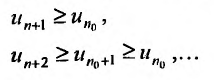
Так как по предположению 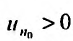, то n-ный член ряда будучи ограниченным снизу положительной постоянной не стремится к нулю. Следовательно, не выполняется необходимое условие сходимости ряда, и поэтому ряд (27.3.6) расходится.

Следствие 1. Пусть существует предел отношения последующего члена ряда (27.3.6) к предыдущему равный r :

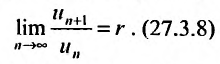
Тогда, если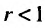 то ряд (27.3.6) сходится: если же 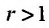то ряд (21.3.6) расходится.

Доказательство. Воспользовавшись определением предела, для фиксированного 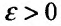, можно утверждать, что начиная с некоторого номера 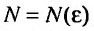, для всех 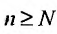, все отношения 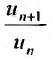будут отличатся от значения предела r на число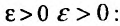

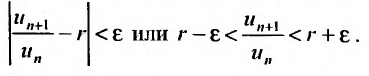
Рассмотрим правую часть двойного неравенства: 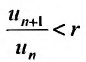. Тогда сославшись на доказанную теорему 27.3.3, в случае если r 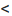1, получаем сходимость ряда. Рассматривая левую часть неравенства

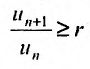, получаем расходимость ряда приr > 1. Следствие доказано.

Пример №19

Рассмотрим ряд , сходимость которого исследуем, используя признак Даламбера, т.е. следствие 1.

Решение:

Выпишем вначале значения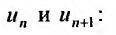

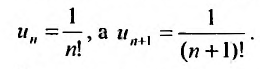
Затем вычислим предел отношения последующего члена ряда к предыдущему:

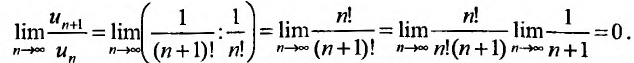
Так как этот предел меньше 1, то, в силу следствия 1, данный ряд сходится.

Заметим, что при исследовании сходимости ряда обычно (как правило, но не всегда) применяют следствие 1 из теоремы 27.3.3.

Теорема 27.3.4. (признак Kouiu). Если для ряда

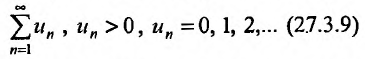
с положительными членами, начиная с некоторого номера 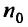. выполняется неравенство 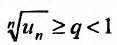для всех 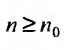, то ряд (27.3.6) сходится. Если же существует такой номер 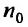, начиная с которого выполняется неравенство 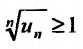для всех 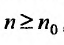, то данный ряд расходится.

Доказательство. Пусть существует такой номер 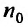, что при всех 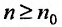выполняется неравенство 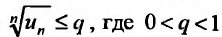Тогда, возводя обе части неравенства в степень n, получим 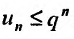. Так как сходится геометрический ряд 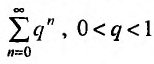, то на основании признака сравнения, получаем, что ряд 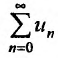сходится. Если же существует номер 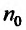, такой что 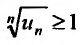для всех 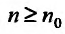, то ясно, что 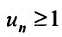, и значит 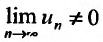(не выполняется необходимый признак сходимости), поэтому ряд 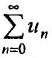расходится.

Следствие 2. Пусть существует предел корня n -ой степени из n-го члена ряда (27.3.9):

Тогда, если 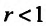, то ряд (27.3.9) сходится, если же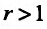, то ряд (27.3.9) расходится.

Доказательство. Из определения предела следует, что для фиксированного 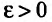существует номер 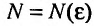, начиная с которого выполняется неравенство 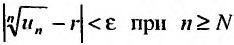Это неравенство равносильно неравенству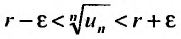. Из правой части неравенства следует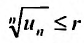, поскольку 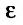сколь угодно малое число. Тогда из теоремы 27.3.4, получаем сходимость ряда (27.3.9). Рассматривая левую часть неравенства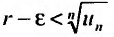, получим 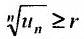и если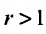, то из теоремы 27.3.4 следует расходимость ряда (27.3.9). Следствие доказано.

Пример №20

Рассмотрим ряд 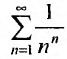, сходимость которого исследуем по признаку Коши, т.е. применим следствие 2.

Решение:

Выпишем значение n-го члена ряда 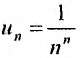н вычислим предел корня n -ой степени: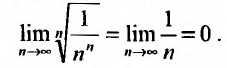

Так как этот предел меньше 1, то, согласно следствию 2, ряд сходится.

Замечание. Если пределы (27.3.8) и (27.3.10) равны 1, то для исследования сходимости ряда (27.3.9) нужно применять другие признаки, с которыми можно ознакомиться в [3].

Интегральный признак сходимости

Рассмотрим признак, достоинство которого состоит в исключительно высокой его чувствительности. Этим признаком проводится исследование сходимости там, где сформулированные признаки Д’Аламбсра и Коши «не работают».

Каждый член числового ряда 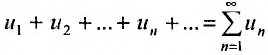можно рассматривать как значение функции f от его номера:

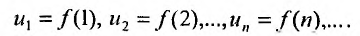
Эта функция определена пока только для целых положительных значений аргумента. Поэтому, доопределив значение функции f для всех нецелых значений аргумента, больших единицы, мы сможем, говорить о функции f(x), принимающей значения для любого 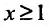и при х = n, равные членам числового ряда. Теорема 27.3.5. Пусть дан ряд

члены которого положительны и не возрастают 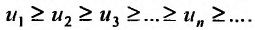Если функция f, определённая для всех 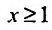, неотрицательна и монотонно убывает, то ряд (27.3.11) сходится или расходится тогда и только тогда, когда сходится или

расходится интеграл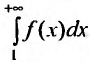

Доказательство. Пусть члены ряда (27.3.11) удовлетворяют условиям теоремы. Изобразим их графически, откладывая по оси Ох независимую переменную, а по оси Оу – соответствующие значения .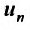

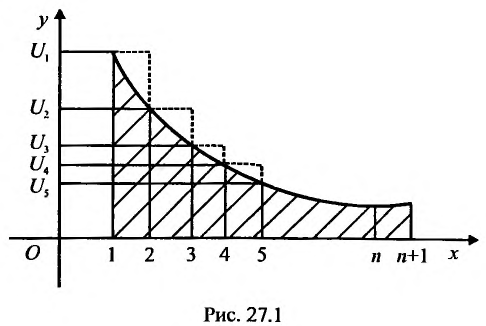
При таком графическом изображении сумма n первых членов ряда 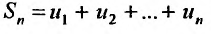представляет сумму площадей описанных прямоугольников, которая заключает внутри себя площадь, ограниченной кривой 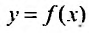, осью Ох и прямыми 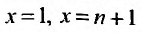и поэтому будет выполняться неравенство:

С другой стороны, криволинейная трапеция содержит сумму площадей вписанных прямоугольников, которая равна 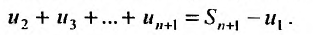Поэтому, выполняется неравенство:

Из (27.3.12) и (27.3.13) следует неравенство:

Предположим, что несобственный интеграл 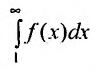сходится. Это означает, что 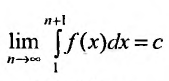является конечным числом. Тогда из неравенства (27.3.14) следует, что последовательность частичных сумм 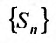возрастающая и ограничена при всех n. Тогда в силу теоремы: “возрастающая последовательность, ограниченная сверху, сходится”, числовой ряд (27.3.11) сходится. Если же несобствснный интеграл 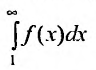расходится, т.е. 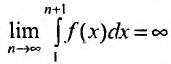, то из неравенства (27.3.12) следует, что последовательность частичных сумм 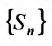не ограничена. Тогда в силу определения 27.1.3 ряд будет расходящимся.

Пример №21

Исследовать сходимость ряда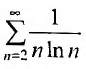

Решение:

Применим интегральный признак. Рассмотрим функцию 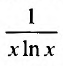которая положительна и убывает при х> 2, и исследуем сходимость несобственного интеграла:

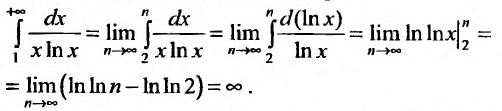
Так как несобственный интеграл расходится, то расходится и ряд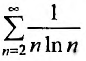 в силу инте1рального признака Коши.

Замечание. Исследовать сходимость данного ряда при помощи следствий 1 и 2 не представляется возможным, так как соответствующие пределы равны 1.

Пример №22

Исследовать сходимость ряда Дирихле

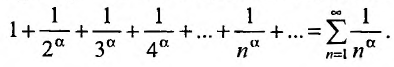
Решение:

Если 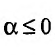, то общий член ряда 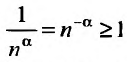не стремится к нулю. На основании следствия из необходимого признака сходимости, следует расходимость ряда Дирихле при .

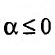Пусть а > 0, тогда необходимый признак, очевидно, выполняется. Применим интегральный признак Коши. Введем функцию

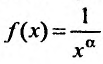, которая положительная и не возрастает при 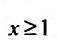и исследуем сходимость несобственного интеграла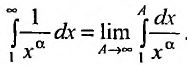

Вычислим определенный интеграл, записанный под знаком предела:

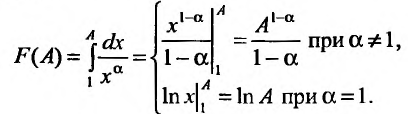
Если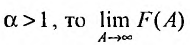 существует и равен 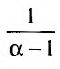а при 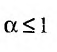указанный предел не существует.

Таким образом, при a>1 несобственный интеграл 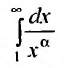сходится, следовательно, сходится и ряд Дирихле, а при 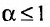несобственный интеграл расходится, следовательно, расходится и ряд Дирихле.

Среднее арифметическое, размах, мода и медиана

1. Алгебра
2. Среднее арифметическое, размах, мода и медиана