Следующее действие, которое можно выполнять с обыкновенными дробями, – вычитание. В рамках этого материала мы рассмотрим, как правильно вычислить разность дробей с одинаковыми и разными знаменателями, как вычесть дробь из натурального числа и наоборот. Все примеры будут проиллюстрированы задачами. Заранее уточним, что мы будем разбирать лишь случаи, когда разность дробей дает в итоге положительное число.
Как найти разность дробей с одинаковыми знаменателями
Начнем сразу с наглядного примера: допустим, у нас есть яблоко, которое разделили на восемь частей. Оставим пять частей на тарелке и заберем две из них. Это действие можно записать так:
58-28
В итоге у нас осталось 3 восьмых доли, поскольку 5−2=3. Получается, что 58-28=38.
Благодаря этому простому примеру мы увидели, как именно работает правило вычитания для дробей, знаменатели которых одинаковы. Сформулируем его.
Чтобы найти разность дробей с одинаковыми знаменателями, нужно из числителя одной вычесть числитель другой, а знаменатель оставить прежним. Это правило можно записать в виде ab-cb=a-cb.
Такую формулу мы будем использовать и в дальнейшем.
Возьмем конкретные примеры.
Вычтите из дроби 2415 обыкновенную дробь 1715.
Решение
Мы видим, что эти дроби имеют одинаковые знаменатели. Поэтому все, что нам нужно сделать, – это вычесть 17 из 24. Мы получаем 7 и дописываем к ней знаменатель, получаем 715.
Наши подсчеты можно записать так: 2415-1715=24-1715=715
Если необходимо, можно сократить сложную дробь или выделить целую часть из неправильной, чтобы считать было удобнее.
Найдите разность 3712-1512.
Решение
Воспользуемся описанной выше формулой и подсчитаем: 3712-1512=37-1512=2212
Легко заметить, что числитель и знаменатель можно разделить на 2 (об этом мы уже говорили ранее, когда разбирали признаки делимости). Сократив ответ, получим 116. Это неправильная дробь, из которой мы выделим целую часть: 116=156.
Как найти разность дробей с разными знаменателями
Такое математическое действие можно свести к тому, что мы уже описывали выше. Для этого просто приведем нужные дроби к одному знаменателю. Сформулируем определение:
Чтобы найти разность дробей, у которых разные знаменатели, необходимо привести их к одному знаменателю и найти разность числителей.
Рассмотрим на примере, как это делается.
Вычтите из 29 дробь 115.
Решение
Знаменатели разные, и нужно привести их к наименьшему общему значению. В данном случае НОК равно 45. Для первой дроби необходим дополнительный множитель 5, а для второй – 3.
Подсчитаем: 29=2·59·5=1045115=1·315·3=345
У нас получились две дроби с одинаковым знаменателем, и теперь мы легко можем найти их разность по описанному ранее алгоритму: 1045-345=10-345=745
Краткая запись решения выглядит так: 29-115=1045-345=10-345=745.
Не стоит пренебрегать сокращением результата или выделением из него целой части, если это необходимо. В данном примере нам этого не нужно делать.
Найдите разность 199 – 736.
Решение
Приведем указанные в условии дроби к наименьшему общему знаменателю 36 и получим соответственно 769 и 736.
Считаем ответ: 7636-736=76-736=6936
Результат можно сократить на 3 и получить 2312. Числитель больше знаменателя, а значит, мы можем выделить целую часть. Итоговый ответ – 11112.
Краткая запись всего решения – 199-736=11112.
Как вычесть из обыкновенной дроби натуральное число
Такое действие также легко свести к простому вычитанию обыкновенных дробей. Это можно сделать, представив натуральное число в виде дроби. Покажем на примере.
Найдите разность 8321 – 3.
Решение
3 – то же самое, что и 31. Тогда можно подсчитать так: 8321-3=2021.
Если в условии необходимо вычесть целое число из неправильной дроби, удобнее сначала выделить из нее целое, записав ее в виде смешанного числа. Тогда предыдущий пример можно решить иначе.
Из дроби 8321 при выделении целой части получится 8321=32021.
Теперь просто вычтем 3 из него: 32021-3=2021.
Как вычесть обыкновенную дробь из натурального числа
Это действие делается аналогично предыдущему: мы переписываем натуральное число в виде дроби, приводим обе к единому знаменателю и находим разность. Проиллюстрируем это примером.
Найдите разность: 7-53.
Решение
Сделаем 7 дробью 71. Делаем вычитание и преобразуем конечный результат, выделяя из него целую часть: 7-53=513.
Есть и другой способ произвести расчеты. Он обладает некоторыми преимуществами, которыми можно воспользоваться в тех случаях, если числители и знаменатели дробей в задаче – большие числа.
Если та дробь, которую нужно вычесть, является правильной, то натуральное число, из которого мы вычитаем, нужно представить в виде суммы двух чисел, одно из которых равно 1. После этого нужно вычесть нужную дробь из единицы и получить ответ.
Вычислите разность 1 065 -1362.
Решение
Дробь, которую нужно вычесть – правильная, ведь ее числитель меньше знаменателя. Поэтому нам нужно отнять единицу от 1065 и вычесть из нее нужную дробь: 1065-1362=(1064+1)-1362
Теперь нам нужно найти ответ. Используя свойства вычитания, полученное выражение можно записать как 1064+1-1362. Подсчитаем разность в скобках. Для этого единицу представим как дробь 11.
Получается, что 1-1362=11-1362=6262-1362=4962.
Теперь вспомним про 1064 и сформулируем ответ: 10644962.
Используем старый способ, чтобы доказать, что он менее удобен. Вот такие вычисления вышли бы у нас:
1065-1362=10651-1362=1065·621·62-1362=6603062-1362==66030-1362=6601762=106446
Ответ тот же, но подсчеты, очевидно, более громоздкие.
Мы рассмотрели случай, когда нужно вычесть правильную дробь. Если она неправильная, мы заменяем ее смешанным числом и производим вычитание по знакомым правилам.
Вычислите разность 644 – 735.
Решение
Вторая дробь – неправильная, и от нее надо отделить целую часть.
735=1435
Теперь вычисляем аналогично предыдущему примеру: 630-35=(629+1)-35=629+1-35=629+25=62925
Свойства вычитания при работе с дробями
Те свойства, которыми обладает вычитание натуральных чисел, распространяются и на случаи вычитания обыкновенных дробей. Рассмотрим, как использовать их при решении примеров.
Найдите разность 244-32-56.
Решение
Схожие примеры мы уже решали, когда разбирали вычитание суммы из числа, поэтому действуем по уже известному алгоритму. Сначала подсчитаем разность 254-32, а потом отнимем от нее последнюю дробь:
254-32=244-64=194194-56=5712-1012=4712
Преобразуем ответ, выделив из него целую часть. Итог – 31112.
Краткая запись всего решения:
254-32-56=254-32-56=254-64-56==194-56=5712-1012=4712=31112
Если в выражении присутствуют и дроби, и натуральные числа, то рекомендуется при подсчетах сгруппировать их по типам.
Н айдите разность 98+1720-5+35.
Решение
Зная основные свойства вычитания и сложения, мы можем сгруппировать числа следующим образом: 98+1720-5+35=98+1720-5-35=98-5+1720-35
Завершим расчеты: 98-5+1720-35=93+1720-1220=93+520=93+14=9314
Содержание:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
- Вычитание смешанных дробей
Определение
Вычитание дробей является действием, обратным к
сложению. Вычесть из одной дроби другую –
это означает найти такую третью дробь, которая в сумме со второй дробью дает первую.
Вычитание дробей с одинаковыми знаменателями
Чтобы вычесть дроби с одинаковыми знаменателями, нужно от
числителя первой дроби отнять числитель второй, а
знаменатель оставить без изменений.
Пример
Задание. Найти разность дробей
$frac{10}{11}$ и $frac{7}{11}$
$$frac{10}{11}-frac{7}{11}=frac{10-7}{11}=frac{3}{11}$$
Ответ. $frac{10}{11}-frac{7}{11}=frac{3}{11}$
Вычитание дробей с разными знаменателями
Чтобы вычислить дроби с разными знаменателями, нужно вначале привести их к наименьшему
общему знаменателю, а затем отнимать их как дроби с одинаковым знаменателем.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Вычесть дроби $frac{2}{5}$ и $frac{1}{3}$
Решение. Заданные дроби имеют разные знаменатели, приводим их к общему, который равен 15 (как НОК знаменателей 5 и 3),
тогда дополнительные множители соответственно к первой дроби –
$15:5=3$ , ко второй – $15:3=5$ . Получаем:
$$frac{2}{5}-frac{1}{3}=frac{2^{3}}{5}-frac{1^{5}}{3}=frac{2 cdot 3-1 cdot 5}{15}=frac{6-5}{15}=frac{1}{15}$$
Ответ. $frac{2}{5}-frac{1}{3}=frac{1}{15}$
Вычитание смешанных дробей
Чтобы вычесть одно смешанное число из другого смешанного числа, надо, если это возможно, от целого отнять целое, а от дроби отнять дробь.
Пример
Задание. Найти разность $6 frac{7}{11}-2 frac{1}{22}$
Решение. Выполним вычитание по описанному выше правилу
$$6 frac{7}{11}-2 frac{1}{22}=(6-2)+left(frac{7^{2}}{11}-frac{1}{22}right)=$$
$$=4+frac{7 cdot 2-1 cdot 1}{22}=4+frac{14-1}{22}=4+frac{13}{22}=4 frac{13}{22}$$
Ответ. $6 frac{7}{11}-2 frac{1}{22}=4 frac{13}{22}$
В случае, когда дробь вычитаемого больше, чем дробь уменьшаемого, поступают следующим образом: берут одну единицу
(целое) из целого числа уменьшаемого, записывают его как неправильную дробь, числитель и знаменатель которой равны между
собой и равны знаменателю дробной части, и прибавляют к дробной части, далее отнимают две смешанные дроби, как описано выше.
Пример
Задание. Выполнить вычитание $5 frac{4}{9}-1 frac{11}{12}$
Решение. Дробь $frac{4}{9}$ меньше (
сравнение дробей ), чем дробь $frac{11}{12}$ (так как $4 cdot 12 = 36 < 9 cdot 11 = 99$ ), тогда
$$5 frac{4}{9}-1 frac{11}{12}=5+frac{4}{9}-1 frac{11}{12}=4+1+frac{4}{9}-1 frac{11}{12}=$$
$$=4+frac{9}{9}+frac{4}{9}-1 frac{11}{12}=4 frac{9+4}{9}-1 frac{11}{12}=4 frac{13}{9}-1 frac{11}{12}=$$
$$=(4-1)+left(frac{13^{4}}{9}-frac{11^{3}}{12}right)=3+frac{13 cdot 4-11 cdot 3}{36}=$$
$$=3+frac{52-33}{36}=3+frac{19}{36}=3 frac{19}{36}$$
Ответ. $5 frac{4}{9}-1 frac{11}{12}=3 frac{19}{36}$
Аналогичным образом поступают, когда надо вычесть из целого числа дробное.
Пример
Задание. Найти разность
$4-3 frac{3}{5}$
Решение. Выполним вычитание дробей по описанному выше правилу
$$4-3 frac{3}{5}=3+1-3 frac{3}{5}=3+frac{5}{5}-3 frac{3}{5}=3 frac{5}{5}-3 frac{3}{5}=$$
$$=(3-3)+left(frac{5}{5}-frac{3}{5}right)=0+frac{5-3}{5}=frac{2}{5}$$
Ответ. $4-3 frac{3}{5}=frac{2}{5}$
Замечание. Производить операции со
смешанными числами можно и иначе: записать смешанное число в виде
неправильной дроби и уже работать далее как с
обыкновенными дробями.
Читать следующую тему: умножение дробей.
При вычитании дробей, как и при сложении, могут встретиться несколько случаев.
Вычитание дробей с одинаковыми знаменателями
При вычитании дробей с одинаковыми знаменателями от числителя уменьшаемого (первой дроби) отнимают
числитель вычитаемого (второй дроби), а знаменатель оставляют прежним.
Пример.
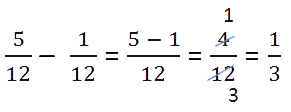
Запомните!
![]()
Прежде чем записать конечный ответ, проверьте, нельзя ли сократить полученную дробь.
В буквенном виде правило вычитания дробей с одинаковыми знаменателями
записывают так:
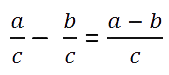
Вычитание правильной дроби из единицы
Когда нужно вычесть из единицы правильную дробь, единицу представляют в виде
неправильной дроби, знаменатель которой, равен знаменателю вычитаемой дроби.
Пример.
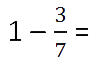
Знаменатель вычитаемой дроби равен 7, значит, единицу представляют как неправильную
дробь
и вычитают по правилу вычитания дробей с одинаковыми знаменателями.
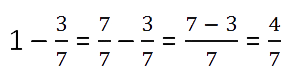
Вычитание правильной дроби из целого числа
Чтобы из целого числа вычесть правильную дробь нужно представить это натуральное число
в виде смешанного числа.
Для этого занимаем единицу в натуральном числе и представляем её в виде неправильной дроби,
знаменатель которой равен знаменателю вычитаемой дроби.
Пример.
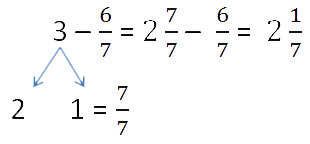
В примере единицу мы заменили неправильной дробью
и вместо 3 записали смешанное
число и от дробной части отняли дробь.
Вычитание смешанных чисел
При вычитании смешанных чисел отдельно из целой части вычитают целую часть, а из дробной части
вычитают дробную часть.
При подобных расчётах могут встретиться разные случаи.
Первый случай вычитания смешанных чисел
У дробных частей одинаковые знаменатели и числитель дробной части
уменьшаемого (из чего вычитаем) больше или равен числителю дробной части вычитаемого
(что вычитаем).
Пример.
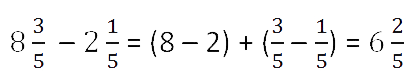
Второй случай вычитания смешанных чисел
У дробных частей разные знаменатели.
В этом случае вначале нужно
привести к общему знаменателю
дробные части, а затем
выполнить вычитание целой части из целой, а дробной из дробной.
Пример.
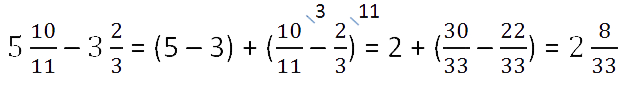
Третий случай вычитания смешанных чисел
Дробная часть уменьшаемого меньше дробной части вычитаемого.
Пример.
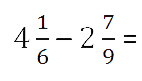
Так как у дробных частей разные знаменатели, то как и
во втором случае, вначале приведём обыкновенные дроби к общему знаменателю.
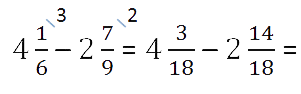
Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого.
3 < 14
Поэтому, вспомнив
вычитание правильной дроби из целого числа, займём единицу из целой части и представим
эту единицу в виде неправильной дроби с одинаковым знаменателем и числителем равным 18.
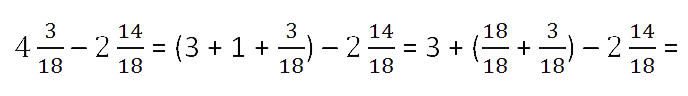
Сложим полученную неправильную дробь
и дробную часть
уменьшаемого и получим:
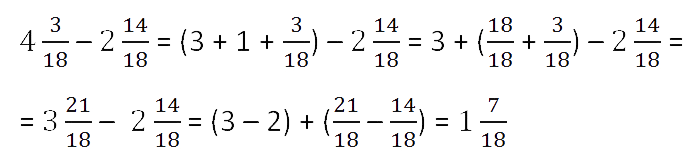
Все рассмотренные случаи можно описать с помощью правил вычитания
смешанных чисел.
- Привести дробные части уменьшаемого и вычитаемого к наименьшему общему знаменателю.
- Если дробная часть уменьшаемого меньше дробной части
вычитаемого, то занимаем у целой части уменьшаемого единицу. Эту единицу
превращаем в неправильную дробь с одинаковым числителем и знаменателем равными наименьшему общему знаменателю. - Прибавляем полученную неправильную дробь к дробной части уменьшаемого.
- Вычитаем из целой части целую, а из дробной — дробную.
- Проверяем, нельзя ли сократить и выделить целую часть в конечной дроби.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
13 ноября 2019 в 6:24
Валя Гутник

Профиль
Благодарили: 0
Сообщений: 7

Валя Гутник
Профиль
Благодарили: 0
Сообщений: 7
как вычитать дроби с разным знаменателем
−
0
Спасибо
Ответить
15 апреля 2020 в 13:34
Ответ для Валя Гутник
Саша Алекс

Профиль
Благодарили: 0
Сообщений: 1

Саша Алекс
Профиль
Благодарили: 0
Сообщений: 1
Хз
0
Спасибо
Ответить
18 марта 2019 в 18:37
Никита Рулькевич

Профиль
Благодарили: 0
Сообщений: 2

Никита Рулькевич
Профиль
Благодарили: 0
Сообщений: 2
0
Спасибо
Ответить
18 марта 2019 в 18:51
Ответ для Никита Рулькевич
Никита Рулькевич

Профиль
Благодарили: 0
Сообщений: 2

Никита Рулькевич
Профиль
Благодарили: 0
Сообщений: 2
11 ![]()
0
Спасибо
Ответить
4 сентября 2015 в 12:08
Зарина-И-Владимир Вебер

Профиль
Благодарили: 0
Сообщений: 1

Зарина-И-Владимир Вебер
Профиль
Благодарили: 0
Сообщений: 1
?12
? 7
? ?
?я незнаю ответ помогите пожалуста
0
Спасибо
Ответить
2 сентября 2016 в 14:33
Ответ для Зарина-И-Владимир Вебер
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Сначала — действие в скобках. Переводим в дробь целую часть, приводим к общему знаменателю, производим действие, далее производим умножение.
= (
?) · = · = = == 2=2,5
0
Спасибо
Ответить
7 апреля 2015 в 13:14
Женечка Беляевская

Профиль
Благодарили: 0
Сообщений: 1

Женечка Беляевская
Профиль
Благодарили: 0
Сообщений: 1
вычитание дроби из целого числа 9-
0
Спасибо
Ответить
8 апреля 2015 в 0:39
Ответ для Женечка Беляевская
Алёна Гермес

Профиль
Благодарили: 0
Сообщений: 2

Алёна Гермес
Профиль
Благодарили: 0
Сообщений: 2
9-3/4 = 9/1-3/4 = 36/4-3/4 = 33/4 = 8
Целое число представляем в виде дроби, затем приводим к общему знаменателю, путем умножения первой дроби на знаменаетль второй и знаменателя первой на вторую дробь. Получаем неправельную дробь, и превращаем её в правильную, делим 33 на 4 и получаем 8 и остаток от деления 1.
0
Спасибо
Ответить
14 апреля 2015 в 17:00
Ответ для Женечка Беляевская
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
9- = 8 — =8 =8
0
Спасибо
Ответить
6 апреля 2015 в 14:02
Алексей Старков

Профиль
Благодарили: 0
Сообщений: 1

Алексей Старков
Профиль
Благодарили: 0
Сообщений: 1
(1 — 1/2): (1/2 — 1/3) =
0
Спасибо
Ответить
7 апреля 2015 в 3:34
Ответ для Алексей Старков
Алёна Гермес

Профиль
Благодарили: 0
Сообщений: 2

Алёна Гермес
Профиль
Благодарили: 0
Сообщений: 2
1) (1 — 1/2) = 1/1 — 1/2 = 2/2 — 1/2 = 1/2
Находим общий заменатель, перемножая первую дробь на знаменатель второй, и вторую на знаменатель первой.
2) (1/2 — 1/3) = 3/6 — 2/6 = 1/6
Находим общий знаменатель.
3) 1/2: 1/6 = 1/2 · 6/1 = 6/2 =3/1 = 3
Что бы разделить одну дробь на другую, нужно перевернуть вторую дробь и разделить её на первую. Затем следует сократить дробь.
0
Спасибо
Ответить
14 апреля 2015 в 17:08
Ответ для Алексей Старков
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
(1- ): ( — )
1)
— =
2)
=
3)
– = =
0
Спасибо
Ответить
14 апреля 2015 в 17:10
Ответ для Алексей Старков
Asel Talantbekovna

Профиль
Благодарили: 0
Сообщений: 8

Asel Talantbekovna
Профиль
Благодарили: 0
Сообщений: 8
последнее дествие исправлю!
: =
0
Спасибо
Ответить
9 апреля 2019 в 17:24
Ответ для Алексей Старков
Настя Бородина

Профиль
Благодарили: 0
Сообщений: 1

Настя Бородина
Профиль
Благодарили: 0
Сообщений: 1
самый понятный овет
0
Спасибо
Ответить
Перед тем как перейти к сложению дробей, вспомним теоретические основы. Итак, дробь — это форма записи числа:
где a — числитель, b — знаменатель.
Дробь называется правильной — если числитель меньше знаменателя (к примеру, 1/3), неправильной — если числитель больше знаменателя (например, 5/2).
Вычитание обыкновенных дробей
Вычитание дробей — это арифметическое действие, в результате которого получается новое число, содержащее разность заданных чисел.
Разберем на конкретных примерах: как находить разность дробей с одинаковыми и разными знаменателями, как из натурального числа вычесть дробь и наоборот, познакомимся с вычитанием смешанных дробей.
Вычитание дробей с одинаковыми знаменателями
Чтобы вычесть дроби с одинаковыми знаменателями нужно из числителя первой дроби вычесть числитель второй, а знаменатели оставить без изменения. В общем виде это будет выглядеть следующим образом:
Пример 1:
7 8
—
2 8
Решение:
7 8
—
2 8
=
7 — 2 8
=
5 8
Таким образом, чтобы вычесть дроби с одинаковыми знаменателями нужно найти разность их числителей, а знаменатель оставить без изменения.
Как вычитать дроби с разными знаменателями
В общем виде, вычитание дробей с разными знаменателями, выглядит следующим образом:
a b
—
c d
=
a ∙ m1 — c ∙ m2 e
где e — наименьший общий знаменатель (НОЗ — наименьшее число, которое делится без остатка и на b и на d), m1 и m2 — дополнительные множители (m1 = e : b, m2 = e : d).
Пример 3:
5 3
—
2 7
Решение:
5 3
—
2 7
=
5 ∙ 7 21
—
2 ∙ 3 21
=
35 21
—
6 21
=
35 — 6 21
=
29 21
=
1
8 21
Подробнее про нахождение НОЗ — смотрите тут.
Как из целого числа вычесть дробь?
Вычитание обыкновенной дроби из целого числа, сводится к представлению целого числа в виде дроби, в которой знаменатель будет единицей, а числитель самим числом, к примеру:
Дальнейшее вычисление происходит по стандартному алгоритму.
Как из обыкновенной дроби вычесть целое число?
Порядок действий, при вычитании целого числа из дробного, аналогичен, т.е. представляем целое число в виде дроби со знаменателем — 1 и находим разность, согласно представленным выше алгоритмам вычитания.
Как вычитать смешанные дроби?
Вычитание смешанных дробей сводится к переводу их к неправильному виду и дальнейшим действиям согласно вышеописанным алгоритмам. Перевод смешанного числа в неправильную дробь, в общем виде, выглядит следующим образом:
Пример 4:
3
2 4
—
3 5
Решение:
3
2 4
—
3 5
=
3 ∙ 4 + 2 4
—
3 5
=
14 4
—
3 5
=
14 ∙ 5 20
—
3 ∙ 4 20
=
70 20
—
12 20
=
70 — 12 20
=
58 20
=
29 10
=
2
9 10
Правила вычитания дробей
Резюмируя вышесказанное, выведем общий алгоритм вычитания дробей:
- Если дробь смешанная — приводим её к неправильному виду;
- Если дроби имеют одинаковые знаменатели — из числителя первой дроби вычитаем числитель второй;
- Если дроби имеют разные знаменатели — находим НОЗ и дополнительные множители, находим разность числителей;
- При необходимости сокращаем и приводим к неправильному виду.
Смотрите также:
- Смотрите также
- Калькуляторы
- Последние примеры
Калькулятор вычитания дробей
Оцените материал:
![]() Загрузка…
Загрузка…
При нахождении наименьшего общего знаменателя при сложении (вычитании) обыкновенных дробей учащиеся часто поступают нерационально, принимая в качестве общего знаменателя произведение знаменателей исходных дробей.
Можно использовать следующий прием, использующий навык сокращения дробей
Пример 1. Найти сумму дробей с разными знаменателями
Составили дробь из знаменателей дробей слагаемых и после ее сокращения на 7 получили дополнительные множители к дробям слагаемым:
2 – дополнительный множитель к дроби со знаменателем 21,
3 – дополнительный множитель к дроби со знаменателем 14
Т.е. дополнительные множители соответствуют исходным знаменателям “крест-накрест”
Пример 2. Найти разность дробей с разными знаменателями
Составили дробь из знаменателей, сократили ее и получили дополнительные множители, которые соответствуют исходным знаменателям “крест-накрест”, как в пропорции
Способ можно применять для нахождения наименьшего общего кратного двух чисел (это очевидно, т.к. наименьший общий знаменатель является наименьшим общим кратным исходных знаменателей)
Пример 3. Найти наименьшее общее кратное
Составили дробь из чисел, для которых надо найти наименьшее общее кратное, сократили ее последовательно (сначала на 2, потом на 7, потом на 3) – получили несократимую дробь.
Числитель составленной дроби умножаем на знаменатель дроби после сокращения (84 умножаем на 3).
Знаменатель составленной дроби умножаем на числитель дроби после сокращения (126 умножаем на 2).
В обоих случаях получаем наименьшее общее кратное при условии, что получена именно несократимая дробь.
Алгоритм усложняется, если надо найти общий знаменатель трех и более дробей. В этом случае надо найти общий знаменатель первых двух дробей, потом найти общий знаменатель результата и следующей дроби и т.д.
Алгоритм можно применять также при сложении (вычитании) алгебраических дробей.
