Как найти разность векторов в пространстве - Сайт, где вы сможете решить свои вопросы

Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.

Определение

Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.

Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.

Доказательство:

В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.

Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.

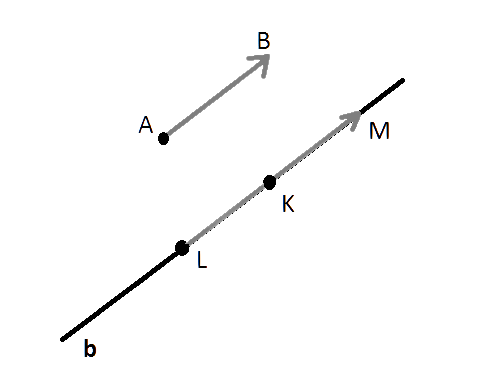
Единственность нашего вектора следует из того, что мы построили и видим.

Теорема доказана.

Определение

Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.

Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.

Разность векторов

Определение

Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.

По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т. е. вектор a.

Формулами это записывается так:

b + c = a

a – b = c

Как найти разность векторов аналитическим способом

В двухмерном пространстве векторов a {x₁, y₁} и b {x₂, y₂} разность векторов можно вычислить, как показано ниже:

c {x₃, y₃} = {x₁ — x₂, y₁ — y₂}.

Вычитание векторов в 3-мерном пространстве выглядит следующим образом:

c {x₃; y₃; z₃} = {x₁ — x₂, y₂ — y₂, z₁ — z₂}.

Как найти разность векторов графическим способом

Нужно воспользоваться правилом треугольника. Последовательность действий следующая:

Постройте по координатам векторы, для которых требуется найти разность;
Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.

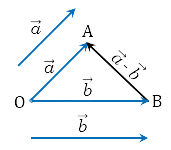
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:

Постройте исходные направленные отрезки;
Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
Постройте сумму, т. е. соедините начало первого отрезка и конец второго.

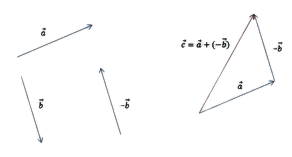
Нет времени решать самому?

Наши эксперты помогут!

Примеры вычисления разности векторов

Примеры

Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.

Решение:

Действуем по выше указанному правилу

a — b = {1 — 4; 2 — 8} = {-3; -6}

Ответ: с{-3; -6}.

Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.

Решение:

Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.

a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}

Ответ: c {-3; -6; 4}.

На рисунке векторы

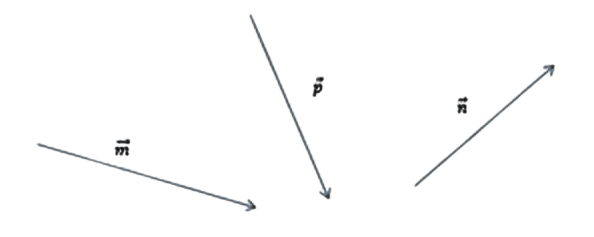
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.

Решение:

Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.

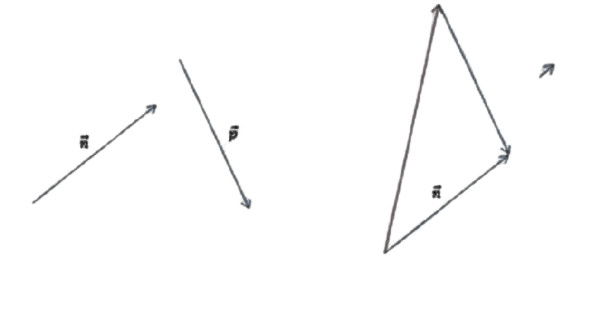
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.

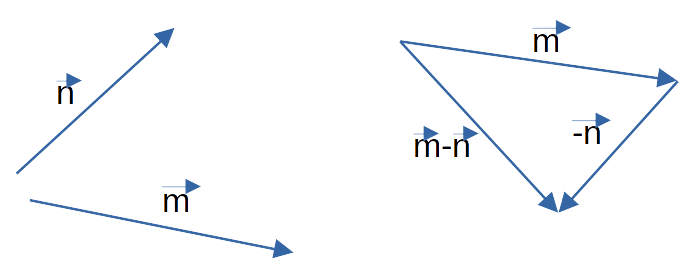
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:

m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m;
(m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p;
(m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.

Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.

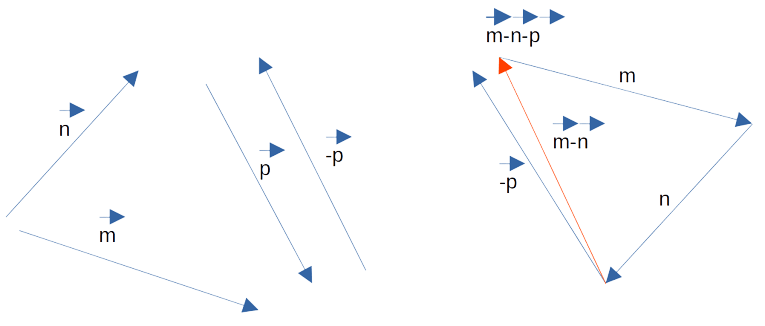
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.

Источник

Содержание:

Формула
Примеры нахождения разности векторов

Формула

Чтобы найти разность векторов $bar{a}-bar{b}$, заданных на плоскости координатами $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, необходимо вычесть из
координат первого вектора соответствующие
координаты второго, то есть

$$bar{a}-bar{b}=left(a_{x}-b_{x} ; a_{y}-b_{y}right)$$

В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их разность равна

$$bar{a}-bar{b}=left(a_{x}-b_{x} ; a_{y}-b_{y} ; a_{z}-b_{z}right)$$

Примеры нахождения разности векторов

Пример

Задание. Найти разность векторов $bar{a}-bar{b}$, где
$bar{a}=(3 ; 0)$ и $bar{b}=(1 ; 2)$

Решение. Для нахождения разности векторов
$bar{a}$ и
$bar{b}$, вычтем их соответствующие координаты:

$$bar{a}-bar{b}=(3 ; 0)-(1 ; 2)=(3-1 ; 0-2)=(2 ;-2)$$

Ответ. $bar{a}-bar{b}=(2 ;-2)$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти разность векторов
$bar{a}-bar{b}-bar{c}$, заданных в трехмерном пространстве своими координатами $bar{a}=(2 ;-3 ; 1), bar{b}=(1 ; 0 ;-2)$ и $bar{c}=(-1 ; 2 ; 3)$

Решение. Для нахождения искомой разности векторов вычтем их соответствующие координаты:

$$begin{aligned} bar{a}-bar{b}-bar{c}=(2 ;-3 ; 1)-(1 ; 0 ;-2)-(-1 ; 2 ; 3)=& \=(2-1-(-1) ;-3-0-2 ; 1-(-2)-3)=(2 ;-5 ; 0) end{aligned}$$

Ответ. $begin{aligned} bar{a}-bar{b}-bar{c}=(2 ;-5 ; 0) end{aligned}$

Читать дальше: как найти проекцию вектора.

Источник

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

$vec{a}(x_{a};: y_{a};: z_{a})$

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

$vec{a}=vec{AB}(x_{B}-x_{A};: y_{B}-y_{A};: z_{B}-z_{A})$

Длина вектора vec{AB} в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:

$|vec{a}|=sqrt{x^{2}_{a}+y^{2}_{a}+z^{2}_{a}}=sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}$ Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

$x_{M}=frac{x_{A}+x_{B}}{2};: : y_{M}=frac{y_{A}+y_{B}}{2};: : z_{M}=frac{z_{A}+z_{B}}{2}$

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Сумма векторов:

$vec{a}+vec{b}=vec{c}(x_{a}+x_{b};: y_{a}+y_{b};: z_{a}+z_{b})$

Разность векторов:

$vec{a}-vec{b}=vec{d}(x_{a}-x_{b};: y_{a}-y_{b};: z_{a}-z_{b})$

Произведение вектора на число:

$lambda cdot vec{a}=vec{p}(lambda x_{a};: lambda y_{a};:lambda z_{a} )$

Скалярное произведение векторов:

$vec{a}cdot vec{b}=|vec{a}|cdot |vec{b}|cdot cosvarphi =x_{a}cdot x_{b}+y_{a}cdot y_{b}+z_{a}cdot z_{b}$

Косинус угла между векторами:

$cosvarphi =frac{vec{a}cdot vec{b}}{|vec{a}|cdot vec{|b|}}=frac{x_{a}cdot x_{b}+y_{a}cdot y_{b}+z_{a}cdot z_{b}}{sqrt{x^{2}_{a}+y^{2}_{a}+z^{2}_{a}}cdot sqrt{x^{2}_{b}+y^{2}_{b}+z^{2}_{b}}}$

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами vec{AE} и vec{BK} . Для этого нужны их координаты.

$, \ A(0;0;0)\ B(1;0;0)\ E(frac{1}{2};0;1)\ K(1;frac{1}{2};1)$

Запишем координаты векторов:

$vec{AE}left (frac{1}{2};0;1 right )$

$vec{BK}left (0;frac{1}{2};1 right )$

и найдем косинус угла между векторами vec{AE} и vec{BK} :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

$Aleft ( frac{1}{2};-frac{1}{2};0 right )$

$Bleft ( frac{1}{2};frac{1}{2};0 right )$

$Cleft ( -frac{1}{2};frac{1}{2};0 right )$

Из прямоугольного треугольника AOS найдем $OS=frac{sqrt{2}}{2}.$

Координаты вершины пирамиды: $Sleft ( 0;0;frac{sqrt{2}}{2} right ).$

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

$Eleft ( frac{1}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

$Kleft ( -frac{1}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

Найдем координаты векторов и :

$overrightarrow{AE}left ( -frac{1}{4};frac{3}{4};frac{sqrt{2}}{4} right )$

$overrightarrow{BK}left ( -frac{3}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

и угол между ними:

$cosvarphi =frac{overrightarrow{AE}cdot overrightarrow{BK}}{left |overrightarrow{AE} right |cdot left |overrightarrow{BK} right |}=frac{1}{6}$

Покажем теперь, как вписать систему координат в треугольную призму.

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

$A_{1}(0;0;1)$

$B(frac{1}{2};frac{sqrt{3}}{2};0)$

$B_{1}(frac{1}{2};frac{sqrt{3}}{2};1)$

$C_{1}(-frac{1}{2};frac{sqrt{3}}{2};1)$

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

$D(frac{1}{4};frac{sqrt{3}}{4};1)$

Найдем координаты векторов и $overrightarrow{BC}_{1}$ , а затем угол между ними:

$overrightarrow{AD}(frac{1}{4};frac{sqrt{3}}{4};1)$

$overrightarrow{BC_{1}}(-1;0;1)$

$cosvarphi =frac{overrightarrow{AD}cdot overrightarrow{BC_{1}}}{left |overrightarrow{AD} right |cdot left |overrightarrow{BC_{1}} right |}=frac{3}{2sqrt{10}}$

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

Для точки M:

То есть A + C + D = 0.

Для точки N:

Аналогично для точки K:

Получили систему из трех уравнений:

$left{begin{matrix} A+C+D=0\ 2A-2B+D=0\ 4A+B+2C+D=0 end{matrix}right.$ .

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

$left{begin{matrix} A+C-2=0\ 2A-2B-2=0\ 4A+B+2C-2=0 end{matrix}right.$ ;

$left{begin{matrix} A+C=2\ A-B=1\ 4A+B+2C=2 end{matrix}right.$ .

Выразим C и B через A и подставим в третье уравнение:

$left{begin{matrix} C=2-A\ B=A-1\ 4A+A-1+4-2A=2 end{matrix}right.$ .

Решив систему, получим:

$, \ A=-frac{1}{3}\ , \ B=-frac{4}{3}\ , \ C=frac{7}{3}$

Уравнение плоскости MNK имеет вид:

$-frac{1}{3}x-frac{4}{3}y+frac{7}{3}z-2=0.$

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку $M(x_{0}, y_{0}, z_{0}),$ имеет вид:

$A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0.$

Угол между плоскостями равен углу между нормалями к этим плоскостям:

$cosvarphi =frac{left |vec{n}_{1}cdot vec{n}_{2} right |}{|vec{n}_{1}|cdot |vec{n}_{2}|}$

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть: $vec{n}_{1}=overrightarrow{AC}(1;1;0).$

Напишем уравнение плоскости AEF.

$, \ A(0;0;0)\ E(frac{1}{2};0;1)\ , \ F(0;frac{1}{2};1)$

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

$left.begin{matrix} A\ , \ E\ , \ F end{matrix}right|$ $, \ 0cdot A+0cdot B+0cdot C+D=0\ , \ frac{1}{2}cdot A+0cdot B+1cdot C+D=0\ , \ 0cdot A+frac{1}{2}cdot B+1cdot C+D=0$

Упростим систему:

$left{begin{matrix} D=0\ frac{1}{2}A+C=0\ , \ frac{1}{2}B+C=0 end{matrix}right.$ .

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

$cosvarphi =frac{|2+2|}{sqrt{2}cdot sqrt{9}}=frac{4}{sqrt{2}cdot 3}=frac{4}{sqrt{2}cdot 3}=frac{2sqrt{2}}{3}$

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Итак, AA₁ = √3

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор $vec{n_{1}}(1;0;0)$ .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

$B_{1}left ( 5;, 0;, sqrt{3} right )$

Координаты вектора $overrightarrow{B_{1}D}$ — тоже:

$overrightarrow{B_{1}D}left ( -5;, sqrt{33};, -sqrt{3} right )=overrightarrow{n}_{2}$

Находим угол между плоскостями, равный углу между нормалями к ним:

$cos, varphi =frac{5}{sqrt{25+33+3}}=frac{5}{sqrt{61}}$

Зная косинус угла, находим его тангенс по формуле

$1+tg^{2}varphi =frac{1}{cos^{2}varphi }$

Получим:
$tg, varphi =frac{6}{5}.$

Ответ: $frac{6}{5}.$

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

$sin, varphi =frac{left | overrightarrow{n}cdotoverrightarrow{a} right |}{left | overrightarrow{n} right |cdot |overrightarrow{a}|}$

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

$Eleft ( 1;, frac{1}{2};, 1 right )$

Находим координаты вектора $overrightarrow{AE}left ( 0;, frac{1}{2};, 1 right )$ .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

$sin, varphi =frac{left | overrightarrow{AC}cdot overrightarrow{AE} right |}{|overrightarrow{AC}|cdot|overrightarrow{AE}|}=frac{2}{2cdot sqrt{2}cdot sqrt{5}}=frac{1}{sqrt{10}}$

Ответ: $frac{1}{sqrt{10}}.$

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

$h=frac{|Ax_{0}+By_{0}+Cz_{0}+D|}{sqrt{A^{2}+B^{2}+C^{2}}}$

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = $frac{6}{sqrt{5}}$ . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

$A_{1}left ( 0, ;0;, frac{6}{sqrt{5}} right )$

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

$left.begin{matrix} A_{1}\ B\ D end{matrix}right|$ $begin{matrix} frac{6}{sqrt{5}}C+D=0\ sqrt{10}A+D=0\ 3sqrt{10}B+D=0 end{matrix}$

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

$h=frac{|Ax_{0}+By_{0}+Cz_{0}+D|}{sqrt{A^{2}+B^{2}+C^{2}}}=frac{6sqrt{10}}{sqrt{50+36+4}}=frac{6sqrt{10}}{sqrt{90}}=2.$

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

Вектор – это направленный прямолинейный отрезок, то есть отрезок, имеющий
определенную длину и определенное направление. Пусть точка А – начало вектора, а точка B – его конец, тогда вектор обозначается символом или . Вектор называется противоположным
вектору и может быть
обозначен .

Сформулируем ряд базовых определений.

Длиной
или модулем
вектора  называется
длина отрезка и обозначается . Вектор нулевой длины (его суть – точка) называется нулевым  и направления
не имеет. Вектор единичной длины, называется единичным. Единичный вектор,
направление которого совпадает с направлением вектора , называется ортом вектора  .

Векторы
называются коллинеарными, если они лежат на одной прямой или на
параллельных прямых, записывают. Коллинеарные векторы могут иметь совпадающие или
противоположные направления. Нулевой вектор считают коллинеарным любому
вектору.

Векторы
называются равными , если они коллинеарны, одинаково направлены и имеют
одинаковые длины.

Три вектора в пространстве называются компланарными,
если они лежат в одной плоскости или на параллельных плоскостях. Если среди
трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы
компланарны.

Рассмотрим в
пространстве прямоугольную систему координат 0xyz. Выделим на осях координат 0x, 0y, 0z единичные векторы (орты) и
обозначим их через соответственно.
Выберем произвольный вектор

пространства и совместим его начало с началом
координат. Спроектируем вектор
на координатные
оси и обозначим проекции через a_x, a_y, a_z
соответственно. Тогда нетрудно показать, что

. (2.25)

Эта
формула является основной в векторном исчислении и называется разложением
вектора по ортам координатных осей. Числа a_x, a_y, a_z называются координатами вектора . Таким образом, координаты вектора являются его
проекциями на оси координат. Векторное равенство (2.25) часто записывают в
виде

. Мы будем использовать обозначение вектора в фигурных
скобках, чтобы визуально легче различать координаты вектора и координаты точки.
С использованием формулы длины отрезка, известной из школьной геометрии, можно
найти выражение для вычисления модуля вектора

:

, (2.26)

то
есть модуль вектора равен корню квадратному из суммы квадратов его координат.

Обозначим углы между вектором
и осями
координат через α, β, γ соответственно. Косинусы этих углов называются
для вектора направляющими, и для них выполняется соотношение:Верность данного равенства можно показать с помощью
свойства проекции вектора на ось, которое будет рассмотрено в нижеследующем
пункте 4.

Пусть в трехмерном пространстве заданы векторы своими
координатами. Имеют место следующие
операции над ними: линейные (сложение, вычитание, умножение на число и
проектирование вектора на ось или другой вектор); не линейные – различные
произведения векторов (скалярное, векторное, смешанное).

1. Сложение двух векторов производится покоординатно, то
есть если

Данная
формула имеет место для произвольного конечного числа слагаемых.

Геометрически
два вектора складываются по двум правилам:

а) правило треугольника –
результирующий вектор суммы двух векторов соединяет начало первого из них с
концом второго при условии, что начало второго совпадает с концом первого
вектора; для суммы векторов –
результирующий вектор суммы соединяет начало первого из них с концом последнего
вектора-слагаемого при условии, что начало последующего слагаемого совпадает с
концом предыдущего;

б)
правило
параллелограмма (для двух
векторов) – параллелограмм строится на векторах-слагаемых как на сторонах,
приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой
векторов.

2. Вычитание двух векторов производится
покоординатно, аналогично сложению, то есть если , то

Геометрически два
вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов
является диагональ, соединяющая концы векторов, причем результирующий вектор
направлен из конца вычитаемого в конец уменьшаемого вектора.

Важным следствием
вычитания векторов является тот факт, что если известны координаты начала и
конца вектора, то для вычисления координат вектора необходимо из координат его конца
вычесть координаты его начала. Действительно, любой вектор пространства может быть
представлен в виде разности двух векторов, исходящих из начала координат: . Координаты векторов и совпадают с
координатами точек А и В, так как начало координат О(0;0;0). Таким образом, по правилу
вычитания векторов следует произвести вычитание координат точки А из координат точки В.

3. Умножение вектора на число λ покоординатно:.

При λ>0
– вектор сонаправлен ; λ<0 – вектор противоположно направлен ; |λ|>1 – длина вектора увеличивается в λ раз; |λ|<1 – длина вектора уменьшается в λ раз.

4. Пусть в пространстве задана
направленная прямая (ось l), вектор задан
координатами конца и начала. Обозначим проекции точек A и B на ось l
соответственно через A’ и B’.

Проекцией вектора на ось l называется длина вектора , взятая со
знаком «+», если вектор и ось l сонаправлены, и со
знаком «–», если и l противоположно направлены.

Если
в качестве оси l взять некоторый другой вектор , то получим проекцию вектора на вектор .

Рассмотрим некоторые
основные свойства проекций:

1) проекция вектора на ось l равна произведению модуля
вектора на косинус угла
между вектором и осью, то есть ;

2.) проекция вектора на ось
положительна (отрицательна), если вектор образует с осью острый (тупой) угол, и
равна нулю, если этот угол – прямой;

3) проекция суммы нескольких
векторов на одну и ту же ось равна сумме проекций на эту ось.

Сформулируем определения и
теоремы о произведениях векторов, представляющих нелинейные операции над
векторами.

5. Скалярным произведением векторов и называется
число (скаляр), равное произведению длин этих векторов на косинус угла φ между
ними, то есть

. (2.27)

Очевидно, что скалярный квадрат любого ненулевого вектора равен квадрату его длины, так как в этом случае угол , поэтому его косинус (в 2.27) равен 1.

Теорема 2.2. Необходимым и достаточным условием
перпендикулярности двух векторов является равенство нулю их скалярного
произведения

Следствие. Попарные скалярные произведения единичных орт равны нулю, то есть

Теорема 2.3. Скалярное произведение двух векторов ,
заданных своими координатами, равно сумме произведений их одноименных координат, то есть

(2.28)

С помощью скалярного произведения векторов можно
вычислить угол между ними.
Если заданы два ненулевых вектора
своими координатами , то косинус угла φ между ними:

(2.29)

Отсюда
следует условие перпендикулярности ненулевых векторов
и :

(2.30)

Нахождение проекции вектора на направление,
заданное вектором , может осуществляться по формуле

(2.31)

С помощью скалярного произведения векторов находят
работу постоянной силы на
прямолинейном участке пути.

Предположим, что под действием постоянной силы материальная точка перемещается прямолинейно из
положения А в положение B. Вектор силы образует угол φ с вектором перемещения (рис. 2.14). Физика утверждает, что работа силы при перемещении
равна .

Следовательно, работа постоянной силы
при прямолинейном перемещении точки ее приложения равна скалярному произведению
вектора силы на вектор перемещения.

Пример
2.9. С
помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах

Решение. Вычислим модули векторов и их скалярное произведение
по теореме (2.3):

Отсюда согласно формуле (2.29) получим косинус
искомого угла

Пример 2.10. Затраты сырьевых и материальных ресурсов, используемых
на производство одной тонны творога, заданы в таблице 2.2 (руб.).

Какова общая цена этих ресурсов, затрачиваемых на изготовление одной
тонны творога?

Таблица 2.2

Решение. Введем в рассмотрение два вектора: вектор затрат
ресурсов на тонну продукции и вектор цены единицы
соответствующего ресурса .

Тогда . Общая цена
ресурсов , что представляет собой скалярное произведение
векторов . Вычислим его по формуле (2.28) согласно теореме 2.3:

Таким образом, общая цена затрат на производство одной
тонны творога составляет 279 541,5 рублей

Примечание. Действия с векторами, осуществленные в примере 2.10,
можно выполнить на персональном компьютере. Для нахождения скалярного
произведения векторов в MS Excel используют функцию СУММПРОИЗВ( ), где в качестве
аргументов указываются адреса диапазонов элементов матриц, сумму произведений
которых необходимо найти. В MathCAD
скалярное произведение двух векторов выполняется при помощи соответствующего
оператора панели инструментов Matrix

Пример 2.11. Вычислить работу, произведенную силой , если точка ее приложения перемещается прямолинейно
из положения A(2;4;6) в положение A(4;2;7). Под каким углом к AB направлена сила ?

Решение. Находим вектор перемещения, вычитая из координат его конца координаты
начала

. По формуле (2.28) (единиц работы).

Угол φ между и
находим по
формуле (2.29), то есть

6. Три некомпланарных вектора , взятые в указанном порядке, образуют правую
тройку, если при наблюдении из конца третьего вектора кратчайший
поворот от первого вектора ко второму
вектору совершается против часовой стрелки, и левую,
если по часовой стрелке.

Векторным
произведением вектора на вектор называется
вектор , удовлетворяющий следующим условиям:

– перпендикулярен векторам и ;

– имеет длину, равную , где φ – угол, образованный векторами
и ;

– векторы образуют правую
тройку (рис. 2.15).

Теорема 2.4. Необходимым и достаточным
условием коллинеарности двух векторов является равенство нулю их векторного
произведения

Теорема 2.5. Векторное произведение векторов , заданных своими координатами, равно определителю
третьего порядка вида

(2.32)

Примечание. Определитель (2.25)
раскладывается по свойству 7 определителей

Следствие 1. Необходимым и достаточным условием коллинеарности двух
векторов является пропорциональность их соответствующих координат

Следствие 2. Векторные произведения единичных орт равны

Следствие 3. Векторный квадрат любого вектора равен нулю

Геометрическая
интерпретация векторного произведения состоит в том, что длина результирующего
вектора численно равна площади S
параллелограмма, построенного на векторах–сомножителях как на сторонах,
приведенных к одному началу. Действительно, согласно определению, модуль
векторного произведения векторов равен . С другой стороны, площадь параллелограмма,
построенного на векторах и , также равна

. Следовательно,

. (2.33)

Также с помощью векторного произведения можно
определить момент силы относительно точки и линейную скорость вращения.

Пусть в точке A приложена
сила  и пусть O –
некоторая точка пространства (рис. 2.16). Из курса физики известно, что моментом
силы  относительно
точки O называется вектор , который проходит через точку O и удовлетворяет следующим условиям:

– перпендикулярен плоскости, проходящей через точки O, A, B;

– его модуль численно равен произведению силы на плечо .

– образует правую тройку с векторами и .

Следовательно,
момент силы относительно
точки O представляет собой векторное произведение

. (2.34)

Линейная скорость точки М твердого тела, вращающегося с
угловой скоростью вокруг
неподвижной оси, определяется формулой Эйлера , O – некоторая неподвижная

точка оси (рис. 2.17).

Пример 2.12. С помощью
векторного произведения найти площадь треугольника ABC, построенного на векторах
, приведенных к одному началу.

Решение. Найдем векторное произведение заданных векторов по
формуле (2.32).

. Согласно формуле (2.33) модуль векторного
произведения двух неколлинеарных векторов численно равен площади
параллелограмма, построенного на данных векторах как на сторонах, приведенных к
общему началу, то есть . Тогда площадь треугольника
. Следовательно, искомая площадь равна (единиц
площади)

7. Рассмотрим произведение трех векторов , составленное следующим образом: . Здесь первые два вектора перемножаются векторно, а
результирующий вектор – скалярно на третий. Такое произведение называется смешанным
произведением трех векторов
(векторно–скалярным произведением).

Теорема 2.6. Необходимым и достаточным условием компланарности
трех векторов является равенство нулю их смешанного произведения

Теорема 2.7. Если три вектора заданы своими координатами, то их смешанное
произведение представляет собой определитель третьего порядка, составленный из
координат векторов- сомножителей соответственно, то есть

(2.35)

Нетрудно показать, что объем параллелепипеда,
построенного на векторах как на
сторонах, приведенных к общему началу, численно равен модулю смешенного
произведения этих векторов .

Объем треугольной пирамиды, построенной на этих же
векторах, равен

(2.36)

Пример 2.13. Вершинами пирамиды служат точки . Вычислить объем пирамиды.

Решение. Найдем
координаты векторов

. Вычислим смешанное произведение этих векторов:

По формуле (2.36) объем пирамиды, построенной на
векторах равен
(единиц объема)

Рассмотрим очень важный вопрос о
разложении вектора по базису. Приведем
следующие определения.

Система векторов называется
линейно зависимой, если существуют такие числа , хотя бы одно из которых отлично от нуля, что имеет
место равенство

(2.37)

Отсюда всегда можно один из линейно
зависимых векторов выразить через линейную комбинацию остальных. Действительно,
допустим для определенности, что . Тогда на это число разделим равенство (2.37), имеем:

получим выражение вектора через
остальные векторы

Линейно независимыми называют векторы, если равенство
(2.37) выполняется только тогда, когда
все

В системе векторов число линейно
независимых векторов равняется рангу матрицы, которая составлена из координат
этих векторов (смотри раздел I.5).

Базисом n – мерного
пространства E_n называют любую совокупность линейно независимых векторов n – мерного пространства.

Произвольный вектор n
– мерного пространства можно представить
в виде линейной комбинации векторов базиса

таким образом:

Числа
называются координатами
вектора в базисе
векторов .

Линейное пространство называется
конечномерным и имеет размерность n, если в этом
пространстве существует система из n линейно независимых векторов (базис) такая,
что каждое ее расширение приводит к линейной зависимости системы.

Например, в трехмерном пространстве
существует базис единичных орт  такой, что любое расширение этой системы
линейно независимых векторов, то есть каждый вектор  трехмерного
пространства, приводит к линейной зависимости векторов (является линейной
комбинацией орт ): Коэффициенты {x₁, x₂, x₃} такого разложения вектора
по ортам  являются координатами вектора  в трехмерном
пространстве.

Вопросы для самопроверки

Источник

Разность векторов – это вектор с координатами, равными разности координат первого и второго векторов, и направлением, совпадающим с направлением отрезка, исходящим из конца второго вектора и направленным в конец первого вектора.

Обозначения[править]

Введём обозначения:

r₁=(x₁,y₁,z₁) — первый вектор;

r₂=(x₂,y₂,z₂) — второй вектор.

Формула[править]

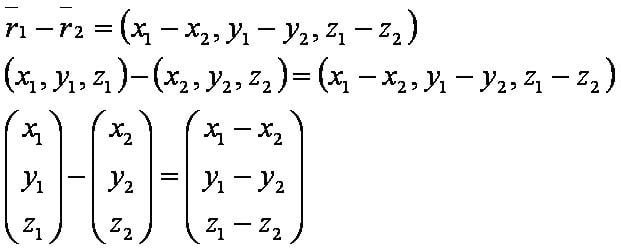
Рисунок[править]

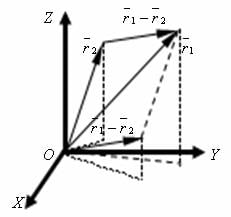
Другие операции:[править]

нахождение длины вектора;
сложение векторов;
вычитание векторов;
умножение вектора на число;
скалярное произведение;
векторное произведение;
смешанное произведение;
двойное векторное произведение;
нахождение угла между векторами;
ортогонализация векторов.

Литература[править]

Корн Г., Корн Т. Справочник по математике для научных работников и инженеров — М.: Наука, 1970.

Ссылки[править]

Участник:Logic-samara

Источник

Разность векторов

Как найти разность векторов аналитическим способом

Как найти разность векторов графическим способом

Примеры вычисления разности векторов

Формула

Примеры нахождения разности векторов

Векторы в пространстве и метод координат

Система координат в пространстве

Плоскость в пространстве задается уравнением:

Обозначения[править]

Формула[править]

Рисунок[править]

Другие операции:[править]

Литература[править]

Ссылки[править]

Вам также может понравиться

Как найти свой ответ на дзене

Как найти родственников в финляндии

Как найти колонку джибиэль

Добавить комментарий Отменить ответ