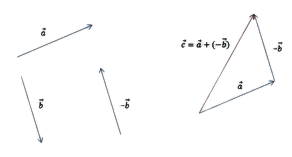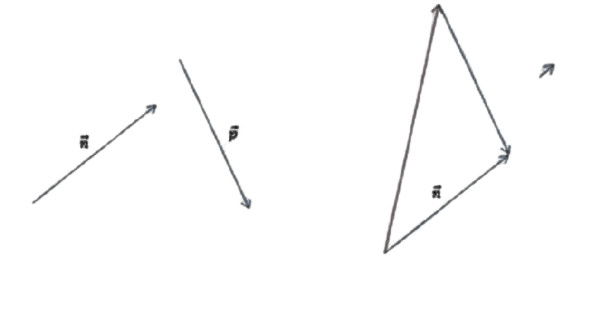Содержание:
- Формула
- Примеры нахождения разности векторов
Формула
Чтобы найти разность векторов $bar{a}-bar{b}$, заданных на плоскости координатами $bar{a}=left(a_{x} ; a_{y}right)$ и $bar{b}=left(b_{x} ; b_{y}right)$, необходимо вычесть из
координат первого вектора соответствующие
координаты второго, то есть
$$bar{a}-bar{b}=left(a_{x}-b_{x} ; a_{y}-b_{y}right)$$
В случае если векторы заданы в пространстве, то есть $bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то их разность равна
$$bar{a}-bar{b}=left(a_{x}-b_{x} ; a_{y}-b_{y} ; a_{z}-b_{z}right)$$
Примеры нахождения разности векторов
Пример
Задание. Найти разность векторов $bar{a}-bar{b}$, где
$bar{a}=(3 ; 0)$ и $bar{b}=(1 ; 2)$
Решение. Для нахождения разности векторов
$bar{a}$ и
$bar{b}$, вычтем их соответствующие координаты:
$$bar{a}-bar{b}=(3 ; 0)-(1 ; 2)=(3-1 ; 0-2)=(2 ;-2)$$
Ответ. $bar{a}-bar{b}=(2 ;-2)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти разность векторов
$bar{a}-bar{b}-bar{c}$, заданных в трехмерном пространстве своими координатами $bar{a}=(2 ;-3 ; 1), bar{b}=(1 ; 0 ;-2)$ и $bar{c}=(-1 ; 2 ; 3)$
Решение. Для нахождения искомой разности векторов вычтем их соответствующие координаты:
$$begin{aligned} bar{a}-bar{b}-bar{c}=(2 ;-3 ; 1)-(1 ; 0 ;-2)-(-1 ; 2 ; 3)=& \=(2-1-(-1) ;-3-0-2 ; 1-(-2)-3)=(2 ;-5 ; 0) end{aligned}$$
Ответ. $begin{aligned} bar{a}-bar{b}-bar{c}=(2 ;-5 ; 0) end{aligned}$
Читать дальше: как найти проекцию вектора.
Вектор – направленный отрезок, имеющий как начало, так и конец, иначе – величина характеризуемая числовым значением и направлением, обозначается
Координаты вектора – его проекции на координатные оси Ox, Oy и Oz, обозначаются
Разность двух векторов равна сумме первого вектора и противоположного второму вектора ( то есть второй вектор с противоположным знаком), и разность двух одинаковых векторов равна нулевому вектору. Координаты разности векторов равны разности соответствующих координат этих векторов, на плоскости:
в пространстве:
Вычитание векторов
Содержание:
- Как происходит вычитание векторов
- Как производится вычитание векторов по координатам
-
Основные правила вычисления
- Правило треугольника
- Правило параллелограмма
- Примеры задач на понятие разности векторов
Как происходит вычитание векторов
Определение
Вычитание векторов — это арифметическое действие в геометрии, при котором из одного вектора отнимают другой.
Чтобы вычесть (overrightarrow b) из (overrightarrow а), нужно найти такой (overrightarrow с), сложение которого с вектором (overrightarrow b) составляло бы (overrightarrow а).
Таким образом, формула разности будет выглядеть так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(overrightarrow а-overrightarrow b=overrightarrow а+left(-overrightarrow bright))
Если задан (overrightarrow а), то можно построить противоположный ему (-overrightarrow а), равный по длине, но противоположно направленный. Тогда происходит сведение двух противоположно направленных векторов к нулевому:
(overrightarrow а+left(-overrightarrow аright)=0)
Как производится вычитание векторов по координатам
Если необходимо произвести вычитание векторов по координатам, то следует просто вычесть соответствующие точки. То есть если из (overrightarrow а) отнимается (overrightarrow b), то из X1 отнимаем X2, из Y1 Y2 и из Z1 Z2.
Проиллюстрируем координатное пространство:
Основные правила вычисления
Для того, чтобы найти значение разности векторов, можно использовать несколько способов.
Правило треугольника
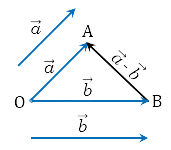
Чтобы графически продемонстрировать разность, необходимо отложить от произвольной точки вектор (overrightarrow а), из его начала (overrightarrow b). Тогда вектор, начало которого совпадает с концом ( overrightarrow b), а конец — с концом (overrightarrow a), и будет искомым вектором разности (overrightarrow a;-;overrightarrow b). Проиллюстрируем это:
Правило параллелограмма
Если два неколлинеарных, то есть непараллельных вектора (overrightarrow а) и (overrightarrow b) имеют общее начало, то их разностью является вектор, совпадающий с диагональю параллелограмма, построенного на (overrightarrow а) и (overrightarrow b), причем начало этой диагонали совпадает с концом (overrightarrow b), а конец — с концом (overrightarrow а).
Если векторы (overrightarrow а) и (overrightarrow b) заданы в некотором промежутке:
(overrightarrow a=left(а_1;а_2right),;overrightarrow b=left(b_1;b_2right))
то, чтобы найти координаты их разности (overrightarrow a;-;overrightarrow b), необходимо от точек (overrightarrow a) отнять соответствующие точки (overrightarrow b):
(overrightarrow a;-;overrightarrow b=left(a_1;a_2right)-left(b_1;b_2right)=left(a_1-b_1;a_2-b_2right))
Проиллюстрируем правило многоугольника:
Примеры задач на понятие разности векторов
Задача 1
Дано
(overrightarrow a;=left(2;-1right),;overrightarrow b=left(0;2right))
Найти: (overrightarrow с=2overrightarrow a-3overrightarrow b;)
Решение
Найдем координаты (2overrightarrow a) и (3overrightarrow b). Для этого умножим каждую на два и три:
(2overrightarrow а=2timesleft(2;-1right)=left(2times2;2timesleft(-1right)right)=left(4;-2right), 3overrightarrow b=3timesleft(0;2right)=left(3times0;3times2right)=left(0;6right))
Тогда искомый вектор:
(overrightarrow с=2overrightarrow a-3overrightarrow b=left(4;-2right)-left(0;6right)=left(4-0;;-2-6right)=left(4;-8right))
Ответ: (overrightarrow с=left(4;-8right).)
Задача 2
Дано
(Аleft(1;-1;0right),;Вleft(2;3;-1right),;Сleft(0;-1;0right),;Dleft(1;0;2right))
Найти: координаты (overrightarrow{AB}-overrightarrow{CD}.)
Решение
Для начала найдем проекции (overrightarrow{AB}) и (overrightarrow{CD}).
Для этого от координат конца вектора, то есть точек B и D, нужно отнять соответствующие проекции его начала, то есть точек А и С.
(overrightarrow{AB}=left(2-1;3-left(-1right);-1-0right)=left(1;4;-1right),;overrightarrow{CD}=left(1-0;0-left(-1right);2-0right)=left(1;1;2right))
Тогда для нахождения координат разности (overrightarrow{AB}-overrightarrow{CD}), от координат первого вычтем координаты второго:
(overrightarrow{AB}-overrightarrow{CD}=left(1;4;-1right)-left(1;1;2right)=left(1-1;4-1;-1-2right)=left(0;3;-3right))
Ответ: (overrightarrow{AB}-overrightarrow{CD}=left(0;3;-3right))
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Для того, чтобы уяснить, что собой представляет разность векторов, введём понятие откладывания вектора от определённой точки и понятие суммы векторов.
Определение
Если некоторая точка A является началом вектора a, то говорят, что он является отложенным от точки A.
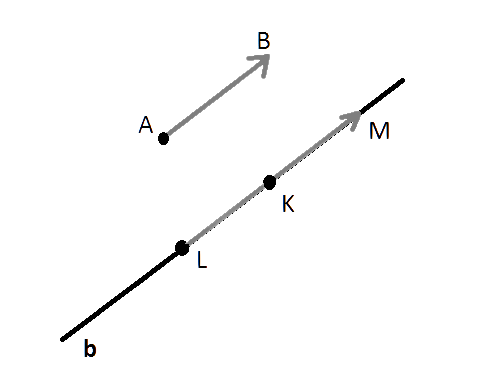
Теорема. От каждой точки можно отложить только один вектор, имеющий заданный модуль и направление. Докажем эту теорему.
Доказательство:
В случае, когда вектор нулевой, то теорема очевидна. Нулевые вектора в одной и той же точки совпадают между собой, т. е. являются одним и тем же вектором.
Сделаем построение. Точкой A обозначим начало вектора a, а точкой B его конец. Пусть у нас имеется некоторая точка K. Проведём через неё прямую b, которая параллельна вектору a. Отложим на данной прямой равные по своей абсолютной величине вектору a отрезки KL и KM. Из векторов, образованных этими отрезками искомым можно назвать только сонаправленный с a.
Единственность нашего вектора следует из того, что мы построили и видим.
Теорема доказана.
Определение
Суммой векторов a и b называется вектор с тем же началом, что вектор a и концом, как у вектора b. При этом вектор b должен начинаться в той же самой точке, в которой заканчивается вектор a.
Равные векторы, начинающиеся в разных точках, нередко обозначают одной и той же буквой. Иногда про подобные векторы говорят, как об одном и том же векторе, отложенном из разных мест.
Разность векторов
Определение
Разностью векторов a и b называется сумма вектора a c вектором, который противоположно направлен к вектору b.
По-другому это определение можно сформулировать следующим образом: разностью двух векторов a и b называется вектор c, который при сложении с вычитаемым b образует уменьшаемое, т. е. вектор a.
Формулами это записывается так:
b + c = a
a – b = c
Как найти разность векторов аналитическим способом
В двухмерном пространстве векторов a {x1, y1} и b {x2, y₂} разность векторов можно вычислить, как показано ниже:
c {x3, y3} = {x₁ — x2, y1 — y₂}.
Вычитание векторов в 3-мерном пространстве выглядит следующим образом:
c {x3; y3; z₃} = {x₁ — x2, y₂ — y₂, z1 — z2}.
Как найти разность векторов графическим способом
Нужно воспользоваться правилом треугольника. Последовательность действий следующая:
- Постройте по координатам векторы, для которых требуется найти разность;
- Совместите концы построенных векторов. Для этого нужно построить два равных заданным направленных отрезка, концы у которых будут в одной и той же точке;
- Соедините начала построенных отрезков и укажите их направление. Вектор c, называемый разностью векторов, будет иметь своё начало в той же точке, где начинается вектор, именуемый уменьшаемым и заканчивается в точке начала вычитаемого. Смотрите рисунок ниже.
Есть ещё один способ графического нахождения разности векторов. Он предусматривает следующий порядок действий:
- Постройте исходные направленные отрезки;
- Отразите вычитаемый отрезок. Для этого постройте противоположно направленный и равный ему отрезок и затем совместите начало этого отрезка с уменьшаемым;
- Постройте сумму, т. е. соедините начало первого отрезка и конец второго.
Нет времени решать самому?
Наши эксперты помогут!
Примеры вычисления разности векторов
Примеры
Вычислить вектор c, который представляет собой разность вектора a ={1;
2} и вектора b = {4; 8}.
Решение:
Действуем по выше указанному правилу
a — b = {1 — 4; 2 — 8} = {-3; -6}
Ответ: с{-3; -6}.
Вычислить вектор c, который является разностью векторов a = {1; 2; 5} и
b = {4; 8; 1}.
Решение:
Почти всё делается, как в уже рассмотренном примере, только добавляется третья координата.
a — b = {1 — 4; 2 — 8; 5 — 1} = {-3; -6; 4}
Ответ: c {-3; -6; 4}.
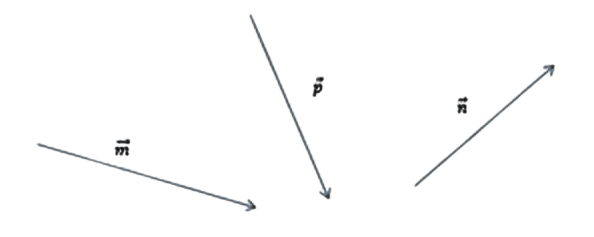
На рисунке векторы
Требуется построить разности: p — n, m —
n,m — n — p и найти ту из них, которая
имеет наименьший модуль.
Решение:
Для изображения p — n проще всего воспользоваться правилом треугольника. Параллельным переносом
отрезки
следует соединить таким образом, чтобы совпали их конечные точки. Далее нужно соединить начальные точки и
определить направление. В нашем случае вектор разности берёт своё начало там же, где и вычитаемый n.
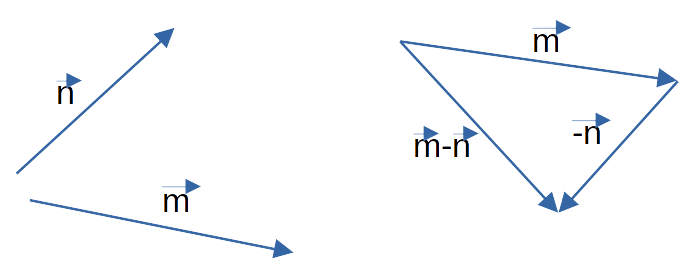
Для изображения m — n правильнее будет воспользоваться вторым графическим способом нахождения разности
векторов. Сначала построим вектор противоположный n и найдём его суммы с вектором m.
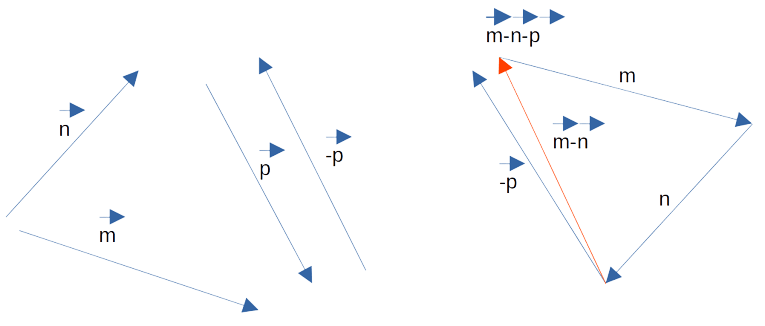
Для нахождения разности m — n — p разобьём это выражение на два действия. Возможны следующие варианты:
- m — (n + p). Сначала нужно построить сумму,
затем уже вычесть её из m; - (m — n) — p. Сначала находим m — n,
осле этого от полученной разности отнимаем p; - (m— p) — n. Сначала определяем m — p, затем от
полученного результата отнимаем n.
Из вычислений выше нам известна разность m — n. Для получения решения нам нужно вычесть из неё
p.
Используя определение 3 построим разность векторов на рисунке. На нём изображён окончательный результат
и промежуточный.
Теперь нужно определить наименьший модуль. В нашем случае для этого можно лишь визуально оценить длины p — n,
m — n и m — n — p. Из построения сразу видно, что наименьшим модулем обладает вектор разности m — n —
p.
Как найти разность векторов
ФОРМУЛА
Чтобы найти разность векторов(
overline{a}-overline{b}
), заданных на плоскости координатами (
overline{a}=left(a_{x} ; a_{y}right)quad{и}quad overline{b}=left(b_{x} ; b_{y}right)
) , необходимо вычесть из координат первого вектора соответствующие координаты второго, т.е.
(
overline{a}-overline{b}=left(a_{x}-b_{x} ; a_{y}-b_{y}right)
)
Если векторы заданы в пространстве, то есть (
tilde{a}=left(a_{x} ; a_{y} ; a_{z}right)quad{и}quad overline{b}=left(b_{x} ; b_{y} ; b_{z}right)
)тогда их различие
(
overline{a}-overline{b}=left(a_{x}-b_{x} ; a_{y}-b_{y} ; a_{z}-b_{z}right)
)
ПРИМЕР
overline{a}-overline{b}, text { где } overline{a}=(3 ; 0)quad{и}quad overline{b}=(1 ; 2)
)
overline{a}quad иquad overline{b}
) вычитаем их соответствующие координаты: (
overline{a}-overline{b}=(3 ; 0)-(1 ; 2)=(3-1 ; 0-2)=(2 ;-2)
)
overline{a}-overline{b}=(2 ;-2)
)
ПРИМЕР
overline{a}-overline{b}-overline{c}
) , заданных в трехмерном пространстве их координатами (
overline{a}=(2 ;-3 ; 1), overline{b}=(1 ; 0 ;-2)
) и (
overline{c}=(-1 ; 2 ; 3)
)
(
overline{a}-overline{b}-overline{c}=(2 ;-3 ; 1)-(1 ; 0 ;-2)-(-1 ; 2 ; 3)=
)
(
=(2-1-(-1) ;-3-0-2 ; 1-(-2)-3)=(2 ;-5 ; 0)
)
overline{a}-overline{b}-overline{c}=(2 ;-5 ; 0)
)