Как найти стороны прямоугольного треугольника
Онлайн калькулятор
Чтобы вычислить длины сторон прямоугольного треугольника вам нужно знать следующие параметры (либо-либо):
- для гипотенузы (с):
- длины катетов a и b
- длину катета (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину катета (a или b) и противолежащий к нему острый угол (α или β, соответственно)
- для катета:
- длину гипотенузы (с) и длину одного из катетов
- длину гипотенузы (с) и прилежащий к искомому катету (a или b) острый угол (β или α, соответственно)
- длину гипотенузы (с) и противолежащий к искомому катету (a или b) острый угол (α или β, соответственно)
- длину одного из катетов (a или b) и прилежащий к нему острый угол (β или α, соответственно)
- длину одного из катетов (a или b) и противолежащий к нему острый угол (α или β, соответственно)
Введите их в соответствующие поля и получите результат.
Найти гипотенузу (c)
Найти гипотенузу по двум катетам
Чему равна гипотенуза (сторона с) если известны оба катета (стороны a и b)?
Формула
следовательно: c = √ a² + b²
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 3 см, а катет b = 4 см:
c = √ 3² + 4² = √ 9 + 16 = √ 25 = 5 см
Найти гипотенузу по катету и прилежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и прилежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а прилежащий к нему ∠β = 60°:
c = 2 / cos(60) = 2 / 0.5 = 4 см
Найти гипотенузу по катету и противолежащему к нему острому углу
Чему равна гипотенуза (сторона с) если известны один из катетов (a или b) и противолежащий к нему угол?
Формула
Пример
Для примера посчитаем чему равна гипотенуза прямоугольного треугольника если катет a = 2 см, а противолежащий к нему ∠α = 30°:
c = 2 / sin(30) = 2 / 0.5 = 4 см
Найти гипотенузу по двум углам
Найти гипотенузу прямоугольного треугольника только по двум острым углам невозможно.
Найти катет
Найти катет по гипотенузе и катету
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и второй катет?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 5 см, а катет b = 4 см:
a = √ 5² – 4² = √ 25 – 16 = √ 9 = 3 см
Найти катет по гипотенузе и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и прилежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если гипотенуза c = 5 см, а ∠α = 60°:
b = 5 ⋅ cos(60) = 5 ⋅ 0.5 = 2.5 см
Найти катет по гипотенузе и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известны гипотенуза и противолежащий к искомому катету острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если гипотенуза c = 4 см, а ∠α = 30°:
a = 4 ⋅ sin(30) = 4 ⋅ 0.5 = 2 см
Найти катет по второму катету и прилежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и прилежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет b прямоугольного треугольника если катет a = 2 см, а ∠β = 45°:
b = 2 ⋅ tg(45) = 2 ⋅ 1 = 2 см
Найти катет по второму катету и противолежащему к нему острому углу
Чему равен один из катетов прямоугольного треугольника если известен другой катет и противолежащий к нему острый угол?
Формула
Пример
Для примера посчитаем чему равен катет a прямоугольного треугольника если катет b = 3 см, а ∠β = 35°:
Прямоугольный треугольник
Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).
Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.
Стороны, прилежащие к прямому углу, называются катетами .
Признаки равенства прямоугольных треугольников
Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).
Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).
Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.
3. Теорема Пифагора:
, где – катеты, – гипотенуза. Видеодоказательство
4. Площадь прямоугольного треугольника с катетами :
5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:
6. Центр описанной окружности – есть середина гипотенузы.
7. Радиус описанной окружности есть половина гипотенузы :
8. Медиана, проведенная к гипотенузе, равна ее половине
9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:
Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.
Виды треугольников
Треугольники различаются между собой по характеру углов и по характеру сторон.
Виды треугольников по углам
- Остроугольный треугольник – это треугольник, у которого все углы острые, то есть меньше 90°.
- Прямоугольный треугольник – это треугольник, у которого один из углов является прямым, то есть равен 90°.
Стороны, образующие прямой угол называются катетами, а сторона, лежащая напротив прямого угла, называется гипотенузой.
Виды треугольников по сторонам
- Разносторонний треугольник – это треугольник, у которого все стороны имеют разную длину.
- Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой.
Равные стороны называются боковыми сторона треугольника, а третья сторона, не равная двум другим, называется его основанием.
[spoiler title=”источники:”]
http://izamorfix.ru/matematika/planimetriya/vidy_treug.html
[/spoiler]
Танюшка Шур1,5 K
Люблю смотреть российские сериалы, играть в шахматы и путешествовать. · 22 дек 2018
4 клеточки вниз, 3 вправо и соединить концы прямой линией.
Этот треугольник будет со сторонами 4,3,5
Проверим это с помощью теоремы Пифагора:
5^2=25 = 4^2+3^2= 16+9=25
1,2 K
Комментировать ответ…Комментировать…
Вы знаете ответ на этот вопрос?
Поделитесь своим опытом и знаниями
Войти и ответить на вопрос
- Учебники
- 5 класс
- Математика 👍
- Мерзляк
- №340
авторы: Мерзляк, Полонский, Якир.
издательство: Вентана-Граф, 2018 г.
Посмотреть глоссарий
Математика 5 класс Мерзляк. Номер №340
- Предыдущее
- Следующее
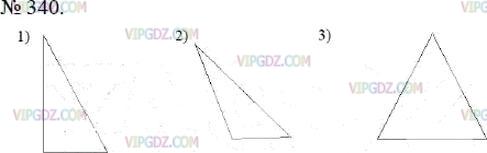
Начертите:
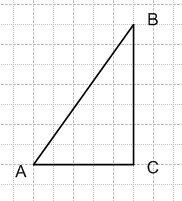
1) разносторонний прямоугольный треугольник;
2) разносторонний тупоугольный треугольник;
3) равнобедренный остроугольный треугольник.
reshalka.com
Математика 5 класс Мерзляк. Номер №340
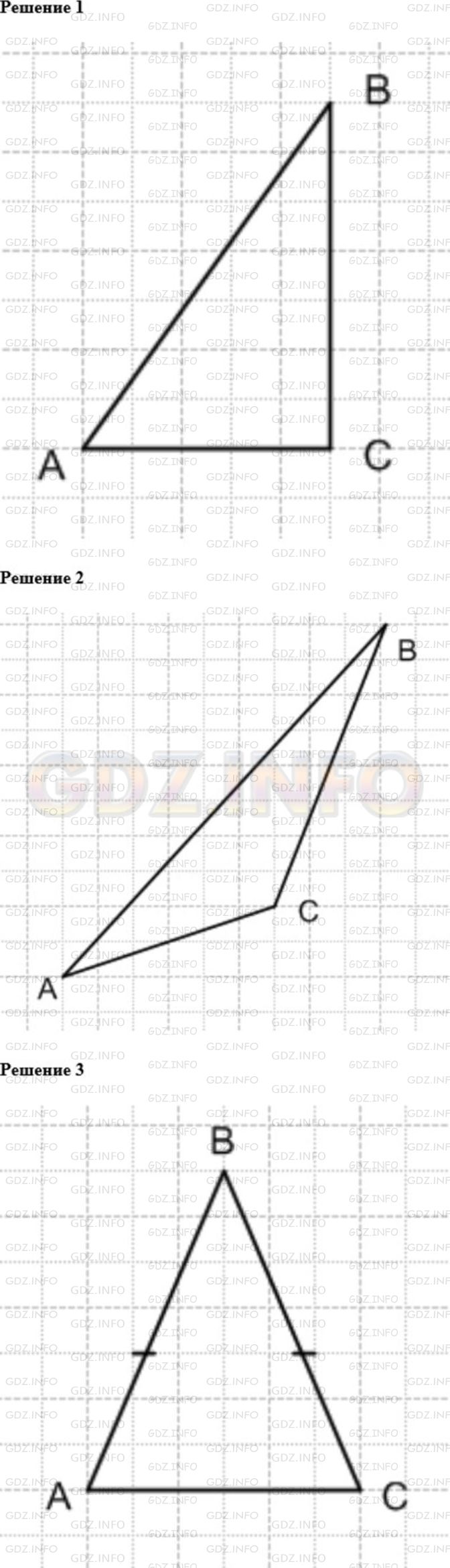
Решение 1
Получай решения и ответы с помощью нашего бота
Посмотреть калькулятор Натуральные числа
Решение 2
Решение 3
- Предыдущее
- Следующее
Нашли ошибку?
Посмотреть глоссарий
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
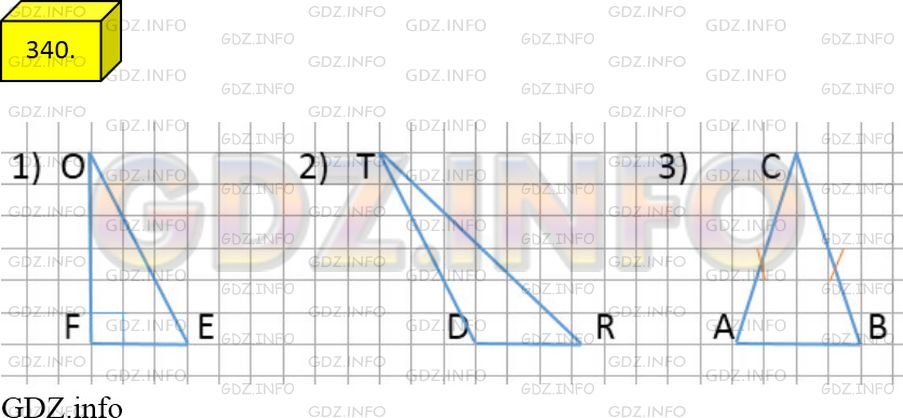
Номер № 340
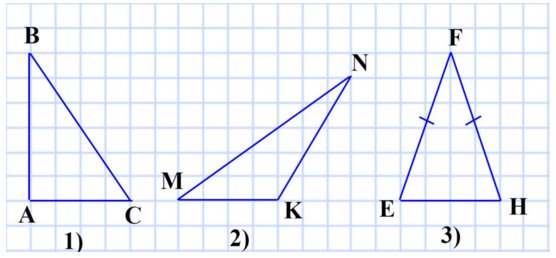
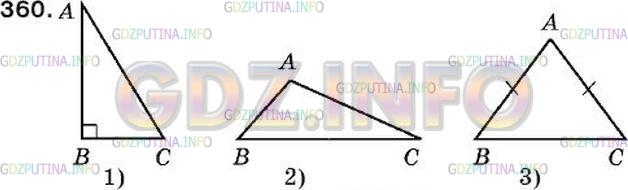
340. Начертите:
- разносторонний прямоугольный треугольник;
- разносторонний тупоугольный треугольник;
- равнобедренный остроугольный треугольник.
Решение:
1) ABC – разносторонний прямоугольный треугольник;
2) MNK – разносторонний тупоугольный треугольник;
3) EFH – равнобедренный остроугольный треугольник.
<< № 339№ 340№ 341 >>
Выбрать другой номер
Если вам понравился сайт, поделитесь страничкой в соцсетях, чтобы не потерять его:
ГДЗ по классам
2 класс
3 класс
4 класс
5 класс
6 класс
7 класс
8 класс
9 класс
10 класс
11 класс
ГДЗ и решебники
вип уровня
Условие
Начертите:
1) разносторонний прямоугольный треугольник;
2) разносторонний тупоугольный треугольник;
3) равнобедренный остроугольный треугольник.
Решение 1
Решение 2
Решение 3
Решение 4
Другие задачи из этого учебника