Как найти разрешающую строку в симплекс методе

Общая
постановка задачи

Симплексный
метод – метод последовательного
улучшения плана.

Метод
является универсальным, так как позволяет
решить практически любую задачу
линейного программирования. Математическая
модель задачи приводится к каноническому
(стандартному) виду. Заполняется опорная
симплекс – таблица с использованием
коэффициентов целевой функции и системы
ограничений. Решается задача по алгоритму.

Идея
симплексного метода заключается в том,
что начиная с некоторого исходного
опорного решения осуществляется
последовательно направленное перемещение
по допустимым решениям к оптимальному.
Значение целевой функции для задач на
максимум не убывает. Так как число
допустимых решений конечно, то через
конечное число шагов получим оптимальное
решение.

Алгоритм
симплексного метода

1.Математическую
модель задачи привести к каноническому
(стандартному) виду.

2.
Построить
начальную симплекс-таблицу исходя из
стандартного вида.

3. Найти разрешающий
столбец. В строке коэффициентов ЦФ найти
значение с самим маленьким отрицательным
числом. Этот столбец и будет разрешающим.

4.
Вычислить разрешающую
строку и ведущий элемент (Почленно
разделить столбец свободных членов на
элементы разрешающего столбца, за
исключением строки ЦФ. Выбрать наименьшее
из частных. Эта строка будет
разрешающей.Ведущий элемент будет на
пересечении разрешающего столбца и
разрешающей строки.).

5.Построить
новую симплекс-таблицу-второй шаг.

При построении
новой таблицы убрать из базиса строку
с переменной разрешающей строки в
предыдущей таблице. Ввести в базис
строку с названием разрешающего столбца
предыдущей таблицы.

• Построение ведущей
  строки в новой таблице. Почленно поделить
  всю разрешающую строку на разрешающий
  элемент.

• Построение других
  строк в новой таблице. Почленно умножить
  ведущую строку на соответствующие этим
  строкам элементы разрешающего столбца
  из предыдущей таблицы и прибавить к
  соответствующим строкам в старой
  таблице.

6. Проверяем таблицу
второго шага на оптимальность. Если в
строке целевой функции нет отрицательных
элементов, тогда таблица имеет оптимальный
план, записать ответ. Если в строке ЦФ
есть отрицательный элемент (элементы),
тогда переходят к следующему (третьему)
шагу, строят новую симплекс-таблицу в
соответствии п.5 и затем проверяют ее
на оптимальность. Построение таблиц
заканчивается с нахождением оптимального
плана.

Прямая задача на
минимум решается следующим образом:

• Написать
  математическую модель двойственной
  задачи в стандартном виде

• Решить двойственную
  модель симплекс – методом

• Записать ответ.

Связь между задачами
двойственной пары в том, что, решая
симплексным методом одну из них,
автоматически получаем решение другой.

Для этого достаточно
воспользоваться соответствием переменных
прямой и двойственной задач в последней
симплекс-таблице.

Х1	x2	…	xn	S1	S2	…	Sm
S1	S2	…	Sm	y1	y2	…	ym

Задача

На предприятии
имеется возможность выпускать n видов
продукции (1,2,…n). При ее изготовлении
используются ресурсы Р1, Р2, Р3. Размеры
прямых затрат ресурсов ограничены
соответственно величинами b1, b2, b3. Расход
i –го ресурса на единицу продукции
j-того вида составляют aij. Цена единицы
продукции j-того вида равна cj ден. ед.
Сформулировать прямую и двойственную
задачу и раскрывать экономический смысл
всех переменных.

Требуется:

Найти оптимальный
план симплекс-методом.

Найти решение
двойственной задачи

Указать дефицитность
ресурсов

Обосновать
эффективность плана производства

Оценить
целесообразность приобретения ресурса

Оценить
целесообразность выпуска новой продукции

Данные :

b1 = 25, b2
= 30, b3 = 42

a11= 2,
a12= 3, a13= 2, a14= 1

a21= 4,
a22= 1, a23= 3, a24= 2

a31= 3, a32= 5, a33= 2,a34= 2

c1= 6, c2= 5, c3= 4, c4= 3

Математическая
модель прямой задачи

max (Z=
6×1+5×2+4×3+3×4)

2×1+3×2+2×3+x4<
25

4×1+x2+3×3+2×4<
30

3×1+5×2+2×3+2×4<
42

x1,
x2,
x3,
x4
>
0

Математическая
модель двойственной задачи

min (Z*=
25y1+30y2+42y3)

2y1+4y2+3y3>
6

3y1+y2+5y3>
5

2y1+3y2+2y3>
4

y1+2y2+2y3>
3

y1,
y2,
y3,
y4
>
0

Стандартный вид

min
(Z=
-6×1-5×2-4×3-3×4)

2×1+3×2+2×3+x4+S1=25

4×1+x2+3×3+2×4+S2=30

3×1+5×2+2×3+2×4+S3=42

x1,
x2,
x3,
x4,
S1,
S2,
S3
>
0

Экономический
смысл переменных

Xi – количество
произведенной продукции

Yj – цена ресурса

Si – количество
оставшегося ресурса

базис	значение	x1	x2	x3	x4	S1	S2	S3	отношение
Z	0	-6	-5	-4	-3	0	0	0
S1	25	2	3	2	1	1	0	0	12,5
S2	30	4	1	3	2	0	1	0	7,5
S3	42	3	5	2	2	0	0	1	14
Таблица 2
базис	значение	x1	x2	x3	x4	S1	S2	S3	отношение
Z	45	0	-3,5	0,5	0	0	1,5	0
S1	10	0	2,5	0,5	0	1	-0,5	0	4
x1	7,5	1	0,25	0,75	0,5	0	0,25	0	30
S3	19,5	0	4,25	-0,3	0,5	0	-0,8	1	4,59
Таблица 3
базис	значение	x1	x2	x3	x4	S1	S2	S3	отношение
Z	59	0	0	1,2	0	1,4	0,8	0
x2	4	0	1	0,2	0	0,4	-0,2	0
x1	6,5	1	0	0,7	0,5	-0,1	0,3	0
S3	2,5	0	0	-1,1	0,5	-1,7	0,1	1

Анализ решения

Продукции 1 вида
производим 6,5 ед., второго вида 4 единицы,
третьего и четвертого вообще не
производим. Прибыль при этом составит
59 ден. единиц.

Ресурс 1 типа стоит
1,4 ден. ед., 2 типа – 0,8 ден. ед. Третий тип
ресурса у нас остался в количестве 2,5
ед., поэтому его покупать не нужно.

Ресурсы 1 и 2 типа
дефицитны, 3 типа избыточен.

Эффективность
производства

Z = 6*6.5+5*4+4*0+3*0=59
Z*=25*1.4+30*0.8+42*0=59 Производство в целом
эффективно

2*1,4+4*0,8+3*0<
6 6=6 Производство 1 вида продукции
эффективно

3*1,4+1*0,8+5*0<
5 5=5 Производство 2 вида продукции
эффективно

2*1,4+3*0,8+2*0<
4 5,2> 4 Производство 3 вида продукции не
эффективно

1*1,4+2*0,8+2*0<
3 3=3 Т.к. x4 не входит в базис, то оптимальный
план не единственен.

Оценить
целесообразность покупки 5 ед. второго
ресурса по цене 10 ден. ед, т.е. единица
ресурса обойдется нам в 2 ден. ед. Мы же
готовы покупать только по 0,8 ден. ед. за
1 единицу ресурса.

а1 = 2, а2 = 2, а3 = 4.
Цена новой продукции равна 4.

2*1,4+2*0,8+2*0<
4 4,4> 4 Производство 5 вида продукции не
эффективно.

Контрольные
вопросы.

1.Определение
математической модели экономической
задачи.

2.Виды математических
моделей ЛП.

3.Составление
математической модели.

4.Экономическая
формулировка математической модели
прямой и двойственной задач.

5.Понятие
двойственности в задачах линейного
программирования.

6.Правило построения
математической модели двойственной
задачи.

7. Первая теорема
двойственности.

8. Вторая теорема
двойственности.

9. Третья теорема
двойственности.

10.Алгоритм
геометрического метода решения задач
ЛП.

11.Симплексный
метод решения задач ЛП и его применение.

12.Алгоритмм
симплексного метода.

13.Анализ решения
задачи по симплекс – таблице, отвечающей
критерию оптимальности.

Соседние файлы в предмете Методы оптимизации

• #
• #

Пример 5.1. Решить следующую задачу линейного программирования симплекс-методом:

Решение:

I итерация:

1 этап: формирование исходной симплекс-таблицы.

Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.

В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:

Приведем целевую функцию к следующему виду:

На основе полученной задачи сформируем исходную симплекс-таблицу:

Таблица 5.3

Исходная симплекс-таблица

2 этап: определение базисного решения.

Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

.

3 этап: проверка совместности системы ограничений ЗЛП.

На данной итерации (в таблице 5.3) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).

4 этап: проверка ограниченности целевой функции.

На данной итерации (в таблице 5.3) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с отрицательным элементом в строке целевой функции (кроме колонки свободных чисел), в которой не было бы хотя бы одного положительного элемента).

5 этап: проверка допустимости найденного базисного решения.

Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.

6 этап: проверка оптимальности.

Найденное базисное решение не является оптимальным, так как согласно признаку оптимальности (признак 4) в строке целевой функции не должно быть отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, согласно алгоритму симплекс-метода переходим к 8 этапу.

8 этап: определение разрешающего элемента.

8.1. Определение разрешающей колонки.

Так как найденное базисное решение допустимое, то поиск разрешающей колонки будем производить по следующей схеме: определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.3, таких колонок две: колонка «х1» и колонка «х2». Из таких колонок выбирается та, которая содержит наименьший элемент в строке целевой функции. Она и будет разрешающей. Колонка «х2» содержит наименьший элемент (–3) в сравнении с колонкой «х1». Следовательно, ее принимаем в качестве разрешенной.

8.2. Определение разрешающей строки.

Для определения разрешающей строки находим положительные оценочные отношения свободных чисел к элементам разрешающей колонки, строка, которой соответствует наименьшее положительное оценочное отношение, принимается в качестве разрешенной.

Таблица 5.4

Исходная симплекс-таблица

В таблице 5.4 наименьшее положительное оценочное отношение соответствует строке «х5», следовательно, она будет разрешающей.

Элемент, расположенный на пересечение разрешающей колонки и разрешающей строки, принимается в качестве разрешающего. В нашем примере – это элемент , который расположен на пересечении строки «х5» и колонки «х2».

9 этап: преобразование симплекс-таблицы.

Разрешающий элемент показывает одну базисную и одну свободную переменные, которые необходимо поменять местами в симплекс-таблице, для перехода к новому «улучшенному» базисному решению. В данном случае это переменные х5 и х2, в новой симплекс-таблице (таблице 5.5) их меняем местами.

9.1. Преобразование разрешающего элемента.

Разрешающий элемент таблицы 5.4 преобразовывается следующим образом:

Полученный результат вписываем в аналогичную клетку таблицы 5.5.

9.2. Преобразование разрешающей строки.

Элементы разрешающей строки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей строки приведены в таблице 5.5.

9.3. Преобразование разрешающей колонки.

Элементы разрешающей колонки таблицы 5.4 делим на разрешающий элемент данной симплекс-таблицы, а результат берется с обратным знаком. Полученные результаты вписываются в аналогичные ячейки новой симплекс-таблицы (таблицы 5.5). Преобразования элементов разрешающей колонки приведены в таблице 5.5.

9.4. Преобразование остальных элементов симплекс-таблицы.

Преобразование остальных элементов симплекс-таблицы (т.е. элементов не расположенных в разрешающей строке и разрешающей колонке) осуществляется по правилу «прямоугольника».

К примеру, рассмотрим преобразование элемента, расположенного на пересечении строки «х3» и колонки «», условно обозначим его «х3». В таблице 5.4 мысленно вычерчиваем прямоугольник, одна вершина которого располагается в клетке, значение которой преобразуем (т.е. в клетке «х3»), а другая (диагональная вершина) – в клетке с разрешающим элементом. Две другие вершины (второй диагонали) определяются однозначно. Тогда преобразованное значение клетки «х3» будет равно прежнему значению данной клетки минус дробь, в знаменателе которой разрешающий элемент (из таблицы 5.4), а в числителе произведение двух других неиспользованных вершин, т.е.:

«х3»: .

Аналогично преобразуются значения других клеток:

«х3 х1»: ;

«х4»: ;

«х4 х1»: ;

«х6»: ;

«х6 х1»: ;

« »: ;

« х1»: .

В результате данных преобразований получили новую симплекс- таблицу (таблица 5.5).

II итерация:

1 этап: составление симплекс-таблицы.

По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

Таблица 5.5

Симплекс-таблица II итерации

2 этап: определение базисного решения.

В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.5):

.

Как видно, при данном базисном решении значение целевой функции =15, что больше чем при предыдущем базисном решении.

3 этап: проверка совместности системы ограничений.

Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.5 не выявлена.

4 этап: проверка ограниченности целевой функции.

Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.5 не выявлена.

5 этап: проверка допустимости найденного базисного решения.

Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.5) содержится отрицательный элемент: –2 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.

8 этап: определение разрешающего элемента.

8.1. Определение разрешающей колонки.

Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.5, такой колонкой является только одна колонка: «х1». Следовательно, ее принимаем в качестве разрешенной.

8.2. Определение разрешающей строки.

Согласно полученным значениям положительных оценочных отношений в таблице 5.6, минимальным является отношение, соответствующее строке «х3». Следовательно, ее принимаем в качестве разрешенной.

Таблица 5.6

Симплекс-таблица II итерации

9 этап: преобразование симплекс-таблицы.

Преобразования симплекс-таблицы (таблицы 5.6) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.7.

III итерация

1 этап: построение новой симплекс-таблицы.

По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

Таблица 5.7

Симплекс-таблица III итерации

2 этап: определение базисного решения.

В результате проведенных симплекс-преобразований получили новое базисное решение (таблица 5.7):

.

3 этап: проверка совместности системы ограничений.

Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.7 не выявлена.

4 этап: проверка ограниченности целевой функции.

Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.7 не выявлена.

5 этап: проверка допустимости найденного базисного решения.

Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 не оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.7) содержится отрицательный элемент: –3 (свободное число данной строки при рассмотрении данного признака не учитывается). Следовательно, переходим к 8 этапу.

8 этап: определение разрешающего элемента.

8.1. Определение разрешающей колонки.

Найденное базисное решение допустимое, определяем колонки с отрицательными элементами в строке целевой функции (кроме колонки свободных чисел). Согласно таблице 5.7, такой колонкой является только одна колонка: «х5». Следовательно, ее принимаем в качестве разрешенной.

8.2. Определение разрешающей строки.

Согласно полученным значениям положительных оценочных отношений в таблице 5.8, минимальным является отношение, соответствующее строке «х4». Следовательно, ее принимаем в качестве разрешенной.

Таблица 5.8

Симплекс-таблица III итерации

9 этап: преобразование симплекс-таблицы.

Преобразования симплекс-таблицы (таблицы 5.8) выполняются аналогично, как и в предыдущей итерации. Результаты преобразований элементов симплекс-таблицы приведены в таблице 5.9.

IV итерация

1 этап: построение новой симплекс-таблицы.

По результатам симплекс-преобразований предыдущей итерации составляем новую симплекс-таблицу:

Таблица 5.9

Симплекс-таблица IV итерации

2 этап: определение базисного решения.

В результате проведенных симплекс-преобразований получили новое базисное решение, согласно таблице 5.9 решение следующее:

.

3 этап: проверка совместности системы ограничений.

Не совместность системы ограничений в соответствии с признаком 1 в таблице 5.9 не выявлена.

4 этап: проверка ограниченности целевой функции.

Неограниченность целевой функции в соответствии с признаком 2 в таблице 5.9 не выявлена.

5 этап: проверка допустимости найденного базисного решения.

Найденное базисное решение в соответствии с признаком 3 допустимое, так как не содержит отрицательных компонент.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.9) нет отрицательных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

7 этап: проверка альтернативности решения.

Найденное решение является единственным, так как в строке целевой функции (таблица 5.9) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

Ответ: оптимальное значение целевой функции рассматриваемой задачи =24, которое достигается при .

Пример 5.2. Решить вышеприведенную задачу линейного программирования при условии, что целевая функция минимизируется:

Решение:

I итерация:

1 этап: формирование исходной симплекс-таблицы.

Исходная задача линейного программирования задана в стандартной форме. Приведем ее к каноническому виду путем введения в каждое из ограничений-неравенств дополнительной неотрицательной переменной, т.е.

В полученной системе уравнений примем в качестве разрешенных (базисных) переменные х3, х4, х5, х6, тогда свободными переменными будут х1,х2. Выразим базисные переменные через свободные:

Приведем целевую функцию к следующему виду:

На основе полученной задачи сформируем исходную симплекс-таблицу:

Таблица 5.10

Исходная симплекс-таблица

2 этап: определение базисного решения.

Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

.

3 этап: проверка совместности системы ограничений ЗЛП.

На данной итерации (в таблице 5.10) признак несовместности системы ограничений (признак 1) не выявлен (т.е. нет строки с отрицательным свободным числом (кроме строки целевой функции), в которой не было бы хотя бы одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной)).

4 этап: проверка ограниченности целевой функции.

На данной итерации (в таблице 5.10) признак неограниченности целевой функции (признак 2) не выявлен (т.е. нет колонки с положительным элементом в строке целевой функции (колонка свободных чисел не рассматривается), в которой не было бы хотя бы одного положительного элемента).

5 этап: проверка допустимости найденного базисного решения.

Так как найденное базисное решение не содержит отрицательных компонент, то оно является допустимым.

6 этап: проверка оптимальности найденного базисного решения.

Найденное базисное решение в соответствии с признаком 4 оптимальное, так как в строке целевой функции симплекс-таблицы (таблица 5.10) нет положительных элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

7 этап: проверка альтернативности решения.

Найденное решение является единственным, так как в строке целевой функции (таблица 5.10) нет нулевых элементов (свободное число данной строки при рассмотрении данного признака не учитывается).

Ответ: оптимальное значение целевой функции рассматриваемой задачи =0, которое достигается при .

Пример 5.3. Решить следующую задачу линейного программирования симплекс-методом:

Решение:

I итерация

1 этап: составление исходной симплекс-таблицы.

Задача линейного программирования задана в каноническом виде. Составим расширенную матрицу и выделим с помощью метода Жордана-Гаусса базисные переменные. Примем в качестве базисных – переменные х1 и х2.

Умножим (поэлементно) первую строку на –3 и сложим со второй:

.

Умножим вторую строку на :

.

Сложим вторую с первой строкой:

.

В результате система ограничений примет следующий вид:

Выразим базисные переменные через свободные:

Выразим целевую функцию также через свободные переменные, для этого подставим полученные значения базисных переменных в целевую функцию:

.

Запишем целевую функцию в следующем виде:

.

Составим исходную симплекс-таблицу:

Таблица 5.11

Исходная симплекс-таблица

2 этап: определение базисного решения.

Согласно определению базисного решения свободные переменные равны нулю, а значения базисных переменных – соответствующим значениям свободных чисел, т.е.:

.

Найденное базисное решение является вырожденным, т.к. имеется базисная переменная х2, равная нулю.

3 этап: проверка совместности системы ограничений ЗЛП.

Так как в таблице 5.11 имеется строка с отрицательным свободным числом (–1), в которой нет ни одного отрицательного элемента (т.е. отрицательного коэффициента при свободной переменной), то согласно признаку несовместности (признак 1) система ограничений данной задачи не совместна (строка целевой функции при рассмотрении данного признака не учитывается). Следовательно, рассматриваемая задача линейного программирования не имеет решения.

Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности ее системы ограничений.

Прочие статьи цикла

Введение

Задача линейного программирования (ЗЛП) состоит в определении значений упорядоченной совокупности переменных x_j, j = 1(1)n при которых линейная целевая функция достигает экстремального значения и при этом выполняются (удовлетворяются) все ограничения (они также линейные) в форме равенств или неравенств. Требуется найти план  Х _<n> = <x₁, x₂, …, x_n>, который обеспечивает получение целевой функцией с экстремальным значением. Идеи моделей линейного планирования (программирования) впервые были высказаны и опубликованы советским математиком Л. В. Канторовичем в 1939 году в работе “математические методы организации и планирования производства”. В 1975 году Л. В. Канторович и Т. Купманс получили Нобелевскую премию по экономическим наукам с формулировкой «за их вклад в теорию оптимального распределения ресурсов». В 1947 г. очень близкие идеи высказаны американским математиком Дж. Данцигом. А еще позднее стали массово появляться работы, посвященные проблемам выбора оптимальных решений в силу их исключительной важности. Признание приоритета за Л. В. Канторовичем не оспаривалось практически никогда, а после присуждения Нобелевской премии тем более. 

Общая постановка задачи

Задача линейного программирования (ЗЛП) состоит в определении значений упорядоченной совокупности переменных x_j, j = 1(1)n при которых линейная целевая функция достигает экстремального значения и при этом выполняются (удовлетворяются) все ограничения в форме равенств или неравенств. Требуется найти план  Х _<n> = <x₁, x₂, …, x_n>, который обеспечивает получение целевой функцией экстремального значения

а) Если система ограничений ЗЛП обладает хотя бы одним решением, она называется совместной в противном случае несовместной; б) Допустимое множество решений ЗЛП не пусто, если система ограничений совместна; в) Множество допустимых решений ЗЛП (если оно не пусто) в общем случае является многогранным множеством. Линейная функция Q(X_<n>) называется функцией цели, целевой функцией (ЦФ), множество планов {X_<n>} удовлетворяющих системе ограничений (2) – (5), ­­- множеством допустимых решений (альтернатив) и обозначается символом R, X_<n>є Ω  Допустимый план X_<n>є Ω, доставляющий целевой функции (1) экстремальное значение, называется оптимальным. Задача в форме (1) – (5) представляет общую задачу линейного программирования.

Cтандартная форма задачи

Если все ограничения задачи заданы в виде строгих равенств и на переменные величины наложено условие неотрицатаельности  x_j ≥0, j = 1(1)n, то такую формулировку называют стандартной:

Экстремумы функций в общем случае связаны простыми соотношениями

Переход от общей задачи к стандартной     

1. Для удобства применения методов решения выполняют преобразование исходной общей задачи. Ограничения неравенства преобразуют в равенства. Вводятся дополнительные переменные по числу неравенств, т. е. формулируют расширенную задачу x_n+1 ≥0, x_n+2 ≥0, … , x_n+k ≥0. Неравенства a_i1x₁+a_i2x₂+…+a_inx_n ≥b_i введением переменной x_n+1≥0 преобразуются в равенства a_i1x₁+a_i2x₂+…+a_inx_n + a_i(n+1)x_n+1=b_i. В ЦФ вновь введённые переменные имеют коэффициенты равные нулю c_n+1=c_n+2=…=c_n+k =0.

2. а) Если в исходной общей задаче на некоторые переменные  x_j , j = 1(1)n,  не наложено условие их неотрицательности, то каждую такую переменную представляют в виде разности положительных новых переменных x’_j – x”_j , где x’_j≥0 и x”_j≥0 , j>r . Способ устранения отрицательных переменных прост, но при этом размерность (число неотрицательных переменных) задачи возрастает.      б) Имеется другой более сложный путь. Каждую x_j ≯ 0 выражают явно через другие, для которых условие x_j ≥0 выполняется. Затем найденные выражения подставляют в ограничения, чтобы исключить их из рассмотрения. При этом размерность задачи даже уменьшается. 

Каноническая форма задачи

Удобство этой формы ЗЛП состоит в том, что она позволяет предельно просто получить первое допустимое решение. Для этой формы должны быть выполнены условия:

• правые части в ограничениях – неотрицательны b_i ≥ 0, i = 1(1)m;

• каждое уравнение содержит переменную x_j ≥0  с коэффициентом при ней равным “1” в этом уравнении и с коэффициентом “0” во всех других уравнениях; эти переменные называют дополнительными или искусственными;

• в ЦФ эти переменные входят с коэффициентом “0”;

• определение опорного плана (начальной вершины) выполняют методом искусственного базиса, что ещё до решения задачи позволяет выяснить факт существования решения.

  Если исходная задача имеет хотя бы один план, то расширенная задача (после введения искусственных переменных в систему ограничений) также содержит этот план в качестве своего допустимого решения

Переменные x₁, x₂, …, x_m называют базисными – остальные свободными (внебазисными).      Вершина допустимой области решений записывается в виде точки <β₁, β₂, …, β_m, 0, 0,…,0>, так как векторы условий для x₁, x₂, …, x_m являются линейно независимыми (образуют подматрицу, где единицы помещаются только на главной диагонали).

Геометрическая интерпретация ЗЛП

Будем рассматривать пример ЗЛП в производстве двух видов продукции на предприятии, использующем при этом четыре виды сырья (см. ранее эту задачу). Этот пример удобен для геометрической интерпретации тем, что пространство решений является двумерным (т. е. плоскость) и все элементы ЗЛП допускают наглядное представление (изображение) в трёхмерном пространстве. Начнём с рассмотрения системы неравенств (ограничений ЗЛП). Заметим, что каждое i-е неравенство в ограничениях ЗЛП определяет полуплоскость в системе координат х₁Ох₂ с граничной прямой a_i1x₁ + a_i2x₂ = b_i , i = 1(1)m.

 Выпишем их и присвоим им имена

Область, формируемая полуплоскостями, может быть получена в виде замкнутого или разомкнутого (неограниченного) многогранника. Путём непосредственного построения границ (прямых) и выявления области пересечения полупространств выясним, является ли многогранное множество ограниченным и не пусто ли оно (рис.). Имеем на плоскости х₁ О х₂ многоугольник А Ո В Ո C Ո D Ո E Ո F . Он является выпуклым (всегда ли?), его граница образована отрезками прямых.

Целевая функция. Что можно сказать о линейной форме (ЦФ)? Это функция двух переменных x₁ и x2, её образ в трёхмерном пространстве – плоскость, проходящая через начало координат. Найдём частные производные ЦФ по х_j

Так как частная производная по переменной х_j представляет наибольшую скорость изменения функции Q в направлении этой оси, то вектор C_<n>= <c₁, c₂> – это вектор наибольшего изменения ЦФ, вектор градиентного направления. Если значения Q зафиксировать Q =Q₁ = const , то уравнение ЦФ превращается в уравнение прямой c₁x₁ + c₂x₂= Q₁= const плоскости х₁О х₂

В трёхмерном пространстве это плоскость параллельная х₁О х₂  на высоте Q₁, в каждой точке <x1, x2, Q_1>  которой значение ЦФ постоянно и равно Q₁. . На плоскости Q этой прямой соответствует линия параллельная плоскости х₁О х₂, которую называют линией уровня (плотницкий уровень) функции c₁x₁ + c₂x₂ . Изменяя Q, получим семейство линий уровня параллельных друг другу. Требованию задачи – поиску экстремума Q соответствует смещение точки по поверхности функции Q в направлении вектора C_<n>= <c₁, c₂>  от начала координат.

Ограничения ЗЛП не позволяют аргументам ЦФ Q(x1, x2) выходить за пределы многоугольной допустимой области. Другими словами, надо найти точку на плоскости Q наиболее удалённую от плоскости х₁О х₂ и проекция которой на х₁О х₂ лежит в области допустимых решений. Координаты x*₁, x*₂ найденной точки и определяют оптимальный план ЗЛП. Покажем, что семейство линий уровня (изолиний) перпендикулярно C_<n>, т. е. перпендикулярно прямой х₂ =с₂х₁/c₁. Из векторного анализа известно, что все линии уровня ЦФ Q перпендикулярны вектору градиенту ЦФ, вычисленному в некоторой точке

Таким образом, перемещаясь вдоль вектора C_<n> или по прямой х₂ =с₂х₁/c₁, легко построить линию уровня (она перпендикулярна х₂ = с₂х₁/c₁ ) и вычислить значение ЦФ Q для этой линии. Экстремум Q, очевидно, будет достигаться в положении касания линией уровня (её проекцией) границы множества допустимых решений. Такое касание может быть трёх типов: в вершине, по ребру, по грани многогранника. Этим типам касания соответствуют: единственное решение в вершине и бесконечное множество решений в других случаях.       Область допустимых решений. Рассмотрим случаи ограниченной и неограниченной области допустимых решений. В последнем случае поиск экстремума Q может приводить к отсутствию решения, так как extr Q → ±∞ или существует опорная прямая линия, касающаяся неограниченного многогранника, и тогда решение существует.

Пример. Описание области допустимых решений. 

Мы можем записать уравнение границы области D заданной неравенствами:

Основные понятия и теоремы линейной алгебры Важным понятием линейной алгебры является понятие линейного векторного пространства. Определение 2.1. Упорядоченная совокупность n действительных чисел называется n-мерным вектором. Определение 2.2. Совокупность всевозможных n-мерных векторов после введения в нее операций сложения и умножения на действительное число называется n-мерным линейным векторным пространством. Частными случаями линейных пространств являются прямая, плоскость, трехмерное пространство. Определение 2.3. Система векторов X₁, X₂, …, X_n называется линейно зависимой, если существуют такие числа λ₁, λ₂, …, λ_n, не равные нулю одновременно, при которых имеет место равенство: λ₁X₁+ λ₂X₂ …+ λ_n X_n=0 , где все λ_i ≥0 и λ₁+ λ₂+ …+ λ_n =1. Если же это равенство возможно лишь в случае, когда все λ_i = 0 (i = 1(1)n) , то система векторов называется линейно независимой. Определение 2.4. Базисом n-мерного векторного пространства называется любая совокупность n линейно независимых векторов этого пространства. В двумерном пространстве за базис могут быть взяты любые два неколлинеарных вектора, в частности, е₁ = (1,0), е₂ = (0, 1). В трехмерном пространстве – любые три некомпланарных вектора, например, е₁ = (1,0,0), е₂ = (0,1,0), е₃ = (0,0,1).

Выпуклой линейной комбинацией точек X₁, X₂, …, X_n называется линейная комбинация вида: X= λ₁X₁+ λ₂X₂ …+ λ_n X_n где все λ_i ≥0 и λ₁+ λ₂+ …+ λ_n =1. В частности, когда имеются две точки X₁ и X₂, то их выпуклая комбинация λX₁+(1- λ)X₂, λ ∈[0,1] представляет собой точку на отрезке, соединяющем эти точки.

Теорема 1. Любой вектор n-мерного векторного пространства можно представить, как линейную комбинацию векторов базиса, притом единственным образом. Определение 2.5. Максимальное число линейно независимых векторов линейного пространства называется размерностью линейного пространства. Линейное пространство обычно обозначают, R_n где n – его размерность. Выпуклой оболочкой точек называется множество всевозможных выпуклых комбинаций этих точек. Множество называется выпуклым, если вместе с двумя любыми его точками оно содержит и их произвольную выпуклую линейную комбинацию. С геометрической точки зрения это означает, что выпуклое множество содержит вместе с любыми двумя своими точками и соединяющий их отрезок. Выпуклое множество совпадает со своей выпуклой оболочкой. Примерами выпуклых множеств являются прямолинейный отрезок, квадрат, круг, прямая, полуплоскость, куб, шар, полупространство и другие. Угловыми точками выпуклого множества называются точки, не являющиеся выпуклой линейной комбинацией двух произвольных точек множества. Например, угловыми точками треугольника являются его вершины, угловыми точками круга – точки окружности. Таким образом, выпуклое множество может иметь конечное или бесконечное число угловых точек, но может не иметь их совсем. Например, прямая, плоскость, полуплоскость, пространство, полупространство угловых точек не имеют. Одним из основных понятий теории линейного программирования является понятие выпуклого многогранника в n-мерном пространстве, частными случаями которого являются при n =  1 отрезок на прямой, при n = 2 выпуклый многоугольник на плоскости. Выпуклым многоугольником называется выпуклое замкнутое ограниченное множество точек на плоскости, имеющее конечное число угловых точек, называемых вершинами. Прямолинейные отрезки, соединяющие две вершины и образующие границу, называются сторонами многоугольника.

Опорной прямой выпуклого многоугольника называется прямая, имеющая с многоугольником, расположенным по одну сторону от нее, хотя бы одну общую точку.

Выпуклым многогранником называется выпуклое замкнутое ограниченное множество точек пространства, имеющее конечное число угловых точек, называемых его вершинами. Многоугольники, ограничивающие многогранник, называются его гранями, а отрезки, по которым пересекаются грани, называются ребрами. Опорной плоскостью многогранника называется плоскость, имеющая с многогранником, расположенным по одну сторону от нее, хотя бы одну общую точку.

Теорема 2.2. Выпуклый n-мерный многогранник является выпуклой линейной комбинацией своих угловых точек.

Следствие 2.3. Из теоремы вытекает, что выпуклый многогранник порождается своими угловыми точками (вершинами): отрезок – двумя точками, треугольник – тремя точками, n – угольник на плоскости – n точками и т. д. В тоже время выпуклая многогранная область, содержащая бесконечно удаленную точку, являясь неограниченным множеством, не определяется однозначно своими угловыми точками: любую ее точку нельзя представить в виде выпуклой линейной комбинации угловых точек.

Элементы выпуклых множеств

Определение 1. Множеством называется совокупность элементов любой природы, для которых задано правило принадлежности к данному множеству.

Определение 2. е – о к р е с т н о с т ь ю точки х называется множество всех точек, расстояние которых до точки х меньше е.

Определение 3. Точка х₁ называется внутренней точкой множества M, если существует такая – окрестность данной точки, все точки которой принадлежат множеству M.

Определение 4. Точка х₂ называется в н е ш н е й т о ч к о й м н о ж е с т в а M, если существует такая – окрестность данной точки, все точки которой не принадлежат множеству М.

Определение 5. Точка х₃ называется г р а н и ч н о й т о ч к о й м н о ж е с т в а M, если в любой её – окрестности существуют точки как принадлежащие множеству M, так и не принадлежащие этому множеству.

Определение 6. Множество М называется з а м к н у т ы м, если оно содержит все свои граничные точки. х 2– незамкнутое множество, Пример. х 2 – замкнутое множество.

Определение 7. Множество М называется в ы п у к л ы м, если вместе с любыми двумя точками, принадлежащими данному множеству, оно содержит и отрезок их соединяющий. В общей форме ЗЛП каждый символ R1, R2, …, Rm означает один из знаков: = или ≠. В такой форме задачи линейного программирования часть переменных может быть подчинена условию неотрицательности (x_i ≥ 0), часть – условию неположительности (x_j ≤ 0), а какие-то переменные, возможно, могут принимать любые значения.

Общий алгоритм симплексного метода ЗЛП

Решается задача

Пусть система невырожденна и совместна, т.е. r_A = r_B = r = m<n  – ранг.

Выделим m = r базисных переменных x₁, x₂, …, x_m , ф = 1(1)m и k = n – m свободных переменных x_m+1, x_m+2, …, x_n , j = m + 1(1)n ; ЦФ и базисные переменные выразим через свободные

Все введённые переменные в новых обозначениях удобно свести в таблицу, которая называется симплексной.

Алгоритм решения

1) Формируем исходный план при свободных переменных; x_j =0, j = m+1(1)n, x_j = β_ф, ф = 1(1)m при β_ф > 0 план x^o_<n> допустим Q(x) =x_o.

2) Проверяем этот план на оптимальность, используя значения γ_j коэффициентов ЦФ в последней строке таблицы. Могут быть два случая:

а) все γ_j ≤0, j = m+1(1)n , при этом увеличение никакой переменной (из свободных) не приведёт к уменьшению ЦФ Q, т. е. план x^o_<n> улучшить нельзя, и он уже оптимален, таким образом, условием оптимальности плана является – отсутствие в таблице γ_j >0.

б) некоторые γ_j > 0.   В этом случае увеличение значений соответствующих свободных переменных x_j (γ_j > 0) будет минимизировать Q, так как

Чтобы Q уменьшалось, такие переменные следует вводить (последовательно) в базис, но, чтобы размерность пространства не изменялась из базиса должны выводиться переменные в число свободных (по одной) формируем множество индексов Г = { j | γ_j >0}.          Какая переменная должна первой вводиться в базис? Вообще последовательно перебирая (вершины симплекса) решение отыскивается при произвольном выборе, но для определённости выбираем новую базисную переменную с индексом v = argmax {x_j}, где j ∈ Г. Теперь определим переменную (базисную), которая будет выводиться из базиса.

В системе уравнений

Начинаем увеличивать х_v до тех пор, пока некоторый х_ф станет отрицательным. Первый же х_ф ≤ 0 будет выводиться из базиса. Определение. Столбец с индексом v и строка с индексом ф = i называются направляющими.

3) Проверка существования решения (ограниченность ЗЛП). В выражениях, связывающих х, ∝, β, х_ф = β_ф -∝_фvх_v, ф=1(1)m, могут быть все ∝_фv < 0 и тогда рост х_v будет неограниченно увеличивать все х_ф, т.е. ни одно отрицательное значение не будет принимать.  Это случай, когда ЦФ Q  не ограничена снизу и, следовательно, ЗЛП не имеет оптимального решения.

Признаком неограниченности ЦФ является отсутствие в направляющем v– м столбце значений ∝_фv > 0. Пусть ЦФ ограничена и некоторые ∝_фv > 0. Сформируем множество индексов S = { ф | ∝_фv >0}. Из базиса необходимо выводить переменную с индексом i, так как она первая обращается в нуль, i = argmin(β_ф/∝_фv), где ф∈S, таким образом, базисная переменная x_i выводится из базиса.

Определение. Коэффициент ∝_фv=∝_iv ,  стоящий на пересечении направляющих строки и столбца называется направляющим (разрешающим, генеральным) элементом таблицы.

4) Формируем новые множества:

Дальнейшие действия алгоритма:

• преобразуем задачу, т.е. все базисные переменные и целевую функцию выражаем через свободные переменные;

• заполняем новую симплексную таблицу;

• делаем все свободные переменные х_j = 0 и находим опорный план;

  Опорный план (вектор) такой Х’_<n>=< β₁,β₂,…,β_v,,…,β_m, 0, 0…,0>; Q(Х’_<n>) ≤ Q₀ ;

• если план не оптимален, то определяем направляющий столбец;

• проверяем существует ли оптимальный план;

• если оптимальный план существует, то находим направляющую строку и вновь изменяем базис и т. д.   

• Переход от одной таблицы к другой связан с трудоемкими расчетами (о чем надо еще написать)    Вводимую в базис переменную х_ν (икс ню) выражаем через свободные переменные и выводимую х_i. Действуем так.

При ручном счете все эти действия проще выполнять с использованием вспомогательных таблиц по правилам специального алгоритма. Эти таблицы имеют прежнюю структуру, но клетки делятся на две полуклетки. В верхней полуклетке оставляем содержимое из прежней таблицы.

При решении задач линейного программирования вычисляются ранги у матрицы ограничений и расширенной матрицы ранги должны быть равны r=m.

Матрица и её ранг. Система mn чисел, расположенных в форме прямоугольной таблицы из m строк и n столбцов, называется матрицей.

Определение. Рангом матрицы [A] называется наибольший порядок, который могут иметь её миноры, не обращающиеся в нуль. Для определения ранга матрицы следует рассмотреть все её миноры порядка р (где р – меньшее из чисел m, n, если m ≠ n или р = m = n); если хотя бы один из них ≠ 0, то ранг [A] равен р; если же все они равны (= 0), то следует рассмотреть все миноры порядка р – 1 и т. д. Практически поступают наоборот: переходят от миноров меньшего порядка к минорам большего порядка, в соответствии со следующим правилом. Если найден минор k-го порядка D_k, отличный от нуля, то остается вычислить только те миноры (k + 1) -го порядка, которые представляют собой «окаймление» D_k, например,

Определение. Минором k-го порядка матрицы [A] (k ≤ m, k ≤ n) называется определитель D, составленный (с сохранением порядка) из k² элементов матрицы, лежащих на пересечении некоторых её k столбцов и k строк См. схему выше минор D из 3-х строк и 3-х столбцов. Обозначается матрица символами:

Приведем пример вычисления ранга матрицы.

С выполнением каждого шага связаны процедуры:

1. Получение опорного плана; 2. устанавливается, является ли данный опорный план оптимальным; 3. если нет, то существует ли оптимальный план вообще, или задача является неограниченной; 4. если оптимальный план существует, то, как перейти на следующем шаге, к новому опорному плану с меньшим значением ЦФ.

Алгоритм СМ применяется к ЗЛП после её приведения к канонической форме, т.е. отыскивается минимум целевой функции min Q(X) на множестве векторов Х_<n>.

Система ограничений совместна r_A = r_B  и detA ≠ 0 невырожденная, т.е. ранг r =m матрицы A_{[m, n]} и расширенной матрицы системы равен m. Имеется множество решений. Для решения системы произвольным (n – m) переменным могут быть приданы любые, в частности, нулевые значения. Эти переменные называются свободными. Обычно их индексируют x_e, e =(m+1)(1)n. Остальные переменные (их называют базисными), однозначно определяются из решения системы

(здесь x_e, e =(m+1)(1)n). Матрица этой системы неособенная и, следовательно, система имеет единственное решение x_j , j =1(1)m.

Исходный опорный план ЗЛП – вектор, содержащий значения всех переменных задачи как базисных, так и свободных, т.е. этот вектор Х_<n>, удовлетворяет ограничениям, но не обеспечивает, как правило, экстремума ЦФ. Общее число опорных планов очевидно равно числу сочетаний из n по m. Оптимальный план можно выявить, перебрав их все. Такой путь громоздок и неприемлем уже при n, m ≈ 10 ÷15.

Алгоритм СМ тоже перебирает опорные планы, но не все, а направленно, т.е. на каждом шаге ЦФ уменьшается. Число шагов имеет тот же порядок, что и число уравнений в ограничениях.

Приведем пояснения некоторым понятиям и терминам, широко используемым в алгоритме решения задач линейного программирования симплексным методом и тесно связанными с ним методами.

Определение. Системой линейных уравнений называют систему следующего вида. Ранг матрицы определяется через миноры  r = – 5.

Решение системы уравнений. Решаем относительно переменных x и y, полагаем z = 1. Получаем единственное решение х = –2/5, y = 3/5, z =1. Все другие решения получаются из этого линейно-независимого фундаментального решения:  х = –2k/5; y = 3k/5;  z = k  или х = 2k , y = 3k, z = 5k. Подобные системы возникают при описании ограничений ЗЛП. Существенную роль при решении ЗЛП играют определители подобных систем (Δ = 0, Δ ≠ 0). При однородной системе определитель должен быть равен нулю.

Определение. Симплекс – выпуклый многоугольник в n-мерном пространстве с n + 1 вершинами, не лежащими в одной гиперплоскости. Симплексы выделены в отдельный класс потому, что в n-мерном пространстве n точек всегда лежат в одной гиперплоскости. Другими словами, симплекс – это простейший многоугольник, содержащий некоторый объем n-мерного пространства. В обычном (трехмерном) пространстве симплекс – это тетраэдр; трехмерный объем совпадает с объемом тела. На плоскости симплекс – это треугольник, двумерный объем – площадь; на прямой – симплекс – отрезок, объем – длина отрезка.

Определение. Гиперпространство, гиперплоскость. Гиперпространство многомерного (n-мерного) пространства – это его подпространство размерности (n – 1). Главное свойство гиперпространства – то, что оно «самое большое» подпространство. Иначе говоря, если к базису выбранного гиперпространства добавить еще один линейно независимый вектор, то можно получить базис всего пространства.

Например, для трехмерного пространства гиперпространством является плоскость (любая), проходящая через начало координат. Для двумерного пространства – гиперпространство – это прямая линия, проходящая через нуль.

Гиперплоскость в n-мерном пространстве обобщает наши представления о роли прямой на плоскости и плоскости в пространстве. Например, в n-мерном пространстве через любые n точек можно провести единственную гиперплоскость (как в трехмерном через три точки общего положения, т.е. не лежащие на одной прямой).

Гиперплоскость определяется линейной формой: а₁х₁ + а₂х₂ + … + а_nx_n = k, где коэффициенты (а₁, а₂, …, а_n) представляют собой координаты вектора А.

Гиперплоскость делит пространство (соответствующей размерности) на два полупространства. Все точки каждого из них определяются неравенствами. Например, в случае прямой линии на плоскости: а₁х₁ + а₂х₂ ≥_Z,  или  а₁х₁ + а₂х₂ >Z _, а₁х₁ + а₂х₂ <_Z  а₁х₁ + а₂х₂ ≤_Z. Эти два варианта различаются тем, к какой полуплоскости мы относим разделяющую прямую.  

Литература

Один из методов решения оптимизационных задач (как правило связанных с нахождением минимума или максимума) линейного программирования называется симплекс-методом. Симплекс-метод включает в себя целую группу алгоритмов и способов решения задач линейного программирования. Один из таких способов, предусматривающий запись исходных данных и их пересчет в специальной таблице, носит наименование табличного симплекс-метода.

Рассмотрим алгоритм табличного симплекс-метода на примере решения производственной задачи, которая сводится к нахождению производственного плана обеспечивающего максимальную прибыль.

Решение задачи табличным симплекс-методом

Решение задачи происходит в несколько последовательных этапов. Разберем их на небольшом примере производственной задачи.

1. Определение исходных данных

В нашем примере, по условиям задачи предприятие выпускает 4 вида изделий, обрабатывая их на 3 станках.

Исходные данные для производственной задачи запишем в формате матриц:

• Матрица A — нормы времени на обработку изделий;
• Матрица B — фонд времени работы станков;
• Матрица C — продажи производимых изделий.

Таким образом, нормы времени (мин./шт.) на обработку изделий на станках, заданы матрицей A:

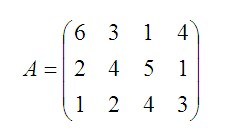
Фонд времени работы станков (мин.) задан в матрице B:

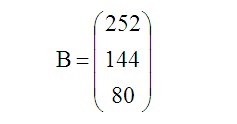
Прибыль от продажи каждой единицы изделия (руб./шт.) задана матрицей C:

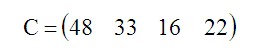
Кроме того, обозначим через X_i планируемое количество изделий каждого вида. Тогда искомый план: X₁, X₂, X₃, X₄.

2. Запись ограничений плана в виде системы неравенств

Запишем ограничения плана в виде системы неравенств:

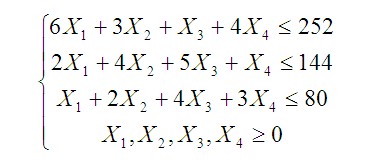
Коэффициенты при переменных в левой части системы неравенств берем из матрицы A, значения из правой части — из матрицы B.

Неравенства задают для каждого станка ограничение на суммарное время обработки им всех видов изделий, которое не должно превышать соответствующий ему фонд времени (т. к. станок чисто физически не может проработать ни минутой больше).

Также добавляем условие, согласно которому переменные не могут быть меньше нуля, так как произвести отрицательное количество изделий невозможно.

3. Определение целевого показателя

В нашей задаче целевой показатель — прибыль, которую следует максимизировать путем составления оптимального плана производства.

Тогда целевая прибыль может быть записана через следующее равенство:

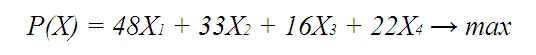
Коэффициенты при переменных берем из матрицы C. То есть мы перемножаем прибыль от производства единицы изделия каждого вида на их планируемое количество, для получения значения суммарной прибыли (которая должна быть максимальной).

4. Приведение системы неравенств к системе линейных уравнений

Для решения получившейся задачи на условный экстремум, заменим систему неравенств системой линейных уравнений путем ввода в нее дополнительных неотрицательных переменных (X₅, X₆, X₇).

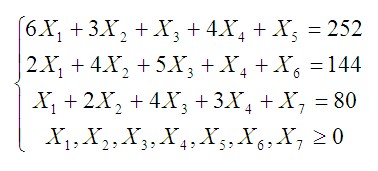
Эти переменные являются фиктивными изделиями, на которые мы списываем неиспользованные остатки фондов времени работы станков.

5. Формирование опорного плана

Примем следующий опорный план (предварительный вариант, который в процессе решения задачи будет итерационно улучшаться):

X₁ = 0, X₂ = 0, X₃ = 0, X₄ = 0, X₅ = 252, X₆ = 144, X₇ = 80.

Здесь основным переменным (количеству изделий производимых в рамках плана) сопоставляем нулевые значения, а дополнительным (фиктивным) переменным — соответствующие величины фондов времени работы станков.

6. Составление симплекс-таблицы

Занесем исходные данные в специальную симплекс-таблицу.

В столбец Базис выписываем дополнительные переменные (X₅..X₇). В колонку H вносим величины фонда времени работы станков. В столбцы X₁..X₇ помещаем коэффициенты при этих переменных из составленной ранее системы уравнений (если переменных в уравнении нет, как например, X₆ и X₇ в первом равенстве, то коэффициенты будут равны 0). Кроме того, следует предусмотреть дополнительный столбец (b) для показателя, который мы будем рассчитывать на следующем этапе.

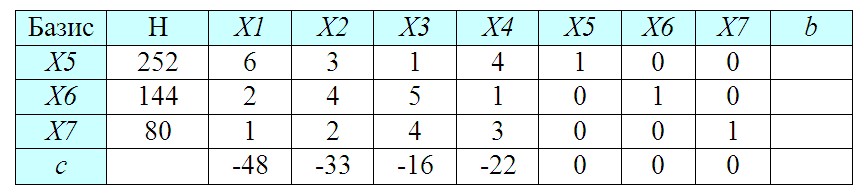
Количество строк в таблице соответствует числу дополнительных переменных (X₅..X₇). В последнюю строку (c) заносим коэффициенты при целевой функции с обратным знаком (коэффициенты при дополнительных переменных X₅..X₇ будут нулевыми).

7. Вычисление показателя b

Выбираем в последней строке наибольшее (по модулю!) отрицательное число.

В нашем примере это -48 (еще раз подчеркнем, что отрицательные числа сравниваем без учета знака).

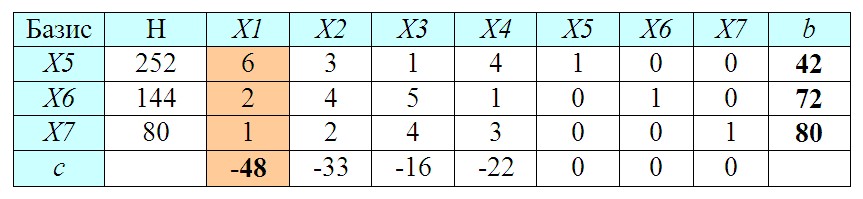
Далее вычислим для столбца, которому соответствует выбранное число, специальный показатель b_i = Н_i / a_i, где a_i — значение ячейки выбранного столбца и соответствующей строки.

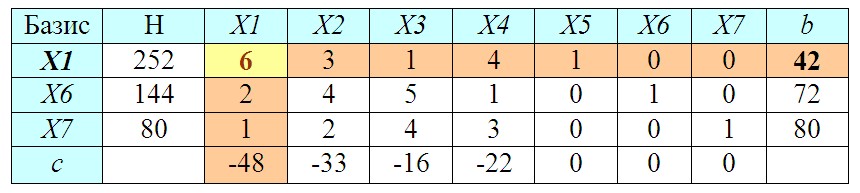
8. Нахождение разрешающего элемента

Среди вычисленных значений b выбираем наименьшее.

Пересечение выбранных столбца и строки даст нам разрешающий элемент (РЭ). Меняем базисную переменную (из первой колонки в выбранной строке) на переменную соответствующую разрешающему элементу (X₅ на X₁).

9. Перерасчет элементов симплекс-таблицы

Теперь необходимо пересчитать все элементы симплекс-таблицы, кроме столбца b (который очищается).

При перерасчете элементов симплекс-таблицы следует придерживаться следующих правил:

• Сам разрешающий элемент (РЭ) обращается в единицу;
• Для элементов разрешающей строки применяется формула: a_ij^* = a_ij / РЭ (то есть каждый элемент делим на значение разрешающего элемента и получаем новые данные);
• Для элементов разрешающего столбца — они просто обнуляются;
• Остальные элементы таблицы пересчитываем по правилу прямоугольника:

  

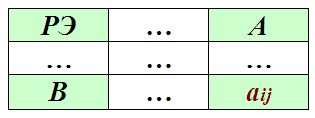
  Формула здесь следующая: a_ij^* = a_ij — ( A × B / РЭ )

  Как видите, мы берем пересчитываемую ячейку и ячейку с разрешающим элементом. Они образуют противоположные углы прямоугольника. Далее перемножаем значения из ячеек 2-х других углов этого прямоугольника. Это произведение (A × B) делим на разрешающий элемент (РЭ) и вычитаем из текущей пересчитываемой ячейки (a_ij) то, что получилось. В итоге имеем новое значение — a_ij^*.

Полученные в результате перерасчета значения заносим в новую симплекс-таблицу:

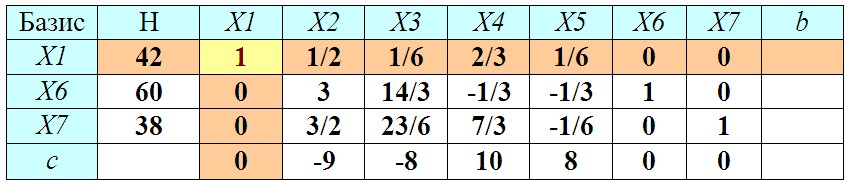
10. Проверяем последнюю строку симплекс-таблицы на наличие отрицательных чисел: если их нет — оптимальный план найден (п. 11), если есть — план требует улучшения (п. 7)

Вновь проверяем последнюю строку (c) на наличие отрицательных чисел. Если их нет — оптимальный план найден, переходим к последнему этапу решения задачи (пункт 11). Если есть — план еще не оптимален, и симплекс-таблицу вновь нужно пересчитать.

Так как у нас в последней строке снова имеются отрицательные числа, начинаем новую итерацию (повторение) вычислений с пункта 7.

В нашем примере мы снова ищем в последней строке наибольшее по модулю отрицательное число, вычисляем для соответствующего ему столбца показатель b, определяем разрешающий элемент, меняем базис и пересчитываем элементы симплекс-таблицы.

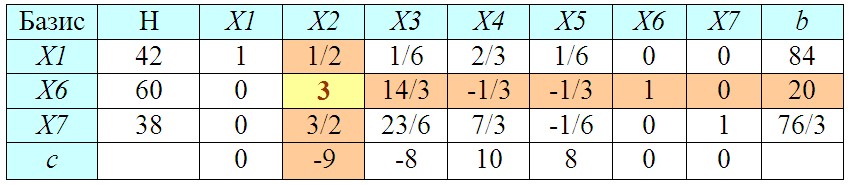
Пересчитав таблицу мы видим, что на сей раз в последней строке нет отрицательных чисел, следовательно оптимальный план (позволяющий получить максимальную прибыль) найден и можно переходить к завершающему пункту решения.

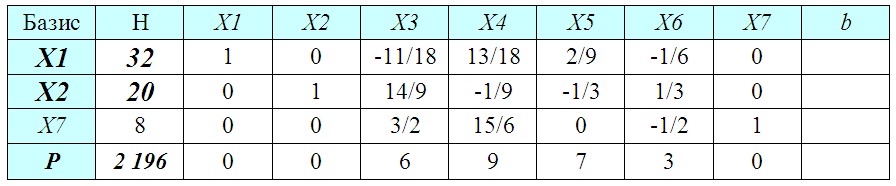
Еще раз обращаю ваше внимание, что отсутствие в последней строке отрицательных элементов указывает на то, что нами найден оптимальный план производства позволяющий получить максимально возможную прибыль при заданных условиях.

11. Определение производственного плана и вычисление общей прибыли

В соответствии с найденным планом (смотрим какие переменные перешли в колонку «Базис») выпускать мы будем изделия X₁ и X₂ (X₇ не учитываем, т. к. это фиктивное изделие, не производимое на предприятии и введенное для приведения системы неравенств к системе уравнений).

Прибыль от производства каждой единицы продукции нам известна (матрица C). Остается перемножить ее с найденными объемами выпуска изделий X₁ и X₂ (значения X₃ и X₄ нулевые, т. к. эти изделия производить оказалось невыгодно), для получения общей (максимально возможной!) прибыли.

Ответ План производства: X₁ = 32 шт., X₂ = 20 шт., X₃ = 0 шт., X₄ = 0 шт., общая прибыль: P = 48 × 32 + 33 × 20 = 2 196 руб.

Статья дополнена и доработана автором 5 ноя 2020 г.

© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.

Рассмотрим симплекс-метод для решения задач линейного программирования (ЛП). Он основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает.
 

Алгоритм симплекс-метода следующий:
 

1. Исходную задачу переводим в канонический вид путем введения дополнительных переменных. Для неравенства вида ≤ дополнительные переменные вводят со знаком (+), если же вида ≥ то со знаком (—). В целевую функцию дополнительные переменные вводят с соответствующими знаками с коэффициентом, равным 0, т.к. целевая функция не должна при этом менять свой экономический смысл.
2. Выписываются вектора P_i из коэффициентов при переменных и столбца свободных членов. Этим действием определяется количество единичных векторов. Правило – единичных векторов должно быть столько, сколько неравенств в системе ограничений.
3. После этого исходные данные вводятся в симплекс-таблицу. В базис вносятся единичные вектора, и исключая их из базиса, находят оптимальное решение. Коэффициенты целевой функции записывают с противоположным знаком.
4. Признак оптимальности для задачи ЛП – решение оптимально, если в f – строке все коэффициенты положительны. Правило нахождения разрешающего столбца – просматривается f – строка и среди ее отрицательных элементов выбирается наименьшее. Вектор P_i его содержащий становится разрешающим. Правило выбора разрешающего элемента – составляются отношения положительных элементов разрешающего столбца к элементам вектора Р₀ и то число, которое дает наименьшее отношение становится разрешающим элементом, относительно которого будет произведен пересчет симплекс-таблицы. Строка, содержащая этот элемент называется разрешающей строкой. Если в разрешающем столбце нет положительных элементов, то задача не имеет решения. После определения разрешающего элемента переходят к пересчету новой симплекс – таблицы.
5. Правила заполнения новой симплекс – таблицы. На месте разрешающего элемента проставляют единицу, а другие элементы полагают равными 0. Разрешающий вектор вносят в базис, из которого исключают соответствующий нулевой вектор, а остальные базисные вектора записывают без изменений. Элементы разрешающей строки делят на разрешающий элемент, а остальные элементы пересчитывают по правилу прямоугольников.
6. Так поступают до тех пор, пока в f – строке все элементы не станут положительными.

Рассмотрим решение задачи с использованием рассмотренного выше алгоритма.
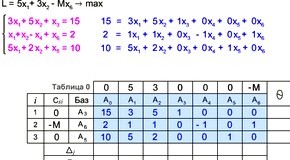
Дано:

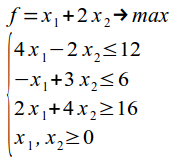
Приводим задачу к каноническому виду:

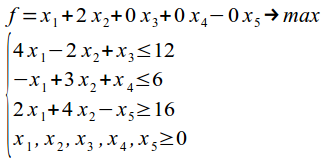
Составляем вектора:

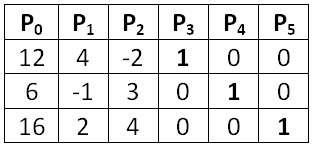
Заполняем симплекс – таблицу:

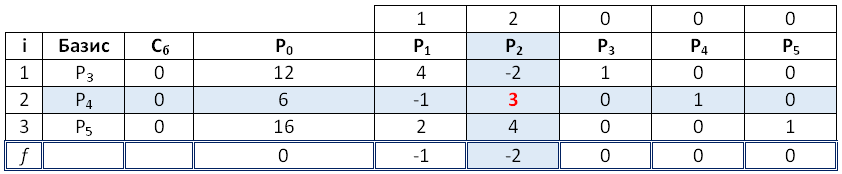
Правило прямоугольников:
Пересчитаем первый элемент вектора Р₀, для чего составляем прямоугольник из чисел: и получаем: .

Аналогичные расчеты выполним для всех остальных элементов симплекс – таблицы:

В полученном плане f – строка содержит один отрицательный элемент – (-5/3), вектора P₁. Он содержит в своем столбце единственный положительный элемент, который и будет разрешающим элементом. Сделаем пересчет таблицы относительно этого элемента:

Отсутствие отрицательных элементов в f – строке означает, что найден оптимальный план:
F* = 36/5, Х = (12/5, 14/5, 8, 0, 0).
 

Рекомендуемая литература

• Ашманов С. А. Линейное программирование, М: Наука, 1998г.,
• Вентцель Е.С. Исследование операций, М: Советское радио, 2001г.,
• Кузнецов Ю.Н., Кузубов В.И., Волошенко А.Б. Математическое программирование, М: Высшая школа, 1986г.

Решение линейного программирования на заказ

Заказать любые задания по этой дисциплине можно у нас на сайте. Прикрепить файлы и указать сроки можно на странице заказа.