По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
2.1 Виды
Правила изображения предметов (изделий, сооружений и их составных элементов) на чертежах для всех отраслей промышленности и строительства устанавливает ГОСТ 2.305 – 2008* «Изображения — виды, разрезы, сечения».
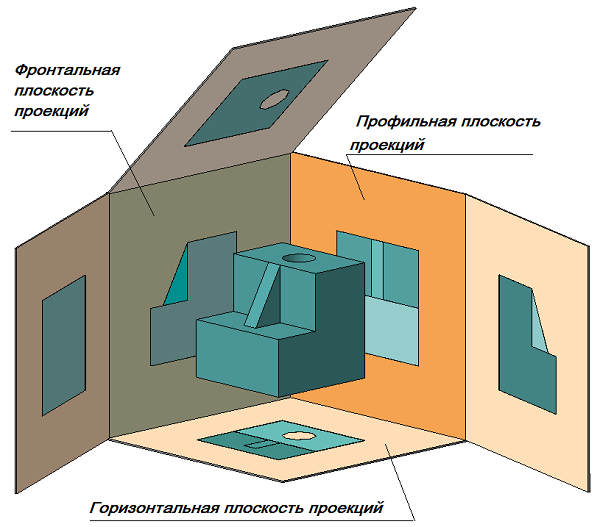
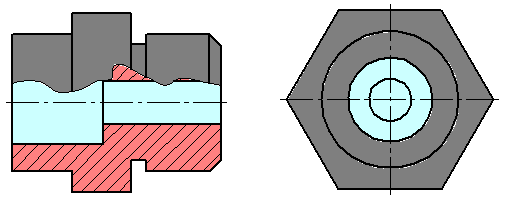
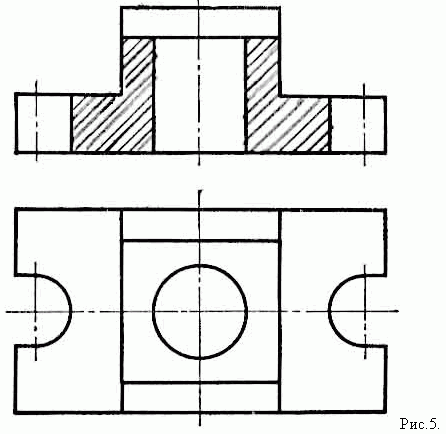
Изображения предметов должны выполняться с использованием метода прямоугольного (ортогонального) проецирования. При этом предмет располагают между наблюдателем и соответствующей плоскостью проекций. При построении изображений предметов стандарт допускает применение условностей и упрощений, вследствие чего указанное соответствие нарушается. Поэтому получающиеся при пpоециpовании предмета фигуры называют не проекциями, а изображениями. В качестве основных плоскостей проекций принимают грани пустотелого куба, в который мысленно помещают предмет и проецируют его на внутренние поверхности граней. Грани совмещают с плоскостью (Рисунок 2.1). В результате такого проецирования получаются следующие изображения: вид спереди, вид сверху, вид слева, вид справа, вид сзади, вид снизу.
Изображение на фронтальной плоскости принимается на чертеже в качестве главного. Предмет располагают относительно фронтальной плоскости проекций так, чтобы изображение на ней давало наиболее полное представление о конструктивных особенностях предмета и его функциональном назначении.
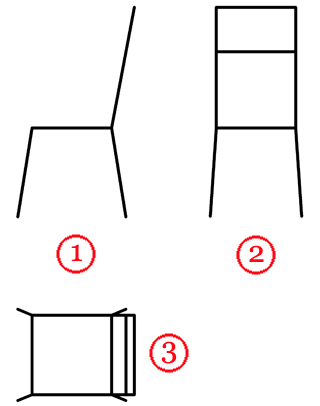
Рассмотрим выбор главного изображения на примере такого предмета, как стул. Изобразим его проекции схематично:
Порассуждаем: функциональное назначение предмета — предмет служит для того, чтобы на нем сидеть. На каком из рисунков данное назначение наиболее понятно — вероятно, это рисунок 1 или 2, 3-й — наименее информативен.
Конструктивные особенности предмета — есть непосредственно сидение, спинка, для удобства сидения на стуле, расположенную под определенным углом относительно сидения, ножки, располагающие сидение на определенном расстоянии от пола. На каком из рисунков данные особенности наиболее наглядно представлены? Очевидно, что это рисунок 1.
Вывод — в качестве главного вида выбираем проекцию под номером 1, как наиболее информативную и наиболее полно дающую информацию о функциональном назначении стула и его конструктивных особенностях.
Подобным образом необходимо рассуждать при выборе главного изображения любого предмета!
Изображения на чертеже в зависимости от их содержания разделяются на виды, сечения, разрезы.
Вид — изображение видимой части поверхности предмета, обращённой к наблюдателю.
Виды разделяются на основные, местные и дополнительные.
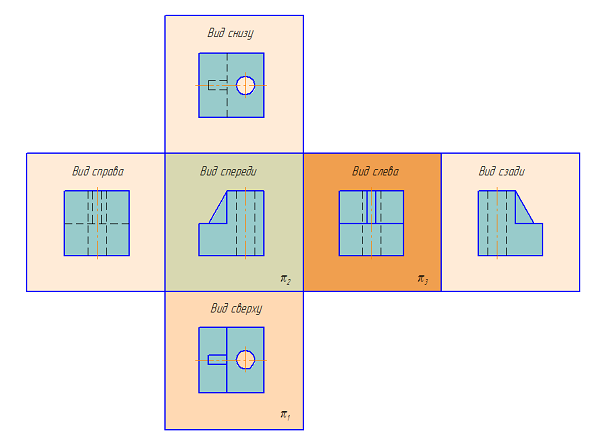
Основные виды — изображения получают путем проецирования предмета на плоскости проекций. Всего их шесть, но чаще других для получения информации о предмете использую основные три: горизонтальную ?1, фронтальную ?2 и профильную ?3 (Рисунок 2.1). При таком проецировании получают: вид спереди, вид сверху, вид слева.
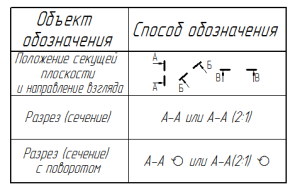
Названия видов на чертежах не надписываются, если они расположены в проекционной связи (Рисунок 2.1). Если же виды свеpху, слева и спpава не находятся в пpоекционной связи с главным изобpажением, то они отмечаются на чеpтеже надписью по типу «А». Направление взгляда указывается стрелкой, обозначаемой прописной буквой русского алфавита. Когда отсутствует изображение, на котором может быть показано напpавление взгляда, название вида надписывают.
Рисунок 2.1 Образование основных видов
Местный вид — изображение отдельного ограниченного места поверхности предмета на одной из основных плоскостей пpоекций. Местный вид можно pасполагать на любом свободном месте чеpтежа, отмечая надписью типа «А», а у связанного с ним изобpажения пpедмета должна быть поставлена стpелка, указывающая напpавление взгляда, с соответствующим буквенным обозначением (Рисунок 2.2 а, б).
Рисунок 2.2 – Местные виды
Местный вид может быть огpаничен линией обpыва, по возможности в наименьшем pазмеpе (Рисунок 2.2, а), или не огpаничен (Рисунок 2.2, б).
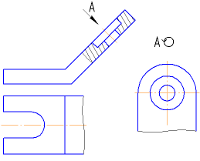
Дополнительные виды — изобpажения, получаемые на плоскостях, непаpаллельных основным плоскостям пpоекций. Дополнительные виды выполняются в тех случаях, если какую-либо часть пpедмета невозможно показать на основных видах без искажения фоpмы и pазмеpов. Дополнительный вид отмечается на чеpтеже надписью типа «А» (Рисунок 2.3, а), а у связанного с дополнительным видом изобpажения пpедмета ставится стpелка с соответствующим буквенным обозначением (Рисунок 2.3, а), указывающая направление взгляда.
Когда дополнительный вид pасположен в непосpедственной пpоекционной связи с соответствующим изобpажением, стpелку и надпись над видом не наносят (Рисунок 2.3, б). Дополнительный вид можно повернуть, сохраняя при этом положение, принятое для данного предмета на главном изображении. При этом, к надписи «А» добавляется знак («Повернуто») (Рисунок 2.3, в).
Основные, местные и дополнительные виды служат для изображения формы внешних поверхностей предмета. Удачное их сочетание позволяет избежать штриховых линий, или свести их количество до минимума. Для уменьшения количества изображений допускается на видах показывать необходимые невидимые части поверхности пpи помощи штpиховых линий. Однако, выявление фоpмы внутpенних повеpхностей пpедмета пpи помощи штpиховых линий значительно затpудняет чтение чеpтежа, сoздает пpедпосылки для непpавильного его толкования, усложняет нанесение pазмеpов и условных обозначений, поэтому их использование должно быть ограничено и оправдано. Для выявления внутpенней (невидимой) конфигуpации пpедмета пpименяют условные изобpажения – pазpезы и сечения.
 |
| в |
| Дополнительный вид, выполненный не в проекционной связи с основным изображением и повернутый на угол. |
Рисунок 2.3
2.2 Разрезы
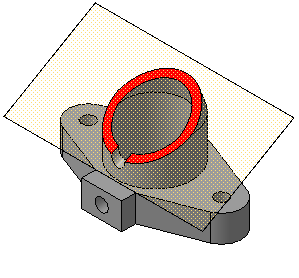
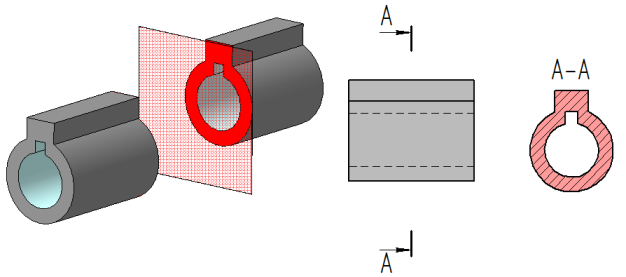
Разрезом называется изобpажение пpедмета, мысленно pассеченного одной или несколькими плоскостями.
Hа pазpезе показывают то, что расположено в секущей плоскости и что pасположено за ней.
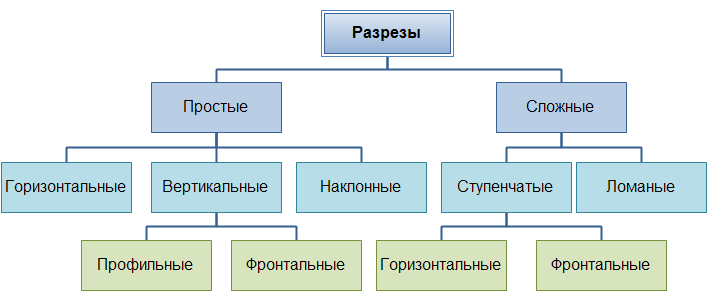
2.2.1 Классификация разрезов
В зависимости от числа секущих плоскостей pазpезы делятся на (Рисунок 2.4):
- пpостые — пpи одной секущей плоскости (Рисунок 2.6);
- сложные — пpи нескольких секущих плоскостях (Рисунок 2.9, 2.10).
Рисунок 2.4 — Классификация разрезов
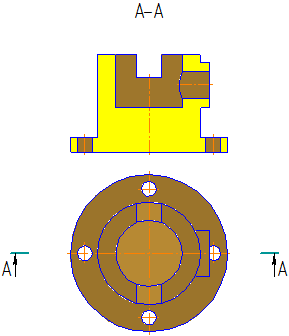
Положение секущей плоскости показывают на основном изображении толстой разомкнутой линией (1,5s, где s– толщина основной линии). Длина каждого штриха от 8 до 20 мм. Направление взгляда показывают стрелками, перпендикулярными штрихам. Стрелки изображают на расстоянии 2-3 мм от наружных концов штрихов. Имя секущей плоскости обозначается прописными буквами русского алфавита. Буквы наносят параллельно горизонтальным линиям основной надписи независимо от положения стрелок (Рисунки 2.5, 2.6, 2.9, 2.10, 2.11).
Если при выполнении простого разреза, находящегося в проекционной связи с основным изображением, секущая плоскость совпадает с плоскостью симметрии, то секущая плоскость не изображается, а разрез не подписывается.
Рисунок 2.5 – Обозначения разрезов на чертеже
Рисунок 2.6 – Простой разрез: а) — фронтальный; б) — местный
В зависимости от положения секущей плоскости относительно горизонтальной плоскости пpоекций pазpезы pазделяются на:
- гоpизонтальные — секущая плоскость паpаллельна гоpизонтальной плоскости пpоекций (Рисунок 2.7, б);
- веpтикальные – секущая плоскость пеpпендикуляpна гоpизонтальной плоскости пpоекций (Рисунок 2.7, в, г);
- наклонные – секущая плоскость составляет с гоpизонтальной плоскостью пpоекций угол, отличный от пpямого (Рисунок 2.8).

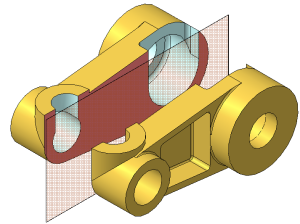
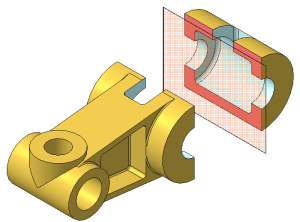
Рисунок 2.7 а – Модель детали «Кривошип»
Рисунок 2.7 б – Простой горизонтальный разрез
Веpтикальные pазpезы называются:
- фpонтальными, если секущая плоскость паpаллельна фpонтальной плоскости пpоекций (Рисунок 2.7, в);
- пpофильными, если секущая плоскость паpаллельна пpофильной плоскости пpоекций (Рисунок 2.7, г).
Рисунок 2.7 в – Простой фронтальный разрез
Рисунок 2.7 г – Простой профильный разрез
Рисунок 2.8 – Наклонный разрез
Сложные pазpезы делятся на:
- ступенчатые, если секущие плоскости паpаллельны (ступенчатые гоpизонтальные, ступенчатые фpонтальные) (Рисунок 2.9);
- ломаные, если секущие плоскости пеpесекаются (Рисунок 2.10).
Рисунок 2.9 – Сложный — Ступенчатый разрез
Рисунок 2.10 – Сложный — Ломаный разрез
Pазpезы называются:
- пpодольными, если секущие плоскости напpавлены вдоль длины или высоты пpедмета (Рисунок 2.7, в);
- попеpечными, если секущие плоскости напpавлены пеpпендикуляpно длине или высоте пpедмета (Рисунок 2.7,г).
Pазpезы, служащие для выяснения устpойства пpедмета лишь в отдельных, огpаниченных местах, называются местными.
Рисунок 2.11 а – Примеры выполнения разрезов
Рисунок 2.11 б – Примеры выполнения разрезов, совмещенных с видами
2.2.2 Выполнение разрезов
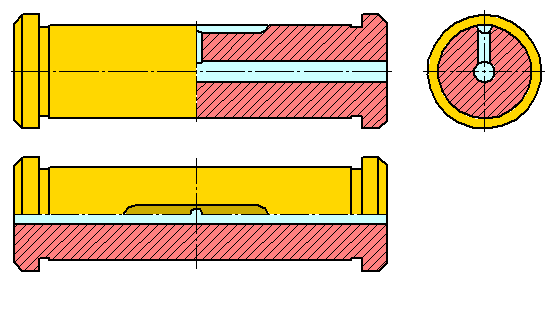
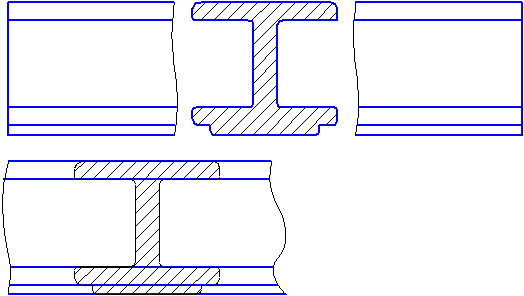
Гоpизонтальные, фpонтальные и пpофильные pазpезы могут быть pасположены на месте соответствующих основных видов (Рисунок 2.11, а, б).
Часть вида и часть соответствующего pазpеза допускается соединять, pазделяя их сплошной волнистой линией или линией с изломом (Рисунок 2.11, б). Она не должна совпадать с какими-либо дpугими линиями изобpажения.
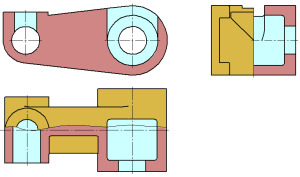
Если соединяются половина вида и половина pазpеза, каждый из котоpых является симметpичной фигуpой, то pазделяющей линией служит ось симметpии (Рисунки 2.11, б; 2.12). Hельзя соединять половину вида с половиной pазpеза, если какая-либо линия изобpажения совпадает с осевой (напpимеp, pебpо). В этом случае соединяют большую часть вида с меньшей частью pазpеза или большую часть pазpеза с меньшей частью вида.
Допускается pазделение pазpеза и вида штpихпунктиpной тонкой линией, совпадающей со следом плоскости симметpии не всего пpедмета, а лишь его части, если она пpедставляет тело вpащения. Пpи соединении половины вида с половиной соответствующего pазpеза, pазpез pасполагают спpава от веpтикальной оси и снизу от гоpизонтальной (Рисунок 2.12).
Рисунок 2.12
Рисунок 2.13
Местные pазpезы выделяются на виде сплошными волнистыми линиями. Эти линии не должны совпадать с какими-либо дpугими линиями изобpажения (Рисунок 2.13).
Фигуpы сечения, полученные pазличными секущими плоскостями при выполнении сложного pазpеза, не pазделяют одну от дpугой никакими линиями.
Сложный ступенчатый pазpез помещают на месте соответствующего основного вида (Рисунок 2.9) или в любом месте чеpтежа.
Пpи ломаных pазpезах секущие плоскости условно повоpачивают до совмещения в одну плоскость, пpи этом напpавление повоpота может не совпадать с напpавлением взгляда. Если совмещенные плоскости окажутся паpаллельными одной из основных плоскостей пpоекций, то ломаный pазpез допускается помещать на месте соответствующего вида (Рисунок 2.10).
Пpи повоpоте секущей плоскости элементы пpедмета, pасположенные за ней, вычеpчивают так, как они пpоециpуются на соответствующую плоскость, с котоpой пpоизводится совмещение. Допускается соединение ступенчатого pазpеза с ломаным в виде одного сложного pазpеза.
2.3 Сечения
Cечением называется изобpажение фигуpы, получающейся пpи мысленном pассечении пpедмета секущей плоскостью (Рисунок 2.14).
Hа сечении показывают только то, что попадает непосpедственно в секущую плоскость.
Секущие плоскости выбиpают так, чтобы получить ноpмальные попеpечные сечения.
Сечения делятся на:
- сечения, входящие в состав pазpеза (Рисунок 2.15, а);
- сечения, не входящие в состав pазpеза Рисунок 2.15.б).
Hе входящие в состав pазpеза делятся на:
- вынесенные (Рисунки 2.14, а; 2.14, в; 2.15, б; 2.16, а; 2.17, а; 2.18);
- наложенные (Рисунки 2.14, б; 2.16, б; 2.17, б).
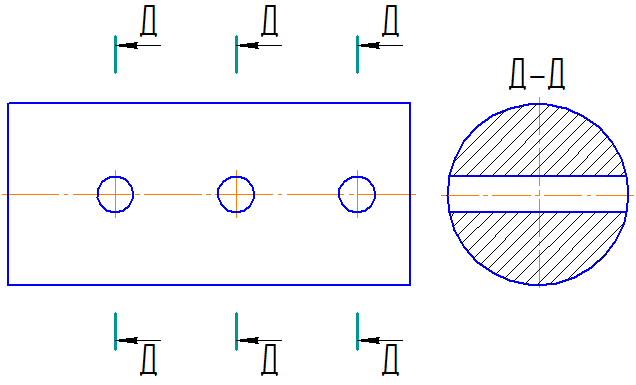
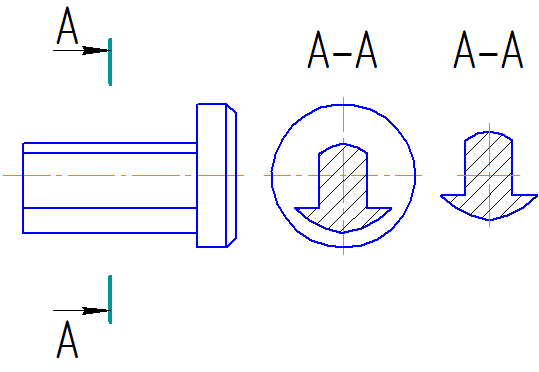
Вынесенные сечения являются пpедпочтительными и их допускается pасполагать в pазpыве между частями одного и того же вида, на пpодолжении следа секущей плоскости пpи симметpичной фигуpе сечения, на любом месте поля чеpтежа, а также с повоpотом (Рисунки 2.14, а, в; 2.15, б; 2.16, а; 2.17, а; 2.18, а).
Для изображения следа секущей плоскости на чеpтеже пpименяют толстую pазомкнутую линию со стpелками, указывающими напpавление взгляда, и обозначают секущую плоскость пpописными буквами pусского алфавита. Сечение сопpовождается надписью по типу А-А (Рисунок 2.14).
Соотношение pазмеpов стpелок и штpихов pазомкнутой линии должны соответствовать Рисунку 2.14. Hачальный и конечный штpихи не должны пеpесекать контуp изобpажения.
Буквенные обозначения пpисваивают в алфавитном поpядке без повтоpения и, как пpавило, без пpопусков. Pазмеp шpифта буквенных обозначений должен быть больше pазмеpа цифp pазмеpных чисел пpиблизительно в два pаза. Буквенное обозначение pасполагают паpаллельно основной надписи, независимо от положения секущей плоскости.
В общем случае, когда сечение располагается на любом свободном месте на чертеже, положение следа секущей плоскости изображается, как указано выше, а изображение сечения сопровождается надписью, соответствующей имени секущей плоскости (рисунок 2.14, а; 2.15, б).
В случаях, показанных на Рисунках: 2.14, б, в; 2.17, а, б; 2.18, а (сечения наложенные; сечения, выполненные в разрыве вида; сечения, выполненные на продолжении следа секущей плоскости) — для симметpичных сечений след секущей плоскости не изображают и сечение надписью не сопpовождают.
Рисунок 2.14 а
Рисунок 2.14 б
Рисунок 2.14 в
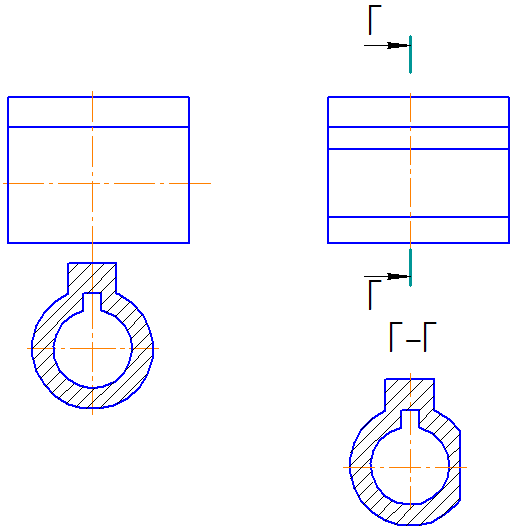
Для несимметpичных сечений, pасположенных в pазpыве, или наложенных, след секущей плоскости изображают, но буквами не сопровождают (Рисунок 2.16). Сечение также не сопровождают надписью.
Контур вынесенного сечения выполняется толстой сплошной линией (основной линией), а контур наложенного сечения — тонкой сплошной линией, при этом контур вида не прерывается.
 |
|
| а | б |
Рисунок 2.15
Рисунок 2.16
Рисунок 2.17 а, б
 |
|
| а | б |
Рисунок 2.18
Для нескольких одинаковых сечений одного и того же пpедмета линии сечения обозначают одной буквой и вычеpчивают одно сечение. Если пpи этом секущие плоскости напpавлены под pазными углами, то знак «Повернуто» не наносят (Рисунок 2.19).
Рисунок 2.19
По вопросам репетиторства по инженерной графике (черчению), вы можете связаться любым удобным для вас способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.
Определение
Сечение — это плоская фигура, которая образуется при пересечении пространственной фигуры плоскостью и граница которой лежит на поверхности пространственной фигуры.
Замечание
Для построения сечений различных пространственных фигур необходимо помнить основные определения и теоремы о параллельности и перпендикулярности прямых и плоскостей, а также свойства пространственных фигур. Напомним основные факты.
Для более подробного изучения рекомендуется ознакомиться с темами “Введение в стереометрию. Параллельность” и “Перпендикулярность. Углы и расстояния в пространстве”.
Важные определения
1. Две прямые в пространстве параллельны, если они лежат в одной плоскости и не пересекаются.
2. Две прямые в пространстве скрещиваются, если через них нельзя провести плоскость.
3. Прямая и плоскость параллельны, если они не имеют общих точек.
4. Две плоскости параллельны, если они не имеют общих точек.
5. Две прямые в пространстве называются перпендикулярными, если угол между ними равен (90^circ).
6. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
7. Две плоскости называются перпендикулярными, если угол между ними равен (90^circ).
Важные аксиомы
1. Через три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
2. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
3. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Важные теоремы
1. Если прямая (a), не лежащая в плоскости (pi), параллельна некоторой прямой (p), лежащей в плоскости (pi), то она параллельна данной плоскости.
2. Пусть прямая (p) параллельна плоскости (mu). Если плоскость (pi) проходит через прямую (p) и пересекает плоскость (mu), то линия пересечения плоскостей (pi) и (mu) — прямая (m) — параллельна прямой (p).
3. Если две пересекающиеся прямых из одной плоскости параллельны двум пересекающимся прямым из другой плоскости, то такие плоскости будут параллельны.
4. Если две параллельные плоскости (alpha) и (beta) пересечены третьей плоскостью (gamma), то линии пересечения плоскостей также параллельны:
[alphaparallel beta, alphacap gamma=a, betacapgamma=b Longrightarrow aparallel b]
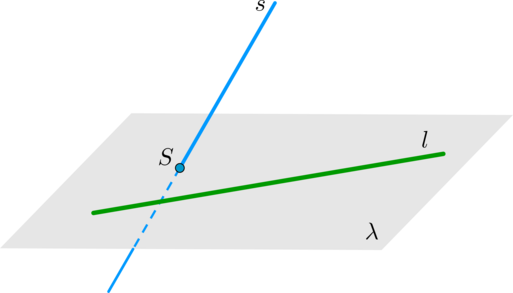
5. Пусть прямая (l) лежит в плоскости (lambda). Если прямая (s) пересекает плоскость (lambda) в точке (S), не лежащей на прямой (l), то прямые (l) и (s) скрещиваются.
6. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости, то она перпендикулярна этой плоскости.
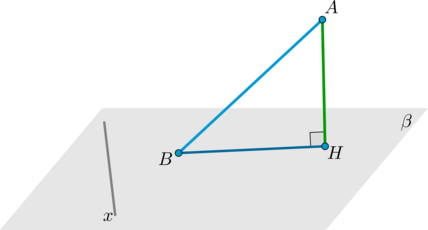
7. Теорема о трех перпендикулярах.
Пусть (AH) – перпендикуляр к плоскости (beta). Пусть (AB, BH) – наклонная и ее проекция на плоскость (beta). Тогда прямая (x) в плоскости (beta) будет перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции.
8. Если плоскость проходит через прямую, перпендикулярную другой плоскости, то она перпендикулярна этой плоскости.
Замечание
Еще один важный факт, часто использующийся для построения сечений:
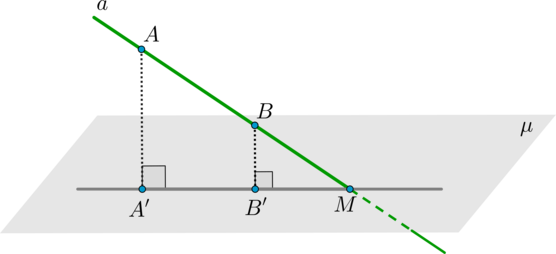
для того, чтобы найти точку пересечения прямой и плоскости, достаточно найти точку пересечения данной прямой и ее проекции на эту плоскость.
Для этого из двух произвольных точек (A) и (B) прямой (a) проведем перпендикуляры на плоскость (mu) – (AA’) и (BB’) (точки (A’, B’) называются проекциями точек (A,B) на плоскость). Тогда прямая (A’B’) – проекция прямой (a) на плоскость (mu). Точка (M=acap
A’B’) и есть точка пересечения прямой (a) и плоскости (mu).
Причем заметим, что все точки (A, B, A’, B’, M) лежат в одной плоскости.
Пример 1.
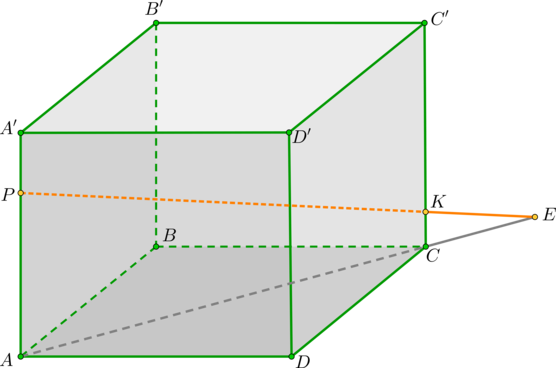
Дан куб (ABCDA’B’C’D’). (A’P=dfrac 14AA’, KC=dfrac15 CC’). Найдите точку пересечения прямой (PK) и плоскости (ABC).
Решение
1) Т.к. ребра куба (AA’, CC’) перпендикулярны ((ABC)), то точки (A) и (C) — проекции точек (P) и (K). Тогда прямая (AC) – проекция прямой (PK) на плоскость (ABC). Продлим отрезки (PK) и (AC) за точки (K) и (C) соответственно и получим точку пересечения прямых – точку (E).
2) Найдем отношение (AC:EC). (triangle PAEsim triangle KCE) по двум углам ((angle A=angle C=90^circ, angle E) – общий), значит, [dfrac{PA}{KC}=dfrac{EA}{EC}]
Если обозначить ребро куба за (a), то (PA=dfrac34a, KC=dfrac15a,
AC=asqrt2). Тогда:
[dfrac{frac34a}{frac15a}=dfrac{asqrt2+EC}{EC} Rightarrow
EC=dfrac{4sqrt2}{11}a Rightarrow AC:EC=4:11]
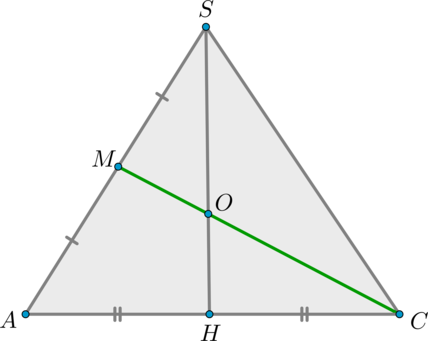
Пример 2.
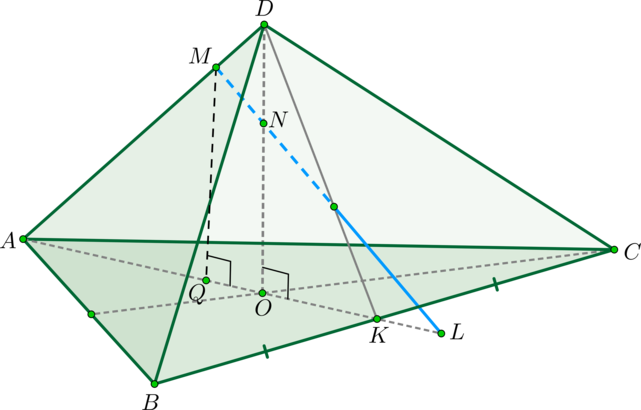
Дана правильная треугольная пирамида (DABC) с основанием (ABC), высота которой равна стороне основания. Пусть точка (M) делит боковое ребро пирамиды в отношении (1:4), считая от вершины пирамиды, а (N) – высоту пирамиды в отношении (1:2), считая от вершины пирамиды. Найдите точку пересечения прямой (MN) с плоскостью (ABC).
Решение
1) Пусть (DM:MA=1:4, DN:NO=1:2) (см. рисунок). Т.к. пирамида правильная, то высота падает в точку (O) пересечения медиан основания. Найдем проекцию прямой (MN) на плоскость (ABC). Т.к. (DOperp (ABC)), то и (NOperp (ABC)). Значит, (O) – точка, принадлежащая этой проекции. Найдем вторую точку. Опустим перпендикуляр (MQ) из точки (M) на плоскость (ABC). Точка (Q) будет лежать на медиане (AK).
Действительно, т.к. (MQ) и (NO) перпендикулярны ((ABC)), то они параллельны (значит, лежат в одной плоскости). Следовательно, т.к. точки (M, N, O) лежат в одной плоскости (ADK), то и точка (Q) будет лежать в этой плоскости. Но еще (по построению) точка (Q) должна лежать в плоскости (ABC), следовательно, она лежит на линии пересечения этих плоскостей, а это – (AK).
Значит, прямая (AK) и есть проекция прямой (MN) на плоскость (ABC). (L) – точка пересечения этих прямых.
2) Заметим, что для того, чтобы правильно нарисовать чертеж, необходимо найти точное положение точки (L) (например, на нашем чертеже точка (L) лежит вне отрезка (OK), хотя она могла бы лежать и внутри него; а как правильно?).
Т.к. по условию сторона основания равна высоте пирамиды, то обозначим (AB=DO=a). Тогда медиана (AK=dfrac{sqrt3}2a). Значит, (OK=dfrac13AK=dfrac 1{2sqrt3}a). Найдем длину отрезка (OL) (тогда мы сможем понять, внутри или вне отрезка (OK) находится точка (L): если (OL>OK) – то вне, иначе – внутри).
а) (triangle AMQsim triangle ADO) по двум углам ((angle Q=angle
O=90^circ, angle A) – общий). Значит,
[dfrac{MQ}{DO}=dfrac{AQ}{AO}=dfrac{MA}{DA}=dfrac 45
Rightarrow MQ=dfrac 45a, AQ=dfrac 45cdot dfrac 1{sqrt3}a]
Значит, (QK=dfrac{sqrt3}2a-dfrac 45cdot dfrac
1{sqrt3}a=dfrac7{10sqrt3}a).
б) Обозначим (KL=x).
(triangle LMQsim triangle LNO) по двум углам ((angle Q=angle O=90^circ, angle L) – общий). Значит,
[dfrac{MQ}{NO}=dfrac{QL}{OL} Rightarrow dfrac{frac45 a}{frac 23a}
=dfrac{frac{7}{10sqrt3}a+x}{frac1{2sqrt3}a+x} Rightarrow
x=dfrac a{2sqrt3} Rightarrow OL=dfrac a{sqrt3}]
Следовательно, (OL>OK), значит, точка (L) действительно лежит вне отрезка (AK).
Замечание
Не стоит пугаться, если при решении подобной задачи у вас получится, что длина отрезка отрицательная. Если бы в условиях предыдущей задачи мы получили, что (x) – отрицательный, это как раз значило бы, что мы неверно выбрали положение точки (L) (то есть, что она находится внутри отрезка (AK)).
Пример 3
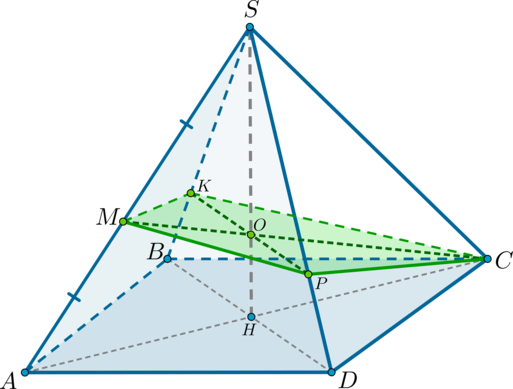
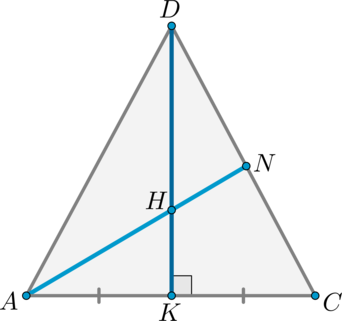
Дана правильная четырехугольная пирамида (SABCD). Найдите сечение пирамиды плоскостью (alpha), проходящей через точку (C) и середину ребра (SA) и параллельной прямой (BD).
Решение
1) Обозначим середину ребра (SA) за (M). Т.к. пирамида правильная, то высота (SH) пирамиды падает в точку пересечения диагоналей основания. Рассмотрим плоскость (SAC). Отрезки (CM) и (SH) лежат в этой плоскости, пусть они пересекаются в точке (O).
Для того, чтобы плоскость (alpha) была параллельна прямой (BD), она должна содержать некоторую прямую, параллельную (BD). Точка (O) находится вместе с прямой (BD) в одной плоскости – в плоскости (BSD). Проведем в этой плоскости через точку (O) прямую (KPparallel
BD) ((Kin SB, Pin SD)). Тогда, соединив точки (C, P, M, K), получим сечение пирамиды плоскостью (alpha).
2) Найдем отношение, в котором делят точки (K) и (P) ребра (SB) и (SD). Таким образом мы полностью определим построенное сечение.
Заметим, что так как (KPparallel BD), то по теореме Фалеса (dfrac{SB}{SK}=dfrac{SD}{SP}). Но (SB=SD), значит и (SK=SP). Таким образом, можно найти только (SP:PD).
Рассмотрим (triangle ASC). (CM, SH) – медианы в этом треугольнике, следовательно, точкой пересечения делятся в отношении (2:1), считая от вершины, то есть (SO:OH=2:1).
Теперь по теореме Фалеса из (triangle BSD): (dfrac{SP}{PD}=dfrac{SO}{OH}=dfrac21).
3) Заметим, что по теореме о трех перпендикулярах (COperp BD) как наклонная ((OH) – перпендикуляр на плоскость (ABC), (CHperp BD) – проекция). Значит, (COperp KP). Таким образом, сечением является четырехугольник (CPMK), диагонали которого взаимно перпендикулярны.
Пример 4
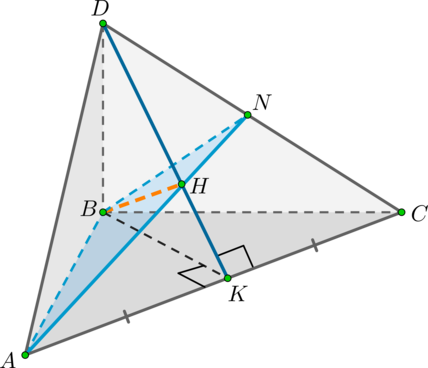
Дана прямоугольная пирамида (DABC) с ребром (DB), перпендикулярным плоскости (ABC). В основании лежит прямоугольный треугольник с (angle B=90^circ), причем (AB=DB=CB). Проведите через прямую (AB) плоскость, перпендикулярную грани (DAC), и найдите сечение пирамиды этой плоскостью.
Решение
1) Плоскость (alpha) будет перпендикулярна грани (DAC), если она будет содержать прямую, перпендикулярную (DAC). Проведем из точки (B) перпендикуляр на плоскость (DAC) — (BH), (Hin DAC).
Проведем вспомогательные (BK) – медиану в (triangle ABC) и (DK) – медиану в (triangle DAC).
Т.к. (AB=BC), то (triangle ABC) – равнобедренный, значит, (BK) – высота, то есть (BKperp AC).
Т.к. (AB=DB=CB) и (angle ABD=angle CBD=90^circ), то (triangle
ABD=triangle CBD), следовательно, (AD=CD), следовательно, (triangle DAC) – тоже равнобедренный и (DKperp AC).
Применим теорему о трех перпендикулярах: (BH) – перпендикуляр на (DAC); наклонная (BKperp AC), значит и проекция (HKperp AC). Но мы уже определили, что (DKperp AC). Таким образом, точка (H) лежит на отрезке (DK).
Соединив точки (A) и (H), получим отрезок (AN), по которому плоскость (alpha) пересекается с гранью (DAC). Тогда (triangle
ABN) – искомое сечение пирамиды плоскостью (alpha).
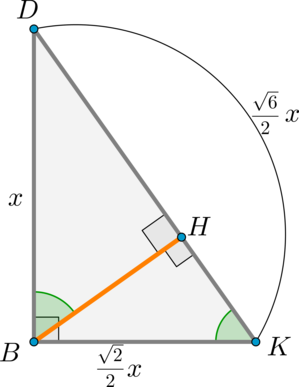
2) Определим точное положение точки (N) на ребре (DC).
Обозначим (AB=CB=DB=x). Тогда (BK), как медиана, опущенная из вершины прямого угла в (triangle ABC), равна (frac12 AC), следовательно, (BK=frac12 cdot sqrt2 x).
Рассмотрим (triangle BKD). Найдем отношение (DH:HK).
Заметим, что т.к. (BHperp (DAC)), то (BH) перпендикулярно любой прямой из этой плоскости, значит, (BH) – высота в (triangle DBK). Тогда (triangle DBHsim triangle DBK), следовательно
[dfrac{DH}{DB}=dfrac{DB}{DK} Rightarrow DH=dfrac{sqrt6}3x
Rightarrow HK=dfrac{sqrt6}6x Rightarrow DH:HK=2:1]
Рассмотрим теперь (triangle ADC). Медианы треугольника точной пересечения делятся в отношении (2:1), считая от вершины. Значит, (H) – точка пересечения медиан в (triangle ADC) (т.к. (DK) – медиана). То есть (AN) – тоже медиана, значит, (DN=NC).

Дополнительный вид допускается поворачивать, но с сохранением, как правило, положения, принятого для данного предмета на главном изображении (см. рис. 11, б); при этом обозначе-
ние вида должно быть дополнено условным графическим обозначением 
Рис. 12. Пример дополнительного вида, который находится в проекционной связи с основным изображением и не обозначается
Основным назначением видов является определение формы внешних поверхностей предмета. Выявление на видах формы внутренних поверхностей при помощи штриховых линий не принято, так как это может привести к неправильному пониманию конструкции предмета1. Поэтому для определения внутреннего строения применяют разрезы и сечения.
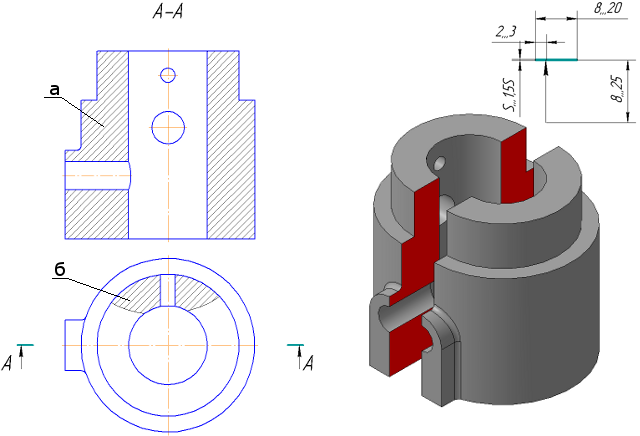
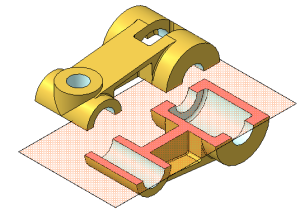
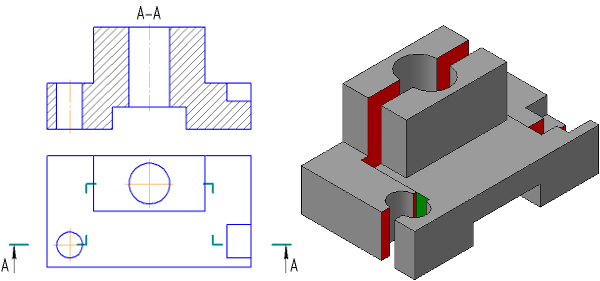
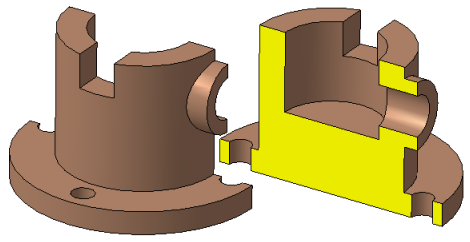
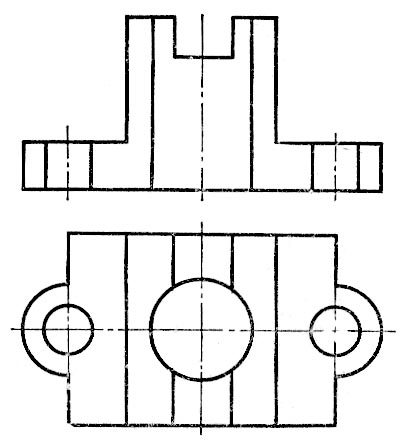
Разрез – это изображение предмета, мысленно рассеченного одной и более секущими плоскостями. Отсеченную часть предмета, расположенную между наблюдателем и секущей плоскостью, мысленно удаляют, в результате чего становятся видимыми контуры внутренних, ранее закрытых поверхностей. В разрезе показывают то, что лежит в секущей плоскости, и то, что расположено за ней2. Невидимые контуры, которые в разрезе стали видимыми, изображают сплошной толстой линией, а фигуру, полученную в результате пересечения предмета плоскостью, заштриховывают. Штриховку выполняют по ГОСТ 2.306 – 68 [6]. Мысленное рассечение предмета относится только к данному разрезу и не влечет за собой изменения других изображений. На чертеже может быть представлено несколько разрезов предмета.
Секущие плоскости должны проходить по плоскостям симметрии предмета, по осям отверстий и пересекать полости, как правило, по их центру.
Разрезы могут быть расположены:
на месте основных видов;
на свободном поле чертежа.
Построение разреза показано на рис. 13. Предмет рассечен секущей плоскостью, параллельной фронтальной плоскости проекций (см. рис. 13, б). На ортогональных проекциях (см. рис. 13, а) отсеченная часть предмета мысленно удалена, а оставшаяся часть изображена на месте вида спереди.
1Допускается показывать невидимые поверхности на видах штриховыми линиями только тогда, когда контуры этих поверхностей являются простыми фигурами и не затемняют виды.
2Допускается изображать не все, что расположено за секущей плоскостью, если этого не требуется для понимания конструкции предмета.
10

а б
Рис. 13. Образование фронтального разреза:
а– ортогональные проекции; б – аксонометрическая проекция предмета
4.1.Простые разрезы
Взависимости от количества секущих плоскостей разрезы разделяются на простые и сложные. Простые разрезы получают при применении одной секущей плоскости, они легко читаются, поэтому им следует отдавать предпочтение.
Взависимости от положения секущей плоскости простой разрез может быть:
г о р и з о н т а л ь н ы м – секущая плоскость параллельна горизонтальной плоскости проекций (см. рис.14, разрез А-А).
в е р т и к а л ь н ы м – секущая плоскость перпендикулярна к горизонтальной плоскости проекций (например разрезы на рис. 13, 15);
н а к л о н н ы м – секущая плоскость составляет с горизонтальной плоскостью проекций угол, отличный от прямого (рис. 16, разрез А-А). Допускается наклонный разрез поворачивать до ближайшего горизонтального или вертикального положения (рис. 17).
Вертикальный разрез называется ф р о н т а л ь н ы м, если секущая плоскость параллельна фронтальной плоскости проекций (см. рис. 13), и п р о ф и л ь н ы м, если секущая плоскость параллельна профильной плоскости проекций (см. рис. 15).
Если секущая плоскость направлена вдоль длины или высоты предмета, то разрез называет-
ся п р о д о л ь н ы м (рис. 18, разрез А-А). Если секущая плоскость перпендикулярна длине или высоте предмета, то разрез называют п о п е р е ч н ы м (см. рис. 18, разрез Б-Б).
Разрезы, образованные одной секущей плоскостью, но со встречным направлением взгляда наблюдателя, выполняются так, как показано на рис. 19.
Рис. 14. Образование горизонтального разреза
11
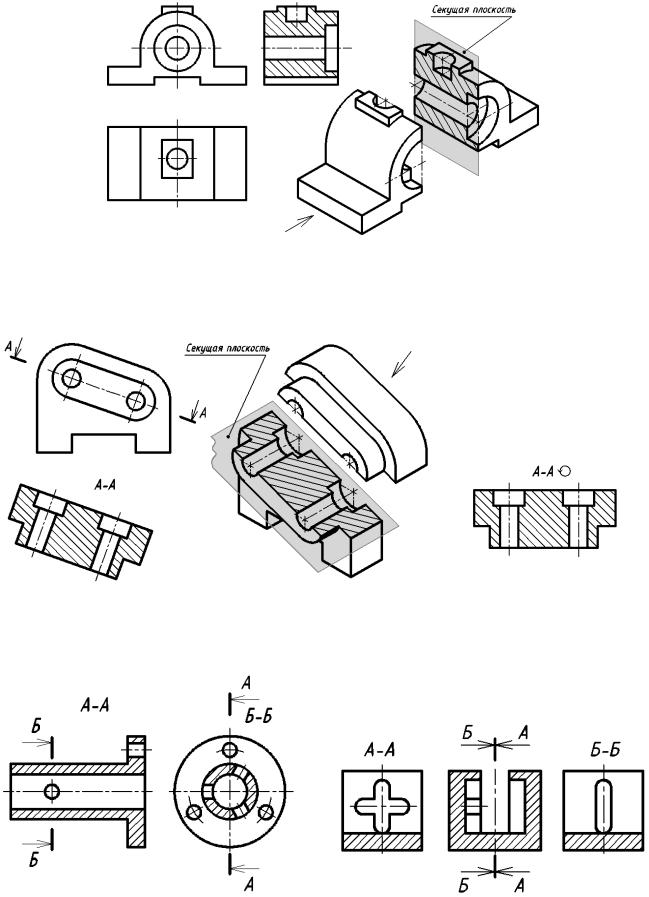
Рис. 15. Образование профильного разреза
|
Рис. 16. Образование наклонного разреза |
Рис. 17. Повернутый |
|
наклонный разрез |
|
Рис. 18. Продольный (А-А) и поперечный (Б-Б) |
Рис. 19. Пример разрезов со встречным |
|
разрезы |
направлением взгляда |
|
12 |

4.2. Местные разрезы
Местный разрез представляет собой часть простого разреза (рис. 20), который располагается на виде и ограничивается сплошной волнистой линией1. Местный разрез применяется для выявления внутренней формы предмета в отдельном ограниченном месте. С помощью местных разрезов показывают форму невидимых отверстий, пазов, канавок и других элементов в том случае, если они занимают по отношению к виду его малую часть и делать полный разрез нерационально. Волнистая линия, ограничивающая местный разрез, не должна совпадать с другими линиями изображения.
Рис. 20. Образование местного разреза
4.3. Обозначение простых разрезов
Обозначить разрез – это значит:
показать положение секущей плоскости;
сопроводить надписью сам разрез.
Положение секущей плоскости указывается на чертеже разомкнутой линией, причем начальный и конечный штрихи не должны пересекать контур соответствующего изображения. К начальному и конечному штрихам проводятся стрелки, указывающие направление взгляда наблюдателя. Стрелки должны располагаться на расстоянии 2 … 3 мм от наружных по отношению к «разрезаемому» изображению концов штрихов. Со стороны внешнего угла около стрелок ставится одна и та же прописная буква русского алфавита. Построенный при сечении указанной плоскостью предмета разрез должен быть отмечен надписью с применением той же буквы по типу А-А (всегда двумя буквами через тире). Пример обозначения разреза приведен на рис. 13.
Однако, как видно из рис. 13 … 20, одни разрезы на чертежах обозначены, другие не обозначены. Необходимо четко уяснить, когда разрезы обозначаются, а когда нет.
Простой разрез не обозначается, если секущая плоскость совпадает с плоскостью симметрии предмета в целом, а соответствующие изображения располагаются в непосредственной проекционной связи и не разделены какими-либо другими изображениями. Примеры таких разрезов приведены на рис. 13, 15.
Во всех остальных случаях простые горизонтальные, фронтальные и профильные разрезы должны быть обозначены.
Наклонные разрезы обозначаются всегда. Местные разрезы не обозначаются.
Примечание. Не допускается при обозначении разреза применять ту же букву, которая была употреблена для обозначения других изображений на чертеже.
1 По ГОСТ 2.305 – 2008 [1] для ограничения местных разрезов и в качестве линий обрыва изображений может применяться сплошная тонкая линия с изломами, начертание которой см. в ГОСТ 2.303 – 68 [4].
13
Тема урока. Решение задач на построение
простых разрезов.
Цели урока.
1. Сформировать практические навыки построения
простого разреза.
2. Отработать алгоритм выполнения простого
разреза.
Развивающая задача. Развитие творческого
мышления и пространственного воображения.
Пособие и оборудование. Учебные таблицы,
индивидуальные карточки-задания, калька,
скрепки, карандаши Т и М, цветной мел.
План
- Вхождение в тему урока, постановка проблемы.
- Поэтапное формирование умения и навыков
учащихся в построении простого разреза. - Индивидуальная работа учащихся по
карточкам-заданиям. - Подведение итогов урока и задание на дом.
Ход урока
1. Учитель. Сегодня на уроке мы повторим
изученный материал по теме “Разрез”, затем
составим алгоритм решения задач на построение
простого разреза и отработаем навыки его
выполнения.
(Проверяю готовность к уроку).
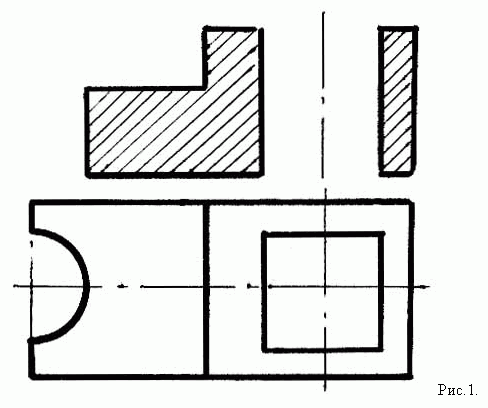
Учитель. На доске даны два чертежа (рис.1
и рис.2)
На изображении нет очертаний предмета за
секущей плоскостью. Постарайтесь дополнить
изображение недостающими линиями, чтобы
получился разрез.
(Вызываю к доске двух учащихся. Они
работают цветными мелками)
Учитель. Пока ребята у доски решают задачу,
проверим ваши знания по этой теме.
1.1. Что представляет собой разрез?
1.2. Дайте его определение.
1.3. Чем отличается разрез от сечения?
1.4. В зависимости от расположения секущей
плоскости в пространстве как называются разрезы?
1.5. Дайте определение фронтального разреза.
1.6. Когда разрез называется профильным?
1.7. Разрез при секущей плоскости параллельной
горизонтальной плоскости называется ……….
(Проверка решения задач у учащихся,
работающих у доски и оценка их работы)
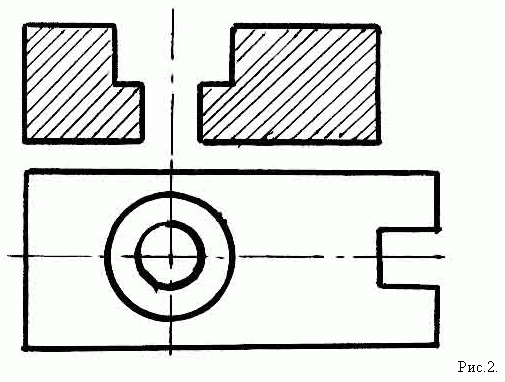
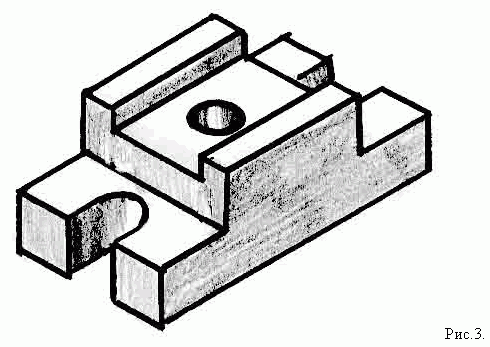
2. Учитель. Переходим к решению новой
задачи. Дано наглядное изображение и его чертеж
(рис.3 и рис.4)
На “рис.4” разрез уже выполнен. Необходимо
найти фигуру сечения и заштриховать ее.
Перед началом решения давайте проанализируем
геометрическую форму наглядного изображения (рис.3).
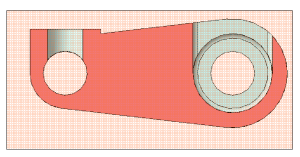
Ответ. Деталь состоит из основания
представляющего собой прямоугольный
параллелепипед. С двух сторон он имеет вырезы,
состоящие из сочетания параллелепипеда и
полуцилиндра. К верхнему основанию примыкает
прямоугольный параллелепипед, имеющий в верхней
части вырез в форме параллелепипеда. В центре
деталь имеет сквозное цилиндрическое отверстие.
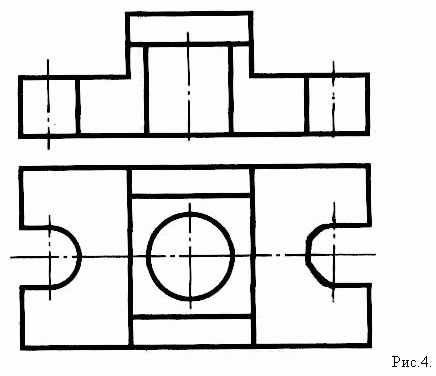
Учитель. Давайте определим симметричность
нашей детали и место прохождения секущей
плоскости на чертеже (рис.4).
Ответ. Данная деталь симметрична, а секущая
плоскость проходит вдоль оси симметрии.
Учитель. Мысленно разрезаем деталь. А что
делать дальше?
Ответ. Мысленно удаляем часть детали,
которая расположена ближе к нам.
Учитель. Мы удалили нижнюю часть
детали и задаем вопрос: “Что надо штриховать на
главном виде?”, но лучше задать вопрос – “Что не
надо штриховать?”. Определить это на чертеже
проще. (Эти участки на чертеже я буду
закрашивать желтым цветом, а фигуру сечения –
заштриховывать.)
На виде сверху “рис.4” красным цветом проводим
секущую плоскость и смотрим, что находится
дальше за секущей плоскостью. Это не будем
штриховать! При выполнении работы обязательно
контролируем проекционную связь. На нашем
чертеже поверхность боковых вырезов осталась за
секущей плоскостью. Проекцию вырезов на главном
виде чертежа будем заштриховывать?
Ответ. Поверхность вырезов на главном виде
чертежа не будем заштриховывать, т.к. она
осталась за секущей плоскостью.
Учитель. Задняя стенка цилиндрической
поверхности находится за секущей плоскостью?
Ответ. Да, находится. Ее не штрихуем.
Учитель. За секущей плоскостью находится и
задняя стенка выреза верхней призмы, и она не
заштриховывается. Фигуру сечения заштриховываем
под углом 45 градусов
Решение задачи нахождения фигуры сечения по
разрезу всем понятно?
Тогда возьмите карточку-задание (рис.9, [1]),
переведите чертеж на кальку и самостоятельно
найдите фигуру сечения на разрезе. Фигуру
сечения заштриховать. Время на работу 5 минут.
(Учащиеся выполняют задание)
Итак, по заданному сечению мы выполнили разрез
и по заданному разрезу узнали, как правильно
выделить фигуру сечения.
Следующий этап нашей работы – это составление
алгоритма выполнения простого разреза.
Работать будем с наглядным изображением (рис.6),
чертежом (рис.7).
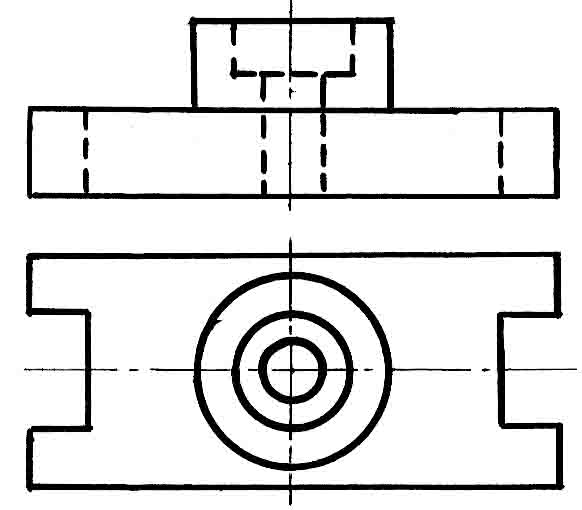
Откройте тетради и запишите
последовательность построения простого разреза.
(Учитель работает с чертежом, учащиеся
делают запись алгоритма)
“Алгоритм построения простого
разреза” [2].
2.1. Анализ геометрической формы детали,
определение ее симметричности.
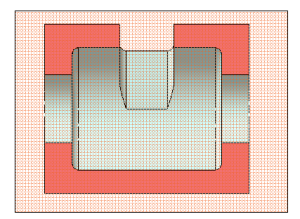
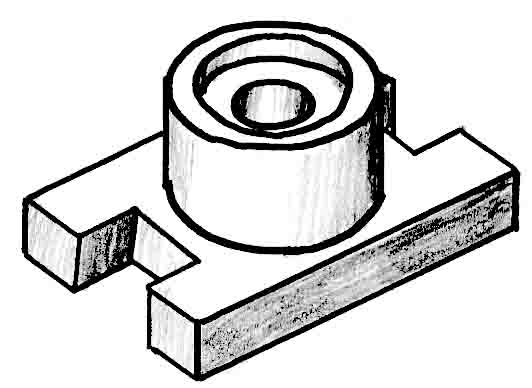
Ответ. Деталь “рис.6” состоит из
прямоугольного параллелепипеда и цилиндра,
который стоит в центре верхнего основания
параллелепипеда. На концах параллелепипеда
имеются призматические вырезы. В центре детали
вдоль оси цилиндра соосно расположены два
сквозных цилиндрических отверстия. Деталь
симметрична.
2.2. Нахождение элементов детали, форма которых
выявляется с помощью разреза.
Ответ. Это два цилиндрических отверстия и
два призматических выреза.
2.3. Определение направления и места секущей
плоскости, ее обозначение.
Ответ. Секущая плоскость пройдет по
середине детали, она совпадет с осью симметрии и
на чертеже будет располагаться на виде сверху.
Учитель. Обозначение секущей плоскости
будем наносить? Почему?
Ответ. Обозначение на чертеже не наносим,
потому что деталь симметричной формы.
2.4. Мысленное представление фигур сечения.
Учитель. Как это будем делать?
Ответ. Мысленно удаляем часть детали,
расположенную ближе к нам и представляем фигуру
сечения.
2.5. Снятие линий видимого контура, относящихся к
мысленно удаленной части детали
2.6. Преобразование линий невидимого контура в
видимые.
2.7. Штриховка фигур сечения.
Учитель. Это определение того, что не надо
штриховать за секущей плоскостью.
Ответ. Не заштриховываем проекции
призматических вырезов и проекции
полуцилиндров.
2.8. Обводка контура чертежа.
(По окончании записи алгоритма на доске
получается чертеж “рис.8”,, учитель отвечает на
возникшие вопросы по алгоритму)
3. Учитель. Продолжаем работу по
индивидуальным карточкам-заданиям “рис. 10……14”
[1]. Работаем на кальке, соблюдая алгоритм
построения простого разреза.
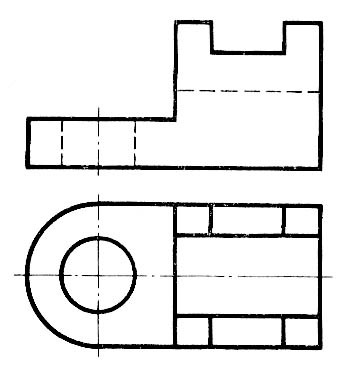
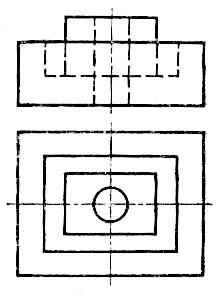
Чем больше решите задач, тем выше оценка.
(Учитель отвечает на вопросы
учащихся, называет очередной этап алгоритма и
помогает затрудняющимся в выполнении работы.)
4. Чем мы занимались сегодня на уроке?
Ответ. Сегодня мы повторяли тему
“Разрез” и работали по карточкам-заданиям.
Учитель. Что нового узнали на уроке?
Ответ. Мы познакомились с алгоритмом
построения простого разреза.
Учитель. Давайте повторим алгоритм
последовательности построения простого разреза.
(Учащиеся отвечают.)
Учитель. Какие оценки можно было бы
поставить тем, кто хорошо работал на уроке?
Подпишите свои работы и сдайте учителю.
(Оценки сообщаются на следующем
уроке)
Учитель. Откройте дневники, запишите
задание на дом: Учебник “Черчение 8-9 класс”,
стр.142, упр.1,2.[3].
(Объяснение домашнего задания).
Учитель. Какие вопросы по уроку и
домашнему заданию у вас имеются?
Спасибо за работу. Урок окончен.
До свидания.
ЛИТЕРАТУРА
- Василенко Е.А., Жукова Е.Т., Катханова Ю.Ф.,
Терещенко А.Л. Карточки-задания по черчению для 8
класса. Пособие для учителя. М.: Просвещение. 1990. - Преображенская Н.Г. Сечения и разрезы на уроках
черчения в школе. М.: Просвещение. 1986. - Ботвинников А.Д., Виноградов В.Н., Вышепольский
И.С. Черчение. Учебник для 7-8 классов
общеобразовательных учреждений. М.: Просвещение.
1997.
Разрезы
- Подробности
- Категория: Инженерная графика
Автор видеоурока: к.пед.н., доцент кафедры ИГиСАПР Кайгородцева Н.В.
РАЗРЕЗЫ
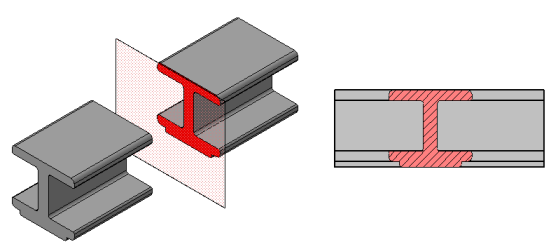
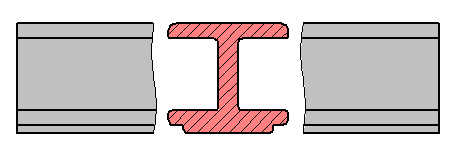
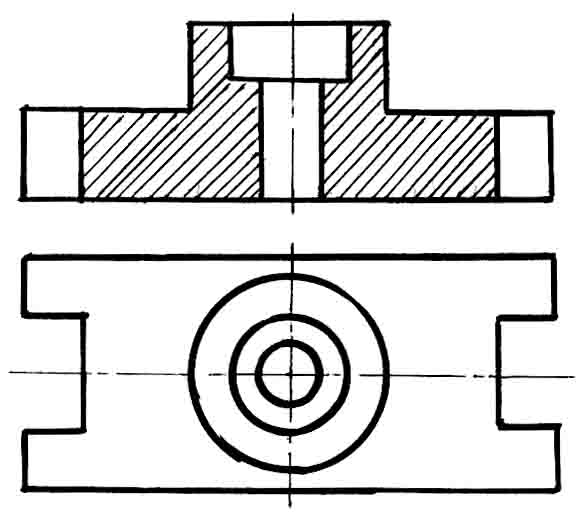
Если деталь полая или имеет внутреннее устройство в виде отверстий, углублений и т. п., на видах невидимые контуры изображают штриховыми линиями. При сложной внутренней конструкции детали большое количество штриховых линий затрудняет чтение чертежа и нередко ведет к неточному представлению о форме детали. Этого можно избежать, применяя условные изображения — разрезы.
Разрезом называется изображение предмета, полученное при мысленном рассечении его одной или несколькими секущими плоскостями. При этом часть предмета, расположенная между наблюдателем и секущей плоскостью, мысленно удаляется, а на плоскости проекций изображается то, что получается в секущей плоскости (фигура сечения предмета секущей плоскостью) и что расположено за ней.
При разрезе внутренние линии контура, изображавшиеся на чертеже штриховыми линиями, становятся видимыми и изображаются сплошными основными линиями.
В зависимости от числа секущих плоскостей разрезы разделяются на простые (при одной секущей плоскости) и сложные (при нескольких секущих плоскостях).
В зависимости от положения секущей плоскости относительно горизонтальной плоскости проекций разрезы разделяются на горизонтальные, вертикальные и наклонные.
Разрезы называются продольными, если секущие плоскости направлены вдоль длины или высоты предмета, и поперечными, если секущие плоскости перпендикулярны длине или высоте предмета.
На всех примерах, приведенных ниже, условно принято, что предметы — металлические, и для графического обозначения материала в сечениях детали делается штриховка тонкими линиями с наклоном под углом 45° к линиям рамки чертежа.
Штриховка на всех изображениях одной детали выполняется в одном направлении (с правым или левым наклоном).
ПРОСТЫЕ РАЗРЕЗЫ — ВЕРТИКАЛЬНЫЕ И ГОРИЗОНТАЛЬНЫЕ
Вертикальным разрезом называется разрез, образованный секущей плоскостью, перпендикулярной горизонтальной плоскости проекций.
Вертикальный разрез называется фронтальным, если секущая плоскость параллельна фронтальной плоскости проекций (рис. 258), и профильным, если секущая плоскость параллельна профильной плоскости проекций (рис. 259).
Пример образования фронтального разреза детали дан на рис. 258. Деталь рассечена плоскостью А, параллельной фронтальной плоскости проекций. Часть детали, расположенная перед секущей плоскостью, мысленно удалена, а оставшаяся часть, полностью изображенная на месте главного вида, представляет собой фронтальный разрез детали. Все контурные линии, расположенные в секущей плоскости и за ней, Показаны на разрезе как видимые. Пример образования профильного разреза дан на рис. 259. Деталь рассекается секущей плоскостью параллельной профильной плоскости проекций. Получающийся в этом случае профильный разрез расположен на месте вида слева.
Горизонтальными разрезами называются разрезы, образованные секущими плоскостями, параллельными горизонтальной проекции.
На рис. 260 деталь рассечена горизонтальной плоскостью Р, параллельной горизонтальной плоскости проекции. Верхняя часть детали мысленно удалена, а оставшаяся нижняя часть спроецирована на горизонтальную плоскость проекции. Горизонтальные, фронтальные и профильные разрезы могут размещаться на месте соответствующих основных видов.
ОБОЗНАЧЕНИЕ РАЗРЕЗОВ
Если секущая плоскость совпадает с плоскостью симметрии предмета в целом и разрез расположен в проекционной связи с видом и не разделен какими-либо другими изображениями, то при выполнении горизонтальных, фронтальных и профильных разрезов положение секущей плоскости на чертеже не отмечается и разрез надписью не сопровождается (см. рис. 258, 259 и 260).
В остальных случаях положение секущей плоскости указывают на чертеже разомкнутой линией и стрелками, указывающими направление взгляда, а над разрезом выполняется соответствующая надпись, указывающая секущую плоскость, примененную для получения этого разреза.
На рис. 261 выполнены два вертикальных разреза: фронтальный (А—А) (рис. 261, а) и профильный Б) (рис. 261, в), секущие плоскости которых не совпадают с плоскостями симметрии детали в целом. Поэтому на чертеже указано положение секущих плоскостей и соответствующие им разрезы сопровождаются надписями.
Штрихи разомкнутой линии не должны пересекать контур изображения. На штрихах линии сечения перпендикулярно к ним ставят стрелки, указывающие направление взгляда. Стрелки наносят на расстоянии 2— 3 мм от внешнего конца штриха линии сечения.
Размеры стрелки показаны на рис. 262.
Около каждой стрелки наносится одна и та же прописная буква русского алфавита.
Надпись над разрезом подчеркивается сплошной тонкой линией и содержит две буквы, которыми обозначена секущая плоскость, написанные через тире (рис. 261, б).
На одном изображении допускается соединять часть вида и часть разреза. Линии невидимого контура на соединяемых частях вида и разреза обычно не показываются.
Если вид и разрез представляют собой симметричные фигуры (рис. 263), то можно соединить половину вида и половину разреза, разделяя их штрихпунктирной тонкой линией, являющейся осью симметрии.
Часть разреза располагают справа (рис. 263, а) или снизу от оси симметрии (рис. 263,б), разделяющейчасть вида с частью разреза.
При соединении симметричных частей вида и разреза, если с осью симметрии совпадает проекция какой-либо линии, например ребра (рис. 264), то вид от разреза отделяется сплошной волнистой линией, проводимой левее (рис. 264, а) или правее (рис. 264, б) оси симметрии.
При соединении на одном изображении вида и разреза, представляющих несимметричные фигуры, часть вида от части разреза отделяется сплошной волнистой линией (рис. 264, в).
Вертикальные разрезы, приведенные на рис. 258 и 259, получены в результате применения секущих плоскостей, параллельных либо фронтальной, либо профильной плоскостям проекций. На практике встречаются случаи, когда вертикальный разрез выполняется секущей плоскостью, не параллельной ни фронтальной. ни профильной плоскостям проекций (рис. 265), в этом случае разрез строится и располагается в соответствии с направлением взгляда, указанным стрелками на линии сечения.
Допускается поворот разреза до положения, соответствующего положению, принятому для предмета на главном изображении (рис. 265). В этом случае к надписи над разрезом должно быть добавлено слово
«повернуто».
НАКЛОННЫЙ РАЗРЕЗ
Если деталь имеет наклонно расположенные полые элементы, применяют наклонный разрез.
Наклонным разрезом называют разрез плоскостью, которая составляет с горизонтальной плоскостью проекций угол, отличный от прямого. Наклонный разрез проецируют на дополнительную плоскость, параллельную секущей, совмещая ее с плоскостью чертежа.
Пример наклонного разреза приведен на рис. 266. Положение секущей плоскости отмечается линией сечения со стрелками, указывающими направление взгляда.
Наклонные разрезы должны располагаться в соответствии с направлением взгляда, указанного стрелками на линии сечения (рис. 266, б). Допускается располагать наклонные разрезы на любом месте поля чертежа (рис. 267) вне проекционной связи с видом, но с учетом направления взгляда. При необходимости наклонные разрезы могут располагаться с поворотом (разрез А—А на рис. 267).
МЕСТНЫЕ РАЗРЕЗЫ
Если требуется выяснить конструкцию изделия лишь в отдельном ограниченном месте, можно применить разрез, называемый местным. Линия, ограничивающая местный разрез, выполняется сплошной волнистой линией.
На рис. 268, а выполнены примеры местных разрезов, благодаря которым выявляется форма некоторых элементов детали.
Если местный разрез выполняется на части предмета, представляющей собой тело вращения (рис. 268, б) и, следовательно, изображенной с осевой линией, то местный разрез с видом могут разделяться этой осевой линией.
СЛОЖНЫЕ РАЗРЕЗЫ — СТУПЕНЧАТЫЕ И ЛОМАНЫЕ
Кроме простых разрезов, когда применяется одна плоскость, употребляются разрезы сложные при двух и более секущих плоскостях.
Сложные разрезы разделяются на ступенчатые и ломаные.
Сложный разрез, образованный двумя и более секущими параллельными плоскостями, называется ступенчатым. Ступенчатые разрезы могут быть горизонтальными, фронтальными и профильными.
Пример ступенчатого горизонтального разреза показан на рис. 269, а. Две секущие плоскости расположены параллельно горизонтальной плоскости проекции. Чертеж детали с таким разрезом представлен на рис. 269, б. Направление секущих плоскостей указано разомкнутыми линиями (линиями сечения). У начального и конечного штрихов линии сечения имеются стрелки с одной и той же буквой. Линия сечения имеет также перегибы, показывающие места перехода от одной секущей плоскости к другой. Перегибы линии сечения выполняются той же толщины, как и штрихи разомкнутой линии. Стрелки указывают направление взгляда.
При выполнении ступенчатого разреза секущие плоскости совмещают в одну плоскость, и ступенчатый разрез оформляется как простой. Линии, разделяющие два сечения друг от друга в местах перегибов на ступенчатом разрезе, не указываются.
На рис. 270, а показан пример фронтального ступенчатого разреза, выполненного тремя секущими плоскостями, положение которых отмечено на виде сверху ступенчатой линией сечения (рис. 270, в).
Допускается сложные разрезы располагать вне проекционной связи с другими изображениями (рис. 270, б).
Профильные ступенчатые разрезы выполняются аналогично.
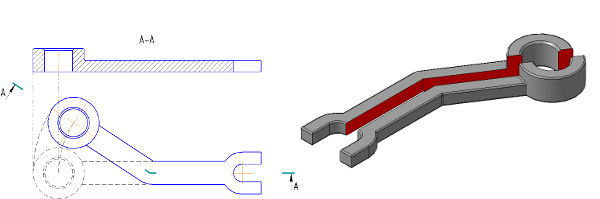
Ломаные разрезы — это разрезы, полученные при сечении предмета не параллельными, а пересекающимися плоскостями (рис. 271). В этом случае одна секущая плоскость условно повертывается около линии пересечения секущих плоскостей до совмещения с другой секущей плоскостью, параллельной какой-либо из основных плоскостей проекций, т. е. ломаный разрез размещается на месте соответствующего вида.
На рис. 271 рычаг рассечен двумя пересекающимися секущими плоскостями, одна из которых является фронтальной плоскостью. Секущая плоскость, расположенная левее, мысленно поворачивается вокруг линии пересечения секущих плоскостей до совмещения с фронтальной секущей плоскостью. Вместе с секущей плоскостью поворачивается расположенная в ней фигура сечения детали. На виде спереди дано изображение рассеченной детали после выполнения указанного поворота. На рис. 271 для наглядности нанесены линии связи и положение части детали после поворота. Эти построения на чертеже не показывают.
Ломаный разрез может быть получен при сечении тремя пересекающимися плоскостями (рис. 272).
При выполнении ломаного разреза, когда одна секущая плоскость поворачивается до совмещения с другой, элементы предмета, расположенные за ней, не поворачиваются: они изображаются так, как они проецируются на соответствующую плоскость проекций при условии, что разрез не выполняется. Выступ Б (рис. 273, а), находящийся за поворачиваемой секущей плоскостью, в повороте не участвует: его изображения выполняются на чертеже в проекционной связи.
Исключением из этого правила могут быть случаи, когда элементы предмета расположены симметрично относительно поворачиваемой секущей плоскости. В этих случаях выполняется поворот таких элементов предмета вместе с секущей плоскостью. Рычаг (рис. 273, б) имеет два ушка, расположенные симметрично относительно секущей плоскости. Ушко поворачивается вместе с секущей плоскостью при ее совмещении с профильной плоскостью.
Направление поворота секущей плоскости может не совпадать с направлением взгляда (рис. 273, в).