Как найти разрядность двоичного кода

Сегодня каждый из нас не представляет жизнь без компьютера. Компьютер — это устройство, которое может работать с разными видами данных (текстовыми, графическими, звуковыми). Чтобы эти данные компьютер мог сохранить, обработать, передать, они должны быть представлены в цифровом виде. Данные в компьютере хранятся, обрабатываются, передаются в двоичном коде.

Как и каждый язык (формальный или естественный), двоичный код имеет свой алфавит и мощность алфавита.

Почему именно (0) и (1)? Потому что в технике проще всего реализовать такие наборы цифр: если есть сигнал, то это (1), если нет — это (0).

Двоичная система кодирования появилась не с созданием компьютера, ещё задолго до этого математик Г. В. Лейбниц использовал двоичные числа.

Рис. (1). Портрет Г. В. Лейбница

Существуют ряд устройств, работающих по принципу двоичного кодирования. Например, обычный выключатель, где свет горит/не горит.

Всем известная азбука Морзе тоже состоит из двух знаков: точки и тире.

Рис. (2). Алфавит азбуки Морзе

Память компьютера можно представить в виде листочка в клетку, и в каждой клетке хранится либо (1), либо (0).

Рис. (3). Представление битов памяти

Что же происходит, когда мы нажимаем на клавиатуре цифру, например (5)?

Каждая клавиша имеет свой порядковый номер (по кодировочной таблице), и именно он переводится в двоичный код.

Рис. (4). Схема двоичного кодирования

Как узнать, сколько бит (клеточек) в памяти компьютера необходимо для кодирования различных знаков?

Как кодируются числа при помощи двоичного кодирования?

Пусть нам нужно закодировать две цифры — (0) и (1). Для кодирования этих цифр нужно (2) ячейки памяти, в одну напишем (0), а в другую — (1).

А если цифр больше? Сколько битов нужно для кодирования каждой цифры? Рассмотрим, как закодировать (4) цифры.

Если будем использовать однозначные числа, то хватит только для кодирования (2) цифр, а нам нужно больше. Попробуем сделать коды двузначными:

Получается, если цифр будет (16), то длина цепочки будет (4)?

Длина цепочки знаков в двоичном коде называется разрядностью двоичного кода.

Рассмотри таблицу.

Задача (1). Определи, сколько нужно знаков для кодирования (11) цифр?

Решение: посмотри в таблицу.

Задача (2). Определи, сколько можно составить различных последовательностей, если длина цепочки (6) символов?

Решение: для решения воспользуемся таблицей.

Если длина цепочки (разрядность двоичного кода) равна (6), следовательно, можно закодировать (64) различные последовательности.

Информатика

7 класс

Урок № 5

Кодирование информации. Двоичный код

Перечень вопросов, рассматриваемых в теме:

• Понятие код.
• Понятие кодирования информации.
• Двоичный код.

Тезаурус:

Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную. Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.

Алфавит языка – конечный набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита – это количество входящих в него символов.

Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием. Двоичное кодирование универсально, так как с его помощью может быть представлена любая информация.

Основная литература:

1. Босова Л. Л. Информатика: 7 класс. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2017. – 226 с.

Дополнительная литература:

1. Босова Л. Л. Информатика: 7–9 классы. Методическое пособие. // Босова Л. Л., Босова А. Ю., Анатольев А. В., Аквилянов Н.А. – М.: БИНОМ, 2019. – 512 с.
2. Босова Л. Л. Информатика. Рабочая тетрадь для 7 класса. Ч 1. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2019. – 160 с.
3. Босова Л. Л. Информатика. Рабочая тетрадь для 7 класса. Ч 2. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2019. – 160 с.
4. Гейн А. Г. Информатика: 7 класс. // Гейн А. Г., Юнерман Н. А., Гейн А.А. – М.: Просвещение, 2012. – 198 с.

Теоретический материал для самостоятельного изучения

Кодирование информации

Для решения своих задач человеку часто приходится преобразовывать имеющуюся информацию из одной формы представления в другую. Например, при чтении вслух происходит преобразование информации из дискретной (текстовой) формы в непрерывную (звук). Во время диктанта на уроке русского языка, наоборот, происходит преобразование информации из непрерывной формы (голос учителя) в дискретную (записи учеников).

Информация, представленная в дискретной форме, значительно проще для передачи, хранения или автоматической обработки. Поэтому в компьютерной технике большое внимание уделяется методам преобразования информации из непрерывной формы в дискретную.

Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную.

Рассмотрим суть процесса дискретизации информации на примере.

На метеорологических станциях имеются самопишущие приборы для непрерывной записи атмосферного давления. Результатом их работы являются барограммы – кривые, показывающие, как изменялось давление в течение длительных промежутков времени. Одна из таких кривых, вычерченная прибором в течение семи часов проведения наблюдений, показана на рисунке 1.

На основании полученной информации можно построить таблицу, содержащую показания прибора в начале измерений и на конец каждого часа наблюдений.

Полученная таблица даёт не совсем полную картину того, как изменялось давление за время наблюдений: например, не указано самое большое значение давления, имевшее место в течение четвёртого часа наблюдений. Но если занести в таблицу значения давления, наблюдаемые каждые полчаса или 15 минут, то новая таблица будет давать более полное представление о том, как изменялось давление.

Таким образом, информацию, представленную в непрерывной форме (барограмму, кривую), мы с некоторой потерей точности преобразовали в дискретную форму (таблицу).

В дальнейшем вы познакомитесь со способами дискретного представления звуковой и графической информации.

Двоичное кодирование

В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.

Алфавит – конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита – это количество входящих в него символов (знаков).

Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 3). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.

Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1. Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа.

Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов. Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рисунке.

Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:

Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 – вдвое больше, чем из двух двоичных символов:

Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный – 32, шестиразрядный – 64 и т. д.

Длину двоичной цепочки – количество символов в двоичном коде – называют разрядностью двоичного кода.

Обратите внимание, что:

4 = 2 ∙ 2,

8 = 2 ∙ 2 ∙ 2,

16 = 2 ∙ 2 ∙ 2 ∙ 2,

32 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 и т. д.

Здесь количество кодовых комбинаций представляет собой произведение некоторого количества одинаковых множителей, равного разрядности двоичного кода.

Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода – буквой i, то выявленная закономерность в общем виде будет записана так:

В математике такие произведения записывают в виде:

N = 2ⁱ.

Запись 2ⁱ читают так: «2 в i-й степени».

Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Двоичный код какой разрядности потребуется, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.

Решение. Так как алфавит племени Мульти состоит из 16 символов, то и кодовых комбинаций им нужно 16. В этом случае длина (разрядность) двоичного кода определяется из соотношения: 16 = 2ⁱ. Отсюда i = 4.

Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рис. 1.13: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.

Универсальность двоичного кодирования

В начале нашей беседы вы узнали, что информация, представленная в непрерывной форме, может быть выражена с помощью символов некоторого естественного или формального языка. В свою очередь, символы произвольного алфавита могут быть преобразованы в двоичный код. Таким образом, с помощью двоичного кода может быть представлена любая информация на естественных и формальных языках, а также изображения и звуки (рис. 6). Это и означает универсальность двоичного кодирования.

Двоичные коды широко используются в компьютерной технике, требуя только двух состояний электронной схемы – «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре 0).

Простота технической реализации – главное достоинство двоичного кодирования. Недостаток двоичного кодирования – большая длина получаемого кода.

Равномерные и неравномерные коды

Различают равномерные и неравномерные коды. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные – разное.

Выше мы рассмотрели равномерные двоичные коды.

Примером неравномерного кода может служить азбука Морзе, в которой для каждой буквы и цифры определена последовательность коротких и длинных сигналов. Так, букве Е соответствует короткий сигнал («точка»), а букве Ш – четыре длинных сигнала (четыре «тире»). Неравномерное кодирование позволяет повысить скорость передачи сообщений за счёт того, что наиболее часто встречающиеся в передаваемой информации символы имеют самые короткие кодовые комбинации.

Разбор решения заданий тренировочного модуля

№1.Тип задания: ввод с клавиатуры пропущенных элементов в тексте

Переведите десятичное число 273 в двоичную систему счисления.

273₁₀=_____

Решение.

Воспользуемся алгоритмом перевода целых чисел из системы с основанием p в систему с основанием q:

1. Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.

2. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.

3. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.

4. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

273₁₀= 100010001.

Ответ: 273₁₀= 100010001.

№2. Тип задания: единичный / множественный выбор.

Четыре буквы латинского алфавита закодированы кодами различной длины:

Определите, какой набор букв закодирован двоичной строкой 0100000100010.

Варианты ответов:

1. BACAD
2. ACAD
3. ABBAD
4. CADDA

Решение. Рассмотрим код: 0100000100010.

Выделим закодированные буквы:

01 000 001 000 10

В A C A D

Ответ: 1. BACAD.

Двоичная система счисления

Двоичный код — понятие, которое кажется сложным большинству людей. Однако на самом деле это одна из самых простых шифровальных систем в мире. Более того, мы сталкиваемся с ней ежедневно в обычной жизни.

Например, в наших компьютерах хранится самая различная информация — текстовые файлы, видеоролики, аудиозаписи и изображения. Но в виде картинок, текстов и мультимедийных файлов эту информацию видим только мы — а сам компьютер воспринимает и обрабатывает любые сведения в форме двоичного кода.

Двоичная система счисления — что это такое?

Двоичный, или, как еще его называют, бинарный код — шифр, состоящий всего из двух символов. Его можно сравнить с азбукой Морзе, где используются только тире и точки в разных комбинациях — морзянкой передают сколь угодно сложные сообщения.

Двоичный код чаще всего представлен нулем и единицей. Но это не обязательно — двоичного кода можно брать и любые другие обозначения, главное, чтобы эти символы были противоположными или взаимоисключающими по сути.

• Двоичное кодирование — это процесс перевода любой информации в двоичную систему, то есть ее запись при помощи шифра, состоящего из двух символов в разных комбинациях.
• И наоборот, декодированием называют процесс обратного перевода — из двоичного кода в привычную для человеческих органов чувств форму информации.

Что такое разрядность двоичного кода?

Одним из важных свойств двоичной системы является понятие разрядности — этим словом называют количество позиций, используемых в конкретном коде для составления комбинаций.

• Например, в кодировке с двумя разрядами базовые символы будут представлены в четырех вариациях — 11, 00, 01 и 10.
• Три разряда будут выглядеть следующим образом — 000, 111, 110, 101, 100, 001, 010.
• Численность разряда можно установить, посчитав количество символов в комбинации.

Смысл разрядного двоичного кода заключается в том, что одно и то же число в нем можно обозначить разными комбинациями символов — например, обозначения 0001, 001, 01 и 1 будут подразумевать одно и то же число «1». Читают разряды не так, как текст, а справа налево. Как правило, на практике код бывает 4, 8, 16, 32 и 64 разрядным — в зависимости от объема информации и специфики решаемой задачи.

У неопытного пользователя может возникнуть вопрос — какой смысл в двоичной системе, и не проще ли обходиться без нее? Однако когда речь идет о сложной вычислительной технике, то оперировать огромным множеством простейших элементов для нее удобнее, нежели обращаться с малочисленными, но сложными символами.

Похожие статьи

Оглавление:

1. Что такое двоичный код?
2. Разрядность двоичного кода
3. Расшифровка двоичного кода
4. Виды двоичных кодов

Всем известна такая способность компьютеров, как
вычисление больших групп данных практически за считанные секунды. Однако не
каждый знает, что это умение электронных машин зависит от наличия тока и
напряжения.

Что такое двоичный код?

Как же компьютеру удаётся быстро обрабатывать огромные
объёмы информации? Помогает ему в этом двоичная система исчисления. Данные,
поступающие в это умное устройство, выглядят как единицы и нули. Каждой единице
и каждому нулю соответствует определённое состояние электропровода:

• 1 — высокое напряжение.
• 0 — низкое.

Или же для единиц — наличие напряжения, а для нулей —
отсутствие.

Основой двоичной системы исчисления являются двоичные
коды. Что такое двоичный код?

Процесс, когда данные преобразуются в нули и единицы,
называют «двоичная конверсия», а окончательное их обозначение — «двоичный код».

Разрядность двоичного кода

Все двоичные числа являются совокупностью битов, то есть,
единиц и нулей, а каждый бит является одним разрядом или одной позицией в
двоичном числе. Часто в задачах по информатике встречается вопрос, какое
количество информации несёт тот или иной двоичный код. Следует знать, что в
каждой цифре двоичного кода содержится количество информации, которое равно одному биту.

Что такое разрядность двоичного кода? Если смотреть с
точки зрения арифметики, то под разрядностью понимается место, которое занимает
цифра при записи чисел. Тогда под разрядностью двоичного кода подразумевается
количество мест знаков (разрядов) или количество битов, которые заранее
отведены для того, чтобы записать число.

Расшифровка двоичного кода

Как же расшифровать двоичный код? Десятичное обозначение
основано на десятичной системе исчисления, которую обычно используют в
повседневной жизни и числовые значения здесь представлены в виде десяти цифр от
нуля до девяти. Каждое из мест в числах в десять раз больше по ценности, чем
место, находящееся справа. Для представления числа больше 9 в десятичной
системе используется ноль, который ставится справа. А единица расположена слева
на следующем, более ценном месте.

Подобным образом устроена и двоичная система, в которой
используют только две цифры — ноль и единицу. Места слева ценнее в два раза,
чем места справа. Так, для двоичного кода характерно, что одноместными числами
могут быть только 0 и 1, а для любых чисел больше единицы требуется уже 2
места.

После 0 и 1 следуют такие двоичные числа:

• 10 (то есть, 1,0).
• 11 (1,1).
• 100 (1,0,0).

В двоичной системе 100 — это эквивалент цифры 4
десятичной системы. Таким образом, любое число можно выразить в виде двоичного
кода, но оно будет занимать больше места. Также, закрепив за каждой буквой
алфавита определённые двоичные числа, можно осуществить перевод в двоичный код
любое слово.

Видео о переводе чисел в двоичный код

К примеру, для передачи сообщения по цифровому каналу
связи, его кодируют, то есть, сопоставляют каждый символ исходного сообщения с
некоторым кодом (кодовым словом). Для этого используются двоичные коды —
последовательность единиц и нулей.

Например, чтобы закодировать слово «мама» выбирается
следующий код:

• М — 00.
• А — 1.
• Ы — 01.
• Л — 0.
• У — 10.

Пробел — 11.

Закодированные буквы соединятся в одну битовую строчку и
будут переданы по сети в таком виде:

МАМА МЫЛА ЛАМУ → 0010011100010111010010

После
того как эта строка будет доставлена к пункту назначения, следует решить
проблему восстановления исходного сообщения. Так, получив сообщение «001001»,
его раскодирование можно осуществить несколькими способами. К примеру,
предположив, что оно состоит только из букв Л (код 0) и А (код 1), получится:

ЛЛАЛЛАААЛЛЛАЛАААЛАЛЛАЛ

Это значит, что вышеприведённый код не декодируется
однозначно. Однозначно декодируемые коды — это такие коды, в которых любые
кодовые сообщения расшифровываются только одним способом.

Равномерные коды

Данная проблема решается путём правильного разбития
битовой цепочки на отдельно закодированные слова. Это можно сделать, к примеру,
с использованием равномерного кода, длина слов в котором всегда одинакова. К
примеру, данная фраза состоит из шести символов, а это значит, что можно
применить трехбитный код.

Например, если закодировать вышеприведённую фразу с
помощью такого кода:

• М — 000.
• А — 001.
• Ы — 010.
• Л — 011.
• Пробел — 101, то получится следующее:

МАМА МЫЛА ЛАМУ →
000001000001101000010011001101011001000100

Это сообщение имеет длину 42 бита. Несмотря на то что оно
длиннее, чем первое, состоящее всего из 22 бит, его значительно легче разобрать
на отдельные слова для раскодирования:

000 001 000 001 101 000 010 011 001 101 011 001 000 100

М  А  М 
А  _  М  Ы  Л 
А  _  Л 
А  М  У 

Хотя такой равномерный код нельзя назвать экономичным,
зато его можно однозначно декодировать.

Видео о переводе букв в двоичный код

Неравномерные коды

Неравномерный двоичный код — что это такое? Его иногда
применяют для сокращения длины сообщений. В неравномерном коде кодовое слово,
соответствующее определённому символу в алфавите, может отличаться по длине от
других слов.

Например, если использовать для кодирования «Мама мыла
ламу» такой код:

• М — 01.
• А — 00.
• Ы — 1011
• Л — 100.
• У — 1010.
• Пробел — 11, то получится:

МАМА МЫЛА ЛАМУ → 0100010011011011100001110000011010

Данное сообщение состоит из 34 бит. Эту битовую цепочку
можно декодировать однозначно, поскольку в первой букве — М, имеющей код 01,
код является уникальным, ведь другие кодовые слова не начинаются с 01. Таким же
образом можно определить вторую букву — А. Свойство, когда кодовые слова не
совпадают с началом других кодовых слов, называют условием Фано, а коды,
декодируемые с помощью свойства Фано, называются префиксными.

Префиксные коды отличаются важным практическим значением
— с их помощью декодируются символы получаемых сообщений по мере их
поступления, не ожидая, когда всё сообщение придёт к получателю.

Виды двоичных кодов

Для представления целых чисел существуют следующие виды
двоичных кодов:

• Знаковые.
• Беззнаковые.

Отрицательные числа могут быть представлены только в
знаковом виде. Хранение целых чисел в компьютере осуществляется в формате с
фиксированной запятой.

Беззнаковые коды

В целых беззнаковых двоичных кодах все двоичные разряды
представлены в степени цифры 2:

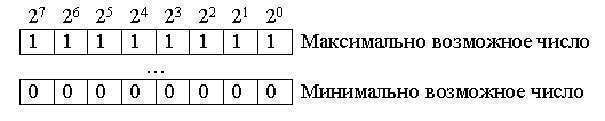
Значение минимально возможного числа равняется нулю, а
максимальное определяется по формуле:

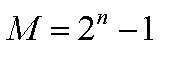
С помощью этих двух чисел определяется диапазон чисел,
представленных в виде двоичного кода.

• Если представлено восьмиразрядное беззнаковое целое
  число, то диапазон чисел записывается с помощью кода: 0…255.
• Если представлен шестнадцатиразрядный код — 0…65535.

В восьмиразрядных процессорах такие числа хранятся в двух
ячейках памяти, которые расположены в соседних адресах. Работа с подобными числами
осуществляется с помощью специальных команд.

Знаковые коды

В прямых целых
знаковых кодах представление знака числа осуществляется с помощью
старшего разряда в слове. Для прямого знакового кода для обозначения знака «+»
используется ноль, а знака «-» — единица. При введении знакового разряда
произойдёт смещение диапазона чисел в сторону отрицательных значений.

• Двоичное восьмиразрядное знаковое целое число
  записывается с помощью такого диапазона: -127…+127.
• Шестнадцатиразрядный код будет записан в диапазоне:
  -32767…+32767.

В восьмиразрядных процессорах такие числа хранятся также
в двух ячейках памяти, адреса которых расположены рядом.

В качестве недостатка этого кода можно назвать
необходимость раздельной обработки знакового и цифрового разрядов. Программы,
работающие в таких алгоритмах, являются довольно сложными. Для того чтобы
выделить и изменить знаковый разряд, придётся применить метод маскирования
разрядов, что приводит к увеличению размера программы и уменьшению её
быстродействия. Для предотвращения возникновения различий в алгоритме обработки
цифрового и знакового разрядов используются обратные двоичные коды.

Отличие знаковых
обратных двоичных кодов от прямых заключается в образовании
отрицательных чисел с помощью инвертирования всех разрядов чисел. Однако при
этом цифровой и знаковый разряды не имеют различий. Такие коды позволяют
значительно упростить алгоритм работы.

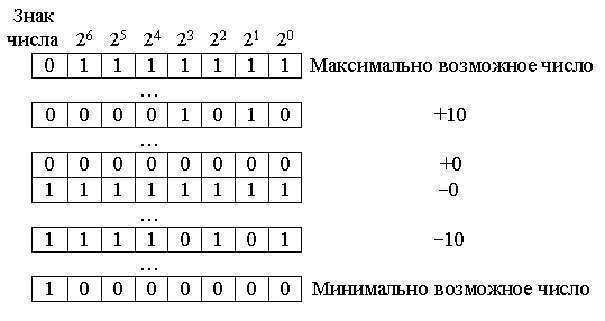
Но, несмотря на это, работа с обратными кодами требует
специального алгоритма для того, чтобы распознавать знаки, вычислять абсолютные
значения чисел, восстанавливать знак результата числа. Также прямой обратный
код числа требует для запоминания нуля использовать два кода в то время, когда
известно, что ноль является положительным числом, и отрицательным он быть не
может никогда.

А Вы знаете, что такое двоичный код и как его расшифровать? Помогли ли Вам в жизни эти знания? Расскажите об этом в комментариях.

Цепочки из двух двоичных символов
Û четыре различных символа произвольного алфавита:

Цепочки из трех двоичных символов
Û восемь различных символов произвольного алфавита.

Разрядность двоичного кода –
количество символов в двоичном коде (длина двоичной цепочки).