Уважаемые коллеги, мы рады предложить вам, разрабатываемый нами учебный курс по программированию ПЛК фирмы Beckhoff с применением среды автоматизации TwinCAT. Курс предназначен исключительно для самостоятельного изучения в ознакомительных целях. Перед любым применением изложенного материала в коммерческих целях просим связаться с нами. Текст из предложенных вам статей скопированный и размещенный в других источниках, должен содержать ссылку на наш сайт heaviside.ru. Вы можете связаться с нами по любым вопросам, в том числе создания для вас систем мониторинга и АСУ ТП.
Системы счисления
Уважаемые коллеги, эта статья будет полностью состоять из теории, мы рассмотрим системы счисления. При чтении этой статьи вы познакомитесь с двоичной и шестнадцатеричной системами счисления. Возможно, кому-то из читателей материал по системам счисления и переводу чисел из одной системы в другую может показаться сложным или скучным. Однако автор настоятельно рекомендует понять хотя бы их базовые принципы, так как в области программирования ПЛК, как и во многих других сферах программирования, они все еще достаточно актуальны и часто требуются на практике.
Бит, байт и размер данных
В прошлых статьях, когда мы рисовали схемы на языке LD, мы использовали тип данных BOOL. BOOL — это простейший тип данных, который может принимать всего два значения: ![]() и
и ![]() , они же FALSE и TRUE и содержит в себе количество информации, соответствующее одному биту. Бит — это наименьшее количество информации. Один бит равен количеству информации, получаемой в результате осуществления одного из двух равновероятных событий. Например, выпадение орла или решки при бросании монетки. Помимо бита для обозначения количества информации применяют понятие байта. В современных системах обычно имеют в виду, что байт состоит из восьми бит. При записи в качестве единицы измерения биты записываются как «бит», а байты как «Б», например,
, они же FALSE и TRUE и содержит в себе количество информации, соответствующее одному биту. Бит — это наименьшее количество информации. Один бит равен количеству информации, получаемой в результате осуществления одного из двух равновероятных событий. Например, выпадение орла или решки при бросании монетки. Помимо бита для обозначения количества информации применяют понятие байта. В современных системах обычно имеют в виду, что байт состоит из восьми бит. При записи в качестве единицы измерения биты записываются как «бит», а байты как «Б», например, ![]() бит,
бит, ![]() Б. Как и для других единиц измерения, для записи количества информации перед единицей измерения используются десятичные приставки СИ. Кроме того, для битов и байтов используют двоичные приставки.
Б. Как и для других единиц измерения, для записи количества информации перед единицей измерения используются десятичные приставки СИ. Кроме того, для битов и байтов используют двоичные приставки.
Иногда при написании десятичных приставок имеются в виду двоичные, то есть при записи ![]() КБ имеется в виду
КБ имеется в виду ![]() Б. Такое использование приставок формально хоть и не является корректным, но очень часто встречается на практике.
Б. Такое использование приставок формально хоть и не является корректным, но очень часто встречается на практике.
Также стоит отметить, что иногда под словом байт подразумевается размер регистров процессора, то есть количество бит, которое процессор может обрабатывать за раз. Размер регистров процессора называется разрядность (или битность) процессора. Из контекста всегда можно понять, что имеется в виду: ![]() бит или один разряд процессора. Современные процессоры, работающие под управлением Windows, имеют разрядность в
бит или один разряд процессора. Современные процессоры, работающие под управлением Windows, имеют разрядность в ![]() или
или ![]() бита.
бита.
Системы счисления
Наверное, всем известно, что компьютеры оперируют данными в виде единиц и нолей. Такая система счисления называется двоичной позиционной. Система счисления — это способ записи цифр. Двоичная система наиболее удобна для применения в электронных схемах. Нулю соответствует отсутствие напряжения, единице — его наличие, или наоборот, в электронике достаточно часто единице соответствует отсутствие напряжение, нулю его наличие.
История знает попытки создания компьютеров на основе других систем счисления. Например, советский компьютер Сетунь, который использовал троичную систему счисления, или американский Mark I с десятичной системой. Но какого-либо серьезного распространения компьютеры, основанные на системах счисления, отличных от двоичной, не получили.

Системы счисления делятся на позиционные, непозиционные и смешанные:
- Позиционные системы счисления — системы счисления, в которых значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда). Например, рассмотрим число
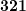 ,
, 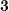 — означает количество сотен,
— означает количество сотен, 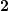 — количество десятков,
— количество десятков, 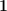 — количество единиц. Так, арабская система счисления, которой все мы пользуемся в повседневной жизни, является десятичной позиционной системой. Обратим внимание на слово «десятичная». В данном примере оно связано с основанием системы счисления, а именно количеством знаков, используемых для записи числа в той или иной системе. В десятичной системе для записи используются цифры
— количество единиц. Так, арабская система счисления, которой все мы пользуемся в повседневной жизни, является десятичной позиционной системой. Обратим внимание на слово «десятичная». В данном примере оно связано с основанием системы счисления, а именно количеством знаков, используемых для записи числа в той или иной системе. В десятичной системе для записи используются цифры 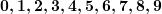 . Основанием является число
. Основанием является число 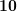 .
. - Смешанные системы счисления, — системы счисления, в которых числа, заданные в некоторой системе счисления с основанием P, изображаются с помощью цифр другой системы счисления с основанием Q, где Q<P. Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд.
- Непозиционные системы счисления — системы счисления, в которых величина, обозначаемая цифрой, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания. Примерами непозиционных счисления являются римская, египетская и система остаточных классов.
Далее в этой статье речь пойдет только о позиционных системах счисления. Как говорилось выше, в компьютерах применяют двоичную позиционную систему счисления. Для начала давайте разберемся, что такое число и чем оно отличается от цифры. Число используется для счета и выражает количество. Цифры — это набор знаков для записи чисел. В арабской системе счисления цифрами являются знаки ![]() , в двоичной —
, в двоичной — ![]() и
и ![]() . Каждая цифра в записи числа, называется разрядом. В информатике разряд числа считается справа налево, начиная с нуля. При записи в десятичной системе числа
. Каждая цифра в записи числа, называется разрядом. В информатике разряд числа считается справа налево, начиная с нуля. При записи в десятичной системе числа ![]() цифра
цифра ![]() является нулевым разрядом, цифра
является нулевым разрядом, цифра ![]() — первым, цифра
— первым, цифра ![]() — вторым разрядом.
— вторым разрядом.
Двоичная система счисления имеет основание ![]() , то есть в ней используется всего две цифры:
, то есть в ней используется всего две цифры: ![]() и
и ![]() . Числа ноль и один в десятичной и в двоичной системах выглядят абсолютно одинаково и записываются как
. Числа ноль и один в десятичной и в двоичной системах выглядят абсолютно одинаково и записываются как ![]() и
и ![]() соответственно. А вот цифры
соответственно. А вот цифры ![]() в двоичной системе нет, поэтому приходится добавить еще один разряд, число два в двоичной системе будет записываться как
в двоичной системе нет, поэтому приходится добавить еще один разряд, число два в двоичной системе будет записываться как ![]() . Что бы записать число три, надо добавить к двойке единицу, выглядит это так
. Что бы записать число три, надо добавить к двойке единицу, выглядит это так ![]() . Для записи числа четыре снова надо добавить еще один разряд, в результате получаем
. Для записи числа четыре снова надо добавить еще один разряд, в результате получаем ![]() . Пять записывается как
. Пять записывается как ![]() и так далее.
и так далее.
| Десятичная | Двоичная |
Шестнадцатеричная система счисления
Двоичная система весьма неудобна для восприятия человеком. Например, число ![]() , записанное в двоичной системе, будет выглядеть как
, записанное в двоичной системе, будет выглядеть как ![]() , а число
, а число ![]() соответствует записи
соответствует записи ![]() . Для более удобного восприятия человеком числа часто представляют в шестнадцатеричной системе счисления. Переводить числа из одной системы счисления в другую мы научимся позже в этой статье.
. Для более удобного восприятия человеком числа часто представляют в шестнадцатеричной системе счисления. Переводить числа из одной системы счисления в другую мы научимся позже в этой статье.
Как и в других позиционных системах счисления, принцип записи чисел в шестнадцатеричной системе схож с рассмотренной выше двоичной системой и всем знакомой с детства десятичной. Разница лишь в том, что следующей после цифры ![]() идет
идет ![]() (десятичная
(десятичная ![]() ), а новый разряд добавляется после цифры
), а новый разряд добавляется после цифры ![]() (десятичная
(десятичная ![]() ). В шестнадцатеричной системе счисления для записи используются следующие цифры:
). В шестнадцатеричной системе счисления для записи используются следующие цифры:
| Десятичная цифра | Шестнадцатеричная цифра |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
Применение именно шестнадцатеричной системы обусловлено легкостью перевода данных в нее из двоичной и обратно, а также наглядностью записи, которая обусловлена тем, что один разряд шестнадцатеричного числа эквивалентен четырем разрядам двоичного числа. То есть байт двоичного кода записывается ровно двумя цифрами шестнадцатеричного числа. Число ![]() , в двоичной системе выглядит как
, в двоичной системе выглядит как ![]() , а в шестнадцатеричной
, а в шестнадцатеричной ![]() . Причем четыре старших разряда двоичного числа
. Причем четыре старших разряда двоичного числа ![]() записываются шестнадцатиричной
записываются шестнадцатиричной ![]() , а четыре младших разряда двоичного числа
, а четыре младших разряда двоичного числа ![]() записываются шестнадцатеричным числом
записываются шестнадцатеричным числом ![]() .
.
В этой статье мы используем сразу три системы счисления. Не всегда можно понять, какая система счисления применяется для записи числа, если это не указанно явно. Например, цифры ![]() могут означать три в двоичной системе, одиннадцать в десятичной и семнадцать в шестнадцатеричной. Во избежание путаницы, в математике принято указывать основание применяемой системы счисления в виде индекса после записанного числа. К примеру, запись
могут означать три в двоичной системе, одиннадцать в десятичной и семнадцать в шестнадцатеричной. Во избежание путаницы, в математике принято указывать основание применяемой системы счисления в виде индекса после записанного числа. К примеру, запись ![]() означает, что применена двоичная система. Если индекс не указан предполагается что применена десятичная система.
означает, что применена двоичная система. Если индекс не указан предполагается что применена десятичная система.
При написании программ достаточно часто возникает необходимость указать в какой системе счисления записано число. В языках МЭК это делается с помощью префиксов добавляемых к числу.
| Префикс | Система счисления |
| двоичная | |
| |
восьмеричная |
| отсутствует | десятичная |
| шестнадцатеричная |
То есть двоичное число ![]() в TwinCAT записывается как
в TwinCAT записывается как ![]() #
#![]() .
.
Восьмеричная система хоть и поддерживается в TwinCAT, но в настоящее время почти не используется. Изложенного выше материала должно быть достаточно для ее понимания.
Перевод чисел из двоичной системы в десятичную и обратно
В сети материала со строгим изложением теоретических выкладок по переводу чисел из одной системы счисления в другую достаточно много. Здесь мы рассмотрим лишь один из удобных на практике способов перевода чисел между различными системами, несильно вдаваясь в теорию этого процесса.
В позиционных системах счисления любое число можно представить в виде ![]() где:
где: ![]() — основание системы счисления.
— основание системы счисления. ![]() — числа, равные цифре, стоящей в разряде k.
— числа, равные цифре, стоящей в разряде k.
Выглядит сложно, но на практике довольно просто, число ![]() можно представить в виде:
можно представить в виде:
![]()
![]()
![]()
Кстати, именно из-за такой формы записи разряды чисел считают, начиная с нуля, а не с единицы.
Число ![]() (десятичное
(десятичное ![]() ) можно представить в виде:
) можно представить в виде:
![]()
![]()
![]()
Вспомнив, что ![]()
![]()
![]()
![]() можно продолжить выражение.
можно продолжить выражение.
![]()
![]()
![]()
Можно заметить, что достаточно запомнить, какое десятичное значение соответствует каждому двоичному разряду и просуммировать их при переводе.
| Номер разряда |
Двоичное значение |
Десятичное значение |
Для перевода из двоичной системы в десятичную и обратно приведенную выше таблицу следует выучить наизусть.
Давайте решим несколько примеров для закрепления:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Перевод из десятичной системы в двоичную производится следующим образом: из десятичного числа вычитается ближайшее меньшее число, из только что выученной нами наизусть таблицы, и записывается соответствующие ему двоичное, после чего действие повторяется с остатком. Когда остатка не осталось, суммируем все записанные двоичные числа.
Приведем пример с числом ![]() :
:
- Ближайшее меньшее к
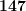 число из таблицы
число из таблицы 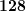 . Записываем
. Записываем 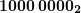 . Остатком будет
. Остатком будет 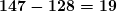 .
. - Повторяем действие. Ближайшее к
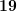 число из таблицы —
число из таблицы — 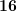 . Пишем
. Пишем 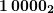 . Остаток
. Остаток 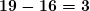 .
. - Ближайшее к
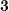 число
число 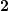 . Записываем
. Записываем 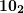 . Остаток
. Остаток 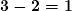 .
. - Числу
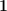 соответствует число
соответствует число 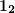 , его и записываем.
, его и записываем. - В результате предыдущих действий мы получили числа
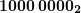 ,
, 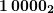 ,
, 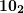 ,
, 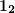 . После сложения получится
. После сложения получится 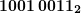 .
.
Как видите, перевод из двоичной системы счисления в десятичную и обратно не составляет большой сложности.
Перевод чисел из двоичной системы в шестнадцатеричную и обратно
В целом порядок перевода в десятичную и в шестнадцатиричную систему схожи. Главное отличие в том, таблица перевода будет повторяться каждые четыре строчки, так как 16=24. Таким образом, выучив всего четыре строчки, вы сможете переводить числа любого размера.
| Номер разряда |
Двоичное значение |
Шестнадцатеричное значение |
В таблице намеренно показано больше чем четыре строчки, что бы читатели могли увидеть как именно повторяются значения.
Повторим некоторые примеры, которые мы приводили для десятичной системы:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Перевод из шестнадцатеричной системы в двоичную производится аналогично переводу из десятичной в двоичную, но проще, так как производится группами по 4 бита. Напомним, из шестнадцатеричного числа вычитается ближайшее меньшее число из таблицы перевода между двоичными и шестнадцатеричными числами, после чего действие повторяется с остатком. После того, как остатка не будет, суммируем все записанные двоичные числа.
Приведем пример с числом ![]() (десятичное
(десятичное ![]() ):
):
- Ближайшее меньшее к
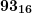 число из таблицы
число из таблицы 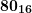 , записываем
, записываем 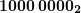 . Остатком будет
. Остатком будет 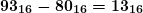 .
. - Повторяем действие, ближайшее к
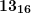 число из таблицы —
число из таблицы — 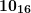 , записываем
, записываем 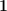
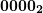 . Остаток
. Остаток 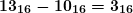 .
. - Ближайшее к
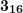 число —
число — 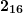 , записываем
, записываем 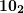 . Остаток
. Остаток 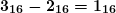 .
. - Числу
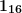 соответствует число
соответствует число 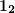 , его и записываем.
, его и записываем. - В результате предыдущих действий мы получили числа
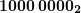 ,
, 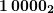 ,
, 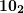 ,
, 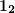 . После сложения получится
. После сложения получится 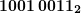 .
.
Еще один простой способ перевода чисел между системами счисления – это использование стандартного калькулятора в Windows (предварительно необходимо переключить в режим «Программист»).
Хотя такой способ может показаться соблазнительным, но стоит научиться переводить в уме числа хотя бы до одного байта (как читатель теперь уже может убедиться самостоятельно, в один байт можно записать числа в диапазоне от ![]() до
до ![]() ). С приобретением практики это станет не сложнее умножения двузначных чисел.
). С приобретением практики это станет не сложнее умножения двузначных чисел.
Сегодня каждый из нас не представляет жизнь без компьютера. Компьютер — это устройство, которое может работать с разными видами данных (текстовыми, графическими, звуковыми). Чтобы эти данные компьютер мог сохранить, обработать, передать, они должны быть представлены в цифровом виде. Данные в компьютере хранятся, обрабатываются, передаются в двоичном коде.
Двоичный код — это строка символов, состоящих из (0) и (1).
Как и каждый язык (формальный или естественный), двоичный код имеет свой алфавит и мощность алфавита.
Алфавит, который состоит из двух символов, называется двоичным алфавитом.
Мощность алфавита — это количество символов, которые в него входят.
Запись информации с помощью двоичного алфавита называют двоичным кодированием.
Почему именно (0) и (1)? Потому что в технике проще всего реализовать такие наборы цифр: если есть сигнал, то это (1), если нет — это (0).
Двоичная система кодирования появилась не с созданием компьютера, ещё задолго до этого математик Г. В. Лейбниц использовал двоичные числа.

Рис. (1). Портрет Г. В. Лейбница
В своей бинарной (двоичной) арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль — небытие, и что Высшее Существо создаёт все сущее из небытия точно таким же образом, как единица и нуль в его системе выражают все числа.
Существуют ряд устройств, работающих по принципу двоичного кодирования. Например, обычный выключатель, где свет горит/не горит.
Всем известная азбука Морзе тоже состоит из двух знаков: точки и тире.

Рис. (2). Алфавит азбуки Морзе
Память компьютера можно представить в виде листочка в клетку, и в каждой клетке хранится либо (1), либо (0).

Рис. (3). Представление битов памяти
Что же происходит, когда мы нажимаем на клавиатуре цифру, например (5)?
Каждая клавиша имеет свой порядковый номер (по кодировочной таблице), и именно он переводится в двоичный код.

Рис. (4). Схема двоичного кодирования
Как узнать, сколько бит (клеточек) в памяти компьютера необходимо для кодирования различных знаков?
Как кодируются числа при помощи двоичного кодирования?
Пусть нам нужно закодировать две цифры — (0) и (1). Для кодирования этих цифр нужно (2) ячейки памяти, в одну напишем (0), а в другую — (1).
А если цифр больше? Сколько битов нужно для кодирования каждой цифры? Рассмотрим, как закодировать (4) цифры.
Если будем использовать однозначные числа, то хватит только для кодирования (2) цифр, а нам нужно больше. Попробуем сделать коды двузначными:
(0) — (00),
(1) — (01),
(2) — (10),
(3) — (11).
Цепочка из двух символов достаточна для кодирования (4) знаков, а если нужно закодировать (8) знаков? Попробуем увеличить длину цепочки:
(0) — (000),
(1) — (001),
(2) — (010),
(3) — (011),
(4) — (100),
(5) — (101),
(6) — (110),
(7) — (111).
Получается, если цифр будет (16), то длина цепочки будет (4)?
Длина цепочки знаков в двоичном коде называется разрядностью двоичного кода.
Рассмотри таблицу.
| Разрядность двоичного кода |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
(9) |
(10) |
|
Количество цифр (комбинаций), которые можно закодировать |
(2) |
(4) |
(8) |
(16) |
(32) |
(64) |
(128) |
(256) |
(512) |
(1024) |
Проанализировав таблицу, можно увидеть зависимость между разрядностью и количеством цифр.
Чтобы получить коды для (2) цифр, нужно взять цепочку из (1) знака, чтобы получить (4) цифры, нужно взять цепочку из (2) знаков, чтобы получить (8) цифр, нужно взять цепочку из (3) знаков и т. д.
(2 = 2);
(4 = 2·2);
(8 = 2·2·2);
(16 = 2·2·2·2);
(32 = 2·2·2·2·2).
Из математики ты знаешь, что степень показывает количество множителей числа на само себя.
Если обозначить количество цифр (комбинаций) через (N), а степень — через (i), получим формулу:
N=2i
.
Задача (1). Определи, сколько нужно знаков для кодирования (11) цифр?
Решение: посмотри в таблицу.
Число (8<11<16), значит, цепочка из (3) символов нам не подходит, а вот цепочки из (4) символов нам достаточно.
Проверим:
(0) — (0000), (1) — (0001), (2) — (0010), (3) — (0011), (4) — (0100), (5) — (0101), (6) — (0110), (7) — (0111), (8) — (1000), (9) — (1001), (10) — (1010), (11) — (1011).
Задача (2). Определи, сколько можно составить различных последовательностей, если длина цепочки (6) символов?
Решение: для решения воспользуемся таблицей.
Если длина цепочки (разрядность двоичного кода) равна (6), следовательно, можно закодировать (64) различные последовательности.
Источники:
Цитата с сайта https://www.livelib.ru/quote/1343718-chto-takoe-matematika-kurant-r-robbins-g (Дата обращения: 14.11.2021.)
Рис. 1. Портрет Г. В.Лейбница By Christoph Bernhard Francke – Herzog Anton Ulrich-Museum Braunschweig, Public Domain, https://commons.wikimedia.org/w/index.php?curid=57268659 (Дата обращения: 14.11.2021.)
Рис. 2. Алфавит азбуки Морзе. © ЯКласс.
Рис. 3. Представление битов памяти. © ЯКласс.
Рис. 4. Схема двоичного кодирования. © ЯКласс.
Совсем недавно на блоге сайт
была опубликована заметка, в помощь тем, кто собирается обновлять свой компьютер или же покупать/собирать новый. А именно, в ней говорилось о том, сколько оперативной памяти нужно компьютеру в зависимости от тех задач, которые передними ставятся: Сколько оперативной памяти нужно?
Следующей нашей заметкой по плану была статья о поддержке различных объемов памяти со стороны операционной системы — о разрядности операционной системы; о том, что не все объемы памяти поддерживаются всеми версиями Windows
. Отдельное спасибо всем читателям, которые в комментариях на блоге упомянули о теме разрядности: после прочтения их я понял, что короткой заметки в блоге на эту тему — мало. Нужен подробный материал на эту тему.
Именно поэтому было решено написать статью, (ликбез, если хотите) по этому вопросу и разместить ее здесь, на ITexpertPortal.com —
в архиве бесплатных обучающих материалов и статей на важные темы компьютерной грамотности.
Итак, вернемся к основной теме, к разрядности операционных систем и к поддержке различных объемов памяти. Вначале ответим на вопрос:
Что такое разрядность вообще?
Научное определение:
В информатике разрядностью электронного (в частности, периферийного) устройства или шины называется количество разрядов (битов), одновременно обрабатываемых этим устройством или передаваемых этой шиной. Термин применим к составным частям вычислительных, периферийных или измерительных устройств: шинам данных компьютеров, процессорам и т.д. Разрядностью компьютера называют разрядность его машинного слова.
(источник — Википедия).
Думаю, все просто и понятно. Разрядность — способность одновременно обрабатывать какое-то количество битов, если говорить проще.
На самом деле, все не так просто, и чтобы осветить полностью этот вопрос и “по-научному” — никакой статьи не хватит. Поэтому, не будем углубляться в курс архитектуры ПК, а затронем чисто практические моменты, с которыми приходится сталкиваться и которые имеют значение для нас — пользователей.
Причем тут объем оперативной памяти?
Существует две версии операционной системы Windows
(по крайней мере пока — только две). Не важно, что именно мы возьмем из современных и актуальных систем: XP, Vista
или 7.
Все эти системы существуют в двух вариантах — 32-битные и 64-битные. Например:
Windows 7 Ultimate 32-bit
(или х86 — равнозначные обозначения)
Windows 7 Ultimate 64-bit (или x64 —
равнозначные обозначения)
Windows Vista Ultimate x86 (x86 —
это обозначение 32-битной версии)
Windows Visa Ultimate x64
(соответственно — 64-битная версия)
Архитектурные различия между 32 и 64-битными версиями Windows,
разумеется, есть. Говорить о них можно долго, но это ни к чему, поверьте мне. 🙂
Самые главные особенности и отличия, которые непосредственно касаются пользователя и с которыми приходится сталкиваться:
1. Максимальный объем оперативной памяти.
2. Разрядность операционной системы.
3. Разрядность процессора.
Вот об этом мы с вами поговорим подробнее…
Максимальный объем оперативной памяти.
32-битная операционная система может адресовать (т.е. может использовать, “видеть”) не более 4 ГБ оперативной памяти. Это самое главное отличие, и самое существенное. Если в вашем компьютере установлено, скажем, 2 ГБ, то 32-битная операционная система работает с таким объемом нормально.
Если вы у становите 4 ГБ памяти и будете работать под управлением 32-битной ОС, то она просто не увидит такой объем. Все, что она сможет использовать — это примерно 3.5 ГБ из 4 ГБ. Остальной объем она не может предоставить для работающих программ. Разумеется, если вы установите в компьютер 8 ГБ памяти, скажем, и при этом будете оставаться на 32-битной системе, то она так же не увидит более 3.5 ГБ из всего установленного объема.
64-битная операционная система может работать с гораздо бОльшими объемами памяти — до 192 ГБ (для Windows 7)
. Т.е. если вы, скажем, захотели установить 8 ГБ памяти, то обязательно нужно переходить на 64-битную ОС, в противном случае, вы просто не сможете использовать столь большой доступный объем.
 Мы рассмотрели, можно сказать, “крайности”, до 2 ГБ и 8 ГБ и более. А как быть с золотой серединой? Что, если у вас уже установлено или же вы планируете увеличить объем памяти до 4 ГБ? Нужно ли в этом случае переходить на 64-битную ОС, чтобы компьютер смог использовать не 3.3, а все 4 ГБ памяти?
Мы рассмотрели, можно сказать, “крайности”, до 2 ГБ и 8 ГБ и более. А как быть с золотой серединой? Что, если у вас уже установлено или же вы планируете увеличить объем памяти до 4 ГБ? Нужно ли в этом случае переходить на 64-битную ОС, чтобы компьютер смог использовать не 3.3, а все 4 ГБ памяти?
Не все так просто… 64-битные версии ОС используют заметно больше памяти. Все переменные теперь уже не 32-битные, а 64-битные. Обычно это увеличивает объём приложений на 20-40%, что приводит и к соответствующему росту объёма занимаемой памяти. На такие файловые форматы, как музыка или видео, это не влияет.
Устанавливать 64-битную версию
Windows
, чтобы лучше использовать 4 Гбайт памяти, смысла не имеет, пусть даже 32-битная версия распознаёт только до 3,5 ГБ памяти. Проблема кроется в том, что вы получите отсутствующую память, однако сразу же её потеряете по той причине, что 64-битная версия требует для себя больше памяти. Так что переход на 64 бита актуален только при памяти большего объёма: 6, 8 ГБ и более.
Итак, если вы решили установить много памяти, и здесь 64-битная ОС нужна точно, то возможно, вас интересует вопрос:
Какими особенностями обладает 64-битная Windows Vista
/7 ?
Визуально — никакими. Т.е. внешне — это обычная ОС, ничем не выделяющаяся от 32-битного варианта. Вы можете определить ее принадлежность к 64-битной архитектуре только зайдя в пункт “свойства системы” в панели управления — там указана разрядность.
Технически — небольшие различия есть. Первое, собственно, что 64-битная ОС “видит” большие объемы памяти и умеет с ними работать. Второе — она позволяет запускать 64-битные приложения.
64-битная ОС позволяет запускать и обычные 32-битные программы. Привычным способом, никаких настроек для этого не требуется. Все как всегда. Просто в 64-битной системе присутствует подсистема выполнения 32-х разрядных приложений. Поэтому, вы с успехом можете устанавливать и работать как с 32-битными, так и с 64-битными приложениями.
Сейчас таких х64-приложений немного, хотя их число постоянно растет. Особенно это касается ресурсоемких программ — графических и видеоредакторов и так далее. Т.е. всех программ, которым нужны в первую очередь большие объемы доступной для работы памяти. Например, чтобы какой-то видеоредактор мог использовать в работе более 4 ГБ из доступной памяти.
Например, компания Adobe заявляла, что современные приложения серии Adobe CS5 — будут
только 64-битные. Это значит, что, скажем, Photoshop CS5, Dreamweaver CS5
и т.п. смогут запустится только на 64-битной системе. На 32-битной ОС они просто не запустятся. Почему?
Потому что в 64-битной ОС могут работать 32-битные приложения, но не наоборот!
Следующий технический момент — 64-битные ОС требуют 64-битных драйверов
.
Как правило, все современные (не старше двух лет) устройства ПК, ноутбуки и периферия имеют на прилагающемся установочном диске две версии драйверов — 32 и 64-битную. Поэтому с современными устройствами проблем не возникнет — как обычно вставляем диск с драйвером в привод и запускаем установку, инсталлятор сам определит версию Windows
и запустит соответствующий разрядности драйвер.
Если диска нет или на нем нет 64-битного драйвера, необходимо посетить официальный сайт разработчика конкретного устройства, чтобы скачать такой драйвер. То же относится и к устаревшему оборудованию.
ОБЯЗАТЕЛЬНО проверьте наличие 64-битных версий ВСЕХ необходимых драйверов еще ДО начала установки 64-битной версии Windows
!
Разрядность процессора.
Где взять/как определить 64-битные приложения?
64-битное программное обеспечение можно определить без труда. На упаковке в системных требованиях, как правило, указывается, что данная программа 64-битная. Это же может быть указано отдельно на упаковке.
Если же вы приобретаете какое-то ПО через интернет, то принадлежность к 64-битной архитектуре тоже указывается.
Вот пример: моя лицензионная коробочная версия Windows Vista Ultimate
. В комплекте два установочных диска — 32 и 64-битная версия ОС:


Не обращайте внимание на “англоязычность” в данном случае, просто ОС была куплена в Соединенных Штатах.
Но это в данном случае — Vista Ultimate
(только Ultimate)
так поставлялась, в двух версиях. Как правило, та же Windows,
например (или любая другая программа) продается ИЛИ
32-битная ИЛИ
64-битная, о чем указано на коробке, как я уже упоминал.
На этом отличия и особенности 64-битных операционных систем Windows, значимые для пользователя заканчиваются.
В остальном — все точно так же, как и на привычных 32-битных Windows XP/Vista/7.
32- или 64-разрядный процессор компьютера – что лучше? Сегодня пользователи этим вопросом не заморачиваются по той простой причине, что все современные сборки ПК, как правило, комплектуются 64-разрядными процессорами. Но еще каких-то 5-6 лет назад споры о том, какой же процессор лучше — 32- или 64-разрядный – были популярнейшей темой различных компьютерных форумов в Интернете.
Что такое разрядность процессора, в чем заключается отличие 32- от 64-разрядного процессора, и как это в конечном счете влияет на работу и производительность ПК с позиции обычного пользователя? В этом всем попытаемся разобраться ниже.
1. Как узнать разрядность установленного на ПК процессора?
Чтобы узнать разрядность установленного на ПК процессора, лучше всего установить специальную программу, функционал которой предусматривает отображение детальной информации об аппаратных составляющих ПК. Например, программы или Speccy – их можно скачать c официальных сайтов совершенно бесплатно.
Запустите одну из этих программ, подождите, пока те просканируют систему и отобразят аппаратные характеристики ПК. Зайдите в раздел меню, в котором содержатся данные о центральном процессоре ПК – вкладки «CPU
» в программе CPU-Z или «Центральный процессор
» в Speccy.
Разрядность процессора отображается в графе «Инструкции
», где выводятся данные о поддержке инструкций. Если процессор 64-разрядный, то в этой графе должно присутствовать об этом указание.

В программе «CPU» в зависимости от производителя процессора это либо «EM64T
» (Intel 64), либо «x86-64
» (AMD 64).

В программе Speccy все чуть проще – графа инструкции отображает либо «AMD 64
», либо «Intel 64
».
Если раздел «Инструкции
» в обеих программах не отображает таких данных, это значит на ПК установлен 32-разрядный процессор.
Но встретить 32-разрядный процессор сегодня не так-то и просто, это должна быть очень старая сборка ПК, ведь начиная с первого 64-разрядного процессора AMD Athlon 64, представленного в 2003 году, и поздних моделей Pentium 4 от Intel, на рынок компьютерной техники производители поставляют только 64-разрядные процессоры.
2. Разрядность: что включает в себя этот термин?
Как видим, определить разрядность процессора, установленного на ПК очень просто, но что же включает в себя сам термин разрядность? Разрядность процессора это – число разрядов (их еще называют битами), которые процессор способен обработать за один раз.
Рост разрядности процессоров был обусловлен развитием компьютерных технологий.
В 1971 году компанией Intel был создан первый 4-разрядный процессор 4004. Чуть позднее появился 8-разрядный 8080, затем 16-разрядный 8086. Первый 32-разрядный процессор 80386 компания Intel создала в 1985 году, и он в дальнейшем стал базой для всех сегодняшних моделей компьютерных процессоров. А вот первенство в создании 64-разрядного процессора принадлежит компании AMD – в 2003 году она создала Athlon 64.
Термин разрядность применяется не только к процессорам, но также и к шинам. К примеру, технические характеристики видеокарт часто содержат указание разрядности шины памяти. Что касается определения термина разрядности шины, то здесь будет виднеться та же суть, что и у термина разрядности процессора. Так, разрядность шины это не что иное, как число бит, одновременно обрабатываемое шиной.
3. Каковы преимущества 64-разрядных процессоров для обычных пользователей ПК?
Для обычных пользователей, использующих ПК сугубо для своих личных нужд в рамках досуга, преимущество 64-разрядных процессоров заключается в возможности задействовать больше 4 Гб оперативной памяти. 64-разрядный процессор позволяет использовать 8, 16, 32 и даже более Гб оперативной памяти в работе ПК. Такая производительность необходима тем, кто использует ПК, загружая его многозадачностью, работая со сложными графическими программами или профессиональными видеоредакторами. И, конечно же, геймеры – для многих новинок игромира, для некоторых мощных видеоигр, начиная с 2011 года, может потребоваться как минимум 8 Гб оперативной памяти, чтобы играть на максимальном качестве игры.
Для использования такого преимущества 64-разрядного процессора, на ПК должна быть установлена 64-разрядная операционная система, специфика которой сможет раскрыть весь мощностной потенциал ПК. А вот если на ПК с 64-разрядным процессором и, к примеру, с 8 Гб оперативной памяти установить 32-разрядную операционную систему, придется довольствоваться ограничениями – оперативная память будет доступна только в объеме 4 Гб. И весь мощностной потенциал «железа» ПК останется нераскрытым.
Определить, на ПК установлена 32- или 64-разрядная Windows, можно, вызвав левой клавишей мышки контекстное меню на иконке «Мой компьютер
» (или «Этот компьюте
р» в Windows 8 и 8.1). В меню выбираем «Свойства
». Откроются основные системные характеристики, где в графе «Тип системы
» и будет указана, какая Windows установлена — 32- или 64-разрядная.

Это же можно определить, не выходя из программы Speccy – в разделе «Операционная система
».

32- и 64-разрядная Windows практически не отличаются ни установкой, ни настройкой, ни использованием. Скачать загрузочный образ Windows в Интернете или купить физический загрузочный диск можно очень легко и с одной, и с другой разрядностью операционной системы.
Помогла ли Вам данная статья?
Существует два вида процессоров: 32-битные и 64-битные. Эти цифры обозначают разрядность процессора. От того, какой процессор вы используете, будет зависеть, какой версией операционной системы пользоваться, как выбирать программы и игры, какое количество ОЗУ можно поставить на свой компьютер. Также можно встретить обозначение x86, которое часто ошибочно принимают за отдельную разрядность процессора. Но прежде всего определим, операционная система какого типа установлена на вашем компьютере.
Как узнать разрядность установленной Windows
Есть несколько способов, позволяющих узнать, сколько бит использует ваша операционная система Windows. Ищите значения x32 или x64, так как они являются основными показателями разрядности системы, а x86 может относиться как к одноядерной, так и к двухъядерной системе. Сначала рассмотрим самый простой и быстрый вариант.
Через свойства компьютера

Через сведения о системе

Различия и преимущества разного количества ядер
Итак, существует два вида процессоров: одноядерные (x32) и двухъядерные (x64). Иногда можно встретить обозначение x86 – это не отдельный вид процессоров, а обозначение архитектуры микропроцессора. Чаще всего цифра x86 свидетельствует о том, что процессор одноядерный, но она также может использоваться и для 64-битного процессора. Поэтому не стоит ориентироваться на неё, всегда ищите обозначение в формате x36 или x64.
Производительность и скорость работы, соответственно, выше у 64-битных процессоров, так как работают сразу два ядра, а не одно. Если вы используете 32-битный процессор, то можете установить на свой компьютер сколько угодно оперативной памяти (ОЗУ), но при этом система будет использовать только 4 ГБ из всей памяти. При наличии 64-битного процессора можно использовать до 32 ГБ оперативной памяти.
 Производительность и скорость работы выше у 64-битных процессоров, так как работают сразу два ядра, а не одно
Производительность и скорость работы выше у 64-битных процессоров, так как работают сразу два ядра, а не одно
Требования для 64-разрядной системы
Главное преимущество процессоров x64 заключается в том, что они поддерживают программы, игры и операционные системы, написанные не только для 64-битных процессоров, но и для 32-битных. То есть, если у вас процессор x32, то вы можете установить только 32-битную операционную систему Windows, но не 64-битную.
Какая разрядность лучше
Из всего вышеописанного можно сделать вывод, что если вы выбираете между одним и двумя ядрами, то предпочтительнее второй вариант, так как большинство современных программ и игр требуют 64 бита. Не исключено, что в будущем от 32-битной системы полностью откажутся, так как её мощности мало на что хватает.
Как перейти на Windows 7 x64
Если вы хотите увеличить производительность системы и объёмы доступной оперативной памяти, а также расширить количество поддерживаемых приложений и игр, то необходимо перейти на 64-битную операционную систему. Сделать это можно единственным способом – стереть старую 32-битную систему и установить новую.
Учтите, что все файлы, находящиеся на компьютере, при выполнении этой операции будут безвозвратно утеряны, так что заранее скопируйте их на сторонний носитель, чтобы не потерять ничего важного.
Итак, после того как вы начнёте установку новой операционной системы, вам будет предложено выбрать язык и подтвердить начало операции, а также выбрать версию системы. Выберите ту, которая имеет разряд x64, и пройдите процесс установки.
 Выбираем тип архитектуры и продолжаем процесс установки
Выбираем тип архитектуры и продолжаем процесс установки
Почему не устанавливается 64-битная Windows
Если установка не удалась – значит, ваш процессор не поддерживает 64-битную систему и рассчитан только на x32. Выход из этой ситуации один – приобрести новый процессор, который будет соответствовать вашим требованиям.
Как определить разрядность процессора
Есть несколько способов, позволяющих определить, какое количество ядер содержит и использует процессор, установленный в вашем компьютере.
Формат слова (разрядность) ЭВМ определяется числом двоичных знаков {битов), которые она может одновременно обработать (табл. 1.3). Производительность ЭВМ зависит от ее разрядности и быстродействия. Электронно-вычислительная машина, имеющая формат слова в 2 раза больший, чем другая ЭВМ, действующая с такой же скоростью, может за определенный отрезок времени выполнить в 2 раза большую работу.
|
Тип ЭВМ |
Стоимость, дол |
Тип ЭВМ |
Формат, бит |
|
IBM |
4,5 |
IBM |
|
|
DEC PDP |
50 000 |
DEC PDP |
|
|
MAKED MINI |
2500 |
NAKED MINI |
|
|
Intel MCS-80 |
Intel MCS-80 |
У большой ЭВМ формат слова в 2 раза больше, чем у мини-ЭВМ, и в 4 раза больше, чем у микро-ЭВМ. Обычно у больших ЭВМ формат слова 32—64 бит, у мини-ЭВМ 12—32 бит, а у микро-ЭВМ 4—16 бит. Таким образом, формат слова является важным показателем вычислительной мощности ЭВМ.
Это особенно важно при выполнении арифметических операций.
Представьте себе, как трудно было бы перемножить два шестизначных числа, если бы оперировали только парой цифр; при таком выполнении умножения задача была бы сложнее не в 6 раз, а в большее число раз из-за необходимости позиционирования и множества переносов. Электронно-вычислительные машины с большим форматом слова могут выполнять сложные арифметические расчеты намного лучше, чем ЭВМ малой разрядности. Такие задачи, как прогноз погоды и имитация полета самолета, больше подходят для больших ЭВМ. Мини- и микро-ЭВМ больше приспособлены для задач управления.
Необходимо отметить, однако, что большой формат слова ЭВМ имеет преимущества, только когда входная информация в двоичной системе имеет большую длину. Если ЭВМ получает за 1 прием только 8-разрядную информацию, то тот факт, что она может обработать слова большей разрядности, преимущества не дает. Для задач управления часто требуется, чтобы ЭВМ в каждый момент времени оперировала данными небольшой разрядности. Эти данные поступают на ЭВМ со шкал, кнопок, концевых выключателей или сенсоров и после обработки передаются на дисплеи, приводы и двигатели. В таких применениях преимуществами обладают ЭВМ с меньшим форматом слова. Электронно-вычислительная машина с меньшим форматом слова может успешно подготавливать данные для ввода в большую ЭВМ. Мини- или микро-ЭВМ, используемые в качестве терминалов, могут значительно увеличивать загрузку большой ЭВМ при очень небольших дополнительных затратах. На рис. 1.8 показана система, к которой 4-разрядный МП получает входные данные в виде 4-разрядных сегментов и размещает их в соответствующих местах 32-разрядного регистра. Когда МП набирает 32 разряда, он посылает сигнал в большую ЭВМ, которая за прием считывает все 32 разряда. Пока МП собирает данные, большая ЭВМ выполняет другие задачи.
Разрядность процессора – загадочная величина, которая часто появляется в статьях, описывающих софт или “железо”. При этом в текстах обычно фигурирует число либо 32, либо 64. О том, что скрывают эти значения, и будет рассказано в статье.
Общее определение
Если рассматривать самые простые определения, то можно сказать, что разрядность – величина, показывающая, сколько бит CPU может обработать за один такт. Сегодня это число равно либо 32, либо 64. Причем первые активно вытесняются, и вероятно, что совсем скоро подобных ЦП не останется вовсе.
В целом для информатики описанный выше тезис верен, но если рассматривать именно разрядность процессора, понятие становится расплывчатым. Устройство неделимое, но, как и многие другие, включает в себя составные части, причем столько, что становится самым сложным компонентом во всем компьютере.
Для того чтобы лучше понять, что скрывает неясное определение, нужно ответить на вопрос: “А какую вообще информацию генерирует и принимает CPU?” Ответов будет несколько: данные, команды и адреса.
Команды
Изначально длина команды, поступающей к CPU за один такт, должна была быть такой же, как и разрядность шины процессора. Для ЦП такое положение вещей является наиболее удобным – не требуется выполнять лишние вычисления. Для программиста подобный подход уже не максимально приемлем, ибо команды занимают всегда фиксированный объем (значит, даже самая простая требует больше места для своего хранения).
Первый факт, о который может споткнуться человек, впервые прочитавший упрощенное определение рассматриваемого объекта: сегодня ЦП могут похвастаться умением работать с командами переменной длины, значит, с этим типом данных разрядность процессора никак не связана. А чтобы развеять все сомнения (или посеять семя для новых), нужно копать дальше.
Данные и адреса
Необходимо ли центральному процессору логически (то есть с точки зрения программиста) уметь хранить данные размером в 32 бита, чтобы называться 32-разрядным? Тут все очевидно – ответ положительный. С адресным пространством не все так просто. Каждый 8-разрядный ЦП мог работать с адресами, которые имели длину в 16 бит. Может, размер данных, которые умеет хранить процессор, и определяет его разрядность?
Перейдем от программных возможностей к физическому устройству. Нужно ли CPU хранить внутри себя адреса и данные в определенном формате? Скажем, чтобы говорить о том, что разрядность процессора равна 32, должен ли он оперировать данными этой длины? Как показывает история, далеко не всегда.

Рассмотрим ЦП, имеющий называние i8080. Он был 8-битным (как говорят спецификации), однако оперировал значениями, которые имели длину 32 разряда, раскидав нолики и единички по спаренным регистрам. CPU Z8000 работал уже не с двойками, а с четверками, значит, и оперировал большими данными за один такт.
Вывод
В CPU вообще ничего не нужно делать для того, чтобы сказать, что он имеет какую-либо разрядность. Создайте удобный инструмент для программиста и рекламу для пользователя – этого будет достаточно. На аппаратном же уровне все новое должно вводиться только при необходимости. Сегодня, пожалуй, процесс перехода от 32-битных устройств к 64 происходит наиболее быстро.
Необходимо ли это? Научные сотрудники сказали, что подобный переход требуется, раньше других, ведь размер машинного слова напрямую влияет на точность вычислений. Когда максимальная разрядность процессора равна 64, а не 32, показатели намного превосходят предшествующие, что дает возможность отказываться от апгрейда оборудования. Разработчики компьютерных игр тоже решили, что от подобного перехода никуда не деться. Требуется ли это простому пользователю, который и научных работ не выполняет, и к видеоиграм относится холодно? На этот вопрос каждый ответит для себя сам.
Для пользователя

Как узнать разрядность процессора, который установлен в вашем компьютере? Сделать это несложно.
- Нажмите сочетание Win+R на клавиатуре, отобразится окно с заголовком “Выполнить”, в него введите cmd.
- На экране появится черная консоль, напоминающая MS-DOS, в ней нужно набрать systeminfo.
- Подождите, пока операционная система соберет данные о компьютере, они будут показаны здесь же.
- Найдите строку “Процессор(ы)”. В ней будет написано имя ЦП. Например, AMD64 Family 16 Model 4 Stepping 3.
- Обычно первые цифры и означают разрядность CPU.

Как узнать разрядность процессора, если при помощи командной строки получить необходимую информацию не получилось?
- Скачайте программу AIDA64.
- В левой части окна отыщите надпись “Системная плата”.
- Теперь кликните дважды по значку с названием “ЦП” или “CPUID”.
- В первом случае обратите внимание на графу “Наборы инструкций”, если здесь присутствует число 64, значит, процессор 64-разрядный, иначе же – ЦП 32-битный.
- Во втором случае просмотрите надписи возле тех чекбоксов, в которых стоят галочки. Здесь находятся подробные описания каждого набора инструкций, из которых можно будет легко понять, какой именно CPU используется в вашем компьютере.
Разрядностью (или битностью) центрального процессора (ЦП) называется количество бит, которые ЦП может обрабатывать за одну команду. Разрядность определяет количество бит, отводимых хранение одной ячейки данных. То есть, если архитектура вашего процессора, например, 32 битная, то он может работать с числами, которые представлены в двоичном коде из 32 бит, причём обрабатывать эти числа он может за одну команду.
Таким же образом (за одну команду) могут обрабатываться данные и меньшей разрядности, просто их старшие биты будут игнорироваться. Современные ЦП могут работать c 8-ми, 16-ти, 32-х и 64-х разрядными типами данных. Все использующиеся сейчас ЦП в компьютерах либо 32, либо 64 разрядные.
Часто, читая описания ЦП, можно встретить обозначение x86 — это значит, что мы имеем дело с 32 битной архитектурой. Если же встречается надпись х64 – то можно сказать, что данный ЦП обладает битностью, равной 64.
Важно! Часто битность ЦП ошибочно принимается за основу при определении максимального объёма памяти, к которому он может обращаться. Это, естественно, не так. Шины адреса и данных практически любого ЦП имеют разную битность и никак не влияют друг на друга.
Значение битности ЦП играет не последнюю роль для пользователей, поскольку битности операционной системы (ОС) и процессора, которые используются друг с другом, должны совпадать. Однако, здесь работает принцип обратной совместимости: на 64 разрядный ЦП может быть установлена операционная система как 32 так и 64 разрядная.
Версия операционной системы в данном случае не играет роли: например, все ОС Windows или Linux, уже начиная с появления первых 64 разрядных ЦП имеют как 32 битные так и 64 битные сборки. То есть, существуют все версии Windows (от XP до 10-й), имеющие как 64 так и 32 битную среду.
Важно! Установить на ЦП семейств х86 ОС, в названии которой фигурирует «х64» невозможно! Мало того, невозможно запускать исполняемые файлы для 64 битных ЦП на 32 битных ОС.
Именно поэтому определение того, какие именно (32 или 64 разрядные) данные используются ЦП весьма важно. Часто от этого зависит работоспособность достаточно больших групп пользователей, использующих одинаковое программное обеспечение.
В данной статье будет рассмотрено, как узнать разрядность процессора при помощи различных способов.
Версия операционной системы в данном случае не играет роли: например, все ОС Windows или Linux, уже начиная с появления первых 64 разрядных ЦП имеют как 32 битные так и 64 битные сборки. То есть, существуют все версии Windows (от XP до 10-й), имеющие как 64 так и 32 битную среду.
Важно! Установить на ЦП семейств х86 ОС, в названии которой фигурирует «х64» невозможно! Мало того, невозможно запускать исполняемые файлы для 64 битных ЦП на 32 битных ОС.
Именно поэтому определение того, какие именно (32 или 64 разрядные) данные используются ЦП весьма важно. Часто от этого зависит работоспособность достаточно больших групп пользователей, использующих одинаковое программное обеспечение.
В данной статье будет рассмотрено, как узнать разрядность процессора при помощи различных способов.
Откроется консоль командного процессора. В ней следует ввести команду «systeminfo». Результатом её выполнения будет длинный перечень параметров системы. Интересующий нас пункт называется «Процессор(ы):» В нём будет написано название модели ЦП. И обязательно указана его битность (либо цифрами 32 или 64, либо надписями «х86» или «х64»).
Через свойства компьютера
Можно определить, какую разрядность поддерживает процессор, посмотрев свойства системы.
Один из способов сделать это – войти в параметр «Система» панели управления и там, в разделе «Тип системы» можно будет увидеть её разрядность. Если она равна 64, то и ЦП тоже 64 битный.
Однако, как уже было сказано ранее, поскольку на 64 разрядный ЦП может быть поставлена 32 разрядная система, необходимо будет уточнить тип используемого ЦП. Для этого следует зайти в «Диспетчер устройств», ссылка на который есть на той же странице, в «Устройствах» выбрать ЦП и открыть в его свойствах вкладку «Сведения».
В этой вкладке интересующий нас параметр называется «ИД оборудования». В нём будет указан тип используемого процессора – 64 или 32 разрядный.
Альтернативой является исследование свойств устройства, называемого в Диспетчере устройств «Компьютер». В нём может содержаться описание применяемого типа ПК с указанием его битности.
Аналогично свойствам процессора, следует зайти в свойства компьютера и во вкладке «Сведения» посмотреть описание устройства. Параметр может также называться «Выводимое имя». В любом случае, в нём будет присутствовать либо надпись «х86», либо «х64», что и будет соответствовать битности используемого ЦП в 32 или 64 соответственно.
Узнать разрядность через интернет
Для этого достаточно набрать в строке поиска фразу «узнать разрядность онлайн». Первые 5-10 результатов поиска дадут ссылки на сайты, определяющие этот параметр. После этого следует перейти на этот сайт и активный контент автоматически опознает количество разрядов ЦП и версию ОС.
Важно! Исполнение активных компонентов может быть заблокировано браузером и в этом случае определить интересующий параметр не получится. Для этого следует разрешить выполнение активного содержимого на странице.
Через BIOS
Самый простой способ, не требующий наличия программного обеспечения вообще. При загрузке ПК следует войти в BIOS, нажав F2 или Del. Далее следует выбрать раздел «System Settings», «Main» или «CPU Settings» – в зависимости от производителя BIOS он может называться по-разному, и посмотреть значение параметра «Processor Type». В нём будет указана фирма производитель, модель ЦП, его частота и разрядность.
Так же можете прочитать статьи на темы: Как включить второе ядро процессора Windows 7 и Мониторинг загрузки процессора и видеокарты в играх
Информатика
7 класс
Урок № 5
Кодирование информации. Двоичный код
Перечень вопросов, рассматриваемых в теме:
- Понятие код.
- Понятие кодирования информации.
- Двоичный код.
Тезаурус:
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную. Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.
Алфавит языка – конечный набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита – это количество входящих в него символов.
Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием. Двоичное кодирование универсально, так как с его помощью может быть представлена любая информация.
Основная литература:
1. Босова Л. Л. Информатика: 7 класс. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2017. – 226 с.
Дополнительная литература:
- Босова Л. Л. Информатика: 7–9 классы. Методическое пособие. // Босова Л. Л., Босова А. Ю., Анатольев А. В., Аквилянов Н.А. – М.: БИНОМ, 2019. – 512 с.
- Босова Л. Л. Информатика. Рабочая тетрадь для 7 класса. Ч 1. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2019. – 160 с.
- Босова Л. Л. Информатика. Рабочая тетрадь для 7 класса. Ч 2. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2019. – 160 с.
- Гейн А. Г. Информатика: 7 класс. // Гейн А. Г., Юнерман Н. А., Гейн А.А. – М.: Просвещение, 2012. – 198 с.
Теоретический материал для самостоятельного изучения
Кодирование информации
Для решения своих задач человеку часто приходится преобразовывать имеющуюся информацию из одной формы представления в другую. Например, при чтении вслух происходит преобразование информации из дискретной (текстовой) формы в непрерывную (звук). Во время диктанта на уроке русского языка, наоборот, происходит преобразование информации из непрерывной формы (голос учителя) в дискретную (записи учеников).
Информация, представленная в дискретной форме, значительно проще для передачи, хранения или автоматической обработки. Поэтому в компьютерной технике большое внимание уделяется методам преобразования информации из непрерывной формы в дискретную.
Дискретизация информации – процесс преобразования информации из непрерывной формы представления в дискретную.
Рассмотрим суть процесса дискретизации информации на примере.
На метеорологических станциях имеются самопишущие приборы для непрерывной записи атмосферного давления. Результатом их работы являются барограммы – кривые, показывающие, как изменялось давление в течение длительных промежутков времени. Одна из таких кривых, вычерченная прибором в течение семи часов проведения наблюдений, показана на рисунке 1.
На основании полученной информации можно построить таблицу, содержащую показания прибора в начале измерений и на конец каждого часа наблюдений.

Полученная таблица даёт не совсем полную картину того, как изменялось давление за время наблюдений: например, не указано самое большое значение давления, имевшее место в течение четвёртого часа наблюдений. Но если занести в таблицу значения давления, наблюдаемые каждые полчаса или 15 минут, то новая таблица будет давать более полное представление о том, как изменялось давление.
Таким образом, информацию, представленную в непрерывной форме (барограмму, кривую), мы с некоторой потерей точности преобразовали в дискретную форму (таблицу).
В дальнейшем вы познакомитесь со способами дискретного представления звуковой и графической информации.
Двоичное кодирование
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит – конечный набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита – это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (рис. 3). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1. Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа.

Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов. Правило получения двоичных кодов для символов алфавита мощностью больше двух можно представить схемой на рисунке.

Двоичные символы (0,1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки (кодовые комбинации) из двух двоичных символов позволяют представить четыре различных символа произвольного алфавита:

Цепочки из трёх двоичных символов получаются дополнением двухразрядных двоичных кодов справа символом 0 или 1. В итоге кодовых комбинаций из трёх двоичных символов получается 8 – вдвое больше, чем из двух двоичных символов:

Соответственно, четырёхразрядный двоичный код позволяет получить 16 кодовых комбинаций, пятиразрядный – 32, шестиразрядный – 64 и т. д.
Длину двоичной цепочки – количество символов в двоичном коде – называют разрядностью двоичного кода.

Обратите внимание, что:
4 = 2 ∙ 2,
8 = 2 ∙ 2 ∙ 2,
16 = 2 ∙ 2 ∙ 2 ∙ 2,
32 = 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 и т. д.
Здесь количество кодовых комбинаций представляет собой произведение некоторого количества одинаковых множителей, равного разрядности двоичного кода.
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода – буквой i, то выявленная закономерность в общем виде будет записана так:

В математике такие произведения записывают в виде:
N = 2i.
Запись 2i читают так: «2 в i-й степени».
Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Двоичный код какой разрядности потребуется, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.
Решение. Так как алфавит племени Мульти состоит из 16 символов, то и кодовых комбинаций им нужно 16. В этом случае длина (разрядность) двоичного кода определяется из соотношения: 16 = 2i. Отсюда i = 4.
Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рис. 1.13: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
Универсальность двоичного кодирования
В начале нашей беседы вы узнали, что информация, представленная в непрерывной форме, может быть выражена с помощью символов некоторого естественного или формального языка. В свою очередь, символы произвольного алфавита могут быть преобразованы в двоичный код. Таким образом, с помощью двоичного кода может быть представлена любая информация на естественных и формальных языках, а также изображения и звуки (рис. 6). Это и означает универсальность двоичного кодирования.

Двоичные коды широко используются в компьютерной технике, требуя только двух состояний электронной схемы – «включено» (это соответствует цифре 1) и «выключено» (это соответствует цифре 0).
Простота технической реализации – главное достоинство двоичного кодирования. Недостаток двоичного кодирования – большая длина получаемого кода.
Равномерные и неравномерные коды
Различают равномерные и неравномерные коды. Равномерные коды в кодовых комбинациях содержат одинаковое число символов, неравномерные – разное.
Выше мы рассмотрели равномерные двоичные коды.
Примером неравномерного кода может служить азбука Морзе, в которой для каждой буквы и цифры определена последовательность коротких и длинных сигналов. Так, букве Е соответствует короткий сигнал («точка»), а букве Ш – четыре длинных сигнала (четыре «тире»). Неравномерное кодирование позволяет повысить скорость передачи сообщений за счёт того, что наиболее часто встречающиеся в передаваемой информации символы имеют самые короткие кодовые комбинации.
Разбор решения заданий тренировочного модуля
№1.Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Переведите десятичное число 273 в двоичную систему счисления.
27310=_____
Решение.
Воспользуемся алгоритмом перевода целых чисел из системы с основанием p в систему с основанием q:
1. Основание новой системы счисления выразить цифрами исходной системы счисления и все последующие действия производить в исходной системе счисления.
2. Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, меньшее делителя.
3. Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
4. Составить число в новой системе счисления, записывая его, начиная с последнего остатка.

27310= 100010001.
Ответ: 27310= 100010001.
№2. Тип задания: единичный / множественный выбор.
Четыре буквы латинского алфавита закодированы кодами различной длины:
Определите, какой набор букв закодирован двоичной строкой 0100000100010.
Варианты ответов:
- BACAD
- ACAD
- ABBAD
- CADDA
Решение. Рассмотрим код: 0100000100010.
Выделим закодированные буквы:
01 000 001 000 10
В A C A D
Ответ: 1. BACAD.
