Как найти разрядность звукового сигнала

Как найти разрядность звукового сигнала

From Wikipedia, the free encyclopedia

For other uses of “8-bit music”, see chiptune.

An analog signal (in red) encoded to 4-bit PCM digital samples (in blue); the bit depth is four, so each sample’s amplitude is one of 16 possible values.

In digital audio using pulse-code modulation (PCM), bit depth is the number of bits of information in each sample, and it directly corresponds to the resolution of each sample. Examples of bit depth include Compact Disc Digital Audio, which uses 16 bits per sample, and DVD-Audio and Blu-ray Disc which can support up to 24 bits per sample.

In basic implementations, variations in bit depth primarily affect the noise level from quantization error—thus the signal-to-noise ratio (SNR) and dynamic range. However, techniques such as dithering, noise shaping, and oversampling can mitigate these effects without changing the bit depth. Bit depth also affects bit rate and file size.

Bit depth is only meaningful in reference to a PCM digital signal. Non-PCM formats, such as lossy compression formats, do not have associated bit depths.[a]

Binary representation[edit]

A PCM signal is a sequence of digital audio samples containing the data providing the necessary information to reconstruct the original analog signal. Each sample represents the amplitude of the signal at a specific point in time, and the samples are uniformly spaced in time. The amplitude is the only information explicitly stored in the sample, and it is typically stored as either an integer or a floating point number, encoded as a binary number with a fixed number of digits: the sample’s bit depth, also referred to as word length or word size.

The resolution indicates the number of discrete values that can be represented over the range of analog values. The resolution of binary integers increases exponentially as the word length increases. Adding one bit doubles the resolution, adding two quadruples it and so on. The number of possible values that can be represented by an integer bit depth can be calculated by using 2n, where n is the bit depth.[1] Thus, a 16-bit system has a resolution of 65,536 (216) possible values.

Integer PCM audio data is typically stored as signed numbers in two’s complement format.[2]

Today, most audio file formats and digital audio workstations (DAWs) support PCM formats with samples represented by floating point numbers.[3][4][5][6] Both the WAV file format and the AIFF file format support floating point representations.[7][8] Unlike integers, whose bit pattern is a single series of bits, a floating point number is instead composed of separate fields whose mathematical relation forms a number. The most common standard is IEEE 754 which is composed of three fields: a sign bit which represents whether the number is positive or negative, an exponent and a mantissa which is raised by the exponent. The mantissa is expressed as a binary fraction in IEEE base-two floating point formats.[9]

Quantization[edit]

The bit depth limits the signal-to-noise ratio (SNR) of the reconstructed signal to a maximum level determined by quantization error. The bit depth has no impact on the frequency response, which is constrained by the sample rate.

Quantization error introduced during analog-to-digital conversion (ADC) can be modeled as quantization noise. It is a rounding error between the analog input voltage to the ADC and the output digitized value. The noise is nonlinear and signal-dependent.

An 8-bit binary number (149 in decimal), with the LSB highlighted

In an ideal ADC, where the quantization error is uniformly distributed between scriptstyle{pm frac{1}{2}} least significant bit (LSB) and where the signal has a uniform distribution covering all quantization levels, the signal-to-quantization-noise ratio (SQNR) can be calculated from

{displaystyle mathrm {SQNR} =20log _{10}({sqrt {1.5}}cdot 2^{mathrm {b} })approx 1.76+6.02{mathrm {b} };mathrm {dB} ,!}

where b is the number of quantization bits and the result is measured in decibels (dB).[10][11]

Therefore, 16-bit digital audio found on CDs has a theoretical maximum SNR of 98 dB and professional 24-bit digital audio tops out as 146 dB. As of 2011, digital audio converter technology is limited to a SNR of about 123 dB[12][13][14] (effectively 21-bits) because of real-world limitations in integrated circuit design.[b] Still, this approximately matches the performance of the human auditory system.[17][18] Multiple converters can be used to cover different ranges of the same signal, being combined to record a wider dynamic range in the long-term, while still being limited by the single converter’s dynamic range in the short term, which is called dynamic range extension.[19][20]

Signal-to-noise ratio and resolution of bit depths (unweighted)

# bits SNR (Audio) SNR (Video) Minimum dB step difference (quantization rounding error) No. of possible values (per sample) Range (per sample) for signed representation
4 25.28 dB 34.31 dB 1.578 dB 16 −8 to +7
8 49.89 dB 58.92 dB 0.1948 dB 256 −128 to +127
11 67.98 dB 77.01 dB 0.0331 dB 2,048 −1,024 to +1,023
12 74.01 dB 83.04 dB 0.01806 dB 4,096 −2,048 to +2,047
16 98.09 dB 107.12 dB 0.00598 dB 65,536 −32,768 to +32,767
18 110.13 dB – 0.000420 dB 262,144 −131,072 to +131,071
20 122.17 dB – 0.000116 dB 1,048,576 −524,288 to +524,287
24 146.25 dB – 0.00000871 dB 16,777,216 −8,388,608 to +8,388,607
32 194.42 dB – 4.52669337E−8 dB 4,294,967,296 −2,147,483,648 to +2,147,483,647
48 290.75 dB – 1.03295150E−12 dB 281,474,976,710,656 −140,737,488,355,328 to +140,737,488,355,327
64 387.08 dB – 2.09836488E−17 dB 18,446,744,073,709,551,616 −9,223,372,036,854,775,808 to +9,223,372,036,854,775,807

Floating point[edit]

The resolution of floating-point samples is less straightforward than integer samples because floating-point values are not evenly spaced. In floating-point representation, the space between any two adjacent values is in proportion to the value. This greatly increases the SNR compared to an integer system because the accuracy of a high-level signal will be the same as the accuracy of an identical signal at a lower level.[21]

The trade-off between floating point and integers is that the space between large floating-point values is greater than the space between large integer values of the same bit depth. Rounding a large floating-point number results in a greater error than rounding a small floating-point number whereas rounding an integer number will always result in the same level of error. In other words, integers have round-off that is uniform, always rounding the LSB to 0 or 1, and floating point has SNR that is uniform, the quantization noise level is always of a certain proportion to the signal level.[21] A floating-point noise floor will rise as the signal rises and fall as the signal falls, resulting in audible variance if the bit depth is low enough.[22]

Audio processing[edit]

Most processing operations on digital audio involve the re-quantization of samples and thus introduce additional rounding error analogous to the original quantization error introduced during analog-to-digital conversion. To prevent rounding error larger than the implicit error during ADC, calculations during processing must be performed at higher precisions than the input samples.[23]

Digital signal processing (DSP) operations can be performed in either fixed point or floating-point precision. In either case, the precision of each operation is determined by the precision of the hardware operations used to perform each step of the processing and not the resolution of the input data. For example, on x86 processors, floating-point operations are performed with single or double precision and fixed-point operations at 16-, 32- or 64-bit resolution. Consequently, all processing performed on Intel-based hardware will be performed with these constraints regardless of the source format.[c]

Fixed point digital signal processors often support specific word lengths in order to support specific signal resolutions. For example, the Motorola 56000 DSP chip uses 24-bit multipliers and 56-bit accumulators to perform multiply-accumulate operations on two 24-bit samples without overflow or truncation.[24] On devices that do not support large accumulators, fixed point results may be truncated, reducing precision. Errors compound through multiple stages of DSP at a rate that depends on the operations being performed. For uncorrelated processing steps on audio data without a DC offset, errors are assumed to be random with zero mean. Under this assumption, the standard deviation of the distribution represents the error signal, and quantization error scales with the square root of the number of operations.[25] High levels of precision are necessary for algorithms that involve repeated processing, such as convolution.[23] High levels of precision are also necessary in recursive algorithms, such as infinite impulse response (IIR) filters.[26] In the particular case of IIR filters, rounding error can degrade frequency response and cause instability.[23]

Dither[edit]

Headroom and noise floor at audio process stages for the purpose of comparison with dither level

The noise introduced by quantization error, including rounding errors and loss of precision introduced during audio processing, can be mitigated by adding a small amount of random noise, called dither, to the signal prior to quantizing. Dithering eliminates non-linear quantization error behavior, giving very low distortion, but at the expense of a slightly raised noise floor. Recommended dither for 16-bit digital audio measured using ITU-R 468 noise weighting is about 66 dB below alignment level, or 84 dB below digital full scale, which is comparable to microphone and room noise level, and hence of little consequence in 16-bit audio.

24-bit and 32-bit audio do not require dithering, as the noise level of the digital converter is always louder than the required level of any dither that might be applied. 24-bit audio could theoretically encode 144 dB of dynamic range, and 32-bit audio can achieve 192 dB, but this is almost impossible to achieve in the real world, as even the best sensors and microphones rarely exceed 130 dB.[27]

Dither can also be used to increase the effective dynamic range. The perceived dynamic range of 16-bit audio can be 120 dB or more with noise-shaped dither, taking advantage of the frequency response of the human ear.[28][29]

Dynamic range and headroom[edit]

Dynamic range is the difference between the largest and smallest signal a system can record or reproduce. Without dither, the dynamic range correlates to the quantization noise floor. For example, 16-bit integer resolution allows for a dynamic range of about 96 dB. With the proper application of dither, digital systems can reproduce signals with levels lower than their resolution would normally allow, extending the effective dynamic range beyond the limit imposed by the resolution.[30] The use of techniques such as oversampling and noise shaping can further extend the dynamic range of sampled audio by moving quantization error out of the frequency band of interest.

If the signal’s maximum level is lower than that allowed by the bit depth, the recording has headroom. Using higher bit depths during studio recording can make headroom available while maintaining the same dynamic range. This reduces the risk of clipping without increasing quantization errors at low volumes.

Oversampling[edit]

Oversampling is an alternative method to increase the dynamic range of PCM audio without changing the number of bits per sample.[31] In oversampling, audio samples are acquired at a multiple of the desired sample rate. Because quantization error is assumed to be uniformly distributed with frequency, much of the quantization error is shifted to ultrasonic frequencies and can be removed by the digital-to-analog converter during playback.

For an increase equivalent to n additional bits of resolution, a signal must be oversampled by

mathrm{number of samples} = (2^n)^2 = 2^{2n}.

For example, a 14-bit ADC can produce 16-bit 48 kHz audio if operated at 16× oversampling, or 768 kHz. Oversampled PCM, therefore, exchanges fewer bits per sample for more samples in order to obtain the same resolution.

Dynamic range can also be enhanced with oversampling at signal reconstruction, absent oversampling at the source. Consider 16× oversampling at reconstruction. Each sample at reconstruction would be unique in that for each of the original sample points sixteen are inserted, all having been calculated by a digital reconstruction filter. The mechanism of increased effective bit depth is as previously discussed, that is, quantization noise power has not been reduced, but the noise spectrum has been spread over 16× the audio bandwidth.

Historical note—The compact disc standard was developed by a collaboration between Sony and Philips. The first Sony consumer unit featured a 16-bit DAC; the first Philips units dual 14-bit DACs. This caused confusion in the marketplace and even in professional circles, because 14-bit PCM allows for 84 dB SNR, 12 dB less than 16-bit PCM. Philips had implemented 4× oversampling with first order noise shaping which theoretically realized the full 96 dB dynamic range of the CD format.[32] In practice the Philips CD100 was rated at 90 dB SNR in the audio band of 20 Hz–20 kHz, the same as Sony’s CDP-101.[33][34]

Noise shaping[edit]

Oversampling a signal results in equal quantization noise per unit of bandwidth at all frequencies and a dynamic range that improves with only the square root of the oversampling ratio. Noise shaping is a technique that adds additional noise at higher frequencies which cancels out some error at lower frequencies, resulting in a larger increase in dynamic range when oversampling. For nth-order noise shaping, the dynamic range of an oversampled signal is improved by an additional 6n dB relative to oversampling without noise shaping.[35] For example, for a 20 kHz analog audio sampled at 4× oversampling with second-order noise shaping, the dynamic range is increased by 30 dB. Therefore, a 16-bit signal sampled at 176 kHz would have a bit depth equal to a 21-bit signal sampled at 44.1 kHz without noise shaping.

Noise shaping is commonly implemented with delta-sigma modulation. Using delta-sigma modulation, Direct Stream Digital achieves a theoretical 120 dB SNR at audio frequencies using 1-bit audio with 64× oversampling.

Applications[edit]

Bit depth is a fundamental property of digital audio implementations. Depending on application requirements and equipment capabilities, different bit depths are used for different applications.

Example applications and supported audio bit depth

Application Description Audio format(s)
CD-DA (Red Book)[36] Digital media 16-bit LPCM
DVD-Audio[37] Digital media 16-, 20- and 24-bit LPCM[A]
Super Audio CD[38] Digital media 1-bit Direct Stream Digital (PDM)
Blu-ray Disc audio[39] Digital media 16-, 20- and 24-bit LPCM and others[B]
DV audio[40] Digital media 12- and 16-bit uncompressed PCM
ITU-T Recommendation G.711[41] Compression standard for telephony 8-bit PCM with companding[C]
NICAM-1, NICAM-2 and NICAM-3[42] Compression standards for broadcasting 10-, 11- and 10-bit PCM respectively, with companding[D]
Ardour DAW by Paul Davis and the Ardour Community 32-bit floating point[43]
Pro Tools 11 DAW by Avid Technology 16- and 24-bit or 32-bit floating point sessions and 64-bit floating point mixing[44]
Logic Pro X DAW by Apple Inc. 16- and 24-bit projects and 32-bit or 64-bit floating point mixing[45]
Cubase DAW by Steinberg Allows audio processing precision to 32 bit float or 64 bit float [46]
Ableton Live[6] DAW by Ableton 32-bit floating point bit depth and 64-bit summing
Reason 7 DAW by Propellerhead Software 16-, 20- and 24-bit I/O, 32-bit floating point arithmetic and 64-bit summing[47]
Reaper 5 DAW by Cockos Inc. 8-bit PCM, 16-bit PCM, 24-bit PCM, 32-bit PCM, 32-bit FP, 64-bit FP, 4-bit IMA ADPCM & 2-bit cADPCM rendering;

8-bit int, 16-bit int, 24-bit int, 32-bit int, 32-bit float, and 64-bit float mixing

GarageBand ’11 (version 6) DAW by Apple Inc. 16-bit default with 24-bit real instrument recording[48]
Audacity Open source audio editor 16- and 24-bit LPCM and 32-bit floating point[49]
FL Studio DAW by Image-Line 16- and 24-bit int and 32-bit floating point (controlled by OS)[50]
  1. ^ DVD-Audio also supports optional Meridian Lossless Packing, a lossless compression scheme.
  2. ^ Blu-ray supports a variety of non-LPCM formats but all conform to some combination of 16, 20 or 24 bits per sample.
  3. ^ ITU-T specifies the A-law and μ-law companding algorithms, compressing down from 13 and 14 bits respectively.
  4. ^ NICAM systems 1, 2 and 3 compress down from 13, 14 and 14 bits respectively.

Bit rate and file size[edit]

Bit depth affects bit rate and file size. Bits are the basic unit of data used in computing and digital communications. Bit rate refers to the amount of data, specifically bits, transmitted or received per second. In MP3 and other lossy compressed audio formats, bit rate describes the amount of information used to encode an audio signal. It is usually measured in kb/s.[51]

See also[edit]

  • Audio system measurements
  • Color depth, corresponding concept for digital images
  • Effective number of bits

Notes[edit]

  1. ^ For example, in MP3, quantization is performed on the frequency domain representation of the signal, not on the time domain samples relevant to bit depth.
  2. ^ While 32-bit converters exist, they are purely for marketing purposes and provide no practical benefit over 24-bit converters; the extra bits are either zero or encode only noise.[15][16]
  3. ^ Intel and AMD x86 hardware can handle higher precision than 64 bit, or even arbitrarily large float points or integers, but processing takes a lot longer than the native types.

References[edit]

  1. ^ Thompson, Dan (2005). Understanding Audio. Berklee Press. ISBN 978-0-634-00959-4.
  2. ^ Smith, Julius (2007). “Pulse Code Modulation (PCM)”. Mathematics of the Discrete Fourier Transform (DFT) with Audio Applications, Second Edition, online book. Retrieved 22 October 2012.
  3. ^ Campbell, Robert (2013). Pro Tools 10 Advanced Music Production Techniques, pg. 247. Cengage Learning. ISBN 978-1133728016. Retrieved 12 August 2013.
  4. ^ Wherry, Mark (March 2012). “Avid Pro Tools 10”. Sound On Sound. Retrieved 10 August 2013.
  5. ^ Price, Simon (October 2005). “Reason Mixing Masterclass”. Sound On Sound. Retrieved 10 August 2013.
  6. ^ a b “Ableton Reference Manual Version 10, 32. Audio Fact Sheet”. Ableton. 2019. Retrieved 3 September 2019.
  7. ^ Kabal, Peter (3 January 2011). “Audio File Format Specifications, WAVE Specifications”. McGill University. Retrieved 10 August 2013.
  8. ^ Kabal, Peter (3 January 2011). “Audio File Format Specifications, AIFF / AIFF-C Specifications”. McGill University. Retrieved 10 August 2013.
  9. ^ Smith, Steven (1997–98). “The Scientist and Engineer’s Guide to Digital Signal Processing, Chapter 4 – DSP Software / Floating Point (Real Numbers)”. www.dspguide.com. Retrieved 10 August 2013.
  10. ^ See Signal-to-noise ratio#Fixed point
  11. ^ Kester, Walt (2007). “Taking the Mystery out of the Infamous Formula, “SNR = 6.02N + 1.76dB,” and Why You Should Care” (PDF). Analog Devices. Retrieved 26 July 2011.
  12. ^ Nwavguy (6 September 2011). “NwAvGuy: Noise & Dynamic Range”. NwAvGuy. Retrieved 2 December 2016. 24 bit DACs often only manage approximately 16 bit performance and the very best reach 21 bit (ENOB) performance.
  13. ^ “PCM4222”. Retrieved 21 April 2011. Dynamic Range (–60dB input, A-weighted): 124dB typical Dynamic Range (–60dB input, 20 kHz Bandwidth): 122dB typical
  14. ^ “WM8741 : High Performance Stereo DAC”. Cirrus Logic. Retrieved 2 December 2016. 128dB SNR (‘A’-weighted mono @ 48 kHz) 123dB SNR (non-weighted stereo @ 48 kHz)
  15. ^ “The great audio myth: why you don’t need that 32-bit DAC”. Android Authority. 19 January 2016. Retrieved 2 December 2016. So your 32-bit DAC is actually only ever going to be able to output at most 21-bits of useful data and the other bits will be masked by circuit noise.
  16. ^ “32-bit capable DACs”. hydrogenaud.io. Retrieved 2 December 2016. all the ’32 bit capable’ DAC chips existent today have actual resolution less than 24 bit.
  17. ^ D. R. Campbell. “Aspects of Human Hearing” (PDF). Archived from the original (PDF) on 21 August 2011. Retrieved 21 April 2011. The dynamic range of human hearing is [approximately] 120 dB
  18. ^ “Sensitivity of Human Ear”. Archived from the original on 4 June 2011. Retrieved 21 April 2011. The practical dynamic range could be said to be from the threshold of hearing to the threshold of pain [130 dB]
  19. ^ US6317065B1, “Multiple A to D converters for enhanced dynamic range”, issued 1999-07-01
  20. ^ Christodoulou, Lakis; Lane, John; Kasparis, Takis (1 March 2010). “Dynamic range extension using multiple A/D converters”. 2010 4th International Symposium on Communications, Control and Signal Processing (ISCCSP): 1–4. doi:10.1109/ISCCSP.2010.5463427. ISBN 978-1-4244-6285-8. S2CID 16501096.
  21. ^ a b Smith, Steven (1997–98). “The Scientist and Engineer’s Guide to Digital Signal Processing, Chapter 28 – Digital Signal Processors / Fixed versus Floating Point”. www.dspguide.com. Retrieved 10 August 2013.
  22. ^ Moorer, James (September 1999). “48-Bit Integer Processing Beats 32-Bit Floating-Point for Professional Audio Applications” (PDF). www.jamminpower.com. Retrieved 12 August 2013.
  23. ^ a b c Tomarakos, John. “Relationship of Data Word Size to Dynamic Range and Signal Quality in Digital Audio Processing Applications”. www.analog.com. Analog Devices. Retrieved 16 August 2013.
  24. ^ “DSP56001A” (PDF). Freescale. Retrieved 15 August 2013.
  25. ^ Smith, Steven (1997–98). “The Scientist and Engineer’s Guide to Digital Signal Processing, Chapter 4 – DSP Software / Number Precision”. Retrieved 19 August 2013.
  26. ^ Carletta, Joan (2003). “Determining Appropriate Precisions for Signals in Fixed-Point IIR Filters”. DAC. CiteSeerX 10.1.1.92.1266.
  27. ^ Choosing a high-performance audio ADC, 14 September 2011, retrieved 7 May 2019
  28. ^ Montgomery, Chris (25 March 2012). “24/192 Music Downloads …and why they make no sense”. xiph.org. Archived from the original on 7 July 2013. Retrieved 26 May 2013. With use of shaped dither, which moves quantization noise energy into frequencies where it’s harder to hear, the effective dynamic range of 16 bit audio reaches 120dB in practice, more than fifteen times deeper than the 96dB claim. 120dB is greater than the difference between a mosquito somewhere in the same room and a jackhammer a foot away…. or the difference between a deserted ‘soundproof’ room and a sound loud enough to cause hearing damage in seconds. 16 bits is enough to store all we can hear, and will be enough forever.
  29. ^ Stuart, J. Robert (1997). “Coding High Quality Digital Audio” (PDF). Meridian Audio Ltd. Archived from the original (PDF) on 7 April 2016. Retrieved 25 February 2016. One of the great discoveries in PCM was that, by adding a small random noise (that we call dither) the truncation effect can disappear. Even more important was the realisation that there is a right sort of random noise to add, and that when the right dither is used, the resolution of the digital system becomes infinite.
  30. ^ “Dithering in Analog-to-Digital Conversion” (PDF). e2v Semiconductors. 2007. Archived from the original (PDF) on 4 October 2011. Retrieved 26 July 2011.
  31. ^ Kester, Walt. “Oversampling Interpolating DACs” (PDF). Analog Devices. Archived from the original (PDF) on 19 May 2012. Retrieved 19 August 2013.
  32. ^ “The history of the CD”. philips.com. Retrieved 7 October 2020.
  33. ^ “Philips CD100”. hifiengine.
  34. ^ “Sony CDP-101”. hifiengine.
  35. ^ “B.1 First and Second-Order Noise Shaping Loops”. Retrieved 19 August 2013.
  36. ^ “Sweetwater Knowledge Base, Masterlink: What is a “Red Book” CD?”. www.sweetwater.com. Sweetwater. 27 April 2007. Retrieved 25 August 2013.
  37. ^ “Understanding DVD-Audio” (PDF). Sonic Solutions. Archived from the original (PDF) on 4 March 2012. Retrieved 25 August 2013.
  38. ^ Shapiro, L. (2 July 2001). “Surround Sound, Page 10”. ExtremeTech. Retrieved 26 August 2013.
  39. ^ “White paper Blu-ray Disc Format, 2.B Audio Visual Application Format Specifications for BD-ROM Version 2.4” (PDF). Blu-ray Disc Association. April 2010. Retrieved 25 August 2013.
  40. ^ Puhovski, Nenad (April 2000). “DV – A SUCCESS STORY”. www.stanford.edu. Archived from the original on 27 October 2004. Retrieved 26 August 2013.
  41. ^ “G.711 : Pulse code modulation (PCM) of voice frequencies” (PDF). International Telecommunication Union. Retrieved 25 August 2013.
  42. ^ “DIGITAL SOUND SIGNALS: tests to compare the performance of five companding systems for high-quality sound signals” (PDF). BBC Research Department. August 1978. Archived from the original (PDF) on 8 November 2012. Retrieved 26 August 2013.
  43. ^ “Ardour Key Features”. Ardour Community. 2014. Retrieved 8 April 2014.
  44. ^ “Pro Tools Documentation, Pro Tools Reference Guide” (ZIP/PDF). Avid. 2013. Retrieved 26 August 2013.
  45. ^ “Logic Pro X: User Guide” (PDF). Apple. January 2010. Retrieved 26 August 2013.[permanent dead link]
  46. ^ “Cubase Pro 10.5 Manual” (PDF). Steinberg. 2020. Retrieved 2 September 2020.
  47. ^ “Reason 7 Operation Manual” (PDF). Propellerhead Software. 2013. Archived from the original (PDF) on 24 May 2013. Retrieved 26 August 2013.
  48. ^ “GarageBand ’11: Set the audio resolution”. Apple. 13 March 2012. Retrieved 26 August 2013.
  49. ^ “Audacity: Features”. wiki.audacityteam.com. Audacity development team. Retrieved 13 September 2014.
  50. ^ “Audio Settings”. www.image-line.com. Retrieved 12 February 2019.
  51. ^ “Sample Rate, Bit-Depth & Bitrate | Exclusivemusicplus”. Exclusivemusicplus. 26 October 2018. Retrieved 30 November 2018.
  • Ken C. Pohlmann (15 February 2000). Principles of Digital Audio (4th ed.). McGraw-Hill Professional. ISBN 978-0-07-134819-5.
Источник

Кодирование звуковой информации

Кодирование звуковой информации

Введение

Не до конца понимаете, как происходит кодирование звуковой информации? Запутались в аналогово-цифровых и цифро-аналоговых преобразователях? Записывайтесь ко мне на индивидуальный урок по информатике и ИКТ. Кроме рассмотрения теоретических сведений мы с вами прорешаем колоссальное количество тематических примеров.

Общие сведения о звуковой информации

В течение дня обычный человек слышит большое количество различных звуков. Давайте попытаемся кратко понять, что же такое звук. Звук – колебания воздуха, которые были созданы неким источником.
Под источником звука можно понимать любой предмет, объект, который способен генерировать звуковые волны:

  • Человек, который что-то произнес.

  • Проезжающий поезд, от которого исходит шум.

  • Музыкальные инструменты, на которых играет музыкант.

В самом широком физическом смысле под звуком следует понимать простую волну. Если говорить о графической интерпретации звука, то звуковые волны следует представлять, как множество синусоидальных графиков функций, каждый из которых имеет ряд обязательных параметров.

Звук обладает множеством характеристик, но ключевыми являются лишь две:

  1. Амплитуда звуковой волны.

  2. Частота звуковой волны.

Об этих свойствах будет детально рассказано в следующем разделе данной статьи.

Сейчас я вам покажу график функций идеальной звуковой волны, которой в природе физически не существует.

Идеальная звуковая волна

Графическое представление идеальной звуковой волны

Также хочу продемонстрировать график функций неидеальной звуковой волны, которая является речью обыкновенного человека.

Неидеальная звуковая волна

Графическое представление неидеальной звуковой волны, которая является речью человека

Посмотрев на оба выше представленных графика функций, у вас должны возникнуть следующие мысли и закономерный вопрос: если перед нами изображен график функций, то где координатная ось, координатная сетка, градуированные шкалы осей ОХ и оси ОY, а также нужно понять, на основании каких закономерностей построены данные графики функций? То есть, какие параметры выступают значением по оси абсцисс и по оси ординат. О данных характеристиках, параметрах будет рассказано ниже.

Характеристики звуковой информации

Как было сказано выше, что звук обладает двумя ключевыми характеристиками: амплитудой и частотой.

Амплитуда – по сути, громкость или сила звука, измеряемая в децибелах. В физике принято сокращение единицы децибел до дБ. Человек в дневное время суток способен воспринимать звуки громкостью от 10-15 дБ. Уровень громкости звука является относительной величиной. Болевой порог для человека составляет уровень громкости звука в 120-130 дБ.

Частота – отношение количества колебаний звуковой волны в единицу времени. Иногда вместо термина «частота звука» используется термин «высота звука». Единицей измерения частоты в мировой системе СИ является герц. Обозначается единица герц как Гц. Человек воспринимает звуковые волны в диапазоне от 20 Гц до 20000 Гц. Звуковые волны, имеющие частотность меньше, чем 20 Гц, называют инфразвуком. Звуковые волны, имеющие частотность выше, чем 20000 Гц, называют ультразвуком.

Влияние частоты на тип звука

Влияние частоты на тип звука

Давайте вернемся к графикам функций идеальной и неидеальной звуковой волны.

Наша задача – разобраться, какая величина откладывается на оси абсцисс, а какая – на оси ординат.

Очевидно, что одной из осей является популярнейшая характеристика большинства физических графиков функций – время. Мы не сможем исследовать поведение звуковой волны, если не будем рассматривать ее в различные отрезки времени. Следовательно, осью абсцисс является параметр время. Единицей измерения является, например, секунда или миллисекунда.

Осью ординат выступает амплитуда или громкость рассматриваемой звуковой волны. Чем больше громкость или выше амплитуда, тем выше проходит график функций, соответствующий анализируемой звуковой волне.

Представим те же самые графики функций звуковых волн, но уже с обозначениями осей координат и их градуировкой.

Частота дискретизации звука

Необходимо знать, что процессор персонального компьютера взаимодействует с любыми данными на уровне двоичного кода. Двоичный или бинарный код – цепочки битов, которые принимают только одно из двух предопределенных значений, – 0 или 1.

Под кодированием звуковой информации следует понимать преобразование аналогового звукового сигнала в формат, понятный процессору персонального компьютера, то есть в двоичный код. Аналоговый или непрерывный звуковой сигнал у нас представлен в виде графика функций, как зависимость амплитуды от времени.

Чтобы оцифровать аналоговый звуковой сигнал разобьем ось, выражающую время, на некоторое количество равных отрезков и произведем замеры амплитуды/громкости в каждом отрезке. Предлагаю произвести разбивку с шагом 0.1 секунды.

Дискретизация – процесс преобразования непрерывного сигнала в дискретный, то есть прерывный сигнал. Под частотой дискретизации следует понимать частоту взятия отсчетов непрерывного во времени сигнала при его дискретизации. В нашем случае дискретизация – операция, связанная с разбивкой оси абсцисс, отвечающей за время, на отдельные одинаковые участки. А частотой дискретизации является значение, равное 10 Гц. То есть мы производим 10 замеров амплитуды звуковой волны за 1 секунду.

Дискретизация неидеальной звуковой волны

Дискретизация неидеальной звуковой волны

Таблица значений громкости звуковой волны при частоте дискретизации 10 Гц:

Время, сек

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Громкость, дБ

90

20

80

30

90

10

40

20

90

20

60

Разрядность звука при кодировании звуковой информации

В теории кодирования звуковой информации понятие разрядности взаимосвязано с понятием квантования. В грубом приближении под квантованием можно понимать операцию, которая преобразует значения громкости или амплитуды звукового сигнала в двоичный код.

Обратимся еще раз к графику функций, который выражает аналоговый неидеальный звуковой сигнал. Значения громкости находятся в диапазоне от 0 до 100 децибел. Следовательно, у нас должна быть возможность запоминания 101 различного состояния, значения. Давайте рассчитаем минимальное количество бит информации, необходимой для кодирования 101 различного значения. Для этого решим простейшее показательное неравенство: 2x ≥ 101. Очевидно, что x = 7, так как 27 = 128 ≥ 100. Следовательно, для кодирования звуковой информации нам будет достаточности разрядности в 7 бит.

Сейчас мы произведем операцию квантования по отношению к замеренной громкости звуковой волны:

 Время, сек

0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1

Громкость, дБ

90

20

80

30

90

10

40

20

90

20

60

Двоичный код

1011010

0010100

1010000

0011110

1011010

0001010

0101000

0010100

1011010

0010100

0111100

На этом этап кодирования звуковой информации можно считать законченным. В оперативной памяти персонального компьютера входной аналоговый звуковой сигнал будет представлен в следующем виде:

101101000101001010000001111010110100001010 01010000010100101101000101000111100

Хочу обратить ваше внимание, что в приведенном примере мы использовали ничтожно малую частоту дискретизации, равную 10 Гц. В современных условиях кодирование звуковой информации осуществляют при частоте дискретизации 44100 Гц. То есть мы провели 10 замеров в течение 1 секунды, а на практике обеспечивают 44100 замеров за 1 секунду. Чем чаще производятся замеры исследуемой величины, тем точнее кодируется звуковая информация.

Для ради эксперимента давайте рассчитаем информационный объем, которые требуется для хранения звуковой волны в нашем примере, при частоте дискретизации 10 Гц и разрядности 7 бит.

V = [Частота дискретизации] ∙ [Разрядность] ∙ [Промежуток времени] = 10 ∙ 7 ∙ 1 = 70 [бит].

Данная формула справедлива для монозвука. Информационный объем для стереозвука рассчитывается по аналогичной формуле, но в начале стоит коэффициент 2. Это связано с тем, что при кодировании стерео звуковой информации используется две дорожки.

Уровни громкости звука

Громкость, дБ

Характеристика

Источник звука

0

Абсолютная тишина

5

Почти идеальная тишина

10

Почти идеальная тишина

Шорох листьев

15

Едва слышно

Качание веток деревьев

20

Едва слышно

Шепот человека

25

Очень тихо

Шепот человека

30

Тихо

Тиканье часов на стене

35

Ниже среднего

Речь человека на расстоянии 10 метров

40

Ниже среднего

Обыкновенная речь человека

45

Ниже среднего

Обыкновенная речь человека

50

Средне

Печатная машинка

55

Выше среднего

Офисное помещение

60

Шумно

Отдел продаж

65-75

Шумно

Громкий разговор, крики, смех

80

Очень громко

Крик человека

85

Очень громко

Громкий крик человека

90

Очень шумно

Движение поезда на расстоянии в 1 метр

95

Очень шумно

Движение метро снаружи

100

Крайне шумно

Оркестр

120

Невыносимо громко

Отбойный молоток

130

Болевой порог

Самолет при взлете

150

Контузия

Старт ракеты

160

Шок, тяжелые травмы слухового аппарата

Ударная волна при взрыве ядерной бомбы

200

Смерть

Шумовое оружие

Громкость звука необходимо учитывать при кодировании звуковой информации, так как ее величина влияет на разрядность кодирования звуковых волн, а следовательно, и на информационный вес закодированного в двоичном коде звукового файла.

Краткие логические выводы

Подытожим алгоритм кодирования звуковой информации:

  1. Анализ входного аналогового сигнала. Как правило данный сигнал выражается графиком функций в системе координат время-громкость.

  2. Проведение операции дискретизации, то есть разбивка входного сигнала на конечное и одинаковые по размерам фрагменты. Чем больше значение частоты дискретизации, тем выше точность преобразования при кодировании звуковой информации.

  3. Проведение операции квантования, то есть перевод значений в двоичный формат.

  4. Запись двоичного кода в звуковой файл, находящегося на жестком диске персонального компьютера.

Если у вас остались какие-либо вопросы по теме «Кодирование звуковой информации», то записывайтесь ко мне на индивидуальный урок по информатике и ИКТ. Кроме теоретических сведений из области кодирования звуковой информации мы будем делать упор и на решение тематических заданий.

Источник

Решение задач на кодирование звуковой информации.

  1. Теоретическая часть

При решении задач учащиеся опираются на следующие понятия:

 Временная дискретизация – процесс, при котором, во время кодирования непрерывного звукового сигнала, звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина амплитуды. Чем больше амплитуда сигнала, тем громче звук.

Глубина звука (глубина кодирования) – количество бит на кодировку звука.

Количество различных уровней громкости рассчитываем по формуле N= 2I , где I – глубина звука.

Частота дискретизации – количество измерений уровня входного сигнала в единицу времени (за 1 сек). Чем больше частота дискретизации, тем точнее процедура двоичного кодирования. Частота измеряется в герцах (Гц).

 Качество двоичного кодирования – величина, которая определяется глубиной кодирования и частотой дискретизации.

Разрядность регистра – число бит в регистре аудио адаптера. Чем больше разрядность, тем меньше погрешность каждого отдельного преобразования величины электрического тока в число и обратно. Если разрядность равна I, то при измерении входного сигнала может быть получено 2I =N различных значений.

  1. Практическая часть. Разбор и решение задачи.

Задача 1. Оцените информационный объём цифрового звукового стерео файла длительностью 20 секунд при глубине кодирования 16 бит и частоте дискретизации 10000 Гц?  Результат представить в Кбайтах, округлить до сотых.

         При решении таких задач надо не забывать следующее:

Что  моно – 1 канал, стерео – 2 канала

Дано:

I = 16 бит

t = 20 сек

η =10000 Гц

I – разрядность звуковой карты,

t – время звучания аудиофайла,

η – частота дискретизации

Решение:

V =2· I · η ·t

V = 2* 16 * 10000*20 = 6400000 бит

6400000/8 = 800000 байт

800000/1024 = 781,25 Кбайт

Ответ:V(Инфор.) = 781,25 Кбайт

Найти: V(информационный объём)-?

Задача 2. Определить размер (в байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при частоте дискретизации 22,05 кГц и разрешении 8 бит.

 Дано:

I = 8 бит=1 байт

t = 10 сек

η = 22,05 кГц = 22,05 * 1000 Гц = 22050 Гц

I – разрядность звуковой карты,

t – время звучания аудиофайла,

η – частота дискретизации

Решение:

V(Инфор.) =  I · η ·t

V(Инфор.) =  22050 *10 *1 = 220500 байт

Ответ: V(Инфор.) = 220500 байт

Найти: V(информационный объём)-?

Задача 3. Объем свободной памяти на диске — 5,25 Мб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 22,05 кГц?

Дано:

I = 16 бит = 2 байт

V(Инфор.) = 5,25Мб = 5505024 байт

η = 22,05 кГц =22,05 * 1000 Гц =22050 Гц

Решение:

V(Инфор.) =  I · η ·t

t = V(Инфор.)/( η · I)

t = 5505024/( 22050 *2 = 124,8 сек

Ответ: t = 124,8 секунды

Найти: t-?
Источник

Звук.

Звук – это звуковая волна, у которой непрерывно меняется амплитуда и частота. При этом амплитуда определяет громкость звука, а частота — его тон. Чем больше амплитуда звуковых колебаний, тем он громче. А частота писка комара больше частоты сигнала автомобиля. Частоту измеряют в Герцах. 1Гц — это одно колебание в секунду.

Кодирование звука.

Компьютер является мощнейшим устройством для обработки различных типов информации, в том числе и звуковой. Но аналоговый звук непригоден для обработки на компьютере, его необходимо преобразовать в цифровой. Для этого используются специальные устройства — аналого-цифровые преобразователи или АЦП. В компьютере роль АЦП выполняет звуковая карта. Каким же образом АЦП преобразует сигнал из аналогового в цифровой вид? Давайте разберемся.

Пусть у нас есть источник звука с частотой 440Гц, пусть это будет гитара. Сначала звук нужно превратить в электрический сигнал. Для этого используем микрофон. На выходе микрофона мы получим электрический сигнал с частотой 440Гц. Графически он выглядит таким образом:

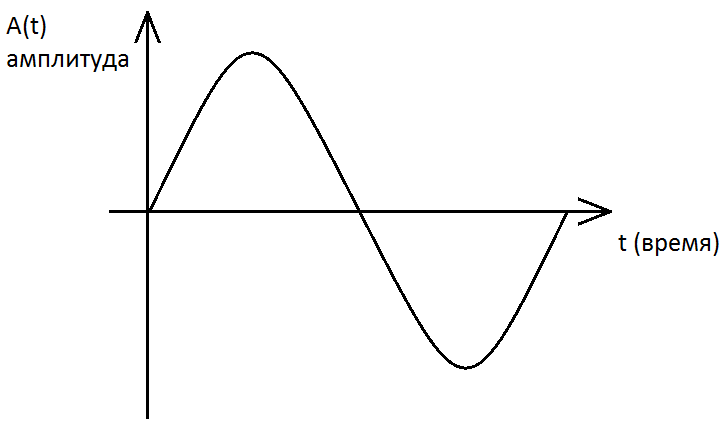
Следующая задача — преобразовать этот сигнал в цифровой вид, то есть в последовательность цифр. Для этого используется временная дискретизация — аналоговый звуковой сигнал разбивается на отдельные маленькие временные участки и для каждого такого участка устанавливается определенная величина интенсивности звука, которая зависит от амплитуды. Другими словами через какие-то промежутки времени мы измеряем уровень аналогового сигнала. Количество таких измерений за одну секунду называется частотой дискретизации. Частота дискретизации измеряется в Герцах. Соответственно, если мы будет измерять наш сигнал 100 раз в секунду, то частота дискретизации будет равна 100Гц.

Вот примеры некоторых используемых частот дискретизации звука:

  • 8 000 Гц — телефон, достаточно для речи;
  • 11 025 Гц;
  • 16 000 Гц;
  • 22 050 Гц — радио;
  • 32 000 Гц;
  • 44 100 Гц — используется в Audio CD;
  • 48 000 Гц — DVD, DAT;
  • 96 000 Гц — DVD-Audio (MLP 5.1);
  • 192 000 Гц — DVD-Audio (MLP 2.0);
  • 2 822 400 Гц — SACD, процесс однобитной дельта-сигма модуляции, известный как DSD — Direct Stream Digital, совместно разработан компаниями Sony и Philips;
  • 5,644,800 Гц — DSD с удвоенной частотой дискретизации, однобитный Direct Stream Digital с частотой дискретизации вдвое больше, чем у SACD. Используется в некоторых профессиональных устройствах записи DSD.

Современные звуковые карты способны оцифровывать звук с частотой дискретизации 96Кгц и даже 192 кГц.

В итоге наш аналоговый сигнал превратится в цифровой, а график станет уже не гладким, а ступенчатым, дискретным:

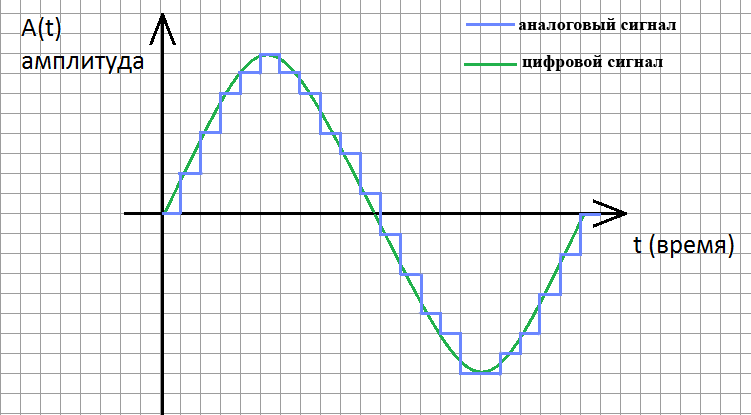
Глубина кодирования звука — это количество возможных уровней сигнала. Другими словами глубина кодирования это точность измерения сигнала. Глубина кодирования измеряется в битах. Например, если количество возможных уровней сигнала равно 255, то глубина кодирования такого звука 8 бит. 16-битный звук уже позволяет работать с 65536 уровнями сигнала. Современные звуковые карты обеспечивают глубину кодирования в 16 и даже 24 бита, а это возможность кодирования 65536  и 16 777 216 различных уровней громкости соответственно.

Зная глубину кодирования, можно легко узнать количество уровней сигнала цифрового звука.  Для этого используем формулу:

N=2i,

где N — количество уровней сигнала, а i — глубина кодирования.

Например, мы знаем, что глубина кодирования звука 16 бит. Значит количество уровней цифрового сигнала равно 216=65536.

Чтобы определить глубину кодирования если известно количество возможных уровней применяют эту же формулу. Например, если известно, что сигнал имеет 256 уровней сигнала, то глубина кодирования составит 8 бит, так как 28=256.

Как понятно из данного вышеприведенного рисунка, чем чаще мы будем измерять уровень сигнала, т.е. чем выше частота дискретизации и чем точнее мы будем его измерять, тем более график цифрового сигнала будет похож на аналоговый график, соответственно, тем выше качество цифрового звука мы получим. И тем больший объем будет иметь файл.

Кроме того, мы рассматривали монофонический (одноканальный) звук, если же звук стереофонический, то размер файла увеличивается в 2 раза, так как он содержит 2 канала.

Рассмотрим пример задачи.

Какой объем будет иметь звуковой монофонический файл содержащий звук, если длительность звука 1 минута, глубина кодирования 8 бит, а частота дискретизации 22050Гц?

Зная частоту дискретизации и длительность звука легко установить количество измерений уровня сигнала за все время. Если частота дискретизации 22050Гц — значит за 1 секунду происходит 22050 измерений, а за минуту таких измерений будет 22050*60=1 323 000.

На одно измерение требуется 8 бит памяти, следовательно на 1 323 000 измерений потребуется 1 323 000*8 = 10 584 000 бит памяти. Разделив полученное число на 8 получим объем файла в байтах — 10584000/8=1 323 000 байт. Далее, разделив полученное число на 1024 получим объем файла в килобайтах — 1 291,9921875 Кбайт. А разделив полученное число еще раз на 1024 и округлив до сотых получим размер файла в мегабайтах — 1 291,9921875/1024=1,26Мбайт.

Ответ: 1,26Мбайт.

Автор:

Источник

Добавить комментарий