Как найти развертку куба

• Авторы
• Научный руководитель
• Файлы
• Литература

Математика изучает объекты, явления, процессы окружающего мира во всех его проявлениях и взаимодействиях. Обустраивая окружающее пространство, человек всегда старается его упорядочить. Одна из часто встречаемых форм бытовых предметов – это прямоугольный параллелепипед. Его форму имеют: шкаф, телевизор, детские кубики, кусочки сахара… Длину, ширину и высоту прямоугольного параллелепипеда называют его измерением. Если все три измерения равны, то его называют кубом.

Знания о площади поверхности куба, его развертках, объёме полезны при расчётах количества обоев, паркета, краски при ремонте квартиры, кубометров леса при постройке дома… Поэтому тема «Куб и его развёртки» является актуальной.

Актуальность применения правил замощения плоскости подтверждает сказ о мастерах.

Двум мастерам было дано задание из одинаковых листов железа изготовить максимальное количество кубов, используя предложенную развертку куба. У первого мастера получилось 5 штук, второй же мастер, применив принципы замощения плоскости, сумел сделать в два раза больше кубов, тем самым показав возможность рационального использования материала

Цель исследования: получение новых знаний о кубе, его развертках и их практических применениях.

Задачи исследования:

1. Изучить элементы куба.

2. Исследовать развёртки куба.

3. Изготовить модели куба.

4. Выполнить замощение плоскости развёртками куба.

5. Изготовить пазлы.

Предмет исследования: куб.

Объект исследования: развёртки куба.

Гипотеза: знания о кубе и его развёртках помогают решать практические задачи.

Методы исследования: практический, наблюдение, опрос, анализ, обобщение, измерения, расчёты, изучение литературы и материалов сайтов.

Теоретический этап исследования

1. Куб и его элементы

По другому куб называют шестигранником или гексаэдром [6]. Куб имеет 6 граней Каждая грань куба – квадрат. У куба 8 вершин. Вершина куба – это самая отдалённая от центра куба точка, которая лежит на пересечении трёх его граней. Каждая вершина принадлежит только трём граням и только трём рёбрам. Куб имеет 12 рёбер. Ребро куба – это отрезок, образованный пересечением двух граней куба. Рёбра имеют одинаковую длину. Каждый конец ребра соединен с двумя соседними рёбрами под прямым углом [3].

Поверхность куба состоит из шести граней. Площадь поверхности куба – это сумма площадей всех граней.

Площадь одной грани куба при длине ребра «а» равна а2. Площадь поверхности куба можно выразить формулой S=6a2.

Площадь одной грани этого куба: 1 дм2, тогда площадь поверхности куба будет равна 6 дм2. Если разбить 1 дм2 на см2 и мм2, мы получим, что площадь поверхности данного куба будет равна 600см2 и 60 000мм2 соответственно.

Объём куба – это совокупность всех точек в пространстве, ограниченных гранями куба. Объём куба при длине ребра «а» можно выразить формулой V=a3.

Кубы с одинаковым размером граней, но сделанные из разных материалов имеют одинаковый объем, одинаковую площадь, но разную массу. Соответственно, кубы, изготовленные из разных материалов, но имеющие одинаковую массу, будут отличаться размерами.

Игральная кость – это популярный источник случайности, который широко применяется в азартных, настольных и ролевых играх.

Традиционная игральная кость – это кубик, который используется как средство генерирования случайных чисел. На каждую грань кубика нанесены числа от 1 до 6. Их принято располагать так, чтобы сумма чисел на противоположных гранях была равна семи. Целью кубика является демонстрация случайно определённого целого числа от одного до шести. Выпадение каждого числа является равновозможным благодаря правильной геометрической форме кубика.

2. Развёртки куба

Развёртка куба – это оболочка, позволяющая увидеть куб со всех сторон. Развертка куба состоит из 6 равных квадратов.

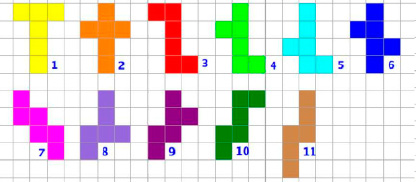
Изучение возможных вариантов развёртки куба, показало, что их всего 11 видов [4].

3. Замощение

Замощение – это покрытие всей плоскости или заполнение всего пространства неперекрывающимися фигурами [5].

Изучение куба показало, что плоскость можно покрыть целиком без пробелов его реберными развёртками одного вида. При этом несколько развёрток одного типа складываются в симметричный элемент орнамента, называемый плиткой, с помощью которой происходит замощение плоскости [2].

Выполнено замощение плоскости различными развёртками куба. Замощение плоскости развертками куба можно использовать при изготовлении пазлов.

Пазл – это увлекательная головоломка очень популярная у взрослых и незаменимый элемент в жизни каждого ребёнка. Пазлы для детей – это увлекательная игра, позволяющая развивать мелкую моторику, логическое мышление, воображение, память, усидчивость, терпение, целеустремленность.

Практический этап исследования

Практическая работа №1

Сделать модель куба из дерева с рёбрами 1 дм, из бумаги с ребром 1 дм. Из бумаги с ребром 1 см.

Заполнить таблицу.

Вывод: площадь поверхности и объёма куба зависит от величины ребра и не зависит от материала. Масса куба зависит от размеров куба и материала, из которого он изготовлен (Приложение 1).

Практическая работа №2

Изготовить тренажёр по переводу единиц измерения площади. На бумажной модели куба разбить одну грань на квадратные сантиметры, на противоположной сделать надпись 100см2, другую грань разбить на квадратные миллиметры, на противоположной грани сделать надпись 10000 мм2. На пятой грани сделать надпись 1 дм2.

Результат: изготовлен тренажёр по переводу единиц измерения площади (Приложение 2).

Практическая работа №3

Изготовить 11 различных развёрток куба с длиной ребра 1дм. Обёртыванием бумажной модели куба убедиться, что все они являются развёртками куба.

Результат: даны названия развёрткам куба: «Буква Т», «Крестик», «Лежачая собачка», «Ружьё», «Стоячая собачка», «Пушка», «Загадочная», «Лесенки».

Проверено, что все 11 многоугольников являются развёртками куба (Приложение 3).

Практическая работа №4

Изготовить модель игральной кости с ребром 5 см. Подбрасыванием кости убедиться, что выпадение очков происходит с равной вероятностью.

Вывод: выпадение очков происходит с равной вероятностью (Приложение 4).

Практическая работа №5

Замостить плоскость различными развёртками куба. Сделать пазлы.

Результаты:

1. Выполнены рисунки по замощению плоскости развёртками куба.

2. Изготовлены пазлы (Приложение 5).

Задача о нахождении кратчайшего расстояния по поверхности куба

В точке А на поверхности куба находится паук, в точке В муха. Найти кратчайшее расстояние по поверхности куба от паука к мухе.

Развертки куба помогают при решении различных задач. Одна из таких задач была предложена для решения воспитанникам нашей школы. Необходимо было указать кратчайший путь от паука, сидящего в точке А, к мухе, находящейся в точке В.

Был проведён опрос воспитанников по нахождению самого короткого пути по поверхности куба.Предложенные варианты ответов изображены цифрами.

Произвели измерения и вычислили длины путей, самый короткий путь оказался четвёртый. Это подтверждает развёртка куба. Самый короткий путь на развёртке – это отрезок АВ. Двигаться надо к точке на ребре куба, отстоящей от нижней грани на четверть ребра (Приложение 6).

Заключение

В результате работы были сделаны следующие выводы:

1. Куб – это геометрическое тело, являющееся правильным шестигранником, каждая грань которого представляет собой квадрат.

2. Куб небольшого размера, на каждую грань которого нанесены числа от 1 до 6, используется как средство генерирования случайных чисел.

3. Развёртки куба позволяют находить решения различных задач.

4. Применение различных развёрток куба и правил замощения плоскости способствуют созданию разнообразных орнаментов и рациональному использованию материала.

5. Замощение плоскости развертками куба можно использовать при изготовлении пазлов для детей, способствующих их полноценному и всестороннему развитию.

Приложения

Приложение 1

Модели куба

Приложение 2

Поверхность куба

Приложение 3

Развёртки куба

Приложение 4

Игральная кость

Приложение 5

Замощение плоскости

Приложение 6

Нахождение кратчайшего пути

Библиографическая ссылка

Ляховский К.С. КУБ И ЕГО РАЗВЁРТКИ // Старт в науке. – 2018. – № 5-6.
;

URL: https://science-start.ru/ru/article/view?id=1223 (дата обращения: 19.05.2023).