- Авторы
- Научный руководитель
- Файлы
- Литература
Ляховский К.С.
1
1 г. Котлас, ЧЧОУ «Школа-интернат № 1 среднего общего образования ОАО «Российские железные дороги», 4 класс
Бубнова Н.И. (Котлас, ЧОУ «Школа-интернат № 1 ;среднего общего образования ОАО «Российские железные дороги»)
1. Моро М.И., Волкова С.И. Для ;тех, кто любит математику. 4 ;класс ;/ Просвещение, 2017.
2. Волкова С.И. Математика и ;конструирование. 4 ;класс, 2014.
3. Атанасян Л.С., Бутузов В.Ф. Геометрия 7–9 ;классы: учеб. для ;образовательных учреждений. 5-е изд. – М.: Просвещение.
4. http://uslide.ru/geometriya/18852–razvyortki-kuba.html.
5. http://easyen.ru/load/m/3_klass/kub_ehlementy_kuba_grani_rebra_vershiny/377–1–0–13873.
6. https://ru.wikipedia.org/wiki.
Математика изучает объекты, явления, процессы окружающего мира во всех его проявлениях и взаимодействиях. Обустраивая окружающее пространство, человек всегда старается его упорядочить. Одна из часто встречаемых форм бытовых предметов – это прямоугольный параллелепипед. Его форму имеют: шкаф, телевизор, детские кубики, кусочки сахара… Длину, ширину и высоту прямоугольного параллелепипеда называют его измерением. Если все три измерения равны, то его называют кубом.
Знания о площади поверхности куба, его развертках, объёме полезны при расчётах количества обоев, паркета, краски при ремонте квартиры, кубометров леса при постройке дома… Поэтому тема «Куб и его развёртки» является актуальной.
Актуальность применения правил замощения плоскости подтверждает сказ о мастерах.
Двум мастерам было дано задание из одинаковых листов железа изготовить максимальное количество кубов, используя предложенную развертку куба. У первого мастера получилось 5 штук, второй же мастер, применив принципы замощения плоскости, сумел сделать в два раза больше кубов, тем самым показав возможность рационального использования материала
Цель исследования: получение новых знаний о кубе, его развертках и их практических применениях.
Задачи исследования:
1. Изучить элементы куба.
2. Исследовать развёртки куба.
3. Изготовить модели куба.
4. Выполнить замощение плоскости развёртками куба.
5. Изготовить пазлы.
Предмет исследования: куб.
Объект исследования: развёртки куба.
Гипотеза: знания о кубе и его развёртках помогают решать практические задачи.
Методы исследования: практический, наблюдение, опрос, анализ, обобщение, измерения, расчёты, изучение литературы и материалов сайтов.
Теоретический этап исследования
1. Куб и его элементы
По другому куб называют шестигранником или гексаэдром [6]. Куб имеет 6 граней Каждая грань куба – квадрат. У куба 8 вершин. Вершина куба – это самая отдалённая от центра куба точка, которая лежит на пересечении трёх его граней. Каждая вершина принадлежит только трём граням и только трём рёбрам. Куб имеет 12 рёбер. Ребро куба – это отрезок, образованный пересечением двух граней куба. Рёбра имеют одинаковую длину. Каждый конец ребра соединен с двумя соседними рёбрами под прямым углом [3].
Поверхность куба состоит из шести граней. Площадь поверхности куба – это сумма площадей всех граней.
Площадь одной грани куба при длине ребра «а» равна а2. Площадь поверхности куба можно выразить формулой S=6a2.
Площадь одной грани этого куба: 1 дм2, тогда площадь поверхности куба будет равна 6 дм2. Если разбить 1 дм2 на см2 и мм2, мы получим, что площадь поверхности данного куба будет равна 600см2 и 60 000мм2 соответственно.
Объём куба – это совокупность всех точек в пространстве, ограниченных гранями куба. Объём куба при длине ребра «а» можно выразить формулой V=a3.
Кубы с одинаковым размером граней, но сделанные из разных материалов имеют одинаковый объем, одинаковую площадь, но разную массу. Соответственно, кубы, изготовленные из разных материалов, но имеющие одинаковую массу, будут отличаться размерами.
Игральная кость – это популярный источник случайности, который широко применяется в азартных, настольных и ролевых играх.
Традиционная игральная кость – это кубик, который используется как средство генерирования случайных чисел. На каждую грань кубика нанесены числа от 1 до 6. Их принято располагать так, чтобы сумма чисел на противоположных гранях была равна семи. Целью кубика является демонстрация случайно определённого целого числа от одного до шести. Выпадение каждого числа является равновозможным благодаря правильной геометрической форме кубика.
2. Развёртки куба
Развёртка куба – это оболочка, позволяющая увидеть куб со всех сторон. Развертка куба состоит из 6 равных квадратов.
Изучение возможных вариантов развёртки куба, показало, что их всего 11 видов [4].
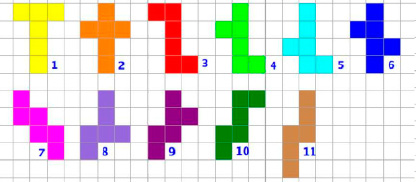
3. Замощение
Замощение – это покрытие всей плоскости или заполнение всего пространства неперекрывающимися фигурами [5].
Изучение куба показало, что плоскость можно покрыть целиком без пробелов его реберными развёртками одного вида. При этом несколько развёрток одного типа складываются в симметричный элемент орнамента, называемый плиткой, с помощью которой происходит замощение плоскости [2].
Выполнено замощение плоскости различными развёртками куба. Замощение плоскости развертками куба можно использовать при изготовлении пазлов.
Пазл – это увлекательная головоломка очень популярная у взрослых и незаменимый элемент в жизни каждого ребёнка. Пазлы для детей – это увлекательная игра, позволяющая развивать мелкую моторику, логическое мышление, воображение, память, усидчивость, терпение, целеустремленность.
Практический этап исследования
Практическая работа №1
Сделать модель куба из дерева с рёбрами 1 дм, из бумаги с ребром 1 дм. Из бумаги с ребром 1 см.
Заполнить таблицу.
|
Ребро |
Площадь поверхности |
Объём |
Масса |
|
|
Куб из дерева |
1 дм |
6 дм2 |
1 дм3 |
650 г |
|
Куб из бумаги |
1 дм |
6 дм2 |
1 дм3 |
50 г |
|
Куб из бумаги |
1 см |
6 см2 |
1 см3 |
0,5 г |
Вывод: площадь поверхности и объёма куба зависит от величины ребра и не зависит от материала. Масса куба зависит от размеров куба и материала, из которого он изготовлен (Приложение 1).
Практическая работа №2
Изготовить тренажёр по переводу единиц измерения площади. На бумажной модели куба разбить одну грань на квадратные сантиметры, на противоположной сделать надпись 100см2, другую грань разбить на квадратные миллиметры, на противоположной грани сделать надпись 10000 мм2. На пятой грани сделать надпись 1 дм2.
Результат: изготовлен тренажёр по переводу единиц измерения площади (Приложение 2).
Практическая работа №3
Изготовить 11 различных развёрток куба с длиной ребра 1дм. Обёртыванием бумажной модели куба убедиться, что все они являются развёртками куба.
Результат: даны названия развёрткам куба: «Буква Т», «Крестик», «Лежачая собачка», «Ружьё», «Стоячая собачка», «Пушка», «Загадочная», «Лесенки».
Проверено, что все 11 многоугольников являются развёртками куба (Приложение 3).
Практическая работа №4
Изготовить модель игральной кости с ребром 5 см. Подбрасыванием кости убедиться, что выпадение очков происходит с равной вероятностью.
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Выпадение очков |
5 |
1 |
4 |
5 |
6 |
3 |
3 |
1 |
2 |
6 |
3 |
5 |
6 |
4 |
2 |
1 |
6 |
2 |
4 |
5 |
Вывод: выпадение очков происходит с равной вероятностью (Приложение 4).
Практическая работа №5
Замостить плоскость различными развёртками куба. Сделать пазлы.
Результаты:
1. Выполнены рисунки по замощению плоскости развёртками куба.
2. Изготовлены пазлы (Приложение 5).
Задача о нахождении кратчайшего расстояния по поверхности куба
В точке А на поверхности куба находится паук, в точке В муха. Найти кратчайшее расстояние по поверхности куба от паука к мухе.
Развертки куба помогают при решении различных задач. Одна из таких задач была предложена для решения воспитанникам нашей школы. Необходимо было указать кратчайший путь от паука, сидящего в точке А, к мухе, находящейся в точке В.
Был проведён опрос воспитанников по нахождению самого короткого пути по поверхности куба.Предложенные варианты ответов изображены цифрами.
|
№ опыта |
Длина линии |
|
1 |
25 см |
|
2 |
23 см |
|
3 |
21 см 5 мм |
|
4 |
20 см 5 мм |
|
5 |
21 см 4 мм |
Произвели измерения и вычислили длины путей, самый короткий путь оказался четвёртый. Это подтверждает развёртка куба. Самый короткий путь на развёртке – это отрезок АВ. Двигаться надо к точке на ребре куба, отстоящей от нижней грани на четверть ребра (Приложение 6).
Заключение
В результате работы были сделаны следующие выводы:
1. Куб – это геометрическое тело, являющееся правильным шестигранником, каждая грань которого представляет собой квадрат.
2. Куб небольшого размера, на каждую грань которого нанесены числа от 1 до 6, используется как средство генерирования случайных чисел.
3. Развёртки куба позволяют находить решения различных задач.
4. Применение различных развёрток куба и правил замощения плоскости способствуют созданию разнообразных орнаментов и рациональному использованию материала.
5. Замощение плоскости развертками куба можно использовать при изготовлении пазлов для детей, способствующих их полноценному и всестороннему развитию.
Приложения
Приложение 1
Модели куба

Приложение 2
Поверхность куба


Приложение 3
Развёртки куба




Приложение 4
Игральная кость



Приложение 5
Замощение плоскости



Приложение 6
Нахождение кратчайшего пути



Библиографическая ссылка
Ляховский К.С. КУБ И ЕГО РАЗВЁРТКИ // Старт в науке. – 2018. – № 5-6.
;
URL: https://science-start.ru/ru/article/view?id=1223 (дата обращения: 20.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Валерия Сирота
«Квантик» №8, 2022

В статье из «Квантика» № 7 за 2022 год мы научились рисовать четырёхмерный кубик. Может, теперь его сделать? Из подручных материалов.
Совсем сделать, конечно, не получится. Ведь у нас всё-таки нет здесь четырёхмерного пространства, в котором такой кубик можно было бы хранить. Но зато можно сделать выкройку — развёртку — и подождать, когда кто-нибудь четырёхмерный её сложит в куб.

Действительно, когда мы делаем трёхмерный бумажный кубик, мы сначала рисуем на бумаге плоскую развёртку из шести квадратов — например, латинский крест (рис. 1). И эта развёртка, заметьте, двумерная! Её могли бы сделать и плоские человечки, живущие на листе бумаги. Потом мы её сворачиваем в куб, а вот это плоские человечки уже не могут: мы используем наше третье измерение.

Трёхмерный куб мы собирали из двумерных граней. А из чего же собирать четырёхмерный? Из трёхмерных кубиков, конечно! В прошлый раз мы выяснили, что их понадобится 8 штук — столько, сколько 3-граней у 4-куба. И склеивать их нужно будет уже не рёбрами, как кубик, а гранями — ведь у двух соседних 3-граней есть общая двумерная (квадратная) грань. Всё, что можно, склеим у себя в трёхмерном пространстве, а остальное они уж там в своём четырёхмерном сложат.

Выкройки, как и для двумерного кубика, могут быть разные. Проще всего сделать «обобщение» латинского креста: ведь мы знаем, что в четырёхмерном кубе все двумерные грани должны соединять какие-то две 3-грани, «свободных» двумерных граней не должно оставаться; так же, как в трёхмерном кубе не болтаются ни к чему не приклеенные рёбра. Итак, берём 8 кубиков и склеиваем их — и вуаля! Развёртка готова (рис. 2).
Теперь нужно разобраться, как наша выкройка будет потом, в четырёхмерье, складываться. Тут придётся потренировать наше почти уже 4-мерное воображение!
Заметьте, что мы не можем разглядеть один из кубиков нашей развёртки ни с какой стороны — он полностью закрыт соседями. Так же и плоские человечки, когда смотрят на латинский крест, не видят центрального квадрата. Но можно сделать такую развёртку, чтобы им были видны все квадраты. Так же и мы — если захотим, можем переклеить одну из будущих 3-граней так, чтобы в новой развёртке нам были видны все кубики.
Из каждой развёртки обычного 3-куба можно получить много развёрток 4-куба: достаточно к каждому её квадрату приклеить кубик, получив похожий на латинский крест «плоский слой» (высотой в один кубик), потом к этому плоскому слою приклеить ещё два кубика: один с одной стороны (к любому кубику слоя!), второй — с другой (тоже к любому кубику). Так, например, получается развёртка на рисунке 2. Но бывают и такие развёртки 4-куба, которые из развёрток 3-куба не получишь.

Теперь, когда вы умеете рисовать и даже почти изготавливать четырёхмерные кубики, вы, конечно, понимаете, что можно рисовать и пятимерные, и шестимерные… А вдруг на самом деле мы живём в каком-нибудь таком «пространстве большей размерности», пяти- или там десятимерном? Так плоские человечки или одномерные червяки могли бы жить у нас в трёхмерии, сами того не замечая и ничего не видя снаружи от своей плоскости… Мы живём, а пятимерные существа иногда подходят и смотрят «оттуда» на наш трёхмерный мир? Что ж, такое не исключено…
А что, если в одном четырёхмерном пространстве находятся сразу два трёхмерных мира (говорят: подпространства)? Могут они там поместиться? А может быть, жителям этих миров можно как-нибудь переходить из одного в другой? Или хотя бы что-нибудь передавать?.. Подумайте: каким может быть такой «портал», соединяющий миры?
(Подсказка. Прежде чем придумывать про 4-мерье, можно «упростить задачу на одно измерение» и посмотреть, как это устроено в нашем трёхмерном пространстве. Какие пространства и как в него могут «помещаться»?)
И ещё. Двумерным человечкам не обязательно жить на плоскости. Они могут жить и на какой-нибудь изогнутой поверхности, например на сфере — на оболочке большого шара… Нам, смотрящим на них снаружи, это было бы хорошо видно. А как они могли бы догадаться об этом сами? Может, и наше трёхмерное пространство — какое-нибудь кривое? Как мы могли бы это проверить?
Художник Мария Усеинова.
Решение задачи 1

Решение задачи 2

А где белый кубик?
Решение задачи 3
Например, так:

Решение задачи 4

Например, можно последовательно переклеить все боковые кубики «латинского креста» друг на друга — оранжевый кубик на рисунке к задаче 2 отклеить от центрального и приклеить к розовому, розовый — к бежевому, бежевый — к фиолетовому. Получится так, как на рисунке.
-
-
November 28 2016, 02:00
- Образование
- Литература
- Дети
- Cancel
Третьеклассники: куб и его развертки
Тему “Куб и его развертки” предложил мне учебник Елены Юрьевны Ивановой
(теперь учебники Ивановой можно купить и здесь )


Задачи на куб и развертки куба
у Истоминой даются в Наглядной геометрии для 2 класса.


Несколько интересных задач я нашла
в тетрадке Беленковой и Лебединцевой для 5 класса ( 2 часть)







там же в приложении можно найти крупную развертку, которую третьекласснику нетрудно склеить.
Мультфильм про замощения из серии “Математические этюды” позволяет детям увидеть все развертки куба
http://www.etudes.ru/ru/etudes/cubisme/
Мне помогают в работе квадратные магнитные рамки MAGFORMERS
которые очень удобо складывать в развертку и потом сворачивать в кубик.
А у каждого ребенка есть деревянные кубики http://www.artotoys.ru/product/kubik-derevjannyj-buk/ ,
на которых очень удобно рисовать карандашом рисунки на гранях, которые легко стираются
Хочу отметить, что игры с кубиками- игральными костями кроме формирования пространственного представления еще готовят ребенка к изучению комбинаторики и теории вероятностей.
Про игры с игральными костями я писала в теме https://klarissa45.livejournal.com/23157.html
Продолжение темы здесь
Цели урока:
- повторить и закрепить элементы куба;
- отработать навык рисования куба «от руки»;
- показать решение логических задач с помощью разворачивания поверхности куба;
познакомить с геодезическими линиями на поверхности куба; - закрепить новый материал в решении задач;
- подвести итог урока – поговорить о практическом применении развертки.
Ход урока
I. Повторение – устный счет.
«Распутать клубок».
Ребятам раздаются листочки с заранее приготовленными заданиями (Приложение 2). Требуется вписать в геометрические фигуры числа так, чтобы все вычисления были правильными и в одинаковые фигуры были бы вписаны одинаковые числа.

Для проверки демонстрируются слайды 2 и 3 (презентация в Приложении 1).
II. Повторение элементов куба.
Демонстрируется слайд 4.
Ученикам задаются следующие вопросы:
- Назовите элементы куба?
- Сколько у куба граней, ребер, вершин?
- Назовите ребро по которому пересекаются верхняя и правая боковая грани?
- Назовите ребро по которому пересекаются передняя и нижняя грани?
- Назовите ребро по которому пересекаются верхняя и задняя грани?
- Назовите ребра, которые сходятся в вершине А; в вершине G?
III. Задача на кратчайшее расстояние.
Вспомним, что расстоянием между двумя точками называют отрезок, соединяющий эти точки. Однако в жизни довольно часто трудно добраться от одного пункта до другого по прямой. Тем не менее, из всех возможных вариантов стараются выбрать самую короткую дорогу.
В пространстве это несколько сложнее, чем на плоскости. В этом мы сейчас убедимся на следующем примере:

«На поверхности прозрачного куба сидит паук и видит сидящую на другой грани куба муху. Чтобы поймать муху пауку нужно как можно скорее до нее добраться, ведь муха может улететь. Другими словами, пауку необходимо двигаться к мухе кратчайшим маршрутом.
Изобразите карандашом путь по которому должен двигаться паук.»
Обсуждение задачи, варианты решений дети показывают у доски, как итог – демонстрация правильного решения с помощью развертки куба.
Решение задачи демонстрируется на слайдах 5 и 6, к слайдам даются следующие комментарии:
«Мысленно отогнем грань куба на которой сидит паук, расположив верхнюю и боковую грани в одной плоскости. Посмотрим на эти грани сверху. Кратчайший путь от паука до мухи теперь найти очень просто. Достаточно соединить отрезком точки в которых они сидят.
По учебнику стр. 238 дети читают:
Линии, которые на чертеже показывают кратчайший путь от одной точки до другой называются геодезическими линиями.
По учебнику стр. 239:
Решая задачу о пауке и мухе мы мысленно разворачивали две грани куба, располагая их в одной плоскости. Фигура, которая получается при полном развертывании называется разверткой куба.»
IV. Закрепление – решение задач с помощью разверток.

- Проложить геодезическую линию от точки A до точки B.

- Сравнить длины ломаных ABC и ADC.
Сравнить длины ломаных MNK MLK. (задача №926)
К задачам подготовлены слайды 7-11.
V. Работа в группах.
Класс разбивается на небольшие группы. Каждой группе раздается набор разверток куба (Приложение 3). Задача каждой группы попытаться сначала по виду развертки определить правильная она или нет. Затем проверить, попытавшись собрать куб из каждой из разверток.
Для проверки приготовлены слайды 12 и 13.
Итог – беседа о практическом применении развертки.
VI. Домашнее задание.
Используя какую-нибудь из правильных разверток из предыдущего задания склеить модель куба.
Анализ урока:
При изучении объемных фигур у детей возникают трудности различного характера: с изображением таких фигур в тетради, при решении задач, при чтении чертежей.
Данный урок направлен на развитие пространственного мышления и на знакомство с новым подходом – вынесением условия задачи и последующим решением в плоскость с помощью развертки.
На уроке осуществляются следующие этапы:
- активизация урока, устный счет с элементами игры;
- подготовительный этап – повторение элементов куба;
- решение проблемной задачи с элементом игры; рассмотрение различных способов ее решения и убедительное решение с помощью развертки;
- этап закрепления нового подхода – решение логических задач на нахождение кратчайшего маршрута на поверхности куба;
- работа в группах на решение обратной задачи: определение возможных разверток куба;
- беседа о практическом применении развертки;
- по ходу урока ребята учатся чертить куб по линейке и «от руки».
Для чего нужна развертка?
Развёртка — режущий инструмент, который нужен для окончательной обработки отверстий после сверления, зенкерования или растачивания. Развёртыванием достигается точность до 6-9 квалитета и шероховатость поверхности до Ra = 0,32…1,25 мкм.
Что такое развертка в черчение?
Разверткой поверхности многогранника называют плоскую фигуру, полученную при последовательным совмещением всех граней поверхности (многогранника) с плоскостью чертежа в последовательности их расположения на многограннике.
Сколько всего разверток куба?
Найти и построить другие развёртки куба (их существует 11).
Как называется головоломка содержащая 11 фигур которые являются развертками куба?
Вскоре после появления кубика Рубика, в 1981 году была запатентована подобная головоломка в форме правильного додекаэдра — мегаминкс.
Для чего Райбер?
инструмент конической формы для фрезерования внутренней поверхности труб, колонн и т. п.
Как правильно работать с разверткой?
Обычно все происходит по такой схеме.
- Выполняются разметка и накернивание.
- Отверстие высверливается.
- Развертка закрепляется в воротке, смазывается и вставляется в отверстие.
- Для его развертывания инструмент вращают по часовой стрелке.
- Финальный этап — проверка параметров отверстия при помощи калибра.
27 авг. 2019 г.
Что значит читать чертежи?
Чтение чертежа – это представление на двумерной плоской поверхности по изображениям объёмной формы предмета и его размеров и содержащее прочие сведения.
Что такое развертки стен?
Развертки стен — это планы стен. На них показан декор (молдинги, например), ниши, выступы, бра, раскладка плитки, декоративное панно и прочее в размерах. Узлы – это детальная проработка некоторых мест (например, сопряжение плитки с ванной на углу или как делать нишу на потолке с невидимой подсветкой).
Сколько ребер у куба?
Верно, у куба 12 ребер. Вершины граней – это вершины куба. Посчитайте, сколько вершин у куба. Правильно, у куба 8 (восемь) вершин.
Сколько граней у куба?
| Куб | |
|---|---|
| Элементы | 6 граней 12 рёбер 8 вершин Χ = 2 |
| Грани | квадраты |
| Конфигурация вершины | 4.4.4 |
| Двойственный многогранник | правильный октаэдр |
Какая заготовка является разверткой кубика?
Развёртка куба – это оболочка, позволяющая увидеть куб со всех сторон. Развертка куба состоит из 6 равных квадратов.
Как найти развертку цилиндра?
Развертка представляет собой прямоугольник длиной с = πD и высотой Н. Прямой круговой цилиндр, усеченный плоскостью, параллельной его оси, показан на рис. 2. Развертка представляет собой прямоугольник высотой Н и длиной L = b + k, где b = πDᵠ/360° и k = 2 √((D/2)2 – a2) = 2a tg (ᵠ/2).
Как работает развертка?
При подаче развертка контактирует с заготовкой заборной областью рабочей части и снимает припуск. Далее отверстие приобретает нужные параметры за счет работы калибрующей части. На ее заднем конце имеется обратный конус. Он нужен для того, чтобы развертка при выходе из детали не повредила отверстие.
Что это такое Райбер?
инструмент конической формы для фрезерования внутренней поверхности труб, колонн и т. п.
Как правильно развернуть отверстие разверткой?
Вставить развертку в предварительно просверленное или полученное методом литья отверстие. Надеть вороток на хвостовик инструмента. Вращать вороток по часовой стрелке (направлению режущих кромок) избегая резких движений. В процессе работы периодически поливать СОЖ на инструмент.
Как выбрать диаметр развертки?
При назначении диаметра развертки необходимо учитывать разбивку; запас на износ; допуски на изготовление самой развертки. Для обеспечения входа в отверстие малый диаметр режущей части выполняется меньше диаметра обработанного отверстия на 1,3—1,4 припуска на развертывание.
Что должно быть на сборочном чертеже?
На сборочном чертеже должны быть указаны: — габаритные размеры изделия (размеры, определяющие внешние очертания изделия); — установочные и присоединительные размеры (размеры, определяющие величины элементов, по которым данное изделие устанавливают на месте монтажа или присоединяют к другому изделию);
