Как найти развертку пирамиды

Построение развертки поверхности пирамиды способом треугольников

Развертка поверхности пирамиды – это плоская фигура, составленная из основания и граней пирамиды, совмещенных с некоторой плоскостью. На примере ниже мы рассмотрим построение развертки способом треугольников.

Задача

Пирамиду SABC пересекает фронтально-проецирующая плоскость α. Необходимо построить развертку поверхности  SABC и нанести на нее линию пересечения.

Решение

На фронтальной проекции S”A”B”C” отмечаем точки D”, E” и F”, в которых след α_v пересекается с отрезками A”S”, B”S” и C”S” соответственно. Определяем положение точек D’, E’, F’ и соединяем их друг с другом. Линия пересечения обозначена на рисунке красным цветом.

Определение длины ребер

Чтобы найти натуральные величины боковых ребер пирамиды, воспользуемся методом вращения вокруг проецирующей прямой. Для этого через вершину S перпендикулярно горизонтальной плоскости H проведем ось i. Поворачивая вокруг нее отрезки SA, SB и SC, переместим их в положение, параллельное фронтальной плоскости V.

Действительные величины ребер равны проекциям S”A”₁, S”₁B”₁ и S”C”₁. Отмечаем на них точки D”₁, E”₁, F”₁, как это показано стрелками на рисунке выше.

Треугольник ABC, лежащий в основании пирамиды, параллелен горизонтальной плоскости. Он отображается на ней в натуральную величину, равную ∆A’B’C’.

Порядок построения развертки

В произвольном месте на чертеже отмечаем точку S₀. Через нее проводим прямую n и откладываем отрезок S₀A₀ = S”A”₁.

Строим грань ABS = A₀B₀S₀ как треугольник по трем сторонам. Для этого из точек S₀ и A₀ проводим дуги окружностей радиусами R₁ = S”B”₁ и r₁ = A’B’ соответственно. Пересечение данных дуг определяет положение точки B₀.

Грани B₀S₀C₀ и C₀S₀A₀ строятся аналогично. Основание пирамиды в зависимости компоновки чертежа присоединяется к любой из сторон: A₀B₀, B₀C₀ или C₀A₀. 

Нанесем на развертку линию, по которой плоскость α пересекается с пирамидой. Для этого на ребрах S₀A₀, S₀B₀ и S₀С₀ отметим соответственно точки D₀, E₀ и F₀. При этом точка D₀ находится на пересечении отрезка S₀A₀ с окружностью радиусом S”D”₁. Аналогично E₀ = S₀B₀ ∩ S”E”₁, F₀ = S₀C₀ ∩ S”F”₁.

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

6.1. Пирамида. Сечение пирамиды плоскостью. Развертка пирамиды

Многогранником называется тело, ограниченное плоскими многоугольниками, которые называется гранями.

Грани, пересекаясь, образуют ребра.
Ребра, пересекаясь, образуют вершины.
Рассмотрим два основных вида многогранников:

Пирамида – многогранник, у которого боковыми гранями являются треугольники, а основанием – многоугольник.

Упражнение

Дана пирамида, основание которой  параллельно π₁. Основание представляет собой некоторый треугольник.

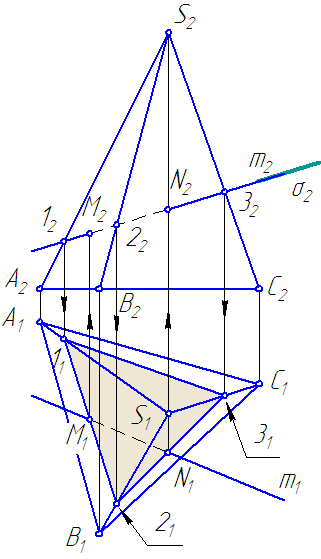
S – вершина пирамиды (Рисунок 6.1).

Рисунок 6.1 – Пересечение поверхности пирамиды прямой

Требуется построить точки пересечения прямой m общего положения с поверхностью пирамиды.

Решение

1.  

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение ∆ (123) поверхности пирамиды с плоскостью σ.

Решение задачи сводится к нахождению линии пересечения плоскостей общего положения (боковые грани пирамиды) и плоскости частного положения (плоскость σ).

Примечание. При наличии круто падающих рёбер (близких к вертикали), построение недостающей проекции точки на ребре по одной данной проекции  необходимо выполнять при помощи пропорционального деления отрезка.

1. В сечении находим точки M и N принадлежащие прямой m.
2. Определяем видимость прямой m.

Развёрткой многогранника называется фигура, полученная в результате последовательного совмещения граней многогранника с плоскостью.

Развёртка всегда строится наружной (лицевой) стороной к наблюдателю.

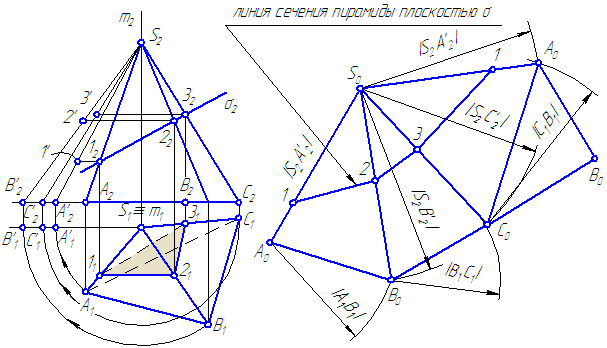
Для построения развёртки пирамиды нужно определить истинные величины всех рёбер пирамиды и построить грани пирамиды в виде треугольников, последовательно присоединяя их друг к другу.

Основание можно присоединить к любой грани, например, АС (Рисунок 6.2).

Рисунок 6.2 – Построение развёртки пирамиды

В упражнении истинные значения ребер определены способом вращения. Для построения линии сечения на развертке, на истинных величинах рёбер построим точки overline{1},overline{2},overline{3}, проведя горизонтальные линии (траектории перемещения точек 1, 2, 3) до пересечения с соответствующими истинными проекциями ребер.

6.2. Призма. Развертка призмы

Призма – многогранник, у которого боковыми гранями являются параллелограммы, а основания – многоугольники, лежащие в параллельных плоскостях.

Упражнение

Дана призма, основания которой параллельны плоскости проекций π₁.

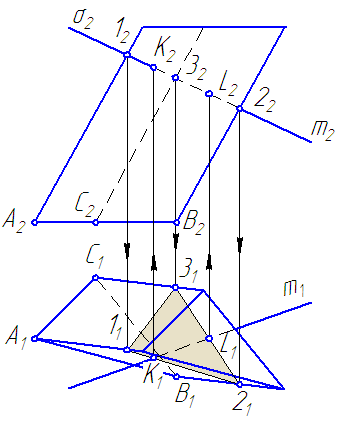
Требуется построить точки пересечения прямой m с поверхностью призмы (Рисунок 6.3).

Рисунок 6.3 – Построение «точек встречи» прямой с поверхностью наклонной призмы

Порядок построения:

1. Вводим через прямую вспомогательную секущую плоскость σ∈m и σ⊥π₂.
2. Строим сечение поверхности призмы с плоскостью σ →(∆(123)).
3. В сечении находим точки K и L принадлежащие прямой m.
4. Определяем видимость прямой m. Если грань АВ на π₂ видна, то точка К на π₂ видима, грань ВС невидима, следовательно, точка Lневидима.

Рассмотрим наклонную призму. Пусть основание призмы параллельно π₁, а ребра параллельны π₂.

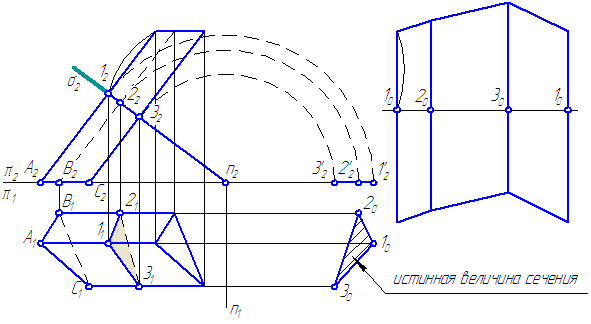
Построим нормальное сечение, то есть сечение плоскостью σ, перпендикулярной ребрам призмы (Рисунок 6.4).

Это сечение развернется в прямую линию. Боковые ребра перпендикулярны к линии сечения.

Рисунок 6.4 – Построение развёртки призмы
Порядок построения:

1.  

1. Найдем истинную величину сечения – (1₀2₀3₀), для чего повернём сечение (123) вокруг оси n⊥π₂, (можно ввести ДПП π₃//σ).
2. Проведём горизонтальную линию на свободном месте листа. Отложим на ней отрезки:
   /1₀-2₀/; /2₀-3₀/; /3₀-1₀/.

1. Проведём направления рёбер перпендикулярно этой линии через точки: 1₀; 2₀; 3₀ и отмерим вверх и вниз расстояния от нормального сечения (на π₂) до верхнего и нижнего основания, откладывая их на линиях-ребрах.

6.3. Взаимное пересечение многогранников

В результате пересечения многогранников получим ломаную линию.

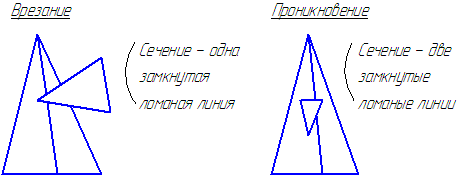
Возможны два случая пересечения многогранников (Рисунок 6.5):

Рисунок 6.5 – Варианты пересечения многогранников

Вершины ломаной – точки пересечения рёбер одного многогранника с гранями другого.

Звенья ломаной – линии пересечения граней.

Для решения задачи нужно найти вершины ломаной, то есть точки пересечения всех рёбер, участвующих в пересечении.

Построенные точки соединить.

Упражнение

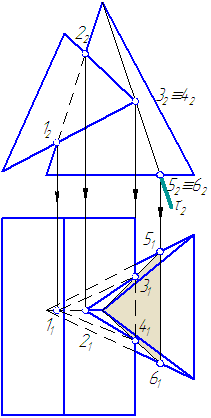
Построить линии пересечения призмы с пирамидой (Рисунок 6.6).

Рисунок 6.6. Построение линии пересечения призмы с пирамидой
Решение

1.  

1. Находим на π₂ проекции точек пересечения ребра пирамиды с проецирующими гранями призмы (точки 1₂ и 2₂). Находим их горизонтальные проекции.
2. Строим точки пересечения ребра призмы с боковыми гранями пирамиды (точки 3₂ и 4₂), для чего используем вспомогательную плоскость τ⊥π₂.
3. Полученные на π₁ точки 3, 2, 4, 1 соединяем отрезками прямых. Причем отрезки 1₁-3₁, 1₁-2₁, 1₁-4₁ невидимы. Получили замкнутую линию пересечения пирамиды с призмой.

Упражнение

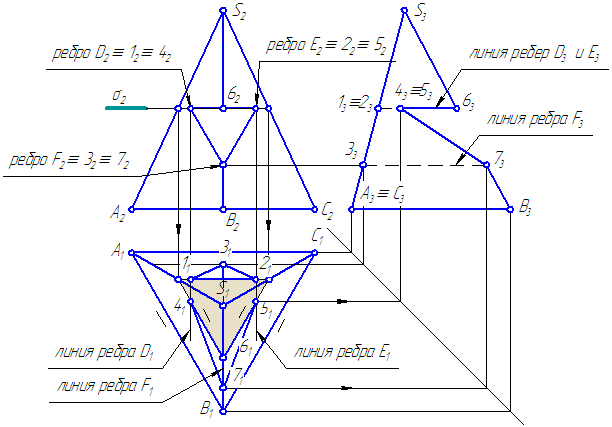
остроить три проекции пирамиды с вырезом и развертку (Рисунок 6.7).

1. По двум проекциям построить третью;
2. На всех трех проекциях построить проекции линии пересечения призматического выреза с пирамидой;
3. Невидимые участки линии пересечения и участки рёбер многогранников показывать штриховой линией;
4. Построить развёртку пирамиды с нанесением линии пересечения.

Рисунок 6.7. Построение проекций пирамиды с вырезом и развертки
Решение:

1. Проводим линии рёбер призмы на всех проекциях.
2. Введём плоскость σ⊥π₂, σ//π₁:

• σ//АВС – основанию пирамиды;
• σ пересекает пирамиду ’ сечение подобно ΔА₁В₁С₁.

Это сечение пересекается:

— с ребром D в двух точках 1 и 4;

— с ребром Е в двух точках 2 и 5.

Грань D₂E₂∩S₂B₂ =6₂.

Ребро F₂∩S₂B₂ =7₂.

Соединим найденные точки: 1-2-3-1; 4-6-5-7-4 и определим видимость.

Построение развертки рассмотрено ранее.

6.4. Задачи для самостоятельной работы

1-4. Построить линию пересечения гранных поверхностей. Показать видимость (Рисунки 6.8 – 6.11).

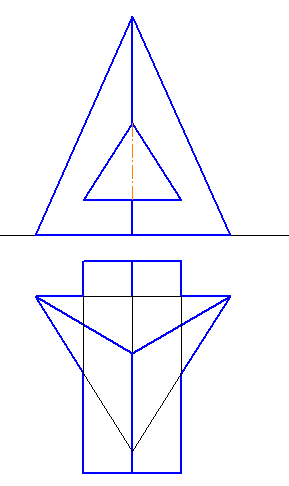
Рисунок 6.8

Рисунок 6.9

Рисунок 6.10

Рисунок 6.11

По вопросам репетиторства по начертательной геометрии, вы можете связаться любым удобным способом в разделе Контакты. Возможно очное и дистанционное обучение по Skype: 1250 р./ак.ч.

Разделы Уроки по теме Рекомендуем

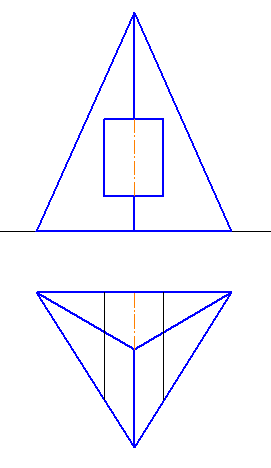
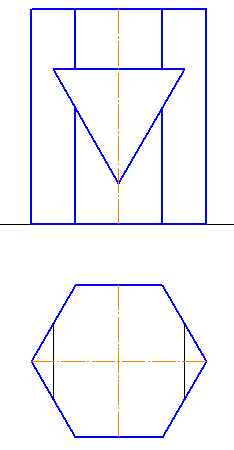
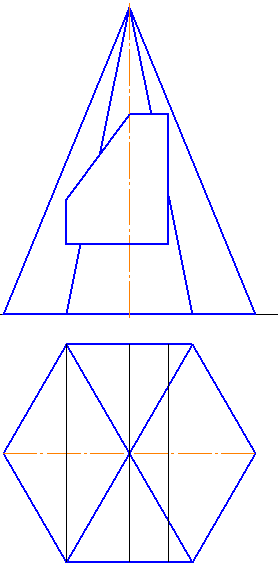
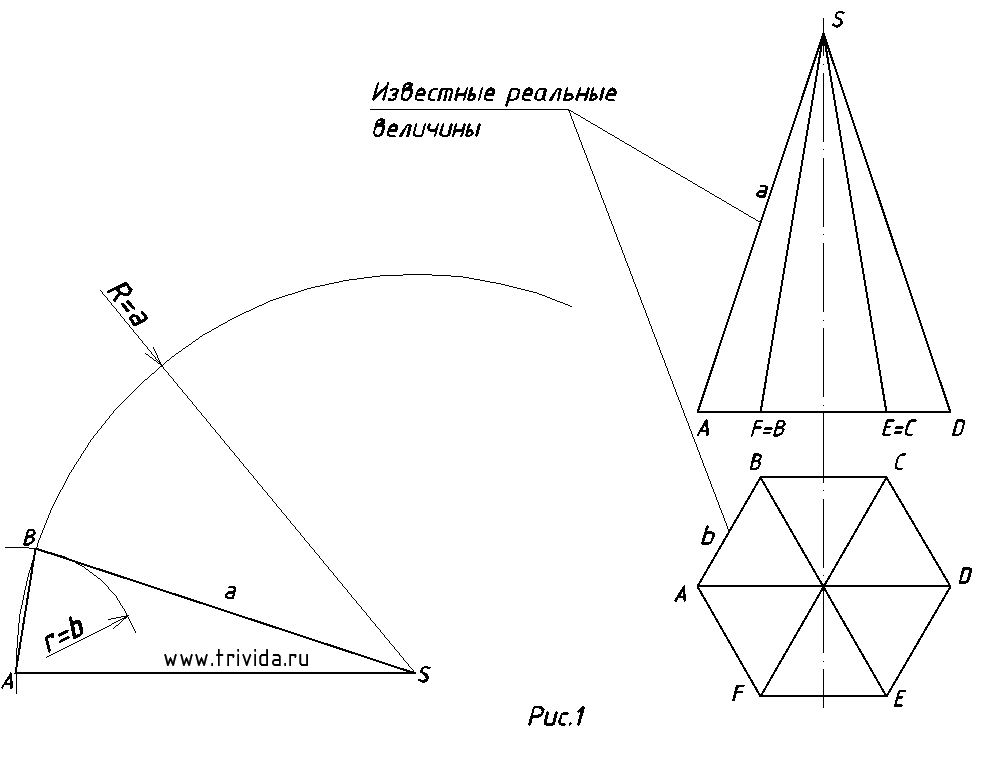
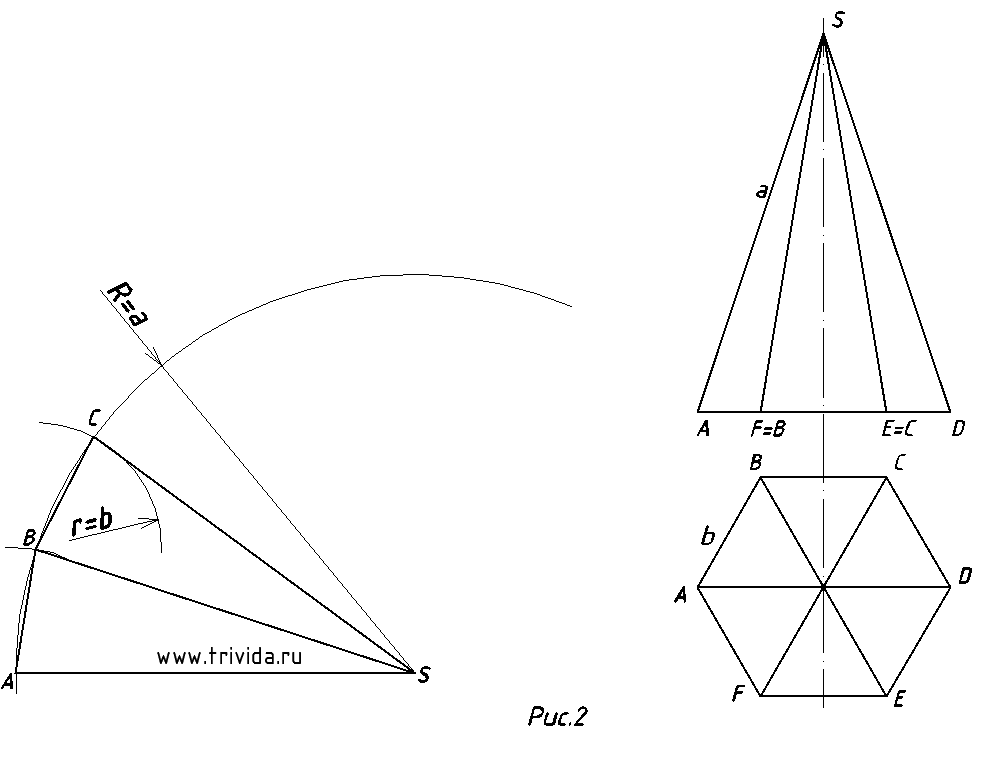
Развертка пирамиды. Как построить развертку шестиугольной пирамиды. Автор: Moroz Дата: 2015-01-19 Если вам нужна пошаговая инструкция как построить развертку пирамиды, то прошу к нашему уроку. Первым делом оцените, развернута ли ваша пирамида аналогичным образом, как на рисунке 1. Если у вас она повернута под 90 градусов, то ребро, помеченное на рисунке как “известные реальные величины” в вашем случае можно будет найти на профильной проекции, которую вам необходимо будет построить. В моем же случае этого не требуется, все необходимые для построения величины у нас уже есть. Важно не забыть, что в данном чертеже только ребра SA и SD на фронтальной проекции отображены в натуральную величину. Все остальные проецируются с искажением длины. Кроме того, на виде сверху все стороны шестиугольника так же спроецированы в натуральную величину. Исходя из этого приступим. 1. Для пущей красоты проведем первую линию горизонтально (рисунок 1). Затем, проведем широкую дугу радиусом R=a, т.е. радиусом равным длине бокового ребра пирамиды. Получим точку А. Из нее сделаем с помощью циркуля засечку на дуге, радиусом r=b (длина стороны основания пирамиды). Получим точку B. У нас уже есть первая грань пирамиды! 2. Из точки B сделаем еще одну засечку таким же радиусом – получим точку C и соединив ее с точками B и S получим вторую боковую грань пирамиды (рисунок 2). 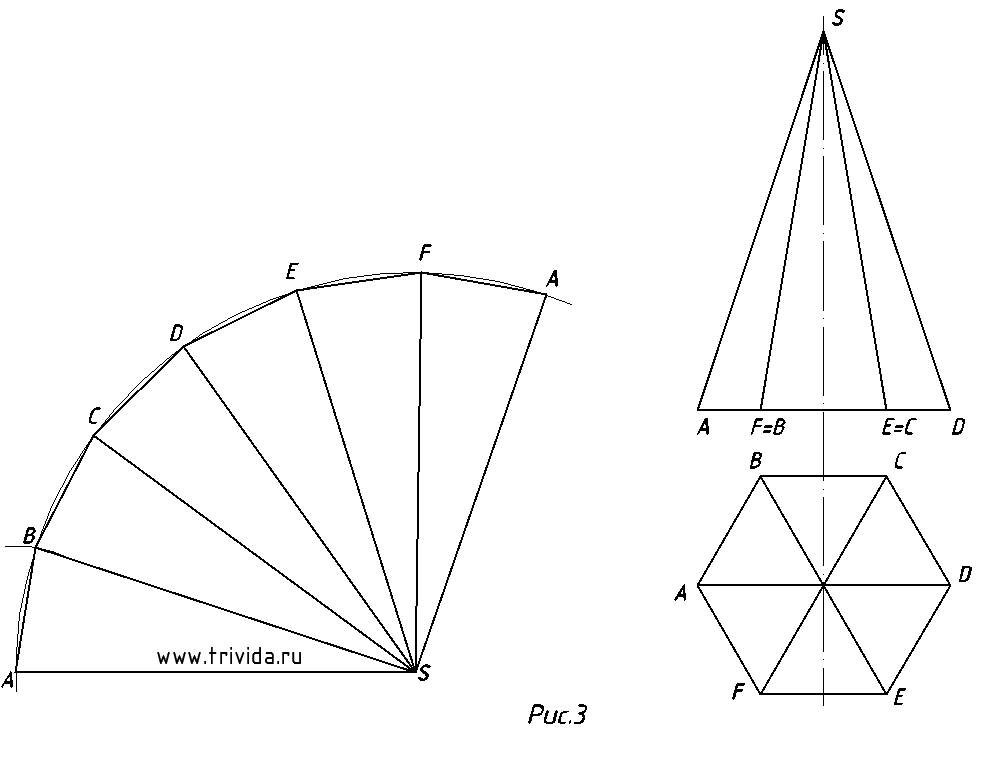3. Повторив данные действия необходимое количество раз (все зависит от того, сколько граней у вашей пирамиды) мы получим такой вот веер (рисунок 3). При правильном построении вы должны получить все точки основания, причем крайние должны повториться. 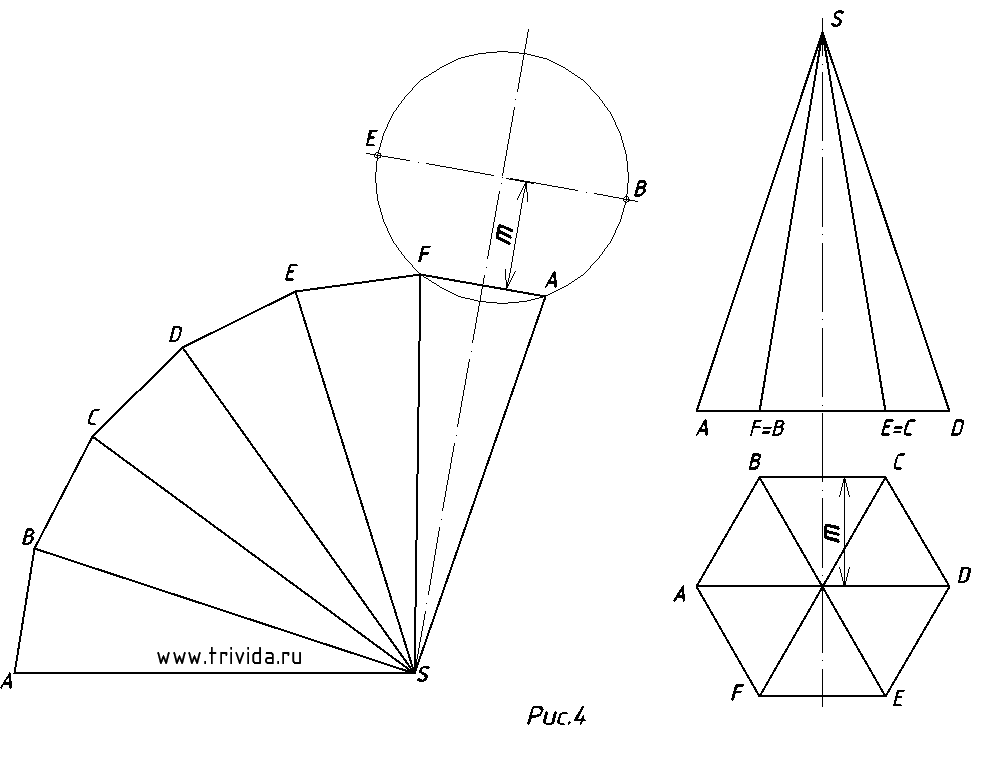4. Это требуют не всегда, но все же оно нужно: добавить основание пирамиды к развертке боковой поверхности. Начертить шести-восьми-пятиугольник все дочитавшие до этого места, полагаю, умеют (как начертить пятиугольник подробно рассказано в этом уроке) Сложность же заключается в том, что фигуру нужно начертить в нужном месте и под нужным углом. Через середину любой грани проведем ось. Из точки пересечения с прямой основания отложим расстояние m, как показано на рисунке 4. Проведя через эту точку перпендикуляр, мы получим оси будущего шестиугольника. Из полученного центра проводим окружность, как вы поступали при построении вида сверху. 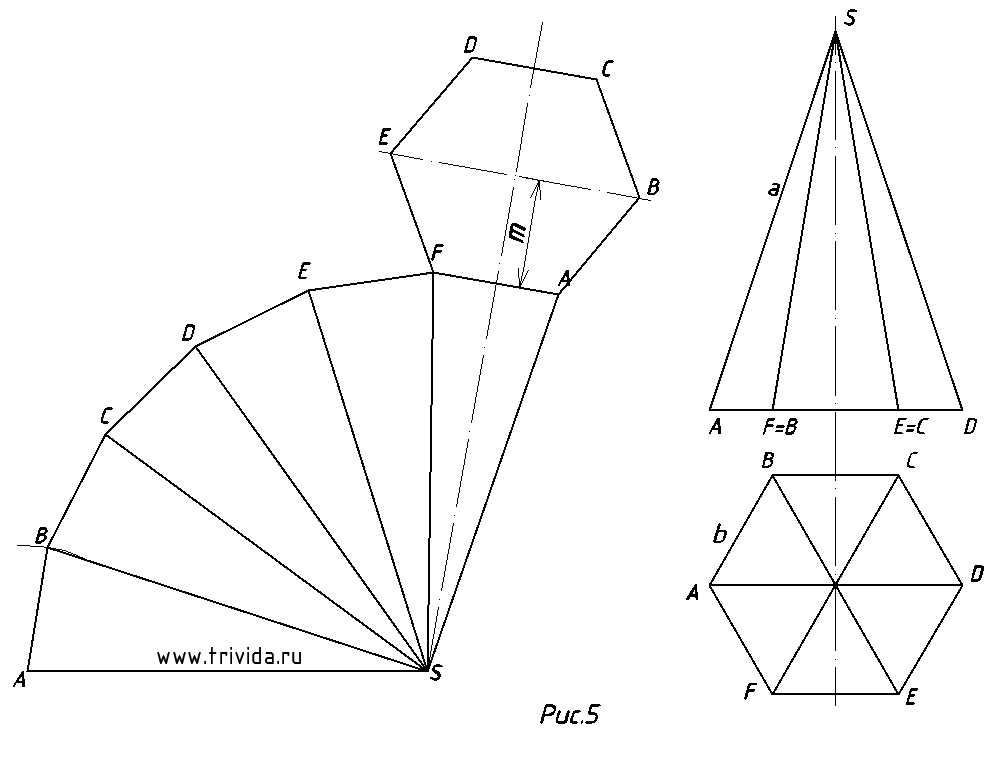Обратите внимание, что окружность должна пройти через две точки боковой грани (в моем случае это F и A) 5. На рисунке 5 показан конечный вид развертки шестиугольной призмы. На этом построение развертки пирамиды завершено. Стройте ваши развертки, учитесь находить решения, будьте въедливыми и никогда не опускайте рук. Спасибо, что зашли. Не забудьте порекомендовать нас друзьям 🙂 Всего хорошего! Просмотров: 105703 Вы можете сказать “спасибо!” автору статьи: пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект “White Bird. Чертежи Студентам” или или запишите наш телефон и расскажите о нас своим друзьям – кто-то наверняка ищет способ выполнить чертежи или создайте у себя на страничке или в блоге заметку про наши уроки – и кто-то еще сможет освоить черчение. А вот это – не реклама. Это напоминание, что каждый из нас может сделать. Если хотите – это просьба. Мы действительно им нужны: Комментарии: Ребята, спасибо, выручили! Даже преподаватель так не объясняет! Спасибо огромное!8 Вот спасибо вам, порадовали! Чего-то такого я и ждал все эти годы :))) Пусть все получается! Спасибо автору, выручил очень) Написано коротко и ясно без заморочек)9 Спасибо большое, очень помогли!) Добавьте свой комментарий:

Последние уроки Как построить диметрию детали? Построение наклонного сечения, заданного на виде слева Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей. Наша почта: zakaz@trivida.ru Наша страница в ВК: Случайный комментарий Сергей: Всем, кто будет в будущем решать, звонить сюда, или кому-то еще – однозначно говорю – сюда. Есть с чем сравнить. В прошлом году заказывал начертательную геометрию в другом месте – устал звонить чтоб отдали чертежи и методичку. Здесь же – отдали готовые чертежи день в день как изначально договорились. Чертежи чистые и препод даже не придрался, хотя меня и предупредили, что могут попросить что-то немного подправить. Еще раз спасибо, очень выручили. Сергей, благодарю вас, что нашли время отписаться. Кстати о времени – нелегко было сделать ваши пять листов за один день. Старайтесь впредь так не затягивать! Обращайтесь, если еще будет нужно, хотя черчение у вас уже закончилось..

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 сентября 2022 года; проверки требуют 4 правки.

Пирами́да (от др.-греч. πυραμίς, род. п. πυραμίδος) — многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину^[1]. По числу углов основания различают пирамиды треугольные (тетраэдр), четырёхугольные и т. д.
Пирамида является частным случаем конуса^[2].

История развития пирамиды в геометрии[править | править код]

Начало геометрии пирамиды было положено в Древнем Египте и Вавилоне, однако активное развитие получило в Древней Греции. Объём пирамиды был известен древним египтянам. Первым греческим математиком, кто установил, чему равен объём пирамиды, был Демокрит
^[3], а доказал Евдокс Книдский. Древнегреческий математик Евклид систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке (книга XI, определение 12^[4]).

Элементы пирамиды[править | править код]

• вершина пирамиды — общая точка боковых граней, не лежащая в плоскости основания;
• основание — грань, которой не принадлежит вершина пирамиды;
• боковые грани — треугольные грани, сходящиеся в вершине;
• боковые рёбра — рёбра, являющиеся сторонами двух боковых граней (и, соответственно, не являющиеся сторонами основания);
• высота пирамиды — перпендикуляр из вершины пирамиды на её основание;
• апофема — высота боковой грани правильной пирамиды, проведённая из её вершины;
• диагональное сечение пирамиды — сечение пирамиды, проходящее через её вершину и диагональ основания.

Развёртка пирамиды[править | править код]

Развёрткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).
Приступая к изучению развёртки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую плёнку. Некоторые из представленных таким образом поверхностей можно путём изгибания совместить с плоскостью. При этом, если отсек поверхности может быть совмещён с плоскостью без разрывов и склеивания, то такую поверхность называют развёртывающейся, а полученную плоскую фигуру — её развёрткой.

Свойства[править | править код]

Если все боковые рёбра равны, то:

• вокруг основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр;
• боковые рёбра образуют с плоскостью основания равные углы;
• также верно и обратное, то есть если боковые рёбра образуют с плоскостью основания равные углы, или если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые рёбра пирамиды равны.

Если боковые грани наклонены к плоскости основания под одним углом, то:

• в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
• высоты боковых граней равны;
• площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани.

Теоремы, связывающие пирамиду с другими геометрическими телами[править | править код]

Сфера[править | править код]

• около пирамиды можно описать сферу тогда, когда в основании пирамиды лежит многоугольник, вокруг которого можно описать окружность (необходимое и достаточное условие)^[5]. Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им. Из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу;
• в пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.

Конус[править | править код]

• Конус называется вписанным в пирамиду, если вершины их совпадают, а его основание вписано в основание пирамиды. Причём вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие);^[6]
• Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые рёбра пирамиды равны между собой (необходимое и достаточное условие);
• Высоты у таких конусов и пирамид равны между собой.

Цилиндр[править | править код]

• Цилиндр называется вписанным в пирамиду, если одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.
• Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания пирамиды. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник (необходимое и достаточное условие).

Формулы, связанные с пирамидой[править | править код]

• Объём пирамиды может быть вычислен по формуле:

где  — площадь основания и  — высота;^[7]

где  — объём параллелепипеда;

• Также объём треугольной пирамиды (тетраэдра) может быть вычислен по формуле^[8]:

где  — скрещивающиеся рёбра ,  — расстояние между и ,  — угол между и ;

• Боковая поверхность — это сумма площадей боковых граней:

• Полная поверхность — это сумма площади боковой поверхности и площади основания:

• Для нахождения площади боковой поверхности в правильной пирамиде можно использовать формулы:

где  — апофема ,  — периметр основания,  — число сторон основания,  — боковое ребро,  — плоский угол при вершине пирамиды.

Особые случаи пирамиды[править | править код]

Правильная пирамида[править | править код]

Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.
Тогда она обладает такими свойствами:

Прямоугольная пирамида[править | править код]

Пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро и является высотой пирамиды.

Тетраэдр[править | править код]

Тетраэдром называется треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды. Кроме того, существует большое различие между понятиями «правильная треугольная пирамида» и «правильный тетраэдр». Правильная треугольная пирамида — это пирамида с правильным треугольником в основании (грани же должны быть равнобедренными треугольниками). Правильным тетраэдром является тетраэдр, у которого все грани являются равносторонними треугольниками.

См. также[править | править код]

• Усечённая пирамида
• Бипирамида

Примечания[править | править код]

Литература[править | править код]

• Александров А. Д., Вернер А. Л. Геометрия. Учебник для 10—11 классов общеобразовательных учреждений. — 2-е изд. — М.: Просвещение, 2003. — 271 с. — ISBN 5-09-010773-4.
• Калинин А. Ю., Терешин Д. А. Стереометрия. 11 класс. — 2-е изд. — М.: Физматкнига, 2005. — 332 с. — ISBN 5-89155-134-9.
• А. П. Киселёв, Геометрия по Киселёву, arΧiv:1806.06942 [math.HO].
• Погорелов А. В. Геометрия: Учебник для 10—11 классов общеобразовательных учреждений. — 8-е изд. — М.: Просвещение, 2008. — 175 с. — 60 000 экз. — ISBN 978-5-09-019708-3.

Ссылки[править | править код]

• Бумажные модели пирамид Архивная копия от 4 января 2010 на Wayback Machine (англ.)
• «Начала» Евклида.

Развертка пирамиды

Построение
развертки боковой поверхности пирамиды
сводится к последовательному построению
ряда треугольников (по трем их сторонам),
каждый из которых равен натуральной
величине соответствующей боковой грани
пирамиды.

Чтобы
построить развертку треугольной пирамиды
(рисунок 15, необходимо определить
натуральные величины ребер пирамиды
любым способом. Если ребер много, то
удобно воспользоваться способом
прямоугольного треугольника. При этом
нужно вынести построения всех треугольников
в сторону от чертежа данной фигуры.
Натуральные величины ребер можно найти
и методом вращения вокруг горизонтально
проецирующей оси i,
проходящей через вершину S.
На рисунке 15 показаны оба способа
нахождения натуральных величин ребер
пирамиды.

После того, как
определим длины ребер SA,
SB, SC,
приступаем к построению развертки. Для
этого через произвольно выбранную точку
S проводим прямую l,
на которой откладываем натуральную
величину ребра AS. Далее
строим вершину B треугольника
ABS методом засечек, затем
вершину С треугольника BCS
и вершину А треугольника CAS.
После этого достраиваем к полученной
развертке боковой поверхности основание
пирамиды АВС, взятое с плоскости П₁,
на которую оно проецируется в натуральную
величину, т.к. является горизонтальной
плоскостью уровня.

На рисунке 15
показано нахождение на развертке точки
К, расположенной на грани ABS.

Рисунок 15

Развертка прямого кругового цилиндра

Полная
развертка прямого кругового цилиндра
представляет собой прямоугольник,
высота которого равна высоте цилиндра,
а основание – длине окружности основания
цилиндра и пристроенные к нему два
круга-основания.

Для получения
приближенной развертки цилиндрической
поверхности заменяем последнюю на
вписанную в нее 12-ти угольную правильную
призму (рисунок 16).

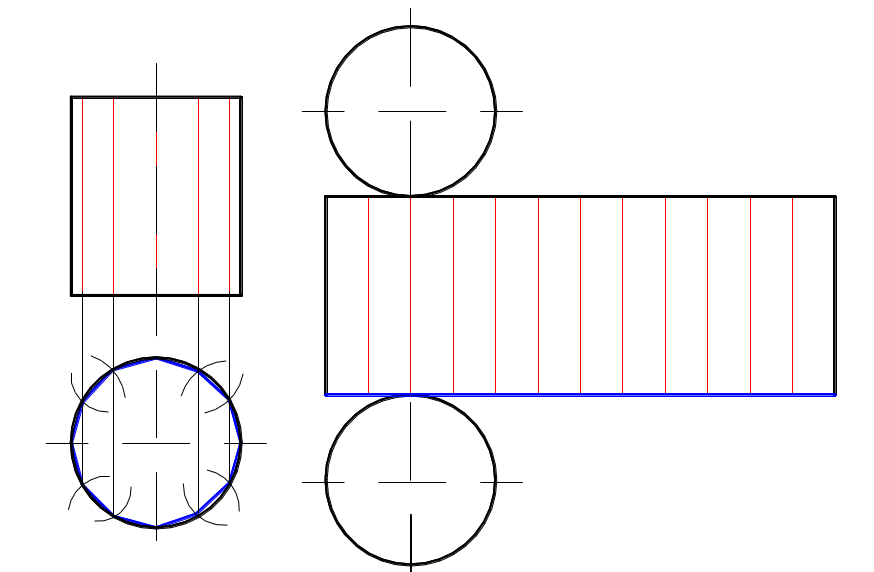
Рисунок 16

Развертка прямого кругового конуса

Полная
развертка прямого кругового конуса
представляет собой сектор, радиус
которого равен образующей конуса, а
длина дуги равна длине окружности
основания конуса и пристроенный к нему
круг основания.

Для получения
приближенной развертки конической
поверхности, усеченной фронтально
проецирующей плоскостью, заменяем
последнюю на вписанную в нее 12-ти угольную
правильную пирамиду (рисунок 17). Для
этого делим окружность основания конуса
своим радиусом на 12 частей . Через эти
точки деления проводим соответственно
12 образующих конуса.

Точка
1 принадлежит правой очерковой образующей
конуса, проецирующейся на П₂ в
натуральную величину, т.к. она является
фронтальной прямой уровня, поэтому на
развертке расстояние от вершины S
до точки 1 равно отрезку S₂1₂.
Для определения расстояний от вершины
S до остальных точек
пересечения образующих конуса с секущей
плоскостью проводим через их фронтальные
проекции прямые, параллельные фронтальной
проекции основания конуса, до пересечения
с одной из очерковых (правой или левой)
образующих конуса. Это соответствует
вращению этих образующих до положения,
параллельного плоскости П₂.

Точки
10 и 11, лежащие на очерке основания конуса,
находим измеряя наименьшую хорду по
дуге окружности.

Рисунок 17

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #