Определение опорных реакций
Способы определения опорных реакций изучаются в курсе теоретической механики. Остановимся только практических вопросах методики вычисления опорных реакций, в частности для шарнирно опертой балки с консолью (рис. 7.4).

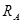
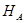
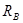
Нахождение и проверка опорных реакций в шарнирной опоре
Для вычисления значений реакций опор составим уравнения статики:
Сумма проекций всех сил (активных и реактивных) на ось z равна нулю: 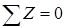
Поскольку на балку действуют только вертикальные нагрузки (перпендикулярные к оси балки), то из этого уравнения находим: горизонтальная реакция неподвижной шарнирной опоры 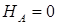
Сумма моментов всех сил относительно опоры А равна нулю: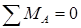
Правило знаков для момента силы: считаем момент силы положительным, если он вращает балку относительно точки против хода часовой стрелки.
Необходимо найти равнодействующую распределенной погонной нагрузки. Распределенная погонная нагрузка равна площади эпюры распределенной нагрузки 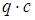
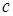
Тогда
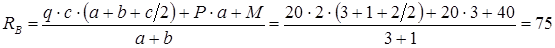
Сумма моментов всех сил относительно опоры B равна нулю: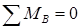
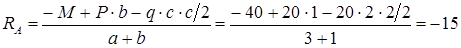
Знак «минус» в результате говорит: предварительное направление опорной реакции 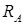
Проверка опорных реакций
Сумма проекций всех сил на ось y должна быть равна нулю: 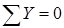
Силы, направление которых совпадает с положительным направлением оси y, проектируются на нее со знаком «плюс»:
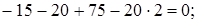
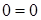
Нахождение опорных реакций в жесткой заделке
Найдем реакции опор в жесткой заделке. Для определения опорных реакций составляются уравнения статики:
Из первого уравнения определяется реакция 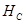
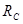
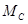
Проверка, как правило, не производится.
Лекция №3
Тема: «Внутренние
усилия в поперечных сечениях стержня»
Вопросы:
1. Опоры и
опорные реакции, и их определение
2. Поперечная
сила и изгибающий момент
3. Взаимосвязь
между изгибающим моментом, поперечной
силой и интенсивностью распределенной
нагрузки
1. Опоры
и опорные реакции, и их определение
При
расчете конструкций в основном встречаются
элементы, испытывающие изгиб.
Стержни,
работающие преимущественно
на изгиб, называют балками. Для того
чтобы балка
могла
испытывать
нагрузку и передавать ее на основание,
она должна
быть соединена с ним опорными связями.
На практике применяют
несколько типов опорных связей, или,
как говорят, несколько
типов опор.
Различают три
основных типа опор:
а)
шарнирно-подвижная опора:
б)
шарнирно-неподвижная опора:
в)
жесткая заделка.
Рис. 1
На
рис. 1 показана шарнирно-подвижная
опора, такая опора позволяет
балке свободно поворачиваться и
перемещаться в горизонтальном
направлении. Поэтому реакция в опоре
будет одна
вертикальная сила. Условное обозначение
такой опоры показано справа.
Рис. 2
На
рис. 2 показана шарнирно-неподвижная
опора. Такая опора
позволяет балке свободно поворачиваться,
но перемещаться она
не может. Поэтому могут возникать две
реакции – вертикальная и горизонтальная
силы. Их можно сложить и получить одну
результатирующую
силу, но нужно знать угол, под которым
oна
будет
направлена. Более удобно будет пользоваться
вертикальной и горизонтальной
составляющими реакции.
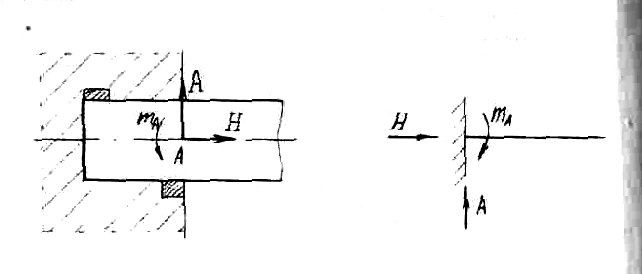
На
рис. 3 показана жесткая заделка. Она
не позволяет балке ни поворачиваться,
ни перемещаться. Поэтому могут возникать
три опорные
реакции: момент, вертикальная и
горизонтальная силы. Если балка не имеет
на конце опоры, то эта часть ее называется
консолью.
Рис. 3
Определим
реакции опор для балки (см. рис. 4).
Рис.4
В опоре
А горизонтальная реакция равна нулю,
так как распределенная
нагрузка q
и сосредоточенная сила F
имеют
вертикальное
направление. Реакции опор
направим
вверх.
Составим два уравнения статического
равновесия сил. Сумма моментов относительно
каждой из опор равна нулю. Уравнения
моментов нужно составлять относительно
опор, так как в этом случае получаются
уравнения с одним неизвестным. Если
составить уравнения
относительно точек В и С, то получим
уравнения с двумя неизвестными,
а их решать сложнее. Моменты против
часовой стрелки будем считать
положительными, по часовой
отрицательными.
где
момент от равномерно распределенной
нагрузки.
Произведение
q
на расстояние, на котором она приложена,
из условия
равновесия системы равно сосредоточенной
силе, приложенной
посредине отрезка. Поэтому момент
равен:
– момент силы F
Внешний
момент m
на плечо не умножается, так
как
это
пара сил, т.е. две равные по величине,
противоположно направленные силы,
имеющие постоянное плечо.
или
.
Проверка:
Сумма всех сил на вертикальную ось Y
должна быть равна
нулю:
.
Момент
m
в условие статического равновесия
не записывают,
так как момент
это две равные по величине, противоположно
направленные силы и в проекции на любую
ось они дадут
ноль.
30-20-2-40+50=0:
80-80=0.
Реакции
определены правильно.
2. Поперечная
сила и изгибающий момент
Пусть
на балку действуют силы
,
реакции опор
.
Определим внутренние усилия в сечении,
расположенном на расстоянии от нулевого
конца (см. рис.5).
Рис. 5
Поскольку
все внешние силы действуют вертикально,
то горизонтальной составляющей у реакции
опоры А
не будет. Балка не будет сжиматься или
растягиваться, т.е. продольная сила в
поперечных сечениях равна нулю. Можно
было взять пример, когда
силы
были бы не вертикальными по направлению.
Тогда бы в опоре А
была бы и вторая реакция
горизонтальная сила, а в сечениях балки
продольная сила N.
В этом случае балка испытывала бы изгиб
с растяжением (сжатием), т.e.
был бы случай сложного сопротивления.
Его мы будем изучать позднее. Вначале
рассматривают более простые задачи и
идут к более сложным, а не наоборот.
Поскольку
внешние силы
лежат в одной плоскости,
проходящей через ось бруса, то возможно
возникновение
тpex
внутренних усилий: изгибающею момента
М,
поперечной силы Q
и
продольной силы N,
которая, как мы отмечали, равна нулю.
Значения М
и Q
определим
из уравнения статического равновесия
левой
части балки:
.
Вывод:
поперечная сила в сечении численно
равна алгебраической
сумме всех внешних сил, а изгибающий
момент
сумме
всех моментов, вычисленных относительно
сечения и приложенных
к рассматриваемой части балки.
Для
поперечных сил и изгибающих моментов
приняты обязательные
правила знаков (см. рис. 6).
Если
сила пытается повернуть рассматриваемую
часть балки по часовой
стрелке, то она вызывает положительную
поперечную силу, и, наоборот, если
действует против часовой стрелки
то поперечная
сила
отрицательная. На рис. 5
сила
вызывает положительное
Q,
а
отрицательное. Следует отметить, что
направление силы положительное для
левой части будет отрицательным для
правой части.
Это вызвано тем, что внутренние силы,
действующие на правую
и левую часть балки обязательно должны
быть равны и противоположно
направлены.
Если
внешняя сила или внешний момент изгибают
балку выпуклостью
вниз, то возникающий изгибающий момент
положительный
и, наоборот, выпуклостью вверх
отрицательный.
Рис. 6
3. Взаимосвязь
между изгибающим моментом,
поперечной силой
и интенсивностью распределенной нагрузки
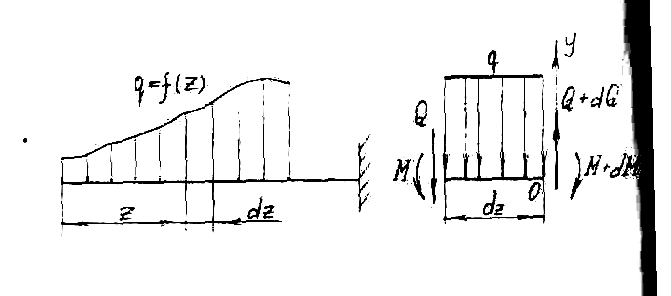
Пусть
на консольную балку (см. рис. 7)
действует
распределенная
нагрузка, изменяющаяся по длине балки.
На расстоянии z
от левого конца возьмем бесконечно
малый отрезок dz.
Рис. 7
Тогда
распределенную нагрузку на нем можно
рассматривать как постоянную.
В левой части рассматриваемого отрезка
будут внутренние усилия Q
и
М,
в правой
с учетом приращения внутренних
усилий Q+dQ
и
M+dM.
Составим
уравнения статического равновесия для
отрезка балки:
(1)
Третьим
членом можно пренебречь, как бесконечно
малой величиной
более высокого порядка, т.е.:
После преобразований
получим:
(2)
т.е. первая
производная от изгибающего момента по
абсциссе (длине балки) есть поперечная
сила.
Если
в формулу (1) подставить значение Q
из
формулы (2),
то
получим:
, (3)
т.е. вторая
производная от изгибающего момента
есть интенсивность распределенной
нагрузки.
Как определить реакции в опорах?
Привет! В этой статье, предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции в опорах, и этому уделяют особое внимание на термехе. А курс термеха, по традиции, читают до сопромата. Для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Что такое реакция опоры?
Реакция опоры – это та сила, которая возникает в опоре от действия внешней нагрузки. В зависимости от конструкции опоры и ее назначения, в ней может появляться разное количество реакций, это может быть как сила, так и момент.
В начале этой статьи, расскажу о том, что должен уже уметь читатель, для успешного освоения данного урока. Если у Вас есть проблемы по поднятым вопросам на старте статьи, переходите по ссылкам на другие материалы на нашем сайте, после чего возвращайтесь к нам на чай реакции. Во второй части статьи, посмотрим, как вычисляются реакции на простейшем примере – балки, загруженной по центру сосредоточенной силой. Тут я покажу, как пользоваться уравнениями равновесия статики, как их правильно составлять. Дальше по плану, научу учитывать распределенную нагрузку, на примере той же балки. И завершать данный урок, будет пример определения реакций для плоской рамы, загруженной всевозможными типами нагрузок. Где применим уже все фишки, о которых я буду рассказывать по ходу урока. Что же, давайте начнем разбираться с реакциями!
Что вы должны уже уметь?
В этом блоке статье, я расскажу, как и обещал, что Вы должны УЖЕ уметь, чтобы понять то, что я буду докладывать дальше, про реакции опор.
Должны уметь находить сумму проекций сил
Да, это то, что Вам когда-то рассказывали на термехе, как собственно, и опорные реакции. Если Вы шарите немного в этих проекциях, то можете смело переходить к следующему пункту. Если же нет, то специально на этот случай, у меня есть другая статья, про проекции сил. Переходите, просвещайтесь, после чего, обязательно, возвращайтесь сюда!
Должны уметь составлять сумму моментов относительно точки
Немного теории! Познакомимся для начала с самим понятием момент силы. Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр. Проиллюстрирую написанное:
На изображении показано, как определить момент силы F, относительно точки O.
Так же, для моментов, нужно задаться каким-то правилом знаков. Сила относительно точки может поворачивать как по часовой стрелке, так и против нее. Я в своих уроках буду придерживаться такого правила:
- Если сила относительно точки крутит ПРОТИВ часовой стрелке, то момент положительный.
- Если она крутит ПО часовой стрелки, то соответственно момент отрицательный.
Причем, это правило условно! Какое правило Вы будете использовать совсем не важно, результат получите тот же самый. В теоретической механике, к примеру, делают также как я рассказываю.
Должны разбираться в основных видах опор
Теперь поговорим о самих опорах. В этой статье, будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.
Шарнирно-подвижная опора препятствует вертикальному перемещению элементу конструкции, в связи с чем, в ней, под действием внешней нагрузки возникает вертикальная реакция. Обозначают ее обычно как Ri, где i — точка крепления опоры.
Шарнирно-неподвижная опора имеет две реакции: вертикальную и горизонтальную. Так как препятствует перемещению в этих двух направлениях.
Вообще-то способов закрепления элементов конструкций и их условных обозначений достаточно много, но в рамках этой статьи их рассматривать не будем.
Примеры определения сил реакций опор
Вроде, всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнем с простейшей расчетной схемы балки.
Определение реакций опор для балки
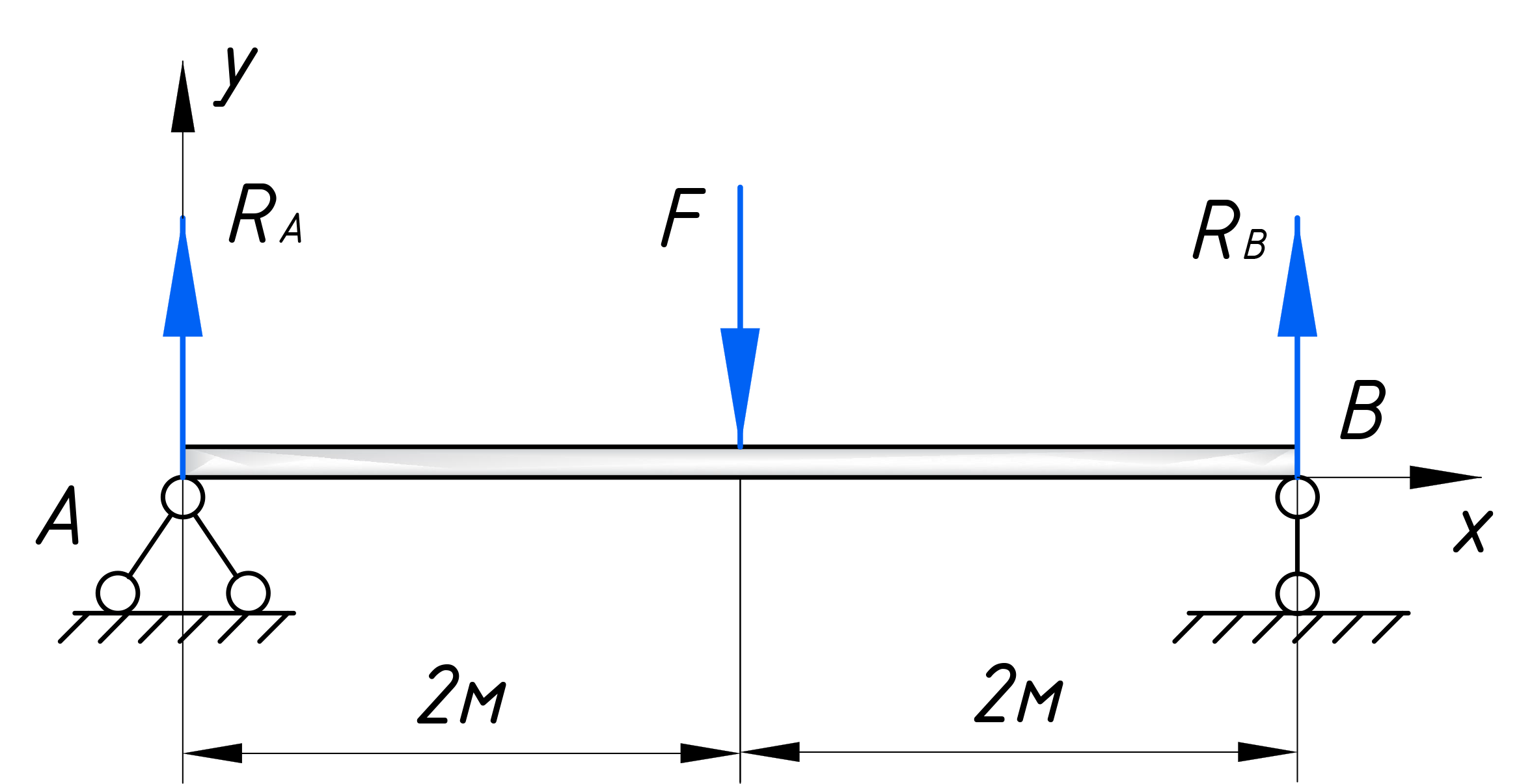
Возьмем балку на двух опорах, длиной 2 метра. Загрузим ее, посередине пролета, сосредоточенной силой:
Для этой расчетной схемы, выгодно записать такое условие равновесия: 
Введем систему координат, пустим ось х вдоль балки, а ось y вертикально. Обозначим реакции в опорах как RA и RB:
Запишем уравнение моментов, относительно точки А. Сила F поворачивает ПО часовой стрелки, записываем ее со знаком МИНУС и умножаем на плечо. Сила RB поворачивает ПРОТИВ часовой стрелки, пишем ее со знаком ПЛЮС и умножаем на плечо. Все это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB.
Первая реакция найдена! Вторая реакция находится аналогично, только теперь уравнение моментов записываем относительно другой точки:
После нахождения реакций, делаем проверку:
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно свернуть до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:
Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:
Определение опорных реакций для плоской рамы
Теперь, после освоения азов по расчету реакций, предлагаю выполнить расчет плоской рамы. Для примера, возьмем раму, загруженную всевозможными видами нагрузок:
Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим глобальную систему координат x и y.
Для такой расчетной схемы, лучше использовать следующую форму условий равновесия:

Записав второе уравнение, сумму проекций на ось х, найдем горизонтальную реакцию HA:
И, наконец, третье уравнение, позволит найти реакцию RA:
Не пугайтесь отрицательного значения реакции! Это значит, что при отбрасывании опоры, мы не угадали с направлением этой силы.
Расчет же показал, что RA, направленна в другую сторону:
В итоге, получили следующие реакции в опорах рамы:
Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумму будет равна нулю, то расчет выполнен верно:
Как видим, расчет реакций выполнен правильно!
На этом заканчиваю данный урок. Если у Вас остались какие-то вопросы по нахождению опорных реакций, смело задавайте их в комментариях к этой статье. Обязательно на все отвечу!
Спасибо за внимание! Если понравилась данная статья, расскажите о ней своим одногруппникам, не жадничайте 🙂
Также рекомендую подписаться на наши соц. сети, чтобы быть в курсе обновлений материалов проекта.
Как определить реакции опор или найти опорные реакции: для балки или рамы
Что такое реакция опоры или опорная реакция?
Реакция опоры или опорная реакция – это силовой фактор, возникающий в опоре, от действия на конструкцию внешней нагрузки. В опорах, как правило, возникают реактивные силы, которые для удобства ручного расчета раскладываются на две составляющие: вертикальную и горизонтальную проекции. В жестких заделках, которые ограничивают все степени свободы конструкций, в том числе поворот сечений, также могут появляться реактивные моменты.
Зачем определять реакции опор?
На элементы конструкций всегда наложены какие-то связи, в виде опор, жестких заделок, стержней, которые ограничивают степени свободы конструкций. Под действием внешней нагрузки в этих связях возникают реакции. И эти реакции опор нужно обязательно учитывать при расчетах на прочность, жесткость и т. д., так как они являются внешними нагрузками. Практически любая задача по сопромату начинается с нахождения реакций связей, именно поэтому статья будет одной из первых на этом сайте.
Пример определения опорных реакций для балки
Давайте рассмотрим пример, на котором я покажу как определяются реакции опор. Причем, постараюсь объяснить максимально просто, буквально на пальцах.
Возьмем простую балку, загруженную сосредоточенной силой F, под действием которой в опорах появляются реакции RA и RB. Также сразу вводим систему координат x, y:
Чтобы узнать численное значение эти реакций, воспользуемся первой формой уравнений равновесия:
Первое уравнение равновесия
Записываем первое уравнение. Так как оси x не параллельна ни одна из сил, то соответственно сумма проекций сил на эту ось будет равна нулю:
Таким будет первое уравнение для этой расчетной схемы.
Второе уравнение равновесия
Второе уравнение, связанно с проекциями на вертикальную ось. Здесь все намного лучше, все силы параллельны этой оси, а значит дадут проекции. Вопрос только с каким знаком, каждая сила пойдет в уравнение. Если направление силы, совпадает с направлением оси, то в уравнение она пойдет со знаком «плюс» (RA и RB). Если же сила направленна в противоположную сторону, как F, в нашем случае, то в уравнении будем записывать ее с минусом. Таким образом, получим второе уравнение равновесия:
Как видите, во втором уравнении у нас находится 2 неизвестные реакции. Чтобы, наконец, решить задачу, давайте запишем третье уравнение равновесия.
Третье уравнение равновесия
Это уравнение отличается от первых двух, так как тут речь идет о моментах. Напомню, момент – это произведение силы на плечо. В свою очередь, плечо – это перпендикуляр, опущенный от центра момента до линии действия силы. То есть это кратчайшее расстояние от центра момента до силы. В качестве центра моментов у нас назначена точка A, по условию сумма моментов всех сил должна быть равна нулю относительно этой точки.

Сила F, относительно точки А, создает момент равный:
Обратите внимание, плечо в данном случае равно 2 метрам. Кроме того, важен знак момента, для этого традиционно используется правило, которое продвинутым студентам известно еще с теоретической механики:
- Если сила, относительно произвольного центра, поворачивает ПРОТИВ часовой стрелки, то момент силы положительный;
- Если сила, относительно произвольного центра, поворачивает ПО часовой стрелке, то момент силы отрицательный.
Для силы F, как видите, момент отрицательный:
Реакция опоры — RB, создает момент равный RB · 4, так как сила поворачивает против часовой стрелки, то в уравнение записываем его со знаком плюс:
Вычисление реакций опор
Вот собственно и все, все уравнения составлены. Теперь осталось только решить их и найти искомые значения реакций опор (F=2 кН):
В этой статье, мы рассмотрели достаточно простой пример. Если вы хотите развить свои навыки по определению реакций опор, узнать различные хитрости по их нахождению, научится определять реакции, когда на конструкцию действуют силы под различными углами, учитывать в уравнениях сосредоточенные моменты и распределенную нагрузку, приступайте к изучению статьи – как определить реакции опор для балки.
Определение реакций опор балки – решение задачи
Как определить реакции опор балки
Пример решения задачи на определение реакций опор балки
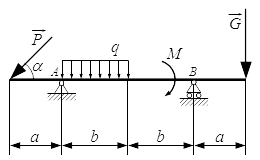
Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и B, вызываемые указанными нагрузками.
Дано:
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;
Решение задачи
Проводим оси x и y системы координат. Начало системы координат поместим в точку A . Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.
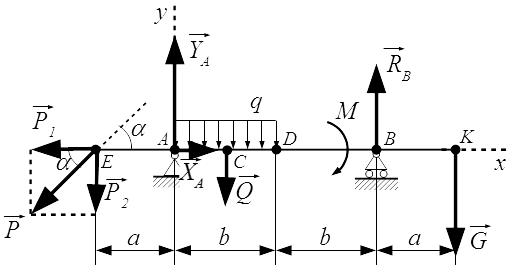
Отбрасываем опоры и заменяем их силами реакций.
В шарнире A , разложим силу реакции на составляющие и вдоль осей координат.
Реакция , в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.
Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
Н .
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м .
Уравнения равновесия для сил
Определяем проекции сил на оси координат.
Разложим силу на составляющие вдоль координатных осей:
.
Абсолютные значения составляющих:
.
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
.
Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
;
;
;
;
.
Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
;
;
;
(П1) .
Сумма проекций всех сил на ось y равна нулю:
;
;
;
(П2) .
Уравнения равновесия для моментов
Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и . Чтобы их определить, нам нужно составить еще одно уравнение.
Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A , перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.
Находим моменты сил относительно выбранной оси.
Силы , и пересекают ось. Поэтому их моменты равны нулю:
; ; .
Сила перпендикулярна плечу AB . Ее момент:
.
Поскольку, относительно оси A , сила направлена против часовой стрелки, то ее момент положительный.
Сила перпендикулярна плечу AK . Поскольку, относительно оси A , эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
.
Аналогичным способом находим моменты остальных сил:
;
.
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
.
Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
;
;
;
(П3) .
Решение уравнений равновесия
Итак, для трех неизвестных величин, мы получили три уравнения:
(П1) .
(П2) .
(П3) .
Решаем эти уравнения. Вычисляем расстояния.
м;
м;
м;
м.
Из уравнения (П1) находим:
Н.
Из уравнения (П3) находим:
Н.
Из уравнения (П2) имеем:
Н.
Абсолютное значение реакции опоры в точке A :
Н.
Проверка правильности решения
Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.
Возьмем ось, проходящую через точку E . Вычисляем сумму моментов сил относительно этой оси:
.
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н . Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм . Мы получили значение -0,03 Нм . Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.
Второй способ решения
Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.
Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
.
Вычисляем моменты сил относительно оси B .
; ; ;
;
;
;
;
.
Сумма моментов сил относительно оси B равна нулю:
;
;
;
(П4) ;
Итак, вторым способом, мы также имеем три уравнения:
(П1) .
(П3) ;
(П4) .
Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):
Н.
Значение реакции совпало со значением, полученным первым способом из уравнения (П2).
Автор: Олег Одинцов . Опубликовано: 14-10-2017 Изменено: 28-12-2021
[spoiler title=”источники:”]
http://sopromats.ru/sopromat/opredelenie-reaktsiy-opor/
http://1cov-edu.ru/mehanika/statika/opredelenie-reaktsij-opor-balki/
[/spoiler]
Содержание:
- Задача с решением 75-14.
- Задача с решением 76-14;
- Задача с решением 77-14.
- Задача с решением 79-14.
- Задача с решением 80-14*.
- Задача с решением 82-14.
- Определение реакций в общем случае
- Пример с решением 58.
- Пример с решением 59.
Как известно, любую плоскую систему сил можно привести к главному вектору 
Если же система сил уравновешена (тело, находящееся под действием такой системы сил, либо неподвижно, либо равномерно вращается около неподвижной оси, либо находится в равномерном и прямолинейном поступательном движении), то 
Эти равенства выражают два необходимых и достаточных условия равновесия любой системы сил.
Для произвольной плоской системы сил из этих двух условий непосредственно получаем три уравнения равновесия:
Первое и второе выражения — уравнения проекций — образуются из условия — 
Если на тело действует система параллельных сил, то уравнений равновесия получится только два: уравнение проекций на ось, параллельную силам, и уравнение моментов
При решении некоторых задач одно или оба уравнения проекций целесообразно заменить уравнениями моментов относительно каких-либо точек, т. е. систему уравнений равновесия можно представить в таком виде:
или
В первом случае линия, проходящая через точки 





Для системы параллельных сил соответственно получаем два уравнения моментов:
В этом случае точки 

В задачах, решаемых при помощи уравнений равновесия, обычно рассматриваются тела, находящиеся в состоянии покоя, тогда система сил, действующих на это тело, уравновешена.
Возможно вам будут полезны данные страницы:
Силы, действующие на тело, делятся на две группы. Одна группа сил называется нагрузками (активные силы), вторая группа сил называется реакциями связей (пассивные силы).
Нагрузки, как правило, бывают заданы. Они имеют числовое значение, точку приложения к телу и направление их действия.
В рассматриваемых ниже задачах используются лишь три разновидности нагрузок: сосредоточенные силы, равномерно распределенные силы* и пары сил (статические моменты)**.
Сосредоточенными называются силы, приложенные к точке тела. Если, например, на тело действуют нагрузки 

на рис. 91, а, действия этих нагрузок можно считать приложенными соответственно к точкам 

Равномерно распреде.генные нагрузки, например кирпичная кладка (рис. 92, а), или собственный вес однородного тела (бруса, балки) постоянного поперечного сечения по всей его длине задается при помощи двух параметров —интенсивности 

- Пара сил (сосредоточенный момент), например, может быть образована двумя одинаковыми грузами
действующими на тело так, как показано на рис. 93, а. Условное изображение пары сил, действующей на тело, показано на рис. 93, б.
Очень часто в каком-либо месте тела возникает совместное действие сосредоточенной силы и момента. Пусть, например, груз 
в каком-либо теле (рис. 94, а). Если перенести действие силы в точку 
Как правило, в задачах по статике реакции связей —искомые величины. Для каждой искомой реакции связи обычно необходимо
знать ее направление и числовое значение (модуль).
Направления реакций идеальных связей —связей без трения — определяют в зависимости от вида связи по следующим правилам.
1. При свободном опирании тела на связь реакция связи направлена от связи к телу перпендикулярно либо к поверхности тела (


Во всех этих случаях связь препятствует движению тела в одном направлении —перпендикулярном к опорной поверхности.
2. Если связями являются нити, цепи, тросы (гибкая связь), то они препятствуют движению тела только будучи натянутыми.
Поэтому реакции нитей, цепей, тросов всегда направлены вдоль их самих в сторону от тела к связи (

3. Если связь тела с какой-либо опорной поверхностью осуществляется при помощи подвижного шарнира (рис. 97), то его реакция направлена перпендикулярно к опорной поверхности. Таким
образом, подвижный шарнир (т. е. шарнир, ось которого может передвигаться вдоль опорной поверхности) представляет собой конструктивный вариант свободного опирания.
4. Если соединение тела со связью осуществляется при помощи неподвижного шарнира (рис. 98), то определить непосредственно направление реакции нельзя, за исключением тех частных случаев, которые описаны ниже.
Шарнирное соединение препятствует поступательному перемещению тела во всех направлениях в плоскости, перпендикулярной к оси шарнира. Направление реакции неподвижного шарнира может быть любым в зависимости от направления действия остальных сил. Потому сначала определяют две взаимно перпендикулярные составляющие 





Направление реакции неподвижного шарнира непосредственно определяют в двух следующих случаях:
а) если, кроме реакции шарнира, все остальные силы (нагрузки и реакция другой связи) образуют систему параллельных сил, то реакция неподвижного шарнира также параллельна всем силам;
б) если, кроме реакции шарнира, на тело действуют еще только две непараллельные силы, то линия действия реакции неподвижного шарнира проходит через ось шарнира и точку пересечения двух других сил (задачи 47-9 и 48-9).
5. Движение тела может быть ограничено жесткой заделкой в какой-либо опоре (рис. 99). В этом случае даже одна жесткая заделка обеспечивает равновесие тела при любых нагрузках.
Так же как и неподвижный шарнир, жесткая заделка препятствует поступательному перемещению тела. Поэтому направление
ее реакции заранее определить нельзя и сначала определяют составляющие 


Таким образом, если опорой тела является жесткая заделка, то со стороны последней на тело действуют реакция заделки, которую можно заменить двумя взаимно перпендикулярными составляющими, и момент заделки.
6. Иногда тело удерживается в равновесии при помощи жестких стержней, шарнирно соединенных с телом и с опорами (рис. 100). В отличие от гибкой связи (см. п. 2) такие стержни могут испытывать не только растяжение, но и сжатие.
Возможны и такие случаи, когда нельзя заранее установить, какие стержни растянуты, а какие сжаты. Поэтому при составлении уравнений равновесия исходят из того, что все стержни растянуты. Если же некоторые стержни окажутся в действительности сжатыми, tq в результате решения числовые значения реакций таких стержней получатся отрицательными.
Задача с решением 75-14.
На горизонтальную балку 




Решение.
1. Рассмотрим равновесие балки 




2. Освободив правый конец балки от связи и заменив ее действие реакцией 
параллельных сил. Поэтому, если освободить и левый конец балки от шарнирно неподвижной опоры, то ее реакция будет также направлена вертикально (рис. 101, б).
3. Составим систему уравнений равновесия вида (5), приняв для одного уравнения за центр моментов точку 
4. Решая уравнения, из (1) находим
из (2)

Подставляя в это уравнение числовые значения, получаем тождество

Значит задача решена правильно.
Реакции опор:

При решении задач рекомендуется не пренебрегать проверкой. От правильности определения реакций опор зависит правильность всего остального решения или расчета.
Задача с решением 76-14;
На консольную балку, имеющую в точке 




Решение.
1. Рассматривая находящуюся в равновесии балку 






2. Освобождаем балку от связей и заменим их действие реакциями. В месте шарнирно-подвижной опоры 


3. Для полученной системы из пяти сил, произвольно расположенных в плоскости, составим систему уравнений равновесия вида (3), расположив ось 

4. Решаем полученные уравнения. Из (1)
Так как
то из (2)
Замечая, что
из (3) получаем
Знак минус, получившийся в последнем случае, показывает, что 
5. При необходимости реакцию 

Модуль реакции шарнира 
Направление реакции 
откуда
6. Проверим правильность решения задачи. Так как при решении не использовано уравнение проекций на ось 
Уравнение составлено по рис. 102, б.
После подстановки в это уравнение известных значений получим:
В данном случае, проверка решения при помощи уравнения проекций не дает возможности установить правильность определения полной реакции 


Подставляем в это уравнение числовые значения, имея в виду, что
Расхождение в результатах, равное 
В следующих задачах проверка решения не приводится и ее рекомендуется производить самостоятельно.
Задача с решением 77-14.
Горизонтальная балка имеет в точке 






Решение.
1. Так же как и в задаче 75-14, балка нагружена двумя параллельными силами, но в отличие от этой задачи здесь реакция подвижного шарнира 


2. Расположив оси 

3. Решаем полученные уравнения. Из уравнения (3) находим
Из уравнения (2) находим
Из уравнения (1) находим
Таким образом, реакция шарнира
а составляющие реакции шарнира
и
4. Проверку решения производим при помощи уравнения моментов относительно точки 
Следующую задачу рекомендуется решить самостоятельно.
Задача с решением 79-14.
На консольную балку, имеющую в точке 





Решение.
1. В этой задаче, кроме сосредоточенной силы 





2. Так же как в задаче 75-14, реакция 

3. Составим два уравнения моментов относительно точек 
Из уравнения (1)
Отрицательное значение реакции 


Из уравнения (2) находим
Таким образом, реакция шарнира 



5. Для проверки решения можно использовать уравнение проекций на вертикальную ось.
Задача с решением 80-14*.
На двухконсольную балку с шарнирно-неподвижной опорой в точке 




Решение.
1. В отличие от предыдущей задачи здесь, кроме сосредоточенной силы и равномерно распределенной-нагрузки, равнодействующая 



2. После освобождения балки от связей и замены связей их реакциями 

3. Составим два уравнения моментов относительно точек 
4. Решая эти уравнения, находим, что

Задача с решением 82-14.
Жестко заделанная у левого конца консольная балка 



Решение.
1. На балку действуют три нагрузки: в точке 





2. Равновесие балки обеспечивается жесткой заделкой у точки 








3. Составим уравнения равновесия — уравнение проекции на оси 

4. Из уравнения (1)
а это означает, что горизонтальная составляющая реакции заделки 

Выше найдено, что 


Из уравнения (3)
Таким образом,

5. Проверку правильности решения можно произвести при помощи уравнения моментов относительно точки 

Следующую задачу рекомендуется решить самостоятельно.
Определение реакций в общем случае
Один из способов определения реакций связей был уже рассмотрен при изучении уравнений равновесия с множителями Лагранжа, когда связи задаются неявными уравнениями или неравенствами. В общем же случае связи, наложенные на систему материальных точек, всегда могут быть заменены соответствующими силами реакций, действие которых эквивалентно действию связей. После такой замены система может рассматриваться как свободная от связей, но подверженная действию как активных, так и пассивных сил. Принцип Бернулли для такой свободной системы дает необходимые и достаточные условия равновесия в виде уравнения
где 



Последние уравнения и служат для определения реакций связи. Если по условиям задачи требуется определять не все, а лишь некоторые силы реакции, то система освобождается только от тех связей, реакции которых необходимо определить. Освобождая систему от связей, тем самым добавляем ей возможные перемещения, которые раньше не допускались связями и на которых будут работать реакции освобожденных связей.
Подсчитывая сумму работ активных сил и сил реакции связей на освобожденном перемещении, получим условия для определения реакций связи.
Пример с решением 58.
Исследовать условия равновесия твердого тела, у которого закреплены две точки 



Решение. Выберем начало неподвижной системы координат в точке 



где 

Для определения реакции в точке 





так что
Из принципа Бериулли для освобожденного твердого тела будем иметь
подставляя сюда значения вариаций координат, получим
или, после сокращения на
где 


Точно таким же путем можно получить реакцию 

так что
Подставляя найденные значения вариаций координат в общее уравнение статики, получим
или
Реакция 


Пример с решением 59.
На гладкой горизонтальной плоскости лежат несколько одинаковых однородных цилиндрических труб. Чтобы трубы не раскатывались, они подпираются двумя брусьями 

Решение. Для определенности рассмотрим пятнадцать труб, расположенных, как указано на чертеже. Чтобы избежать рассмотрения статически неопределимой задачи, предположим, что расстояние между брусками 



где 


Будем предполагать сначала, что последние условия выполняются лишь в виде неравенств. Определив вертикальные координаты центров труб
Запишем принцип Торричелли для системы с удерживающими связями:
или, после подстановки значений
где величины 

Определив из последнего уравнения
и подставив это значение в равенство (с), получим уравнение для независимых параметров
Приравнивая нулю коэффициенты при 

которые можно переписать в виде
Принимая во внимание неравенства (b), получим условия равновесия
Величины

При 
В самом деле,
При уменьшении 

Лишь при выполнении этого неравенства нижине трубы в положении равновесия не будут касаться друг друга. Уменьшая 

Рассмотрим теперь только такие состояния системы, для которых выполняются условия
Уравнение связи для возможных перемещений (d) приобретает вид
Общее уравнение статики для рассматриваемой системы перепишем в виде
Система линейных относительно 

или
Отсюда следует, что в положении равновесия должно быть
Тогда из уравнения связи (а) находим
Как видно из последнего соотношения, при 









и подсчитаем работу всех сил, в том числе и работу силы 
откуда следует
Если 

Заметим, что на рассматриваемом перемещении опускаются вниз четыре трубы. У остальных труб вертикальные координаты не изменяются. Если обозначить через 

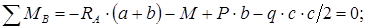






































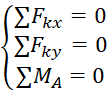
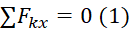
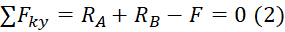
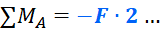
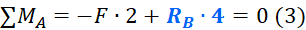
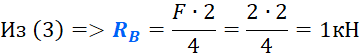
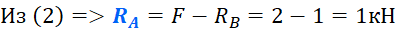









 действующими на тело так, как показано на рис. 93, а. Условное изображение пары сил, действующей на тело, показано на рис. 93, б.
действующими на тело так, как показано на рис. 93, а. Условное изображение пары сил, действующей на тело, показано на рис. 93, б.


























































































































