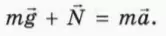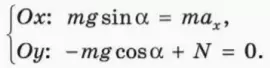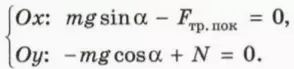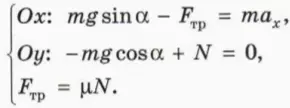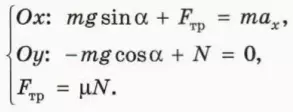Как найти реакцию опоры на наклонной плоскости

Как найти реакцию опоры на наклонной плоскости

Сила реакции опоры — это сила, с которой опора действует на тело. Она направлена перпендикулярно поверхности, поэтому такую силу называют силой нормальной реакции. Обозначают ее символом N и измеряют в Ньютонах.

Тело находится на выпуклой или вогнутой поверхности

Рассмотрим рисунок 1. Тело находится на опоре и давит на нее своим весом. Опора реагирует на воздействие тела и отвечает ему силой (vec{N}). Эта сила направлена перпендикулярно поверхности, вдоль вектора нормали, поэтому ее называют нормальной силой.

Примечания:

  • Нормаль – значит, перпендикуляр.
  • Искривленную, т.е., выпуклую, или вогнутую поверхность, можно считать частью сферы. Центр сферы – точка, она находится внутри сферы, от этой точки к поверхности сферы можно провести радиус.

(vec{N} left( H right) ) – сила, с которой опора действует на тело.

Сферическое тело находится на выпуклой – а) и вогнутой – б) поверхности. Поверхность - опора отвечает телу силой реакции N

Рис. 1. Тело (шар) опирается на выпуклую – а) и вогнутую – б) поверхность. А поверхность реагирует на вес тела силой нормальной реакции

Когда тело находится на выпуклой поверхности (рис. 1а), реакция направлена вдоль радиуса от центра сферы наружу, за ее пределы.

Если же тело находится на вогнутой части (рис. 1б) поверхности, реакция (vec{N}) направлена по радиусу внутрь сферической поверхности к ее центру.

Тело опирается на поверхность в двух точках

На рисунках 2а и 2б изображено продолговатое тело (к примеру, стержень), опирающееся на поверхности двумя своими точками.

Стержень опирается на поверхность двумя точками, в каждой из точек сила реакции N расположена перпендикулярно поверхности

Рис. 2. Однородный стержень опирается на поверхность двумя точками, в каждой из точек сила реакции располагается перпендикулярно поверхности

В точках соприкосновения поверхность отвечает телу силой (vec{N}) своей реакции. Видно, что в каждая сила реакции направлена перпендикулярно поверхности.

Cилы реакции (vec{N_{1}}) и (vec{N_{2}})  имеют различные направления и в общем случае не равны по модулю.

[large vec{N_{1}} ne vec{N_{2}}]

Примечание: Сила — это вектор. Между векторами можно ставить знак равенства, только, когда совпадают характеристики векторов.

Как рассчитать силу нормальной реакции

Пусть тело давит на опору своим весом. В местах соприкосновения тела с опорой наблюдается упругая деформация. При этом опора стремится избавиться от возникшей деформации и вернуться в первоначальное состояние. Силы, с которыми опора упруго сопротивляется воздействию тела, имеют электромагнитную природу. Когда сближаются электронные оболочки атомов тела и опоры, между ними возникает сила отталкивания. Она и является силой реакции опоры на воздействие тела.

Примечание: Сила реакции (vec{N}) распределяется по всей площади соприкосновения тела и опоры. Но для удобства ее обычно считают сосредоточенной силой. Ее изображают на границах соприкасающихся поверхностей исходящей из точки, расположенной под центром масс тела.

Для того, чтобы рассчитать силу реакции, нужно понимать законы Ньютона, уметь составлять силовые уравнения и знать, что такое равнодействующая.

На рисунке 3 изображены тела, находящиеся на горизонтальной – а) и наклонной – б) поверхностях.

Силу реакции рассчитывают, составляя силовые уравнения для сил, расположенных перпендикулярно поверхностям

Рис. 3. Тело опирается на поверхность горизонтальную – а) и наклонную – б), составляя силовые уравнения для сил, расположенных перпендикулярно соприкасающимся поверхностям, рассчитывают силу реакции опоры

Рассмотрим подробнее рисунок 3а. Тело на горизонтальной поверхности находится в покое. Значит, выполняются условия равновесия тела.

По третьему закону Ньютона, сила, с которой тело действует на опору, равна по модулю весу тела и направлена противоположно весу.

[large boxed{ N = m cdot g }]

(m vec{g} left( H right) ) – сила, с которой тело действует на опору;

(vec{N} left( H right) ) – сила, с которой опора отвечает телу;

Рисунок 3б иллюстрирует тело на наклонной поверхности. Перпендикулярно соприкасающимся поверхностям проведена ось Oy. Проекция силы (m vec{g}) на ось — это (mg_{y}), она будет направлена противоположно реакции опоры (vec{N}) и численно равна ей.

Примечание: Выражение «численно равна» нужно понимать, как «длины векторов равны».

[large boxed{ N = m cdot g cdot cos(alpha) }]

(alpha  left(text{рад} right) ) – угол между силой (mg) и осью Oy.

Итоги

  1. Сила, с которой опора сопротивляется воздействию тела, называется силой реакции опоры, она имеет электромагнитную природу.
  2. Ее, как и любую силу, измеряют в Ньютонах, обозначают так: (vec{N}).
  3. Реакция опоры направлена перпендикулярно поверхности, поэтому ее называют силой нормальной реакции.
  4. Сила (vec{N}) распределена по площади соприкосновения, но для удобства ее обычно считают сосредоточенной силой. Ее изображают исходящей из точки, расположенной под центром масс тела на границах между поверхностями тела и опоры.
  5. Чтобы рассчитать силу реакции, нужно знать законы Ньютона, уметь составлять силовые уравнения и понимать, что такое равнодействующая.
Источник


Загрузить PDF


Загрузить PDF

Сила нормальной реакции – сила, действующая на тело со стороны опоры (или сила, противодействующая другим силам в любом данном сценарии). Ее вычисление зависит от конкретных условий и известных величин.

  1. Изображение с названием Find Normal Force Step 1

    1

    В случае тела, покоящегося на горизонтальной поверхности, сила нормальной реакции противодействует силе тяжести.

    • Представьте себе тело, лежащее на столе. Сила тяжести действует по направлению к земле, но так как тело не разрушает стол и не падает на землю, существует некоторая противодействующая сила. Эта сила и есть сила нормальной реакции.

  2. Изображение с названием Find Normal Force Step 2

    2

    Формула для нахождения силы нормальной реакции для тела, покоящегося на горизонтальной поверхности: N = m*g[1]

    • В этой формуле N – сила нормальной реакции, m – масса тела, g – ускорение свободного падения.
    • В случае тела, находящегося в состоянии покоя на горизонтальной поверхности и на которое не действуют внешние силы, сила нормальной реакции равна весу. Для сохранения тела в состоянии покоя, сила нормальной реакции должна быть равна силе тяжести, действующую на опору. В данном случае сила тяжести, действующая на опору, является весом, то есть произведением массы тела на ускорение свободного падения.
    • Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г.

  3. Изображение с названием Find Normal Force Step 3

    3

    Умножьте массу тела на ускорение свободного падения. Вы найдете вес, который в данном случае равен силе нормальной реакции (так как тело в находится в покое на горизонтальной поверхности).

    • Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.[2]
    • Пример: вес = m*g = 4,2*9,8 = 41,16 Н.

  4. Изображение с названием Find Normal Force Step 4

    4

    Запишите ответ.

    • Пример: сила нормальной реакции равна 41,16 Н.

    Реклама

  1. Изображение с названием Find Normal Force Step 5

    1

    Формула для вычисления силы нормальной реакции, действующей на тело, покоящееся на наклонной поверхности: N = m * g * cos(x).[3]

    • В этой формуле N – сила нормальной реакции, m – масса тела, g – ускорение свободного падения, х – угол наклона поверхности.
    • Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г, находящегося на наклонной поверхности с углом наклона 45 градусов.

  2. Изображение с названием Find Normal Force Step 6

    2

    Найдите косинус угла. Косинус угла равен отношению прилежащей (к этому углу) стороны к гипотенузе. [4]

    • Косинус зачастую вычисляется с помощью калькулятора, но вы также можете найти его вручную.
    • Пример: соs(45) = 0,71.

  3. Изображение с названием Find Normal Force Step 7

    3

    Найдите вес. Вес равен произведению массы тела на ускорение свободного падения.

    • Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.
    • Пример: вес = m*g = 4,2*9,8 = 41,16 Н.

  4. Изображение с названием Find Normal Force Step 8

    4

    Перемножьте два найденных значения. Для вычисления силы нормальной реакции умножьте вес на косинус угла наклона.

    • Пример: N = m * g * cos(x) = 41,16 * 0,71 = 29,1

  5. Изображение с названием Find Normal Force Step 9

    5

    Запишите ответ.

    • Обратите внимание, что в случае тела, находящегося на наклонной поверхности, сила нормальной реакции меньше веса.
    • Пример: сила нормальной реакции равна 29,1 Н.

    Реклама

  1. Изображение с названием Find Normal Force Step 10

    1

    Формула для вычисления силы нормальной реакции в случае, когда внешняя сила, действующая на тело, направлена вниз: N = m * g + F * sin(x).

    • В этой формуле N – сила нормальной реакции, m – масса тела, g – ускорение свободного падения, х – угол между горизонтальной поверхностью и направлением действия внешней силы.
    • Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г, на которое действует внешняя сила 20,9 Н под углом 30 градусов.

  2. Изображение с названием Find Normal Force Step 11

    2

    Найдите вес. Вес равен произведению массы тела на ускорение свободного падения.

    • Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.
    • Пример: вес = m*g = 4,2*9,8 = 41,16 Н.

  3. Изображение с названием Find Normal Force Step 12

    3

    Найдите синус угла. Синус угла равен отношению противолежащей (к этому углу) стороны к гипотенузе. [5]

    • Пример: sin(30) = 0,5.

  4. Изображение с названием Find Normal Force Step 13

    4

    Умножьте синус угла на внешнюю силу.

    • Пример: 0,5 * 20,9 = 10,45

  5. Изображение с названием Find Normal Force Step 14

    5

    Сложите это значение и вес. Вы найдете силу нормальной реакции.

    • Пример: 10,45 + 41,16 = 51,61

  6. Изображение с названием Find Normal Force Step 15

    6

    Запишите свой ответ. Обратите внимание, что в случае тела, на которое действует сила, направленная вниз, сила нормальной реакции больше веса.

    • Пример: сила нормальной реакции равна 51,61 Н.

    Реклама

  1. Изображение с названием Find Normal Force Step 16

    1

    Формула для вычисления силы нормальной реакции в случае, когда внешняя сила, действующая на тело, направлена вверх: N = m * g – F * sin(x).

    • В этой формуле N – сила нормальной реакции, m – масса тела, g – ускорение свободного падения, х – угол между горизонтальной поверхностью и направлением действия внешней силы.
    • Пример: найдите силу нормальной реакции, действующую на тело массой 4,2 г, на которое действует внешняя сила 20,9 Н под углом 50 градусов.

  2. Изображение с названием Find Normal Force Step 17

    2

    Найдите вес. Вес равен произведению массы тела на ускорение свободного падения.

    • Обратите внимание, что ускорение свободного падения на поверхности Земли является постоянной величиной: g = 9,8 м/с2.
    • Пример: вес = m*g = 4,2*9,8 = 41,16 Н.

  3. Изображение с названием Find Normal Force Step 18

    3

    Найдите синус угла. Синус угла равен отношению противолежащей (к этому углу) стороны к гипотенузе. [6]

    • Пример: sin(50) = 0,77.

  4. Изображение с названием Find Normal Force Step 19

    4

    Умножьте синус угла на внешнюю силу.

    • Пример: 0,77 * 20,9 = 16,01

  5. Изображение с названием Find Normal Force Step 20

    5

    Вычтите это значение из веса. Вы найдете силу нормальной реакции.

    • Пример: 41,16 – 16,01 = 25,15

  6. Изображение с названием Find Normal Force Step 21

    6

    Запишите свой ответ. Обратите внимание, что в случае тела, на которое действует сила, направленная вверх, сила нормальной реакции меньше веса.

    • Пример: сила нормальной реакции равна 25,15 Н.

    Реклама

  1. Изображение с названием Find Normal Force Step 22

    1

    Формула для вычисления силы трения: F = μ * N.

    • В этой формуле F – сила трения, μ – коэффициент трения, N – сила нормальной реакции.
    • Коэффициент трения характеризует силу, необходимую для движения одного материала по поверхности другого.

  2. Изображение с названием Find Normal Force Step 23

    2

    Перепишите формулу, обособив силу нормальной реакции. Если вам даны сила трения и коэффициент трения, вы можете найти силу нормальной реакции по формуле: N = F / μ.

    • Обе части исходной формулы были разделены на μ, в результате чего сила нормальной реакции была обособлена на одной стороне, а сила трения и коэффициент трения – на другой.
    • Пример: найдите силу нормальной реакции, когда сила трения равна 40 Н, а коэффициент трения равен 0,4.

  3. Изображение с названием Find Normal Force Step 24

    3

    Разделите силу трения на коэффициент трения. Вы найдете силу нормальной реакции.

    • Пример: N = F/μ = 40/0,4 = 100

  4. Изображение с названием Find Normal Force Step 25

    4

    Запишите ответ. Вы можете проверить ответ, подставив его в исходную формулу для вычисления силы трения.

    • Пример: сила нормальной реакции равна 100 Н.

    Реклама

Что вам понадобится

  • Карандаш
  • Бумага
  • Калькулятор

Об этой статье

Эту страницу просматривали 59 392 раза.

Была ли эта статья полезной?

Источник

Друзья, сегодня разберем с вами задачку на стыке механики и кинематики. Потренируемся в нахождение работ различных сил, посмотрим на связь этих работ с потенциальной и кинетической энергиями. Рассмотрим это на примере следующей задачи…

Задача

Тело массой 3 кг под действием силы F перемещается вниз по наклонной плоскости на расстояние L = 5 м, расстояние тела от поверхности Земли при этом уменьшается на h = 3 м. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 20 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F ? (Ответ дайте в джоулях.) Ускорение свободного падения примите равным 10 м/с², коэффициент трения μ = 0.5.

Решение:

Любая задача по физике начинается с рисунка, сделаем его:

Рисунок к задаче
Рисунок к задаче

Из геометрии задачи и наклона плоскости сразу найдем косинус и синус нужного нам угла:

Нахождение работ всех сил при движении тела по наклонной плоскости

1. Зная высоту, мы сразу можем найти изменение потенциальной энергии груза при таком съезжании с наклонной плоскости. Сразу заметим, что работа силы тяжести и есть изменение потенциальной энергии груза:

Нахождение работ всех сил при движении тела по наклонной плоскости

2. Работу силы F можно найти сразу, посчитав до числа. Т.е. в этой задаче дается избыточный набор параметров, это делается для того, чтобы сбить с толку решающего, увести по ложному пути или заставить больше прорешать 🙂 Но мы специально этим займемся:

Нахождение работ всех сил при движении тела по наклонной плоскости

3. Найдем работу силы трения скольжения. Для этого нам сначала понадобится найти нормальную реакцию опоры.

Нахождение работ всех сил при движении тела по наклонной плоскости

4. Работа нормальной реакции опоры всегда равна нулю, т.к. движение происходит вдоль наклонной плоскости, а реакция опоры всегда ей перпендикулярна, т.е. между векторами силы и перемещения угол в 90 градусов, что обнуляет скалярное произведение.

5. Вспомним теорему о кинетической энергии. Изменение кинетической энергии мате­риальной точки на некотором ее перемещении равно алгебраической сумме работ всех действующих на эту точку сил на том же перемещении.

Найдем скорость в конце наклонной плоскости двумя способами:
1. Из закона об изменении кинетической энергии
2. Из кинематики, предварительно найдя ускорение тела

Нахождение работ всех сил при движении тела по наклонной плоскости

Выражение для скорости сошлись, значит всё хорошо.

Задача решена. Знаете другие способы решить задачу? Напишите в комментариях 🙂

Понравилась заметка? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в Instagram
Репетитор IT mentor в telegram

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 сентября 2021 года; проверки требует 1 правка.

Си́ла норма́льной реа́кции (иногда нормальная реакция опоры) — сила, действующая на тело со стороны опоры и направленная перпендикулярно («по нормали», «нормально») к поверхности соприкосновения. Распределена по площади зоны соприкосновения. Подлежит учёту при анализе динамики движения тела. Фигурирует в законе Амонтона — Кулона.

Одним из часто обсуждаемых примеров для иллюстрации силы нормальной реакции является случай нахождения небольшого тела на наклонной плоскости. При этом для простоты считается, что сила реакции приложена в одной точке соприкосновения.

Для расчёта в этом случае используется формула

N — сила нормальной реакции, f — сила трения покоя

|vec N|= mg cos theta,

где |vec N| — модуль вектора силы нормальной реакции, m — масса тела, g — ускорение свободного падения, theta  — угол между плоскостью опоры и горизонтальной плоскостью.

Выписанной формулой отражается тот факт, что вдоль направления, перпендикулярного наклонной плоскости, движения нет. Это значит, что величина силы нормальной реакции равна проекции силы тяжести mg на указанное направление.

Из закона Амонтона — Кулона следует, что для модуля вектора силы нормальной реакции при скольжении тела справедливо соотношение:

{displaystyle |{vec {N}}|={frac {|{vec {F}}|}{mu }},}

где {vec {F}} — сила трения скольжения, а mu  — коэффициент трения.

Cила трения покоя (именно она, а не |vec{F}|, действует при отсутствии движения, см. рис.) вычисляется по формуле |vec f|= mg sin theta. Можно экспериментально найти такое значение угла {displaystyle theta =theta _{crit}}, при котором тело приходит в движение, то есть трение покоя сменяется трением скольжения. В этих условиях сила трения покоя будет равна силе трения скольжения: {displaystyle mgsin theta _{crit}=mu mgcos theta _{crit}}. Отсюда выражается коэффициент трения: {displaystyle mu =mathrm {tg} theta _{crit}}.

Литература[править | править код]

  • Сивухин Д. В. Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — 520 с.
Источник

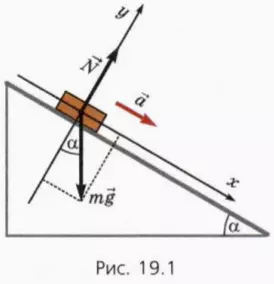
1. Тело на гладкой наклонной плоскости

Напомним: когда говорят о гладкой поверхности, подразумевают, что трением между телом и этой поверхностью можно пренебречь.

На тело массой m, находящееся на гладкой наклонной плоскости, действуют сила тяжести m и сила нормальной реакции (рис. 19.1).

Удобно ось x направить вдоль наклонной плоскости вниз, а ось y – перпендикулярно наклонной плоскости вверх (рис. 19.1). Угол наклона плоскости обозначим α.

Уравнение второго закона Ньютона в векторной форме имеет вид

? 1. Объясните, почему справедливы следующие уравнения:

? 2. Чему равна проекция ускорения тела на ось x?

? 3. Чему равен модуль силы нормальной реакции?

? 4. При каком угле наклона ускорение тела на гладкой плоскости в 2 раза меньше ускорения свободного падения?

? 5. При каком угле наклона плоскости сила нормальной реакции в 2 раза меньше силы тяжести?

При выполнении следующего задания полезно заметить, что ускорение тела, находящегося на гладкой наклонной плоскости, не зависит от направления начальной скорости тела.

? 6. Шайбу толкнули вверх вдоль гладкой наклонной плоскости с углом наклона α. Начальная скорость шайбы v0.
а) Какой путь пройдет шайба до остановки?
б) Через какой промежуток времени шайба вернется в начальную точку?
в) С какой скоростью шайба вернется в начальную точку?

? 7. Брусок массой m находится на гладкой наклонной плоскости с углом наклона α.
а) Чему равен модуль силы, удерживающей брусок на наклонной плоскости, если сила направлена вдоль наклонной плоскости? Горизонтально?
б) Чему равна сила нормальной реакции, когда сила направлена горизонтально?

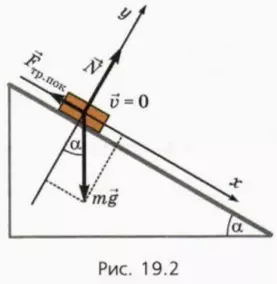
2. Условие покоя тела на наклонной плоскости

Будем теперь учитывать силу трения между телом и наклонной плоскостью.

Если тело покоится на наклонной плоскости, на него действуют сила тяжести m, сила нормальной реакции и сила трения покоя тр.пок (рис. 19.2).

Сила трения покоя направлена вдоль наклонной плоскости вверх: она препятствует соскальзыванию бруска. Следовательно, проекция этой силы на ось x, направленную вдоль наклонной плоскости вниз, отрицательна:

Fтр.пок x = –Fтр.пок

? 8. Объясните, почему справедливы следующие уравнения:

? 9. На наклонной плоскости с углом наклона α покоится брусок массой m. Коэффициент трения между бруском и плоскостью равен μ. Чему равна действующая на брусок сила трения? Есть ли в условии лишние данные?

? 10. Объясните, почему условие покоя тела на наклонной плоскости выражается неравенством

μ ≥ tgα.

Подсказка. Воспользуйтесь тем, что сила трения покоя удовлетворяет неравенству Fтр.пок ≤ μN.

Последнее неравенство можно использовать для измерения коэффициента трения: угол наклона плоскости плавно увеличивают, пока тело не начинает скользить по ней (см. лабораторную работу 4).

? 11.Лежащий на доске брусок начал скользить по доске, когда ее угол наклона к горизонту составил 20º. Чему равен коэффициент трения между бруском и доской?

? 12. Кирпич массой 2,5 кг лежит на доске длиной 2 м. Коэффициент трения между кирпичом и доской равен 0,4.
а) На какую максимальную высоту можно поднять один конец доски, чтобы кирпич не сдвинулся?
б) Чему будет равна при этом действующая на кирпич сила трения?

Сила трения покоя, действующая на тело, находящееся на наклонной плоскости, не обязательно направлена вдоль плоскости вверх. Она может быть направлена и вниз вдоль плоскости!

? 13. Брусок массой m находится на наклонной плоскости с углом наклона α. Коэффициент трения между бруском и плоскостью равен μ, причем и μ < tg α. Какую силу надо приложить к бруску вдоль наклонной плоскости, чтобы сдвинуть его вдоль наклонной плоскости:
а) вниз? б) вверх?

3. Движение тела по наклонной плоскости с учетом трения

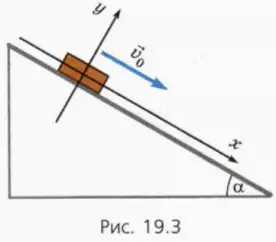
Пусть теперь тело скользит по наклонной плоскости вниз (рис. 19.3). При этом на него действует сила трения скольжения, направленная противоположно скорости тела, то есть вдоль наклонной плоскости вверх.

? 15. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 16. Чему равна проекция ускорения тела на ось x?

? 17. Брусок скользит по наклонной плоскости вниз. Коэффициент трения между бруском и плоскостью равен 0,5. Как изменяется со временем скорость бруска, если угол наклона плоскости равен:
а) 20º? б) 30º? в) 45º? г) 60º?

? 18. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Чему ранен коэффициент трения между бруском и доской? С каким по величине и направлению ускорением будет скользить брусок вниз по доске, наклоненной на угол 30º? 15º?

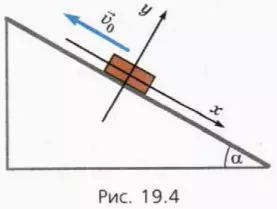
Пусть теперь начальная скорость тела направлена вверх (рис. 19.4).

? 19. Изобразите на чертеже в тетради силы, действующие на тело, и объясните, почему справедливы следующие уравнения:

? 20. Чему равна проекция ускорения тела на ось x?

? 21. Брусок начинает скользить по доске, когда ее наклоняют на угол 20º к горизонту. Брусок толкнули вверх по доске. С каким ускорением он будет двигаться, если доска наклонена на угол: а) 30º? б) 15º? В каком из этих случаев брусок остановится в верхней точке?

? 22.Шайбу толкнули вверх по наклонной плоскости с начальной скоростью v0. Угол наклона плоскости α, коэффициент трения между шайбой и плоскостью μ. Спустя некоторое время шайба вернулась в начальное положение.
а) Сколько времени двигалась шайба вверх до остановки?
б) Какой путь прошла шайба до остановки?
в) Сколько времени после этого шайба возвращалась в начальное положение?

? 23. После толчка брусок двигался в течение 2 с вверх по наклонной плоскости и затем в течение 3 с вниз до возвращения в начальное положение. Угол наклона плоскости 45º.
а) Во сколько раз модуль ускорения бруска при движении вверх больше, чем при движении вниз?
б) Чему равен коэффициент трения между бруском и плоскостью?

Зацените!! Езда Электро-Велосипеда по воде

Дополнительные вопросы и задания

24. Брусок соскальзывает без начальной скорости с гладкой наклонной плоскости высотой h (рис. 19.5). Угол наклона плоскости равен α. Какова скорость бруска в конце спуска? Есть ли здесь лишние данные?

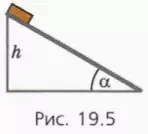
25. (Задача Галилея) В вертикальном диске радиуса R просверлен прямолинейный гладкий желоб (рис. 19.6). Чему равно время соскальзывания бруска вдоль всего желоба из состояния покоя? Угол наклона желоба α, в начальный момент брусок покоится.

26. По гладкой наклонной плоскости с углом наклона α скатывается тележка. На тележке установлен штатив, на котором на нити подвешен груз. Сделайте чертеж, изобразите силы, действующие на груз. Под каким углом к вертикали расположена нить, когда груз покоится относительно тележки?

27. Брусок находится на вершине наклонной плоскости длиной 2 м и высотой 50 см. Коэффициент трения между бруском и плоскостью 0,3.
а) С каким по модулю ускорением будет двигаться брусок, если толкнуть его вниз вдоль плоскости?
б) Какую скорость надо сообщить бруску, чтобы он достиг основания плоскости?

28. Тело массой 2 кг находится на наклонной плоскости. Коэффициент трения между телом и плоскостью 0,4.
а) При каком угле наклона плоскости достигается наибольшее возможное значение силы трения?
б) Чему равно наибольшее значение силы трения?
в) Постройте примерный график зависимости силы трения от угла наклона плоскости.
Подсказка. Если tg α ≤ μ, на тело действует сила трения покоя, а если tg α > μ – сила трения скольжения.

Источник

Добавить комментарий