Привет! В этой статье предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции опор, чему учат еще в рамках дисциплины — «теоретическая механика». Но для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.
Так как этот урок для чайников, я многие моменты буду упрощать и рассказывать только самое основное, чтобы написанное здесь, было понятно даже самому неподготовленному студенту — заочнику.
В рамках статьи рассмотрим 4 примера: двухопорная балка, загруженная посередине пролёта сосредоточенной силой, такая же балка, но загруженная распределённой нагрузкой, консольная балка и плоская рама.
Что такое реакция опоры?
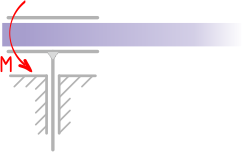
Чтобы лучше понять, что такое реакция опоры (опорная реакция), давай рассмотрим следующий пример — балку (стержень) лежащую на опорах:

На балку давит нагрузка – сила, в свою очередь, балка давит на опоры. И чтобы балка лежала на опорах (никуда не проваливалась), опоры выполняют свою основную функцию — удерживают балку. А чтобы удерживать балку, опоры должны компенсировать тот вес, с которым балка давит на них. Соответственно, действие опор можно представить в виде некоторых сил, так называемых — реакций опор.

Для балки, и нагрузка, и реакции опор, будут являться внешними силами, которые нужно обязательно учитывать при расчёте балки. А чтобы учесть опорные реакции, сначала нужно научиться определять их, чем, собственно, и займёмся на этом уроке.
Виды связей и их реакции
Связи – это способы закрепления элементов конструкций. Опоры, которые я уже показывал ранее – это тоже связи.
В этой статье будем рассматривать три вида связей: жёсткая заделка, шарнирно-подвижная и шарнирно-неподвижная опора.
Жёсткая заделка

Жёсткая заделка — это один из вариантов закрепления элементов конструкций. Этот тип связи препятствует любым перемещениям, тем самым для плоской задачи, может возникать три реакции: вертикальная (RA), горизонтальная (HA) и момент (MA).

Шарнирно-подвижная и шарнирно-неподвижная опора
В этой статье будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

В шарнирно-неподвижной опоре возникает две реакции: вертикальная и горизонтальная. Так как опора препятствует перемещению в этих двух направлениях. В шарнирно-подвижной опоре возникает только вертикальная реакция.

Однако, видов связей и их условных обозначений достаточно много, но в рамках этой статьи их все рассматривать не будем. Так как, изученные ранее виды связей, являются основными и практически всегда, при решении задач по сопромату, ты будешь сталкиваться именно с ними.
Что такое момент силы?
Также необходимо разобраться с понятием момент силы.
Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр.
Проиллюстрирую написанное:

Правило знаков для моментов
Также для моментов, нужно задаться каким-то правилом знаков. Я в своих уроках буду придерживаться такого правила:
- если сила относительно точки стремится повернуть ПРОТИВ часовой стрелки, то момент положительный;
- если она стремится повернуть ПО часовой стрелке, то момент отрицательный.

Всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнём с простейшей расчётной схемы балки.
Определение реакций для двухопорной балки
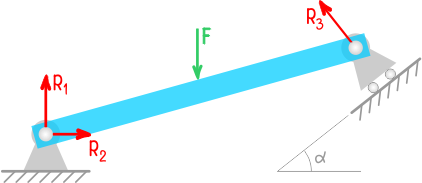
Возьмём балку, загруженную посередине сосредоточенной силой и опирающейся на шарнирно-неподвижную и шарнирно-подвижную опору:

Введём систему координат: направим ось x вдоль балки, а ось y вертикально. Обозначим реакции в опорах как HA, RA и RB:

Для тех, кто пришёл сюда, ещё будучи на этапе изучения теоретической механики, а я знаю, таких будет много, важно отметить, что в сопромате не принято указывать знаки векторов над силами.
В термехе же, в обязательном порядке, преподаватель от тебя настойчиво будет требовать указывать знак вектора над всеми силами, вот так:

Условия равновесия системы
Чтобы найти все реакции, нужно составить и решить три уравнения — уравнения равновесия:

Данные уравнения являются условиями равновесия системы. А так как мы предполагаем, что опоры обеспечивают это состояние равновесия (удерживают балку). То составив и решив уравнения равновесия — найдём значения опорных реакций.
Первое уравнение называется уравнением проекций — суммой проекций всех сил на координатную ось, которая должна быть равна нулю. Два других уравнения называются уравнениями моментов — суммами моментов всех сил относительно точек, которые должны быть равны нулю.
Уравнения равновесия
Как видишь, чтобы научиться находить реакции опор, главное — научиться правильно составлять уравнения равновесия.

Уравнение проекций
Запишем первое уравнение — уравнение проекций для оси x.
В уравнении будут участвовать только те силы, которые параллельны оси x. Такая сила у нас только одна — HA. Так как HA направлена против положительного направления оси x, в уравнение её нужно записать с минусом:
Тогда HA будет равна:
Поздравляю, первая реакция найдена!
Уравнения моментов
А теперь самое интересное…запишем уравнение моментов, относительно точки A, с учётом ранее рассмотренного правила знаков для моментов.
Так как сила F поворачивает ПО часовой стрелке, записываем её со знаком «МИНУС» и умножаем на плечо.
Так как сила RB поворачивает ПРОТИВ часовой стрелки, пишем её со знаком «ПЛЮС» и умножаем на плечо. И, наконец, всё это приравниваем к нулю:
Из полученного уравнения выражаем реакцию RB:

Вторая реакция найдена! Третья реакция находится аналогично, но только теперь уравнение моментов записываем относительно другой точки:

Проверка правильности найденных опорных реакций
Чем хороши задачи на определение реакций, так это тем, что правильность расчёта реакций легко проверить. Для этого достаточно составить дополнительное уравнение равновесия, подставить все численные значения и если сумма проекций сил или сумма моментов будет равна нулю, то и реакции, значит, найдены — верно, а если нет, то ищем ошибку.
Составим дополнительное уравнение проекций для оси y и подставим все численные значения:
Как видишь, реакции опор найдены правильно.
Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно «свернуть» до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:

Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:



Расчёт реакций для консольной балки
Давай рассмотрим теперь пример с жёсткой заделкой – консольную балку. Заодно посмотрим, как учесть силу, приложенную под углом (α = 30°).

Силу, направленную под определённым углом, нужно разложить на две составляющие – горизонтальную и вертикальную. А их значения найти из силового треугольника:


Покажем реакции в заделке и выполним расчёт:

Для этой задачи выгоднее использовать другую форму условий равновесия:

А выгодна она тем, что из каждого записанного уравнения будем сразу находить реакцию:

Не пугайся отрицательного значения реакции! Это значит, что при указании реакции, мы не угадали с её направлением. Расчёт же показал, что MA, направлена не по часовой стрелке, а против.
В теоретической механике, когда реакции получают с «минусом» обычно не заморачиваются и не меняют их направление на схеме, так и оставляют в ответе отрицательное значение, оговаривая, что да реакция найдена, но с учётом знака, на самом деле направлена в другую сторону. Потому что найденные реакции в задачах на статику, являются конечной точкой расчёта.
У нас же, в сопромате после нахождения опорных реакций, всё только начинается. Найдя реакции, мы всего лишь находим ВСЕ силы действующие на элемент конструкции, а дальше по сценарию стоит задача определить внутренние усилия, возникающие в этом элементе, расчёты на прочность и т. д. Поэтому на схеме, обязательно следует указывать истинное направление реакций. Чтобы потом, когда будут рассчитываться внутренние усилия ничего не напутать со знаками.
Если получили отрицательное значение, нужно отразить это на схеме:

С учётом изменений на схеме реакция будет равна:
Сделаем проверку, составив уравнение равновесие, ещё не использованное – сумму моментов относительно, скажем, точки B, которая, при правильном расчёте, конечно, должна быть равна нулю:
![]()
Если не менять направление реакции, то в проверочном уравнении нужно учесть этот «минус»:

Можешь посмотреть еще один пример, с похожей схемой, для закрепления материала, так сказать.
Реакции опор для плоской рамы
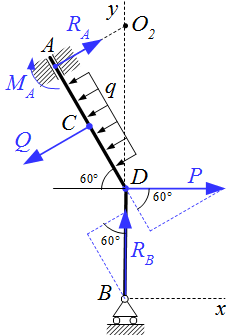
Теперь предлагаю выполнить расчёт плоской рамы. Для примера возьмём расчётную схему, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим систему координат x и y.

Выполняем расчёт реакций опор:


Меняем направление реакции RA:

В итоге получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумма будет равна нулю, то расчет выполнен верно:

Как видим, расчет реакций выполнен правильно!
Определением реакций опор называют расчет величины и направления реактивных (т.е. ответных) сил и моментов, возникающих в опорах конструкций под действием системы заданных внешних нагрузок.
В рассмотренных ниже примерах, для наглядности, заданные внешние нагрузки показаны синим или зеленым цветом, а реакции опор — красным или оранжевым.
При решении задач, определяемые реакции опор могут обозначаться по разному:
- буквой R (от англ. Reaction). В этом случае, для уточнения точки приложения и направления силы могут добавляться соответствующие индексы (например, RAy — это реакция в точке A направленная вдоль оси Y);
- буквами V (Vertical) и H (Horizontal) обозначаются соответственно вертикальная и горизонтальная составляющие полной реакции (например, HB — это реакция в точке B направленная вдоль оси балки);
- Также возможно обозначение реакций по осям координат — YA, XB и т.д.
Сохранить или поделиться с друзьями
Рассмотрим решение всех типов задач по расчету величины и направления опорных реакций в заделках, шарнирных опорах и стержнях:
Примеры нахождения реакций опор
Примеры нахождения реакций опор для различных способов закрепления и нагружения бруса, балок, рам и других элементов конструкций.
Реакции опоры и стержня системы
Невесомая балка удерживается в горизонтальном положении шарнирно-неподвижной опорой в т. A и вертикальным стержнем BC.
В точке D к балке приложена сосредоточенная сила F=30кН под углом 50°.
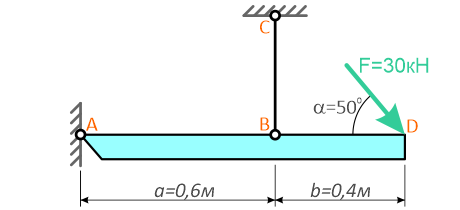
Требуется найти реакции, возникающие в опоре A и стержне BC.
Решение
Для решения задачи, покажем систему координат x-y и зададим произвольное направление реакций.
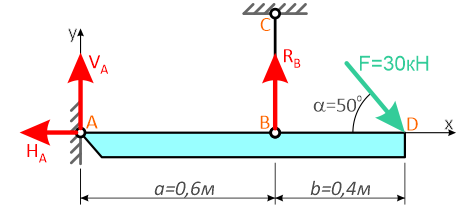
В точке A реакция в опоре раскладывается на две составляющие — вертикальную VA и горизонтальную HA.
Реакция в стержне (RB) всегда направлена вдоль самого стержня.
Для определения трех реакций требуется три уравнения равновесия.
Это будут два уравнения суммы моментов относительно точек в опорах и сумма проекций всех сил на ось x равные нулю.
Составим их:
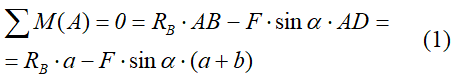
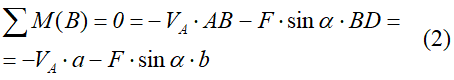
![]()
Из полученных уравнений выражаем и находим искомые реакции опор
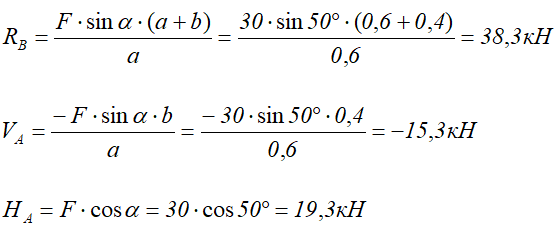
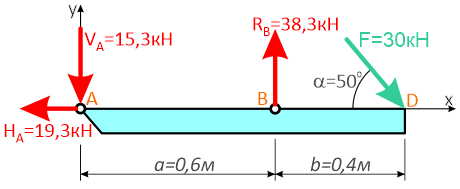
Вертикальная реакция в опоре A получилась отрицательной, это значит что она направлена в противоположную сторону.
Направляем ее вниз, изменив знак на «плюс».
Выполним проверку найденных реакций, проецируя все силы на ось y.
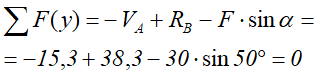
Равенство нулю суммы проекций всех сил и реакций показывает то, что реакции опор найдены верно.
Таким образом, заданная балка удерживается в равновесии под действием одной активной и трех реактивных сил.
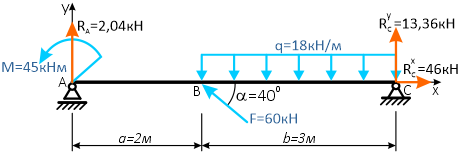
Расчет реакций опор балки
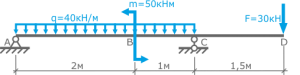
Простая балка на двух шарнирных опорах нагружена системой усилий, включающей силу F=60кН, приложенную под углом 40°, момент M=45кНм и равномерно распределенную нагрузку q=18кН/м.
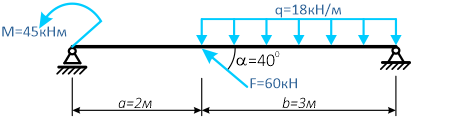
Требуется определить реакции в опорах A и C.
Решение
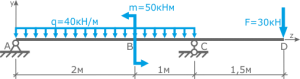
Вычерчиваем заданную схему в масштабе, показываем численные значения нагрузок, систему координат x-y и задаем произвольное направление реакций.
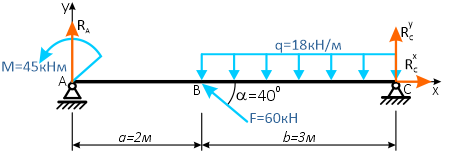
Здесь, в шарнирно-подвижной опоре будет только одна составляющая реакции.
Для упрощения решения, распределенную нагрузку можно заменить её равнодействующей, которая при равномерном распределении q будет приложена по её центру
![]()
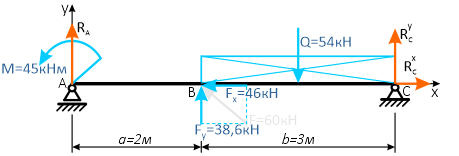
а силу F можно разложить на составляющие, спроецировав её на оси x и y.
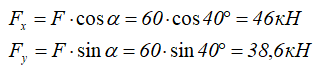
В следющих примерах эти действия выполнять не будем, проводя вычисления напрямую со значениями q и F.
Аналогично тому, как это делалось при решении предыдущей задачи, записываем уравнения равновесия балки: нулевые суммы моментов всех нагрузок и искомых реакций относительно опор
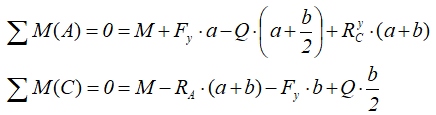
и проекций сил на ось балки
![]()
Откуда находим все три опорные реакции
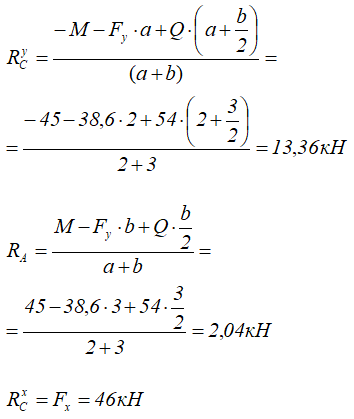
Все результаты положительны, следовательно, направление реакций было выбрано верно.
Проверяем найденные значения.
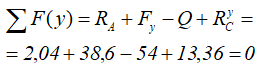
Величина реакций рассчитана правильно.
Подробное решение данного типа задач
Остальные задачи по определению опорных реакций с детальным разбором выполняемых действий:
При растяжении-сжатии стержней
Определение реакций в опорах стержней и стержневых систем при действии продольных сил.
- Расчет опорной реакции при растяжении-сжатии
- Расчет опорной реакции ступенчатого бруса
- Опорная реакция в заделке стержня с продольно распределенной нагрузкой
При кручении
Примеры расчета опорных моментов и реакций в подшипниках вала при кручении.
- Определение неизвестного крутящего момента вала
- Определение реакций подшипников пространственно нагруженного вала
- Расчет уравновешивающего момента вала
При изгибе балок и рам
Определение реакций в шарнирных опорах и заделках консольных балок и рам при действии систем внешних сил, моментов и распределенных нагрузок.
- Определение реакций в опорах двухопорной балки
- Расчет опорных реакций консольной балки
- Определение опорных реакций в жесткой заделке при изгибе
- Определение реакций опор балки, когда сила приложена под углом
- Проверка опорных реакций балки
- Расчет реакций в опорах рамы
- Определение опорных реакций балки (Видео)
Наш короткий видеоурок по расчету реакций опор балки:
Другие видео
Другие примеры определения реакций опор
Расчет реакций в опорах нестандартных систем.
- Определение реакции шарнира и опоры
- Реакции в шарнирах
- Реакции опор и шарнира
- Расчет веса противовеса и реакций в шарнирах
- Величина груза обеспечивающая равновесие и реакции в подшипниках
- Определение усилий в стержнях
- Натяжение троса и реакция опоры
- Реакции опор в точках системы
- Опорные реакции невесомой конструкции
- Опорные реакции в скользящей заделке
- Давление в шарнире и реакции в бискользящей заделке
- Реакции в скользящей заделке
- Расчет усилия в стержне
Типы опор и их реакции
В механике различают тела свободные: возможность перемещения, которых в любом направлении ничем не ограничена, и несвободные, когда перемещение данного тела ограничивают другие тела.
Сами тела ограничивающие свободу перемещения данного тела называют опорами (связями), а силы, с которыми опоры удерживают данное тело в равновесии, называют реакциями опор.
Направление реакций зависит от вида опор и схемы нагружения.
При решении задач очень важно правильно заменить опоры их реакциями, иначе записанные уравнения равновесия окажутся неверными.
И здесь важно помнить о том, что реакции могут появляться только по тем направлениям, в которых перемещение невозможно.
Рассмотрим определение реакций в основных типах опор:
Другие видео
Реакция гладкой поверхности
Пусть некоторое тело опирается на гладкую поверхность.
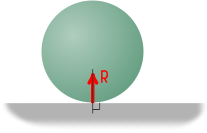
Здесь перемещение тела возможно только вдоль поверхности.
Движение перпендикулярно ей исключено.
Потому что перемещению в сторону поверхности препятствует сама поверхность, а при движении от нее нарушится сама связь.
Таким образом, гладкая поверхность препятствует перемещению тела только в направлении нормали, поэтому реакция гладкой поверхности всегда направлена по нормали к этой поверхности.
При взаимодействии криволинейных поверхностей аналогично, реакция направлена нормально к касательной в точке контакта тел.
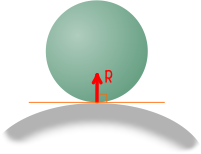
То же самое будет при контакте в двух точках.
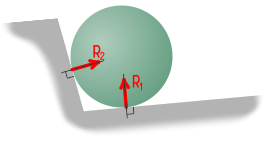
Реакция ребра
В случае, когда прямая балка опирается на ребро, реакции будут направлены перпендикулярно опираемой или опирающейся плоскости в точке их касания.
При повороте балки реакция всегда будет оставаться нормальной к соответствующей поверхности.
Гибкая связь
Для тела, подвешенного на нерастяжимой нити или тросе, связь не позволяет телу удаляться от точки подвеса в направлении самой нити.
Поэтому реакция гибкий связи будет направлена всегда только вдоль самой нити.
Реакции в стержнях
Как и в предыдущем пункте, в стержнях, которые с помощью шарниров соединяют какие-либо элементы с опорами, реакции направлены вдоль самих стержней.
Но в отличие от нитей, здесь может быть одно из двух направлений: растягивающее стержень или сжимающее его.
Реакции в шарнирных опорах
На плоскости возможны только три направления перемещения:
Линейные — вдоль осей x и y, и вращение относительно оси Z.
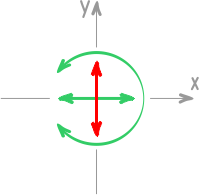
Поэтому в двумерных системах каждая опора может давать не более трех реакций.
Если свободное тело закрепить шарнирно-неподвижной опорой, которая допускает вращение, но исключает любые линейные перемещения, то в такой опоре могут возникать две реакции.
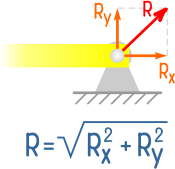
Они являются осевыми проекциями полной реакции опоры, которая может быть найдена как корень из суммы квадратов её составляющих.
Направление вектора полной реакции зависит от схемы нагружения элемента.
Встречаются разные способы изображения шарнирно-неподвижных опор в расчетных схемах.
В шарнирно-подвижных опорах, помимо вращения возможно линейное перемещение вдоль поверхности, поэтому здесь будет только одна, нормальная к поверхности, составляющая реакции, которая по направлению и величине будет совпадать с полной.
У таких опор так же существуют дополнительные варианты схематичного изображения.
Пример направления реакций опор для балки на двух шарнирных опорах.
Реакции в заделках
Вид связи, при котором брус жестко закреплен в опоре называется глухой заделкой.
В этом случае исключены любые перемещения элемента.
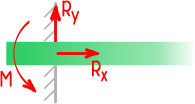
Поэтому в плоских заделках может возникать до трех реакций: горизонтальная и вертикальная составляющие полной реакции, а также момент.
Скользящая заделка допускает линейное перемещение вдоль одной из осей.
Следовательно, по этой оси реакции не будет.
В бискользящей заделке исключается только угловое перемещение элемента.
Здесь из реакций будет один момент.
Реакции опор в трехмерных системах
В пространстве возможно уже шесть направлений движения:
Поступательные вдоль каждой из осей и вращение относительно них.
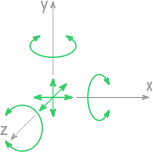
Поэтому в трехмерных системах опоры могут давать до шести реакций.
Шкив на валу, закрепленном подшипниками, может вращаться относительно продольной оси вала.
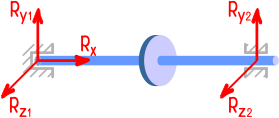
Любые другие перемещения невозможны.
В силу конструктивных особенностей подшипников моментов в них не возникает.
Здесь имеют место только реактивные силы.
В радиальном подшипнике (который справа) все реакции поперечны оси вала.
В радиально-упорном (который слева) добавляется еще и продольная.
В трехмерном шарнире исключены любые линейные перемещения и возможны только повороты относительно трех осей, что дает до трех составляющих полной реакции R.
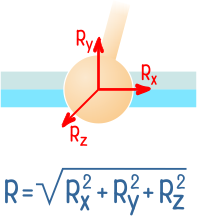
В жесткой заделке при общем случае нагружения может возникать до шести реакций: трёх сил и трех моментов.
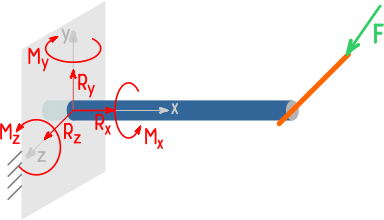
Пример замены опор их реакциями для трехмерной системы:
Порядок расчета опорных реакций
В рассмотренных выше примерах при определении реакций в опорах выполняется следующая последовательность действий:
- Вычерчивается (в масштабе) расчетная схема элемента с указанием всех размеров и приложенных внешних нагрузок;
Расчетная схема балки - Выбирается система координат и обозначаются характерные сечения бруса;
Система координат для балки - Определяется количество и возможное направление связей;
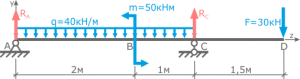
Направление опорных реакций балки - Записываются уравнения статики (по количеству неизвестных реакций);
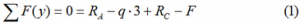
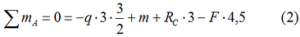
- Из уравнений равновесия находим величину и направление (по знаку) опорных реакций.
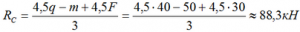
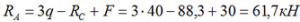
Опорные реакции балки
После расчетов выполняется проверка найденных значений.
Более подробно порядок расчета опорных реакций рассматривается в разделе «Статика» теоретической механики.
Другие примеры решения задач >
Сила реакции опоры — это сила, с которой опора действует на тело. Она направлена перпендикулярно поверхности, поэтому такую силу называют силой нормальной реакции. Обозначают ее символом N и измеряют в Ньютонах.
Тело находится на выпуклой или вогнутой поверхности
Рассмотрим рисунок 1. Тело находится на опоре и давит на нее своим весом. Опора реагирует на воздействие тела и отвечает ему силой (vec{N}). Эта сила направлена перпендикулярно поверхности, вдоль вектора нормали, поэтому ее называют нормальной силой.
Примечания:
- Нормаль – значит, перпендикуляр.
- Искривленную, т.е., выпуклую, или вогнутую поверхность, можно считать частью сферы. Центр сферы – точка, она находится внутри сферы, от этой точки к поверхности сферы можно провести радиус.
(vec{N} left( H right) ) – сила, с которой опора действует на тело.

Рис. 1. Тело (шар) опирается на выпуклую – а) и вогнутую – б) поверхность. А поверхность реагирует на вес тела силой нормальной реакции
Когда тело находится на выпуклой поверхности (рис. 1а), реакция направлена вдоль радиуса от центра сферы наружу, за ее пределы.
Если же тело находится на вогнутой части (рис. 1б) поверхности, реакция (vec{N}) направлена по радиусу внутрь сферической поверхности к ее центру.
Тело опирается на поверхность в двух точках
На рисунках 2а и 2б изображено продолговатое тело (к примеру, стержень), опирающееся на поверхности двумя своими точками.

Рис. 2. Однородный стержень опирается на поверхность двумя точками, в каждой из точек сила реакции располагается перпендикулярно поверхности
В точках соприкосновения поверхность отвечает телу силой (vec{N}) своей реакции. Видно, что в каждая сила реакции направлена перпендикулярно поверхности.
Cилы реакции (vec{N_{1}}) и (vec{N_{2}}) имеют различные направления и в общем случае не равны по модулю.
[large vec{N_{1}} ne vec{N_{2}}]
Примечание: Сила — это вектор. Между векторами можно ставить знак равенства, только, когда совпадают характеристики векторов.
Как рассчитать силу нормальной реакции
Пусть тело давит на опору своим весом. В местах соприкосновения тела с опорой наблюдается упругая деформация. При этом опора стремится избавиться от возникшей деформации и вернуться в первоначальное состояние. Силы, с которыми опора упруго сопротивляется воздействию тела, имеют электромагнитную природу. Когда сближаются электронные оболочки атомов тела и опоры, между ними возникает сила отталкивания. Она и является силой реакции опоры на воздействие тела.
Примечание: Сила реакции (vec{N}) распределяется по всей площади соприкосновения тела и опоры. Но для удобства ее обычно считают сосредоточенной силой. Ее изображают на границах соприкасающихся поверхностей исходящей из точки, расположенной под центром масс тела.
Для того, чтобы рассчитать силу реакции, нужно понимать законы Ньютона, уметь составлять силовые уравнения и знать, что такое равнодействующая.
На рисунке 3 изображены тела, находящиеся на горизонтальной – а) и наклонной – б) поверхностях.

Рис. 3. Тело опирается на поверхность горизонтальную – а) и наклонную – б), составляя силовые уравнения для сил, расположенных перпендикулярно соприкасающимся поверхностям, рассчитывают силу реакции опоры
Рассмотрим подробнее рисунок 3а. Тело на горизонтальной поверхности находится в покое. Значит, выполняются условия равновесия тела.
По третьему закону Ньютона, сила, с которой тело действует на опору, равна по модулю весу тела и направлена противоположно весу.
[large boxed{ N = m cdot g }]
(m vec{g} left( H right) ) – сила, с которой тело действует на опору;
(vec{N} left( H right) ) – сила, с которой опора отвечает телу;
Рисунок 3б иллюстрирует тело на наклонной поверхности. Перпендикулярно соприкасающимся поверхностям проведена ось Oy. Проекция силы (m vec{g}) на ось — это (mg_{y}), она будет направлена противоположно реакции опоры (vec{N}) и численно равна ей.
Примечание: Выражение «численно равна» нужно понимать, как «длины векторов равны».
[large boxed{ N = m cdot g cdot cos(alpha) }]
(alpha left(text{рад} right) ) – угол между силой (mg) и осью Oy.
Итоги
- Сила, с которой опора сопротивляется воздействию тела, называется силой реакции опоры, она имеет электромагнитную природу.
- Ее, как и любую силу, измеряют в Ньютонах, обозначают так: (vec{N}).
- Реакция опоры направлена перпендикулярно поверхности, поэтому ее называют силой нормальной реакции.
- Сила (vec{N}) распределена по площади соприкосновения, но для удобства ее обычно считают сосредоточенной силой. Ее изображают исходящей из точки, расположенной под центром масс тела на границах между поверхностями тела и опоры.
- Чтобы рассчитать силу реакции, нужно знать законы Ньютона, уметь составлять силовые уравнения и понимать, что такое равнодействующая.
- Теоретическая механика в университете
- Статика твердого тела. Решение примеров
- Основные понятия и законы статики
- Связи и их реакции
- Момент силы относительно точки
- Момент силы относительно оси
- Момент пары сил
- Преобразование сходящейся системы сил
- Преобразование произвольной системы сил
- Условия равновесия систем сил
- Равновесие произвольной системы сил
- Кинематика. Решение примеров
- Основные понятия кинематики
- Способы задания движения точки
- Определение кинематических характеристик точки
- Ускорение точки
- Кинематика твердого тела
- Плоско-параллельное движение твердого тела
- Сложное движение точки
- Динамика. Решение примеров
- Основные понятия динамики
- Аксиомы динамики
- Дифференциальные уравнения динамики
- Общие теоремы динамики
- Принцип Даламбера
- Примеры решения задач
Теоретическая механика – это раздел механики, в котором излагаются основные законы механического движения и механического взаимодействия материальных тел.
Теоретическая механика является наукой, в которой изучаются перемещения тел с течением времени (механические движения). Она служит базой других разделов механики (теория упругости, сопротивление материалов, теория пластичности, теория механизмов и машин, гидроаэродинамика) и многих технических дисциплин.
Механическое движение — это изменение с течением времени взаимного положения в пространстве материальных тел.
Механическое взаимодействие – это такое взаимодействие, в результате которого изменяется механическое движение или изменяется взаимное положение частей тела.
Статика твердого тела
Статика — это раздел теоретической механики, в котором рассматриваются задачи на равновесие твердых тел и преобразования одной системы сил в другую, ей эквивалентную.
- Основные понятия и законы статики
- Абсолютно твердое тело (твердое тело, тело) – это материальное тело, расстояние между любыми точками в котором не изменяется.
- Материальная точка – это тело, размерами которого по условиям задачи можно пренебречь.
- Свободное тело – это тело, на перемещение которого не наложено никаких ограничений.
- Несвободное (связанное) тело – это тело, на перемещение которого наложены ограничения.
- Связи – это тела, препятствующие перемещению рассматриваемого объекта (тела или системы тел).
- Реакция связи — это сила, характеризующая действие связи на твердое тело. Если считать силу, с которой твердое тело действует на связь, действием, то реакция связи является противодействием. При этом сила — действие приложена к связи, а реакция связи приложена к твердому телу.
- Механическая система – это совокупность взаимосвязанных между собой тел или материальных точек.
- Твердое тело можно рассматривать как механическую систему, положения и расстояние между точками которой не изменяются.
- Сила – это векторная величина, характеризующая механическое действие одного материального тела на другое.
Сила как вектор характеризуется точкой приложения, направлением действия и абсолютным значением. Единица измерения модуля силы – Ньютон. - Линия действия силы – это прямая, вдоль которой направлен вектор силы.
- Сосредоточенная сила – сила, приложенная в одной точке.
- Распределенные силы (распределенная нагрузка) – это силы, действующие на все точки объема, поверхности или длины тела.
Распределенная нагрузка задается силой, действующей на единицу объема (поверхности, длины).
Размерность распределенной нагрузки – Н/м3 (Н/м2, Н/м). - Внешняя сила – это сила, действующая со стороны тела, не принадлежащего рассматриваемой механической системе.
- Внутренняя сила – это сила, действующая на материальную точку механической системы со стороны другой материальной точки, принадлежащей рассматриваемой системе.
- Система сил – это совокупность сил, действующих на механическую систему.
- Плоская система сил – это система сил, линии действия которых лежат в одной плоскости.
- Пространственная система сил – это система сил, линии действия которых не лежат в одной плоскости.
- Система сходящихся сил – это система сил, линии действия которых пересекаются в одной точке.
- Произвольная система сил – это система сил, линии действия которых не пересекаются в одной точке.
- Эквивалентные системы сил – это такие системы сил, замена которых одна на другую не изменяет механического состояния тела.
Принятое обозначение: .
. - Равновесие – это состояние, при котором тело при действии сил остается неподвижным или движется равномерно прямолинейно.
- Уравновешенная система сил – это система сил, которая будучи приложена к свободному твердому телу не изменяет его механического состояния (не выводит из равновесия).
 .
. - Равнодействующая сила – это сила, действие которой на тело эквивалентно действию системы сил.
 .
. - Момент силы – это величина, характеризующая вращающую способность силы.
- Пара сил – это система двух параллельных равных по модулю противоположно направленных сил.
Принятое обозначение: .
.
Под действием пары сил тело будет совершать вращательное движение. - Проекция силы на ось – это отрезок, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой оси.
Проекция положительна, если направление отрезка совпадает с положительным направлением оси. - Проекция силы на плоскость – это вектор на плоскости, заключенный между перпендикулярами, проведенными из начала и конца вектора силы к этой плоскости.
- Закон 1 (закон инерции). Изолированная материальная точка находится в покое либо движется равномерно и прямолинейно.
Равномерное и прямолинейное движение материальной точки является движением по инерции. Под состоянием равновесия материальной точки и твердого тела понимают не только состояние покоя, но и движение по инерции. Для твердого тела существуют различные виды движения по инерции, например равномерное вращение твердого тела вокруг неподвижной оси. - Закон 2. Твердое тело находится в равновесии под действием двух сил только в том случае, если эти силы равны по модулю и направлены в противоположные стороны по общей линии действия.
Эти две силы называются уравновешивающимися.
Вообще силы называются уравновешивающимися, если твердое тело, к которому приложены эти силы, находится в покое. - Закон 3. Не нарушая состояния (слово «состояние» здесь означает состояние движения или покоя) твердого тела, можно добавлять и отбрасывать уравновешивающиеся силы.
Следствие. Не нарушая состояния твердого тела, силу можно переносить по ее линии действия в любую точку тела.
Две системы сил называются эквивалентными, если одну из них можно заменить другой, не нарушая состояния твердого тела. - Закон 4. Равнодействующая двух сил, приложенных в одной точке, приложена в той же точке, равна по модулю диагонали параллелограмма, построенного на этих силах, и направлена вдоль этой
диагонали.
По модулю равнодействующая равна:

- Закон 5 (закон равенства действия и противодействия). Силы, с которыми два тела действуют друг на друга, равны по модулю и направлены в противоположные стороны по одной прямой.
Следует иметь в виду, что действие — сила, приложенная к телу Б, и противодействие — сила, приложенная к телу А, не уравновешиваются, так как они приложены к разным телам. - Закон 6 (закон отвердевания). Равновесие нетвердого тела не нарушается при его затвердевании.
Не следует при этом забывать, что условия равновесия, являющиеся необходимыми и достаточными для твердого тела, являются необходимыми, но недостаточными для соответствующего нетвердого тела. - Закон 7 (закон освобождаемости от связей). Несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив действие связей соответствующими реакциями связей.
- Связи и их реакции
- Гладкая поверхность ограничивает перемещение по нормали к поверхности опоры. Реакция направлена перпендикулярно поверхности.
- Шарнирная подвижная опора ограничивает перемещение тела по нормали к опорной плоскости. Реакция направлена по нормали к поверхности опоры.
- Шарнирная неподвижная опора противодействует любому перемещению в плоскости, перпендикулярной оси вращения.
- Шарнирный невесомый стержень противодействует перемещению тела вдоль линии стержня. Реакция будет направлена вдоль линии стержня.
- Глухая заделка противодействует любому перемещению и вращению в плоскости. Ее действие можно заменить силой, представленной в виде двух составляющих и парой сил с моментом.
- Момент силы относительно оси
- Момент силы относительно оси — это момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Момент считается положительным, если с положительного конца оси поворот, который сила стремится совершить, виден происходящим против хода часовой стрелки, и отрицательным – если по ходу часовой стрелки.

- Чтобы найти момент силы относительно оси, нужно:
1) Провести плоскость перпендикулярную оси z.
2) Спроецировать силу на эту плоскость и вычислить величину проекции
на эту плоскость и вычислить величину проекции  .
.
3) Провести плечо h из точки пересечения оси с плоскостью на линию действия проекции силы и вычислить его длину.
и вычислить его длину.
4) Найти произведение этого плеча и проекции силы с соответствующим знаком. - Свойства момента силы относительно оси.
Момент силы относительно оси равен нулю, если:
1) , то есть сила
, то есть сила  параллельна оси.
параллельна оси.
2) h=0, то есть линия действия силы пересекает ось.
- Момент пары сил
- Момент пары сил равен произведению одной силы на кратчайшее расстояние между линиями действия сил пары, которое называется плечом пары (пара сил оказывает на тело вращающее действие)
 ,
,
где: — силы, составляющие пару;
— силы, составляющие пару;
h — плечо пары.
Момент пары считают положительным, если силы стремятся вращать плечо против хода часовой стрелки. - Свойства пары сил.
1) Сумма проекций сил пары на любую ось равна нулю.
2) Не изменяя момента пары можно одновременно соответственно изменять значение сил и плечо пары.
3) Пару можно переносить в плоскости ее действия при этом действие пары на тело не изменится.
Кинематика
Кинематика — раздел теоретической механики, в котором рассматриваются общие геометрические свойства механического движения, как процесса, происходящего в пространстве и во времени. Движущиеся объекты рассматривают как геометрические точки или геометрические тела.
- Основные понятия кинематики
- Закон движения точки (тела) – это зависимость положения точки (тела) в пространстве от времени.
- Траектория точки – это геометрическое место положений точки в пространстве при ее движении.
- Скорость точки (тела) – это характеристика изменения во времени положения точки (тела) в пространстве.
- Ускорение точки (тела) – это характеристика изменения во времени скорости точки (тела).
- Способы задания движения точки
- Задать движение точки — значит задать изменение ее положения по отношению к выбранной системе отсчета. Существуют три основные системы отсчета: векторная, координатная, естественная.
- В векторной системе положение точки относительно начала отсчета задается радиус-вектором.
Закон движения: .
. - В системе координат OXYZ положение точки задается тремя координатами X, Y, Z.
Закон движения: x = x(t), y = y(t); z = z(t). - В естественной системе отсчета положение точки задается расстоянием S от начала отсчета до этой точки вдоль траектории.
Закон движения: .
.
Движение точки, при естественном способе задания движения, определено если известны:
1) Траектория движения.
2) Начало и направление отсчета дуговой координаты.
3) Уравнение движения.
При естественном способе задания движения, в отличии от других способов, используются подвижные координатные оси, движущиеся вместе с точкой по траектории. Такими осями являются:
Касательная (τ) – направлена в сторону возрастания дуговой координаты по касательной к траектории.
Главная нормаль (n) – направлена в сторону вогнутости кривой.
Бинормаль (b) – направлена перпендикулярно к осям τ, n.
- Кинематика твердого тела
- В кинематике твердых тел решаются две основные задачи:
1) задание движения и определение кинематических характеристик тела в целом;
2) определение кинематических характеристик точек тела. - Поступательное движение твердого тела
Поступательное движение — это движение, при котором прямая, проведенная через две точки тела, остается параллельной ее первоначальному положению.
Теорема: при поступательном движении все точки тела движутся по одинаковым траекториям и имеют в каждой момент времени одинаковые по модулю и направлению скорости и ускорения.
Вывод: поступательное движение твердого тела определяется движением любой его точки, в связи с чем, задание и изучение его движения сводится к кинематике точки. - Вращательное движение твердого тела вокруг неподвижной оси
Вращательное движение твердого тела вокруг неподвижной оси — это движение твердого тела, при котором две точки, принадлежащие телу, остаются неподвижными в течение всего времени движения.
Положение тела определяется углом поворота . Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
. Единица измерения угла – радиан. (Радиан — центральный угол окружности, длина дуги которого равна радиусу, полный угол окружности содержит 2π радиана.)
Закон вращательного движения тела вокруг неподвижной оси .
.
Угловую скорость и угловое ускорение тела определим методом дифференцирования:
 — угловая скорость, рад/с;
— угловая скорость, рад/с;
 — угловое ускорение, рад/с².
— угловое ускорение, рад/с².
Если рассечь тело плоскостью перпендикулярной оси, выбрать на оси вращения точку С и произвольную точку М, то точка М будет описывать вокруг точки С окружность радиуса R. За время dt происходит элементарный поворот на угол , при этом точка М совершит перемещение вдоль траектории на расстояние
, при этом точка М совершит перемещение вдоль траектории на расстояние  .
.
Модуль линейной скорости:
 .
.
Ускорение точки М при известной траектории определяется по его составляющим :
:
 ,
,
где .
.
В итоге, получаем формулы
тангенциальное ускорение: ;
;
нормальное ускорение: .
.
Динамика
Динамика — это раздел теоретической механики, в котором изучаются механические движении материальных тел в зависимости от причин, их вызывающих.
- Основные понятия динамики
- Инерционность — это свойство материальных тел сохранять состояние покоя или равномерного прямолинейного движения, пока внешние силы не изменят этого состояния.
- Масса — это количественная мера инерционности тела. Единица измерения массы — килограмм (кг).
- Материальная точка — это тело, обладающее массой, размерами которого при решении данной задачи пренебрегают.
- Центр масс механической системы — геометрическая точка, координаты которой определяются формулами:

где mk, xk, yk, zk — масса и координаты k-той точки механической системы, m — масса системы.
В однородном поле тяжести положение центра масс совпадает с положением центра тяжести. - Момент инерции материального тела относительно оси – это количественная мера инертности при вращательном движении.
Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки от оси:
 .
.
Момент инерции системы (тела) относительно оси равен арифметической сумме моментов инерции всех точек:

- Сила инерции материальной точки — это векторная величина, равная по модулю произведению массы точки на модуль ускорения и направленная противоположно вектору ускорения:

- Сила инерции материального тела — это векторная величина, равная по модулю произведению массы тела на модуль ускорения центра масс тела и направленная противоположно вектору ускорения центра масс:
 ,
,
где — ускорение центра масс тела.
— ускорение центра масс тела. - Элементарный импульс силы — это векторная величина
 , равная произведению вектора силы
, равная произведению вектора силы  на бесконечно малый промежуток времени dt:
на бесконечно малый промежуток времени dt:
 .
.
Полный импульс силы за Δt равен интегралу от элементарных импульсов:
 .
. - Элементарная работа силы — это скалярная величина dA, равная скалярному произведению вектора силы
 на бесконечно малое перемещение
на бесконечно малое перемещение  .
.
Скалярное произведение векторов равно произведению их модулей на косинус угла между направлениями векторов:
 ,
,
где α — угол между направлениями векторов перемещения и силы. - Работа силы
 на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению:
на конечном перемещении точки её приложения равна интегралу от элементарной работы, взятому по перемещению:
 .
.
Единица измерения работы — Джоуль (1 Дж = 1 Н·м). - Количество движения материальной точки — это векторная величина
 , равная произведению массы m на её скорость
, равная произведению массы m на её скорость  :
:
 .
. - Количество движения механической системы равно векторной сумме количества движения её точек.
 или
или
 ,
,
где m — масса механической системы, — вектор скорости центра масс системы.
— вектор скорости центра масс системы. - Кинетическая энергия материальной точки — это скалярная величина Т, равная половине произведения массы точки на квадрат её скорости:
 .
. - Кинетическая энергия механической системы равна сумме кинетических энергий всех её точек:
 .
.
- Принцип Даламбера
- Формулировка принципа Даламбера: если в любой момент времени к действующим на точку силам присоединить силы инерции, то полученная система сил будет уравновешенной:
 .
. - Для механической системы:
 .
.
Примеры решения задач
Решение примеров по теме: «Статика твердого тела»
Пример 1. Условия равновесия
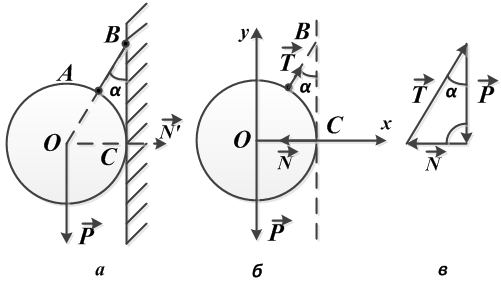
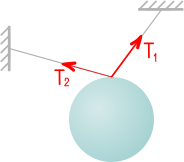
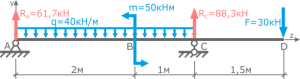
Висящий на нити, под углом в сорок пять градусов к гладкой стене шар весом в десять Ньютон, находится в состоянии равновесия (рис. а). Необходимо определить давление однородного шара на гладкую стенку и натяжение нити.
Дано: P = 10 Н; α = 45°
Найти: N, T — ?
Решение.
Отбрасываем связи, а их действие на шар заменяем реакциями.
Реакция стенки N направлена перпендикулярно стенке (от точки касания С к центру шара О), реакция нити Т — вдоль нити от точки А к точке В.
Тем самым выявляется полная система сил, приложенных к покоящемуся шару.
Это система сил, сходящихся в центре О шара, и состоящая из веса шара Р (активная сила), реакции стенки N и реакции нити Т (рис. б).
Реакции N и Т по величине неизвестны. Для их определения следует воспользоваться условиями равновесия (в той или иной форме — геометрической, аналитической).
При геометрическом способе решения строится замкнутый многоугольник сил и используются соотношения школьной геометрии (теорема синусов, теорема косинусов, теорема Пифагора и т.д.).
В данном случае это замкнутый силовой треугольник (рис. в), из которого получаем:

После подстановки в формулы числовых значений, получим:
 .
.
Ответ:  .
.
Решение примеров по теме: «Кинематика»
Пример 2. Уравнение траектории точки
Дано:
Движение точки задано уравнениями  ;
;
(x, у — в сантиметрах, t — в секундах).
Найти: уравнение траектории точки в координатной форме.
Решение. Для определения уравнения траектории из уравнений движения исключаем время t. Для этого из первого уравнения выражаем  и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
и подставляем это значение во второе уравнение, преобразованное к функциям одинарного угла:
 .
.
Опуская промежуточные выражения, получаем уравнение траектории:
 .
.
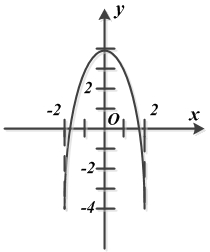 Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).
Уравнение определяет параболу, расположенную симметрично относительно оси у, с вершиной в точке (0, 4). Траекторией служит кусок этой параболы, заключенный между точками с координатами (-2, -4) и (2, -4).
Ответ:  .
.
Решение примеров по теме: «Динамика»
Пример 3. Основной закон динамики точки
Свободная материальная точка, масса которой десять килограмм, движется прямолинейно с ускорением пол метра в секунду в квадрате. Определить силу, приложенную к точке.
Дано: m = 10 кг; a = 0,5 м/с2.
Найти: F — ?
Решение.
Согласно основному закону динамики:  .
.
Подставив значения в формулу, получим:

Ответ: сила, сообщающая массе, равной 10 кг,
ускорение 0,5 м/с2, равна 5 Н.
В помощь студенту
- Формулы, правила, законы, теоремы, уравнения, примеры решения задач
- Теоретические основы электротехники
- Электрические машины
- Высшая математика
Список литературы:
Бать М.И., Джанелидзе Г.Ю., Кельзон А.С. Теоретическая механика в примерах и задачах.
Буторин Л.В., Бусыгина Е.Б. Теоретическая механика. Учебно-практическое пособие.
Как определить реакции в опорах?
Привет! В этой статье, предлагаю поговорить о реакциях опор, еще известных как опорные реакции. Для успешного освоения курса – «сопротивление материалов», каждый студент должен уметь определять реакции в опорах, и этому уделяют особое внимание на термехе. А курс термеха, по традиции, читают до сопромата. Для тех, кто проспал механику на первом курсе, я подготовил данную статью, чтобы каждый желающий мог приобрести навыки по расчету опорных реакций.

Что такое реакция опоры?
Реакция опоры – это та сила, которая возникает в опоре от действия внешней нагрузки. В зависимости от конструкции опоры и ее назначения, в ней может появляться разное количество реакций, это может быть как сила, так и момент.
В начале этой статьи, расскажу о том, что должен уже уметь читатель, для успешного освоения данного урока. Если у Вас есть проблемы по поднятым вопросам на старте статьи, переходите по ссылкам на другие материалы на нашем сайте, после чего возвращайтесь к нам на чай реакции. Во второй части статьи, посмотрим, как вычисляются реакции на простейшем примере – балки, загруженной по центру сосредоточенной силой. Тут я покажу, как пользоваться уравнениями равновесия статики, как их правильно составлять. Дальше по плану, научу учитывать распределенную нагрузку, на примере той же балки. И завершать данный урок, будет пример определения реакций для плоской рамы, загруженной всевозможными типами нагрузок. Где применим уже все фишки, о которых я буду рассказывать по ходу урока. Что же, давайте начнем разбираться с реакциями!
Что вы должны уже уметь?
В этом блоке статье, я расскажу, как и обещал, что Вы должны УЖЕ уметь, чтобы понять то, что я буду докладывать дальше, про реакции опор.
Должны уметь находить сумму проекций сил
Да, это то, что Вам когда-то рассказывали на термехе, как собственно, и опорные реакции. Если Вы шарите немного в этих проекциях, то можете смело переходить к следующему пункту. Если же нет, то специально на этот случай, у меня есть другая статья, про проекции сил. Переходите, просвещайтесь, после чего, обязательно, возвращайтесь сюда!
Должны уметь составлять сумму моментов относительно точки
Немного теории! Познакомимся для начала с самим понятием момент силы. Момент силы — это произведение силы на плечо. Где плечо — это кратчайшее расстояние от точки до силы, то есть перпендикуляр. Проиллюстрирую написанное:

На изображении показано, как определить момент силы F, относительно точки O.
Так же, для моментов, нужно задаться каким-то правилом знаков. Сила относительно точки может поворачивать как по часовой стрелке, так и против нее. Я в своих уроках буду придерживаться такого правила:
- Если сила относительно точки крутит ПРОТИВ часовой стрелке, то момент положительный.
- Если она крутит ПО часовой стрелки, то соответственно момент отрицательный.

Причем, это правило условно! Какое правило Вы будете использовать совсем не важно, результат получите тот же самый. В теоретической механике, к примеру, делают также как я рассказываю.
Должны разбираться в основных видах опор
Теперь поговорим о самих опорах. В этой статье, будем работать с двумя типами опор: шарнирно-подвижной и шарнирно-неподвижной.

Шарнирно-подвижная опора препятствует вертикальному перемещению элементу конструкции, в связи с чем, в ней, под действием внешней нагрузки возникает вертикальная реакция. Обозначают ее обычно как Ri, где i — точка крепления опоры.
Шарнирно-неподвижная опора имеет две реакции: вертикальную и горизонтальную. Так как препятствует перемещению в этих двух направлениях.

Вообще-то способов закрепления элементов конструкций и их условных обозначений достаточно много, но в рамках этой статьи их рассматривать не будем.
Примеры определения сил реакций опор
Вроде, всю подготовительную информацию дал, теперь будем рассматривать конкретные примеры. И начнем с простейшей расчетной схемы балки.
Определение реакций опор для балки
Возьмем балку на двух опорах, длиной 2 метра. Загрузим ее, посередине пролета, сосредоточенной силой:

Для этой расчетной схемы, выгодно записать такое условие равновесия:  То есть, будем составлять две суммы моментов относительно опорных точек, из которых можно сразу выразить реакции в опорах. В шарнирно-неподвижной опоре горизонтальная реакция будет равна нулю, ввиду того, что горизонтальные силы отсутствуют. Последним уравнением, взяв сумму проекций на вертикальную ось, сможем проверить правильность нахождения опорных реакций, это сумма должна быть равна нулю.
То есть, будем составлять две суммы моментов относительно опорных точек, из которых можно сразу выразить реакции в опорах. В шарнирно-неподвижной опоре горизонтальная реакция будет равна нулю, ввиду того, что горизонтальные силы отсутствуют. Последним уравнением, взяв сумму проекций на вертикальную ось, сможем проверить правильность нахождения опорных реакций, это сумма должна быть равна нулю.
Введем систему координат, пустим ось х вдоль балки, а ось y вертикально. Обозначим реакции в опорах как RA и RB:

Запишем уравнение моментов, относительно точки А. Сила F поворачивает ПО часовой стрелки, записываем ее со знаком МИНУС и умножаем на плечо. Сила RB поворачивает ПРОТИВ часовой стрелки, пишем ее со знаком ПЛЮС и умножаем на плечо. Все это приравниваем к нулю:

Из полученного уравнения выражаем реакцию RB.

Первая реакция найдена! Вторая реакция находится аналогично, только теперь уравнение моментов записываем относительно другой точки:


После нахождения реакций, делаем проверку:

Определение реакций опор для балки с распределенной нагрузкой
Теперь рассмотрим балку, загруженную распределенной нагрузкой:

Перед тем как посчитать реакции опор, распределенную нагрузку нужно свернуть до сосредоточенной силы. Если умножить интенсивность q на длину участка, на которой действует нагрузка, получим силу Q. Сила Q будет находиться ровно посередине балки, как и сила F в нашем первом примере:


Подробно комментировать нахождение реакций в опорах здесь, не буду. Просто приведу решение:






Определение опорных реакций для плоской рамы
Теперь, после освоения азов по расчету реакций, предлагаю выполнить расчет плоской рамы. Для примера, возьмем раму, загруженную всевозможными видами нагрузок:

Проводим ряд действий с расчетной схемой рамы:
- заменяем опоры на реакции;
- сворачиваем распределенную нагрузку до сосредоточенной силы;
- вводим глобальную систему координат x и y.

Для такой расчетной схемы, лучше использовать следующую форму условий равновесия:
 Составив первое уравнение, относительно точки A, сразу найдем реакцию в опоре B:
Составив первое уравнение, относительно точки A, сразу найдем реакцию в опоре B:



Записав второе уравнение, сумму проекций на ось х, найдем горизонтальную реакцию HA:


И, наконец, третье уравнение, позволит найти реакцию RA:


Не пугайтесь отрицательного значения реакции! Это значит, что при отбрасывании опоры, мы не угадали с направлением этой силы.
Расчет же показал, что RA, направленна в другую сторону:

В итоге, получили следующие реакции в опорах рамы:

Осталось проверить наши расчеты! Для этого предлагаю записать уравнение моментов, относительно точки B. И если, эта сумму будет равна нулю, то расчет выполнен верно:



Как видим, расчет реакций выполнен правильно!
На этом заканчиваю данный урок. Если у Вас остались какие-то вопросы по нахождению опорных реакций, смело задавайте их в комментариях к этой статье. Обязательно на все отвечу!
Спасибо за внимание! Если понравилась данная статья, расскажите о ней своим одногруппникам, не жадничайте 🙂
Также рекомендую подписаться на наши соц. сети, чтобы быть в курсе обновлений материалов проекта.
Методы определения реакций опор твердого тела
Как определить реакции опор твердого тела
Чтобы определить реакции опор твердого тела нужно выполнить следующие шаги.
- Вместо связей в опорах приложить силы реакций.
- Если есть распределенная нагрузка, то заменить ее равнодействующей силой. Ее величина равна площади эпюры нагрузки. Точка приложения находится в центре тяжести эпюры. Так для равномерно распределенной на отрезке нагрузки, ее равнодействующая приложена к середине этого отрезка.
- Выбрать систему координат. Ее начало желательно выбрать в точке крепления одной из опор.
- Составить уравнения равновесия.
Векторная сумма всех действующих на тело сил (включая реакции опор) равна нулю:
(1) .
Векторная сумма моментов этих сил относительно начала системы координат O равна нулю:
(2) . - Составить проекции уравнений равновесия (1) и (2) на оси системы координат.
Суммы проекций сил на оси координат равны нулю:
(1.x) ;
(1.y) ;
(1.z) .
Суммы моментов сил относительно координатных осей равны нулю:
(2.x) ;
(2.y) ;
(2.z) . - Для трехмерной задачи мы получим систему из шести уравнений, решая которую, определяем шесть неизвестных проекций реакций опор.
- Для плоской задачи, в которой все действующие силы направлены вдоль осей x и y, получаем три уравнения равновесия: (1.x), (1.y) и (2.z). Из них определяем три неизвестные проекции реакций опор.
- Для упрощения расчетов, иногда бывает полезно спроектировать уравнения равновесия (1) и (2) на другие оси, и составить дополнительные уравнения для моментов относительно других точек. См. Три формы уравнений равновесия твердого тела
- Если полученная система не имеет решения, то при такой схеме закрепления тела равновесие не возможно.
- Если число неизвестных превышает число линейно независимых уравнений, то задача имеет бесконечно много решений, она статически неопределима. Такую задачу можно решить только методами сопротивления материалов. Пример: плоское тело с четырьмя опорами.
Далее мы рассмотрим вопросы, связанные с определением реакций опор твердого тела более подробно и разберем пример решения задачи.
Методы определения реакций опор твердого тела
Рассмотрим некоторое твердое тело, на которое действуют заданные внешние силы. Пусть оно определенным образом закреплено в некоторых точках – опорах, и находится в состоянии равновесия. Эти точки закрепления также называются связями. Это могут быть шарниры, заделки, поверхности и т. п.
Отбросим опоры, и приложим вместо них силы. Они называются силами реакций опор. Их направления определяются устройствами соответствующих опор. В некоторых опорах реакции возникают в виде пары сил, которые задаются значением момента пары. Нам нужно найти такие значения сил реакций, чтобы при их действии на тело, оно покоилось, как это происходит в закрепленном состоянии.
Воспользуемся двумя законами, которые выполняются, если тело находится в покое.
1) Векторная сумма всех действующих на тело внешних сил равна нулю:
(M.1) .
2) Векторная сумма моментов всех внешних сил относительно любой точки O равна нулю:
(M.2) .
Эти законы называются уравнениями равновесия. В них также включены силы (пары сил) реакций опор.
Самый простой способ составления уравнений равновесия
Разберем самый простой способ составления уравнений равновесия. С его помощью можно гарантированно получить значения сил реакций опор или определить, что схема закрепления тела в опорах является статически неопределимой.
Выберем прямоугольную систему координат с началом в любой точке. Часто за начало системы координат удобно выбрать точку крепления одной из опор, но это не обязательно. Итак, пусть мы выбрали систему координат Oxyz с началом в точке O .
Спроектируем (M.1) на оси этой системы. В результате мы получим три уравнения, связывающие проекции сил на оси xyz :
(M.1.x) ;
(M.1.y) ;
(M.1.z) .
Здесь – n сил, действующих на тело. В их состав также включены и силы реакций опор.
Составим уравнения равновесия (M.2) для моментов, относительно осей Ox , Oy , Oz системы координат:
(M.2.x) ;
(M.2.y) ;
(M.2.z) .
Заметим, что эти уравнения являются проекциями векторного уравнения (M.2) на оси Ox , Oy и Oz .
Уравнения (M.1.x), (M.1.y), (M.1.z) и (M.2.x), (M.2.y), (M.2.z) представляют собой полную систему уравнений равновесия твердого тела. Если мы попытаемся добавить сюда еще одно уравнение, то оно будет являться линейной комбинацией уже существующих уравнений, и никак не повлияет на численные значения определяемых реакций опор. Например, мы можем выбрать еще одну ось, и спроектировать на нее уравнение (M.1) для сил. Или мы можем составить уравнение для моментов (M.2) относительно другой точки, отличной от начала координат. В результате получим дополнительные уравнения, но число линейно независимых уравнений от этого не изменится.
Таким образом, для одного тела, методами статики, мы можем составить максимум шесть независимых уравнений равновесия. В некоторых случаях их число может быть еще меньше.
Так, в случае плоской системы сил, у нас будет всего три независимых уравнения. Чтобы в этом убедиться, выберем систему координат, у которой оси Ox и Oy лежат в плоскости действия сил. Ось Oz перпендикулярна. Тогда проекции всех сил на ось Oz равны нулю. Поэтому уравнение (M.1.z) выполняется автоматически, и его можно вычеркнуть. В уравнениях (M.2.x) и (M.2.y) все силы или пересекают оси Ox и Oy, или параллельны им. Поэтому их моменты относительно этих осей равны нулю. Тогда и уравнения (M.2.x) и (M.2.y) выполняется автоматически. Их также можно вычеркнуть. Остаются три уравнения равновесия (M.1.x), (M.1.y) и (M.2.z).
Неизвестными в уравнениях равновесия являются проекции сил реакций опор на оси координат, или проекции пар сил. При решении этих уравнений могут возникнуть следующие случаи.
- Число неизвестных совпадает с числом линейно независимых уравнений. Тогда задача статически определима, и мы можем получить значения неизвестных реакций, решив линейную систему уравнений.
- Число неизвестных меньше числа линейно независимых уравнений и система не имеет решений – при такой схеме закрепления тела равновесие не возможно.
- Число неизвестных превышает число независимых уравнений – система имеет бесконечное множество решений. Выбрать единственное решение, используя только методы статики, нельзя. Задача является статически неопределимой. Такие задачи решаются методами сопротивления материалов. Например, если балка имеет четыре опоры, то у нас минимум четыре неизвестные величины и три уравнения равновесия (для плоской системы сил). В этом случае, для определения реакций, необходимо учитывать возникающие в балке деформации и напряжения.
Эффективные способы составления уравнений равновесия
Уравнений (M.1) и (M.2) достаточно для определения опорных реакций, но иногда бывает удобным дополнить их другими уравнениями, из которых можно определить реакции более легким способом.
Один из способов заключается в соответствующем выборе начала системы координат. Так, если за ее начало взять точку крепления одной из опор тела, то сила реакции в этой опоре будет пересекать начало координат, и поэтому ее момент будет равен нулю (это не относится к паре сил). Тогда компоненты этих сил реакций не будут входить в уравнения для моментов (M.2.x), (M.2.y), (M.2.z).
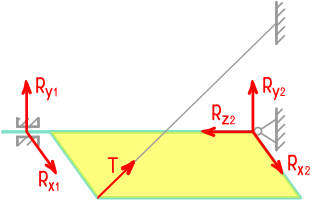
 Спроектировав уравнение равновесия для сил на ось AD, находим реакцию RB
Спроектировав уравнение равновесия для сил на ось AD, находим реакцию RB
Уравнения (М.1.x) – (М.1.z) представляют собой проекции векторного уравнения (М.1) на оси координат. Но это уравнение можно спроектировать на любую ось. Тогда в него не войдут силы, перпендикулярные выбранной оси. На рисунке слева изображено тело ADB. Реакция в скользящей заделке A состоит из силы RA и пары сил с моментом MA; в опоре на катках B – из силы RB. Для определения только одной реакции RB, мы можем спроектировать уравнение для сил на ось AD (см. рисунок). Поскольку реакция перпендикулярна этой оси, то ее проекция на AD равна нулю. Равномерно распределенная нагрузка q, и ее равнодействующая Q также перпендикулярна AD. В результате получим уравнение, содержащее только одну реакцию RB:
;
;
.
Отсюда сразу определяем RB:
.
Поскольку в равновесии сумма моментов сил равна нулю относительно любой точки, то можно выбрать дополнительную точку, и относительно нее составить уравнение для моментов:
.
Число линейно независимых уравнений при этом не изменится, но мы можем дополнить систему более простым уравнением. См. Три формы уравнений равновесия твердого тела.
Вернемся к нашему примеру ⇑. Пусть нам нужно определить только момент . Тогда можно выбрать точку O2 на пересечении линий действия сил и . Поскольку эти силы пересекают O2, то их моменты относительно этой точки равны нулю. Составим уравнение для моментов:
.
Спроектируем его на ось z, перпендикулярную плоскости рисунка:
;
;
.
Отсюда находим :
.
Для трехмерного распределения сил, уравнения (M.2.x), (M.2.y) и (M.2.z) являются проекциями векторного уравнения для моментов (M.2) на оси координат. Но это уравнение можно спроектировать на любую ось, не обязательно параллельной одной из осей системы координат, как мы делали для сил.
Далее приводится подробно разобранный пример решения задачи, в котором требуемая реакция определяется из одного уравнения за счет соответствующего выбора оси, относительно которой вычисляются суммы моментов сил.
Определение реакций опор твердого тела – решение задачи
Автор: Олег Одинцов . Опубликовано: 30-10-2017 Изменено: 06-01-2022
Как определить реакции опор или найти опорные реакции: для балки или рамы
Что такое реакция опоры или опорная реакция?
Реакция опоры или опорная реакция – это силовой фактор, возникающий в опоре, от действия на конструкцию внешней нагрузки. В опорах, как правило, возникают реактивные силы, которые для удобства ручного расчета раскладываются на две составляющие: вертикальную и горизонтальную проекции. В жестких заделках, которые ограничивают все степени свободы конструкций, в том числе поворот сечений, также могут появляться реактивные моменты.
Зачем определять реакции опор?
На элементы конструкций всегда наложены какие-то связи, в виде опор, жестких заделок, стержней, которые ограничивают степени свободы конструкций. Под действием внешней нагрузки в этих связях возникают реакции. И эти реакции опор нужно обязательно учитывать при расчетах на прочность, жесткость и т. д., так как они являются внешними нагрузками. Практически любая задача по сопромату начинается с нахождения реакций связей, именно поэтому статья будет одной из первых на этом сайте.
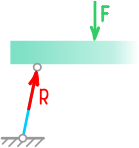
Пример определения опорных реакций для балки
Давайте рассмотрим пример, на котором я покажу как определяются реакции опор. Причем, постараюсь объяснить максимально просто, буквально на пальцах.
Возьмем простую балку, загруженную сосредоточенной силой F, под действием которой в опорах появляются реакции RA и RB. Также сразу вводим систему координат x, y:
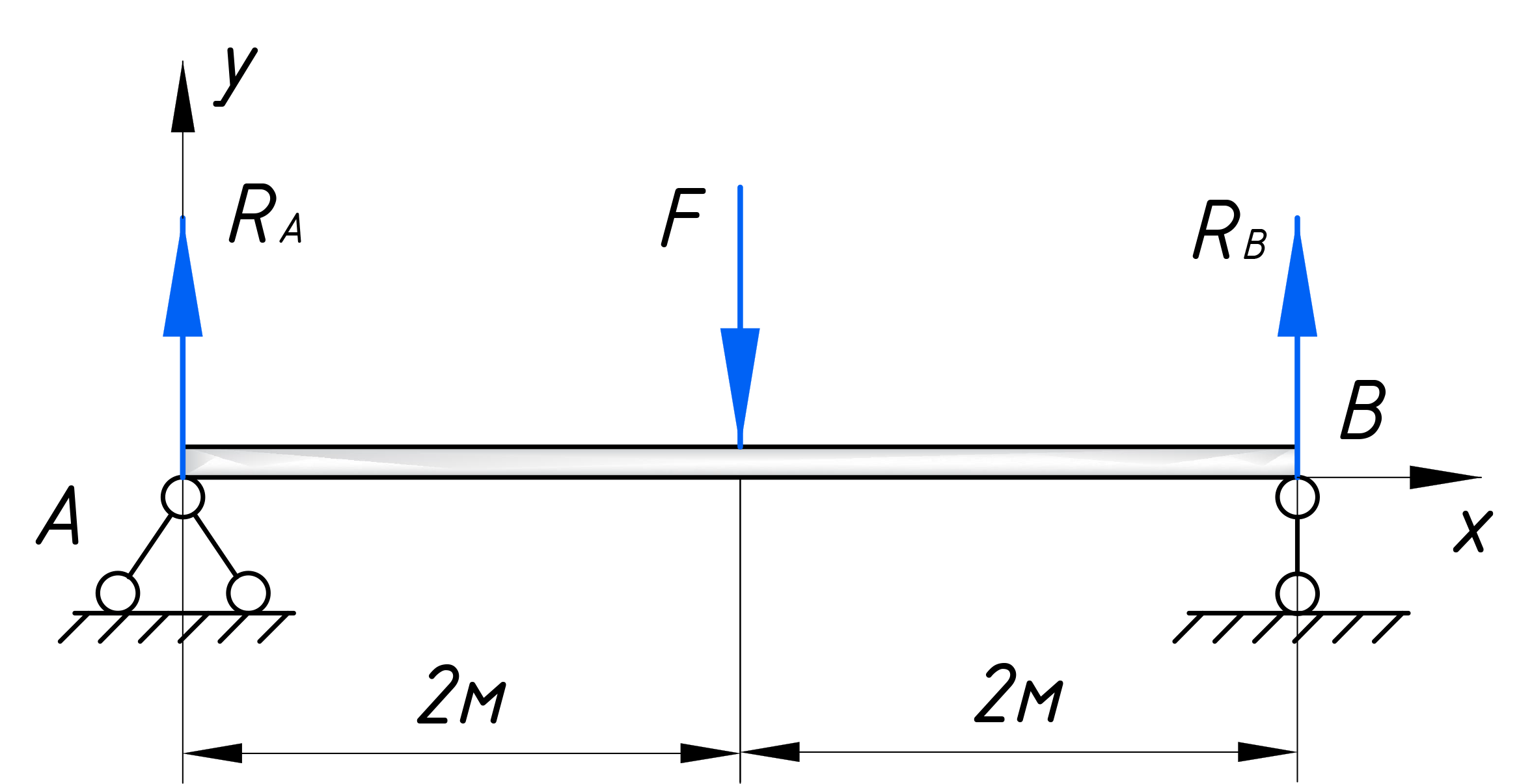
Чтобы узнать численное значение эти реакций, воспользуемся первой формой уравнений равновесия:
Первое уравнение равновесия
Записываем первое уравнение. Так как оси x не параллельна ни одна из сил, то соответственно сумма проекций сил на эту ось будет равна нулю:
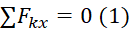
Таким будет первое уравнение для этой расчетной схемы.
Второе уравнение равновесия
Второе уравнение, связанно с проекциями на вертикальную ось. Здесь все намного лучше, все силы параллельны этой оси, а значит дадут проекции. Вопрос только с каким знаком, каждая сила пойдет в уравнение. Если направление силы, совпадает с направлением оси, то в уравнение она пойдет со знаком «плюс» (RA и RB). Если же сила направленна в противоположную сторону, как F, в нашем случае, то в уравнении будем записывать ее с минусом. Таким образом, получим второе уравнение равновесия:
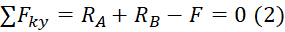
Как видите, во втором уравнении у нас находится 2 неизвестные реакции. Чтобы, наконец, решить задачу, давайте запишем третье уравнение равновесия.
Третье уравнение равновесия
Это уравнение отличается от первых двух, так как тут речь идет о моментах. Напомню, момент – это произведение силы на плечо. В свою очередь, плечо – это перпендикуляр, опущенный от центра момента до линии действия силы. То есть это кратчайшее расстояние от центра момента до силы. В качестве центра моментов у нас назначена точка A, по условию сумма моментов всех сил должна быть равна нулю относительно этой точки.
 Начинаем рассуждать и записывать уравнение. Реакция RA не дает момента, относительно точки А, так как линия действия этой силы пересекает эту точку и соответственно плечо равно нулю. А там, где нет плеча, нет и момента.
Начинаем рассуждать и записывать уравнение. Реакция RA не дает момента, относительно точки А, так как линия действия этой силы пересекает эту точку и соответственно плечо равно нулю. А там, где нет плеча, нет и момента.
Сила F, относительно точки А, создает момент равный:
Обратите внимание, плечо в данном случае равно 2 метрам. Кроме того, важен знак момента, для этого традиционно используется правило, которое продвинутым студентам известно еще с теоретической механики:
- Если сила, относительно произвольного центра, поворачивает ПРОТИВ часовой стрелки, то момент силы положительный;
- Если сила, относительно произвольного центра, поворачивает ПО часовой стрелке, то момент силы отрицательный.
Для силы F, как видите, момент отрицательный:
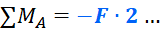
Реакция опоры — RB, создает момент равный RB · 4, так как сила поворачивает против часовой стрелки, то в уравнение записываем его со знаком плюс:
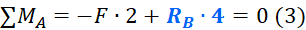
Вычисление реакций опор
Вот собственно и все, все уравнения составлены. Теперь осталось только решить их и найти искомые значения реакций опор (F=2 кН):
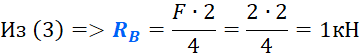
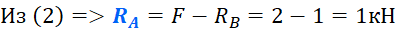
В этой статье, мы рассмотрели достаточно простой пример. Если вы хотите развить свои навыки по определению реакций опор, узнать различные хитрости по их нахождению, научится определять реакции, когда на конструкцию действуют силы под различными углами, учитывать в уравнениях сосредоточенные моменты и распределенную нагрузку, приступайте к изучению статьи – как определить реакции опор для балки.
[spoiler title=”источники:”]
http://1cov-edu.ru/mehanika/statika/opredelenie-reaktsij-opor-tverdogo-tela/
http://sopromats.ru/sopromat/opredelenie-reaktsiy-opor/
[/spoiler]
