Как найти реакцию связи в теоретической механике

Связями называют тела, ограничивающие свободу перемещения рассматриваемого тела.

Реакции связей — это усилия, с которыми связи действуют на данное тело.

Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными.

Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

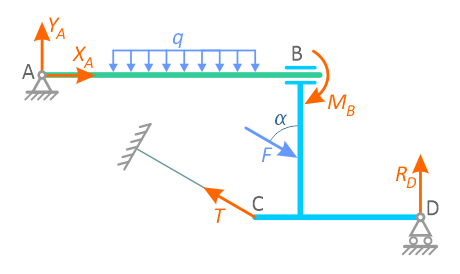
Очень важно правильно расставить реакции связей, иначе написанные уравнения окажутся неверными.

Рассмотрим реакции связей основных типов, встречающихся при решении задач: гладкой поверхности, ребра, гибкой нити, стержня, шарнирных опор и заделок, а также примеры замены связей их реакциями.

Реакции гладкой поверхности и ребра

Ниже приведены примеры замены связей гладкой поверхности и ребра их реакциями.
На рисунках 1.1–1.8 показаны примеры замены реакциями сил, расположенных в плоскости.

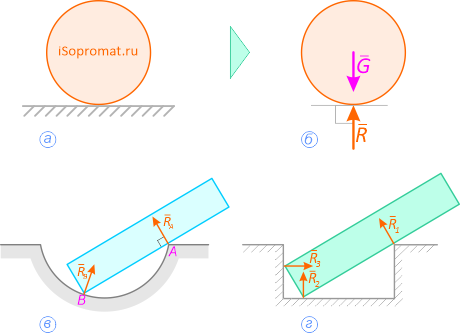
а – тело весом G на гладкой поверхности;
б – действие поверхности заменено реакцией – силой R;
в – в точке А связь «опорная точка» или ребро;
г – реакции направлены перпендикулярно
опираемой или опирающейся плоскостям

Рисунок 1.1

Реакция гладкой поверхности всегда направлена по нормали к этой поверхности (рисунок 1.1).

Реакции связей нити и стержня

Реакция «невесомого» троса (нити, цепи, стержня) всегда направлена вдоль самого троса (нити, цепи, стержня) (рисунок 1.2).

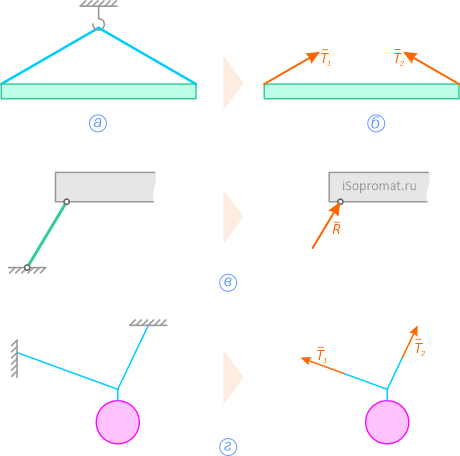
а – балка висит на двух тросах;
б – действие тросов заменено силами Т₁ и Т₂;
в – связь «идеальный стержень»;
г – связь «идеальная нить»

Рисунок 1.2

Реакции связей шарнирных опор

Шарнирные опоры допускают вращение относительно шарнира, поэтому в них не возникает вращающий момент.

Шарнирно-неподвижная опора может изображаться по-разному (рисунок 1.3,а или 1.3,б). Она может быть заменена либо силой R с углом α (рисунок 1.3,в), либо двумя силами, например, X_A и Y_A (рисунок 1.3,г).

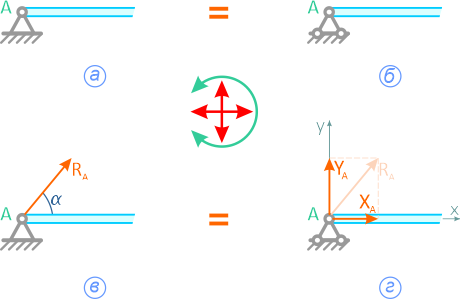
Рисунок 1.3

Всегда можно перейти от R и α к X_A и Y_A (и наоборот):

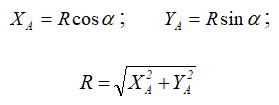
Шарнирно-подвижная опора (рисунок 1.4,а, б, в) допускает (в данном случае) горизонтальное перемещение и не допускает вертикальное.

Реакция R может быть направлена только по нормали к опорной поверхности (рисунок 1.4, г).

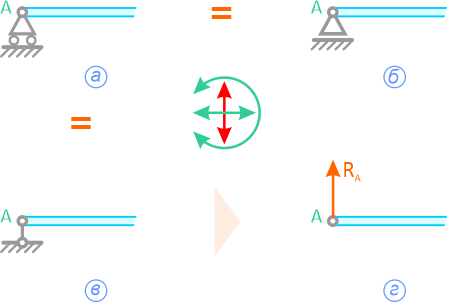
Рисунок 1.4

В следующем примере, связи шарнирно-неподвижной опоры в точке A и шарнирно-подвижной опоры в точке B отброшены (рисунок 1.5, б), а их действие заменено силами X_A, Y_A и R_B.

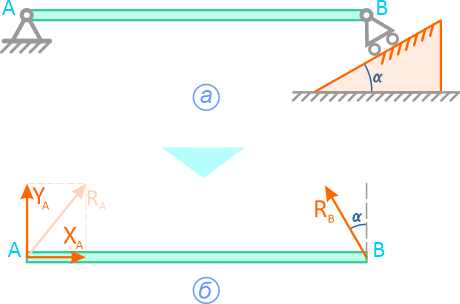
Рисунок 1.5

Подробнее про связи и реакции связей смотрите в нашем видео:

Другие видео

Реакции связи в заделках

Все виды заделок исключают поворот, поэтому в них всегда возникает связь «момент».

Соединение стержня и втулки в плоскости (рисунок 1.6) – скользящая заделка. Отбросив втулку – получаем действие на стержень силы R_D и момента M_D.

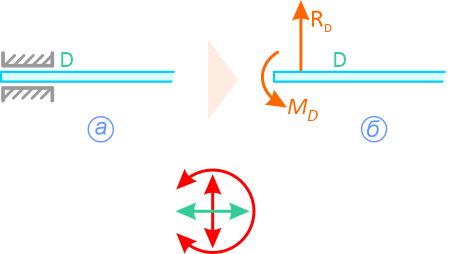
Рисунок 1.6

На рисунке 1.7, а изображена бискользящая заделка. В плоскости данная опора допускает поступательное перемещение стержня как по горизонтали, так и по вертикали, но препятствует повороту (в плоскости). Реакцией такой опоры будет только момент M_C (рисунок 1.7, б).

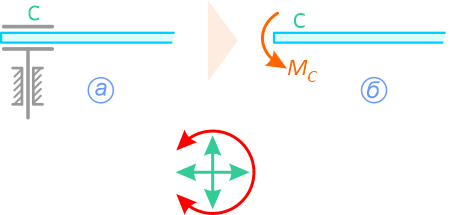
Рисунок 1.7

Консоль (глухая или жесткая заделка) не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила R_A с углом α (или X_A и Y_A) и момент Μ_A (рисунок 1.8).

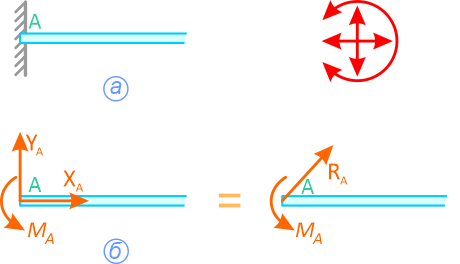
Рисунок 1.8

Реакции пространственных связей

Трехмерная шарнирно-неподвижная опора, или сферический шарнир (рисунок 1.9, а), заменяется системой сил (рисунок 1.9, б) X_A, Y_A и Z_A, т.е. силой, неизвестной по величине и направлению.

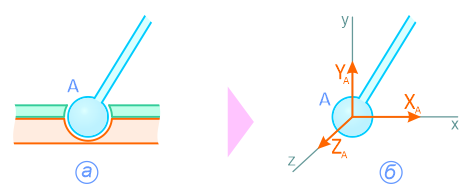
Рисунок 1.9

На рисунке 1.10, а показан вал с колесом, закрепленный в опорах: в точке A – подпятник или стакан, в точке B – втулка или подшипник. Действие опор заменено силами X_A, Y_A, Z_A и X_B, Z_B (рисунок 1.10, б).

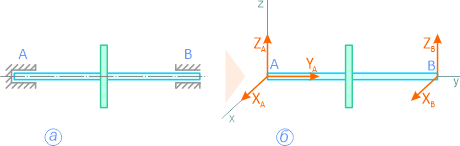
Рисунок 1.10

На следующих рисунках показаны примеры замены различных типов связей их реакциями.

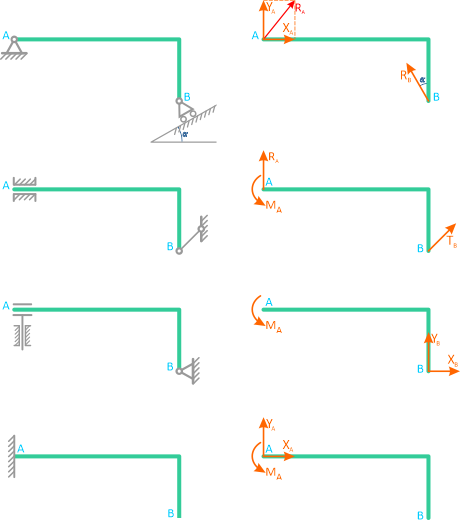
Рисунок 1.11

Трехмерная система удерживаемая в равновесии тремя типами связей: скользящей заделкой, шарнирно неподвижной опорой и тросом.

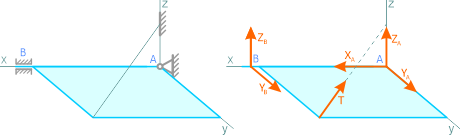
Рисунок 1.12

В общем случае пространственного нагружения, в глухой заделке может возникать до шести реакций связей: три силы и три момента.

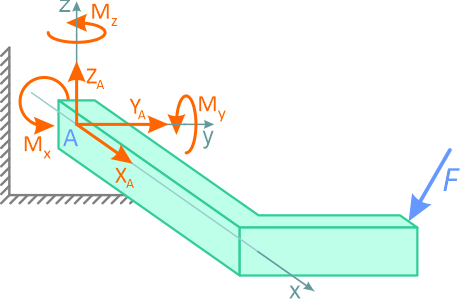
Рисунок 1.13

Величина и истинное направление сил реакций связей определяются из уравнений равновесия рассматриваемой системы.
Для плоской системы сил составляется 3 уравнения

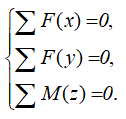
Для пространственной системы — до шести уравнений статики.

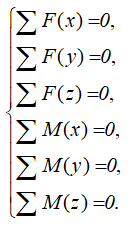
Из которых выражаются и рассчитываются искомые реакции.

Пример определения сил реакций связей

Задача
Жесткая рама закреплена в точке A шарнирной связью, а в точке B удерживается в состоянии статического равновесия опорой на катках, с упором в наклонную плоскость под углом 30°.

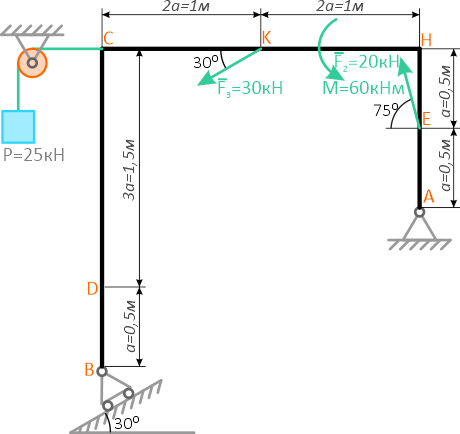
В точке C к раме привязан трос, перекинутый через блок и несущий на конце груз весом P=25кН.
На раму действует пара сил с моментом M=60кНм и две силы F₂ и F₃ приложенные в точках K и E и расположенные под углами 30° и 75° к горизонтальной оси.

Требуется определить реакции связей в точках A и B, вызываемые заданными действующими нагрузками.
При расчетах, принять размер a=0,5м.

Решение
Рассмотрим равновесие рамной пластины.
Проведем координатные оси x-y и изобразим действующие на пластину внешние нагрузки: силы F, пару сил с моментом M, натяжение троса T (по модулю T=P) и реакции связей X_A, Y_A, R_B.

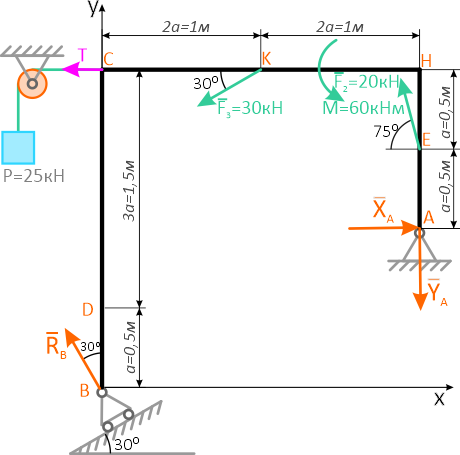
Реакцию неподвижной шарнирной опоры A изображаем двумя составляющими её связями. Реакция на катке направлена перпендикулярно опорной плоскости.
Для полученной плоской системы сил составим три уравнения равновесия системы.

При вычислении моментов сил F относительно точки A воспользуемся теоремой Вариньона, т.е. разложим силы на составляющие F_x=Fcosα и F_y=Fsinα и учтём что m_A(F)=m_A(F_x)+m_A(F_y).

Запишем уравнения сумм проекций сил на оси x и y, а также суммы моментов относительно любой точки системы, например, точки A.

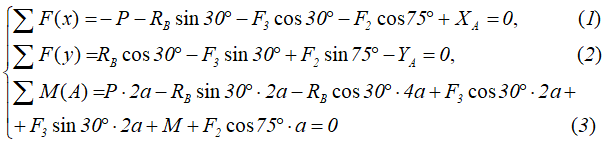
Решая полученную систему уравнений, определяем неизвестные реакции связей катка и шарнирно-неподвижной опоры.

Из уравнения (3) находим реакцию катка

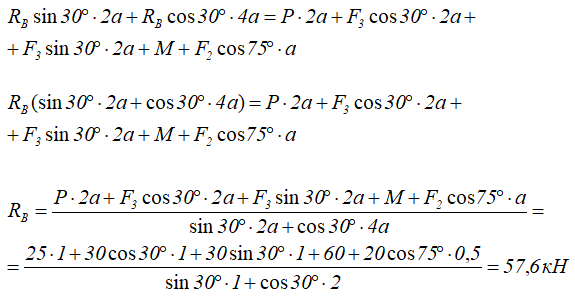
Из уравнения (1) горизонтальную реакцию в точке A

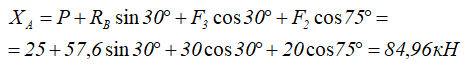
Из уравнения (2) — вертикальную.

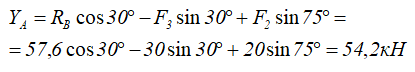
Положительные значения найденных реакций говорят о том, что направление связей было выбрано, верно.

Проверку можно выполнить, составив уравнение суммы моментов, в котором будут записаны все искомые реакции, например, относительно точки D:

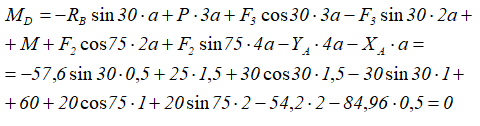
Ноль, полученный в ответе, означает правильность составления и решения уравнений

Ответ: Получены следующие значения сил реакций связей: в катке R_B=57,6кН, в шарнирной опоре X_A=84,96кН и Y_A=54,2кН.

Другие примеры решения задач >
Проекция силы на ось >

Связи и их реакции

Тело, перемещению
которого в пространстве препятствует
какие-нибудь другие тела, скрепленные
или соприкасающиеся с данным, называется
несвободным.
Все то, что ограничивает перемещение
данного тела в пространстве, называется
связями.

Пример. Груз висит
на веревке, ящик стоит на полу и т.д.

Сила, с которой
данная связь действует на тело, препятствуя
тем или иным его перемещениям, называется
силой реакции
(противодействия) связи
или просто
реакцией связи.

Силы, приложенные
к телу, но не являющиеся реакциями,
называются активными.

Направление силы
реакции связи противоположно той, куда
связь не дает перемещаться телу.

Направления реакций некоторых основных видов связи

1. Гладкая поверхность

Реакция
связиN
гладкой поверхности или опоры направлена
по нормали к поверхностям соприкасающихся
тел в точке касания и приложена в этой
точке.

а) б) в)

Рис. 1.5

Если одна из
соприкасающихся поверхностей является
точкой, то реакция направлена по нормали
к другой поверхности (рис. 1.5).

2. Нить, стержень.

Реакция
Т натянутой нити и нагруженного стержняS
направлена вдоль этих связей и приложена
в точке контакта (рис. 1.6).

а) б)

Рис. 1.6

3.
Цилиндрический шарнир (подшипник,
петля).

РеакцияR
цилиндрического шарнира лежит в
плоскости, перпендикулярной оси шарнира,
и может иметь любое направление в этой
плоскости. Для определения R
ее раскладывают на два взаимноперпендикулярных
направления: R_x
и R_y
(рис. 1.7).

Рис. 1.7

4.
Подвижная шарнирная опора.

Реакция
связиR
направлена перпендикулярно плоскости
возможного перемещения шарнира (рис.
1.8).

5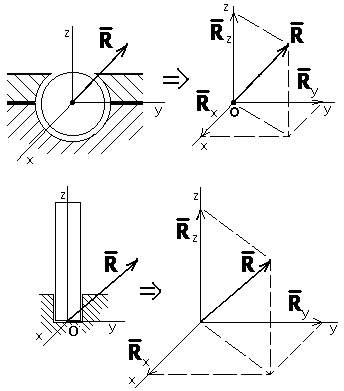

Рис. 1.8

а)

б)

Рис. 1.9

. Шаровый шарнир и подпятник (рис.
1.9, рис. 1.10).

а) б)

Рис. 1.10

Реакция
шарового шарнира и подпятника может
иметь любое направление в пространстве.

А

Рис. 1.11

ксиома связей. Всякое
несвободное тело можно рассматривать
как свободное, если отбросить связи и
заменить их действие реакциями этих
связей (рис. 1.11).

Сложение сил

Геометрический
способ сложения сил

В

а)

б)

Рис. 1.12

еличина, равная геометрической
сумме сил какой-либо системы называется
главным вектором этой системы сил.

Пусть
на твердое тело действует плоская
система сил (F₁,
F₂,
F₃,
…, F_n)
(рис. 1.12).

Из
произвольно выбранной точки О откладывается
векторF₁,
из его конца откладывается вектор F₂
и т.д. Вектор R,
замыкающий силовой многоугольник,
является результирующим:

Сложение двух сил

Пусть на тело
действуют две силы, лежащие в одной
плоскости (рис. 1.13).

.

Р

Рис. 1.13

езультирующая сила определяется
по правилу параллелограмма, модуль силы
определяется по теореме косинусов или
синусов:

; .

Сложение трех
сил не лежащих в одной плоскости

Рассмотрим
три силы,,не лежащие в одной плоскости (рис. 1.14).
Результирующая силаравна:

.

Направление силы
определим по направляющим косинусам:

Рис. 1.14

;
;
.

Разложение сил

Разложение сил
по двум заданным направлениям

Пусть
надо силуF
разложить по направлениям AB
и AD
(рис. 1.15).

Рис. 1.15

.

Задача сводится
к построению параллелограмма, у которого
стороны расположены по направлениям
AB
и AD
и данная сила F
является диагональю. Тогда стороны
параллелограмма будут искомыми силами.

Разложение сил
по трем заданным направлениям.

П

Рис. 1.16

усть направления силы не лежат в
одной плоскости. Тогда задача сводится
к построению параллелепипеда, у которого
диагональю является данная сила, а ребра
параллельны заданным направлениям
(рис. 1.16).

.

Вопросы для
самоконтроля

1. Что изучает
   статика?

2. Что такое абсолютно
   твердое тело?

3. Основные виды
   связей и их реакции?

4. Геометрическое
   сложение сил?

Задачи, рекомендуемые
для самостоятельного решения: 1.1 – 1.6
[2]

Литература: [1],
[3],
[4].

Лекция 2.

Действия над
силами. Система сходящихся сил

Проекция силы
на ось и на плоскость

Проекция
силы на ось.
Пусть сила F
образует с осью OX
угол 
(рис. 2.1), тогда проекция этой силы на ось
будет:

F_x
= Fcos.

П

Рис. 2.1

роекция силы на ось есть величина
скалярная.

Проекция
силы на плоскость.
Проекцией силы F
на плоскость OXY
называется вектор F_xy
= OB₁,
заключенный между проекциями начала и
конца силы F
на эту плоскость (рис. 2.2.)

П

Рис. 2.2

роекция силы на плоскость есть
величина векторная, так как она кроме
численного значения характеризуется
направлением на плоскости. По модулюF_xy
= Fcos,
где 
– угол между направлением силы F
и ее проекцией F_xy.

Аналитический
способ задания сил.
Для аналитического способа задания
силы необходимо выбрать систему координат
OXYZ
и спроектировать силу на оси координат
(рис. 2.3).

Направляющие
косинусы определяются по формулам:

Рис. 2.3

;

;

.

.

Для плоской системы
сил:

;

;

;

.

Соседние файлы в папке 3й курс 5 семестр

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Содержание:

1. Связи и их классификация
2. Пример с решением задачи 1.
3. Пример с решением задачи 2.

Связи и их классификация

В механике необходимо более подробно рассмотреть связи, налагаемые на точки механической системы. Механической сиотемой, как известно, называют любую совокупность материальных точек. Условия, ограничивающие свободу перемещения точек механической системы, называютя связями. Математически связи могут быть выражены уравнениями или неравенствами, в которые входят время, координаты всех или части точек системы и их производные по времени различных порядков. Для одной точки уравнение связи в общем случае можно выразить в форме

В дальнейшем ограничимся рассмотрением связей, в уравнения которых могут входить производные по времени от координат не выше первого порядка.

Для механической системы, состоящей из точек, уравнений связей представятся системой уравнений

Считается, что индекс принимает все или часть значений от до как для координат, так и для их производных.

Если в уравнения связей (2) входят только координаты точек и не входят производные от координат, то связи называются геометрическими. Уравнение геометрической связи для системы имеет форму

Если в уравнения связей кроме координат входят еще и их производные по времени (проекции скоростей точек на оси координат) или только одни производные, кроме времени, то связи называются кинематическими. В этом случае уравнения связей являются дифференциальными уравнениями для координат точек.

Из геометрических связей дифференцированием можно получить связи кинематические. Из кинематических связей геометрические получаются не всегда, так как дифференциальные уравнения не всегда могут быть проинтегрированы.

Иногда дифференциальное уравнение связи можно представить как производную по времени от некоторой функции координат и, возможно, времени

После интегрирования такая кинематическая связь становится геометрической.

Все геометрические и интегрируемые кинематические связи называются голономными. Неинтегрируемые кинематические связи, которые нельзя свести к геометрическим, являются неголономными. Важный класс механических систем о неголономными связями (неголоном-ных систем) интенсивно исследуется в настоящее время, и эти исследования еще далеки от завершения. В дальнейшем изложении систематически системы с такими связями не рассматриваются.

Возможно вам будут полезны данные страницы:

При движении механической системы координаты точек и их производные по времени, входящие в уравнения связей, могут зависеть от времени. Кроме того, в уравнения связей время может входить явно, помимо координат и их производных. Связи, в уравнения которых время явно не входит, называются стационарными или склерономными. Если время входит явно в уравнение связи, то связь называется нестационарной или реономной. Нестационарные связи обычно реализуются посредством движущихся или деформирующихся тел.

В простейшем случае одной точки нестационарная геометрическая связь в форме движущейся или деформируемой поверхности имеет уравнение

Связи называют неосвобождающими или двусторонними, если они выражаются математически уравнениями, и освобождающими или од-посторонними, если они выражаются неравенствами. Для одной точки скрепленной с концом жесткого стержня, другой конец которого закреплен в неподвижной точке связь (жесткий стержень) является геометрической, неосвобождающей (рис. 94). Ее уравнение

где — длина стержня. Если стержень заменить нитью такой же длины, то связь (нить) будет освобождающей. Она математически выражается неравенством

Если при движении точка окажется от точки на расстоянии, меньшем длины нити, то нить уже не стесняет свободу перемещения точки. Связь освобождает точку от своего действия (пунктир на рис, 94). В дальнейшем освобождающие связи рассматривать не будем.

Все связи можно разделить на реальные и идеальные. К идеальным связям относятся все связи без трения. Некоторые связи g трением тоже относятся к идеальным. Понятие идеальных связей дается после введения понятия возможного перемещения системы.

Для формулирования принципа возможных перемещений, определяющего условия равновесия механической системы, требуется ввести понятие возможного, или виртуального, перемещения. Для одной точки возможным перемещением называется такое бесконечно малое (э.гементарное) мысленное перемещение, которое допускается в рассматриваемый момент времени наложенными на точку связями. Для возможного перемещения не требуется времени на его совершение. Это мысленное перемещение, которое могла бы совершить точка при наложенных на нее связях в рассматриваемый момент времени. В отличие от элементарного (бесконечно малого) действительного перемещения точки которое совершает точка за время под действием приложенных сил при заданных начальных условиях и наложенных связях, возможное перемещение определяется только связями в данный момент Проекции возможного перемещения на оси координат, или вариации координат, обозначают а проекции элементарного действительного перемещения на оси координат, или дифференциалы координат при изменении времени на обозначают

Если связью для точки является, например, движущаяся поверхность, уравнение которой то действительное перемещение точки за время является в общем случае векторной суммой перемещений по поверхности и вместе с поверхностью. Все возможные перемещения точки в данный момент времени расположатся на поверхности в попожении, которое она занимает в рассматриваемый момент времени. Действительное перемещение при заданных начальных условиях и силах, которое точка может совершить от момента времени до момента только одно. Возможных перемещений у точки в момент времени бесконечно много.

• Все они допускаются связью (поверхностью) и как отрезки бесконечно малой длины расположатся в касательной плоскости к поверхности в точке, в которой находитсл рассматриваемая точка в данный момент времени.

Возможное перемещение как и действительное является вектором и потому всегда изображаемся направленным прямолинейным отрезком Очевидно, что элементарное действительное перемещение точки принадлежит к чисау возможных, если связь стационарна, т. е действительное перемещение не содержит перемещения ьместе со связью.

Возможное перемещение точки считают изохронной вариацией радиус-вектрра. т. е. его полным дифференциалом, но при фиксированном времени, когда изменяются (варьируются) только координаты точки. Соответственно — изохронные вариации координат точки. допускаемые связями. Действительное перемещение является полным дифференциалом радиус-вектора, который определяется по изменению координат точки в зависимости от изменения времени; — полные дифференциалы координат точки при изменении независимого переменного на величину

Возможным перемещением системы называют любую совокупность возможных перемещений точек системы. В общем случае система может иметь несколько и даже бесконечно много возможных перемещений. Вследствие уравнений связей, наложенных на систему, не все возможные перемещения являются независимыми. Число независимых возможных перемещений называют числом степеней свободы системы.

Свободная точка имеет три степени свободы. В этом случае возможные перемещения (вариации) (или выраженные через вариации каких-либо других координат) являются независимыми. Если точка движется по поверхности то связаны соотношением

которое получают разложением в степенной ряд функции при пренебрежении слагаемыми второго и более высокого порядка по отношению к Независимых вариаций координат, а следовательно, и степеней свободы будет две. Время при этом не варьируется, оно фиксировано. Связь между вариациями координат не зависит от того, входит время явно в уравнения связей или нет. Проекции на оси координат действительного перемещения точки если связь выражается уравнением в отличие от возможных определяется зависимостью

которая тоже получается разложением в степенной ряд функции и отбрасыванием слагаемых второй и более высоких степеней величин Если точка движется по кривой линии, то степеней свободы у нее будет только одна, так как кривую линию можно представить как пересечение двух поверхностей.

Элементарную работу силы на возможном перемещении ее точки приложения вычисляют_по_ обычным формулам для элементарной работы, например, и другим формулам для элементарной работы. Для механической системы, состоящей из N точек, к которым приложены силы, элементарная работа этих сил на каком-либо возможном перемещении системы соответственно выразится так:

Элементарная работа сил при этом зависит от выбора возможного перемещения системы.

Обозначим силы реакций связей для точек системы Тогда связи системы называются идеальными, если для любого возможного перемещения системы выполняется условие

Условие (6) является определением идеальных связей. Важно отметить, что это условие должно выполняться для всех возможных перемещений системы. При этом вся совокупность связей является идеальной. Может быть идеальной каждая из связей в отдельности. Приведем примеры идеальных связей.

• 1. В абсолютно твердом теле точки связаны идеальными связями. Силами реакций связей в этом случае являются внутренние силы, для которых было доказано, что сумма элементарных работ этих сил на любых элементарных перемещениях точек тела равна нулю.
• 2. Абсолютно гладкая поверхность или абсолютно гладкая линия, является идеальной связью для точки. Возможные перемещения точки с такими связями направлены по касательным к поверхности или линии. Силы реакций в этих случаях направлены по нормалям к ним, т.е. перпендикулярны силам. Так, например, все шарниры (поверхности) без трения, подвижные и неподвижные, являются связями, идеальными для тел, соединенных такими связями. Шарниры без трения, как связи идеальные, эквивалентны связям между точками в твердом теле.
• 3. Гибкие нерастяжимые связи типа нитей, канатов, тросов и т. п., соединяющих точки системы, являются связями идеальными. В каждом сечении такой связи силы реакций (силы натяжения) равны по модулю и противоположны по направлению, а возможные перемещения у их точек приложения одни и те же. Сумма элементарных работ сил натяжении для всех мыслимых сечений таких связей равна нулю.
• 4. Закрепленные точки системы по отдельности являются связями идеальными, так как их возможные перемещения равны нулю.
• 5. Шероховатая поверхность для катков, катящихся по ней без скольжения, при отсутствии трения качения и, следовательно, соприкосновения в одной точке или по одной линии, скорости точек которых равны нулю, является связью идеальной. Возможные перемещения в точке или в точках линии соприкосновения равны нулю в каждый момент времени, так как равны нулю скорости в точках соприкосновения, как и для закрепленных точек.

Принцип возможных перемещений, илн принцип Лагранжа, содер* жит необходимые и достаточные условия равновесия некоторых механических систем. Он формулируется следующим образом: для равновесия механической системы, подчиненной идеальным, стационарным и неосвобождтощим связям, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, приложенных к точкам системы, была равна нулю на любом возможном перемещении системы, если скорости точек системы в рассматриваемый момент времени равны нулю, т. е.

где — активная сила, приложенная к точке системы; — радиус-вектор этой точки (рис. 95).

Докажем необходимость условия (7) для равновесия системы, т. е. докажем, что если система находится в равновесии, то активные силы удовлетворяют условию (7). Действительно, если механическая система находится в равновесии, то для каждой ее точки активная сила и сила реакции связей удовлетворяют условию равновесия статики для сил, приложенных к точке:

Умножая обе части этого равенства скалярно на возможное перемещение точки и суммируя по всем точкам системы, получим

По условию идеальности связей, и для активных сил получаем условие (7).

Докажем достаточность условия (7) для равновесия системы, т. е. что если это условие выполняется для активных сил, действующих на точки системы, то система находится в равновесии при выполнении других условий принципа возможных перемещений. Теорема о достаточности условия (7) для равновесия системы доказывается методом от противного. Предполагается, что условие (7) и все остальные условия теоремы выполняются, а система вышла из равновесия. Если теорема о достаточности справедлива, то должно возникнуть противоречие с условиями теоремы. Итак, пусть все условия теоремы выполняются, а система вышла из равновесия. При этом по крайней мере для одной гочки системы не будет выполняться условие равновесия для сил, т. е.

Дадим системе возможное перемещение. Так как связи стационарные, то элементарное действительное перемещение для каждой точки системы под действием не равной нулю равнодействующей силы принадлежит к числу возможных перемещений и их совокупность можно выбрать в качестве возможного перемещения системы.

Скорости точек системы в рассматриваемый момент времени по условию равны нулю;

Следовательно, элементарные действительные перемещения будут направлены по ускорениям j04eK, т. е. по равнодействующим силам. Умножая (8) скалярно на получим

по крайней мере для одной точки системы, вышедшей из равновесия. Суммируя (9) по всем точкам системы, будем иметь

Для идеальных связей

Поэтому из (9′) получаем

что находится в противоречии с условием (7). Следовательно, система не может выйти из равновесия при выполнении условий принципа возможных перемещений. Принцип полностью доказан.

Без дополнительного условия о равенстве нулю скоростей точек системы в рассматриваемый момент принцип возможных перемещений утверждает только то, что равны нулю ускорения точек системы. Вместе с равенством нулю скоростей точек это дает равновесие системы в тот момент, в который выполняется для активных сил условие (7).

При длительном выполнении этого условия система соответственно будет находиться в равновесии тоже длительно, т. е. скорости и ускорения точек равны нулю, если скорости точек системы равны нулю в начале интервала длительности.

В принцип возможных перемещений не входят силы реакций связей. Но его можно применять также и для определения неизвестных сил реакций связей. Для этого связь, силы реакции которой необходимо определить, отбрасывают (освобождают систему от этой свяаи), заменяя ее силами реакции Эти силы добавляют к активным силам.

Оставшиеся связи системы должны быть идеальными. Иногда неидеальную связь заменяют идеальной, компенсируя неидеальность соответствующими силами. Так, если связью для тела является шероховатая поверхность, то ее можно заменить гладкой поверхностью, добавляя к активным силам силу трения скольжения и в более общем случае — еще и пару сил, препятствующую качению. Связь в виде заделки для твердого тела можно заменить неподвижным шарниром, плоским или шаровым соответственно, добавляя момент заделки, векторный или алгебраический. Таким образом, в принцип возможных перемещений входят в действительности не активные силы, а все приложенные к точкам системы силы, кроме сил реакций идеальных связей, которые по условиям задач не требуется определять.

Пример с решением задачи 1.

В механизме (рис. 96) кривошип может поворачиваться вокруг горизонтальной оси, проходящей через точку

По стержню может перемещаться ползун шарнирно соединенный со стержнем который может скользить вдоль вертикальных направляющих. К кривошипу приложена пара сил с моментом Определить при равновесии механизма вертикальную силу приложенную к стержню в зависимости от угла Силами трения и тяжести звеньев механизма пренебречь. Решение. Связи в механизме стационарные и неосвобождающие. Они не имеют трения, а потому идеальные. Применим к механизму принцип возможных перемещений:

Активными силами являются пара сил с моментом и сила Дадим системе возможное перемещение, повернув мысленно стержень на элементарный угол в сторону возрастания угла Тогда согласно принципу возможных перемещений

где — возможное перемещение точки Стержень твердый, поэтому перемещения его концов и равны, т. е.

У механизма только одна степень свободы, следовательно, и зависят друг от друга. Установим предварительно зависимость от Имеем

Путем варьировании этого уравнения связи, аналогичного вычислению полного дифференциала от обеих частей уравнения, получим

Подставляя это значение в (а) и вынося за скобки, имеем

Величину 0ф можно выОрагь отличной от нуля, а потому

Дополнительно установим зависимость между и непосредственно, не используя процесс варьирования уравнения связи. При повороте стержня на угол точка переместится вместе с соответствующей точкой стержня перпендикулярно стержню на и, кроме того, ползун передвинется вдоль стержня на для того, чтобы точка переместилась только по вертикали на так как другие направления перемещения точки не разрешаются вертикальными направляющими стержня Вектор возможного перемещения точки изобразится диагональю прямоугольника, построенною на перемещениях и Из прямоугольника для его диагонали имеем

или

так как

Пример с решением задачи 2.

Состазная балка состоит из двух балок и шарнирно соединенных в точке Конец балки заделан в стену (рио, 97, а). Определить момент заделки если на балку действуют равные вертикальные силы а также момент пары сил. Размеры указаны на рисунке. Силами тяжести балок пренебречь.

Решение. Заменим заделку в для плоской системы приложенных сил плоским шарниром и моментом заделки (рис. 97, 6), Оставшиеся связи являются идеальными, если пренебречь трением в шарнирах и катковой опоре. Они стационарные и неоевобождающие. Применим к составной балке (после замены заделки шарниром и моментом заделки) принцип возможных перемещений:

Приложенными силами являются и пары сил с моментами и

Дадим системе возможное перемещение, повернув мысленно балку на элементарный угол вокруг Связи допускают такое перемещение Составная балка займет положение, показанное на рисунке пунктиром. Катковая опора при этом смещается в горизонтальном направлении, но приложенные силы не совершают работы на горизонтальных перемещениях.

Согласно принципу возможных перемещений,

Отрицательной является элементарная работа тех сил, возможные перемещения точек приложения которых противоположны направлению действия сил. Аналогично определены знаки элементарной работы моментов пар сил, возможные перемещения следует брать как прямолинейные отрезки, направленные по касательным к дугам окружностей, т. е по лииням действия сил.

У составной балки только одна степень свободы, и поэтому она имеет одно произвольное возможное перемещение, например Для остальных возможных перемещений имеем;

Возможное перемещение точки выражается через углы и

поэтому

Подставляя полученные значения возможных перемещений в (а) и учитывая, что получим

Так как то

Связи и реакции связей

Все
законы и теоремы статики справедливы для свободного твердого тела.

Все
тела делятся на свободные и связанные.

Свободные
тела — тела, перемещение которых не ограничено.

Связанные
тела — тела, перемещение которых ограничено дру­гими телами.

Тела, ограничивающие перемещение других
тел, называют свя­зями.

Силы,
действующие от связей и препятствующие перемещению, называют реакциями
связей.

Реакция
связи всегда направлена с той стороны, куда нельзя перемещаться.

Всякое связанное тело можно представить свободным,
если связи заменить их реакциями (принцип освобождения от связей).

Все
связи можно разделить на несколько типов.

Связь — гладкая опора (без
трения)

Рисунок 1

Реакция
опоры приложена в точке опоры и всегда направлена перпендикулярно опоре (рис.
1).

Гибкая связь (нить,
веревка, трос, цепь) Груз подвешен на двух нитях (рис. 2).

Рисунок 2

Жесткий стержень

На
схемах стержни изображают толстой сплошной линией (рис. 3).

Рисунок 3

Стержень
может быть сжат или растянут. Ре­акция стержня направлена вдоль стержня. Стер­жень
работает на растяжение или сжатие. Точное направление реакции определяют,
мысленно убрав стержень и рассмотрев возможные перемещения те­ла без этой
связи.

Возможным перемещением точки
называется такое бесконечно малое мысленное перемещение, которое допуска­ется в
данный момент наложенными на него связями.

Убираем
стержень 1, в этом случае стержень 2 падает вниз. Сле­довательно, сила от
стержня 1 (реакция) направлена вверх. Убираем стержень 2. В этом случае точка А
опускается вниз, отодвигаясь от стены. Следовательно, реакция стержня 2
направлена к стене.

Шарнирная опора

Шарнир
допускает поворот вокруг точки закрепления. Различа­ют два вида шарниров.

Подвижный шарнир

Стержень,
закрепленный на шарнире, может поворачивать­ся вокруг шарнира, а точка
крепления может перемещаться вдоль направляющей (площадки) (рис. 4).

Рисунок 4

Реакция
подвижного шарни­ра направлена перпендикулярно опорной поверхности, т. к. не допускается только перемещение поперек опорной
поверхности.

Неподвижный шарнир

Точка
крепления пере­мещаться не может. Стер­жень может свободно повора­чиваться
вокруг оси шарни­ра. Реакция такой опоры про­ходит через ось шарнира, но
неизвестна по направлению. Ее принято изображать в ви­де двух составляющих:
горизонтальной и вертикальной (Rx;
Rу)
(рис. 5).

Рисунок 5

Защемление или «заделка»

Любые перемещения точки крепле­ния
невозможны.

Под
действием внешних сил в опоре возникают реактивная сила и реактив­ный момент М_R,
препятствующий пово­роту (рис. 6).

Рисунок 6

Реактивную силу принято предста­влять в виде двух
составляющих вдоль осей координат

Примеры решения задач

Пример 1. Груз подвешен на
стержнях и канатах и находится в равновесии (рис. 7). Изобразить систему сил,
действующих на шарнир А.

Рисунок 7

Решение

1.
Реакции стержней направлены вдоль стержней, реакции гибких связей направлены
вдоль нитей в сторону натяжения (рис. 7а).

2.
Для определения точного направления усилий в стержнях мы­сленно убираем
последовательно стержни 1 и 2. Анализируем воз­можные перемещения точки А.

Неподвижный
блок с действующими на него силами не рассма­триваем.

3.
Убираем стержень 1, точка А поднимается и отходит от сте­ны,
следовательно, реакция стержня 1 направлена к стене.

4.
Убираем стержень 2, точка А поднимается и приближается к стене,
следовательно, реакция стержня 2 направлена от стены вниз.

5.
Канат тянет вправо.

6.
Освобождаемся от связей (рис. 7б).

Пример 2. Шар подвешен на
нити и опирается на стену (рис. 8а). Определить реакции нити и гладкой опоры
(стенки).

Рисунок 8

Решение

1.
Реакция нити — вдоль ни­ти к точке В вверх (рис. 8б).

2.
Реакция гладкой опоры (стенки) — по нормали от поверх­ности опоры.

Контрольные вопросы и задания

4.
Укажите возможное направление реакций в опорах (рис. 9).

Рисунок 9