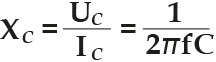Реактивное сопротивление XL и XC
Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.
Элементы, обладающие реактивным сопротивлением, называют реактивными.
Реактивное сопротивление катушки индуктивности.
При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении – положительна и препятствует его убыванию,
оказывая таким образом сопротивление изменению тока на протяжении всего периода.
В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС,
равное ей по амплитуде и противоположное по знаку.
При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения,
что образует расхождение во времени тока и напряжения в 1/4 периода.
Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС,
равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.
Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая
пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток 
Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока 
сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать 
В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома,
где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:
Реактивное сопротивлениие индуктивностей называют индуктивным.
Реактивное сопротивление конденсатора.
Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда –
накопления и отдачи энергии электрическим полем между его обкладками.
В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное.
Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю.
Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току,
обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее
уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума.
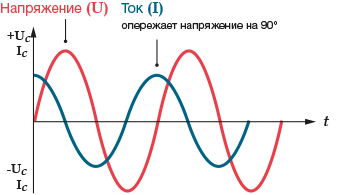
Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = Uampsin(ωt)
запишем выражение мгновенного значения тока следующим образом:
i = UampωCsin(ωt+π/2).
Отсюда выразим соотношение среднеквадратичных значений 
Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:
Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.
Калькулятор расчёта реактивного сопротивления
Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.
Расчитать реактивное сопротивление ёмкости или индуктивности:
Реактивное сопротивление ёмкости
XC = 1 /(2πƒC)
Реактивное сопротивление индуктивности
XL = 2πƒL
Расчитать ёмкость и индуктивность от сопротивления:
Расчёт ёмкости: C = 1 /(2πƒXC)
Расчёт индуктивности: L = XL /(2πƒ)
Похожие страницы с расчётами:
Расcчитать импеданс.
Расcчитать частоту резонанса колебательного контура LC.
Расcчитать реактивную мощность и компенсацию.
Всё о реактивном сопротивлении конденсатора
Содержание
- 1 Конструктивные особенности конденсатора
- 2 Как проверить конденсатор омметром
- 3 Как добиться протекания электротока через конденсатор
- 4 Реактивное сопротивление конденсатора
- 5 Пример расчета емкости в цепи переменного тока
- 6 Видео по теме
Сопротивление конденсатора или емкости (емкостное сопротивление) — это мера противодействия изменению тока в этом компоненте. Согласно определению, электросопротивление характеризует противодействие электрической цепи в целом или отдельного ее компонента электротоку.
Конструктивные особенности конденсатора
В отличие от омического сопротивления, вызывающего безвозвратные потери энергии в цепи, при использовании идеальной емкости потерь электрической энергии нет. Конструктивно конденсатор — это две токопроводящие обкладки, разделенные слоем непроводящего диэлектрика. Из чего следует, что компонент не пропускает постоянный ток. Конструкция конденсатора предполагает бесконечное его сопротивление.
Как проверить конденсатор омметром
Существует простой экспериментальный способ проверки целостности конденсатора омметром. При подключении к щупам омметра (самая простая схема которого — включенные последовательно элемент питания, резистор и чувствительный микроамперметр) исправного компонента стрелка прибора резко отклоняется (определяется емкостью конденсатора), после чего возвращается к началу шкалы.
Если «бесконечное» сопротивление связано с изолирующими свойствами диэлектрика, бросок показаний можно объяснить лишь кратковременным протеканием тока через конденсатор при подключении его к источнику напряжения. При полной зарядке идеального конденсатора до напряжения элемента питания прохождение тока через него прекращается.
Как добиться протекания электротока через конденсатор
Чтобы добиться протекания электротока через конденсатор в противоположном направлении, достаточно переполюсовать источник напряжения. Отсюда логический вывод — при постоянном изменении на выводах конденсатора полярности источника питания ток через конденсатор будет непрерывным, что можно интерпретировать как оказание им некоторого конечного сопротивления протекающему через него току.
При переполюсовке источника напряжения на конденсатор, по сути, подается переменное напряжение прямоугольной формы. При этом форма тока через компонент не повторяет форму напряжения на нем. И лишь при подаче переменного синусоидального напряжения через конденсатор протекает переменный синусоидальный ток.
Реактивное сопротивление конденсатора
Воспользовавшись законом Ома, можно приписать конденсатору определенное электрическое «сопротивление». Этот параметр может быть рассчитан как результат деления напряжения на компоненте к току через него. Но в отличие от резистора, где переменный ток совпадает по фазе с напряжением, емкостный ток в конденсаторе опережает напряжение на 90 градусов.
Чем чаще меняется полярность переменного напряжения на конденсаторе (чем выше его частота), тем больше протекающий ток. Из этого следует, что емкостное или реактивное сопротивление конденсатора обратно пропорционально частоте тока.
Исходя из математических соображений, разнице фаз между током и напряжением в 90 градусов соответствует мнимое сопротивление. Отсюда выводится формула, с помощью которой можно найти емкостное сопротивление конденсатора:
Иногда для емкостного сопротивления конденсатора используют положительное число, равное 1/(2πfC). Этого достаточно для вычисления тока через компонент при приложении к нему определенного переменного напряжения и решения обратной задачи. Расчет экспериментально определяемого реактивного сопротивления конденсатора осуществляется по напряжению на нем и току через него.
Но при включении конденсатора в сложную электрическую цепь (с резисторами и индуктивностями) не следует забывать о том, что в общем виде его сопротивление мнимое. Используя математические формализмы (действия с комплексными числами), удается применять для расчета электрических цепей известные правила последовательного и параллельного соединения сопротивлений и законы Кирхгофа.
Пример расчета емкости в цепи переменного тока
Предположим, что надо запитать от бытовой электросети напряжением 220 В и частотой 50 Гц низковольтную лампочку накаливания с номинальным током 0.28 А при отсутствии понижающего трансформатора. Требуется найти емкость последовательно включенного с лампочкой конденсатора.
Пренебрегая падением напряжения на лампочке, считаем все напряжение сети приложенным к конденсатору. Тогда реактивное сопротивление конденсатора находим, руководствуясь законом Ома:
Xc=U/I=220/0.28=786 Ом.
Параметр C из выражения Xc=1/(2πfC) может быть рассчитан через Xc. Следовательно, C=1/(Xc·2πf).
После подстановки получим:
C=1/(786·2·3.14·50)=0.000004 Ф=4 мкФ.
Таким образом, экспериментальную низковольтную лампочку с номинальным током 0.28 А можно запитать от домашней сети переменного тока через емкость 4 мкФ.
Видео по теме
Калькулятор электрического сопротивления ёмкости
При подключении конденсатора в цепь переменного тока возникает совокупность процессов заряда и разряда ёмкости,
т.е. накопление и отдача энергии электрическим полем между обкладками. По мере заряда ёмкости, ток через нее уменьшается.
Конденсатор будет заряжаться до максимального значения, пока ток не сменит направление на противоположное.
В моменты максимального значения напряжения на конденсаторе, ток в нём будет равен нулю.
Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
Ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току Xc.
X C — сопротивление, Ом;
f — частота, Гц;
C — ёмкость, Ф.
Сопротивление конденсатора переменному току это отношение действующих значений напряжения к току.
Оно обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.
Фазы кривых тока и напряжения на конденсаторе смещены на 90 градусов, при этом ток опережает напряжение.
Расчет электрического сопротивления ёмкости
Для расчета введите значение ёмкости конденсатора и частоту переменного тока
Калькулятор вычисления действующих значений тока или напряжения на конденсаторе.
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Реактивное сопротивление конденсатора – онлайн
Расчет реактивного сопротивления конденсатора
Реактивное сопротивление — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).
Реактивное сопротивление конденсатора вычисляется по формуле:
XC = 1/(2πƒC)
где:
- π – число ПИ
- ƒ – Частота тока
- C – Ёмкость конденсатора
Так же вы можете рассчитать реактивное сопротивление конденсатора онлайн.
Сопротивление конденсатора калькулятор – онлайн
Частота:
Популярные сообщения из этого блога
Найти тангенс фи , если известен косинус фи
Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ
Индекс Руфье калькулятор
Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле: Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в
Найти косинус фи (cos φ), через тангенс фи (tg φ)
tg фи=… чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:
Прежде, чем мы приступим к расчётам разнообразных пассивных и активных фильтров, не плохо было бы сориентироваться в пространстве и
задуматься – а за счёт чего происходит процесс частотной фильтрации сигналов, какой неведомый зверь должен выбежать на свист царевича
после преобразования частотно-зависимыми цепями, и что это за цепи такие – частотно-зависимые?
Большая Энциклопедия Нефти и Газа учит нас, что частотно-зависимыми цепями называются электрические цепи с использованием емкостных и
резистивных элементов. Спасибо, господа нефтяники и газовики – будем знать. От себя добавлю, что индуктивные элементы в
частотно-зависимом хозяйстве также иногда пригождаются.
Для постоянного тока ни конденсаторы, ни катушки индуктивности никакого интереса не представляют. Сопротивление идеального конденсатора –
бесконечность, индуктивности – ноль. Другое дело – переменный ток, тут наши частотно-зависимые элементы, начинают приобретать
определённые значения сопротивлений, называемые реактивными сопротивлениями. Ясен пень, значения этих сопротивлений зависят от
частоты протекающего тока.
Для особо продвинутых, вымучаю из себя умную фразу – “Реактивное сопротивление – электрическое сопротивление переменному току,
обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах”.
Графики, фазовые сдвиги, интегралы и прочие атрибуты студенческих знаний, как правило, мало кого интересуют. Если я не прав,
пусть первыми бросят в меня камень и с лёгкостью найдут необходимую информацию на других сайтах. А мы ребята весёлые, поэтому
сразу перейдём к делу и напишем всего пару формул:
Xс = 1 / 2πƒС, Xl = 2πƒL, где
Xc – сопротивление конденсатора переменному току, а Xl – сопротивление индуктивности переменному току.
РИСУЕМ ТАБЛИЧКУ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ КОНДЕНСАТОРА
|
Ёмкость конденсатора С |
||
|
Подаваемая частота f |
||
| |
||
| Реактивное сопротивление Xc (Ом) |
||
| Реактивное сопротивление Xc (кОм) |
ТО ЖЕ САМОЕ ДЛЯ РАСЧЁТА РЕАКТИВНОГО СОПРОТИВЛЕНИЯ ИНДУКТИВНОСТИ
|
Индуктивность катушки L |
||
|
Подаваемая частота f |
||
| |
||
| Реактивное сопротивление Xl (Ом) |
||
| Реактивное сопротивление Xl (кОм) |
В реальной жизни конденсаторы, помимо ёмкости, обладают также собственными последовательным и параллельным сопротивлениями и
индуктивностью, а катушки индуктивности – омическим сопротивлением провода обмотки и межвитковой паразитной ёмкостью.
Нужно Вам вооружаться этими знаниями, или нет, судить не возьмусь, а вот то, что электролитические конденсаторы имеют обыкновение
иногда взрываться при превышении допустимых уровней напряжений, либо перегреве, вызванным утечками вследствие старения –
знать надо обязательно.
Делают они это, ни кем не посоветовавшись, эффектно, громко, с выделение токсичных паров электролита в виде облака из дыма,
и с лёкгостью могут выбить глаз пытливому радиолюбителю.
Так что, если не хотите превратиться в одноглазого шахматиста из Васюков, соблюдайте технику безопасности, покупайте электролиты
приличных производителей.