Все мы ежедневно сталкиваемся с электроприборами, кажется, без них наша жизнь останавливается. И у каждого из них в технической инструкции указана мощность. Сегодня мы разберемся что же это такое, узнаем виды и способы расчета.
Содержание
- 1 Мощность в цепи переменного электрического тока
- 1.1 Понятие активной мощности
- 1.2 Понятие реактивной мощности
- 1.2.1 Емкостные и индуктивные нагрузки
- 1.2.2 Коэффициент мощности cosφ
- 1.3 Понятие полной мощности. Треугольник мощностей
- 2
- 3 Как измеряют cosφ на практике
Мощность в цепи переменного электрического тока
Электроприборы, подключаемые к электросети работают в цепи переменного тока, поэтому мы будем рассматривать мощность именно в этих условиях. Однако, сначала, дадим общее определение понятию.
Мощность — физическая величина, отражающая скорость преобразования или передачи электрической энергии.
В более узком смысле, говорят, что электрическая мощность – это отношение работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
Если перефразировать данное определение менее научно, то получается, что мощность – это некое количество энергии, которое расходуется потребителем за определенный промежуток времени. Самый простой пример – это обычная лампа накаливания. Скорость, с которой лампочка превращает потребляемую электроэнергию в тепло и свет, и будет ее мощностью. Соответственно, чем выше изначально этот показатель у лампочки, тем больше она будет потреблять энергии, и тем больше отдаст света.
Поскольку в данном случае происходит не только процесс преобразования электроэнергии в некоторую другую (световую, тепловую и т.д.), но и процесс колебания электрического и магнитного поля, появляется сдвиг фазы между силой тока и напряжением, и это следует учитывать при дальнейших расчетах.
При расчете мощности в цепи переменного тока принято выделять активную, реактивную и полную составляющие.
Понятие активной мощности
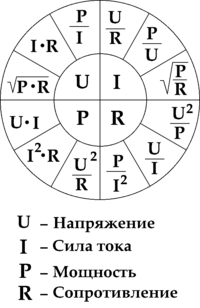
Активная «полезная» мощность — это та часть мощности, которая характеризует непосредственно процесс преобразования электрической энергии в некую другую энергию. Обозначается латинской буквой P и измеряется в ваттах (Вт).
Рассчитывается по формуле: P = U⋅I⋅cosφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, cos φ – косинус угла сдвига фазы между напряжением и током.
ВАЖНО! Описанная ранее формула подходит для расчета цепей с напряжением 220В, однако, мощные агрегаты обычно используют сеть с напряжением 380В. В таком случае выражение следует умножить на корень из трех или 1.73
Понятие реактивной мощности
Реактивная «вредная» мощность — это мощность, которая образуется в процессе работы электроприборов с индуктивной или емкостной нагрузкой, и отражает происходящие электромагнитные колебания. Проще говоря, это энергия, которая переходит от источника питания к потребителю, а потом возвращается обратно в сеть.
Использовать в дело данную составляющую естественно нельзя, мало того, она во многом вредит сети питания, потому обычно его пытаются компенсировать.
Обозначается эта величина латинской буквой Q.
ЗАПОМНИТЕ! Реактивная мощность измеряется не в привычных ваттах (Вт), а в вольт-амперах реактивных (Вар).
Рассчитывается по формуле:
Q = U⋅I⋅sinφ,
где U и I – среднеквадратичное значение напряжения и силы тока цепи соответственно, sinφ – синус угла сдвига фазы между напряжением и током.
ВАЖНО! При расчете данная величина может быть как положительной, так и отрицательной – в зависимости от движения фазы.
Емкостные и индуктивные нагрузки
Главным отличием реактивной (емкостной и индуктивной) нагрузки – наличие, собственно, емкости и индуктивности, которые имеют свойство запасать энергию и позже отдавать ее в сеть.
Индуктивная нагрузка преобразует энергию электрического тока сначала в магнитное поле (в течение половины полупериода), а далее преобразует энергию магнитного поля в электрический ток и передает в сеть. Примером могут служить асинхронные двигатели, выпрямители, трансформаторы, электромагниты.
ВАЖНО! При работе индуктивной нагрузки кривая тока всегда отстает от кривой напряжения на половину полупериода.
Емкостная нагрузка преобразует энергию электрического тока в электрическое поле, а затем преобразует энергию полученного поля обратно в электрический ток. Оба процесса опять же протекают в течение половины полупериода каждый. Примерами являются конденсаторы, батареи, синхронные двигатели.
ВАЖНО! Во время работы емкостной нагрузки кривая тока опережает кривую напряжения на половину полупериода.
Коэффициент мощности cosφ
Коэффициент мощности cosφ (читается косинус фи)– это скалярная физическая величина, отражающая эффективность потребления электрической энергии. Проще говоря, коэффициент cosφ показывает наличие реактивной части и величину получаемой активной части относительно всей мощности.
Коэффициент cosφ находится через отношение активной электрической мощности к полной электрической мощности.
ОБРАТИТЕ ВНИМАНИЕ! При более точном расчете следует учитывать нелинейные искажения синусоиды, однако, в обычных расчетах ими пренебрегают.
Значение данного коэффициента может изменяться от 0 до 1 (если расчет ведется в процентах, то от 0% до 100%). Из расчетной формулы не сложно понять, что, чем больше его значение, тем больше активная составляющая, а значит лучше показатели прибора.
Понятие полной мощности. Треугольник мощностей
Полная мощность – это геометрически вычисляемая величина, равная корню из суммы квадратов активной и реактивной мощностей соответственно. Обозначается латинской буквой S.

Также рассчитать полную мощность можно путем перемножения напряжения и силы тока соответственно.
S = U⋅I
ВАЖНО! Полная мощность измеряется в вольт-амперах (ВА).
Треугольник мощностей – это удобное представление всех ранее описанных вычислений и соотношений между активной, реактивной и полной мощностей.
Катеты отражают реактивную и активную составляющие, гипотенуза – полную мощность. Согласно законам геометрии, косинус угла φ равен отношению активной и полной составляющих, то есть он является коэффициентом мощности.
Как найти активную, реактивную и полную мощности. Пример расчета
Все расчеты строятся на указанных ранее формулах и треугольнике мощностей. Давайте рассмотрим задачу, наиболее часто встречающуюся на практике.
Обычно на электроприборах указана активная мощность и значение коэффициента cosφ. Имея эти данные несложно рассчитать реактивную и полную составляющие.
Для этого разделим активную мощность на коэффициент cosφ и получим произведение тока и напряжения. Это и будет полной мощностью.
Далее, исходя из треугольника мощностей, найдем реактивную мощность равную квадрату из разности квадратов полной и активной мощностей.
Как измеряют cosφ на практике
Значение коэффициента cosφ обычно указано на бирках электроприборов, однако, если необходимо измерить его на практике пользуются специализированным прибором – фазометром. Также с этой задачей легко справится цифровой ваттметр.

Если полученный коэффициент cosφ достаточно низок, то его можно компенсировать практически. Осуществляется это в основном путем включения в цепь дополнительных приборов.
- Если необходимо скорректировать реактивную составляющую, то следует включить в цепь реактивный элемент, действующий противоположно уже функционирующему прибору. Для компенсации работы асинхронного двигателя, для примера индуктивной нагрузки, в параллель включается конденсатор. Для компенсации синхронного двигателя подключается электромагнит.
- Если необходимо скорректировать проблемы нелинейности в схему вводят пассивный корректор коэффициента cosφ, к примеру, это может быть дроссель с высокой индуктивностью, подключаемый последовательно с нагрузкой.
Мощность – это один из важнейших показателей электроприборов, поэтому знать какой она бывает и как рассчитывается, полезно не только школьникам и людям, специализирующимся в области техники, но и каждому из нас.
Что такое активная и реактивная мощность, кто их придумал и какие формулы существуют для их расчета – все это несложные вопросы физики, если рассказать о них простыми словами. Поймут даже чайники.
Содержание
- Мощность в цепи переменного электрического тока
- Что такое активная мощность
- Что такое реактивная мощность
- Что такое полная мощность
- Смысл реактивной нагрузки
- Треугольник мощностей
- Формулы и единицы измерения
- Как найти активную, реактивную и полную мощность
Мощность в цепи переменного электрического тока
Многих пугает все разнообразие мощностей, которое описывается в задачниках по физике. Но все не так сложно, если ознакомиться с теорией, написанной простыми словами. Что такое активная и реактивная мощность, как они соотносятся между собой и что на самом деле означает выражение на полную мощность.

Для начала стоит вспомнить, что же собственно подразумевается под мощностью в физике. Это соотношение передаваемой энергии от одной системы к другой в течение определенного времени передачи. Мощность обычно измеряют в Ваттах (сокращенно Вт/W), которые представляют собой 1 джоуль энергии, который передается другой системе за 1 секунду.

И лишь в астрофизике или теоретической физике могут применяться другие величины для мощности, но они уже не являются системными по умолчанию. В электричестве под этим понятием подразумевается именно передача электроэнергии. Далее речь пойдет о сетях переменного тока, которые используются в быту и производстве.
Если говорить о практическом значении физики, то, в первую очередь, интерес будет представлять активная мощность. Реактивная мощность интересует тех, кто собирается заниматься процессами ее компенсации.
На заметку! Следует отметить уникальность единицы измерения активной мощности, которая отличается среди всех остальных типов мощностей.
Мощность переменного тока может быть разделена на:
- P — активную;
- Q — реактивную;
- S — полную.

Что такое активная мощность
Активная мощность — это некая часть мощности, связанная непосредственно с трансформацией в какой-либо другой вид энергии. Она измеряется в таких единицах измерения, как ватты, сокращенно Вт. Когда речь заходит о формулах, в них активная мощность обозначается буквой Р. Она также связана с неким периодом частоты переменного типа тока. Логично, что этот тип мощности может описывать процессы лишь с участием переменного тока.
Бытовые электроприборы обладают различной мощностью. В чем измеряется их активная мощность, уже шла речь выше: в ваттах. Другая проблема, что производители бытовых приборов часто указывают лишь пиковую мощность, которую устройство готово демонстрировать лишь на протяжении ограниченного временного промежутка.

Одна из наименьших активных мощностей у зарядных устройств – всего около 2 Вт в час. Одна из наибольших у бытовых моек высокого давления – мощность доходит до 3500 Вт. Где-то посередине окажутся стиральные машины, водонагреватели и блендеры.
Интересно! Единица измерения активной мощности, ватты, названа в честь шотландского инженера и изобретателя Джеймса Уатта, жившего на рубеже XVIII – XIX веков.
Среди наименее известных изобретений механика значится машина для копирования скульптур и барельефов. А наиболее известна первая придуманная им единица для измерения мощности – это была лошадиная сила. Здесь речь шла не о движении, производимом в горизонтальной плоскости, а о способности лошадей поднимать людей или грузы в шахтах.
Что такое реактивная мощность
Реактивная мощность – это та часть мощности, которая вернется в сеть обратно. Более детально этот процесс можно описать так: это «вредоносный» процесс, который не полезен для всей системы, он характерен для устройств с нагрузкой индуктивного или емкостного типа.

Логично, что эта часть мощности никак не помогает полезным процессам, не является активной. Задача состоит в том, чтобы компенсировать реактивную мощность. Ее обозначают заглавной буквой Q, а единица измерения реактивной мощности: вольт-амперы, которые обозначаются как Вар.
Что такое полная мощность
Если кратко, то в бытовом аспекте многие путают активную и полную мощность, называя «полной» активную. На самом деле полная мощность – это сочетание активной и неполезной реактивной.
Так что в сети переменного тока считают вместе рассеиваемую и поглощаемую мощность, и получают общее значение. Мощность в этом случае обозначается буквой S. Для ее измерения также используются единицы Вар.
Смысл реактивной нагрузки
Что такое реактивная мощность в рамках производства – это потеря средств. Как только она становится повышенной, предприятие может начать тратить на электроэнергию больше, чем изначально рассчитывалось.
Полная мощность должна включать как можно меньше работы для двигателей вхолостую, нормальным считаются показатели от 60% и выше. Важно перенаправить все так, чтобы избежать чрезмерного перегрева проводников сети. Чаще всего это достигается тем, что устанавливается устройство под названием конденсаторный блок.

Что такое реактивная мощность – мощность, которая появляется в тех сетях, в которых присутствуют реактивные элементы. Энергия накапливается в цепи, после чего она возвращается обратно.
Таким образом, устройства нагреваются при работе, что можно заметить по длительной работе даже такого маломощного предмета ежедневного быта, как зарядное устройство для смартфона.
Для электроприбора есть нормальный коэффициент реактивной мощности. Обычно он составляет от 0,9 до 0,5. Производители указывают его в инструкции по эксплуатации или в паспорте устройства.
Смысл реактивной нагрузки состоит в том, что она создает сдвиг по времени между напряжением и фазами тока. Расчеты и применение формул для вычисления реактивной мощности позволяют не только достигать высокой производительности устройств при меньших затратах на электроэнергию, но и помогают избегать аварийных ситуаций.

Часто возникает вопрос, как правильно определять коэффициент реактивной мощности в случае с бытовыми электросетями перед домашним счетчиком.
Для этого используется формула:
tgφ = Q/P = Eq/Еw
В данном случае Еw – это активная мощность, а вот Eq – это уже реактивная.
Треугольник мощностей
Формула расчета полной, активной и реактивной мощностей достаточно понятно может описывать взаимоотношения этих трех аспектов. Но яснее их взаимоотношения можно выразить на плоскости в виде треугольника мощностей. Так как все они тригонометрически соотносятся. Угол, который возникает между полной и активной мощностями называется фазовым углом и ясно показан на рисунке.

Формулы и единицы измерения
Единица измерения реактивной мощности такая же, как у полной – вольт-амперы, Вар, а для расчета активной используется единица в виде Вт.

Что такое активная и реактивная мощность в совокупности – так называемая полная мощность. Она рассчитывается по следующей простой формуле:
√ (Активная мощность2 + Реактивная мощность2)
То есть требуется найти квадратный корень из суммы квадрата активной и квадрата реактивной мощностей.
Как найти реактивную мощность:
√ (Полная мощность2 – Активная мощность2)
То есть квадратный корень из вычитания квадрата активной мощности из квадрата полной мощности. Когда речь заходит о вычислении активной мощности, то применяется, соответственно, формула:
√ (Полная мощность2 – Реактивная мощность2)
Квадрат из вычитания квадрата реактивной мощности из квадрата полной мощности.

Также могут понадобиться другие формулы для точных вычислений в некоторых случаях. Для однофазных цепей может применяться своя формула:
P = V I cosθ
А в трехфазных цепях уже будет действовать следующий вариант:
P = √3 VL IL cosθ
Важно! Во всех случаях необходимо внимательно следить за единицами измерений. Киловатты необходимо еще до вычисления по формулам переводить в ватты. Киловольтамперы, соответственно, переводят в вольтамперы.
Как найти активную, реактивную и полную мощность
Коэффициент реактивной мощности позволяет оптимизировать работу и избежать нагрева устройства. Профессионалы обычно используют большее количество параметров в расчетах, чтобы компенсировать негативные моменты реактивной мощности. Но для решения рядовых задач по физике вполне применима приведенная выше формула.

Полная мощность, активная и реактивная мощность для чайников может быть представлена несколькими формулами. Важно лишь помнить о ситуационных единицах измерения, об актуальных обозначениях и о треугольнике мощностей, чтобы справиться с расчетами.
 Баланс мощностей цепи переменного тока│Активная, реактивная и полная мощности
Баланс мощностей цепи переменного тока│Активная, реактивная и полная мощности
Помогла ли вам статья?
( 2 оценки, среднее 5 из 5 )
Многие потребители электроэнергии не подозревают того, что часть учтённого электричества расходуется бесполезно. В зависимости от вида нагрузки уровень потерь электроэнергии может достигать от 12 до 50%. При этом счетчики электроэнергии засчитывают эти потери, относя их к полезной работе, за что приходится платить. Виной завышения оплаты за потребление электроэнергии, не выполняющей полезной работы, является реактивная мощность, присутствующая в сетях переменных токов.
Чтобы понять, за что мы переплачиваем и как компенсировать влияние реактивных мощностей на работу электрических установок, рассмотрим причину появления реактивной составляющей при передаче электроэнергии. Для этого придётся разобраться в физике процесса, связанного с переменным напряжением.
Что такое реактивная мощность?
Для начала рассмотрим понятие электрической мощности. В широком смысле слова, этот термин означает работу, выполненную за единицу времени. По отношению к электрической энергии, понятие мощности немного откорректируем: под электрической мощностью будем понимать физическую величину, реально характеризующую скорость генерации тока или количество переданной либо потреблённой электроэнергии в единицу времени.
Понятно, что работа электричества в единицу времени определяется электрической мощностью, измеряемой в ваттах. Мгновенную мощность на участке цепи находят по формуле: P = U×I, где U и I – мгновенные значения показателей параметров напряжения и силы тока на данном участке.
Строго говоря, приведённая выше формула справедлива только для постоянного тока. Однако, в цепях синусоидального тока формула работает лишь тогда, когда нагрузка потребителей чисто активная. При резистивной нагрузке вся электрическая энергия расходуется на выполнение полезной работы. Примерами активных нагрузок являются резистивные приборы, такие как кипятильник или лампа накаливания.
При наличии в электрической цепи ёмкостных или индуктивных нагрузок, появляются паразитные токи, не участвующие в выполнении полезной работы. Мощность этих токов называют реактивной.
На индуктивных и ёмкостных нагрузках часть электроэнергии рассеивается в виде тепла, а часть препятствует выполнению полезной работы.
К устройствам с индуктивными нагрузками относятся:
- электромоторы;
- дроссели;
- трансформаторы;
- электромагнитные
реле и другие устройства, содержащие обмотки.
Ёмкостными сопротивлениями обладают конденсаторы.
Физика процесса
Когда мы имеем дело с цепями постоянного тока, то говорить о реактивной мощности не приходится. В таких цепях значения мгновенной и полной мощности совпадают. Исключением являются моменты включения и отключения ёмкостных и индуктивных нагрузок.
Похожая ситуация происходит при наличии чисто активных сопротивлений в синусоидальных цепях. Однако если в такую электрическую цепь включены устройства с индуктивными или ёмкостными сопротивлениями, происходит сдвиг фаз по току и напряжению (см. рис.1).
При этом на индуктивностях наблюдается отставание тока по фазе, а на ёмкостных элементах фаза тока сдвигается так, что ток опережает напряжение. В связи с нарушением гармоники тока, полная мощность разлагается на две составляющие. Ёмкостные и индуктивные составляющие называют реактивными, бесполезными. Вторая составляющая состоит из активных мощностей.

Угол сдвига фаз используется при вычислениях значений активных и реактивных ёмкостных либо индуктивных мощностей. Если угол φ = 0, что имеет место при резистивных нагрузках, то реактивная составляющая отсутствует.
Важно запомнить:
- резистор потребляет исключительно активную мощность, которая выделяется в виде тепла и света;
- катушки индуктивности провоцируют образование реактивной составляющей и возвращают её в виде магнитных полей;
- Ёмкостные элементы (конденсаторы) являются причиной появления реактивных сопротивлений.
Треугольник мощностей и cos φ
Для наглядности изобразим полную мощность и её составляющие в виде векторов (см. рис. 2). Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.

Применяя теорему Пифагора, вычислим модуль вектора S:
![]()
Отсюда можно найти реактивную составляющую:
![]()
Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.
Если угол сдвига фаз принимает нулевое значение, то cos φ = 1, а это значит что P = S, то есть полная мощность состоит только из активной мощности, а реактивность отсутствует. При сдвиге фаз на угол π/2 , cos φ = 0, откуда следует, что в цепи господствуют только реактивные токи (на практике такая ситуация не возникает).
Из этого можно сделать вывод: чем ближе к 1 коэффициент Pf , тем эффективнее используется ток. Например, для синхронных генераторов приемлемым считается коэффициент от 0,75 до 0,85.
Формулы
Поскольку реактивная мощность зависит от угла φ, то для её вычисления применяется формула: Q = UI×sin φ. Единицей измерения реактивной составляющей является вар или кратная ей величина – квар.
Активную составляющую находят по формуле: P = U*I×cosφ. Тогда
![]()
Зная коэффициент Pf (cos φ), мы можем рассчитать номинальную мощность потребителя тока по его номинальному напряжению, умноженному на значение силы потребляемого тока.
Способы компенсации
Мы уже выяснили, как влияют реактивные токи на работу устройств и оборудования с индуктивными или ёмкостными нагрузками. Для уменьшения потерь в электрических сетях с синусоидальным током их оборудуют дополнительными устройствами компенсации.
Принцип действия установок компенсации основан на свойствах индуктивностей и ёмкостей по сдвигу фаз в противоположные стороны. Например, если обмотка электромотора сдвигает фазу на угол φ, то этот сдвиг можно компенсировать конденсатором соответствующей ёмкости, который сдвигает фазу на величину – φ. Тогда результирующий сдвиг будет равняться нулю.
На практике компенсирующие устройства подключают параллельно нагрузкам. Чаще всего они состоят из блоков конденсаторов большой ёмкости, расположенных в отдельных шкафах. Одна из таких конденсаторных установок изображена на рисунке 3. На картинке видно группы конденсаторов, используемых для компенсации сдвигов напряжений в различных устройствах с индуктивными обмотками.

Компенсацию реактивной мощности ёмкостными нагрузками хорошо иллюстрируют графики на рисунке 4. Обратите внимание на то, как эффективность компенсации зависит от напряжения сети. Чем выше сетевое напряжение, тем сложнее компенсировать паразитные токи (график 3).

Устройства компенсации часто устанавливаются в производственных цехах, где работает много устройств на электроприводах. Потери электричества при этом довольно ощутимы, а качество тока сильно ухудшается. Конденсаторные установки успешно решают подобные проблемы.
Нужны ли устройства компенсации в быту?
На первый взгляд в домашней сети не должно быть больших
реактивных токов. В стандартном наборе бытовых потребителей преобладают
электрическая техника с резистивными нагрузками:
- электрочайник (Pf = 1);
- лампы накаливания
(Pf = 1); - электроплита (Pf =
1) и другие нагревательные приборы;
Коэффициенты
мощности современной бытовой техники, такой как телевизор, компьютер и т.п.
близки к 1. Ими можно пренебречь.
Но если речь идёт о холодильнике (Pf = 0,65), стиральной машине и микроволновой печи, то уже стоит задуматься об установке синхронных компенсаторов. Если вы часто пользуетесь электроинструментом, сварочным аппаратом или у вас дома работает электронасос, тогда установка устройства компенсации более чем желательна.
Экономический эффект от установки таких устройств
ощутимо скажется на вашем семейном бюджете. Вы сможете экономить около 15%
средств ежемесячно. Согласитесь, это не так уж мало, учитывая тарифы не
электроэнергию.
Попутно вы решите следующие вопросы:
- уменьшение нагрузок на индуктивные элементы и на проводку;
- улучшение качества тока, способствующего стабильной работе электронных устройств;
- понижение уровня высших гармоник в бытовой сети.
Для того чтобы ток и напряжение работали синфазно, устройства компенсации следует размещать как можно ближе к потребителям тока. Тогда реальная отдача индуктивных электроприёмников будет принимать максимальные значения.
Видео в тему
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).
Мгновенная электрическая мощность[править | править код]
Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.
По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки 



Мощность, по определению — это работа в единицу времени.
Введём обозначения:
— напряжение на участке
(принимаем его постоянным на интервале
);
— количество зарядов, прошедших от
к
за время
;
— работа, совершённая зарядом
при движении по участку
;
— мощность.
Записывая вышеприведённые рассуждения, получаем:
Для единичного заряда на участке 
Для всех зарядов:
Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть 
Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:
Если участок цепи содержит резистор c электрическим сопротивлением 
Дифференциальные выражения для электрической мощности[править | править код]
Мощность, выделяемая в единице объёма, равна:
где:
— напряжённость электрического поля;
— плотность тока.
Отрицательное значение скалярного произведения (векторы 

В случае изотропной среды в линейном приближении:
где 
В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:
где 
Мощность постоянного тока[править | править код]
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:
Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:
где 
Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:
где 
Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность 
Мощность переменного тока[править | править код]
В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для большинства простых практических расчётов не слишком полезна непосредственно. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.
Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол 
Активная мощность[править | править код]
Единица измерения в СИ — ватт[1].
Среднее за период 
В цепях однофазного синусоидального тока 








В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отражённой мощностью.
Реактивная мощность[править | править код]
Единица измерения, по предложению Международной электротехнической комиссии, – вар (вольт-ампер реактивный); (русское обозначение: вар; международное: var). В терминах единиц СИ, как отмечено в 9-ом издании Брошюры СИ, вар когерентен произведению вольт-ампер. В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения в области «электротехника»[1][2]:
Вар определяется как реактивная мощность цепи с синусоидальным переменным током при действующих значениях напряжения 1 В и тока 1 А, если сдвиг фазы между током и напряжением 
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения 





Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.
Необходимо отметить, что величина 




Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.
Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии, возвращаемой от индуктивной и ёмкостной нагрузки в источник переменного напряжения.
Полная мощность[править | править код]
Единица измерения — В·А, вольт-ампер (русское обозначение: В·А; международное: V·A). В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «электротехника»[1][2].
Полная мощность — величина, равная произведению действующих значений периодического электрического тока 


где:
— активная мощность;
— реактивная мощность (при индуктивной нагрузке
, а при ёмкостной
).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:
Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.
Комплексная мощность[править | править код]
Мощность, аналогично импедансу, можно записать в комплексном виде:
где:
— комплексное напряжение;
— комплексный ток;
— импеданс;
— оператор комплексного сопряжения.
Модуль комплексной мощности 





Измерения[править | править код]
- Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра, амперметра и фазометра.
- Для измерения коэффициента реактивной мощности применяют фазометры
- Государственный эталон мощности — ГЭТ 153—2012 Государственный первичный эталон единицы электрической мощности в диапазоне частот от 1 до 2500 Гц. Институт-хранитель: ВНИИМ
Потребление мощности некоторыми электроприборами[править | править код]
| Электрический прибор | Мощность,Вт |
|---|---|
| Лампочка фонарика | 1 |
| Сетевой роутер, хаб | 10…20 |
| Системный блок ПК | 100…1700 |
| Системный блок сервера | 200…1500 |
| Монитор для ПК ЭЛТ | 15…200 |
| Монитор для ПК ЖК | 2…40 |
| Лампа люминесцентная бытовая | 5…30 |
| Лампа накаливания бытовая | 25…150 |
| Холодильник бытовой | 15…700 |
| Электропылесос | 100… 3000 |
| Электрический утюг | 300…2 000 |
| Стиральная машина | 350…2 000 |
| Электрическая плитка | 1000…2000 |
| Сварочный аппарат бытовой | 1000…5500 |
| Двигатель лифта невысокого дома | 3 000…15 000 |
| Двигатель трамвая | 45 000…75 000 |
| Двигатель электровоза | 650 000 |
| Электродвигатель шахтной подъёмной машины | 1 000 000…5 000 000 |
| Электродвигатель прокатного стана | 6 000 000…32 000 000 |
Выходная мощность[править | править код]
Измеряется как долговременная (RMS[en]), так и кратковременная (PMO, PMPO) мощности, способные отдавать усилителями мощности.
- также см.: КПД
См. также[править | править код]
- Ваттметр
- Электрический ток
- Коэффициент мощности
- Список параметров напряжения и силы электрического тока
- Закон Ома
- КПД
Примечания[править | править код]
- ↑ 1 2 3 Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 26—27. — 240 с. — ISBN 5-7050-0118-5.
- ↑ 1 2 Положение о единицах величин, допускаемых к применению в Российской Федерации Архивная копия от 2 ноября 2013 на Wayback Machine Утверждено Постановлением Правительства РФ от 31 октября 2009 г. N 879.
- ↑ Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1977. — С. 213.
Литература[править | править код]
- ГОСТ 8.417-2002 Единицы величин.
- ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации.
- Л. А. Бессонов . Теоретические основы электротехники. Электрические цепи: учебник
для бакалавров. — 12-е изд., испр. и доп. — М.: Юрайт, 2016. — 702 с. — (Бакалавр. Углубленный курс). — 1000 экз. — ISBN 978-5-9916-3210-2.
- Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193 — 2009. — 146 с.
Ссылки[править | править код]
- Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. ToeHelp.Ru. Дата обращения: 7 марта 2022.
- Для чего нужна компенсация реактивной мощности. Школа для электрика (2010). Дата обращения: 7 марта 2022.
- . ред. Д. Макаров : Как рассчитать мощность электрического тока? Заметки электрика. ASUTPP. Дата обращения: 7 марта 2022.
Мощность
переменного тока – величина, периодически
изменяющаяся. Ее мгновенное значение
![]()
Пусть
ток отстает по фазе от напряжения на
угол
![]() ,
,
т.е.![]()
![]() .
.
Тогда мгновенное значение мощности
![]()
Но

Тогда
Мгновенная
мощность имеет постоянную составляющую
и переменную двойной
частоты. Диаграммы изменения
![]() приведены на рис.40. На интервалах,
приведены на рис.40. На интервалах,
когдаu
и i
имеют
одинаковое направление, мгновенная
мощность положительна,
энергия потребляется от источника. На
интервалах, когда u
и i
имеют
противоположное направление, мгновенная
мощность отрицательна и энергия
возвращается источнику.

t
Среднее
значение мгновенной мощности за период
переменного напряжения (или тока)
называется активной
мощностью
и обозначается, как и в целях постоянного
тока, прописной буквой Р. Так как среднее
значение гармонической составляющей
на периоде повторения равно нулю, то
![]()
(37)
Активная
мощность физически представляет собой
энергию, которая выделяется в единицу
времени в виде теплоты на участке цепи
с сопротивлением R:
![]()
где
![]() – активная составляющая напряжения.
– активная составляющая напряжения.
Единицей измерения
активной мощности является ватт (Вт).
Под
реактивной
мощностью
Q
понимают произведение
![]() (38)
(38)
В
зависимости от знака
![]() реактивная мощность может быть как
реактивная мощность может быть как
положительной, так и отрицательной.
Единица измерения
здесь та же, что и у активной мощности,
но для различия используется вольт-ампер
реактивный (ВАр).
Реактивная
мощность характеризует собой ту энергию,
которой обмениваются генератор и
приемник (если реактивных элементов в
приемнике нет, то
![]() мгновенная мощность не имеет отрицательных
мгновенная мощность не имеет отрицательных
значений, реактивная мощность равна
нулю).
Полная (или
кажущаяся) мощность
S=UI
(39)
Единица
полной мощности –![]() .
.
Полную
мощность можно характеризовать как
максимальную активную мощность, которую
мог бы отдать генератор при активной
нагрузке. Мощности Р, Q
и S
связаны следующей зависимостью:
![]()
(40)
Очень важной
характеристикой цепей переменного тока
является отношение
![]()
(41)
Для
лучшего использования электрических
генераторов желательно иметь максимально
возможное значение
![]() .
.
Например, для питания приемника мощностью
10000 кВт при![]() источник питания должен быть рассчитан
источник питания должен быть рассчитан
на мощность 14300 кВА, а при![]() – на 10000 кВА.
– на 10000 кВА.
Высокое
значение
![]() желательно также для уменьшения потерь
желательно также для уменьшения потерь
в ЛЭП. При неизменной активной мощности
Р приемника ток в линии тем меньше, чем
больше значение![]() :
:
![]()
Большинство
реальных потребителей электроэнергии
имеют индуктивный характер нагрузки,
т.е. в сети ток отстает от напряжения.
Отмеченное можно проиллюстрировать
схемой на рис.41, а (конденсатор отключен)
и векторной диаграммой на рис.41,б

При отключенном
конденсаторе имеем:
![]()
Подключение
в схему конденсатора приведет к изменению
тока I, что можно проследить по векторной
диаграмме на рис.42 (для удобства построений
здесь вектор
![]() направлен вертикально, но взаимное
направлен вертикально, но взаимное
расположение векторов![]() и
и![]() не изменилось).
не изменилось).

На
диаграмме обозначено:
![]() и
и![]() –
–
активная и реактивная составляющие
токаI;
![]() и
и![]() – активная и реактивная составляющие
– активная и реактивная составляющие
тока![]() .
.
Для схемы с конденсатором получим
![]()
Отсюда
требуемая емкость для уменьшения
отставания тока от величины
![]() до
до
величины![]()
![]()
Если требуется
полная компенсация угла сдвига фаз, то
![]() .
.
Компенсация
сдвига фаз существенна для энергоемких
потребителей, например, промышленных
предприятий. Осуществляется она в местах
ввода линии питания в распределительном
устройстве. Экономически выгодно
подключать конденсаторы на возможно
более высокое напряжение, так как
величина
![]() обратно пропорциональна квадрату
обратно пропорциональна квадрату
напряжения.
Рассмотрим простой
прием расчета активной и реактивной
мощностей. Пусть задан некоторый комплекс
![]()
Введем
понятие сопряженного комплекса. Под
комплексом
![]() сопряженным
сопряженным
с комплексом А, будем понимать комплекс
![]() .
.
Обозначим
напряжение на некотором участке цепи
![]() ,
,
ток поэтому участку![]() .
.
Угол между напряжением и током![]() .
.
Умножим комплекс напряжения на сопряженный
комплекс тока![]() и обозначим полученный комплекс черезS
и обозначим полученный комплекс черезS
![]()
Значок
~ (тильда) над S
обозначает комплекс (а не сопряженный
комплекс) полной мощности, составленный
при участим сопряженного комплекса
тока
![]() .
.
Таким
образом, активная мощность Р есть
действительная часть (Rе),
а реактивная мощность О – мнимая часть
(Im)
произведения
![]() :
:

(42)
Для определения
же полной мощности следует пользоваться
только формулой (40).
Из
закона сохранения энергии следует, что
в любой цепи должен соблюдаться баланс
мощностей.
Для цепей переменного тока он формулируется
следующим образом: сумма активных
мощностей источников равна сумме
активных мощностей приемников, а сумма
реактивных мощностей источников равна
сумме реактивных мощностей приемников.
При этом под
реактивной мощностью приемников энергии
понимается сумма произведений квадратов
токов ветвей на реактивные сопротивления
ветвей с учетом их знака.
Реактивная
мощность, получаемая индуктивным
элементом, положительна, а емкостным –
отрицательна. Поэтому баланс для полных
мощностей не соблюдается (на основании
(39)
![]() ,
,
но в этом выражении знакQ
роли не играет).
Для
экспериментального определения мощности
применяются специальные приборы –
ваттметры. Ваттметр содержит две обмотки
и соответственно две пары зажимов для
подключения его в цепь. Одна обмотка
включается в цепь последовательно,
подобно амперметру, вторая – параллельно
участку цепи, подобно вольтметру. На
схемах ваттметр изображается в виде
кружка с буквой W,
из которого выходят четыре конца, как
показано на рис.43.
Д ля
ля
правильного включения в цепь начала
обмоток обозначаются звездоч-ками.
Ваттметр устроен таким образом, что
измеряет произведение эффективных
значений напряжения![]() на
на
ток I и на косинус угла сдвига между
током и напряжением (предполагается,
что ток втекает в вывод последовательной
обмотки, отмеченной звездочкой, а
напряжение на параллельной обмотке
равно разности потенциалов между выводом
со звездочкой – точка на рис.43 – и
выводом без звездочки – точкаb
на рисунке) Как правило, ваттметр включают
в схему так, что он измеряет активную
мощность. По можно при определенном
подклюю-чении измерять и реактивную
мощность.
Пример 15.
Приборы,
подключенные к цепи на рис.44, дали
следующие показания:
![]()
Требуется
вычислить комплексное сопротивление
Z
и комплексные проводимости Y
цепи для случаев: а)
![]() >0;
>0;
б)
![]() <0.
<0.

Модуль сопротивления
и его аргумент:

Искомые комплексные
сопротивления и проводимости цепи:
a)
![]()
![]()

б)![]()

Для
определения знака
![]() необходимо провести следующий опыт:
необходимо провести следующий опыт:
подключить параллельно нагрузкеZ
конденсатор небольшой емкости и
проследить реакцию амперметра.
Если
нагрузка имела емкостный характер, то
добавление емкостной нагрузки приведет
к увеличению тока и увеличению показания
амперметра. В этом случае
![]() отрицательно.
отрицательно.
Если
же подключение конденсатора приводит
к уменьшению тока, то
![]() положительно (см., например, векторную
положительно (см., например, векторную
диаграмму на рис.42, поясняющую компенсацию
сдвига фаз).
Пример 16.
![]()

Требуется определить
все токи, проверить баланс мощностей,
построить векторную диаграмму.
Рассчитаем
реактивные сопротивления:
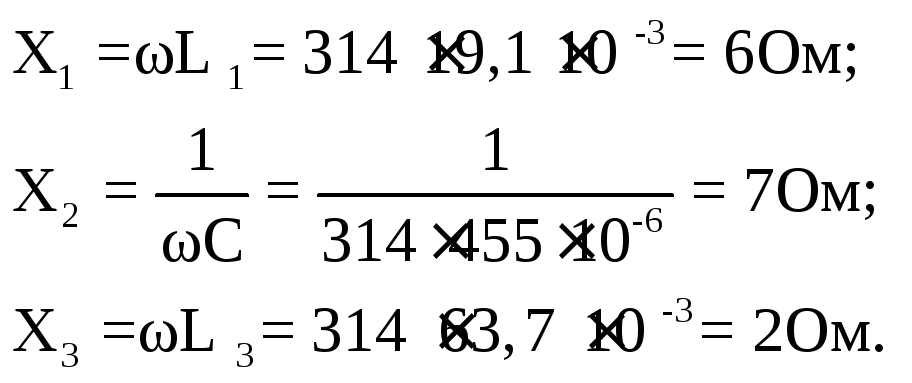
Комплекс
эффективного значения приложенного к
цепи напряжения в
![]() раз меньше комплексной амплитуды,
раз меньше комплексной амплитуды,
поэтому
![]()
Введем обозначение
комплексных сопротивлений:

Полное сопротивление
цепи

В неразветвленной
части цепи проходит ток
![]()
Токи в параллельных
ветвях, согласно формуле (23), могут быть
выражены через ток в неразветвленной
части цепи

Найдем активные
мощности всей цепи и отдельных ее ветвей:
![]()
![]()
С учетом погрешности
вычислений баланс активных мощностей
выполняется.
Наконец, определим
реактивные мощности всей цепи и отдельных
ее ветвей:

Отсюда
видно, что выполняется и баланс реактивных
мощностей.
На рис.46 приведена
векторная диаграмма
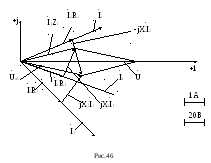
Порядок
построения диаграммы следующий: по
результатам расчетов отложены векторы
токов![]() ,
,
затем по направлению![]() отложен вектор
отложен вектор![]() и перпендикулярно к нему в сторону
и перпендикулярно к нему в сторону
опережения – вектор![]() Их сумма дает вектор
Их сумма дает вектор![]() .
.
Далее в фазе![]() построен вектор
построен вектор![]() и перпендикулярно к нему в сторону
и перпендикулярно к нему в сторону
отставания – вектор![]() ,
,
а их сумма дает вектор напряжения на
параллельном участке![]() .
.
Тот же вектор может быть получен, если
в фазе с![]() отложить
отложить![]() и к нему прибавить вектор
и к нему прибавить вектор![]() опережающий
опережающий![]() на 90°. Сумма векторов
на 90°. Сумма векторов![]() и
и![]() дает
дает
вектор приложенного напряжения![]()




















