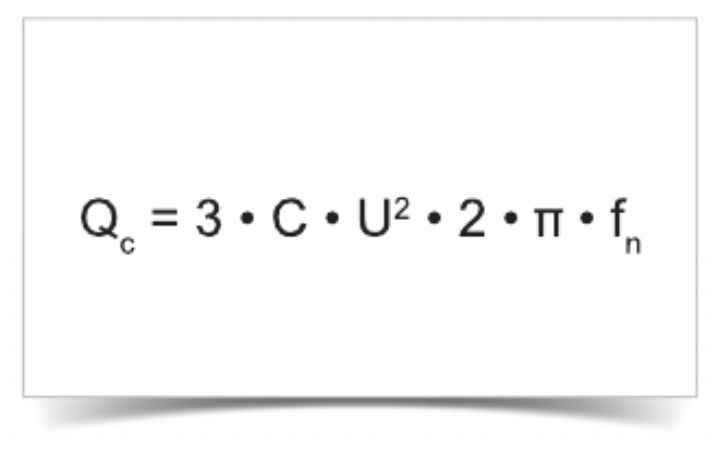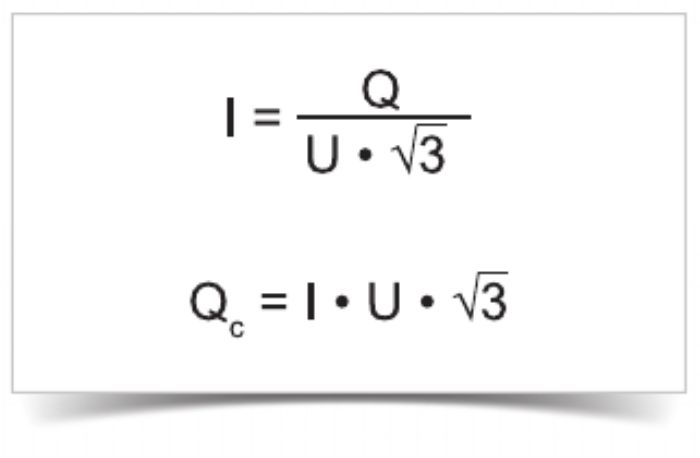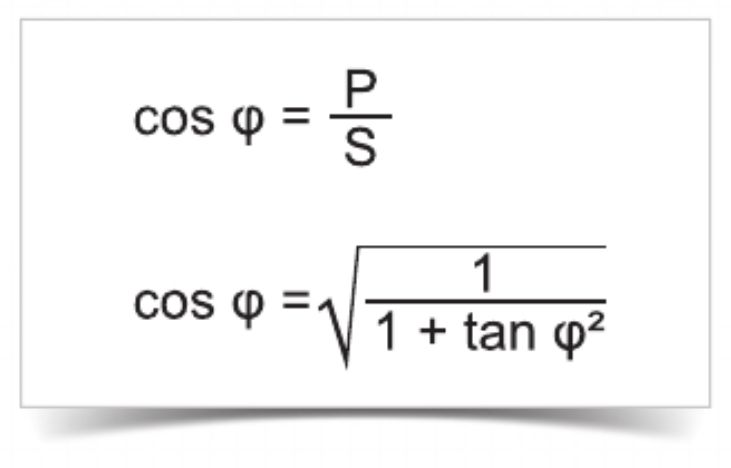Как найти реактивную мощность конденсатора

Как найти реактивную мощность конденсатора

Формулы для расчета конденсатора

Реактивная мощность конденсатора однофазная

Пример: 66.5 кА с 400 В / 50 Гц

0.0000665 · 400² · 2 · 3.14 · 50 = 3,340 ВАр = 3.34 кВАр

рис 119.jpeg   

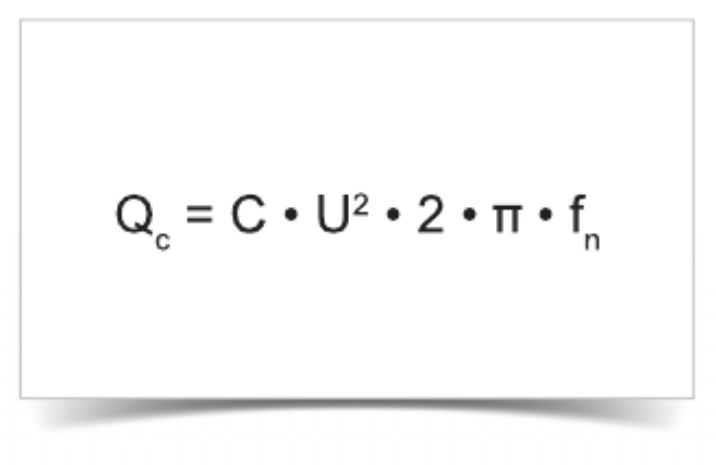
Реактивная мощность конденсатора при соединении треугольником

Пример: 3 х 57 кА с 480 В / 50 Гц

3 · 0.000057 · 4802 · 2 · 3.14 · 50 = 12,371 ВАр = 12.37 кВАр

рис 121.jpeg
  

Реактивная мощность конденсатора при соединении звездой

Пример: 3 х 33,2 кА с 400 В / 50 Гц

3 · 0.0000332 · (400 / 1.73)2 · 2 · 3.14 · 50 = 1670 ВАр = 1.67 кВАр

рис 123.jpeg
 

 Ток конденсатора в фазовом проводнике

Пример: 24 кВАр с 400 В

25,000 / (400 · 1.73) = 36 A

рис 125.jpeg
 

 Частота последовательного резонанса (fr) и коэффициента расстройки (p) у конденсаторов, перестраиваемых постоянным напряжением

 Пример: p = 0,07 (расстройка 7 %) в сети 50 Гц

рис 127.jpeg   

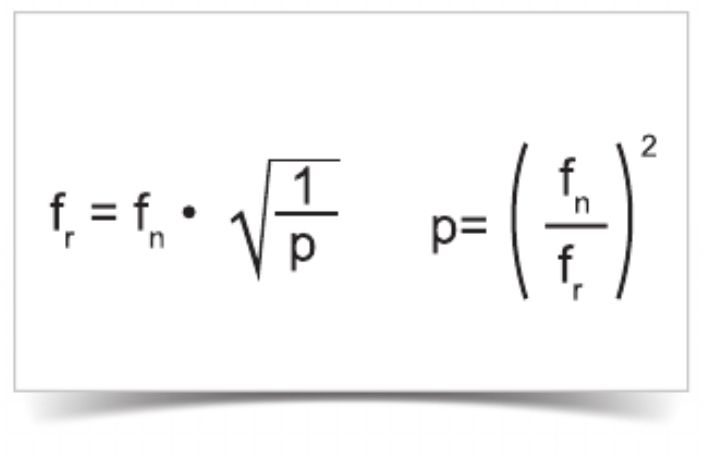
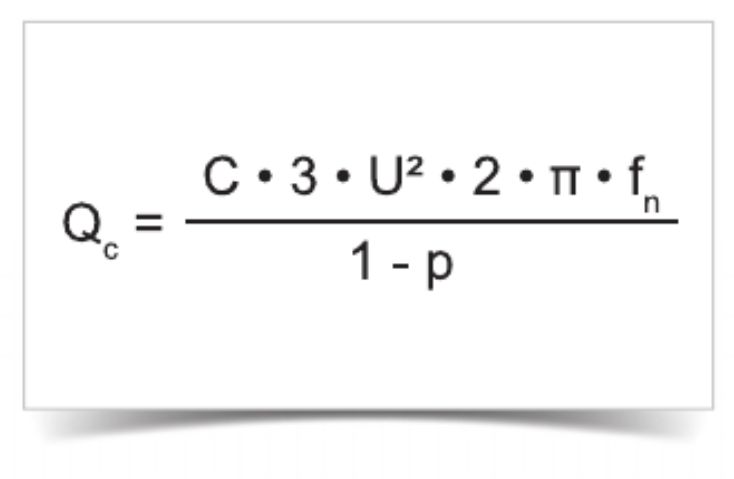
Необходимая номинальная трехфазная мощность конденсатора в варианте с расстройкой

Пример: 3 x 308 мкФ при 400 В / 50 Гц с p = расстройка 7 % 0,000308 · 3 · 4002 · 2 · 3,14 · 50 / (1 – 0,07) = 50 кВАр

Какой конденсатор нужно для этого использовать?

Это значит, что для ступени 50 кВАр необходим конденсатор 440 В 56 кВАр

рис 112.jpeg    

  Коэффициент мощности и пересчет cos в tan
рис 114.jpeg   рис 116.jpeg

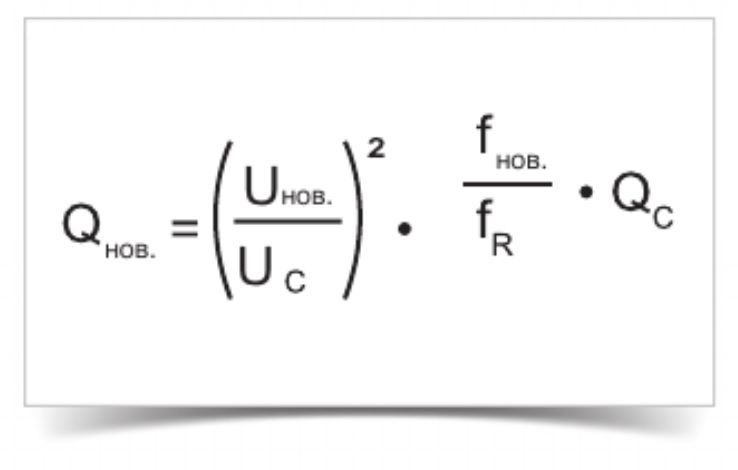
  Пересчет реактивной мощности конденсатора в зависимости от напряжения в сети

Расчет реактивной мощности Qнов. · C – константа.

Пример:

Сеть: 400 В, 50 Гц, 3-фазный

Номинальные характеристики конденсатора: 480 В, 70 кВАр, 60 Гц, 3-фазный,

треугольный, незапертый

Вопрос: чему равна результирующая номинальная мощность конденсатора?

   Результирующая компенсационная мощность этого 480-вольтного конденсатора, подключенного к сети 400 В 50 Гц, составляет всего 40,5 кВАр.

Обозначения

QC Номинальная мощность конденсатора

P Коэффициент фильтрации

UC Напряжение конденсатора

UN Номинальное напряжение

NC Эффективность фильтрования Qнов. Новая реактивная мощность Uнов. Новое напряжение

fnew Новая частота

fR Номинальная частота конденсатора

Источник

Определить реактивную мощность конденсатора

Реактивная мощность конденсатора формула

  • Рреактив = U²*2*π*f*C;

Где:

  •  U – действующее значение переменного напряжения, В;
  •  f – частота переменного тока, Гц;
  •  С – емкость конденсатора, Ф.

Реактивная мощность конденсатора онлайн калькулятор.

Значение переменного напряжения, В:

Частота переменного тока, Гц;

Ёмкость конденсатора:

Реактивная мощность на конденсаторе:

Поделиться в соц сетях:

Популярные сообщения из этого блога

Найти тангенс фи , если известен косинус фи

Калькулятор коэффициент мощности cos fi в tg fi Как найти тангенс фи, если известен косинус фи формула: tg φ = (√(1-cos²φ))/cos φ Калькулятор онлайн – косинус в тангенс cos φ: tg φ: Поделиться в соц сетях: Найти синус φ, если известен тангенс φ Найти косинус φ, если известен тангенс φ

Индекс Руфье калькулятор

Проба Руфье калькулятор онлайн. Первые упоминания теста относиться к 1950 году. Именно в это время мы находим первое упоминание  доктора Диксона о “Использование сердечного индекса Руфье в медико-спортивном контроле”. Проба Руфье – представляет собой нагрузочный комплекс, предназначенный для оценки работоспособности сердца при физической нагрузке. Индекс Руфье для школьников и студентов. У испытуемого, находящегося в положении лежа на спине в течение 5 мин, определяют число пульсаций за 15 сек (P1); После чего в течение 45 сек испытуемый выполняет 30 приседаний. После окончания нагрузки испытуемый ложится, и у него вновь подсчитывается число пульсаций за первые 15 с (Р2); И в завершении за последние 15 сек первой минуты периода восстановления (Р3); Оценку работоспособности сердца производят по формуле:  Индекс Руфье = (4(P1+P2+P3)-200)/10; Индекс Руфье для спортсменов Измеряют пульс в положении сидя (Р1); Спортсмен выполняет 30 глубоких приседаний в

Найти косинус фи (cos φ), через тангенс фи (tg φ)

tg фи=…  чему равен cos фи? Как перевести тангенс в косинус формула: cos(a)=(+-)1/sqrt(1+(tg(a))^2) Косинус через тангенс, перевести tg в cos, калькулятор – онлайн tg φ: cos φ: ± Поделиться в соц сетях:

Источник

4.5.1. Общие сведения

Когда
конденсатор подключен к переменному
синусоидальному напряжению, в нем
возникает синусоидальный ток, опережающий
напряжение на 90о(рис. 4.5.1).

Рис. 4.5.1

Мгновенная
мощность, потребляемая конденсатором
(как и любой другой цепью) определяется
как произведение напряжения и тока:

p
= ui

График изменения этой мощности можно
построить, перемножая попарно ординаты
графиков u(t)
иi(t), взятые
в один и тот же момент времени. Полученная
таким образом кривая (рис. 4.5.1) представляет
собой синусоиду двойной частоты с
амплитудой.

QC
= UCm

ICm /2
= UC

IC.

Когда p>0, конденсатор
заряжается, потребляя энергию и запасая
ее в электрическом поле. Когдаp<0,
он отдает ее другим элементам цепи,
являясь источником энергии. ВеличинаQCявляется максимальной мощностью,
потребляемой или отдаваемой конденсатором,
и называетсяемкостной реактивной
мощностью.

Средняя (активная)
мощность, потребляемая конденсатором,
равна нулю.

4.5.2. Экспериментальная часть Задание

Выведите
кривые тока и напряжения конденсатора
на экран виртуального осциллографа,
перенесите их на график и постройте
кривую изменения мгновенных значений
мощности перемножением мгновенных
значений напряжения и тока.

Порядок выполнения эксперимента

  • Соберите
    цепь согласно схеме (рис. 4.5.2), подсоедините
    к ней регулируемый источник синусоидального
    напряжения с параметрами: U
    = 5Bиf= 1 кГц.

Рис. 4.5.2

  • Включите
    виртуальные приборы V0,A1 и осциллограф.

  • «Подключите»
    два входа осциллографа к приборам V0
    иA1, а остальные отключите.

  • Установите
    параметры развёртки осциллографа так,
    чтобы на экране было изображение
    примерно одного-двух периодов напряжения
    и тока.

  • Включите
    блок «Приборы II», выберите
    из меню функции «Активная мощность» и
    «Реактивная мощность», подключите их
    кV1 иA1,
    запишите значения реактивной мощностиQCи убедитесь, что активная мощность
    близка к нулю.

  • Занесите
    данные осциллографирования напряжения
    и тока конденсатора в табл. 4.5.1
    соответственно указанным моментам
    времени. Выполните вычисления мгновенных
    значений мощности.

Таблица 4.5.1

Время t,
мс

Ток iC,
мА

Напряжение
uC,
В

p
= uCiC,
мВт

0

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

1,0

  • Перенесите
    данные табл. 4.5.1 на график (рис.4.5.3).

Рис. 4.5.3

  • По графику
    p(t) определите
    максимальное значение (реактивную
    мощность) и сравните ее с реактивной
    мощностью, измеренной варметром.

По осциллограмме: QC= …… мВт;

По варметру: QC= …… ВАр.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Реактивная мощность

Реактивная мощность обусловлена способностью реактивных элементов накапливать и отдавать электрическую или магнитную энергию.

Eмкостная нагрузка в цепи переменного тока за время половины периода накапливает заряд в обкладках конденсаторов и отдаёт его обратно в источник.
Индуктивная нагрузка накапливает магнитную энергию в катушках и возвращает её в источник питания в виде электрической энергии.

Напряжение на выводах реактивного элемента будет достигать максимального значения во время смены направления тока, следовательно,
расхождение во времени между напряжением и током в пределах элемента составит четверть периода (сдвиг фаз 90°).

Угол сдвига фаз φ в цепи нагрузки определяется соотношением активного и реактивного сопротивлений нагрузки.

Реактивная мощность характеризует потери, созданные реактивными элементами в цепи переменного тока, и выражается формулой
Q = UIsinφ.

Природу потерь в цепи с реактивными элементами можно рассмотреть с помощью графиков на рисунках.


      φ = 90°     sin90° = 1     cos90° = 0

При отсутствии активной составляющей в нагрузке, сдвиг фаз между напряжением и током составит 90°.
В начале периода, когда напряжение максимально – ток будет равен нулю, следовательно, мгновенное значение мощности UI в это время будет равно нулю.

В течении первой четверти периода, мощность можно видеть на графике, как произведение UI,
которое станет равным нулю при максимуме тока и нулевом значении напряжения.

В следующую четверть периода на графике UI принимает отрицательное значение, следовательно, мощность возвращается обратно в источник питания.
То же самое произойдёт и в отрицательном полупериоде тока. В результате средняя (активная) потребляемая мощность P avg за период будет равна нулю.

В таком случае:
Реактивная мощность Q = UIsin90° = UI
Потребляемая мощность P = UIcos90° = 0
Полная мощность S = UI = √(P² + Q²) будет равна реактивной мощности
Коэффициент мощности P/S = 0

При отсутствии реактивных элементов и сдвига фаз в нагрузках, мгновенная мощность в полупериоде Umax*Imax будет максимальной,
и в следующем полупериоде произведение отрицательного напряжения с отрицательным током дадут положительный результат – полезную мощность в нагрузке.


      φ = 0°     sin90° = 0     cos90° = 1

В этом случае:
Реактивная мощность Q = UIsin0 = 0
Потребляемая мощность P = UIcos0 = UI

Полная мощность S = UI = √(P² + Q²) будет равна потребляемой мощности
Коэффициент мощности P/S = 1

Ниже представлен рисунок графиков со сдвигом фаз 45°, для случая равенства активного и реактивного сопротивлений в нагрузке.


   φ = 45°     sin45° = cos45° = √2/2 ≈ 0.71

Здесь:
Реактивная мощность Q = UIsin45° = 0.71UI
Потребляемая мощность P = UIcos45° = 0.71UI
Полная мощность S = √(P² + Q²) = UI
Коэффициент мощности P/S = 0.71

В примерах рассмотрены случаи с индуктивной нагрузкой, когда ток отстаёт от напряжения (положительный сдвиг фаз).

В случаях с ёмкостной нагрузкой, процессы и расчёты аналогичны,
только напряжение будет отставать от тока (отрицательный сдвиг фаз).

Угол сдвига фаз в сети определится соотношением активного и реактивного сопротивлений нагрузок в
параллельном соединении следующим образом:

XL и XС соответственно индуктивное и ёмкостное сопротивление нагрузок.
Преобладание индуктивных нагрузок будет уменьшать общее индуктивное сопротивление.

Из выражения видно, что угол в этом случае будет принимать положительный знак,
а преобладание ёмкостных нагрузок будет уменьшать ёмкостное сопротивление и вызывать отрицательный сдвиг.
При равенстве индуктивного и ёмкостного сопротивлений, угол сдвига будет равен нулю.
В бытовых и производственных потребителях индуктивное сопротивление обычно существенно преобладает над ёмкостным.

Подробнее о вычислениях общего угла сдвига φ для вариантов соединений активного и
реактивного сопротивлений в нагрузках можно ознакомиться на страничке электрический импеданс.

Компенсация реактивной мощности

Огромное количество индуктивных нагрузок в сети суммарно обладает колоссальной реактивной мощностью,
которая возвращается в генераторы и не совершает никакой полезной работы, расходуя энергию на нагрев кабелей и проводов ЛЭП,
перегружает трансформаторы, снижая их КПД, тем самым уменьшая пропускную способность активных токов.

Если параллельно индуктивной нагрузке подключить конденсатор,
фаза тока в цепи источника будет смещаться в противоположную сторону, компенсируя угол, созданный индуктивностью нагрузки.
При определённом соотношении номиналов,
можно добиться отсутствия сдвига фаз, следовательно, и отсутствия реактивных токов в цепи источника питания.
Ёмкость конденсатора определяется реактивным (индуктивным) сопротивлением нагрузки, которое необходимо компенсировать:

C = 1/(2πƒX),

X = U²/Q – реактивное сопротивление нагрузки,

Q – реактивная мощность нагрузки.

Компенсация реактивных токов в сети позволяет значительно уменьшить потери на активном сопротивлении проводов ЛЭП, кабелей и обмоток трансформаторов питающей сети.
В целях компенсации реактивной мощности на производственных предприятиях, где основными потребителями энергии являются асинхронные электродвигатели,
индукционные печи, люминесцентное освещение, которые обладают индуктивным сопротивлением, часто применяют специальные конденсаторные
установки, способные в ручном или автоматическом режиме поддерживать нулевой сдвиг фаз, тем самым минимизировать реактивные потери.

В масштабах энергосистемы компенсация происходит непосредственно на электростанциях путём контроля сдвига фаз и обеспечения соответствующего тока
подмагничивания роторных обмоток синхронных генераторов станций.

Компенсация реактивной мощности – одна из составляющих комплекса мер по Коррекции Коэффициента Мощности (ККМ) в электросети
(Power Factor Correction – PFC в англоязычной литературе). Применяется в целях уменьшения потерь электроэнергии, как на паразитную реактивную, так и нелинейную составляющую искажений тока в энергосистеме. Более подробно с материалом о ККМ (PFC) можно ознакомиться на странице – коэффициент мощности.

Онлайн-калькулятор расчёта реактивной мощности и её компенсации.

Достаточно вписать значения и кликнуть мышкой в таблице.

Реактивная мощность Q = √((UI)²-P²)

Реактивное сопротивление X = U²/Q
Компенсирующая ёмкость C = 1/(2πƒX)

Похожие страницы с расчётами:

Рассчитать импеданс.

Рассчитать частоту резонанса колебательного контура LC.

Рассчитать реактивное сопротивление катушки индуктивности L и конденсатора C.

Альтернативные статьи:

Дизель-генератор.

Источник

Добавить комментарий