|
|
Макеты страниц
Как и в общей теории колебательных движений, в теории переменных токов большую пользу приносят векторные диаграммы. Очевидно, что синусоидально изменяющуюся электродвижущую силу

можно изобразить как проекцию на ось ординат вращающегося против часовой стрелки с угловой скоростью  вектора, длина которого равна и начальное положение которого в момент
вектора, длина которого равна и начальное положение которого в момент  совпадало с осью абсцисс.
совпадало с осью абсцисс.
Спросим себя, как изобразится в векторной диаграмме ток, протекающий под влиянием синусоидальной электродвижущей силы через катушку, обладающую индуктивностью 

Рис. 341. Векторная диаграмма для случая Индуктивного сопротивления.

Рис. 342. Векторная диаграмма для случая емкостного сопротивления.
Мы видели, что ток в этом случае отстает на четверть периода от напряжения. Отставание на четверть периода представится в векторной диаграмме отставанием вектора тока на  таким образом, вектор «индуктивного» тока будет перпендикулярен к вектору напряжения (рис. 341), отставая от него на 90. Величина этого вектора
таким образом, вектор «индуктивного» тока будет перпендикулярен к вектору напряжения (рис. 341), отставая от него на 90. Величина этого вектора

Если мы имеем дело с прохождением переменного тока через конденсатор, то ток опережает электродвижущую силу на четверть периода. Это значит, что вектор, изображающий «емкостный» ток, должен опережать вектор напряжения на  (рис. 342). Величина этого вектора, как мы видели выше, определяется соотношением
(рис. 342). Величина этого вектора, как мы видели выше, определяется соотношением

Для случая активного омического сопротивления ток совпадает по фазе с напряжением. Это значит, что вектор тока совпадает по направлению с вектором напряжения, Величина его, конечно, определяется законом Ома.
Ток, вектор которого совпадает с вектором напряжения, называют активным током. Токи же, векторы которых отстают от вектора напряжения или опережают его на  называют реактивными токами. Выбор такого названия объясняется тем, что именно активные токи определяют потребление мощности цепью переменного тока, тогда как на возбуждение реактивного тока (т. е. тока, который отстает от напряжения или опережает его на четверть периода) генератор расходует в течение каждой четверти периода столько же энергии, сколько в следующую четверть периода этот реактивный ток отдает генератору обратно (см. рис. 337); в итоге получается, что реактивный ток не производит работы.
называют реактивными токами. Выбор такого названия объясняется тем, что именно активные токи определяют потребление мощности цепью переменного тока, тогда как на возбуждение реактивного тока (т. е. тока, который отстает от напряжения или опережает его на четверть периода) генератор расходует в течение каждой четверти периода столько же энергии, сколько в следующую четверть периода этот реактивный ток отдает генератору обратно (см. рис. 337); в итоге получается, что реактивный ток не производит работы.
В более общем случае, когда сдвиг фазы между током и напряжением определяется углом  (в радианах), работа, производимая переменным током за целое (или полуцелое) число периодов, пропорциональна
(в радианах), работа, производимая переменным током за целое (или полуцелое) число периодов, пропорциональна 
Действительно, пусть ток отстает от напряжения на угол 

Тогда работа тока за период определяется интегралом

а средняя мощность, потребляемая током, определяется отношением этой работы к продолжительности периода:

Если ввести эффективные значения тока и напряжения, то

При  т. е. при чисто реактивных токах, мощность, передаваемая по электрической цепи от генератора к нагрузке, в среднем равна нулю.
т. е. при чисто реактивных токах, мощность, передаваемая по электрической цепи от генератора к нагрузке, в среднем равна нулю.
При каких-либо заданных величинах напряжения и тока, чем меньше разность фаз между ними и соответственно чем ближе  к единице, тем большая мощность передается током от генератора к нагрузке; поэтому
к единице, тем большая мощность передается током от генератора к нагрузке; поэтому  называют коэффициентом мощности цепи.
называют коэффициентом мощности цепи.
Во многих случаях реактивные токи необходимы. Так, если переменным током мы питаем электромагнит, предназначенный, скажем, для подъема железных предметов, то катушка электромагнита, представляя собой в идеальном случае чисто индуктивное сопротивление, будет потреблять от сети реактивный ток, отстающий от напряжения сети на 
Однако в большинстве случаев, в частности при питании трансформаторов, которые служат для преобразования переменных напряжений, важен активный ток, который создается при нагрузке вторичной обмотки трансформатора (§ 84). Реактивный же ток, который необходим для создания магнитного поля в сердечнике трансформатора, носит, в сущности, вспомогательный характер; он непосредственно не производит никакой полезной работы.
Предположим, что к сети подключено, как это часто бывает, большое количество трансформаторов. Каждый из них потребляет известный реактивный ток для создания магнитного поля сердечника. Это значительно ухудшает коэффициент мощности установки.
Однако есть возможность добиться совпадения вектора тока с вектором напряжения, воспользовавшись явлением резонанса (§ 83). Для этого включают в сеть, кроме трансформаторов, также и емкость С, подобрав ее так, чтобы ее реактивный ток был равен суммарному реактивному току трансформаторов.
Тогда во внешней цепи будет течь только активный ток, реактивные же токи трансформаторов и емкости взаимно компенсируют друг друга. Они будут циркулировать лишь в цепи: емкость — обмотки трансформаторов, не заходя в питающую сеть и в генератор электроцентрали. Для питающей линии и для генератора электроцентрали  и условия их работы будут наивыгоднейшими.
и условия их работы будут наивыгоднейшими.
Это мероприятие имеет существенное экономическое значение. Совершенно ясно, что электроцентраль и линии электропередачи, не загруженные бесполезным реактивным током, могут быть в большей мере загружены токами активными.
Следует отметить, что представление о реактивном токе как о токе, фаза  которого сдвинута на относительно напряжения и который поэтому в среднем не производит никакой работы и не сопровождается рассеянием энергии (на нагревание проводов), конечно, является идеализацией (схематическим упрощением) процессов, происходящих в действительности при прохождении переменного тока через катушки или конденсаторы. Заключение, что фазы токов, проходящих через катушку или конденсатор, отличаются от фазы напряжения на 90°, являлось бы точным только в том случае, если бы прохождение этих токов не было связано с нагреванием проводов и другими потерями (как это было предположено в предыдущем параграфе). Но ток, проходящий через катушку, в отношении нагревания проводов, происходящего по закону Джоуля-Ленца, ничем не отличается от активного тока той же частоты (а при большой частоте сопротивление обмотки катушки вследствие скин-эффекта может оказаться значительным).
которого сдвинута на относительно напряжения и который поэтому в среднем не производит никакой работы и не сопровождается рассеянием энергии (на нагревание проводов), конечно, является идеализацией (схематическим упрощением) процессов, происходящих в действительности при прохождении переменного тока через катушки или конденсаторы. Заключение, что фазы токов, проходящих через катушку или конденсатор, отличаются от фазы напряжения на 90°, являлось бы точным только в том случае, если бы прохождение этих токов не было связано с нагреванием проводов и другими потерями (как это было предположено в предыдущем параграфе). Но ток, проходящий через катушку, в отношении нагревания проводов, происходящего по закону Джоуля-Ленца, ничем не отличается от активного тока той же частоты (а при большой частоте сопротивление обмотки катушки вследствие скин-эффекта может оказаться значительным).
Кроме того, часть энергии тока рассеивается вследствие гистерезисных потерь в сердечнике катушки (если он имеется) и токов Фуко в окружающих проводниках, например в металлических «экранах», в которые помещают катушки радиоаппаратов. Может иметь место также утечка тока вследствие несовершенства изоляции и т. п. Потери энергии тока, но обычно меньшие, чем в катушках, наблюдаются и при прохождении тока через конденсаторы. В этом случае они вызываются главным образом некоторым отставанием во времени от напряженности поля поляризации диэлектрика (в той ее части, на которую оказывает
влияние молекулярно-тепловое движение), а также иногда наличием небольших ионных токов проводимости в диэлектрике конденсатора.
Вследствие потерь ток через катушку или конденсатор никогда не является чисто реактивным, т. е. сдвиг его фазы относительно напряжения никогда не бывает точно равным а всегда оказывается меньше, чем на угол  который называют иглом потерь. Под действием напряжения
который называют иглом потерь. Под действием напряжения  в идеальной катушке должен был бы проходить чисто реактивный ток
в идеальной катушке должен был бы проходить чисто реактивный ток  с амплитудой —
с амплитудой —  в действительности же, как показано в конце следующего параграфа (в виде пояснения выведенного там обобщенного закона Ома), возбуждается ток с амплитудой, уменьшившейся вследствие потерь до значения
в действительности же, как показано в конце следующего параграфа (в виде пояснения выведенного там обобщенного закона Ома), возбуждается ток с амплитудой, уменьшившейся вследствие потерь до значения  этот фактический ток через катушку представляет собой сумму возникшего в связи с потерями активного тока
этот фактический ток через катушку представляет собой сумму возникшего в связи с потерями активного тока  и реактивного тока
и реактивного тока

с амплитудой, уменьшившейся до величины  что
что  из рис. 343. Согласно рис. 343
из рис. 343. Согласно рис. 343


Рис. 343. Вследствие потерь амплитуда тока через катушку уменьшается до величины  а амплитуда реактивного тока — до величины
а амплитуда реактивного тока — до величины  где
где  угол
угол  потерь.
потерь.
Аналогичные соотношения и такая же диаграмма справедливы и для тока через конденсатор. Так как активный ток — это ток, фаза которого совпадает с напряжением, то очевидно, что мощность, рассеиваемая вследствие потерь, равна  Та же мощность будет рассеиваться в цепи, составленной из идеальной катушки с той же индуктивностью
Та же мощность будет рассеиваться в цепи, составленной из идеальной катушки с той же индуктивностью  и некоторого сопротивления
и некоторого сопротивления  включенного последовательно с ней (называемого сопротивлением потерь), если это сопротивление
включенного последовательно с ней (называемого сопротивлением потерь), если это сопротивление  определено как раз из условия равенства рассеиваемых мощностей:
определено как раз из условия равенства рассеиваемых мощностей:

Как упоминалось выше,

Поэтому получается, что

Подставляя это значение амплитуды активного тока в приведенное выше выражение для тангенса угла потерь, приходим к формуле, которую считают основной при анализе влияния потерь на режим переменного тока в электрических цепях:

По смыслу вывода этой формулы понятно, что аналогичное соотношение справедливо и для тангенса угла потерь в цепи с конденсатором

В радиотехнических расчетах часто применяют величину, обратную тангенсу угла потерь, которую называют добротностью электрической цепи (см. стр. 460 и 485):

Потери в катушках большой индуктивности в высокой мере зависят от конструкции и магнитных свойств сердечника и выполнения обмотки. При правильной конструкции потери в сердечнике и в обмотке (не одинаково зависящие от частоты) должны быть по возможности уравнены.
Для уменьшения потерь на токи Фуко сердечники набирают из тонких листов трансформаторного железа (толщиной 0,5-0,35 мм), покрытых для изоляций их друг от друга тонким (0,05 мм) слоем лака. Потери в таких сердечниках составляют около  на килограмм массы сердечника. Сечение проводов выбирают с учетом возрастания их сопротивления вследствие скин-эффекта так, чтобы при эксплуатации потери в обмотке были приблизительно равны потерям в сердечнике. Суммарно потери в сердечнике и обмотке трансформаторов большой мощности (порядка
на килограмм массы сердечника. Сечение проводов выбирают с учетом возрастания их сопротивления вследствие скин-эффекта так, чтобы при эксплуатации потери в обмотке были приблизительно равны потерям в сердечнике. Суммарно потери в сердечнике и обмотке трансформаторов большой мощности (порядка  составляют 3—4%, а в трансформаторах очень большой мощности (порядка
составляют 3—4%, а в трансформаторах очень большой мощности (порядка  несколько десятых долей процента
несколько десятых долей процента
Потери в небольших трансформаторах лабораторного типа и в «силовых» трансформаторах, применяемых в радиоаппаратуре, обычно бывают не меньше 10—12% (чаще около  Еще большую часть мощности (как правило, 30%) составляют потери в дросселях и трансформаторах усилителей звуковой частоты. Первичная обмотка трансформаторов для токов звуковой частоты состоит из 2000—5000 витков и имеет индуктивность
Еще большую часть мощности (как правило, 30%) составляют потери в дросселях и трансформаторах усилителей звуковой частоты. Первичная обмотка трансформаторов для токов звуковой частоты состоит из 2000—5000 витков и имеет индуктивность 
Катушки резонансных контуров радиочастот имеют индуктивность порядка тысячных (а для коротких волн—миллионных) долей генри. Такая индуктивность создается сравнительно небольшим числом витков провода без ферромагнитного сердечника. В связя с этим потери в радиочастотных катушках невелики — порядка 1% (тангенс угла потерь — от 0,02 до 0,005).
Потери в конденсаторах (за исключением электролитических конденсаторов) обычно не превышают  что соответствует тангенсу угла потерь
что соответствует тангенсу угла потерь  В электролитических конденсаторах тангенс угла потерь может достигать 0,2.
В электролитических конденсаторах тангенс угла потерь может достигать 0,2.
Среди лучших изоляторов (имеющих удельное сопротивление порядка  ом-см) выделяются наименьшим значением тангенса угла потерь: кварц плавленый, слюда—мусковит, парафин и полистирол; для них
ом-см) выделяются наименьшим значением тангенса угла потерь: кварц плавленый, слюда—мусковит, парафин и полистирол; для них 
Оглавление
- ЧАСТЬ ТРЕТЬЯ. УЧЕНИЕ ОБ ЭЛЕКТРИЧЕСТВЕ
- § 2. Количество электричества. Закон Кулона
- § 3. Атомное строение электричества
- § 4. Напряженность электрического поля
- § 5. Теорема Острогдадского — Гаусса
- § 6. Вектор электрической индукции
- § 7. Примеры применения теоремы Остроградского — Гаусса
- § 8. Потенциал электрического поля
- § 9. Формулы электростатики в практической системе единиц
- ГЛАВА II. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 10. Распределение электричества по поверхностй заряженных проводников
- § 11. Электризация проводников в поле и деформация поля проводниками
- § 12. Контактная разность потенциалов
- § 13. Электроемкость
- § 14. Расчет электроемкости конденсаторов
- § 15. Электрическая энергия
- § 16. Энергия поля
- § 17. Электрометры
- § 18. О природе электрических явлений
- ГЛАВА III. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
- § 19. Дипольная и электронная поляризация диэлектриков. Сегнетоэлектрики
- § 20. Деформация поля диэлектриками
- § 21. Электрическая восприимчивость
- § 22. Электронная теория диэлектриков
- § 23. Пьезоэлектрические и пироэлектрические явления
- § 24. Электроконвекционные явления (электрофорез, электроэндосмос и др.)
- ГЛАВА IV. ПОСТОЯННЫЙ ТОК
- § 25. Величина тока. Электродвижущая сила и напряжение
- § 26. Закон Ома. Законы Кирхгофа
- § 27. Закон Джоуля — Ленца
- § 28. Дифференциальная форма законов Ома и Джоуля — Ленца. Соотношение аналогии между проводимостью и емкостью
- ГЛАВА V. ТОК В МЕТАЛЛАХ
- § 29. Сведения об электропроводности. Термометры сопротивления, болометры, тензометры
- § 30. Закон Видемана — Франца. Теория электропроводности металлов
- § 31. Сверхпроводимость
- § 32. Термоэлектрические явления и их применение
- § 33. Зависимость термоэлектродвижущей силы от температуры спаев. Явление Пельтье
- ГЛАВА VI. ТОК В ПОЛУПРОВОДНИКАХ
- § 34. Полупроводники
- § 35. Понятие о зонной теории электропроводности
- § 36. Применения полупроводников
- ГЛАВА VII. ТОК В ЭЛЕКТРОЛИТАХ
- § 37. Электролиз. Законы Фарадея. Электрохимические эквиваленты. Потенциалы разложения
- § 38. Вторичные реакции на электрэдах. Применения электролиза
- § 39. Подвижность ионов и электропроводность растворов
- § 40. Гальванические элементы. Электрохимическая природа коррозии
- § 41. Электродные потенциалы
- § 42. Аккумуляторы
- § 43. Свободная энергия гальванической цепи. Концентрационные элементы
- ГЛАВА VIII. ТОК В ГАЗАХ
- § 44. Ионизация и электропроводность газов
- § 45. Типы и механизм разряда в газах
- § 46. Катодные и анодные лучи
- § 47. Тлеющий разряд
- § 48. Дуговой разряд
- § 49. Искровой разряд. Молния
- ГЛАВА IX. ТОК ЭЛЕКТРОННОЙ ЭМИССИИ. ЭЛЕКТРОННЫЕ ЛАМПЫ
- § 50. Термоэлектронная эмиссия. Формула Ричардсона — Дёшмена
- § 51. Торможение электронного потока. Рентгеновы трубки
- § 52. Пустотные выпрямители тока (диоды, кенотроны)
- § 53. Усилительные электронные лампы (триоды)
- § 54. Фотоэлектрический эффект. Фотоэлементы. Фотореле
- § 55. Вторичная электронная эмиссия. Электронные умножители
- § 56. Динатронный эффект. Экранированные радиолампы
- ГЛАВА X. МАГНИТНОЕ ПОЛЕ
- § 57. Исторические сведения. Закон Кулона для магнитных полюсов
- § 58. Магнитные величины и соотношения, аналогичные электрическим
- § 59. Магнитное поле Земли
- § 60. Магнитное поле тока
- § 61. Закон Био и Савара
- § 62. Магнитодвижущая сила. Поток индукции электромагнита
- § 63. Магнитные свойства веществ и их использование
- § 64. Электронная теория магнетизма
- ГЛАВА XI. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ТОК
- § 65. Формула Ампера и ее трактовка по Фарадею
- § 66. Работа, производимая током при перемещении проводника в магнитном поле. Электромоторы
- § 67. Отклоняющее действие магнитного поля на электронный поток (в вакууме и в металле)
- § 68. Электродинамические измерительные приборы. Гальванометры, Осциллографы
- § 69. Формулы электродинамики в практической системе единиц
- ГЛАВА XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
- § 70. Понятие об электромагнитном поле. Электромагнитная индукция
- § 71. Закон Ленца. Картина электромагнитного поля по Фарадею
- § 72. Закон Фарадея. Индукционное измерение магнитного потока и магнитодвижущей силы. Вихревые токи
- § 73. Явление самоиндукции. Индуктивность. Законы нарастания и спада тока при включении и выключении цепи
- § 74. Энергия магнитного поля тока. Индуктивность и энергия электромагнита. Индуктивность кабеля
- § 75. Взаимная индуктивность. Энергия взаимодействия токов. Коэффициент взаимной индукции катушек с общим сердечником
- § 76. Уравнения Максвелла и уравнения Лорентца
- § 77. Электромагнитное происхождение массы электрона
- ГЛАВА XIII. ПЕРЕМЕННЫЙ ТОК
- § 78. Генерирование переменного тока
- § 79. Работа генератора электрической энергии на нагрузку Эффективные значения напряжения и величины тока
- § 80. Емкостное сопротивление и индуктивное сопротивление
- § 81. Активные и реактивные токи. Коэффициент мощности (cos f). Потери (tg b)
- § 82. Обобщенный закон Ома
- § 83. Электрический резонанс
- § 84. Трансформация тока
- § 85. Трехфазный ток. Синхронные и асинхронные моторы
- ГЛАВА XIV. ЭЛЕКТРИЧЕСКИЕ КОЛЕБАНИЯ И ИХ ПРИМЕНЕНИЕ
- § 86. Индуктор
- § 87. Колебательный контур
- § 88. Вибратор Герца (возбуждение колебательного контура индуктором). Токи Тесла
- § 89. Электромагнитные волны. Вектор Умова — Пойнтинга
- § 90. Излучение электрического диполя. Волны в двухпроводной линии. Антенны
- § 91. Распространение электромагнитных волн. Роль ионосферы. «Радиоокно» в космос
- § 92. Ламповые генераторы электрических колебаний
- § 93. Модуляция электрических колебаний
- § 94. Прием, детектирование и усиление радиосигналов. Супергетеродины
- § 95. Преобразование звуковых колебаний в электрические и электрических в звуковые. Электрозапись и воспроизведение звука
- § 96. Телевидение
- § 97. Сантиметровые волны и их распространение в волноводах
- § 98. Радиолокация. Генерирование ультракоротких волн (клистроны и магнетроны)
Содержание:
Электрические цепи синусоидального тока:
В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.
При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.
Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
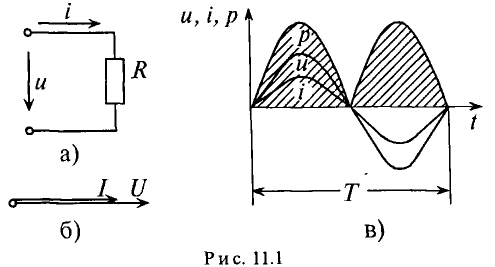
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение 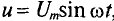
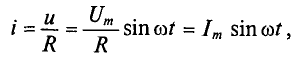
где 
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (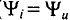 = 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 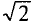 =1,41.
=1,41.
Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.
Активная мощность
Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.
Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.
Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
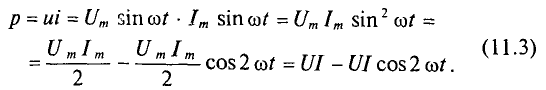
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 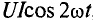 , изменяющейся с двойной частотой.
, изменяющейся с двойной частотой.
Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть
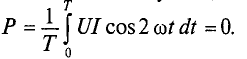
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
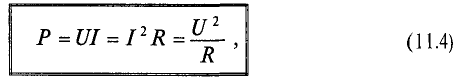
где U- действующее значение напряжения; I— действующее значение тока.
Единицей активной мощности является ватт:
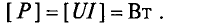
Поверхностный эффект и эффект близости
Сопротивление проводника постоянному току 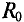 называют омическим сопротивлением и определяют выражением (2.8)
называют омическим сопротивлением и определяют выражением (2.8) 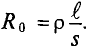 Сопротивление проводника переменному току R называют активным.
Сопротивление проводника переменному току R называют активным.
Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е. 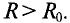
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).
На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.
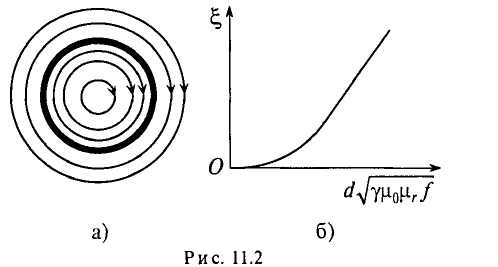
Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.
Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 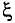 (кси)
(кси)
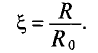
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости 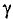 , магнитной проницаемости материала проводника
, магнитной проницаемости материала проводника 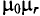 и частоты переменного тока
и частоты переменного тока  , проходящего по проводнику, показан на рис. 11.26.
, проходящего по проводнику, показан на рис. 11.26.
При токах большой частоты  (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
(радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.
На величину активного сопротивления проводника R оказывает влияние и эффект близости.
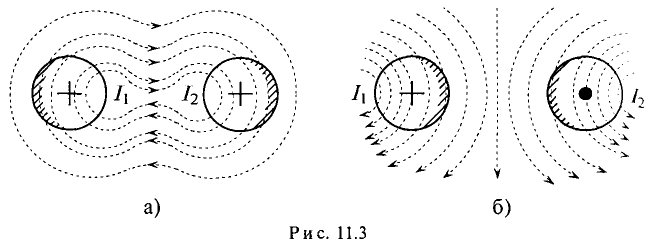
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.
Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).
Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.
Цепь с идеальной индуктивностью
Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.
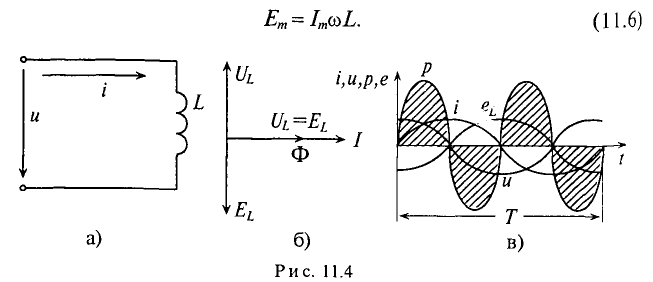
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток 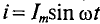 , то этот ток создает в катушке синусоидальный магнитный поток
, то этот ток создает в катушке синусоидальный магнитный поток 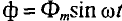 , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
, который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)
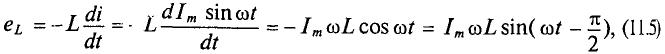
так как 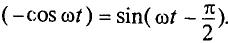
Очевидно, эта ЭДС достигает своего амплитудного значения 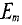 тогда, когда
тогда, когда 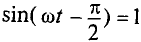 :
:
Тогда 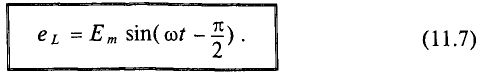
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 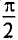 (рис. 11.46, в).
(рис. 11.46, в).
По второму закону Кирхгофа для мгновенных значений можно записать

Откуда 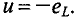
Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):
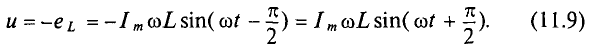
Очевидно, напряжение достигает своего амплитудного значения Um тогда, когда 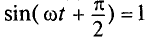 :
:

Следовательно, 
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 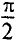 (рис. 11.46, в).
(рис. 11.46, в).
Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).
Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 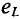 противодействует изменению тока.
противодействует изменению тока.
Если уравнение (11.10) разделить на 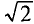 =1,41, то получается
=1,41, то получается 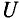 =
=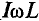 , откуда
, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.
Таким образом,

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
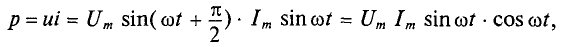
где 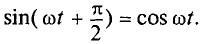
Следовательно, 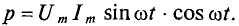
Полученное уравнение умножают и делят на 2:
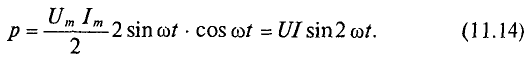
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.
Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (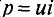 ) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.
То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно
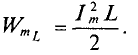
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.
Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.
Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
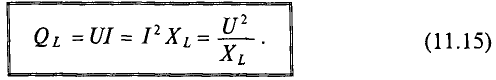
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. XL.
Цепь с емкостью
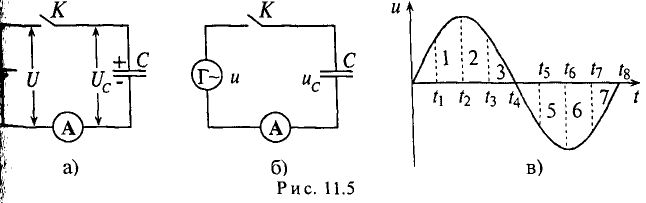
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе Uc не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).
Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе Uc отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
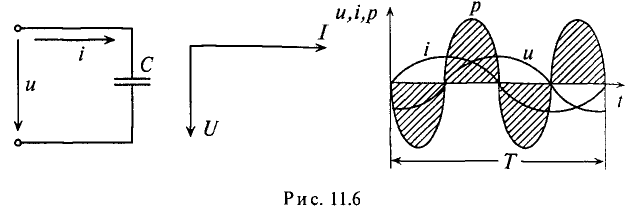
Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 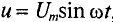 , то в цепи конденсатора проходит ток i (рис. 11.6а):
, то в цепи конденсатора проходит ток i (рис. 11.6а):
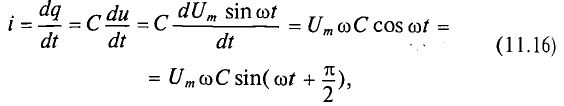
где q= Си согласно (6.3).
Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда 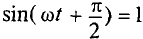 :
:

Тогда 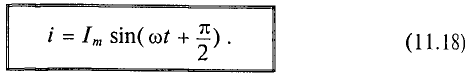
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=
Следовательно, напряжение отстает по фазе от тока на 90° =  (рис. 11.66).
(рис. 11.66).
Если уравнение (11.17) разделить на 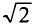 = 1,41, то получится равенство
= 1,41, то получится равенство 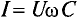 или
или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.
Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление – это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).
Реактивная мощность в цепи с конденсатором
Если в цепи конденсатора емкостью 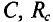 = 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
= 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:
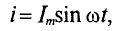
Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно
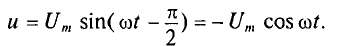
Мгновенная мощность в цепи с конденсатором
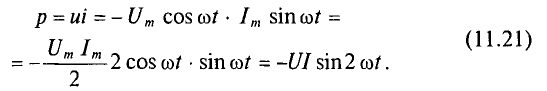
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).
Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.
Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
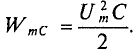
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.
Величина реактивной мощности в цепи конденсатора определяется выражением
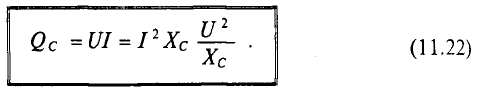
Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) – аналитическом выражении мгновенной мощности в цепи с конденсатором.
Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Хс).
Расчет линейных электрических цепей синусоидального тока
Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.
Цепь с активным сопротивлением и индуктивностью
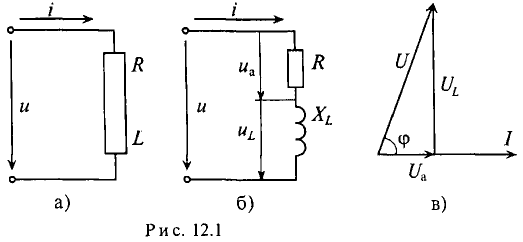
Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 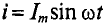 (рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки
(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки 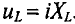
Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением XL (рис. 12.16).
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано 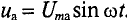 . Индуктивное напряжение
. Индуктивное напряжение 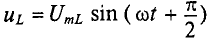 опережает ток на угол 90° =
опережает ток на угол 90° = 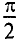 .
.
Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 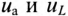 согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений
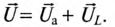
Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).
Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 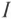 на угол ф. Мгновенное значение этого напряжения может быть записано:
на угол ф. Мгновенное значение этого напряжения может быть записано:
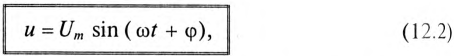
где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение
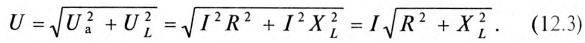
Откуда

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Zk — полное, или кажущееся, сопротивление реальной катушки.
Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.
Треугольники напряжений, сопротивлений, мощностей
Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).
Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:
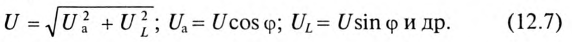
Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:
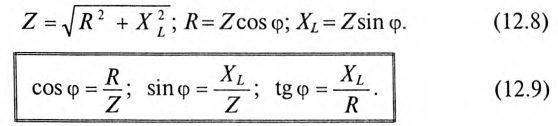
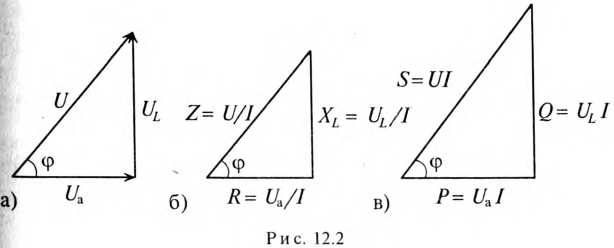
Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).
Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).
Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е. 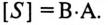
Однако потребляется в цепи только часть полной мощности – активная мощность
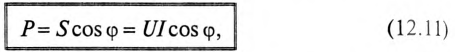
где cos ф показывает, какая часть полной мощности 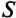 потребляется в цепи, поэтому cos ф называют коэффициентом мощности:
потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:
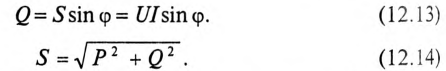
Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.
Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток 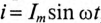 , то он создает падение напряжения на активном сопротивлении
, то он создает падение напряжения на активном сопротивлении 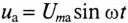 и на емкостном сопротивлении
и на емкостном сопротивлении 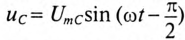 . Векторная диаграмма для этой цепи изображена на рис. 12.36.
. Векторная диаграмма для этой цепи изображена на рис. 12.36.
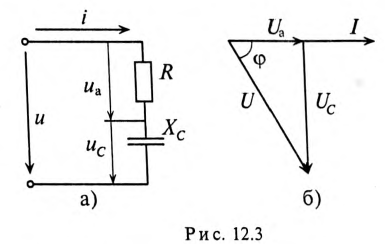
Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф < 90°, т. е.

Действующее значение напряжения U, приложенного к этой цепи, определяется по векторной диаграмме (рис. 12.3):
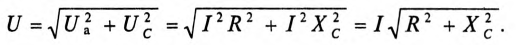
Откуда математическое выражение закона Ома для этой цепи:
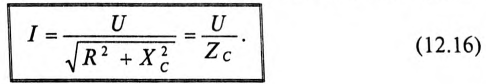
Пример 12.1
К цепи с последовательно включенными сопротивлениями R= 8 Ом и Хс= 6 Ом (рис. 12.3а) приложено напряжение U= 220 В. Определить ток цепи I, напряжение на активном 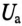 и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
и реактивном Up участках, полную S, активную Р и реактивную Q мощности.
Решение
Для определения тока вычислим полное сопротивление цепи
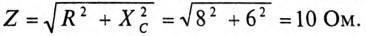
Тогда ток будет равен
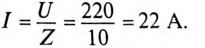
Напряжения на участках:
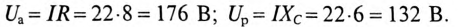
Полная мощность 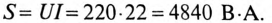
Активная мощность 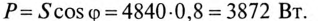
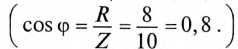
Реактивная мощность 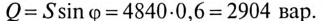
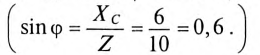
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток 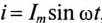 , то он создает падение напряжения на всех участках цепи:
, то он создает падение напряжения на всех участках цепи: 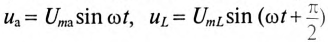 и
и 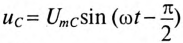 .
.
Мгновенное значение напряжения цепи определяется по формуле
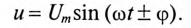
Так как в рассматриваемой цепи включены два реактивных сопротивления XL и Хс, то возможны три режима работы цепи: 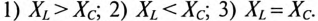
Векторная диаграмма цепи для режима 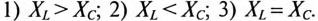 изображена на рис. 12.46.
изображена на рис. 12.46.
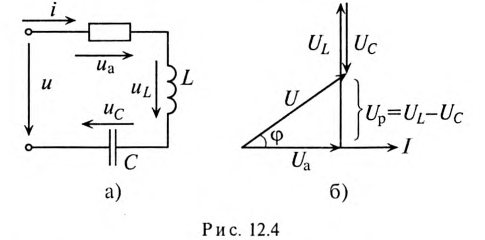
Знак перед углом сдвига фаз ф зависит от режима работы цепи Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т. е. 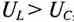 , то цепь имеет индуктивный характер и напряжение U опережает по фазе ток
, то цепь имеет индуктивный характер и напряжение U опережает по фазе ток 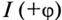 .
.
Если в цепи преобладает емкостное напряжение (сопротивление), т.е. 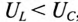 , то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
, то цепь имеет емкостной характер и напряжение U отстает по фазе от тока I (—ф).
Из векторной диаграммы (рис. 12.46) следует:
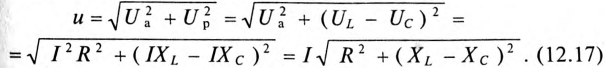
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:
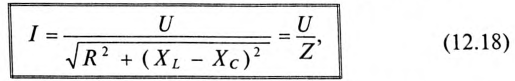
где Z — полное (или кажущееся) сопротивление неразветвленной цепи с R, L и С, т. е.
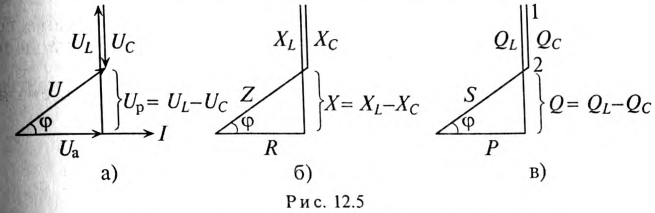
На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла ф можно определить из треугольника сопротивлений (рис. 12.56):
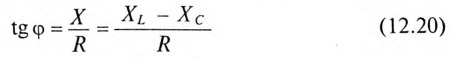
или
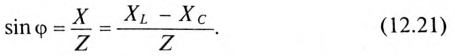
Из выражений (12.20) и (12.21) видно, что если 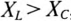 , то угол ф положителен (+ф), если
, то угол ф положителен (+ф), если 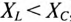 , то угол ф отрицательный (—ф).
, то угол ф отрицательный (—ф).
Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности 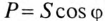 имеется реактивная мощность
имеется реактивная мощность 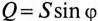 . Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
. Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае Uc) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности QL и Qc изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.
Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= QL– Qc. Эта реактивная мощность (энергия) колеблется между источником и магнитным полем катушки индуктивности, так как 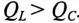
Полная мощность цепи определяется по формуле

Колебательный контур
Электрические цепи, в которых происходят периодические изменения токов, напряжений, энергии называются колебательными.
Для того чтобы исследовать резонансные явления, необходимо иметь представления о процессах в колебательном контуре, состоящем из идеальной катушки и конденсатора без потерь.
Если конденсатор емкостью С зарядить до напряжения Um, то в электрическом поле этого конденсатора накопится энергия, максимальное значение которой согласно выражению (6.21):
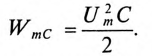
Если к заряженному конденсатору подключить индуктивность L замыканием ключа К (рис. 12.6), то конденсатор будет
разряжаться через индуктивность переменным током i. При этом в индуктивности L создается ЭДС самоиндукции eL, и в магнитном поле ее накапливается энергия, максимальное значение которой (9.12):
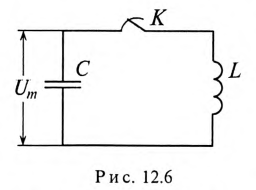
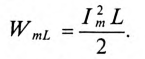
Источником энергии в этом контуре является конденсатор. Ток в контуре, состоящем из индуктивности L и конденсатора С, не прекращается даже когда конденсатор полностью разрядится. За счет ЭДС самоиндукции и энергии, накопившейся в магнитном поле индуктивности, конденсатор будет заряжаться, и энергия магнитного поля индуктивности переходит в электрическое поле конденсатора. При этом источником энергии в этом контуре является индуктивность. Дальше процесс повторяется.
Таким образом, в замкнутом контуре, состоящем из индуктивности и емкости, происходит колебание энергии между электрическим полем конденсатора С и магнитным полем индуктивности L. Поэтому такой замкнутый контур называется колебательным контуром.
Колебание энергии в колебательном контуре происходит с определенной частотой 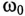 , которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
, которую называют частотой собственных колебаний контура. Частоту собственных колебаний со0 определяют из условия равенства энергии электрического и магнитного полей:
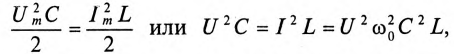
так как из (11.19) в цепи переменного тока с емкостью 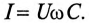
Откуда
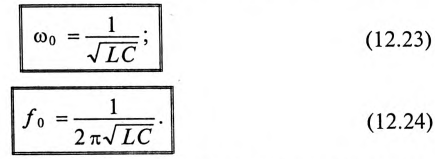
Таким образом, частота собственных колебаний колебательного контура определяется параметрами этого контура L и С.
Если в колебательном контуре отсутствуют потери (идеальный контур), то колебания в нем будут незатухающими с неизменной амплитудой. Если в колебательном контуре имеется активное сопротивление, т.е. возникают потери, то колебания энергии в нем будут затухающие, с уменьшающейся амплитудой, если эти потери не компенсируются.
Резонанс напряжений
Если в цепи синусоидального тока с последовательно соединенными конденсатором емкостью С и катушкой с сопротивлением R И индуктивностью L (рис. 12.7а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.

Из (12.25) следует 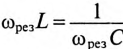 , тогда частота резонанса опреляется выражением
, тогда частота резонанса опреляется выражением

Из (12.26) следует, что резонанс напряжений имеет место в неразветвленной цепи с L и С тогда, когда частота вынужденных колебаний (частота источника) 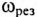 будет равна частоте собственных колебаний резонансного контура
будет равна частоте собственных колебаний резонансного контура 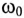 . Следовательно, добиться резонанса напряжений можно изменением частоты источника
. Следовательно, добиться резонанса напряжений можно изменением частоты источника 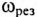 или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний
или изменением параметров колебательного контура L или С. т. е. изменением частоты собственных колебаний 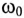 .
.
Полное (кажущееся) сопротивление цепи (рис. 12.7а) при резонансе напряжений определяется по формуле
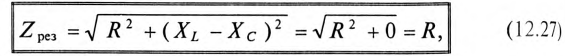
так как XL-Xc=0.
То есть полное сопротивление неразветвленной цепи при резонансе напряжений 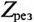 становится минимальным и равным активному сопротивлению цепи R.
становится минимальным и равным активному сопротивлению цепи R.
Следовательно, ток в неразветвленной цепи при резонансе напряжений максимальный:

Реактивные сопротивления при резонансе напряжений равны между собой, т. е.
(12.29)
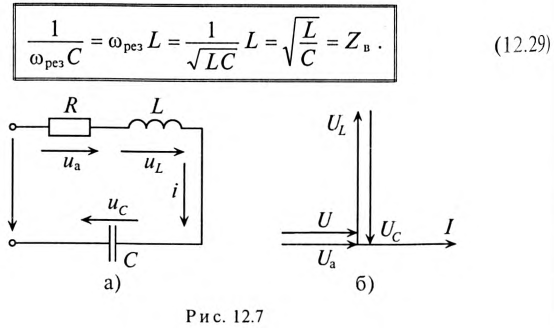
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению 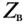 , которое называют характеристическим сопротивлением:
, которое называют характеристическим сопротивлением:
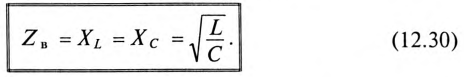
Напряжения на индуктивности UL и на емкости Uc при резонансе напряжений равны между собой, так как равны сопротивления, см. (12.25).
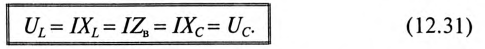
Равенство (12.31) определяет название «резонанс напряжений».
Так как UL и Uc изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении 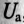 , т. е.
, т. е. 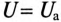 , что видно на векторной диаграмме (рис. 12.76).
, что видно на векторной диаграмме (рис. 12.76).
При резонансе напряжений каждое из реактивных напряжений UL и Uc может оказаться большим, чем напряжение цепи U.
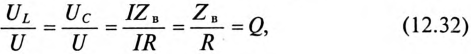
где Q — добротность резонансного контура.
Добротность контура Q показывает, во сколько раз напряжение на индуктивности UL и емкости Uc (каждое) больше напряжения цепи U.
Высокая добротность резонансного контура (при малом активном сопротивлении контура) нашла широкое применение в радиотехнике, в частности в антенном контуре.
Из векторной диаграммы (рис. 12.76) видно, что при резонансе напряжение цепи U совпадает по фазе с током 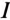 , угол между
, угол между 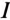 и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:
и U ф = 0 и cos ф = 1. Следовательно, кажущаяся мощность цепи S при резонансе вся потребляется, т. е. является активной:

Колеблющаяся между магнитным полем индуктивности и электрическим полем емкости мощность (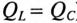 ) не является реактивной, так как не загружает источник и провода.
) не является реактивной, так как не загружает источник и провода.
Из выражения (12.33) следует, что при отсутствии активной Мощности Р (активного сопротивления R) резонансный контур становится при резонансе идеальным колебательным контуром. Следовательно, при наличии активного сопротивления R источник расходует свою мощность на компенсацию потерь в контуре, за счет чего колебания в цепи будут незатухающими.
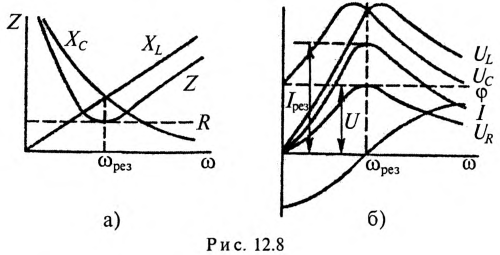
Кроме активного сопротивления R резонансной цепи и напряжения, приложенного к ней, все параметры резонансной цепи (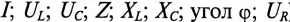 ) изменяются с изменением частоты сети
) изменяются с изменением частоты сети 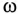 .
.
Эти изменения параметров резонансной цепи наглядно иллюстрируются резонансными кривыми, изображенными на рис. 12.8.
На резонансных кривых четко просматриваются значения этих параметров при частоте резонанса 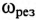 .
.
Общий случай неразветвленной цепи
Для неразветвленной цепи, содержащей несколько активных и реактивных сопротивлений различного характера (рис. 12.9а), справедливо геометрическое равенство напряжений (баланс напряжений)
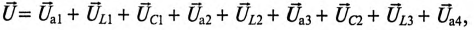
которое лежит в основе построения векторной диаграммы (рис. 12.96).
Таким образом, напряжение цепи равно геометрической сумме напряжений на всех участках этой цепи.
Из векторной диаграммы следует (рис. 12.96)
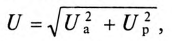
где 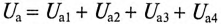 — активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи;
— активное напряжение цепи равно арифметической сумме напряжений на активных участках цепи; 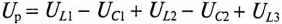 — реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
— реактивное напряжение цепи равно алгебраической сумме напряжений на реактивных участках цепи.
Те же рассуждения можно отнести и к сопротивлениям:
– полное сопротивление цепи 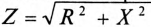 ;
;
– активное сопротивление цепи 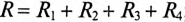 ;
;
– реактивное сопротивление цепи 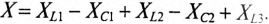
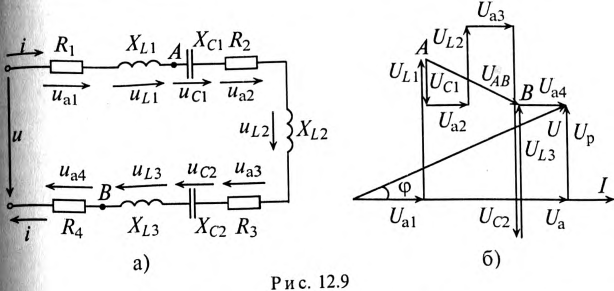
Напряжение на каком-либо участке неразветвленной цепи (рис. 12.9а), например на участке АВ, определяется так:_
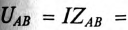
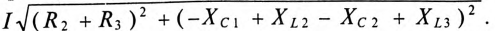
Вектор напряжения UAB показан на векторной диаграмме (рис. 12.96).
Пример 12.2
Напряжение, приложенное к неразветвленной цепи (рис. 12.10) U=220 В, частота тока сети f = 50 Гц. Начальная фаза тока 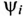 = 0.
= 0.
Сопротивление участков цепи: 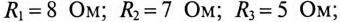
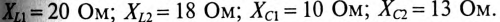
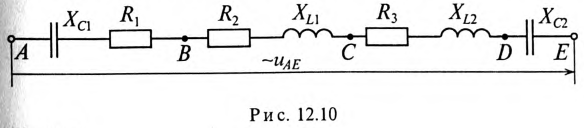
Требуется:
1. Вычислить ток цепи I и записать его мгновенное значение.
2. Записать мгновенное значение напряжения цепи иАЕ, определив предварительно угол ср и характер цепи.
3. Определить напряжение между точками АВ и CD.
4. Построить в масштабе векторную диаграмму цепи, определив едварительно напряжение на каждом сопротивлении.
5. Определить мощности S, Р и Q цепи.
6. Определить частоту, при которой в цепи наступит резонанс напряжений, и ток при резонансе.
7. Определить максимальную энергию, запасенную в магнитном поле катушек WmL и электрическом поле конденсаторов WmC. Как нужно изменить емкость конденсаторов, чтобы в цепи пил резонанс напряжений при частоте f = 50 Гц?
Решение
1. Для определения тока цепи I необходимо вычислить полное сопротивление цепи:
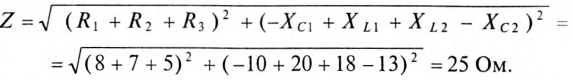
Действующее значение тока 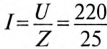 = 8,8 А, а амплитудное значение тока
= 8,8 А, а амплитудное значение тока 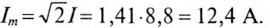
Угловая частота 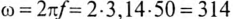 рад/с.
рад/с.
Мгновенное значение тока цепи:
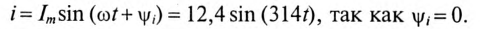
2. Угол сдвига фаз ф и характер цепи определяется через tg ф:
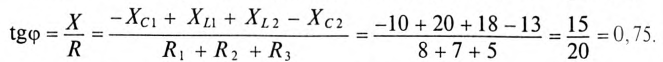
Таким образом, угол ф = 37° (из таблицы), характер цепи индуктивный (+ф).
Тогда мгновенное значение напряжения цепи
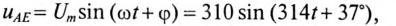
где 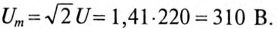
3. Напряжение на участках:
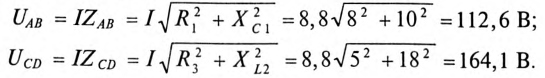
4. Для построения векторной диаграммы определяются напряжения:
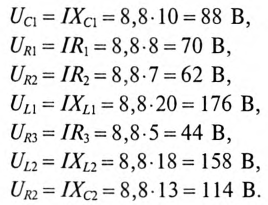
Векторная диаграмма цепи (отображает только характер участков, но не величины напряжений на них) изображена на рис. 12.11.
5. Полная мощность цепи 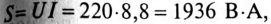 активная мощность Р=
активная мощность Р=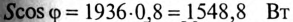 (так как
(так как 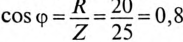 ), реактивная мощность
), реактивная мощность 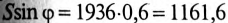 вар, (так как
вар, (так как 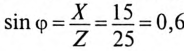 ).
).
6. Для определения частоты резонанса вычисляется индуктивность L и емкость С цепи:
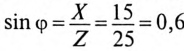
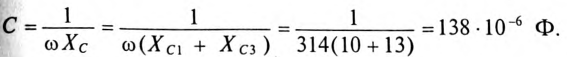
Тогда
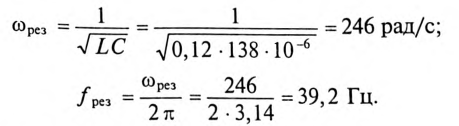
Ток цепи при резонансе 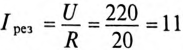 А.
А.
7. Максимальная энергия, запасенная в магнитном поле катушек:
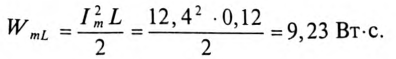
Максимальная энергия, запасенная в электрическом поле конденсаторов:
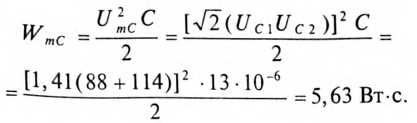
8. Условие резонанса XL = XC.
По условию задачи 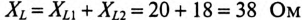 , а
, а 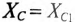
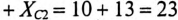 Ом. Этому Хс соответствует емкость С =
Ом. Этому Хс соответствует емкость С = 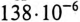 Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
Ф при f = 50 Гц. Для того чтобы выполнить условие резонанса при сохранении частоты 50 Гц, необходимо Хс увеличить до 38 Ом. Чтобы емкостное сопротивление равнялось 38 Ом, величина емкости С должна быть равна
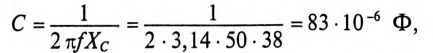
т. е. емкость конденсаторов нужно уменьшить на
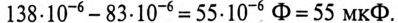
Разветвленная цепь синусоидального тока
Активный и реактивный токи:
Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.
Если к цепи, содержащей активное сопротивление R и индуктивное XL (рис. 13.1а), приложено синусоидальное напряжение 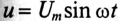 , то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в),
, то синусоидальный ток в цепи, вызванный этим напряжением, отстает от него по фазе на угол ф (рис. 12.1 в), 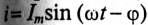 .
.
Векторная диаграмма в этом случае изображена на рис. 13.16.
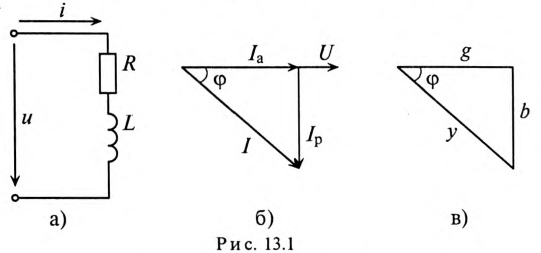
Ток цепи I (рис. 13.16) раскладывается на две составляющие, одна из которых  совпадает по фазе с напряжением, другая
совпадает по фазе с напряжением, другая  — сдвинута на 90°. Составляющая тока
— сдвинута на 90°. Составляющая тока  , совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока
, совпадающая по фазе с напряжением, называется активной составляющей, или активным током. Составляющая тока  , имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
, имеющая относительно напряжения сдвиг по фазе на угол 90°, называется реактивной составляющей, или реактивным током.
Активный и реактивный токи физического смысла не имеют. Они являются расчетными величинами, так как в неразветвленной цепи (рис. 13.1а) ток на всех участках имеет одинаковое значение. Однако понятия активный  и реактивный
и реактивный  токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
токи значительно облегчают расчет разветвленных цепей синусоидального тока. Соотношения между токами определяются из треугольника токов (рис. 13.16)
13.2. Проводимости
Из треугольника токов для рассматриваемой цепи (рис. 13.16) следует: 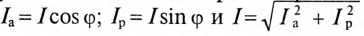 .
.
С другой стороны, известно, что 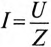 (см. (12.6)), a
(см. (12.6)), a 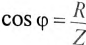 и
и 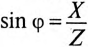 (см. (12.9)).
(см. (12.9)).
Тогда
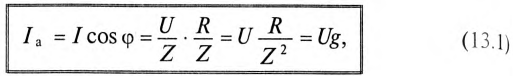
где g — активная проводимость цепи, равная

Величина, на которую умножают напряжение, чтобы получить ток, называют проводимостью.
А так как g определяет активный ток 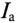 , то ее и называют активной проводимостью.
, то ее и называют активной проводимостью.
Таким образом, активная проводимость g определяется величиной активного сопротивления, деленного на квадрат полного (кажущегося) сопротивления цепи.
Величина реактивного тока определяется выражением
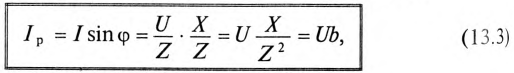
где b — реактивная проводимость цепи, равная

Величина полного тока цепи равна
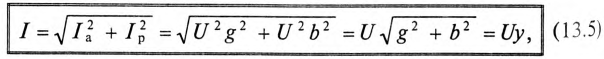
где 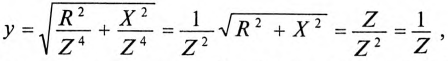 так как для цепи синусоидального тока с
так как для цепи синусоидального тока с 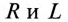 (рис. 13.1а)
(рис. 13.1а) 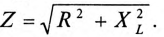
Таким образом, у — полная, или кажущаяся, проводимость цепи:

Полная (кажущаяся) проводимость цепи «у» является обратной величиной полного (кажущегося) сопротивления цепи.
Активная 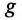 и реактивная
и реактивная 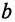 проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е.
проводимости являются соответственно обратными величинами активного R и реактивного X сопротивлений только в том случае, если эти сопротивления (R и X) являются единственными в цепи или ветви, т. е. 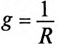 и
и 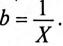
Если же в неразветвленной цепи (или ветви) включены сопротивления 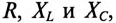 то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
то для определения проводимостей можно воспользоваться выражениями (13.2), (13.4), (13.6). Треугольник проводимостей для рассматриваемой цепи (рис. 13.1а) изображен на рис. 13.1 в. Соотношения между проводимостями определяются из этого треугольника.
Параллельное соединение катушки и конденсатора
Если к источнику синусоидального напряжения 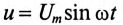 подключить параллельно реальную катушку с активным сопротивлением
подключить параллельно реальную катушку с активным сопротивлением 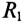 и индуктивным
и индуктивным 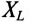 и конденсатор с активным сопротивлением
и конденсатор с активным сопротивлением 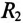 и емкостным
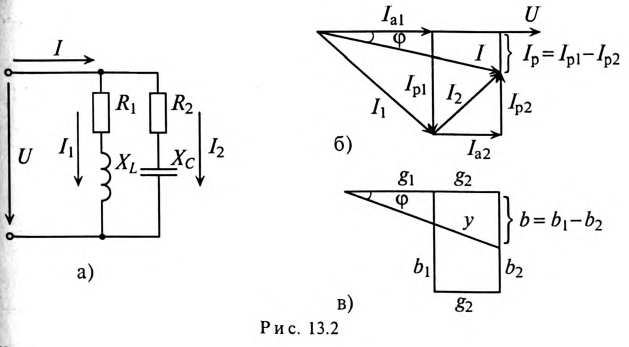
и емкостным 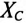 (рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
(рис. 13.2а), то токи в параллельных ветвях этой цепи изменяются по синусоидальному закону:
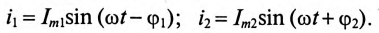
Действующие значения этих токов будут соответственно равны
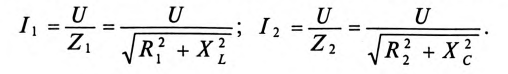
Ток в неразветвленной цепи 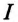 равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
равен геометрической сумме токов в ветвях, так как токи не совпадают по фазе:
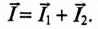
Для определения этого тока строится векторная диаграмма цепи (рис. 13.26), из которой следует:
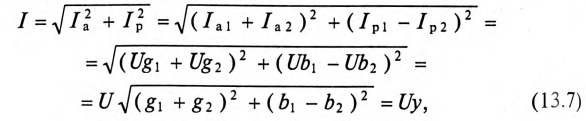
где 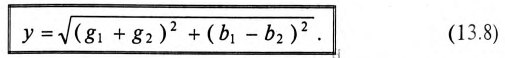
Таким образом, ток в неразветвленной части цепи 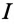 определяется произведением напряжения U и полной проводимости цепи
определяется произведением напряжения U и полной проводимости цепи 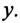
Реактивные проводимости в ветвях имеют различные знаки, так как сопротивления в ветвях различного характера (индуктивное и емкостное).
Треугольник проводимостей рассматриваемой цепи изображен на рис. 13.2в.
Характер разветвленной цепи определяется так же, как и неразветвленной. Если ток цепи 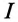 отстает от напряжения
отстает от напряжения 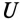 (как в рассматриваемом случае), то цепь индуктивного характера, если же ток
(как в рассматриваемом случае), то цепь индуктивного характера, если же ток 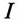 опережает напряжение
опережает напряжение 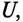 то цепь емкостного характера.
то цепь емкостного характера.
Резонанс токов
Резонанс токов в цепи (рис. 13.2а) с параллельным включением катушки и конденсатора (в различных ветвях) возникает при равенстве реактивных проводимостей в ветвях:
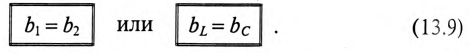
Выражение (13.9) является условием резонанса токов в разветвленных цепях синусоидального тока. Полная (кажущаяся) проводимость при этом условии
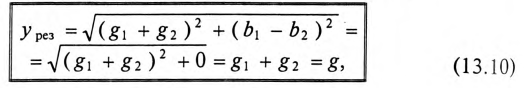
так как 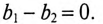
Таким образом, полная проводимость цепи при резонансе токов 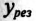 минимальна по величине и равна активной проводимости
минимальна по величине и равна активной проводимости 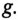 Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину
Следовательно, и ток в неразветвленной части цепи при резонансе токов имеет минимальную величину

Реактивные токи в ветвях при резонансе токов равны между собой

Это равенство и определяет название «резонанс токов».
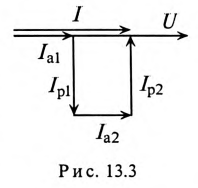
На основании равенства (13.12) строится векторная диаграмма при резонансе токов (рис. 13.3). Реактивные токи находятся в противофазе, поэтому ток в неразветвленной части цепи 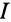 при резонансе токов равен активному току
при резонансе токов равен активному току 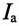 и совпадает по фазе с напряжением, т.е.
и совпадает по фазе с напряжением, т.е. 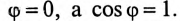 Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
Следовательно, вся мощность цепи 5 при резонансе токов является активной Р:
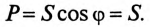
Эта активная мощность компенсирует потери на активном сопротивлении в параллельном резонансном контуре. Мощность (энергия), которая колеблется между электрическим полем конденсатора и магнитным полем индуктивности при резонансе, не является реактивной, так как не загружает источник и провода.
Частота резонанса токов в параллельном резонансном контуре может быть определена из условия резонанса токов, т. е. равенства реактивных проводимостей в ветвях 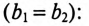
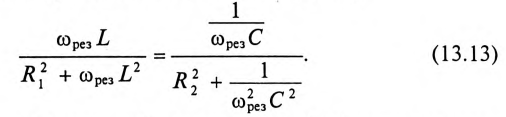
После ряда преобразований равенства (13.13) определяется частота резонанса токов
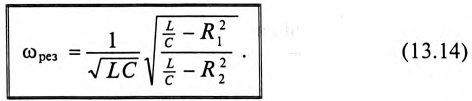
Резонансная частота зависит не только от параметров колебательного контура 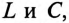 но и от активных сопротивлений в ветвях реального резонансного контура.
но и от активных сопротивлений в ветвях реального резонансного контура.
Если в резонансном контуре отсутствуют активные сопротивления в ветвях, то частота резонанса токов 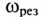 становится равной частоте собственных колебаний идеального резонансного контура
становится равной частоте собственных колебаний идеального резонансного контура
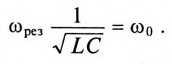
Если в резонансном контуре 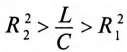 или
или 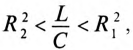 то резонанса токов добиться невозможно.
то резонанса токов добиться невозможно.
Резонанс токов нашел широкое применение в радиотехнике и выпрямительной технике (в резонансных фильтрах) и др.
Пример 13.1
Напряжение, приложенное к параллельно включенным катушке и конденсатору (рис. 13.4а), 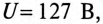 частота сети
частота сети 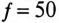 Гц. Параметры цепи:
Гц. Параметры цепи: 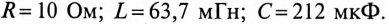 Определить:
Определить:
1) токи всех участков цепи: 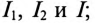
2) углы сдвига фаз этих токов относительно напряжения: 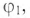
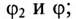
3) полную S, активную Р и реактивную Q мощности цепи;
4) частоту, при которой наступит резонанс токов в этой цепи. Построить векторную диаграмму.
Решение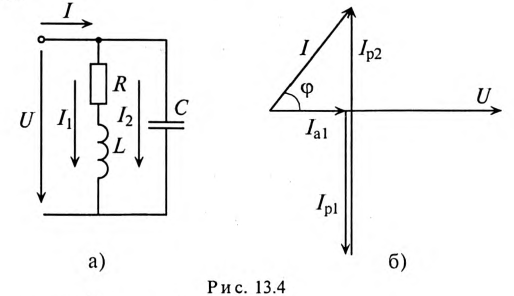
1. Сопротивление участков цепи:
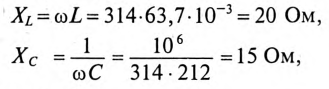
где 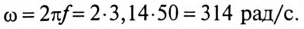
Сопротивление 1-й ветви:
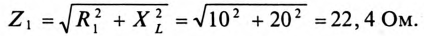
Токи в ветвях соответственно равны
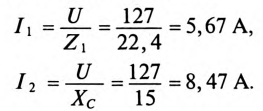
Для определения тока 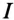 в неразветвленной части цепи определяются проводимости:
в неразветвленной части цепи определяются проводимости:
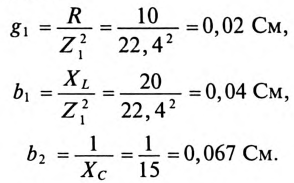
Тогда полная проводимость цепи будет равна
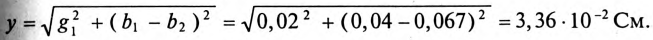
Ток в неразветвленной части цепи
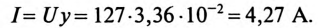
2. Углы сдвига фаз:
.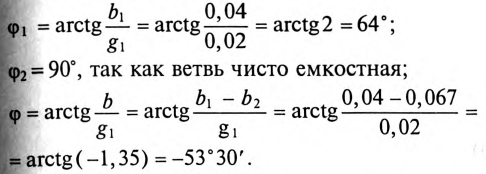
Знак «минус» перед значением угла 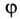 параллельного контура означает, что цепь имеет емкостной характер, так как
параллельного контура означает, что цепь имеет емкостной характер, так как 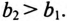
3. Полная мощность цепи 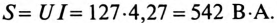
Активная мощность цепи 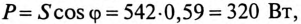 так как
так как 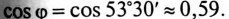
Реактивная мощность цепи 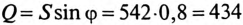 вар, так как
вар, так как 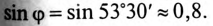
4. Угловая частота резонанса токов в цепи равна
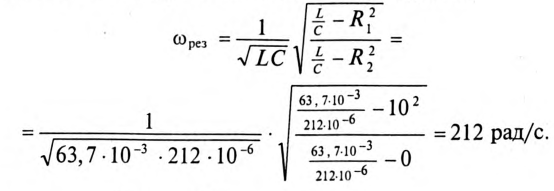
Откуда 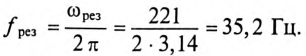
Для построения векторной диаграммы определяют активные и реактивные токи в ветвях:

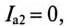 так как в ветви с емкостью отсутствует активное сопротивление, т.е.
так как в ветви с емкостью отсутствует активное сопротивление, т.е. 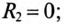
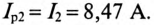
Векторная диаграмма для рассматриваемой цепи изображена на рис. 13.46.
На векторной диаграмме видно, что ток I опережает напряжение U на угол 53°30′ (цепь емкостного характера).
Коэффициент мощности
Номинальные параметры, т.е. мощность источника 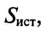 мощность потребителя
мощность потребителя 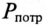 и коэффициент мощности
и коэффициент мощности 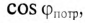 связаны следующим соотношением
связаны следующим соотношением

Из (13.15) следует, что чем меньше 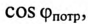 тем большую мощность
тем большую мощность 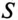 должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
должен иметь источник для питания этого потребителя, т. е. тем больше его габариты, вес, расход материалов, стоимость и др.
Ток в цепи потребителя с определенным 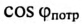 согласно выражению (12.11) равен
согласно выражению (12.11) равен
Из (13.16) видно, что чем меньше 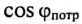 , тем больше ток потребителя
, тем больше ток потребителя 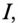 тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД ее и всей системы (3.11). Кроме того, увеличение тока требует для его передачи проводов большего сечения, т. е. большего расхода цветных металлов.
Таким образом, низкий коэффициент мощности потребителя 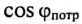 приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.
приводит к увеличению мощности источника, питающего этот потребитель, уменьшению КПД линии электропередачи и к увеличению сечения проводов линий электропередачи. 4В России установлен минимально допустимый коэффициент мощности не менее 0,93, т.е.  должен быть равен или больше 0,93
должен быть равен или больше 0,93 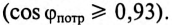
Однако  большинства электрических потребителей переменного тока меньше этой нормы. Так, например,
большинства электрических потребителей переменного тока меньше этой нормы. Так, например,  асинхронных двигателей, в зависимости от нагрузки, составляет
асинхронных двигателей, в зависимости от нагрузки, составляет 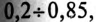 трансформаторов –
трансформаторов – 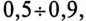 выпрямителей –
выпрямителей – 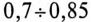 и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
и т.д. Следовательно, коэффициент мощности этих потребителей необходимо повышать.
Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения 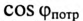 параллельно с ним подключаются конденсаторы (рис. 13.5а).
параллельно с ним подключаются конденсаторы (рис. 13.5а).
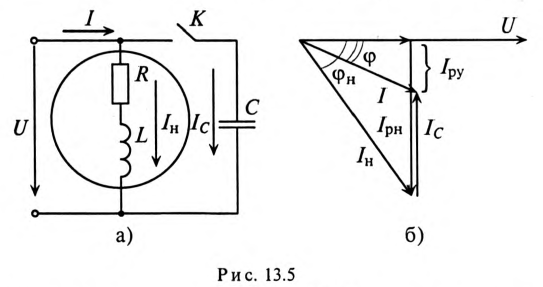
Из векторной диаграммы (рис. 13.56) видно, что с подключением конденсатора С (ключ К замкнут) появляется 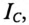 за счет которого уменьшается угол
за счет которого уменьшается угол 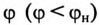 и увеличивается
и увеличивается 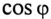 установки. При этом уменьшается ток цепи
установки. При этом уменьшается ток цепи 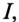 который до подключения конденсатора был равен току нагрузки
который до подключения конденсатора был равен току нагрузки 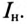
Для повышения коэффициента мощности 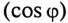 конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения
конденсатор можно включить последовательно с потребителем индуктивного характера. Однако при этом нарушается режим работы (напряжение) потребителя. Поэтому для улучшения 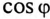 конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
конденсатор подключают параллельно с нагрузкой (рис. 13.5а).
Коэффициент мощности можно повысить, увеличив активную нагрузку. При этом увеличивается потребляемая энергия, что экономически нерационально (уменьшается КПД установки).
Пример 13.2
Асинхронный двигатель, включенный в сеть с напряжением 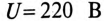 и частотой
и частотой 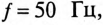 развивает на валу мощность
развивает на валу мощность 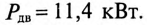 КПД двигателя
КПД двигателя 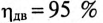 при
при 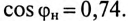 Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить
Определить емкость конденсатора С, который необходимо включить параллельно с двигателем (рис. 13.5а), чтобы повысить 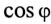 установки до 0,95.
установки до 0,95.
Решение
Мощность, потребляемая двигателем из сети:
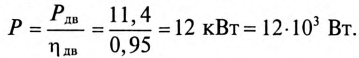
Ток нагрузки 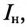 т.е. ток двигателя (рис. 13.5а), равен
т.е. ток двигателя (рис. 13.5а), равен
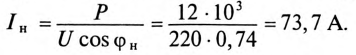
Реактивная составляющая тока двигателя 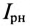 (рис. 13.56)
(рис. 13.56)
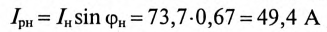
(по таблице 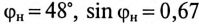 ).
).
Ток установки 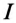 при подключении конденсатора, т. е. при
при подключении конденсатора, т. е. при 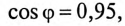 будет равен
будет равен

При 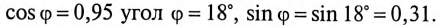 Реактивная составляющая тока установки (рис. 13.56)
Реактивная составляющая тока установки (рис. 13.56)
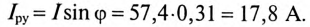
Ток конденсатора 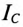 (рис. 13.56)
(рис. 13.56)
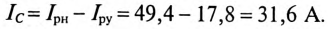
Емкостное сопротивление конденсаторов
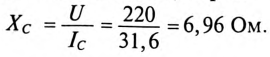
Емкость конденсаторов, которые нужно подключить параллельно двигателю для улучшения 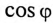 до 0,95:
до 0,95:
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле
Многие потребители электроэнергии не подозревают того, что часть учтённого электричества расходуется бесполезно. В зависимости от вида нагрузки уровень потерь электроэнергии может достигать от 12 до 50%. При этом счетчики электроэнергии засчитывают эти потери, относя их к полезной работе, за что приходится платить. Виной завышения оплаты за потребление электроэнергии, не выполняющей полезной работы, является реактивная мощность, присутствующая в сетях переменных токов.
Чтобы понять, за что мы переплачиваем и как компенсировать влияние реактивных мощностей на работу электрических установок, рассмотрим причину появления реактивной составляющей при передаче электроэнергии. Для этого придётся разобраться в физике процесса, связанного с переменным напряжением.
Что такое реактивная мощность?
Для начала рассмотрим понятие электрической мощности. В широком смысле слова, этот термин означает работу, выполненную за единицу времени. По отношению к электрической энергии, понятие мощности немного откорректируем: под электрической мощностью будем понимать физическую величину, реально характеризующую скорость генерации тока или количество переданной либо потреблённой электроэнергии в единицу времени.
Понятно, что работа электричества в единицу времени определяется электрической мощностью, измеряемой в ваттах. Мгновенную мощность на участке цепи находят по формуле: P = U×I, где U и I – мгновенные значения показателей параметров напряжения и силы тока на данном участке.
Строго говоря, приведённая выше формула справедлива только для постоянного тока. Однако, в цепях синусоидального тока формула работает лишь тогда, когда нагрузка потребителей чисто активная. При резистивной нагрузке вся электрическая энергия расходуется на выполнение полезной работы. Примерами активных нагрузок являются резистивные приборы, такие как кипятильник или лампа накаливания.
При наличии в электрической цепи ёмкостных или индуктивных нагрузок, появляются паразитные токи, не участвующие в выполнении полезной работы. Мощность этих токов называют реактивной.
На индуктивных и ёмкостных нагрузках часть электроэнергии рассеивается в виде тепла, а часть препятствует выполнению полезной работы.
К устройствам с индуктивными нагрузками относятся:
- электромоторы;
- дроссели;
- трансформаторы;
- электромагнитные
реле и другие устройства, содержащие обмотки.
Ёмкостными сопротивлениями обладают конденсаторы.
Физика процесса
Когда мы имеем дело с цепями постоянного тока, то говорить о реактивной мощности не приходится. В таких цепях значения мгновенной и полной мощности совпадают. Исключением являются моменты включения и отключения ёмкостных и индуктивных нагрузок.
Похожая ситуация происходит при наличии чисто активных сопротивлений в синусоидальных цепях. Однако если в такую электрическую цепь включены устройства с индуктивными или ёмкостными сопротивлениями, происходит сдвиг фаз по току и напряжению (см. рис.1).
При этом на индуктивностях наблюдается отставание тока по фазе, а на ёмкостных элементах фаза тока сдвигается так, что ток опережает напряжение. В связи с нарушением гармоники тока, полная мощность разлагается на две составляющие. Ёмкостные и индуктивные составляющие называют реактивными, бесполезными. Вторая составляющая состоит из активных мощностей.

Угол сдвига фаз используется при вычислениях значений активных и реактивных ёмкостных либо индуктивных мощностей. Если угол φ = 0, что имеет место при резистивных нагрузках, то реактивная составляющая отсутствует.
Важно запомнить:
- резистор потребляет исключительно активную мощность, которая выделяется в виде тепла и света;
- катушки индуктивности провоцируют образование реактивной составляющей и возвращают её в виде магнитных полей;
- Ёмкостные элементы (конденсаторы) являются причиной появления реактивных сопротивлений.
Треугольник мощностей и cos φ
Для наглядности изобразим полную мощность и её составляющие в виде векторов (см. рис. 2). Обозначим вектор полной мощности символом S, а векторам активной и реактивной составляющей присвоим символы P и Q, соответственно. Поскольку вектор S является суммой составляющих тока, то, по правилу сложения векторов, образуется треугольник мощностей.

Применяя теорему Пифагора, вычислим модуль вектора S:
![]()
Отсюда можно найти реактивную составляющую:
![]()
Выше мы уже упоминали, что реактивная мощность зависит от сдвига фаз, а значит и от угла этого сдвига. Эту зависимость удобно выражать через cos φ. По определению cos φ = P/S. Данную величину называют коэффициентом мощности и обозначают Pf. Таким образом, Pf = cos φ = P/S.
Коэффициент мощности, то есть cos φ, является очень важной характеристикой, позволяющей оценить эффективность работы тока. Данная величина находится в промежутке от 0 до 1.
Если угол сдвига фаз принимает нулевое значение, то cos φ = 1, а это значит что P = S, то есть полная мощность состоит только из активной мощности, а реактивность отсутствует. При сдвиге фаз на угол π/2 , cos φ = 0, откуда следует, что в цепи господствуют только реактивные токи (на практике такая ситуация не возникает).
Из этого можно сделать вывод: чем ближе к 1 коэффициент Pf , тем эффективнее используется ток. Например, для синхронных генераторов приемлемым считается коэффициент от 0,75 до 0,85.
Формулы
Поскольку реактивная мощность зависит от угла φ, то для её вычисления применяется формула: Q = UI×sin φ. Единицей измерения реактивной составляющей является вар или кратная ей величина – квар.
Активную составляющую находят по формуле: P = U*I×cosφ. Тогда
![]()
Зная коэффициент Pf (cos φ), мы можем рассчитать номинальную мощность потребителя тока по его номинальному напряжению, умноженному на значение силы потребляемого тока.
Способы компенсации
Мы уже выяснили, как влияют реактивные токи на работу устройств и оборудования с индуктивными или ёмкостными нагрузками. Для уменьшения потерь в электрических сетях с синусоидальным током их оборудуют дополнительными устройствами компенсации.
Принцип действия установок компенсации основан на свойствах индуктивностей и ёмкостей по сдвигу фаз в противоположные стороны. Например, если обмотка электромотора сдвигает фазу на угол φ, то этот сдвиг можно компенсировать конденсатором соответствующей ёмкости, который сдвигает фазу на величину – φ. Тогда результирующий сдвиг будет равняться нулю.
На практике компенсирующие устройства подключают параллельно нагрузкам. Чаще всего они состоят из блоков конденсаторов большой ёмкости, расположенных в отдельных шкафах. Одна из таких конденсаторных установок изображена на рисунке 3. На картинке видно группы конденсаторов, используемых для компенсации сдвигов напряжений в различных устройствах с индуктивными обмотками.

Компенсацию реактивной мощности ёмкостными нагрузками хорошо иллюстрируют графики на рисунке 4. Обратите внимание на то, как эффективность компенсации зависит от напряжения сети. Чем выше сетевое напряжение, тем сложнее компенсировать паразитные токи (график 3).

Устройства компенсации часто устанавливаются в производственных цехах, где работает много устройств на электроприводах. Потери электричества при этом довольно ощутимы, а качество тока сильно ухудшается. Конденсаторные установки успешно решают подобные проблемы.
Нужны ли устройства компенсации в быту?
На первый взгляд в домашней сети не должно быть больших
реактивных токов. В стандартном наборе бытовых потребителей преобладают
электрическая техника с резистивными нагрузками:
- электрочайник (Pf = 1);
- лампы накаливания
(Pf = 1); - электроплита (Pf =
1) и другие нагревательные приборы;
Коэффициенты
мощности современной бытовой техники, такой как телевизор, компьютер и т.п.
близки к 1. Ими можно пренебречь.
Но если речь идёт о холодильнике (Pf = 0,65), стиральной машине и микроволновой печи, то уже стоит задуматься об установке синхронных компенсаторов. Если вы часто пользуетесь электроинструментом, сварочным аппаратом или у вас дома работает электронасос, тогда установка устройства компенсации более чем желательна.
Экономический эффект от установки таких устройств
ощутимо скажется на вашем семейном бюджете. Вы сможете экономить около 15%
средств ежемесячно. Согласитесь, это не так уж мало, учитывая тарифы не
электроэнергию.
Попутно вы решите следующие вопросы:
- уменьшение нагрузок на индуктивные элементы и на проводку;
- улучшение качества тока, способствующего стабильной работе электронных устройств;
- понижение уровня высших гармоник в бытовой сети.
Для того чтобы ток и напряжение работали синфазно, устройства компенсации следует размещать как можно ближе к потребителям тока. Тогда реальная отдача индуктивных электроприёмников будет принимать максимальные значения.
Видео в тему
При расчете электрической мощности, потребляемой любым электротехническим или бытовым устройством, обычно учитывается так называемая полная мощность электрического тока, выполняющего определённую работу в цепи данной нагрузки. Под понятием «полная мощность» подразумевается вся та мощность, которая потребляется электроприбором и включает в себя как активную составляющую, так и составляющую реактивную, которая в свою очередь определяется типом используемой в цепи нагрузки. Активная мощность всегда измеряется и указывается в ваттах (Вт), а полная мощность приводится обычно в вольт-амперах (ВА). Различные приборы – потребители электрической энергии могут работать в цепях, имеющих как активную, так и реактивную составляющую электрического тока.
Активная составляющая потребляемой любой нагрузкой мощности электрического тока совершает полезную работу и трансформируется в нужные нам виды энергии (тепловую, световую, звуковую и т.п.). Отдельные электроприборы работают в основном на этой составляющей мощности. Это – лампы накаливания, электроплиты, обогреватели, электропечи, утюги и т.п.
При указанном в паспорте прибора значении активной потребляемой мощности в 1 кВт он будет потреблять от сети полную мощность в 1кВА.
Реактивная составляющая электрического тока возникает только в цепях, содержащих реактивные элементы (индуктивности и ёмкости) и расходуется обычно на бесполезный нагрев проводников, из которых составлена эта цепь. Примером таких реактивных нагрузок являются электродвигатели различного типа, переносные электроинструменты (электродрели, «болгарки», штроборезы и т.п.), а также различная бытовая электронная техника. Полная мощность этих приборов, измеряемая в вольт-амперах, и активная мощность (в ваттах) соотносятся между собой через коэффициент мощности cosφ, который может принимать значение от 0,5 до 0,9. На этих приборах указывается обычно активная мощность в ваттах и значение коэффициента cosφ. Для определения полной потребляемой мощности в ВА, необходимо величину активной мощности (Вт) разделить на коэффициент cosφ.
Пример: если на электродрели указана величина мощности в 600 Вт и cosφ = 0,6, то отсюда следует, что потребляемая инструментом полная мощность составляет 600/0,6=1000 ВА. При отсутствии данных по cosφ можно брать его приблизительное значение, которое для домашнего электроинструмента составляет примерно 0,7.
При рассмотрении вопроса об активной и реактивной составляющих электроэнергии (точнее – её мощности), обычно имеются в виду те явления, которые происходят в цепях переменного тока. Оказалось, что различные нагрузки в цепях переменного тока ведут себя совершенно по-разному. Одни нагрузки используют передаваемую им энергию по прямому назначению (т.е. – для совершения полезной работы), а другой тип нагрузок сначала эту энергию запасает, а потом снова отдаёт её источнику электропитания.
По виду своего поведения в цепях переменного тока, различные потребительские нагрузки делятся на следующие два типа:
1. Активный тип нагрузки поглощает всю получаемую от источника энергию и превращает её в полезную работу (свет от лампы, например), причём форма тока в нагрузке в точности повторяет форму напряжения на ней (сдвиг фаз отсутствует).
2. Реактивный тип нагрузки характеризуется тем, что сначала (в течение некоторого промежутка времени), в нём происходит накопление энергии, поставляемой источником питания. Затем запасённая энергия (в течение определённого промежутка времени) отдаётся обратно в этот источник. К подобным нагрузкам относятся такие элементы электрических цепей, как конденсаторы и катушки индуктивности, а также устройства, содержащие их. При этом в такой нагрузке между напряжением и током присутствует сдвиг фаз, равный 90 градусам. Поскольку основной целью существующих систем электроснабжения является полезная доставка электроэнергии от производителя непосредственно к потребителю (а не перекачивание её туда и обратно) – реактивная составляющая мощности обычно считается вредной характеристикой цепи.
Потери на реактивную составляющую в сети напрямую связаны с величиной рассмотренного выше коэффициента мощности, т.е. чем выше cosφ потребителя, тем меньше будут потери мощности в линии и дешевле обойдётся передача электроэнергии потребителю.
Таким образом, именно коэффициент мощности указывает нам на то, насколько эффективно используется рабочая мощность источника электроэнергии. В целях повышения величины коэффициента мощности (cosφ) во всех видах электрических установок применяются специальные приёмы компенсации реактивной мощности.
Обычно для увеличения коэффициента мощности (за счёт уменьшения сдвига фаз между током и напряжением – угла φ) в действующую сеть включают специальные компенсирующие устройства, представляющие собой вспомогательные генераторы опережающего (емкостного) тока.
Кроме того, очень часто для компенсации потерь, возникающих из-за индуктивной составляющей цепи, в ней используются батареи конденсаторов, подключаемые параллельно рабочей нагрузке и используемые в качестве синхронных компенсаторов.
 none
none
 Опубликована: 2011 г.
Опубликована: 2011 г.

 5
5
![]()
 Вознаградить
Вознаградить
Я собрал
0
1
x
Оценить статью
- Техническая грамотность
- Актуальность материала
- Изложение материала
- Полезность устройства
- Повторяемость устройства
- Орфография
0
Средний балл статьи: 5
Проголосовало: 1 чел.
Что такое активная и реактивная мощность, кто их придумал и какие формулы существуют для их расчета – все это несложные вопросы физики, если рассказать о них простыми словами. Поймут даже чайники.
Содержание
- Мощность в цепи переменного электрического тока
- Что такое активная мощность
- Что такое реактивная мощность
- Что такое полная мощность
- Смысл реактивной нагрузки
- Треугольник мощностей
- Формулы и единицы измерения
- Как найти активную, реактивную и полную мощность
Мощность в цепи переменного электрического тока
Многих пугает все разнообразие мощностей, которое описывается в задачниках по физике. Но все не так сложно, если ознакомиться с теорией, написанной простыми словами. Что такое активная и реактивная мощность, как они соотносятся между собой и что на самом деле означает выражение на полную мощность.

Для начала стоит вспомнить, что же собственно подразумевается под мощностью в физике. Это соотношение передаваемой энергии от одной системы к другой в течение определенного времени передачи. Мощность обычно измеряют в Ваттах (сокращенно Вт/W), которые представляют собой 1 джоуль энергии, который передается другой системе за 1 секунду.

И лишь в астрофизике или теоретической физике могут применяться другие величины для мощности, но они уже не являются системными по умолчанию. В электричестве под этим понятием подразумевается именно передача электроэнергии. Далее речь пойдет о сетях переменного тока, которые используются в быту и производстве.
Если говорить о практическом значении физики, то, в первую очередь, интерес будет представлять активная мощность. Реактивная мощность интересует тех, кто собирается заниматься процессами ее компенсации.
На заметку! Следует отметить уникальность единицы измерения активной мощности, которая отличается среди всех остальных типов мощностей.
Мощность переменного тока может быть разделена на:
- P — активную;
- Q — реактивную;
- S — полную.

Что такое активная мощность
Активная мощность — это некая часть мощности, связанная непосредственно с трансформацией в какой-либо другой вид энергии. Она измеряется в таких единицах измерения, как ватты, сокращенно Вт. Когда речь заходит о формулах, в них активная мощность обозначается буквой Р. Она также связана с неким периодом частоты переменного типа тока. Логично, что этот тип мощности может описывать процессы лишь с участием переменного тока.
Бытовые электроприборы обладают различной мощностью. В чем измеряется их активная мощность, уже шла речь выше: в ваттах. Другая проблема, что производители бытовых приборов часто указывают лишь пиковую мощность, которую устройство готово демонстрировать лишь на протяжении ограниченного временного промежутка.

Одна из наименьших активных мощностей у зарядных устройств – всего около 2 Вт в час. Одна из наибольших у бытовых моек высокого давления – мощность доходит до 3500 Вт. Где-то посередине окажутся стиральные машины, водонагреватели и блендеры.
Интересно! Единица измерения активной мощности, ватты, названа в честь шотландского инженера и изобретателя Джеймса Уатта, жившего на рубеже XVIII – XIX веков.
Среди наименее известных изобретений механика значится машина для копирования скульптур и барельефов. А наиболее известна первая придуманная им единица для измерения мощности – это была лошадиная сила. Здесь речь шла не о движении, производимом в горизонтальной плоскости, а о способности лошадей поднимать людей или грузы в шахтах.
Что такое реактивная мощность
Реактивная мощность – это та часть мощности, которая вернется в сеть обратно. Более детально этот процесс можно описать так: это «вредоносный» процесс, который не полезен для всей системы, он характерен для устройств с нагрузкой индуктивного или емкостного типа.

Логично, что эта часть мощности никак не помогает полезным процессам, не является активной. Задача состоит в том, чтобы компенсировать реактивную мощность. Ее обозначают заглавной буквой Q, а единица измерения реактивной мощности: вольт-амперы, которые обозначаются как Вар.
Что такое полная мощность
Если кратко, то в бытовом аспекте многие путают активную и полную мощность, называя «полной» активную. На самом деле полная мощность – это сочетание активной и неполезной реактивной.
Так что в сети переменного тока считают вместе рассеиваемую и поглощаемую мощность, и получают общее значение. Мощность в этом случае обозначается буквой S. Для ее измерения также используются единицы Вар.
Смысл реактивной нагрузки
Что такое реактивная мощность в рамках производства – это потеря средств. Как только она становится повышенной, предприятие может начать тратить на электроэнергию больше, чем изначально рассчитывалось.
Полная мощность должна включать как можно меньше работы для двигателей вхолостую, нормальным считаются показатели от 60% и выше. Важно перенаправить все так, чтобы избежать чрезмерного перегрева проводников сети. Чаще всего это достигается тем, что устанавливается устройство под названием конденсаторный блок.

Что такое реактивная мощность – мощность, которая появляется в тех сетях, в которых присутствуют реактивные элементы. Энергия накапливается в цепи, после чего она возвращается обратно.
Таким образом, устройства нагреваются при работе, что можно заметить по длительной работе даже такого маломощного предмета ежедневного быта, как зарядное устройство для смартфона.
Для электроприбора есть нормальный коэффициент реактивной мощности. Обычно он составляет от 0,9 до 0,5. Производители указывают его в инструкции по эксплуатации или в паспорте устройства.
Смысл реактивной нагрузки состоит в том, что она создает сдвиг по времени между напряжением и фазами тока. Расчеты и применение формул для вычисления реактивной мощности позволяют не только достигать высокой производительности устройств при меньших затратах на электроэнергию, но и помогают избегать аварийных ситуаций.

Часто возникает вопрос, как правильно определять коэффициент реактивной мощности в случае с бытовыми электросетями перед домашним счетчиком.
Для этого используется формула:
tgφ = Q/P = Eq/Еw
В данном случае Еw – это активная мощность, а вот Eq – это уже реактивная.
Треугольник мощностей
Формула расчета полной, активной и реактивной мощностей достаточно понятно может описывать взаимоотношения этих трех аспектов. Но яснее их взаимоотношения можно выразить на плоскости в виде треугольника мощностей. Так как все они тригонометрически соотносятся. Угол, который возникает между полной и активной мощностями называется фазовым углом и ясно показан на рисунке.

Формулы и единицы измерения
Единица измерения реактивной мощности такая же, как у полной – вольт-амперы, Вар, а для расчета активной используется единица в виде Вт.

Что такое активная и реактивная мощность в совокупности – так называемая полная мощность. Она рассчитывается по следующей простой формуле:
√ (Активная мощность2 + Реактивная мощность2)
То есть требуется найти квадратный корень из суммы квадрата активной и квадрата реактивной мощностей.
Как найти реактивную мощность:
√ (Полная мощность2 – Активная мощность2)
То есть квадратный корень из вычитания квадрата активной мощности из квадрата полной мощности. Когда речь заходит о вычислении активной мощности, то применяется, соответственно, формула:
√ (Полная мощность2 – Реактивная мощность2)
Квадрат из вычитания квадрата реактивной мощности из квадрата полной мощности.

Также могут понадобиться другие формулы для точных вычислений в некоторых случаях. Для однофазных цепей может применяться своя формула:
P = V I cosθ
А в трехфазных цепях уже будет действовать следующий вариант:
P = √3 VL IL cosθ
Важно! Во всех случаях необходимо внимательно следить за единицами измерений. Киловатты необходимо еще до вычисления по формулам переводить в ватты. Киловольтамперы, соответственно, переводят в вольтамперы.
Как найти активную, реактивную и полную мощность
Коэффициент реактивной мощности позволяет оптимизировать работу и избежать нагрева устройства. Профессионалы обычно используют большее количество параметров в расчетах, чтобы компенсировать негативные моменты реактивной мощности. Но для решения рядовых задач по физике вполне применима приведенная выше формула.

Полная мощность, активная и реактивная мощность для чайников может быть представлена несколькими формулами. Важно лишь помнить о ситуационных единицах измерения, об актуальных обозначениях и о треугольнике мощностей, чтобы справиться с расчетами.
 Баланс мощностей цепи переменного тока│Активная, реактивная и полная мощности
Баланс мощностей цепи переменного тока│Активная, реактивная и полная мощности
Помогла ли вам статья?
( 2 оценки, среднее 5 из 5 )

