Как найти реальную годовую ставку процента

Как найти реальную годовую ставку процента

Здравствуйте, друзья!

Как вы считаете, 20 % годовых по вкладу в банке или инвестициям в ценные бумаги – это много или мало?

Чтобы ответить на вопрос, надо сравнить цифру с инфляцией в стране. Если цены растут на 25 % в год, то ваша доходность превращается в обесценивание капитала. Инфляция ее просто “съедает”. Если инфляция равна 5 %, то вы получаете неплохой рост своих денег.

В приведенном примере речь шла о разных процентных ставках, которые надо учитывать при планировании личных финансов.

Рассмотрим, что такое реальная процентная ставка, как она рассчитывается и где используется.

Виды процентных ставок

Реальная процентная ставка – это ставка с учетом текущей или прогнозной инфляции в зависимости от цели расчета. Само название намекает, что процент отражает реальную картину с нашим доходом, а не ту, что нарисована на бумаге.

В этом ключе рассматривается еще одна ставка – номинальная. Она отличается от реальной как раз тем, что не учитывает инфляцию.

Например, по вкладу банк обещает 5 % годовых. Это номинальная ставка. За год инфляция составила 4,5 %. Получается, что вы заработали 5 %, но при этом на 4,5 % у вас обесценились деньги. Реальная ставка составила всего 0,5 %.

Вы можете самостоятельно определить свой фактический доход или платеж, если хотите учесть обесценивание денег. Проблем не будет, если вы оцениваете свою доходность уже по итогам инвестирования или депонирования средств в банке. Все величины известны, и результат точно покажет, что дали вам ваши вложения.

Но инвестору или вкладчику неинтересны прошлые оценки. Ему надо знать, выгодно или нет вкладывать деньги на текущих условиях, но на несколько лет вперед. И одна величина в таком случае будет всегда прогнозной – уровень инфляции. Никто не сможет вам ее назвать и дать 100 % гарантию, что прогноз сбудется. Остается только принять к сведению мнение экспертных органов. Например, Минэкономразвития России прогнозирует инфляцию до 2030 г. по трем сценариям.

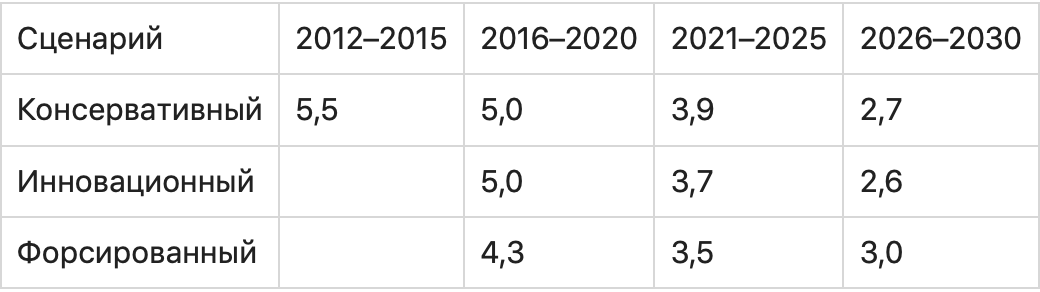
Уже сейчас видно, что специалисты ошиблись в прогнозах как минимум на 2021 г. Это и понятно, ведь разве кто-то мог представить, что не только российская, но и экономики развитых стран в 2020 г. возьмут паузу. Коронавирус внес свои коррективы.

Формула Фишера

Зависимость номинальной и реальной ставок математически описал американский экономист Ирвинг Фишер.

Формула расчета:

Реальная процентная ставка = (Номинальная процентная ставка – Уровень инфляции) / (100 + Уровень инфляции) * 100 %

или

Реальная процентная ставка = (1 + Номинальная процентная ставка) / (1+ Уровень инфляции) – 1

Поясним на примере. Предположим, что у вас есть 100 000 руб. Сегодня вы можете купить на нее определенный объем товара А. Вы кладете деньги на вклад под 3,2 % годовых (условия по вкладу “Сохраняй” от Сбербанка).

Через год банк начислил вам проценты, сумма превратилась в 103 200 руб. А цены на тот же объем товара А выросли в соответствии с инфляцией в стране на 5,5 %. Следовательно, в конце года товар А стоит уже 105 500 руб.

После закрытия вклада и вывода денег со счета вы можете купить уже меньше товара А, чем в начале года: около 97,82 % (103 200 / 105 500 * 100 %). Покупательная способность денег сократилась на: 100 % – 97,82 % = 2,18 %. То есть вложение денег в Сбербанк привело к потере в 2,18 %.

Применим цифры из нашего примера к формуле Фишера и проверим расчеты:

Реальная процентная ставка = (3,2 – 5,5) / (100 + 5,5) * 100 % = –2,18 %

Часто используют и упрощенную формулу, когда из номинальной ставки просто вычитают уровень инфляции и получают реальный процент. В начале статьи мы как раз ее и применили.

При небольших темпах инфляции результат будет почти точным, отличается на десятые доли процента. Но при большом уровне инфляции лучше воспользоваться формулой Фишера.

Она ярко иллюстрирует связь между инфляцией, номинальным и реальным процентом именно в странах с нестабильной экономикой.

Где применяется реальная процентная ставка

Везде, где ожидается доход или производится платеж, выраженный в процентах, можно рассчитать реальную процентную ставку. Это не сделает за вас банк или брокер. Процент, который вы увидите в кредитном договоре, договоре на открытие депозита или брокерском отчете, будет номинальным.

Кредиты

Реальную процентную ставку не рассчитывают по кредиту, хотя она точно так же работает при кредитовании, как и при получении дохода, и даже может внушить заемщику чуть больше оптимизма. Например, сегодня вы взяли кредит под 10 % годовых, а в стране прогнозируется инфляция в 4 % в ближайшие 3–5 лет. Значит, ежегодно ваша реальная ставка будет меньше номинальной на эти 4 %. Это ли не повод для радости?

Представьте, что ежемесячно вы вносите 30 000 руб. в счет погашения кредита. Со временем фактический платеж будет “дешеветь”, потому что 30 000 руб. через 5–10 лет – это не те же 30 000 руб. сегодня, а значительно меньше за счет обесценивания денег. Еще лучше, если у вас получится рефинансирование под меньший процент, тогда эффект будет еще сильнее.

Большее распространение расчет реальной ставки получил при определении доходности вложений: в инвестициях или банковских депозитах.

Инвестиции

Для инвестора большую ценность имеет реальный, а не номинальный процент, который поможет определить доходность от инвестирования в различные инструменты. Например, при выборе облигаций в карточке конкретного инструмента вы увидите сразу несколько видов доходности, но все они номинальные.

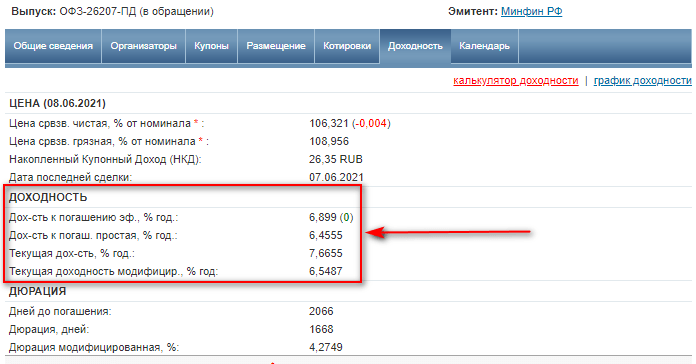
Доходность облигацийЧтобы определить реальную доходность, надо воспользоваться формулой Фишера.

По облигациям в ней будет только одна прогнозная величина, которая может исказить картину в будущем, – это инфляция.

А другой важный параметр точно известен на несколько лет вперед – купонный доход.

В примере выше срок погашения облигации ОФЗ-26207-ПД наступит только в 2027 году. Ежегодный купонный доход на все эти годы составит 8,15 % годовых.

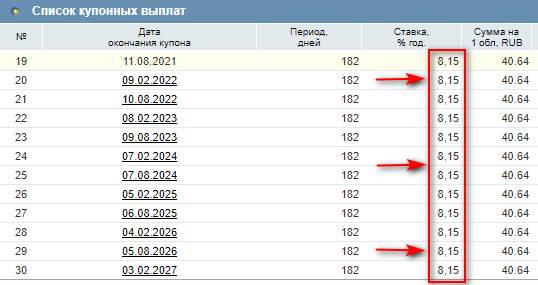
Купонные выплатыПо акциям ситуация другая. Будущее мы можем определить только на основе прогнозных значений доходности и инфляции.

Всем инвесторам известно правило, что доходность в прошлом не является гарантией ее получения в будущем.

Поэтому прогнозировать на основе значений, полученных в предыдущие годы, – неблагодарное занятие.

Остается только фундаментальный анализ компании. Но в любой грамотно проведенный анализ может вмешаться случай и обесценить все сделанные выводы.

Это не значит, что реальную доходность вообще не надо учитывать. Для долгосрочного инвестора определить эффективность своих вложений в тот или иной инструмент можно и по итогам года на основе фактически полученных значений.

Если на протяжении 2–3 лет вы получаете отрицательную реальную доходность, то, наверное, стоит пересмотреть свой портфель и инвестиционную стратегию.

Депозиты

Не обольщайтесь, когда в очередном рекламном ролике от банка вы увидите приятные глазу проценты по депозиту. Это всего лишь ваш будущий номинальный доход, который может показаться уже не таким привлекательным, когда вы рассчитаете реальный с поправкой на инфляцию.

При расчете реальной доходности депозита вы будете, аналогично облигациям, оперировать не к прогнозной инфляции, а к известному проценту, который указан в договоре. Хорошо, когда экономика страны стабильна на протяжении нескольких лет подряд, а деньги обесцениваются в пределах 1–2 %.

Тогда легко рассчитать и свою фактическую прибыль от хранения капитала на депозите. Но эта история не про Россию. Наши граждане видели инфляцию в 4 и 2 500 %, поэтому легко получить нулевую или отрицательную доходность.

Простой пример. Вы положили в банк 1 000 000 руб. на 1 год под 4 % годовых. Инфляция в мае 2021 г. составила 6 % в годовом исчислении. К концу года Банк России ее прогнозирует в районе 5,4–5,8 %. Допустим, что величина составит 5,8 %.

Рассчитаем доход вкладчика:

  1. номинальный доход: 1 000 000 * 1,04 – 1 000 000 = 40 000 руб.;
  2. реальная процентная ставка: (4 – 5,8) / (100 + 5,8) * 100 = –1,70 %;
  3. реальный доход: 1 000 000 * 0,9858 – 1 000 000 = –14 200 руб.

Покупательная способность ваших денег сократилась на 1,70 % или на 14 200 руб.

Заключение

После этой статьи скажите нам, пожалуйста, почему большинство наших сограждан продолжает нести свои деньги в банк? Мы поняли бы это, когда нет других альтернатив. Но сейчас…

Если единственная причина – это надежность вкладов, то почему бы тогда не купить ОФЗ или корпоративные облигации таких компаний, как Сбербанк, ВТБ или Газпром. Дефолт им пока не грозит, а доходность выше, чем по депозиту.

Останавливает, что нужен брокерский счет? Его открыть – дело 5 минут. Пишите, какие еще у вас есть аргументы, чтобы не инвестировать.

Источник

Рассчитываем проценты по вкладу: формула и примеры

Чтобы выяснить, какой доход принесет вклад, недостаточно знать годовую ставку. На прибыльность также методика начисления банком процентов. В финансовой системе существуют понятия простого и сложного процента, позволяющего получить при почти равных условиях разный доход по вкладам.

Рассчитать проценты по вкладу можно самостоятельно без помощи специалиста. В статье разбираем особенности каждой схемы и объясняем, как работать с формулами.

Простые проценты

Это вознаграждение, которое начисляется на начальную сумму вклада за определенный период. Простые проценты не прибавляются к телу депозита и выплачиваются либо по истечении срока договора, либо раз в месяц или год по выбору вкладчика. Если договор продлевается на новый срок, то прибыль за предыдущий период также не суммируется с вкладом.

Такая методика начисления применяется, как правило, для вкладов с возможностью пополнения и снятия средств. Процентная ставка в этом случае ниже, чем при начислении сложных процентов. Это объясняется тем, что ваш вклад — финансовый инструмент получения прибыли банком. И чем меньше уверенности, что вы не заберете деньги раньше срока, тем ниже вероятность долгосрочного инвестирования капиталов банком, а значит — и ниже доход.

Сложные проценты или капитализация

В этом случае доход за оговоренный срок прибавляется к сумме вклада. В последующий период вознаграждение начисляется уже на увеличенный размер депозита. Сумма вклада постепенно растет за счет накапливаемых процентов, итоговый доход становится выше.

Срок капитализации — периодичность, с которой процент суммируется с текущим телом вклада. Банки добавляют проценты раз в месяц, квартал или день. Вам могут предложить депозит с плавающими ставками, когда процент увеличивается с течением времени. Как правило, процент повышается при увеличении срока хранения денег на депозите при условии, что снятий не было.

Доходность вкладов с капитализацией выше за счет увеличения тела кредита, однако наибольший доход дает тот депозит, по которому ограничено движение средств: запрещены снятия и пополнения, или дополнительные взносы разрешены, но с ограничением. Например, сумма всех пополнений не может превышать сумму открытия более, чем в 10 раз.

Расчет простых процентов

Выяснив годовую ставку, периоды и виды начисления процентов, можно посчитать доход по вкладу.

Простые проценты начисляются по следующей формуле:

где:

S — выплаченные проценты,
P — первоначальная сумма вложений,
I — годовая ставка,
T — количество дней вклада,
K — количество дней в году — 365 или 366.

Если вкладчик открыл депозит на 350 000 руб. сроком на 9 месяцев под 4,7%, процентный доход по вкладу составит:

Расчет сложных процентов

Чаще всего банки предлагают программы с ежемесячной капитализацией. Выбирая условия по вкладу, помните об общей закономерности: чем реже проценты прибавляются к телу депозита, тем меньше доход.

Ежедневная капитализация

Рассчитать доход за каждый день действия вклада поможет следующая формула:

где

Дв — сумма на конец срока, включая сумму открытия и начисленный процент,
Р — первоначальный размер депозита,
N — годовая процентная ставка, разделенная на 100,
К — количество дней в году — 365 или 366,
Т — срок вложения в днях.

Если клиент внес 350 000 руб. под 4,7% на 9 месяцев или 273 дня, в конце срока он получит:

Возвести число в большую степень можно на инженерном калькуляторе, где есть функция x^y, воспользоваться онлайн-сервисами или калькуляторами на сайтах банков.

Зная Дв, легко вычислить сумму процентов по вкладу за весь период:

Ежемесячная капитализация

Когда банк суммирует доход по депозиту раз в месяц, расчет ведется по формуле:

где:

Дв — итоговый доход, то есть размер вклада на конец срока включая сумму открытия и начисленный процент,
P — начальный депозит,
N — годовая ставка, разделенная на 100,
T — срок договора в месяцах.

Рассчитаем итоговую сумму с теми же исходными данными:

Процентный доход составит 12 532,56 ₽

Ежеквартальная капитализация

При начислении вознаграждения каждый квартал, а не раз в месяц, понадобится формула:

в ней Т — количество кварталов в сроке, остальные обозначения прежние.

Рассчитаем тот же вклад в конце срока:

Доход в виде процентов составит 12 483 ₽.

Но следует помнить: чем дольше срок размещения депозита, тем выше ставка. Поэтому при внесении денег на депозит надо сравнить условия с фактической ставкой, применяемой по выбранными вами условиям.

Итоги

Из таблицы видна разница доходов по методу простых и сложных процентов при равных условиях.

Проценты по вкладу Доход, руб.

Простые

12 303

Сложные:

ежедневные

12 521

ежемесячные

12 532

ежеквартальные

12 483

Однако нельзя однозначно утверждать о предпочтительности сложных процентов для каждого клиента. Оптимальная схема, тип банковского депозита — накопительный счет или вклад — зависят от ваших планов и потребностей:

  • желаемый срок действия вклада и вероятность досрочного снятия средств
  •  необходимость регулярно пополнять счет или снимать средства
  •  необходимость регулярно снимать проценты

Если закрыт вклад до срока, вне зависимости от того, срочный он или до востребования, банк может применить санкции:

  • Пересчитать процент по простой ставке до востребования. Законодательно ее размер не установлен, но большинство банков выплачивают всего 0,1–0,01%.
  •  Оставить половину или даже треть начальной ставки и тоже сделать перерасчет процентов.

Поэтому перед открытием депозита четко определите его срок и назначение. Райффайзен Банк предлагает банковские вклады без ограничений по снятию и пополнению, где проценты можно получать ежемесячно или добавлять к сумме депозита.

Эта страница полезна?

99

% клиентов считают страницу полезной

Следите за нами в соцсетях и в блоге

Источник

Содержание материала

  1. Почему важно считать кредит самому?
  2. Видео
  3. Как рассчитать годовые проценты по кредиту?
  4. Как самостоятельно рассчитать аннуитетный платеж
  5. Какие данные нужны для расчета платежа по кредиту
  6. Воспользуемся банковскими калькуляторами
  7. Виды ежемесячных выплат по кредитам
  8. Самостоятельный подсчет при аннуитетных платежах
  9. Из чего состоит ежемесячный платеж
  10. Формула расчета процентов по кредиту
  11. Какие данные нужны для расчета
  12. Пример расчета процентов по кредиту
  13. Погашать долг можно по-разному
  14. Как составить график платежей
  15. График выплаты кредита с аннуитетными платежами
  16. График выплаты кредита с дифференцированными платежами

Почему важно считать кредит самому?

Кредитами сейчас сложно кого-то удивить. Каждый среднестатистический россиянин имеет или имел как минимум один-два кредита в своей жизни или собирается его взять. Если вы идете в банк для получения кредита и вам дают несколько предложений, то нужно выбрать самое дешевое и выгодное для вас. Для этого нужно рассчитать кредит самому, например в Excel. Нужно также знать размер ежемесячного платежа, чтоб понять нагрузку займа на ваш бюджет. Это тоже можно сделать самостоятельно.

Видео

Как рассчитать годовые проценты по кредиту?

Для аннуитетного платежа достаточно умножить сумму всего взятого кредита на процентную ставку. Наглядно это выглядит так:

10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.

При дифференцированном платеже сумма годовых процентов рассчитывается немого сложнее, поскольку необходимо помножить остаток по кредиту на процентную ставку и поделить на 12.

То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.

При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.

Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.

Самым оптимальным решением при выборе выплаты по кредиту будет попросить банковского служащего распечатать примерные графики и суммы платежей по обоим кредитам и сравнить, какой из них наиболее выгодный.

Также полезно будет узнать, какой вид платежа предлагается по умолчанию в каком-либо банке.

Как самостоятельно рассчитать аннуитетный платеж

Для самостоятельного расчета понадобится срок кредита, сумма и процентная ставка.

Стандартная формула расчета аннуитетного платежа выглядит так:

Иногда формула может отличаться. Например, если банк предлагает направлять первые платежи только на погашение процентов. Но чаще всего считают по стандартной формуле.

А вот как рассчитывается коэффициент аннуитета:

Для примера возьмем 300 000 рублей, срок 18 месяцев и процентную ставку 15% годовых.

Месячная процентная ставка = 15% / 12 = 1,25%, то есть 0,0125.

Количество платежей равно количеству месяцев — 18.

Подставляем данные в формулу и считаем коэффициент аннуитета:

0,0125 × (1 + 0,0125)18 / ((1 + 0,0125)18 − 1) = 0,062385

Теперь подставляем коэффициент аннуитета в расчет платежа: 300 000 × 0,062385 = 18 715,44 Р — в точности как в кредитном калькуляторе.

Какие данные нужны для расчета платежа по кредиту

Ежемесячный платеж – важная характеристика для многих. Хочется найти золотую середину – платить посильный взнос с наименьшей переплатой.

Рассчитать его можно самостоятельно или через специальные сервисы. Для этого вам понадобятся:

  • ставка,
  • размер желаемого займа,
  • срок, на который вы хотите занять деньги.

Воспользуемся банковскими калькуляторами

Банки побеспокоились о том, чтобы клиенты не мороч

Банки побеспокоились о том, чтобы клиенты не морочили себе голову арифметикой, а сразу получали искомые параметры.

Составлено множество программ, которые названы «калькуляторами». Им стоит только задать основные величины, как они тут же произведут расчёт и покажут всё, что интересует заказчика, вплоть до помесячного графика платежей и суммы переплаты за кредит.

Виды ежемесячных выплат по кредитам

Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.

Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга. Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.

В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.

Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.

Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.

Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.

Самостоятельный подсчет при аннуитетных платежах

Для удобства и наглядности подсчета обозначим одинаковые входные данные по кредиту:

  1. Процентная ставка — 18%.
  2. Период кредитования — 24 месяца.
  3. Сумма кредита — 500000 рублей.

Классическая формула для расчета аннуитетного платежа выглядит так:

Разовый аннуитетный платеж = Сумма кредита * Ка

где Ка — это коэффициент аннуитета.

Ка = ((ЕПС* (1 + ЕПС)n)/( (1 + ЕПС)n -1)

где ЕПС — ежемесячная процентная ставка.

Подставляя данные из примера, ЕПС будет выглядеть как 18%/12 = 1,5% = 0,015.

Итоговый расчет примет вид:

500 000 * (0,015 * (1 + 0,015)24)/((1 + 0,015)24 -1) = 24 962,05 рублей в месяц.

Данные полностью совпадают с примером, приведенным выше, где описан подсчет с помощью функции в Excel.

Итоговая сумма, которую выплатит заемщик за весь период пользования кредитом при точном соблюдении графика выплат:

24 962,05 * 24 = 599 089,24 рублей.

Общая сумма переплаты при аннуитетных платежах с приведенными в примере данными составит 99 089,24 рублей.

Из чего состоит ежемесячный платеж

Расплачиваться за взятые в долг деньги придется ежемесячно. Этот взнос складывается из основного долга и процентов, взятых в разном соотношении. В каком именно – зависит от типа платежей.

Вы можете заплатить меньше или больше установленной выплаты. Если заплатите меньше, вас накажут за просрочку штрафами и пени. Они могут прибавиться к следующей выплате. А если заплатите больше – поможете себе и снизите размер общей переплаты.

Формула расчета процентов по кредиту

S = (s3 x i x Kk / Kr) / 100

  • S = вычисляемые проценты;
  • S3 = общая сумма кредита;
  • i = процентная ставка по кредиту;
  • Kk = кол-во дней по платежам;
  • Kr = кол-во дней на календарный год.

Какие данные нужны для расчета

  • Сумма, выданная в кредит;
  • Процентная ставка за год;
  • Кол-во календарных дней в текущем году.

Пример расчета процентов по кредиту

65000 рублей – сумма переплаты в год. Для того чтобы посчитать сумму переплаты в месяц нужно 65000 рублей разделить на 12.

Погашать долг можно по-разному

Видов платежей два. Они бывают аннуитетными или дифференцированными, и от того, какой вы изберёте, зависит картина выплат.

С точки зрения банка, ежемесячный платёж распадается на несколько частей. Главными в них является тело долга и проценты, но есть и прочие составляющие.

Банк в первую очередь заботится о выплатах процентов, поскольку это его доход. Поэтому в первых платежах, какой бы вид вы ни выбрали, основная часть отводится именно им. По мере продвижения к концу срока доля процентной части уменьшается, а доля основного долга, соответственно, увеличивается.

Если платёж аннуитетный, то его величина остаётся постоянной на всём протяжении погашения долга.

Дифференцированный платёж имеет переменный размер,

Дифференцированный платёж имеет переменный размер, но в нём тоже есть постоянная часть: это доля основного долга. Процентная часть плавающая, она от максимума в первом платеже постепенно уменьшается до нуля в последнем, поскольку рассчитывается от величины оставшейся части долга (ОстДолга).

, поскольку в этом случае переплата меньше. Банку, соответственно, интереснее аннуитетные, и в последнее время они решительно преобладают. Делается это, якобы, во благо заёмщика, ведь с постоянным платежом ему удобнее обращаться.

Если срок небольшой и проценты невелики, то и разница некритична. А вот на многолетних ипотеках, да ещё с высокими процентами, расхождение весьма ощутимо.

Как составить график платежей

Самый простой способ — воспользоваться кредитным калькулятором: график платежей составляется автоматически.

Еще мы написали калькулятор в экселе, в котором можно прикинуть график платежей и ежемесячные платежи при обоих способах погашения.

Если вы хотите рассчитать график платежей самостоятельно, давайте разберемся на примере ранее рассчитанного платежа: кредит на 300 000 рублей, 18 месяцев под 15% годовых.

При аннуитетном способе ежемесячный платеж неизменный из месяца в месяц. Как мы посчитали выше, в нашем случае он составит 18 715,44 Р.

В целом график платежей уже понятен, но мы дополнительно можем посчитать, каким будет соотношение основного долга и процентов в каждом месяце.

Сначала считаем проценты:

Остаток долга × Процентная ставка × Количество дней в месяце / Количество дней в году

Если год не високосный, а в месяце 30 дней, получится 3698,63 Р — это сумма процентов, которые мы заплатим в первом месяце. На погашение основного долга пойдет остаток от нашего ежемесячного платежа: 18 715,44 Р − 3698,63 Р = 15 016,81 Р.

Во втором месяце сумма процентов начислится на сумму кредита минус платеж по основному долгу в первом месяце: 300 000 Р − 15 015,81 Р = 284 983,19 Р.

Считаем проценты во втором месяце. Предположим, что во втором месяце 31 день: 284 983,19 × 15% × 31 / 365 = 3630,61 Р.

На погашение основного долга во втором месяце пойдет 15 084,83 Р (18 715,44 − 3630,61).

Таким образом можно посчитать соотношение процентов и основного долга в каждом месяце кредита.

График выплаты кредита с аннуитетными платежами

Номер платежа Сумма платежа Сумма в погашение тела кредита Сумма платежа в погашение процентов Остаток долга
1 18 715,44 15 016,81 3698,63 284 983,19
2 18 715,44 15 084,83 3630,61 269 898,37
3 18 715,44 15 387,92 3327,51 254 510,44
4 18 715,44 15 473,04 3242,39 239 037,40
5 18 715,44 15 670,17 3045,27 223 367,24
6 18 715,44 16 053,39 2662,05 207 313,85
7 18 715,44 16 074,31 2641,12 191 239,53
8 18 715,44 16 357,69 2357,75 174 881,84
9 18 715,44 16 487,49 2227,95 158 394,35
10 18 715,44 16 762,63 1952,81 141 631,73
11 18 715,44 16 911,09 1804,35 124 720,64
12 18 715,44 17 126,53 1588,91 107 594,11
13 18 715,44 17 388,93 1326,50 90 205,18
14 18 715,44 17 566,25 1149,19 72 638,93
15 18 715,44 17 819,89 895,55 54 819,04
16 18 715,44 18 017,06 698,38 36 801,98
17 18 715,44 18 246,59 468,85 18 555,40
18 18 768,91 18 555,39 213,51

Первый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 016,81

Сумма платежа в погашение процентов

3698,63

Остаток долга 284 983,19

Второй платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 084,83

Сумма платежа в погашение процентов

3630,61

Остаток долга 269 898,37

Третий платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 387,92

Сумма платежа в погашение процентов

3327,51

Остаток долга 254 510,44

Четвертый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 473,04

Сумма платежа в погашение процентов

3242,39

Остаток долга 239 037,40

Пятый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

15 670,17

Сумма платежа в погашение процентов

3045,27

Остаток долга 223 367,24

Шестой платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 053,39

Сумма платежа в погашение процентов

2662,05

Остаток долга 207 313,85

Седьмой платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 074,31

Сумма платежа в погашение процентов

2641,12

Остаток долга 191 239,53

Восьмой платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 357,69

Сумма платежа в погашение процентов

2357,75

Остаток долга 174 881,84

Девятый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 487,49

Сумма платежа в погашение процентов

2227,95

Остаток долга 158 394,35

Десятый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 762,63

Сумма платежа в погашение процентов

1952,81

Остаток долга 141 631,73

Одиннадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

16 911,09

Сумма платежа в погашение процентов

1804,35

Остаток долга 124 720,64

Двенадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 126,53

Сумма платежа в погашение процентов

1588,91

Остаток долга 107 594,11

Тринадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 388,93

Сумма платежа в погашение процентов

1326,50

Остаток долга 90 205,18

Четырнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 566,25

Сумма платежа в погашение процентов

1149,19

Остаток долга 72 638,93

Пятнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

17 819,89

Сумма платежа в погашение процентов

895,55

Остаток долга 54 819,04

Шестнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

18 017,06

Сумма платежа в погашение процентов

698,38

Остаток долга 36 801,98

Семнадцатый платеж

Сумма платежа

18 715,44

Сумма в погашение тела кредита

18 246,59

Сумма платежа в погашение процентов

468,85

Остаток долга 18 555,40

Восемнадцатый платеж Сумма платежа 18 768,91 Сумма в погашение тела кредита 18 555,39 Сумма платежа в погашение процентов 213,51 Остаток долга

При дифференцированном платеже проценты в первом месяце будут такими же — 3698,63 Р. Дальше же принцип расчета процентов аналогичен, а сумма основного долга будет каждый месяц уменьшаться равномерно — на 16 666,67 Р (300 000 / 18). Ежемесячный платеж будет складываться из этих двух сумм.

В результате в первые месяцы платеж будет больше, чем при аннуитетном способе, а итоговая переплата будет меньше.

График выплаты кредита с дифференцированными платежами

Номер платежа Сумма платежа Сумма в погашение тела кредита Сумма платежа в погашение процентов Остаток долга
1 20 365,30 16 666,67 3698,63 283 333,33
2 20 276,26 16 666,67 3609,59 266 666,67
3 19 954,34 16 666,67 3287,67 250 000,00
4 19 851,60 16 666,67 3184,93 233 333,33
5 19 639,27 16 666,67 2972,60 216 666,67
6 19 248,86 16 666,67 2582,19 200 000,00
7 19 214,61 16 666,67 2547,95 183 333,33
8 18 926,94 16 666,67 2260,27 166 666,67
9 18 789,95 16 666,67 2123,29 150 000,00
10 18 515,98 16 666,67 1849,32 133 333,33
11 18 365,30 16 666,67 1698,63 116 666,67
12 18 152,97 16 666,67 1486,30 100 000,00
13 17 899,54 16 666,67 1232,88 83 333,33
14 17 728,31 16 666,67 1061,64 66 666,67
15 17 488,58 16 666,67 821,92 50 000,00
16 17 303,65 16 666,67 636,99 33 333,33
17 17 091,32 16 666,67 424,66 16 666,67
18 16 858,45 16 666,67 191,78

Первый платеж

Сумма платежа

20 365,30

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3698,63

Остаток долга 283 333,33

Второй платеж

Сумма платежа

20 276,26

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3609,59

Остаток долга 266 666,67

Третий платеж

Сумма платежа

19 954,34

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3287,67

Остаток долга 250 000,00

Четвертый платеж

Сумма платежа

19 851,60

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

3184,93

Остаток долга 233 333,33

Пятый платеж

Сумма платежа

19 639,27

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2972,60

Остаток долга 216 666,67

Шестой платеж

Сумма платежа

19 248,86

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2582,19

Остаток долга 200 000,00

Седьмой платеж

Сумма платежа

19 214,61

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2547,95

Остаток долга 183 333,33

Восьмой платеж

Сумма платежа

18 926,94

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2260,27

Остаток долга 166 666,67

Девятый платеж

Сумма платежа

18 789,95

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

2123,29

Остаток долга 150 000,00

Десятый платеж

Сумма платежа

18 515,98

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1849,32

Остаток долга 133 333,33

Одиннадцатый платеж

Сумма платежа

18 365,30

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1698,63

Остаток долга 116 666,67

Двенадцатый платеж

Сумма платежа

18 152,97

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1486,30

Остаток долга 100 000,00

Тринадцатый платеж

Сумма платежа

17 899,54

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1232,88

Остаток долга 83 333,33

Четырнадцатый платеж

Сумма платежа

17 728,31

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

1061,64

Остаток долга 66 666,67

Пятнадцатый платеж

Сумма платежа

17 488,58

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

821,92

Остаток долга 50 000,00

Шестнадцатый платеж

Сумма платежа

17 303,65

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

636,99

Остаток долга 33 333,33

Семнадцатый платеж

Сумма платежа

17 091,32

Сумма в погашение тела кредита

16 666,67

Сумма платежа в погашение процентов

424,66

Остаток долга 16 666,67

Восемнадцатый платеж Сумма платежа 16 858,45 Сумма в погашение тела кредита 16 666,67 Сумма платежа в погашение процентов 191,78 Остаток долга

Теги

Источник

Процентная ставка — сумма, указанная в процентном выражении к сумме кредита, которую платит получатель кредита за пользование им в расчёте на определённый период (месяц, квартал, год).

С позиции теории денег, процентная ставка — цена денег как средства сбережения.

Процентный доход — доход от предоставления капитала в долг в разных формах (ссуды, кредиты), либо это доход от инвестиций в ценные бумаги.

История процентных ставок[править | править код]

В последние два столетия базовые процентные ставки устанавливаются либо национальными правительствами, либо центральными банками. Например, Федеральная резервная ставка по федеральным фондам США колебалась от 0,25 % до 19 % в период с 1954 по 2008 год, в то время как базовые ставки Банка Англии колебались от 0,5 % до 15 % в период с 1989 по 2009[1][2], а разброс базовых ставок в Германии был от близкого к 90 % в 1920-х годах до примерно 2 % в 2000-х годах[3][4]. Во время попытки преодолеть спираль гиперинфляции в 2007 году, Резервный банк Зимбабве повысил процентные ставки по займам до 800 %[5].

Виды процентных ставок[править | править код]

Существует несколько видов процентных ставок.

Фиксированная и плавающая ставки[править | править код]

В зависимости от того, изменяется ли ставка в течение времени, выделяют фиксированную и плавающую процентные ставки:

  • Фиксированная процентная ставка — постоянна, устанавливается на определённый срок и не зависит от каких-либо обстоятельств[6].
  • Плавающая процентная ставка подлежит периодическому пересмотру[7]. Изменение ставки осуществляется на основании колебаний тех или иных показателей. Классическим примером таких показателей является Лондонская межбанковская ставка предложения (LIBOR, средневзвешенная ставка на лондонском межбанковском рынке кредитных ресурсов). Соответственно плавающая ставка LIBOR+5 % будет означать, что номинальная величина процентной ставки на 5 % выше ставки LIBOR.

Декурсивная и антисипативная ставки[править | править код]

В зависимости от времени выплаты процентов, существует два типа процентных ставок:[8]

  • декурсивная ставка — процент выплачивается в конце вместе с основной суммой кредита
  • антисипативная ставка — процент выплачивается в момент предоставления кредита (авансом) и определяется на основании конечной суммы долга.

Для кредитора выгоднее антисипативная ставка, а для заёмщика — декурсивная. Так, если величина процентной ставки составляет 10 %, то при декурсивной ставке при кредите в 1000 р. кредитор получит 1100 р. в конце срока. При антисипативной ставке он даст заёмщику 900 р. и в конце срока получит 1000 р.

Реальная и номинальная ставки[править | править код]

Различают номинальную и реальную процентную ставку.

Номинальная процентная ставка — рыночная процентная ставка без учета инфляции, отражающая текущую оценку денежных активов.

Реальная процентная ставка — номинальная процентная ставка за вычетом темпов инфляции[9].

Взаимосвязь реальной, номинальной ставки и инфляции в общем случае описывается следующей (приближённой) формулой

{displaystyle i_{r}=i_{n}-pi ,}

где

i_n — номинальная процентная ставка,
i_{r} — реальная процентная ставка,
pi  — ожидаемый или планируемый уровень инфляции.

Ирвинг Фишер предложил более точную формулу взаимосвязи реальной, номинальной ставок и инфляции, выражаемую названной в его честь формулой Фишера:

{displaystyle i_{r}={frac {1+i_{n}}{1+pi }}-1={frac {i_{n}-pi }{1+pi }}.}

При pi =0 и pi =i_{n} обе формулы дают одинаковое значение. Легко видеть, что при небольших значениях уровня инфляции pi результаты мало отличаются, но если инфляция велика, то следует применять формулу Фишера.

Согласно Фишеру, реальная процентная ставка численно должна быть равна предельной производительности капитала.

Размеры процентных ставок[править | править код]

Номинальные процентные ставки по кредитам могут быть больше нуля, равны нулю («беспроцентный кредит») и меньше нуля[10] («отрицательные» проценты). Если реальные процентные ставки достигают большой величины, это приводит к возникновению ростовщичества.

См. также[править | править код]

  • Процентный доход
  • Стоимость денег с учётом фактора времени
  • Годовая процентная доходность
  • Ставка рефинансирования
  • Учетная ставка
  • Ломбардная ставка
  • Европейская межбанковская ставка предложения (EURIBOR)
  • Лондонская межбанковская ставка предложения (LIBOR)
  • Капитализация процентов
  • Соглашение о будущей процентной ставке (FRA)
  • Правило семидесяти
  • Инфляция
  • Компаундинг
  • Сложные проценты

Примечания[править | править код]

  1. ↑ Interest Rate History. Архивировано 16 октября 2008 года.. Retrieved 2008-10-27
  2. ↑ UK interest rates lowered to 0,5 %. Дата обращения: 31 октября 2011. Архивировано 7 марта 2009 года.
  3. ↑ Homer, Sylla & Sylla, 1996, p. 509.
  4. ↑ Bundesbank. BBK — Statistics — Time series database. Архивировано 12 февраля 2009 года.. Retrieved 2008-10-27
  5. ↑ Zimbabwe currency revised to help inflation. Дата обращения: 31 октября 2011. Архивировано из оригинала 11 февраля 2009 года.
  6. ↑ Фиксированная процентная ставка. Национальная экономическая энциклопедия. Дата обращения: 16 июля 2013. Архивировано из оригинала 27 декабря 2014 года.
  7. ↑ Борисов А. Б. Плавающая процентная ставка // Большой экономический словарь. — М.: Книжный мир, 2003. — 895 с. — ISBN 5-8041-0049-1.
  8. ↑ Борисов А. Б. Процентная ставка // Большой экономический словарь. — М.: Книжный мир, 2003. — 895 с. — ISBN 5-8041-0049-1.
  9. ↑ Ставка процентная : [арх. 4 января 2023] // Социальное партнёрство — Телевидение. — М. : Большая российская энциклопедия, 2016. — С. 135. — (Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов ; 2004—2017, т. 31). — ISBN 978-5-85270-368-2.
  10. ↑ Моисеев С. Р. Деньги с отрицательной процентной ставкой. Архивировано 2 февраля 2020 года. // Деньги и кредит, 2017. — № 10. — С. 16—26.

Литература[править | править код]

  • Нечаев В. М., Яроцкий В. Г. Процент, в экономике и с юридической точки зрения // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
  • Джон К. Халл. Глава 4. Процентные ставки // Опционы, фьючерсы и другие производные финансовые инструменты = Options, Futures and Other Derivatives. — 6-е изд. — М.: «Вильямс», 2007. — С. 133—165. — ISBN 0-13-149908-4.
  • Homer, Sidney; Sylla, Richard. A History of Interest Rates. — Rutgers University Press, 1996. — ISBN 978-0-8135-2288-3.
Источник

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

Источник

Добавить комментарий