Открыть эту статью в PDF
Формула и значение
Уравнение Фишера (или Формула Фишера) устанавливает связь между реальными и номинальными процентными ставками. В точном виде оно записывается так:
Где
r — реальная процентная ставка
n — номинальная процентная ставка
i — инфляция
Распространен также приблизительный вариант записи этого уравнения:
Погрешность применения приблизительной формулы будет довольно невелика для небольших значений инфляции и процентов, но растет с ростом ставок. Например, для инфляции 5% и номинальной ставки 10% точное значение реальной ставки составит 4,76%, а вариант, рассчитанный по упрощенной формуле, дает значение 5%. В экономических расчетах такой погрешностью часто можно пренебречь.
Применение
Уравнение Фишера активно используется в инвестиционном анализе для сравнения вариантов инвестиций, включающих в будущие денежные потоки инфляцию, и вариантов, которые не индексируются на инфляцию. Например, оно может применяться для сравнения облигаций, защищенных от инфляции, с традиционными видами облигаций.
Другое применение уравнения Фишера — преобразование ожидаемых денежных потоков инвестиционных проектов из номинальных в реальные цены и наоборот. Переход к реальным ценам может упростить анализ проекта, но имеет ряд ограничений, связанных с тем, что не все компоненты бюджета проекта в равной степени подвержены влиянию инфляции.
В экономике уравнение Фишера является частью теории, устанавливающей взаимосвязь между процентными ставками, инфляцией и денежной политикой государства.
Возникновение уравнения Фишера
Уравнение для связи номинальных и реальных процентных ставок было впервые предложено Ирвингом Фишером в 1896 году в книге «Удорожание и проценты» (‘Appreciation and Interest’), в которой он изучал динамику стоимости валюты, опирающейся на золото и серебро и цен на пшеницу. Позднее эта теория была проработана еще глубже в его книге «Процентные ставки» (‘Rate of Interest’, 1907).
Интересно, что Фишер в своем исследовании не использует понятие инфляции — его анализ касается ожидаемого роста стоимости используемых валют. Также, Фишер не был первым, кто предложил эту зависимость для прогнозирования курсов валют и процентных ставок. Первое известное упоминание принципа, заложенного в уравнении Фишера, встречается в исследовании «Обсуждение касательно валют британских плантаций в Америке» (‘A Discourse Concerning the Currencies of the British Plantations in America’), написанном Вильямом Дугласом в 1740 году. Тем не менее, именно Фишер проработал идею взаимосвязи реальных и номинальных ставок достаточно глубоко, чем и заслужил использование своего имени в названии уравнения.
Такие статьи мы публикуем регулярно. Чтобы получать информацию о новых материалах, а также быть в курсе учебных программ, вы можете подписаться на новостную рассылку.
Если вам необходимо отработать определенные навыки в области инвестиционного или финансового анализа и планирования, посмотрите программы наших семинаров.
Спасибо, Вы зарегистрированы
на семинар «Альт-Инвест»!
Наш менеджер свяжется с Вами в ближайшее время.
Спасибо, Ваша заявка принята!
Мы отправили Вам письмо для проверки контактной информации на адрес info@alt-invest.ru.
Подтвердите, пожалуйста, свой адрес, и заявка будет направлена консультанту. После этого мы свяжемся с Вами для уточнения наиболее удобного времени и формата презентации.
Спасибо, Вы почти подписаны на новостную рассылку «Альт-Инвест»!
Мы отправили Вам письмо для подтверждения вашего e-mail на адрес info@alt-invest.ru.
Теперь проверьте почту.
Спасибо за интерес к нашим программам!
Мы отправили Вам письмо, где сказано как получить демо-версию, на адрес info@alt-invest.ru.
Теперь проверьте свою почту.
Здравствуйте, друзья!
Как вы считаете, 20 % годовых по вкладу в банке или инвестициям в ценные бумаги – это много или мало?
Чтобы ответить на вопрос, надо сравнить цифру с инфляцией в стране. Если цены растут на 25 % в год, то ваша доходность превращается в обесценивание капитала. Инфляция ее просто “съедает”. Если инфляция равна 5 %, то вы получаете неплохой рост своих денег.
В приведенном примере речь шла о разных процентных ставках, которые надо учитывать при планировании личных финансов.
Рассмотрим, что такое реальная процентная ставка, как она рассчитывается и где используется.
Виды процентных ставок
Реальная процентная ставка – это ставка с учетом текущей или прогнозной инфляции в зависимости от цели расчета. Само название намекает, что процент отражает реальную картину с нашим доходом, а не ту, что нарисована на бумаге.
 В этом ключе рассматривается еще одна ставка – номинальная. Она отличается от реальной как раз тем, что не учитывает инфляцию.
В этом ключе рассматривается еще одна ставка – номинальная. Она отличается от реальной как раз тем, что не учитывает инфляцию.
Например, по вкладу банк обещает 5 % годовых. Это номинальная ставка. За год инфляция составила 4,5 %. Получается, что вы заработали 5 %, но при этом на 4,5 % у вас обесценились деньги. Реальная ставка составила всего 0,5 %.
Вы можете самостоятельно определить свой фактический доход или платеж, если хотите учесть обесценивание денег. Проблем не будет, если вы оцениваете свою доходность уже по итогам инвестирования или депонирования средств в банке. Все величины известны, и результат точно покажет, что дали вам ваши вложения.
Но инвестору или вкладчику неинтересны прошлые оценки. Ему надо знать, выгодно или нет вкладывать деньги на текущих условиях, но на несколько лет вперед. И одна величина в таком случае будет всегда прогнозной – уровень инфляции. Никто не сможет вам ее назвать и дать 100 % гарантию, что прогноз сбудется. Остается только принять к сведению мнение экспертных органов. Например, Минэкономразвития России прогнозирует инфляцию до 2030 г. по трем сценариям.
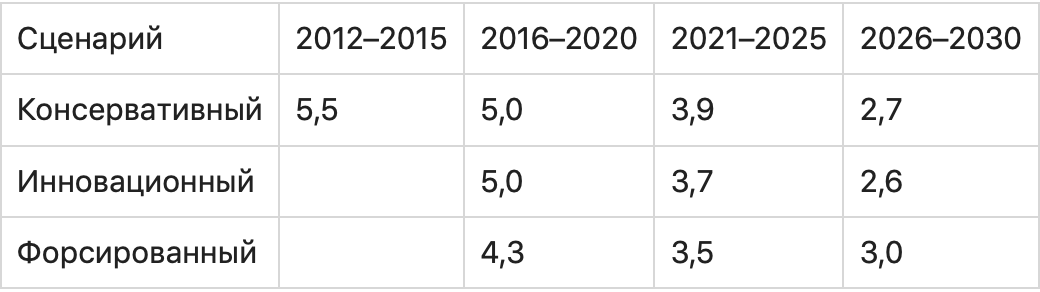 Уже сейчас видно, что специалисты ошиблись в прогнозах как минимум на 2021 г. Это и понятно, ведь разве кто-то мог представить, что не только российская, но и экономики развитых стран в 2020 г. возьмут паузу. Коронавирус внес свои коррективы.
Уже сейчас видно, что специалисты ошиблись в прогнозах как минимум на 2021 г. Это и понятно, ведь разве кто-то мог представить, что не только российская, но и экономики развитых стран в 2020 г. возьмут паузу. Коронавирус внес свои коррективы.
Формула Фишера
Зависимость номинальной и реальной ставок математически описал американский экономист Ирвинг Фишер.
Формула расчета:
Реальная процентная ставка = (Номинальная процентная ставка – Уровень инфляции) / (100 + Уровень инфляции) * 100 %
или
Реальная процентная ставка = (1 + Номинальная процентная ставка) / (1+ Уровень инфляции) – 1
Поясним на примере. Предположим, что у вас есть 100 000 руб. Сегодня вы можете купить на нее определенный объем товара А. Вы кладете деньги на вклад под 3,2 % годовых (условия по вкладу “Сохраняй” от Сбербанка).
Через год банк начислил вам проценты, сумма превратилась в 103 200 руб. А цены на тот же объем товара А выросли в соответствии с инфляцией в стране на 5,5 %. Следовательно, в конце года товар А стоит уже 105 500 руб.
После закрытия вклада и вывода денег со счета вы можете купить уже меньше товара А, чем в начале года: около 97,82 % (103 200 / 105 500 * 100 %). Покупательная способность денег сократилась на: 100 % – 97,82 % = 2,18 %. То есть вложение денег в Сбербанк привело к потере в 2,18 %.
Применим цифры из нашего примера к формуле Фишера и проверим расчеты:
Реальная процентная ставка = (3,2 – 5,5) / (100 + 5,5) * 100 % = –2,18 %
 Часто используют и упрощенную формулу, когда из номинальной ставки просто вычитают уровень инфляции и получают реальный процент. В начале статьи мы как раз ее и применили.
Часто используют и упрощенную формулу, когда из номинальной ставки просто вычитают уровень инфляции и получают реальный процент. В начале статьи мы как раз ее и применили.
При небольших темпах инфляции результат будет почти точным, отличается на десятые доли процента. Но при большом уровне инфляции лучше воспользоваться формулой Фишера.
Она ярко иллюстрирует связь между инфляцией, номинальным и реальным процентом именно в странах с нестабильной экономикой.
Где применяется реальная процентная ставка
Везде, где ожидается доход или производится платеж, выраженный в процентах, можно рассчитать реальную процентную ставку. Это не сделает за вас банк или брокер. Процент, который вы увидите в кредитном договоре, договоре на открытие депозита или брокерском отчете, будет номинальным.
Кредиты
Реальную процентную ставку не рассчитывают по кредиту, хотя она точно так же работает при кредитовании, как и при получении дохода, и даже может внушить заемщику чуть больше оптимизма. Например, сегодня вы взяли кредит под 10 % годовых, а в стране прогнозируется инфляция в 4 % в ближайшие 3–5 лет. Значит, ежегодно ваша реальная ставка будет меньше номинальной на эти 4 %. Это ли не повод для радости?
Представьте, что ежемесячно вы вносите 30 000 руб. в счет погашения кредита. Со временем фактический платеж будет “дешеветь”, потому что 30 000 руб. через 5–10 лет – это не те же 30 000 руб. сегодня, а значительно меньше за счет обесценивания денег. Еще лучше, если у вас получится рефинансирование под меньший процент, тогда эффект будет еще сильнее.
Большее распространение расчет реальной ставки получил при определении доходности вложений: в инвестициях или банковских депозитах.
Инвестиции
Для инвестора большую ценность имеет реальный, а не номинальный процент, который поможет определить доходность от инвестирования в различные инструменты. Например, при выборе облигаций в карточке конкретного инструмента вы увидите сразу несколько видов доходности, но все они номинальные.
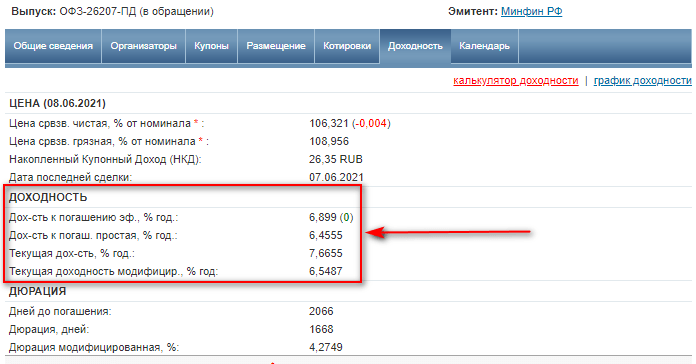 Чтобы определить реальную доходность, надо воспользоваться формулой Фишера.
Чтобы определить реальную доходность, надо воспользоваться формулой Фишера.
По облигациям в ней будет только одна прогнозная величина, которая может исказить картину в будущем, – это инфляция.
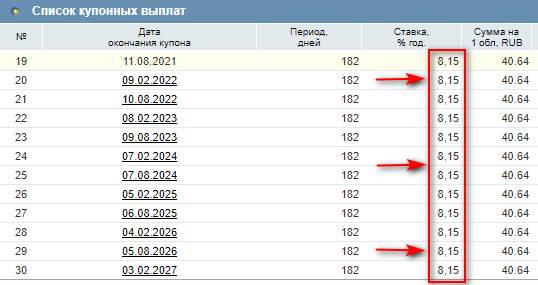
А другой важный параметр точно известен на несколько лет вперед – купонный доход.
В примере выше срок погашения облигации ОФЗ-26207-ПД наступит только в 2027 году. Ежегодный купонный доход на все эти годы составит 8,15 % годовых.
 По акциям ситуация другая. Будущее мы можем определить только на основе прогнозных значений доходности и инфляции.
По акциям ситуация другая. Будущее мы можем определить только на основе прогнозных значений доходности и инфляции.
Всем инвесторам известно правило, что доходность в прошлом не является гарантией ее получения в будущем.
Поэтому прогнозировать на основе значений, полученных в предыдущие годы, – неблагодарное занятие.
Остается только фундаментальный анализ компании. Но в любой грамотно проведенный анализ может вмешаться случай и обесценить все сделанные выводы.
Это не значит, что реальную доходность вообще не надо учитывать. Для долгосрочного инвестора определить эффективность своих вложений в тот или иной инструмент можно и по итогам года на основе фактически полученных значений.
Если на протяжении 2–3 лет вы получаете отрицательную реальную доходность, то, наверное, стоит пересмотреть свой портфель и инвестиционную стратегию.
Депозиты
Не обольщайтесь, когда в очередном рекламном ролике от банка вы увидите приятные глазу проценты по депозиту. Это всего лишь ваш будущий номинальный доход, который может показаться уже не таким привлекательным, когда вы рассчитаете реальный с поправкой на инфляцию.
При расчете реальной доходности депозита вы будете, аналогично облигациям, оперировать не к прогнозной инфляции, а к известному проценту, который указан в договоре. Хорошо, когда экономика страны стабильна на протяжении нескольких лет подряд, а деньги обесцениваются в пределах 1–2 %.
Тогда легко рассчитать и свою фактическую прибыль от хранения капитала на депозите. Но эта история не про Россию. Наши граждане видели инфляцию в 4 и 2 500 %, поэтому легко получить нулевую или отрицательную доходность.
Простой пример. Вы положили в банк 1 000 000 руб. на 1 год под 4 % годовых. Инфляция в мае 2021 г. составила 6 % в годовом исчислении. К концу года Банк России ее прогнозирует в районе 5,4–5,8 %. Допустим, что величина составит 5,8 %.
 Рассчитаем доход вкладчика:
Рассчитаем доход вкладчика:
- номинальный доход: 1 000 000 * 1,04 – 1 000 000 = 40 000 руб.;
- реальная процентная ставка: (4 – 5,8) / (100 + 5,8) * 100 = –1,70 %;
- реальный доход: 1 000 000 * 0,9858 – 1 000 000 = –14 200 руб.
Покупательная способность ваших денег сократилась на 1,70 % или на 14 200 руб.
Заключение
После этой статьи скажите нам, пожалуйста, почему большинство наших сограждан продолжает нести свои деньги в банк? Мы поняли бы это, когда нет других альтернатив. Но сейчас…
Если единственная причина – это надежность вкладов, то почему бы тогда не купить ОФЗ или корпоративные облигации таких компаний, как Сбербанк, ВТБ или Газпром. Дефолт им пока не грозит, а доходность выше, чем по депозиту.
Останавливает, что нужен брокерский счет? Его открыть – дело 5 минут. Пишите, какие еще у вас есть аргументы, чтобы не инвестировать.
From Wikipedia, the free encyclopedia
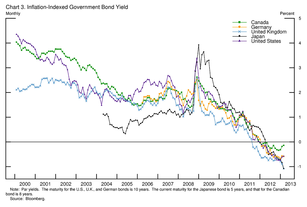
Yields on inflation-indexed government bonds of selected countries and maturities.
The real interest rate is the rate of interest an investor, saver or lender receives (or expects to receive) after allowing for inflation. It can be described more formally by the Fisher equation, which states that the real interest rate is approximately the nominal interest rate minus the inflation rate.
If, for example, an investor were able to lock in a 5% interest rate for the coming year and anticipated a 2% rise in prices, they would expect to earn a real interest rate of 3%.[1] The expected real interest rate is not a single number, as different investors have different expectations of future inflation. Since the inflation rate over the course of a loan is not known initially, volatility in inflation represents a risk to both the lender and the borrower.
In the case of contracts stated in terms of the nominal interest rate, the real interest rate is known only at the end of the period of the loan, based on the realized inflation rate; this is called the ex-post real interest rate. Since the introduction of inflation-indexed bonds, ex-ante real interest rates have become observable.[2]
Compensation for lending[edit]
An individual who lends money for repayment at a later point in time expects to be compensated for the time value of money, or not having the use of that money while it is lent. In addition, they will want to be compensated for the expected value of the loss of purchasing power when the loan is repaid. These expected losses include the possibility that the borrower will default or be unable to pay on the originally agreed upon terms, or that collateral backing the loan will prove to be less valuable than estimated; the possibility of changes in taxation and regulatory changes which would prevent the lender from collecting on a loan or having to pay more in taxes on the amount repaid than originally estimated; and the loss of buying power compared to the money originally lent, due to inflation.
- Nominal interest rates measure the sum of the compensations for all three sources of loss, plus the time value of the money itself.
- Real interest rates measure the compensation for expected losses due to default and regulatory changes as well as measuring the time value of money; they differ from nominal rates of interest by excluding the inflation compensation component.
On an economy-wide basis, the “real interest rate” in an economy is often considered to be the rate of return on a risk-free investment, such as US Treasury notes, minus an index of inflation, such as the rate of change of the CPI or GDP deflator.
Fisher equation[edit]
The relation between real and nominal interest rates and the expected inflation rate is given by the Fisher equation
where
- i = nominal interest rate;
- r = real interest rate;
= expected inflation rate.
For example, if somebody lends $1000 for a year at 10%, and receives $1100 back at the end of the year, this represents a 10% increase in her purchasing power if prices for the average goods and services that she buys are unchanged from what they were at the beginning of the year. However, if the prices of the food, clothing, housing, and other things that she wishes to purchase have increased 25% over this period, she has, in fact, suffered a real loss of about 15% in her purchasing power. (Notice that the approximation here is a bit rough; since 1.1/1.25 – 1 = 0.88 – 1 = -.12, the actual loss of purchasing power is exactly 12%.)
If the inflation rate and the nominal interest are relatively low, the Fisher equation can be approximated by
After-tax real interest rate[edit]
The real return actually gained by a lender is lower if there is a non-zero tax rate imposed on interest earnings. Generally taxes are imposed on nominal interest earnings, not adjusted for inflation. If the tax rate is denoted as t, the before-tax nominal earning rate is i, the amount of taxes paid (per dollar or other unit invested) is i × t, and so the after-tax nominal earning is i × (1–t ). Hence the expected after-tax real return to the investor, using the simplified approximate Fisher equation above, is given by
- Expected real after-tax return =
Variations in inflation[edit]
The inflation rate will not be known in advance. People often base their expectation of future inflation on an average of inflation rates in the past, but this gives rise to errors. The real interest rate ex-post may turn out to be quite different from the real interest rate (ex-ante real interest rate) that was expected in advance. Borrowers hope to repay in cheaper money in the future, while lenders hope to collect on more expensive money. When inflation and currency risks are underestimated by lenders, then they will suffer a net reduction in buying power.
The complexity increases for bonds issued for a long-term, where the average inflation rate over the term of the loan may be subject to a great deal of uncertainty. In response to this, many governments have issued real return bonds, also known as inflation-indexed bonds, in which the principal value and coupon rises each year with the rate of inflation, with the result that the interest rate on the bond approximates a real interest rate. (E.g., the three-month indexation lag of TIPS can result in a divergence of as much as 0.042% from the real interest rate, according to research by Grishchenko and Huang.[3]) In the US, Treasury Inflation Protected Securities (TIPS) are issued by the US Treasury.
The expected real interest rate can vary considerably from year to year. The real interest rate on short term loans is strongly influenced by the monetary policy of central banks. The real interest rate on longer term bonds tends to be more market driven, and in recent decades, with globalized financial markets, the real interest rates in the industrialized countries have become increasingly correlated. Real interest rates have been low by historical standards since 2000, due to a combination of factors, including relatively weak demand for loans by corporations, plus strong savings in newly industrializing countries in Asia. The latter has offset the large borrowing demands by the US Federal Government, which might otherwise have put more upward pressure on real interest rates.
Related is the concept of “risk return”, which is the rate of return minus the risks as measured against the safest (least-risky) investment available. Thus if a loan is made at 15% with an inflation rate of 5% and 10% in risks associated with default or problems repaying, then the “risk adjusted” rate of return on the investment is 0%.
Importance in economic theory[edit]

Effective federal funds rate and prescriptions from alternate versions of the Taylor Rule
The amount of physical investment—in particular the purchasing of new machines and other productive capacity—that firms engage in partially depends on the level of real interest rates because such purchases typically must be financed by issuing new bonds. If real interest rates are high, the cost of borrowing may exceed the real physical return of some potentially purchased machines (in the form of output produced); in that case those machines will not be purchased. Lower real interest rates would make it profitable to borrow to finance the purchasing of a greater number of machines.
The real interest rate is used in various economic theories to explain such phenomena as capital flight, business cycles and economic bubbles. When the real rate of interest is high, because demand for credit is high, then the usage of income will, all other things being equal, move from consumption to saving, and physical investment will fall. Conversely, when the real rate of interest is low, income usage will move from saving to consumption, and physical investment will rise. Different economic theories, beginning with the work of Knut Wicksell, have had different explanations of the effect of rising and falling real interest rates. Thus — assuming risks are constant — international capital moves to markets that offer higher real rates of interest from markets that offer low or negative real rates of interest. Capital flows of this kind often reflect speculation in financial and foreign exchange rate markets.
Real federal funds rate[edit]
In setting monetary policy, the U.S. Federal Reserve (and other central banks) uses open market operations, affecting the amounts of very short-term funds (federal funds) supplied and demanded and thus affecting the federal funds rate. By targeting this at a low rate, they can encourage borrowing and thus economic activity; or the reverse by raising the rate. Like any interest rate, there are a nominal and a real value defined as described above. Further, there is a concept called the “equilibrium real federal funds rate” (r*, or “r-star”), alternatively called the “natural rate of interest” or the “neutral real rate”, which is the “level of the real federal funds rate, if allowed to prevail for several years, [that] would place economic activity at its potential and keep inflation low and stable.” There are various methods used to estimate this amount, using tools such as the Taylor Rule. It is possible for this rate to be negative.[4]
Negative real interest rates[edit]
The real interest rate solved from the Fisher equation is
If there is a negative real interest rate, it means that the inflation rate is greater than the nominal interest rate. If the Federal funds rate is 2% and the inflation rate is 10%, then the borrower would gain 7.27% of every dollar borrowed per year.
Negative real interest rates are an important factor in government fiscal policy. Since 2010, the U.S. Treasury has been obtaining negative real interest rates on government debt, meaning the inflation rate is greater than the interest rate paid on the debt.[5] Such low rates, outpaced by the inflation rate, occur when the market believes that there are no alternatives with sufficiently low risk, or when popular institutional investments such as insurance companies, pensions, or bond, money market, and balanced mutual funds are required or choose to invest sufficiently large sums in Treasury securities to hedge against risk.[6][7] Lawrence Summers stated that at such low rates, government debt borrowing saves taxpayer money, and improves creditworthiness.[8][9] In the late 1940s through the early 1970s, the US and UK both reduced their debt burden by about 30% to 40% of GDP per decade by taking advantage of negative real interest rates, but there is no guarantee that government debt rates will continue to stay so low.[6][10] Between 1946 and 1974, the US debt-to-GDP ratio fell from 121% to 32% even though there were surpluses in only eight of those years which were much smaller than the deficits.[11]
See also[edit]
- Real versus nominal value (economics)
- Shadow Rate (a variation on the real interest rate)
- Inflation
- Deflation
- IS–LM model
- Macroeconomics
- Financial repression
- Natural rate of interest
References[edit]
- ^ Marc Levinson, 2006, “Guide to Financial Markets”, The Economist, page 24
- ^ “FRB: Speech with Slideshow–Bernanke, Long-Term Interest Rates–March 1, 2013”. www.federalreserve.gov. Retrieved 2017-03-07.
- ^ Grishchenko, Olesya V.; Jing-zhi Huang (June 2012). “Inflation Risk Premium: Evidence from the TIPS Market” (PDF). Finance and Economics Discussion Series. Divisions of Research & Statistics and Monetary Affairs Federal Reserve Board, Washington, D.C. Retrieved 26 May 2013.
- ^ U.S. Federal Reserve-Remarks by Vice Chairman Roger W. Ferguson Jr. October 29, 2004
- ^ Saint Louis Federal Reserve (2012) “5-Year Treasury Inflation-Indexed Security, Constant Maturity” FRED Economic Data chart from government debt auctions (the x-axis at y=0 represents the inflation rate over the life of the security)
- ^ a b Carmen M. Reinhart and M. Belen Sbrancia (March 2011) “The Liquidation of Government Debt” National Bureau of Economic Research working paper No. 16893
- ^ David Wessel (August 8, 2012) “When Interest Rates Turn Upside Down” Wall Street Journal (full text Archived 2013-01-20 at the Wayback Machine)
- ^ Lawrence Summers (June 3, 2012) “Breaking the negative feedback loop” Reuters
- ^ Matthew Yglesias (May 30, 2012) “Why Are We Collecting Taxes?” Slate
- ^ William H. Gross (May 2, 2011) “The Caine Mutiny (Part 2)” PIMCO Investment Outlook
- ^ “Why the U.S. Government Never, Ever Has to Pay Back All Its Debt” The Atlantic, February 1, 2013
External links[edit]
- “Equilibrium Real Interest Rate,” by Roger Ferguson, 2004.
- On the distinction between real return and nominal bonds, by Peter Spiro, 2004.
- Real interest rates by country via Quandl
На чтение 7 мин Просмотров 31.6к.
Умение рассчитать реальную и номинальную ставку процента может пригодиться как при получении кредита, так и в случае предоставления ссуды или инвестирования. Всего экономическая теория насчитывает 11 видов процентных ставок, которые отличаются друг от друга методикой расчета и случаями применения.
Содержание
- Классификация и виды процентных ставок
- Понятие реальной и номинальной ставки процента
- Отличие реальной процентной ставки от номинальной
- Взаимосвязь между реальной и номинальной ставкой процента
- Эффект Фишера
- Расчет реальной и номинальной ставки процента
- Формула для расчета реальной и номинальной ставки процента
- Пример расчета реальной и номинальной ставки процента
- Пример расчета номинальной ставки процента
- Пример расчета номинальной ставки процента
Классификация и виды процентных ставок
Процентные ставки принято классифицировать по трем признакам: изменяемость во времени, период выплаты дивидендов, уровень инфляции.
- Фиксированная процентная ставка устанавливается один раз в определенном размере и со временем не может изменяться.
- Плавающая процентная ставка отличается тем, что не остается на одном уровне и постоянно меняется. Как правило, ее размер связывают с уровнем инфляции или межбанковской ставкой.
- Декурсивной называют процентную ставку, которая устанавливается в том случае, если проценты по кредиту выплачиваются в конце срока действия договора.
- Антисипативная ставка является полным аналогом декурсивной. Все дело в том, что ее устанавливают при выплате дивидендов в начале срока кредитования. То есть заемщик, сначала выплачивает проценты по займу, а только потом основную сумму долга.
- Уровень инфляции оказывает большое влияние на фактическую стоимость финансового инструмента. Именно для определения предполагаемой доходности рассчитывают реальную ставку.
- Номинальная ставка рассчитывается с учетом капитализации процентов. Однако при ее вычислении исключается уровень инфляции.
Экономическая теория различает и иные виды процентных ставок, такие как безрисковую, форвардную, межбанковскую, эффективную и процентную ставку овернайт.
Понятие реальной и номинальной ставки процента
Реальная ставка процента представляет собой номинальную ставку с учетом предполагаемого уровня инфляции.
Номинальная ставка – это обратное значение реальному выражению. Она не включает в себя уровень инфляции и рассчитывается исключительно с учетом капитализации.
Важно обратить внимание на то, что реальная ставка значительно отличается от полной. Если первое выражение – это рыночная ставка, которая уменьшена на процент инфляции, то полной называют ставку, включающую все платежи по финансовому инструменту.
Важно! Как правило, реальную и номинальную ставку процента не рассчитывают по кредитам. Ее применяют в случае инвестирования или определения доходности по вкладам.
Отличие реальной процентной ставки от номинальной
Единственное отличие реальной процентной ставки от номинальной в том, что при расчете первого значения учитывается уровень инфляции.
Номинальная ставка применяется при определении доходности по финансовому инструменту, а реальная отражает уровень покупательской способности будущей прибыли.
Например, если сегодня инвестор положил на вклад 1 млн. рублей под 10% годовых на 5 лет, то в конце срока действия договора он получит 1,5 млн. рублей. В данном случае 10% — это и есть номинальная ставка. Но, как правило, с течением времени покупательская способность денег уменьшается. И то, что можно приобрести на 1,5 млн. сегодня, нельзя купить завтра. Для определения данного показателя и рассчитывается реальная ставка, которая вычисляется как разница между номинальной ставкой и процентом инфляции.
Допустим, что за 5 лет действия договора уровень инфляции составил 4%. 10% — 4% = 6% — это и есть реальная ставка, а фактическая доходность инвестора уже составит не 1,5 млн. рублей, а 1,2 млн. рублей. То есть, на руки он получит 1,5 млн. рублей, а сможет купить на них товаров только на 1,2 млн. руб., так как их стоимость со временем увеличилась.
Взаимосвязь между реальной и номинальной ставкой процента
Реальная и номинальная процентные ставки взаимосвязаны между собой. Соотношение четко прослеживается через уравнения, приведенные экономистом Ирвингом Фишером.
Так, для того, чтобы вычислить номинальную процентную ставку, к реальному значению прибавляют процент инфляции. А для расчета реальной ставки используют следующую формулу:
(1 + НС) / (1 + ПИ) — 1, или (НС – ПИ) / (1 – ПИ), где
НС – номинальная ставка;
ПИ – процент инфляции.
То есть первое арифметическое выражение будет равно второму.
Эффект Фишера
Взаимосвязь между реальной и номинальной процентной ставкой можно увидеть, ознакомившись с количественной теорией денег. Ирвинг Фишер предположил, что для избегания инфляции государство обязано контролировать объем денежной массы в экономике страны. Именно из-за недостатка регулирования возникает инфляция.
Важно! Номинальная ставка процента увеличивается пропорционально темпам инфляции.
Эффектом Фишера называют ситуацию, когда реальная ставка процента остается неизменной из-за соответствующего уровня инфляции. Более наглядно данное явление можно просмотреть на простом примере.
Допустим, что инвестор вложил 1 млн. рублей в перспективный проект под 10% годовых на 5 лет. Ожидаемый уровень инфляции составлял 5%. В таком случае номинальной ставкой будет 10%, а реальной – 5%. Но, фактическая инфляция составила 10%. Тогда и реальная ставка уменьшилась, а ее значение равно 0. То есть, получив прибыль от проекта в 10% годовых, покупательская способность дохода осталась неизменной. Инвестор мог бы приобрести такой же объем товаров 5 лет назад, что и сегодня.
Расчет реальной и номинальной ставки процента
Расчет реальной и номинальной ставки процента напрямую зависит от определения первого и второго показателя. Ведь, как говорит экономическая теория, реальная и номинальная ставки прямо взаимосвязаны между собой.
При вычислениях не стоит забывать и об уровне инфляции. Именно он оказывает влияние на конечное значение.
Расчет показателей рекомендуется начинать с вычисления эффективной процентной ставки. Для ее определения используется специальная формула. Она понадобиться для выявления номинальной ставки процента. С целью исключения ошибок рекомендуется использовать следующий алгоритм:
- рассчитать эффективную процентную ставку;
- найти число начислений за год;
- вычислить номинальную ставку, используя формулу.
С другой стороны, если известна реальная ставка процента, то найти номинальную можно иным путем. Для этого реальное значение уменьшают на уровень инфляции.
Расчет реальной ставки процента основан на применении теории Фишера. В таком случае она определяется по формуле, приведенной экономистом.
Формула для расчета реальной и номинальной ставки процента
Для расчета реальной и номинальной ставки процента понадобиться знать одно из значений. Каждый показатель вычисляют с применением формул.
| Показатель | Формула | Расшифровка формулы |
| Номинальная ставка | РС + ПИ | РС – реальная ставка;
ПИ – процент инфляции |
| ЧН * ((1 + ЭС)1 / ЧН — 1 | ЧН – число начислений за год;
ЭС – эффективная ставка; |
|
| Эффективная ставка | (Зкп / Знп – 1) * 100 | Зкп, Знп – значения на конец и начало периода соответственно |
| Реальная ставка | НС — ПИ | НС – номинальная ставка;
ПИ – процент инфляции |
| (НС – ПИ) / (1 + ПИ) | ПИ – процент инфляции;
НС – номинальная ставка |
Важно! Найти реальную ставку без предварительного вычисления номинальной невозможно.
Пример расчета реальной и номинальной ставки процента
Для того чтобы понять алгоритм вычисления реальной и номинальной ставки процента, произведем расчет показателей на примере по следующим условиям.
Инвестор вложил в проект 1 млн. рублей на 3 года под 10% годовых. Выплата дивидендов осуществляется каждый квартал, то есть за год вложенная сумма увеличиться 4 раза. Процент инфляции за 3 года составит 4%. Надо отметить, что в конце инвестирования предполагается получение дохода в размере 1,3 млн. рублей.
Вычисления начнем с определения номинальной ставки. Для ее нахождения используем формулу расчета эффективной ставки.
Пример расчета номинальной ставки процента
Номинальная ставка процента находится по формуле РС + ПИ, где РС – реальная ставка, ПИ – процент инфляции.
В связи с тем, что в данный момент реальная ставка неизвестна, в ходе вычисления показателя используем другое арифметическое выражение:
ЧН * ((1 + ЭС)1 / ЧН – 1, где
ЧН – число начислений за год;
ЭС – эффективная ставка.
Эффективную ставку процента найдем по формуле (Зкп / Знп – 1) * 100, где Зкп, Знп – значения суммы инвестиций на конец и начало периода соответственно.
1,3 млн. руб. / 1 млн. руб. * 100 = 30%.
То есть, в год инвестор будет получать по 10% номинального дохода в размере 100 тыс. рублей.
Теперь можно найти номинальную ставку:
4 * ((1 + 0,3) 1 / 12 – 1 = 0,12 или 12%.
Таким образом, номинальная ставка процента с учетом капитализации составила 12%.
Пример расчета номинальной ставки процента
После того, как номинальная ставка процента найдена, можно приступать к расчету реальной. Для этого достаточно уменьшить первый показатель на процент инфляции, который по условиям задачи равен 4%.
12% — 4% = 8%.
Реальную ставку можно найти и другим путем, используя формулу (НС – ПИ) / (1 + ПИ), где ПИ – процент инфляции, а НС – номинальная ставка.
(12% — 4%) / (1 + 4%) = (0,12 – 0,04) / (1 + 0,04) = 0,077 или 7,7%.
Таким образом, реальная ставка составит 8%. Второй результат немного отличается от первого расчета. Все дело в том, что в ходе вычисления было использовано больше факторов, влияющих на реальную ставку, а ее значение получается более точное.
Проанализировав расчеты номинальной и реальной ставки можно сделать вывод о том, что фактическая доходность от инвестирования в проект средняя. Несмотря на то, что к окончанию срока договора покупательская способность прибыли снизится, инвестор получит доход, так как процент инфляции составит 4%, а реальная ставка 7,7%.
Уравнение Фишера (также называемое эффектом Фишера и гипотезой Фишера) — уравнение, описывающее связь между темпом инфляции, номинальной и реальной ставками процента. Названо в честь Ирвинга Фишера.
Уравнение[править | править код]
Уравнение имеет следующий вид[1].
,
где 


Экономический смысл[править | править код]
Уравнение в приближенной форме (см. Вывод) описывает явление, которое называется эффектом Фишера. Эффект состоит в том, что номинальная ставка процента может измениться по двум причинам:
- из-за изменений реальной ставки процента;
- из-за изменения темпа инфляции.
Уровень цен в экономике со временем меняется. Инвестор также размещает деньги под проценты на определенный срок. Поэтому он заинтересован в том, чтобы получить не только определенный доход, но и компенсировать падение покупательной способности денег в будущем. Например, если инвестор положил на банковский счёт сумму денег, приносящую 10 % годовых ежегодно, то номинальная ставка составит 10 %. При уровне инфляции 6 % реальная ставка составит только 4 %.
В уравнении может использоваться как фактический темп инфляции 

Вывод[править | править код]
Уравнение в приведенной выше форме является приближенным. Оно выполняется тем точнее, чем меньше по модулю значения 

,
Точная запись уравнения выглядит следующим образом:
Если раскрыть скобки, то получится следующая запись:
или
С точки зрения математического анализа, если 





Пусть, например, 

Точную запись можно также преобразовать к следующему виду, предложенному Фишером:
В тривиальных случаях при 

См. также[править | править код]
- Процентная ставка
- Инфляционные ожидания
Примечания[править | править код]
- ↑ Вечканов и др., 2008, с. 55.
Литература[править | править код]
- Вечканов Г. C., Вечканова Г. Р. Макроэкономика. — СПб.: Питер, 2008. — С. 55. — (Серия «Краткий курс»). — ISBN 978-5-91180-108-3.
- Четыркин Е. М. Финансовая математика: Учеб.. — М.: Дело, 2000. — 400 с.











