У этого термина существуют и другие значения, см. Ребро.
Ребро в геометрии — отрезок, соединяющий две вершины многоугольника или многогранника (в размерностях 3 и выше)[1]. В многоугольниках ребро является отрезком, лежащим на границе[2] и чаще называется стороной многоугольника. В трёхмерных многогранниках и в многогранниках большей размерности ребро — это отрезок, общий для двух граней[3]. Отрезок, соединяющий две вершины и проходящий через внутренние или внешние точки, ребром не является и называется диагональю.
Связь с рёбрами графа[править | править код]
Любой многогранник может быть представлен его рёберным скелетом[en], то есть графом, вершинами которого служат геометрические вершины многогранника, а рёбра графа соответствуют геометрическим рёбрам[4]. И обратно, графы, являющиеся скелетами трёхмерных многогранников по теореме Штайница — то же самое, что вершинно k-связные планарные графы[5].
Число рёбер в многограннике[править | править код]
Любая поверхность выпуклого многогранника имеет эйлерову характеристику
где 


Инцидентность другим граням[править | править код]
В многоугольнике в каждой вершине сходятся два ребра (стороны). По теореме Балинского по меньшей мере 

Аналогично, в трёхмерном многограннике в точности две двумерные грани имеют общее ребро[7], в то время как в многогранниках более высоких размерностей общее ребро могут иметь три и более двумерных граней.
Альтернативная терминология[править | править код]
В теории выпуклых многогранников высоких размерностей (свыше 3) фасета (сторона 

См. также[править | править код]
- Продолжение стороны[en]
Примечания[править | править код]
- ↑ Ziegler, 1995, с. 51, Definition 2.1.
- ↑ Weisstein, Eric W. «Polygon Edge.» From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/PolygonEdge.html Архивная копия от 26 июля 2020 на Wayback Machine
- ↑ Weisstein, Eric W. «Polytope Edge.» From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/PolytopeEdge.html Архивная копия от 24 мая 2016 на Wayback Machine
- ↑ Senechal, 2013, с. 81.
- ↑ Pisanski, Randić, 2000, с. 174–194.
- ↑ Balinski, 1961, с. 431–434.
- ↑ Wenninger, 1974, с. 1.
- ↑ Seidel, 1986, с. 404–413.
Литература[править | править код]
- Günter M. Ziegler. Lectures on Polytopes. — Springer, 1995. — Т. 152. — (Graduate Texts in Mathematics).
- M. L. Balinski. On the graph structure of convex polyhedra in n-space // Pacific Journal of Mathematics. — 1961. — Vol. 11. — Вып. 2. — doi:10.2140/pjm.1961.11.431.
- Magnus J. Wenninger. Polyhedron Models. — Cambridge University Press, 1974. — ISBN 9780521098595.
- Marjorie Senechal. Shaping Space: Exploring Polyhedra in Nature, Art, and the Geometrical Imagination. — Springer, 2013. — ISBN 9780387927145.
- Tomaž Pisanski, Milan Randić. Geometry at work / Catherine A. Gorini. — Washington, DC: Math. Assoc. America, 2000. — Т. 53. — (MAA Notes).. См., в частности, теорему 3, стр. 176.
- Raimund Seidel. Proceedings of the Eighteenth Annual ACM Symposium on Theory of Computing (STOC ’86). — 1986. — doi:10.1145/12130.12172.
Ссылки[править | править код]
- Olshevsky, George. «Edge». Glossary for Hyperspace. Архивировано с оригинала 4 февраля 2007.
- Weisstein, Eric W. Polygonal edge (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Polyhedral edge (англ.) на сайте Wolfram MathWorld.
From Wikipedia, the free encyclopedia
-

A polygon is bounded by edges; this square has 4 edges.
-

Every edge is shared by three or more faces in a 4-polytope, as seen in this projection of a tesseract.
In geometry, an edge is a particular type of line segment joining two vertices in a polygon, polyhedron, or higher-dimensional polytope.[1] In a polygon, an edge is a line segment on the boundary,[2] and is often called a polygon side. In a polyhedron or more generally a polytope, an edge is a line segment where two faces (or polyhedron sides) meet.[3] A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal.
Relation to edges in graphs[edit]
In graph theory, an edge is an abstract object connecting two graph vertices, unlike polygon and polyhedron edges which have a concrete geometric representation as a line segment.
However, any polyhedron can be represented by its skeleton or edge-skeleton, a graph whose vertices are the geometric vertices of the polyhedron and whose edges correspond to the geometric edges.[4] Conversely, the graphs that are skeletons of three-dimensional polyhedra can be characterized by Steinitz’s theorem as being exactly the 3-vertex-connected planar graphs.[5]
Number of edges in a polyhedron[edit]
Any convex polyhedron’s surface has Euler characteristic
where V is the number of vertices, E is the number of edges, and F is the number of faces. This equation is known as Euler’s polyhedron formula. Thus the number of edges is 2 less than the sum of the numbers of vertices and faces. For example, a cube has 8 vertices and 6 faces, and hence 12 edges.
Incidences with other faces[edit]
In a polygon, two edges meet at each vertex; more generally, by Balinski’s theorem, at least d edges meet at every vertex of a d-dimensional convex polytope.[6]
Similarly, in a polyhedron, exactly two two-dimensional faces meet at every edge,[7] while in higher dimensional polytopes three or more two-dimensional faces meet at every edge.
Alternative terminology[edit]
In the theory of high-dimensional convex polytopes, a facet or side of a d-dimensional polytope is one of its (d − 1)-dimensional features, a ridge is a (d − 2)-dimensional feature, and a peak is a (d − 3)-dimensional feature. Thus, the edges of a polygon are its facets, the edges of a 3-dimensional convex polyhedron are its ridges, and the edges of a 4-dimensional polytope are its peaks.[8]
See also[edit]
- Extended side
References[edit]
- ^ Ziegler, Günter M. (1995), Lectures on Polytopes, Graduate Texts in Mathematics, vol. 152, Springer, Definition 2.1, p. 51, ISBN 9780387943657.
- ^ Weisstein, Eric W. “Polygon Edge.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/PolygonEdge.html
- ^ Weisstein, Eric W. “Polytope Edge.” From MathWorld–A Wolfram Web Resource. http://mathworld.wolfram.com/PolytopeEdge.html
- ^ Senechal, Marjorie (2013), Shaping Space: Exploring Polyhedra in Nature, Art, and the Geometrical Imagination, Springer, p. 81, ISBN 9780387927145.
- ^ Pisanski, Tomaž; Randić, Milan (2000), “Bridges between geometry and graph theory”, in Gorini, Catherine A. (ed.), Geometry at work, MAA Notes, vol. 53, Washington, DC: Math. Assoc. America, pp. 174–194, MR 1782654. See in particular Theorem 3, p. 176.
- ^ Balinski, M. L. (1961), “On the graph structure of convex polyhedra in n-space”, Pacific Journal of Mathematics, 11 (2): 431–434, doi:10.2140/pjm.1961.11.431, MR 0126765.
- ^ Wenninger, Magnus J. (1974), Polyhedron Models, Cambridge University Press, p. 1, ISBN 9780521098595.
- ^ Seidel, Raimund (1986), “Constructing higher-dimensional convex hulls at logarithmic cost per face”, Proceedings of the Eighteenth Annual ACM Symposium on Theory of Computing (STOC ’86), pp. 404–413, doi:10.1145/12130.12172, S2CID 8342016.
External links[edit]
- Weisstein, Eric W. “Polygonal edge”. MathWorld.
- Weisstein, Eric W. “Polyhedral edge”. MathWorld.
Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида
Когда человек слышит слово “пирамида”, то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .
Что такое пирамида в общем случае?
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.
 Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
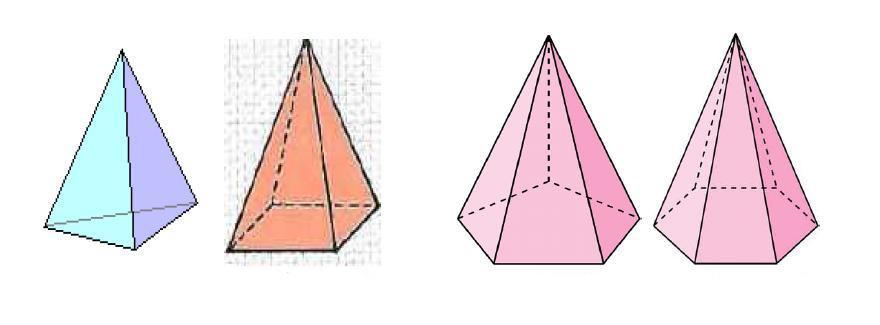
Мы видим что первая фигура имеет треугольное основание, вторая – четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.
Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:
- в основании должен находиться правильный многоугольник;
- боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.
Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.
Правильная четырехугольная пирамида
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).
Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.
Египетские пирамиды в Гизе являются правильными четырехугольными.
Далее приведем формулы, позволяющие определить все характеристики этой фигуры.
Четыре основных линейных параметра
Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.
Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:
Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):
Очевидно, что боковое ребро b всегда больше апофемы ab.
Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.
Площадь и объем фигуры
Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:
Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:
Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.
Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:
S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.
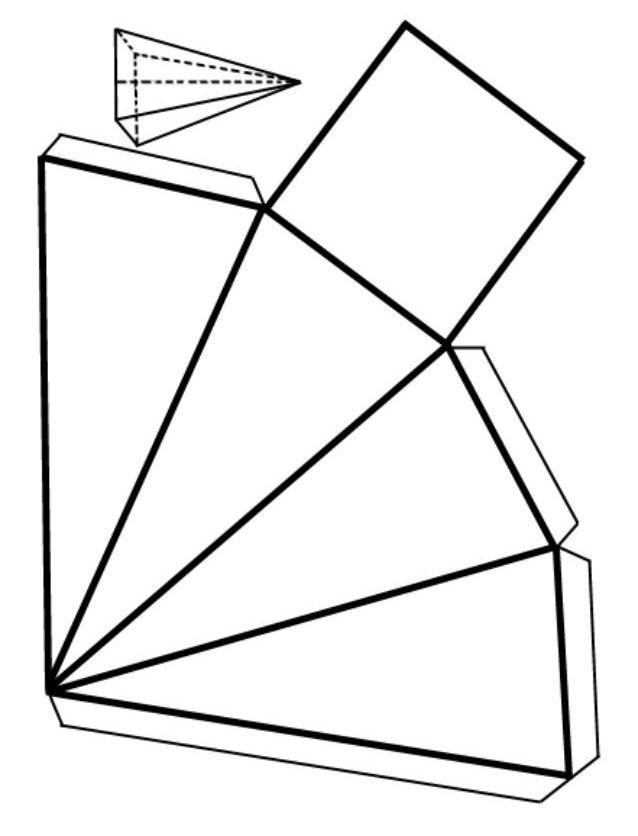
Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:
То есть V равен третьей части произведения высоты фигуры на площадь ее основания.
Свойства правильной усеченной четырехугольной пирамиды
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.
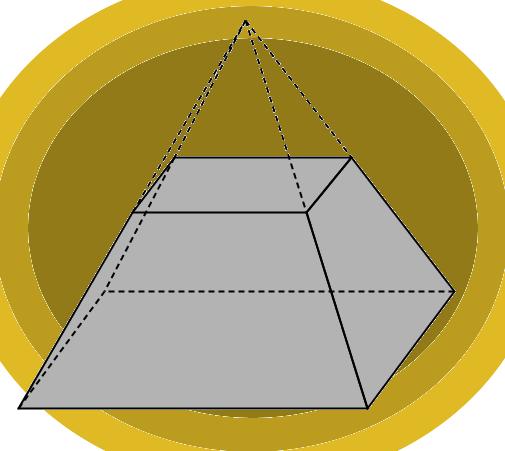
Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание – это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.
Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.
Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:
V = 1/3 × h × (So1 + So2 + √(So1 × So2))
Здесь h – расстояние между основаниями фигуры, So1, So2 – площади нижнего и верхнего оснований.
Как найти ребра правильного четырехугольника
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Площадь поверхности правильной четырехугольной призмы выражается через сторону ее основания a и боковое ребро H формулой
Подставим значения a и S:
откуда находим, что
Пирамида и ее боковые ребра. Формулы. Боковое ребро пирамиды Хеопса
Одной из геометрических фигур, свойства которых изучают в школах в курсе стереометрии, является пирамида. Рассмотрим, что собой представляет эта фигура, а также подробно охарактеризуем важный линейный параметр – боковое ребро пирамиды.
Пирамида как фигура геометрии
Прежде чем рассматривать понятие о боковом ребре пирамиды, следует дать определение этой пространственной фигуры. Если говорить коротко, то пирамида представляет собой поверхность, ограниченную одним n-угольником и n треугольниками. Рисунок ниже показывает один из возможных вариантов этой фигуры.
 Вам будет интересно: Микроскопы “Микромед”: обзор, описание, характеристики
Вам будет интересно: Микроскопы “Микромед”: обзор, описание, характеристики
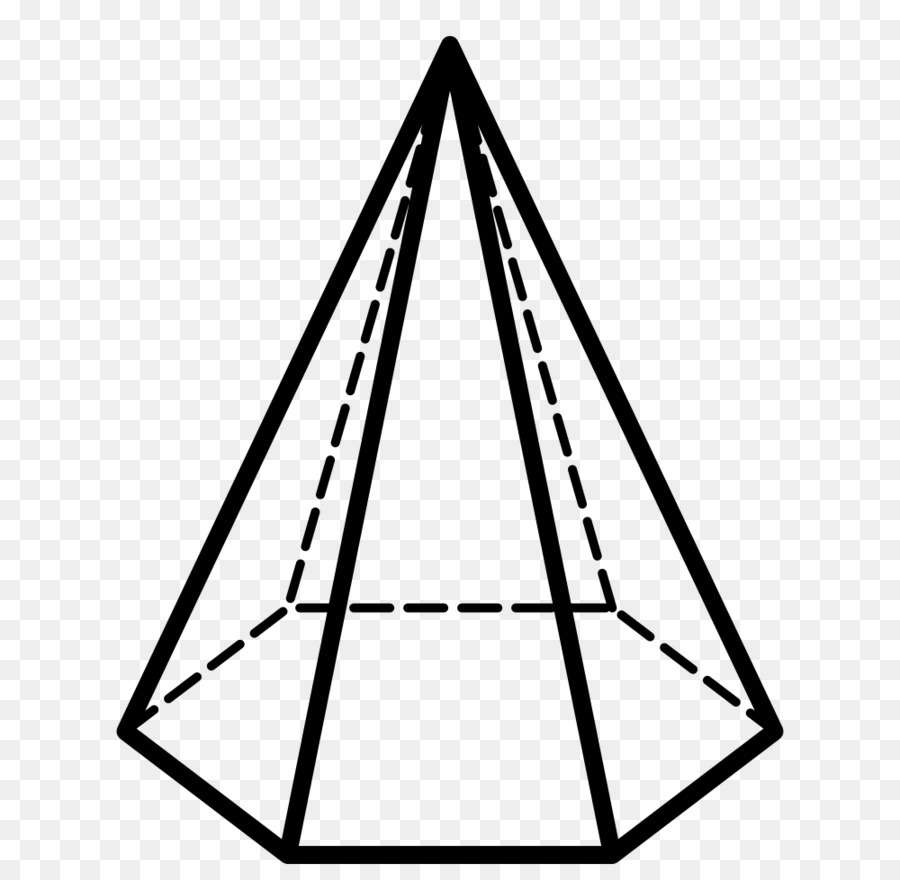
С геометрической точки зрения получить пирамиду можно таким способом: взять n-угольник и соединить все его углы с некоторой точкой в пространстве, которая не должна лежать в плоскости n-угольника.
Заметим, что, независимо от количества сторон n в исходном многоугольнике, всегда при соединении его углов с единственной точкой получаются треугольники. Их совокупность образует боковую поверхность пирамиды, а исходный многоугольник является ее основанием. Точка, в которой соединяются все треугольники, получила название вершины пирамиды.
Элементы пирамиды
Каждая пирамида образована тремя главными элементами:
Граней или сторон у фигуры всегда n + 1. Это легко видеть на приведенном в предыдущем пункте рисунке. Шестиугольное основание является одной гранью. Оставшиеся 6 сторон представляют собой треугольники, опирающиеся на стороны основания и пересекающиеся в вершине пирамиды.
Ребра представляют собой совокупность точек пересечения соседних граней. Фигура имеет два типа этих элементов:
- ребра основания;
- боковые ребра пирамиды.
Их количества, независимо от числа сторон n основания, всегда равны друг другу, то есть фигура имеет 2 × n ребер. Если с ребрами основания все понятно (они являются сторонами n-угольника), то для боковых ребер следует уточнить, что они представляют собой отрезки, соединяющие углы основания с высотой рассматриваемой фигуры.
Наконец, третьим типом элементов пирамиды будут вершины. У фигуры имеется n + 1 вершина. Однако n из них образованы основанием и двумя боковыми гранями. Лишь одна единственная вершина не связана с основанием. Она играет важную роль при изучении количественных характеристик пирамиды, например, ее высоты или апофемы.
Правильные пирамиды
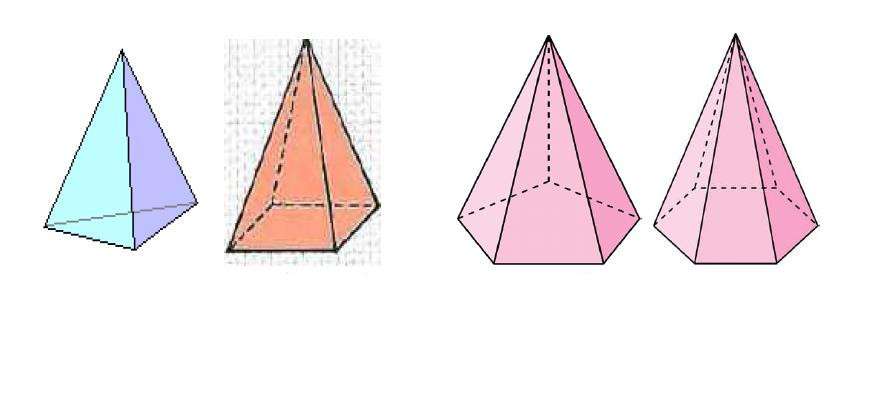
Пирамиды могут быть наклонными и прямыми, правильными и неправильными, выпуклыми и вогнутыми. Все названные типы фигур отличаются друг от друга многоугольным основанием и особенностями поведения высоты.
Предположим, что имеется пирамида, у которой высота (опущенный из вершины к основанию перпендикуляр) падает на многоугольник точно в его геометрическом центре. В этом случая фигура называется прямой. Если же многоугольник является равносторонним, то помимо прямой, пирамида также будет правильной. Напомним, что центр геометрический плоской фигуры аналогичен центру масс в физике. Для квадрата он совпадает с точкой пересечения диагоналей, а для треугольника – с точкой, где медианы пересекаются.
Пирамиды правильные удобно изучать ввиду их симметрии. Так, боковые ребра правильной пирамиды и ее боковые грани равны друг другу. Частным случаем является ситуация, когда боковые грани будут образованы равносторонними треугольниками.
Далее рассмотрим, какими формулами следует пользоваться, чтобы определить размеры боковых ребер пирамид — правильной четырехугольной и треугольной.
Треугольная пирамида
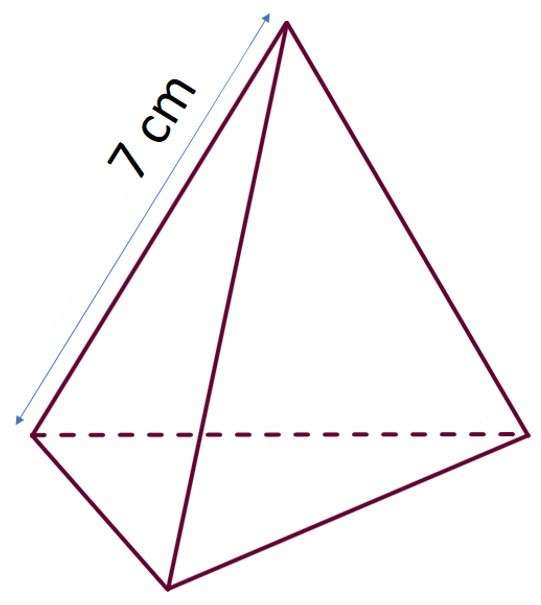
Существуют четыре линейных параметра, которые описывают размеры правильной пирамиды. К ним относятся сторона основания a, боковое ребро b, высота h и апофема hb. Ниже приведем формулы, которые позволяют рассчитать длину бокового ребра для треугольной пирамиды правильной. Основание этой фигуры представляет треугольник с равными сторонами, что позволяет записать следующие равенства:
Обе формулы являются следствием теоремы Пифагора для треугольников, в которых боковое ребро b является гипотенузой.
Четырехугольная пирамида
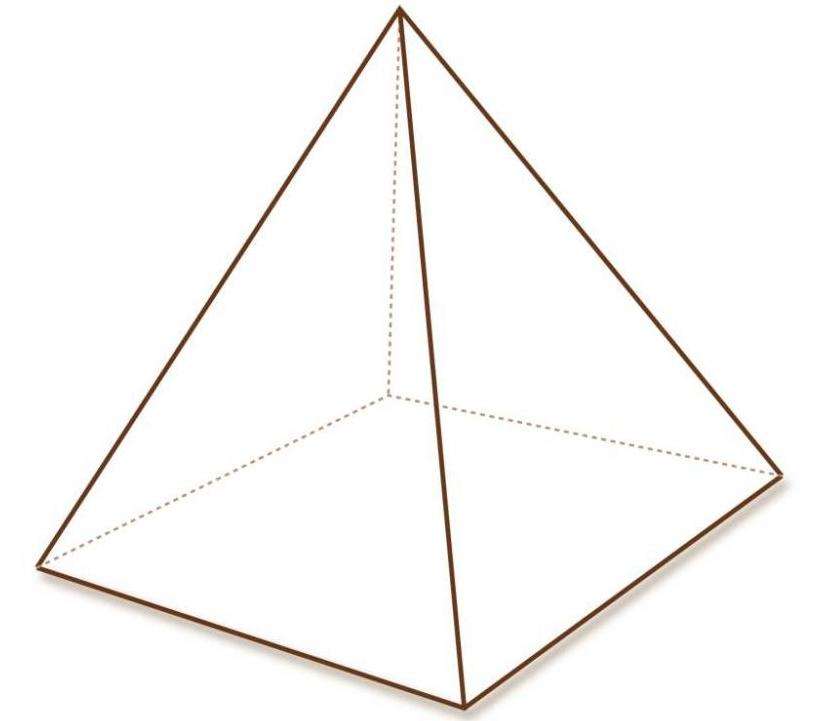
Эта фигура, пожалуй, является самой известной среди остальных пирамид благодаря величественным древним египетским сооружениям. Боковое ребро пирамиды четырехугольной правильной можно определить по таким формулам:
Как и в предыдущем случае, эти выражения являются следствием свойства катетов и гипотенузы прямоугольного треугольника.
Отметим, что формула расчета бокового ребра правильной пирамиды четырехугольной через ее апофему и сторону основания аналогична таковой для треугольной фигуры. Это совпадение не является случайным, поскольку боковые грани обеих пирамид – это равнобедренные треугольники.
Задача на определение бокового ребра пирамиды Хеопса

Каждый человек знает, что первое чудо света – пирамида Хеопса, обладает головокружительными размерами. Она является самой большой из всех пирамид, находящихся в египетской Гизе. Стороны ее основания образуют квадрат с точностью до нескольких десятков сантиметров. Средняя длина стороны пирамиды оценивается в 230,363 метра. Высота пирамиды в настоящее время составляет около 137 метров, однако исходная высота каменного гиганта была 146,50 метров.
Воспользуемся приведенными выше цифрами, чтобы определить, чему равно боковое ребро правильной пирамиды четырехугольной, посвященной фараону Хеопсу.
Поскольку нам известна высота h и длина стороны a монумента, то следует применить такую формулу для b:
Подставляя в нее известные данные, получаем, что боковое ребро правильной четырехугольной пирамиды равно 273 метра, что немногим меньше периметра футбольного поля (300 метров).
[spoiler title=”источники:”]
http://ege.sdamgia.ru/problem?id=27063
http://24simba.ru/zdorove-i-bezopasnost/6790-piramida-i-ee-bokovye-rebra-formuly-bokovoe-rebro-piramidy-heopsa/
[/spoiler]
Что такое ребро в геометрии для детей?
край. • сторона многоугольника или отрезка.
Что такое ребра в математике?
Край где встречаются два лица. Вершина — это угол, в котором сходятся ребра. Множественное число – вершины.
Что такое ребро в 3D-форме?
Края. Ан Край – это место, где встречаются два лица. Например, у куба 12 ребер, у цилиндра — два, а у сферы — ни одного.
Что такое примеры ребер?
Для многоугольника: Отрезок линии на границе, соединяющий одну вершину (угловую точку) с другой. Пример: Этот пятиугольник имеет 5 ребер. Для многогранника: Отрезок, на котором сходятся две грани.
Смотрите также, из чего состоят континенты.
Как найти край фигуры?
Что такое края фигуры?
Край — это место, где сходятся две грани формы. На 2D-фигурах ребра линии между каждой вершиной. В 3D-фигурах это линии, разделяющие каждую грань.
Что такое ребро в треугольнике?
Ребра — это линии, которые соединяются, образуя вершины. … У квадрата четыре стороны и четыре вершины. В треугольнике три и того, и другого. Квадратная пирамида, трехмерная фигура, имеет разное количество ребер и вершин. У него пять вершин или углов, но восемь ребер, соединяющих эти вершины вместе.
Что такое ребро куба?
Ответ: Ребро куба отрезок линии, соединяющий две вершины. Всего в кубе 12 ребер. Давайте подробно разберемся со свойствами куба. Пояснение: … Отрезок, соединяющий две вершины, называется ребром.
Что такое края и углы?
Как существительные разница между краем и углом
в том, что ребро – это граничная линия поверхности в то время как угол – это точка, где встречаются две сходящиеся линии; угол, внешний или внутренний.
Сколько ребер в конусе?
Конусы, сферы и цилиндры не имеют краев потому что у них нет плоских сторон. Место, где встречаются два или более ребра, называется вершиной. Вершина подобна углу.
Что такое края сферы?
Вот список форм вместе с количеством ребер.
| Форма | Количество ребер (E) |
|---|---|
| Сфера | 0 край |
| Цилиндр | 3 ребра |
| Прямоугольная призма | 12 ребер |
| Треугольная призма | 9 ребер |
Как рассчитать преимущество?
Что такое край в структуре данных?
край — край представляет путь между двумя вершинами или линию между двумя вершинами. В следующем примере линии от A до B, от B до C и т. д. представляют ребра.
См. Также, почему Цезарь Август приказал провести перепись
Есть ли у окружности край?
Если ребро замкнутой фигуры должно быть прямым, то круг не имеет краев, поскольку никакая часть окружности не является прямой.
Что такое ребро призмы?
То базовые края призмы – это ребра основания призмы. Вершина призмы – это точка пересечения двух ребер основания. Боковые ребра призмы — это отрезки, соединяющие соответствующие вершины оснований призмы.
Как найти ребро призмы?
Сколько ребер у трехмерного треугольника?
Треугольные призмы
Он состоит из 5 граней (2 треугольника, 3 прямоугольника). Треугольные призмы имеют 6 вершин и 9 ребер!
Как вы описываете край?
Что такое ребро 2D-формы?
Край — это место, где сходятся две грани формы. На 2D-фигурах ребра линии между каждой вершиной. В 3D-фигурах это линии, разделяющие каждую грань.
Как найти стороны треугольника?
Теорема Пифагора: длины ребер прямоугольного треугольника
Наиболее распространенное применение теоремы Пифагора состоит в том, чтобы использовать известные длины двух сторон прямоугольного треугольника, чтобы найти длину третьей стороны, используя алгебру и формула а² + b² = с².
Чему равен край прямоугольника?
четыре края
У прямоугольника четыре стороны. Прямоугольник — это двумерная фигура, имеющая четыре прямые стороны, которые пересекаются под четырьмя углами в 90 градусов. В отличие от…
Как найти ребро куба?
Чему равно ребро прямоугольной призмы?
12 ребер
Прямоугольная призма имеет 12 ребер. Край — это место, где встречаются две грани. Прямоугольная призма имеет 6 граней, каждая из которых имеет 4 ребра.
Как найти ребра куба?
12
Сколько ребер у яйца?
Доступ к ответам на вопросы по математике. Решения NCERT для класса 3 по математике. Глава 5. Формы и конструкции.
| Название вещи | Есть ли у него углы | Количество ребер |
|---|---|---|
| Мяч | Нет | |
| Ластик | да | 12 |
| Яйцо | Нет | |
| Лист бумаги | да | 4 |
См. Также, какова основная цель правительства.
Что такое ребра и вершины в графе?
На диаграмме графа вершина обычно изображается кружком с меткой, а ребро представлено линией или стрелкой, идущей от одной вершины к другой.
Какая фигура имеет ровно 9 ребер?
треугольная призма
Треугольная призма – это призма с двумя треугольными основаниями и тремя прямоугольными сторонами. У него 6 вершин, 9 ребер и 5 граней.
Сколько ребер у пирамиды?
Треугольная пирамида
Все стороны равнобедренных треугольников. Пирамида с треугольным основанием имеет 4 грани, 4 вершины, включая вершину и 6 ребер.
Сколько ребер у призмы?
Прямоугольная призма имеет 6 граней, 8 вершин (или углов) и 12 ребер.
Что такое ребро в цилиндре?
Кубы и прямоугольные параллелепипеды имеют 12 ребер. Конусы имеют 1 ребро. Цилиндры имеют 2 ребра.
Сколько ребер у куба?
12
Как найти ребра вершины?
Сумма значений степени вершины равна вдвое больше ребер, так как каждое ребро было подсчитано с обоих концов. В вашем случае 6 вершин степени 4 означают, что существует (6 × 4)/2 = 12 ребер.
Что такое процент EDGE?
Преимущество Дома — это термин, используемый для описания математическое преимущество что азартная игра и, следовательно, коммерческое место для азартных игр имеет над вами власть, когда вы играете в течение долгого времени. Это преимущество приводит к гарантированному процентному возврату в место проведения с течением времени, а для вас – к гарантированному процентному проигрышу вашей ставки.
Как использовать формулу Келли?
Формула Келли: Келли % = W – (1-W)/R, где:
- Kelly % = процент капитала, который нужно вложить в одну сделку.
- W = исторический процент выигрышей торговой системы.
- R = историческое среднее соотношение выигрышей/проигрышей.
Узнайте о гранях, ребрах и вершинах — 3D-фигуры | Базовая геометрия для детей | Лапша Кидз
Грани Ребра Вершины-Трехмерные фигуры-Геометрическая формула Эйлера
Геометрия края 101
Грани, ребра и вершины | Визуализация твердых фигур | Ч-15.2 – 7-й НЦЭРТ | Эдусарал
Где ребро куба?
Куб — это многогранник, поверхность которого состоит из шести квадратов. Грани куба – это стороны куба, которые представляют собой квадрат. Ребра куба – это стороны граней куба.
Как найти 1 ребро куба?
Следственно длина ребра куба равняется корню квадратному из площади его грани, то есть:а=? S, гдеа – длина ребра куба,S – площадь грани куба.
Как найти ребро куба из площади?
Формулы
| Периметр куба (общая длина ребра) | O = | 12 × a |
|---|---|---|
| Площадь одной стороны | P = | a × a = a² |
| Площадь куба (поверхность) | Q = | 6 × P1 = 6 × a² |
| Объем куба | V = | a × a × a = a³ |
| Диагоналная (стороны/стены) | u2 = | a √2 ≈ a × 1,41 |
•6 сент. 2017 г.
Где длина у куба?
Разделите диагональ одной из граней куба на √2, чтобы найти длину ребра куба. Таким образом, если в задаче дана диагональ грани (любой) куба, то вы можете найти длину ребра куба, разделив диагональ на √2.
Как выглядит куб?
Куб (др. -греч. κύβος); иногда гекса́эдр или правильный гекса́эдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы….
| Куб | |
|---|---|
| Тип | правильный многогранник |
| Комбинаторика | |
| Элементы | 6 граней 12 рёбер 8 вершин Χ = 2 |
| Грани | квадраты |
Чему равно ребро куба?
— грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата. Определение. Ребро куба — это отрезок, образованный пересечением двух граней куба.
Чему равен ребро куба?
— грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата. Определение. Ребро куба — это отрезок, образованный пересечением двух граней куба.
Как найти площадь в кубе?
Площадь куба — это сумма площади всех его сторон. Все стороны куба равны, поэтому, чтобы найти площадь куба, надо найти площадь одной из его сторон и умножить на 6.
Как найти площадь куба 4 класс?
Площадь куба — это сумма площади всех его сторон. Все стороны куба равны, поэтому, чтобы найти площадь куба, надо найти площадь одной из его сторон и умножить на 6.
Какой океан в Варадеро?
Варадеро — самый известный курортный город Кубы. Находится на полуострове Икакос и омывается водами Атлантики и Мексиканского залива.
Сколько метров кубических в кубе?
Куби́ческий метр (кубометр) — единица объёма, производная в Международной системе единиц (СИ), а также в системах единиц МКГСС и МТС. Одному кубическому метру равен объём куба с длиной ребра 1 метр.
Сколько пар параллельных сторон куба?
Всего куб имеет 24 пары скрещивающихся рёбер. Количество пар параллельных граней – 3.
Что такое ребро у квадрата?
Ребро в геометрии — отрезок, соединяющий две вершины многоугольника или многогранника (в размерностях 3 и выше). В многоугольниках ребро является отрезком, лежащим на границе и чаще называется стороной многоугольника.
Сколько квадратных метров в 1 куб?
| Сколько квадратных метров в 1 кубе | ||
|---|---|---|
| Длина | Толщина, ширина | м2 / м.кв. |
| 6 метров, 6000 мм. | 50*100 | 19.998 |
| 50*150 | 19.998 | |
| 50*200 | 20.004 |
Как узнать площадь по размерам?
Чтобы найти площадь прямоугольника ABCD достаточно перемножить длины его сторон a и b. где S — площадь прямоугольника, a — длина первой стороны, b — длина второй стороны.
Как посчитать площадь куба формула?
Площадь куба — это сумма площади всех шести его сторон. Вот формула: 6 x s2, где «s» — это сторона куба.
Как найти площадь куба?
Площадь поверхности куба через сторону Формула для нахождения площади поверхности куба через его сторону: S = 6 a 2 {S = 6 a^2} S=6a2, где a — сторона куба.

