Поможем))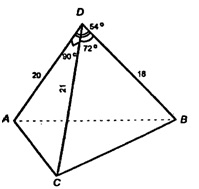
Рассмотрим грань ABD
Из теоремы косинусов:
АВ2 = AD2 + BD2 – 2 • AD • BD • cos54°≈ 400 + 324 – 2 • 20 • 18 •
• 0,05878 = 724 – 720 • 0,5878 ≈ 300,784;![]()
По теореме Пифагора АС2 = AD2 + CD2 ;![]()
СВ2 = CD2 + DB2 – 2 • DC • BD • cos72°;
СВ2 = 441 +324-2 • 21 • 18 • 0,3090 = 765 – 233,603 = 531,396;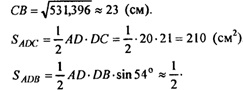 20•18 • 0,8090 = 180 • 0,8090 = 145,62 ≈ 146 (см2).
20•18 • 0,8090 = 180 • 0,8090 = 145,62 ≈ 146 (см2).![]()
21 ∙ 18 ∙ 0,9511 = 189 ∙ 0,9511 = 179,75 ≈ 180 (см2).
Итого: а) ≈ 17 см, ≈ 23 см, 29 см; б) 210 см2, ≈ 146 см2, ≈ 180 см2.
Материал урока.
В начале изучения
курса «Стереометрии» мы говорили, что все геометрические тела делятся на тела
вращения и многогранники. В процессе изучения геометрии в десятом классе, мы
будем подробно рассматривать с вами свойства тех или иных фигур.
Сегодня мы
познакомимся с такой фигурой как тетраэдр. Прежде чем приступить к изучению
пространственной фигуры, давайте вернемся в планиметрию и вспомним такую фигуру
как многоугольник.
Напомню, что многоугольником
называется либо замкнутая линия без самопересечений либо часть плоскости, ограниченная
этой линией, включая ее саму.
Для стереометрии
нам естественно подходит второе определение. Это определение показывает, что
каждый многоугольник представляет собой плоскую поверхность.
Напомним, что простейшим
многоугольником является треугольник. Возьмем треугольник ABC
и точку D, которая не лежит в плоскости треугольника ABC. Соединим точку D с каждой
вершиной треугольника ABC. Таким образом, мы получим
три новых треугольника DAB, DBC,
DCA. Тогда фигуру, которая состоит из четырех
треугольников ABC, DAB, DBC, DCA, называют тетраэдром и
обозначают так: DABC.
Треугольники, из
которых состоит тетраэдр, называются гранями, стороны этих треугольников
называют ребрами, вершины этих треугольников называются вершинами
тетраэдра.
Нетрудно посчитать,
что тетраэдр имеет четыре грани, 6 ребер и четыре вершины. Два ребра тетраэдра,
которые не имеют общих вершин, называются противоположными. Давайте
запишем пары противоположных ребер тетраэдра, который изображен на рисунке.
Это будут ребра AD и BC, BDи AC, CD и AB.
Иногда одну из граней тетраэдра называют основанием, а три другие – боковыми
гранями.
Слово тетраэдр
произошло от древнегреческих слов теторес – четыре и эдра –
основание или грань.
Если все грани
тетраэдра – равносторонние треугольники, то такой тетраэдр называется правильным.
Правильный тетраэдр является одним из пяти правильных многогранников. Они еще
называются телами Платона. Это — тетраэдр, гранями которого
являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр,
имеющий восемь треугольных граней, додекаэдр, гранями которого являются
двенадцать правильных пятиугольников, и икосаэдр с двадцатью
треугольными гранями.
Последователи
Пифагорейской философской школы форму тетраэдра придавали стихии огня.
Тетраэдр, все грани
которого равные между собой треугольники, называется равногранным тетраэдром.
Если ребра
тетраэдра, которые прилегают к одной вершине, перпендикулярны между собой, то
такой тетраэдр называется прямоугольным.
Тетраэдры обычно
изображаются в виде выпуклого или невыпуклого четырехугольника с диагоналями. При
этом штриховыми линиями изображаются невидимые ребра.
На этом рисунке
невидимым является только ребро AC.
А на этом рисунке
невидимыми являются ребра ЕК, KF, KL.
Тетраэдр образует
жёсткую, статически определимую конструкцию. Тетраэдр, выполненный из стержней,
часто используется в качестве основы для пространственных несущих конструкций
пролётов зданий, перекрытий, балок, ферм, мостов.
Ярким примером
тетраэдра является разработанное для Нового Орлеана «здание-город», которое
возвышается на 360 метров, включает в себя 20000 квартир, суммарная жилая
площадь которых 2040000 квадратных метров. Здание использует экологичное
энергоснабжение — энергию ветра, воды и солнца. Кроме квартир в тетраэдре
помещаются коммерческие организации, три отеля, культурные объекты, школа,
больницы и казино. И, учитывая место, под которое создавался проект, его
немаловажная особенность — способность держаться на плаву.
Решим насколько
задач.
Задача. Назовите
все пары скрещивающихся рёбер тетраэдра . Сколько таких пар рёбер имеет тетраэдр?
Решение.
Напомним, что две
прямые называются скрещивающимися, если они не лежат в одной плоскости.
Нетрудно увидеть,
что скрещивающимися будут ребра AB и СD,
АC и BD, АD
и BC. То есть в тетраэдре есть три пары скрещивающихся
ребер.
Задача. В
тетраэдре
,
,
,
,
,
. Найти рёбра основания
данного
тетраэдра.
Решение.
Задача. Пусть
точки и
– середины рёбер
и
тетраэдра
. Доказать, что прямая
параллельна плоскости
.
Доказательство.
Что и
требовалось доказать.
Подведем итоги
урока. Сегодня на уроке мы познакомились с пространственным многогранником
– тетраэдром. Познакомились с элементами тетраэдра, решили несколько задач по
данной теме.
Как найти рёбра основания тетраэдра
Четверка – «тетра» – в названии объемной геометрической фигуры указывает на количество образующих ее граней. А число граней правильного тетраэдра, в свою очередь, однозначно определяет конфигурацию каждой из них – четыре поверхности могут составить объемную фигуру, только имея форму правильного треугольника. Вычисление длин ребер составленной из правильных треугольников фигуры особой сложности не представляет.
Инструкция
В фигуре, составленной из абсолютно одинаковых граней, основанием можно считать любое из них, поэтому задача сводится к вычислению длины произвольно выбранного ребра. Если вам известна полная площадь поверхности тетраэдра (S), для вычисления длины ребра (a) извлеките из нее квадратный корень и разделите полученный результат на кубический корень из тройки: a = √S/³√3.
Площадь одной грани (s), очевидно, должна быть вчетверо меньше полной площади поверхности. Поэтому для расчета длины грани по этому параметру трансформируйте формулу из предыдущего шага к такому виду: a = 2*√s/³√3.
Если в условиях дана только высота (H) тетраэдра, для нахождения длины стороны (а), составляющей каждую грань, утройте это единственное известное значение, а затем разделите на квадратный корень из шестерки: a = 3*H/√6.
При известном из условий задачи объеме (V) тетраэдра для вычисления длины ребра (a) придется извлекать кубический корень из этой величины, увеличенной в двенадцать раз. Рассчитав эту величину, разделите ее еще и на корень четвертой степени из двойки: a = ³√(12*V)/⁴√2.
Зная диаметр описанной около тетраэдра сферы (D) тоже можно найти длину ее ребра (a). Чтобы это сделать, увеличьте диаметр вдвое, а затем разделите на квадратный корень из шестерки: a = 2*D/√6.
По диаметру вписанной в эту фигуру сферы (d) длина ребра определяется почти так же, разница лишь в том, что диаметр надо увеличивать не вдвое, а в целых шесть раз: a = 6*d/√6.
Радиус окружности (r), вписанной в любую грань этой фигуры, тоже позволяет вычислить нужную величину – умножьте его на шестерку и разделите на квадратный корень из тройки: a = r*6/√3.
Если в условиях задачи дана суммарная длина всех ребер правильного тетраэдра (P), для нахождения длины каждого из них просто разделите это число на шесть – именно столько ребер имеет эта объемная фигура: a = P/6.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,655 -
гуманитарные
33,653 -
юридические
17,917 -
школьный раздел
611,939 -
разное
16,901
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
