Куб является первым представителем в ряду правильных многогранников, благодаря тому, что все его ребра равны между собой. Все грани куба являются квадратами, в которых ребро куба становится стороной квадрата и связано отношениями с его площадью и диагональю. Найти ребро куба, зная диагональ основания, можно разделив ее на корень из двух.
Также можно найти ребро куба, зная площадь основания:
Поскольку у куба могут быть даны площади боковой и полной его поверхности, приведем необходимые формулы ребра куба и для них:

Если исходить из понятия ребра, как части объемного тела, то в таком случае становится возможным вычислить ребро куба, зная его объем:
Одной из немаловажных деталей куба является его диагональ, соединяющая противоположные вершины верхнего и нижнего оснований, впрочем, для куба это могут быть любые два противоположных основания, так как все его грани конгруэнтны. Диагональ куба D, соединенная с диагональю основания d и ребром a дает прямоугольный треугольник, в котором из теоремы Пифагора можно найти ребро куба следующим образом.
a2+d2=D2
3a2=D2
В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
- Определение куба
-
Свойства куба
- Свойство 1
-
Свойство 2
- Свойство 3
-
Формулы для куба
- Диагональ
- Диагональ грани
- Площадь полной поверхности
- Периметр ребер
-
Объем
- Радиус описанного вокруг шара
- Радиус вписанного шара
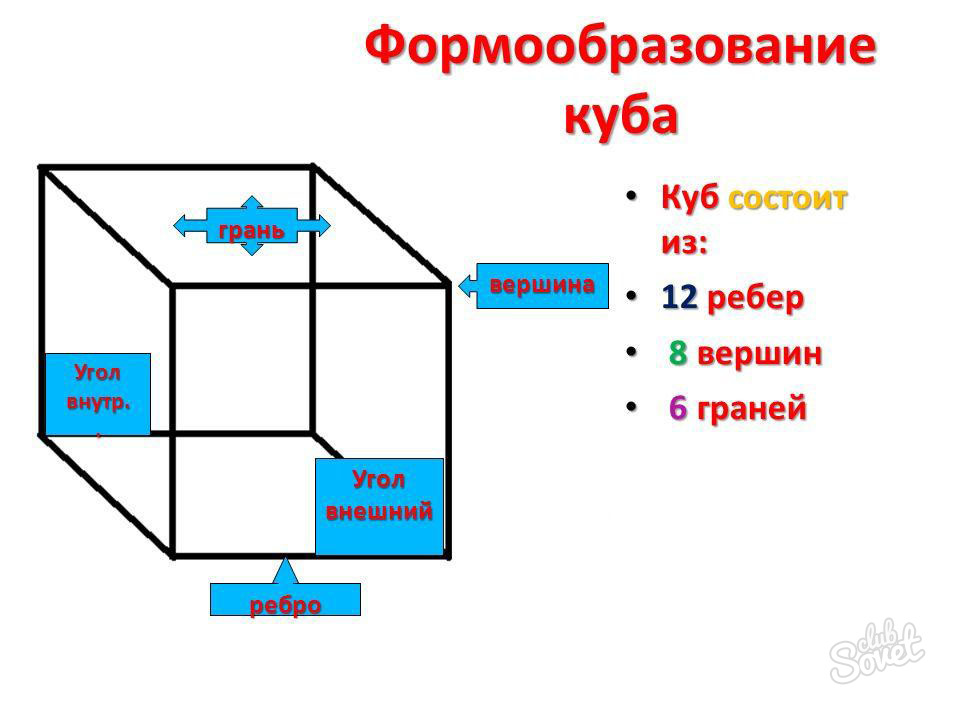
Определение куба
Куб – это правильный многогранник, все грани которого являются квадратами.
- Вершины куба – это точки, являющиеся вершинами его граней.
Всего их 8: A, B, C, D, A1, B1, C1 и D1. - Ребра куба – это стороны его граней.
Всего их 12: AB, BC, CD, AD, AA1, BB1, CC1, DD1, A1B1, B1C1, C1D1 и A1D1. - Грани куба – это квадраты, из которого состоит фигура.
Всего их 6: ABCD, A1B1C1D1, AA1B1B, BB1C1C, CC1D1D и AA1D1D.
Примечание: куб является частным случаем параллелепипеда или призмы.
Свойства куба
Свойство 1
Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:
- ABCD || A1B1C1D1
- AA1B1B || CC1D1D
- BB1C1C || AA1D1D
Свойство 2
Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.
- AC1 = BD1 = A1C = B1D (диагонали куба).
- О – точка пересечения диагоналей:
AO = OC1 = BO = OD1 = A1O = OC = B1O = OD.
Свойство 3
Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.
Например, на рисунке выше угол между гранями ABCD и AA1B1B является прямым.
Формулы для куба
Примем следующие обозначения, которые будут использоваться далее:
- a – ребро куба;
- d – диагональ куба или его грани.
Диагональ
Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани
Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности
Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер
Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем
Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара
Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара
Радиус вписанного в куб шара равен половине длины его ребра.
Длина ребра куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Длина ребра куба
Чтобы найти длину ребра куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Длина ребра куба через объём
Чему равна длина ребра куба, если:
объём Vкуба =
a =
0
Округление ответа:
Длина ребра куба через диагональ
Чему равна длина ребра куба, если:
диагональ d =
a =
0
Округление ответа:
Длина ребра куба через площадь поверхности куба
Чему равна длина ребра куба, если:
Sпов =
a =
0
Округление ответа:
Теория
Как найти ребро куба зная его объём
Чему равна длина ребра куба a, если объём куба Vкуба:
Формула
a = 3√Vкуба
Пример
Для примера, посчитаем чему равна длина ребра куба a, если его объём Vкуба = 8 см³:
a = 3√8 = 2 см
Как найти ребро куба зная его диагональ
Чему равна длина ребра куба a, если его диагональ d:
Формула
a = d ⁄√3
Пример
Для примера, посчитаем чему равна длина ребра куба a, если длина его диагонали d = 9 см:
a = 9 ⁄ √3 ≈ 9/1.732 ≈ 5.196 см
Как найти ребро куба через площадь поверхности
Чему равна длина ребра куба a, если площадь его поверхности Sпов:
Формула
a = √Sпов⁄ 6
Пример
Для примера, посчитаем чему равна длина ребра куба a, если площадь его поверхности Sпов = 150 см²:
a = √150 / 6 = √25 = 5 см
См. также
Радиус описанной сферы куба
Свойства
Если описать вокруг куба сферу, то ее диаметр будет соединять противоположные вершины куба, образуя диагональ куба. Таким образом, радиус описанной сферы куба равен половине диагонали, следовательно, сама диагональ куба равна удвоенному радиусу описанной сферы. (рис.2.3) D=2R
Так как эта же диагональ связывает теоремой Пифагора в прямоугольном треугольнике диагональ стороны куба и ребро куба, то становится возможным вычислить и их через радиус описанной сферы куба, используя формулы диагонали. D=a√3 a=D/√3=2R/√3 a^2+d^2=D^2 (2R/√3)^2+d^2=(2R)^2 d^2=(8R^2)/3 d=√(8/3) R
Чтобы вычислить площадь грани куба, нужно рассмотреть ее в плоскости. Стороной куба является квадрат, поэтому его площадь равна стороне квадрата, то есть ребру куба, во второй степени. Площадь боковой поверхности куба состоит из четырех боковых граней-квадратов, а площадь полной поверхности – из шести граней, поэтому для их вычисления нужно умножить площадь одной грани на их количество. Чтобы найти площади куба через радиус сферы, описанной вокруг него, нужно подставить вместо ребра куба удвоенный радиус, деленный на корень из трех. S=a^2=(2R/√3)^2=(4R^2)/3 S_(б.п.)=4S=(16R^2)/3 S_(п.п.)=6S=(24R^2)/3
Объем куба, зная радиус описанной вокруг него сферы, вычисляется возведением в третью степень выражения для ребра куба. V=a^3=(2R/√3)^3=(8R^3)/(3√3)
Периметр куба, как умноженное на 12 ребро куба, представлено через радиус описанной вокруг сферы окружности в виде отношения радиуса, умноженного на 24, к корню из трех. P=12a=24R/√3
Чтобы вычислить радиус сферы, вписанной в куб, через радиус сферы, описанной около него, нужно разделить ребро куба на два, то есть разделить радиус описанной сферы на корень из трех. r=a/2=2R/(2√3)=R/√3
Калькулятор расчета стороны правильного многоугольника через радиусы окружностей
В публикации представлены онлайн-калькуляторы и формулы для расчета длины стороны правильного многоугольника через радиус вписанной или описанной окружности.
Расчет длины стороны
Инструкция по использованию: введите радиус вписанной (r) или описанной (R) окружности, укажите количество вершин правильного многоугольника (n), затем нажмите кнопку “Рассчитать”. В результате будет вычислена длина стороны фигуры (a).
Квадрат. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти сторону, периметр, диагональ квадрата, радиус вписанной в квадрат окружности, радиус описанной вокруг квадрата окружности и т.д.. Для нахождения незвестных элементов, введите известные данные в ячейки и нажмите на кнопку “Вычислить”. Теоретическую часть и численные примеры смотрите ниже.
Определение 1. Квадрат − это четырехугольник, у которого все углы равны и все стороны равны (Рис.1):
Можно дать и другие определение квадрата.
Определение 2. Квадрат − это прямоугольник, у которого все стороны равны.
Определение 3. Квадрат − это ромб, у которого все углы прямые (или равны).
Свойства квадрата
- Длины всех сторон квадрата равны.
- Все углы квадрата прямые.
- Диагонали квадрата равны.
- Диагонали пересекаются под прямым углом.
- Диагонали квадрата являются биссектрисами углов.
- Диагонали квадрата точкой пересечения делятся пополам.
Изложеннные свойства изображены на рисунках ниже:
Диагональ квадрата
Определение 4. Диагональю квадрата называется отрезок, соединяющий несмежные вершины квадрата.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. У квадрата две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
 . . |
(1) |
Из равенства (1) найдем d:
 . . |
(2) |
Пример 1. Сторона квадрата равна a=53. Найти диагональ квадрата.
Решение. Для нахождения диагонали квадрата воспользуемся формулой (2). Подставляя a=53 в (2), получим:
Ответ:
Окружность, вписанная в квадрат
Определение 5. Окружность называется вписанной в квадрат, если все стороны касаются этого квадрата (Рис.3):
Формула вычисления радиуса вписанной окружности через сторону квадрата
Из рисунка 3 видно, что диаметр вписанной окружности равен стороне квадрата. Следовательно, формула вычисления радиуса вписанной окружности через сторону квадрата имеет вид:
 |
(3) |
Пример 2. Сторона квадрата равна a=21. Найти радиус вписанной окружности.
Решение. Для нахождения радиуса списанной окружности воспользуемся формулой (3). Подставляя a=21 в (3), получим:
Ответ:
Формула вычисления сторон квадрата через радиус вписанной окружности
Из формулы (3) найдем a. Получим формулу вычисления стороны квадрата через радиус вписанной окружности:
 |
(4) |
Пример 3. Радиус вписанной в квадрат окружности равен r=12. Найти сторону квадрата.
Решение. Для нахождения стороны квадраиа воспользуемся формулой (4). Подставляя r=12 в (4), получим:
Ответ:
Окружность, описанная около квадрата
Определение 6. Окружность называется описанной около квадрата, если все вершины квадрата находятся на этой окружности (Рис.4):
Формула радиуса окружности описанной вокруг квадрата
Выведем формулу вычисления радиуса окружности, описанной около квадрата через сторону квадрата.
Обозначим через a сторону квадрата, а через R − радиус описанной около квадрата окружности. Проведем диагональ BD (Рис.4). Треугольник ABD является прямоугольным треугольником. Тогда из теоремы Пифагора имеем:
 |
(5) |
Из формулы (5) найдем R:
 |
(6) |
или, умножая числитель и знаменатель на 
 . . |
(7) |
Пример 4. Сторона квадрата равна a=4.5. Найти радиус окружности, описанной вокруг квадрата.
Решение. Для нахождения радиуса окружности описанной вокруг квадрата воспользуемся формулой (7). Подставляя a=4.5 в (7), получим:
Ответ:
Формула стороны квадрата через радиус описанной около квадрата окружности
Выведем формулу вычисления стороны квадрата, через радиус описанной около квадрата окружности.
Из формулы (1) выразим a через R:
 . . |
(8) |
Пример 5. Радиус описанной вокруг квадрата окружности равен 
Решение. Для нахождения стороны квадрата воспользуемся формулой (8). Подставляя 
Ответ:
Периметр квадрата
Периметр квадрата − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Поскольку стороны квадрата равны, то периметр квадрата вычисляется формулой:
 |
(9) |
где 
Пример 6. Сторона квадрата равен 
Решение. Для нахождения периметра квадрата воспользуемся формулой (9). Подставляя 
Ответ:
Признаки квадрата
Признак 1. Если в четырехугольнике все стороны равны и один из углов четырехугольника прямой, то этот четырехугольник является квадратом.
Доказательство. По условию, в четырехугольнике противоположные стороны равны, то этот четырехугольник праллелограмм (признак 2 статьи Параллелограмм). В параллелограмме противоположные углы равны. Следовательно напротив прямого угла находится прямой угол. Тогда сумма остальных двух углов равна: 360°-90°-90°=180°, но поскольку они также являются противоположными углами, то они также равны и каждый из них равен 90°. Получили, что все углы четырехугольника прямые и, по определению 1, этот четырехугольник является квадратом.
Признак 2. Если в четырехугольнике диагонали равны, перпендикулярны и точкой пересечения делятся пополам, то такой четырехугольник является квадратом (Рис.5).
Доказательство. Пусть в четырехугольнике ABCD диагонали пересекаются в точке O и пусть
 |
(10) |
Так как AD и BC перпендикулярны, то
Из (10) и (11) следует, что треугольники OAB, OBD, ODC, OCA равны (по двум сторонам и углу между ними (см. статью на странице Треугольники. Признаки равенства треугольников)). Тогда
 |
(12) |
Эти реугольники также равнобедренные. Тогда
Из (13) следует, что
 |
(14) |
Равенства (12) и (14) показывают, что четырехугольник ABCD является квадратом (определение 1).
[spoiler title=”источники:”]
http://matworld.ru/geometry/kvadrat.php
[/spoiler]
Как найти ребро куба
Нередко встречаются задачи, в которых необходимо найти ребро куба, зачастую это следует проделать на основе информации о его объеме, площади грани или её диагонали. Существует несколько вариантов определения ребра куба.
1
В том случае, если известна площадь куба, то можно легко определить ребро. Грань куба представляет собой квадрат со стороной, равной ребру куба. Соответственно, её площадь равняется квадрату ребра куба. Следует воспользоваться формулой: а=√S, где а – это длина ребра куба, а S – это площадь грани куба.
2
Найти ребро куба по его объему – еще более простая задача. Нужно учитывать, что объем куба равен кубу (в третьей степени) длины ребра куба. Получается, что длина ребра равняется кубическому корню из его объема. То есть, мы получаем следующую формулу: а=√V, где а – это длина ребра куба, а V – объем куба.
3
По диагоналям также можно найти ребро куба. Соответственно, нам необходимы: а – длина ребра куба, b – длина диагонали грани куба, c – длина диагонали куба. По теореме Пифагора получаем: a^2+a^2=b^2, и отсюда можно легко вывести следующую формулу: a=√(b^2/2), по которой извлекается ребро куба.
4
Еще раз по теореме Пифагора (a^2+a^2=b^2) можно получить следующую зависимость: a^2+a^2+a^2=c^2, из которой выводим: 3*a^2=c^2, следовательно, ребро куба можно получить следующим образом: a=√(c^2/3).
https://www.youtube.com/watch?v=Z8neEwmKe4s