Длина ребра куба
- Главная
- /
- Математика
- /
- Геометрия
- /
- Длина ребра куба
Чтобы найти длину ребра куба воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Длина ребра куба через объём
Чему равна длина ребра куба, если:
объём Vкуба =
a =
0
Округление ответа:
Длина ребра куба через диагональ
Чему равна длина ребра куба, если:
диагональ d =
a =
0
Округление ответа:
Длина ребра куба через площадь поверхности куба
Чему равна длина ребра куба, если:
Sпов =
a =
0
Округление ответа:
Теория
Как найти ребро куба зная его объём
Чему равна длина ребра куба a, если объём куба Vкуба:
Формула
a = 3√Vкуба
Пример
Для примера, посчитаем чему равна длина ребра куба a, если его объём Vкуба = 8 см³:
a = 3√8 = 2 см
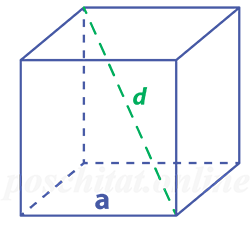
Как найти ребро куба зная его диагональ
Чему равна длина ребра куба a, если его диагональ d:
Формула
a = d ⁄√3
Пример
Для примера, посчитаем чему равна длина ребра куба a, если длина его диагонали d = 9 см:
a = 9 ⁄ √3 ≈ 9/1.732 ≈ 5.196 см
Как найти ребро куба через площадь поверхности
Чему равна длина ребра куба a, если площадь его поверхности Sпов:
Формула
a = √Sпов⁄ 6
Пример
Для примера, посчитаем чему равна длина ребра куба a, если площадь его поверхности Sпов = 150 см²:
a = √150 / 6 = √25 = 5 см
См. также
Ребро куба
Стороны фигур
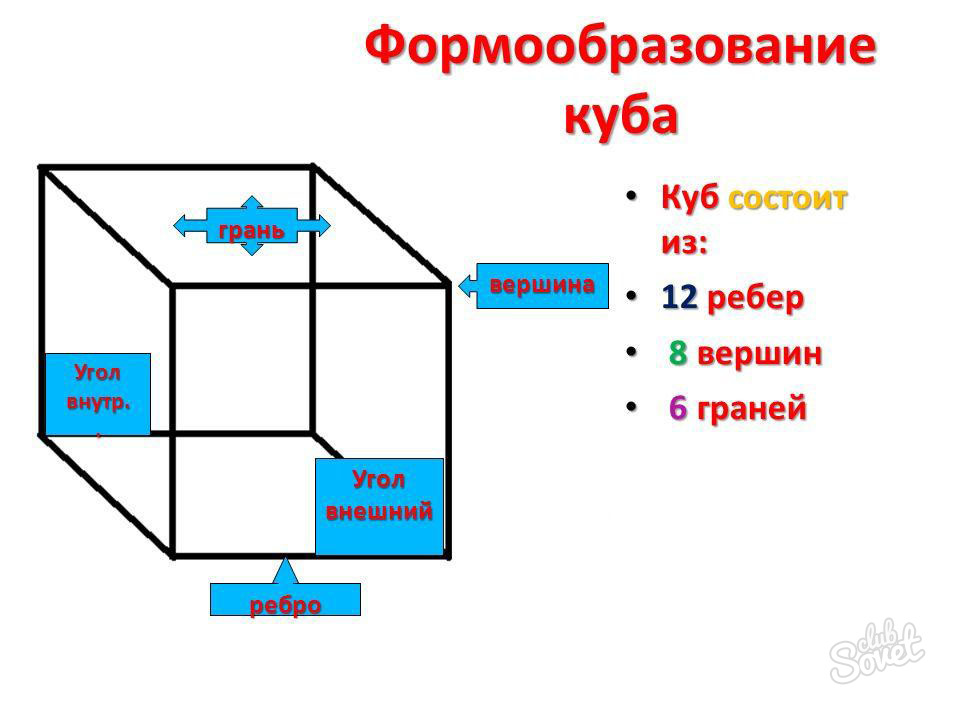
Куб — это четырехугольная призма, все шесть граней которой являются квадратами.
Калькулятор расчета длины ребра куба через объем
Длины трех ребер куба (длина, ширина, высота) имеют равные измерения. Объем куба равен длине ребра, возведенной в третью степень.
V = a3 ,
где Y — объем куба, а — ребро куба.
Если известен объем куба V, длину ребра (а) рассчитываем по формуле:
Калькулятор расчета длины ребра куба через диагональ
Проведенный внутри куба отрезок, соединивший вершины, расположенные на противоположных сторонах, является диагональю куба. Соединив диагональ и боковое ребро, исходящее из вершины диагонали через диагональ основания, получим прямоугольный треугольник. Его гипотенузой будет диагональ куба, а катетами — боковое ребро и диагональ основания. Через теорему Пифагора находим диагональ куба:
d = a√3 ,
где а — ребро куба, d — диагональ куба.
Если известна диагональ куба, его ребро определяем как отношение диагонали к корню из 3 по формуле:
a = d/√3 ,
Как найти ребро куба
Нередко встречаются задачи, в которых необходимо найти ребро куба, зачастую это следует проделать на основе информации о его объеме, площади грани или её диагонали. Существует несколько вариантов определения ребра куба.
1
В том случае, если известна площадь куба, то можно легко определить ребро. Грань куба представляет собой квадрат со стороной, равной ребру куба. Соответственно, её площадь равняется квадрату ребра куба. Следует воспользоваться формулой: а=√S, где а – это длина ребра куба, а S – это площадь грани куба.
2
Найти ребро куба по его объему – еще более простая задача. Нужно учитывать, что объем куба равен кубу (в третьей степени) длины ребра куба. Получается, что длина ребра равняется кубическому корню из его объема. То есть, мы получаем следующую формулу: а=√V, где а – это длина ребра куба, а V – объем куба.
3
По диагоналям также можно найти ребро куба. Соответственно, нам необходимы: а – длина ребра куба, b – длина диагонали грани куба, c – длина диагонали куба. По теореме Пифагора получаем: a^2+a^2=b^2, и отсюда можно легко вывести следующую формулу: a=√(b^2/2), по которой извлекается ребро куба.
4
Еще раз по теореме Пифагора (a^2+a^2=b^2) можно получить следующую зависимость: a^2+a^2+a^2=c^2, из которой выводим: 3*a^2=c^2, следовательно, ребро куба можно получить следующим образом: a=√(c^2/3).
https://www.youtube.com/watch?v=Z8neEwmKe4s
как узнать ребро куба??? как узнать ребро куба если известен объём куба??? Подскажите формулу этого вычисления.
Павел Иванов
Знаток
(281),
закрыт
7 лет назад
♥~Polina~♥
Ученик
(224)
7 лет назад
Объём куба – это ребро куба в третьей степени. То есть, формула нахождения объёма – а*а*а, исходя из этого, чтобы узнать ребро мы объём делим на три. Если Объём это V, а ребро это а, то a=V:3.
GeselleГений (63461)
7 лет назад
корень кубичный надо извлекать, а не на три делить 🙁
а что делать если корень не знаешь раз такой умный
Куб является первым представителем в ряду правильных многогранников, благодаря тому, что все его ребра равны между собой. Все грани куба являются квадратами, в которых ребро куба становится стороной квадрата и связано отношениями с его площадью и диагональю. Найти ребро куба, зная диагональ основания, можно разделив ее на корень из двух.
Также можно найти ребро куба, зная площадь основания:
Поскольку у куба могут быть даны площади боковой и полной его поверхности, приведем необходимые формулы ребра куба и для них:

Если исходить из понятия ребра, как части объемного тела, то в таком случае становится возможным вычислить ребро куба, зная его объем:
Одной из немаловажных деталей куба является его диагональ, соединяющая противоположные вершины верхнего и нижнего оснований, впрочем, для куба это могут быть любые два противоположных основания, так как все его грани конгруэнтны. Диагональ куба D, соединенная с диагональю основания d и ребром a дает прямоугольный треугольник, в котором из теоремы Пифагора можно найти ребро куба следующим образом.
a2+d2=D2
3a2=D2