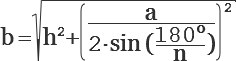Сторона основания пирамиды является стороной правильного многоугольника, исходя из этого, можно найти все параметры пирамиды, связанные с основанием, воспользовавшись формулами для правильных многоугольников.
P=n(a+b)
S=(na^2)/(4 tan〖(180°)/n〗 )
Чтобы найти радиус окружности, вписанной в основание правильной пирамиды, нужно разделить сторону основания на два тангенса из 180 градусов, деленных на количество сторон в основании. (рис.34.1)
r=a/(2 tan〖(180°)/n〗 )
Радиус окружности, описанной вокруг основания правильной пирамиды, равен отношению стороны основания к двум синусам того же угла. (рис.34.2)
R=a/(2 sin〖(180°)/n〗 )
Угол γ между сторонами правильного многоугольника, заложенного в основание пирамиды, легко найти, умножив 180 градусов на количество сторон многоугольника без двух, и деленное на полное количество сторон. (рис.34.3)
γ=180°(n-2)/n
Зная боковое ребро в совокупности со стороной основания, можно вычислить высоту пирамиды и ее апофему из прямоугольных треугольников, которые они образуют. (рис.34.5, 35.1)
h=√(b^2-R^2 )=√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 )
l=√(b^2-a^2/4)
Косинус угла между боковым ребром и основанием будет равен отношению радиуса окружности, описанной вокруг основания, к боковому ребру пирамиды, а косинус угла между апофемой и основанием – отношению радиуса вписанной в основание окружности к апофеме. (рис.34.4,34.5)
cosα=R/b=a/(2b sin〖(180°)/n〗 )
cosβ=r/l=a/(2 tan〖(180°)/n〗 √(b^2-a^2/4))
Площадь боковой поверхности пирамиды складывается из площадей треугольников, являющихся ее гранями, каждая из которых равна половине произведения апофемы на сторону основания, а площадь полной поверхности представляет собой сумму площади боковой поверхности и площади основания.
S_(б.п.)=lan/2=(√(b^2-a^2/4) an)/2
S_(п.п.)=an(l/2+a/(4 tan〖(180°)/n〗 ))=an(√(b^2-a^2/4)/2+a/(4 tan〖(180°)/n〗 ))
Чтобы найти объем пирамиды, необходимо вычислить треть от произведения ее высоты на площадь основания, последовательно подставив выражения для площади и высоты в формулу.
V=1/3 S_(осн.) h=(na^2 √(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(12 tan〖(180°)/n〗 )
Радиус сферы, которая может быть вписана в пирамиду, равен трем объемам, деленным на площадь полной поверхности пирамиды, а радиус сферы, описанной вокруг пирамиды – квадрату бокового ребра, деленному на две высоты. (рис.34.6,34.7)
r_1=3V/S_(п.п.) =(a√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))/(tan〖(180°)/n〗 (2√(b^2-a^2/4)+a/tan〖(180°)/n〗 ) )
R_1=b^2/2h=b^2/(2√(b^2-(a/(2 sin〖(180°)/n〗 ))^2 ))
/
/
/ Длина ребра пирамиды
Длина ребра пирамиды
Установить Длина ребра пирамиды на мобильный
Найти боковое ребро правильной пирамиды
зная длину стороны основания и высоту
|
||
|
Сторона основания пирамиды a |
||
|
Число сторон основания пирамиды n |
||
| Высота пирамиды h | ||
|
|
||
| Длина бокового ребра b |
Скачать калькулятор
Рейтинг: 2.7 (Голосов 6)
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Сообщить об ошибке
Смотрите также
| Сторона треугольника | Стороны прямоугольного треугольника | Сторона квадрата |
| Стороны прямоугольника | Стороны ромба | Боковое ребро параллелепипеда |
олег
979 дн. назад
а если стороны основания разные?
- reply
Михаил
595 дн. назад
Значит пирамида не правильная.
- reply
Добавить комментарий:
Я не робот
Пирамида – это объемная многогранная геометрическая фигура, состоящая из основания и треугольных
граней, собирающихся в одной точке. У нее есть: вершина, ребра (боковые и основные), боковые грани,
основание, высота и апофема – прямая, соединяющая вершину с границей вписанной в основание
окружности. Правильная пирамида –та, у которой все боковые ребра равны и находятся под одним углом к
основанию, а вершина проецируется на центр окружности, описанной вокруг основания. Тетраэдр –
частный случай правильной пирамиды, в которой боковые ребра равны основным и между собой.
Боковые ребра правильной пирамиды – выходящие из ее вершины, общие для боковых граней стороны. Длина
бокового ребра обозначается латинской буквой «b». Это одно из базовых значений, через которое можно
найти остальные элементы пирамиды. Во многих математических задачах требуется вычислить его или
подставить в формулы.
- Боковое ребро правильной треугольной пирамиды через высоту
и ребро основания - Боковое ребро правильной треугольной пирамиды через высоту
и радиус описанной окружности вокруг правильной треугольной пирамиды - Ребро основания правильной треугольной пирамиды через обьём
и высоту
Ребро основания правильной треугольной пирамиды через объём и высоту
Та часть пространства, которую занимает правильная треугольная пирамида называется ее объемом.
Является физической величиной. Его можно найти через, например, через высоту и сторону основания.
Если нам известен объем и высота правильной треугольной пирамиды, то не составит особого труда найти
ребро основания. Для этого используется формула:
a = √((V * 4 * √3) / H)
где V — объём, H — высота.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретную задачу. Необходимо найти ребро основания, зная что
высота H равна 56 см, a объем 268 см³, подставив все в формулу получим следующий результат: a = √((V * 4 * √3) / H) = √((268 * 4 * √3) / 56) = 5,76 см. Боковое
ребро (b) = 5,76 см.
Боковое ребро правильной треугольной пирамиды через высоту и ребро основания
Боковое ребро правильной пирамиды можно найти по теореме Пифагора, поскольку высота, опущенная в
основание пирамиды, опускается в центр вписанной и описанной окружности для данного многоугольника.
Таким образом формула для нахождения бокового ребра правильной треугольной пирамиды через высоту и
ребро основания будет следующей:
b = √(H² + (a / 2 sin (60º)²))
где H — высота, a — ребро основания.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 44 мм, a ребро основания
a равно 63 мм, подставив все в формулу получим следующий результат: b = √(H² + (a / 2 sin (60º)²)) = √(44² + (63 / 2 sin (60º)²)) = 57,09 мм.
Боковое ребро (b) = 57.08765 мм.
Боковое ребро правильной треугольной пирамиды через высоту и радиус описанной окружности вокруг
правильной треугольной пирамиды
Если пирамида вписана в окружность, то ее называют описанной вокруг пирамиды. Около пирамиды можно
описать сферу тогда и только тогда, когда около основания пирамиды можно описать
окружность. Основание перпендикуляра, опущенного из вершины такой пирамиды на плоскость ее
основания, является центром описанной около основания окружности. Если нам известна высота и радиус
этой описанной окружности, то мы сможем найти боковое ребро. Формула подходит только для правильной
треугольной пирамиды:
b = √(H² + R²)
где H — высота правильной треугольной пирамиды, R — радиус описанной вокруг
окружности.
Цифр после
запятой:
Результат в:
Пример. Рассмотрим конкретные данные. Пусть высота H равна 73 мм, a радиус описанной
вокруг окружности 114 мм, подставив все в формулу получим следующий результат: b = √(H² + R²) = √(73² + 114²) = 135 мм. Боковое
ребро (b) = 135 мм.
Почти все формулы пирамиды основываются на теореме Пифагора. Таким образом, можно вывести боковое
ребро правильной треугольной пирамиды через высоту и радиус описанной окружности, опираясь на
прямоугольный треугольник, гипотенуза которого является искомой величиной. По одному из основных
свойств правильной пирамиды, ее высота соединяет вершину с центрами окружностей, вписанных и
описанных вокруг пирамиды. Так внутри формируются 2 треугольника с углом 90°. Один состоит из
высоты, бокового ребра и соединяет их с радиусом описанной окружности, другой составляет высота и
апофема, соединённые с радиусом вписанной окружности.
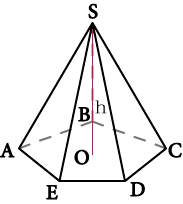
Боковое ребро правильной пирамиды, формула
 |
Боковое ребро правильной пирамиды находится по формуле [ b = sqrt{ h^2 + Big( frac{a}{2sin(frac{180°}{n})} Big) ^2 } ] |
b — Боковое ребро правильной пирамиды (SA или SB или SC или SD или SE)
n — число сторон правильного многоугольника – основания правильной пирамиды
a — сторона правильного многоугольника (AB или BC или CD или DE или EA) – основания правильной пирамиды
h — высота правильной пирамиды (OS)
Боковое ребро правильной пирамиды выводится из следующих формул
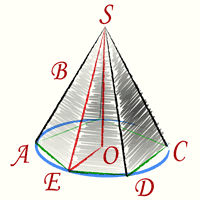
Синим цветом на рисунке изображена описанная вокруг основания правильной пирамиды окружность. Треугольник SOE прямоугольный.
Его стороны: OS — высота правильной пирамиды (h), OE —
радиус описанной окружности вокруг правильного многоугольника (основание правильной пирамиды (R)),
SE — Боковое ребро правильной пирамиды (b).
По теореме Пифагора
[ SE = b = sqrt{ h^2 + R^2 } ]
подставив сюда только радиус описанной окружности получается формула (1).
Вычислить, найти боковое ребро правильной пирамиды по формуле(1)
Боковое ребро правильной пирамиды |
стр. 277 |
|---|
Как найти боковое ребро в правильной четырехугольной пирамиде?
Знаток
(250),
закрыт
11 лет назад
Сэм
Высший разум
(154068)
11 лет назад
В правильной пирамиде все боковые рёбра равны, все боковые грани – равные равнобедренные тр-ки. Высота боковой грани называется апофемой правильной пирамиды.
Следовательно, имеем боковую грань (равнобедр. тр-к с основанием=12 и высотой (апофемой) =15 см Высота равнобедр. тр-ка делит основание пополам и образует прямоуг. тр-к со стороной основания и бок. ребром пирамиды. Тогда по Пифагору:
Бок. ребро=корень кв. из (6^2+15^2)=корень кв. из 261.
Наверное, так.