Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида
Когда человек слышит слово “пирамида”, то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .
Что такое пирамида в общем случае?
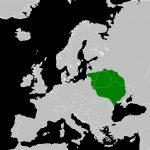
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.
 Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
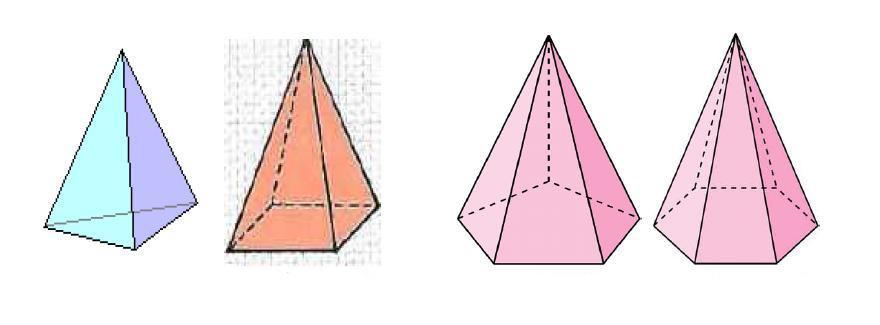
Мы видим что первая фигура имеет треугольное основание, вторая – четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.
Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:
- в основании должен находиться правильный многоугольник;
- боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.
Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.
Правильная четырехугольная пирамида
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).
Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.
Египетские пирамиды в Гизе являются правильными четырехугольными.
Далее приведем формулы, позволяющие определить все характеристики этой фигуры.
Четыре основных линейных параметра
Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.
Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:
Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):
Очевидно, что боковое ребро b всегда больше апофемы ab.
Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.
Площадь и объем фигуры
Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:
Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:
Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.
Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:
S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.
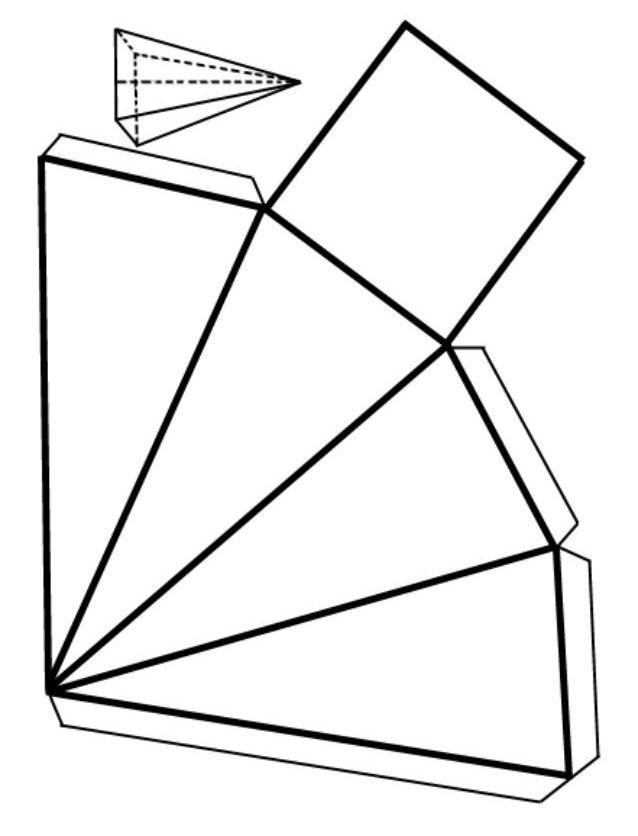
Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:
То есть V равен третьей части произведения высоты фигуры на площадь ее основания.
Свойства правильной усеченной четырехугольной пирамиды
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.
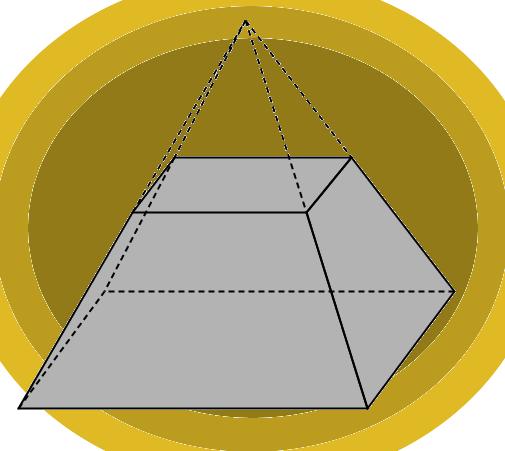
Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание – это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.
Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.
Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:
V = 1/3 × h × (So1 + So2 + √(So1 × So2))
Здесь h – расстояние между основаниями фигуры, So1, So2 – площади нижнего и верхнего оснований.
Как найти ребра правильного четырехугольника
Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760.
Площадь поверхности правильной четырехугольной призмы выражается через сторону ее основания a и боковое ребро H формулой
Подставим значения a и S:
откуда находим, что
Пирамида и ее боковые ребра. Формулы. Боковое ребро пирамиды Хеопса
Одной из геометрических фигур, свойства которых изучают в школах в курсе стереометрии, является пирамида. Рассмотрим, что собой представляет эта фигура, а также подробно охарактеризуем важный линейный параметр – боковое ребро пирамиды.
Пирамида как фигура геометрии
Прежде чем рассматривать понятие о боковом ребре пирамиды, следует дать определение этой пространственной фигуры. Если говорить коротко, то пирамида представляет собой поверхность, ограниченную одним n-угольником и n треугольниками. Рисунок ниже показывает один из возможных вариантов этой фигуры.
 Вам будет интересно: Микроскопы “Микромед”: обзор, описание, характеристики
Вам будет интересно: Микроскопы “Микромед”: обзор, описание, характеристики
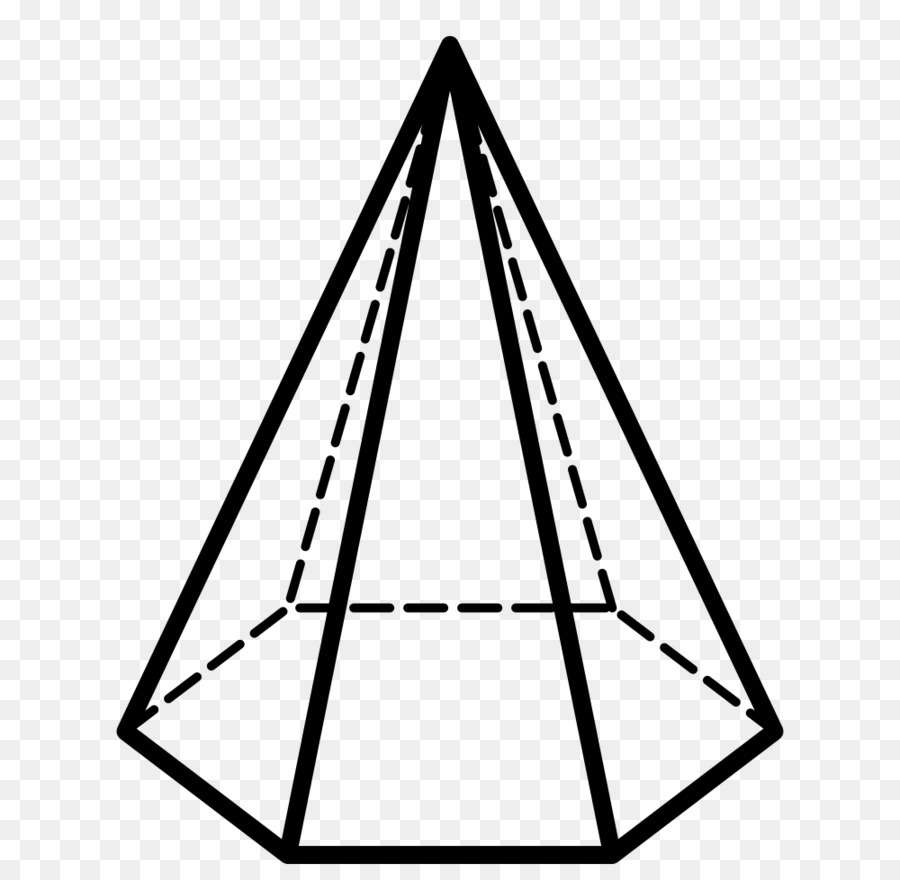
С геометрической точки зрения получить пирамиду можно таким способом: взять n-угольник и соединить все его углы с некоторой точкой в пространстве, которая не должна лежать в плоскости n-угольника.
Заметим, что, независимо от количества сторон n в исходном многоугольнике, всегда при соединении его углов с единственной точкой получаются треугольники. Их совокупность образует боковую поверхность пирамиды, а исходный многоугольник является ее основанием. Точка, в которой соединяются все треугольники, получила название вершины пирамиды.
Элементы пирамиды
Каждая пирамида образована тремя главными элементами:
Граней или сторон у фигуры всегда n + 1. Это легко видеть на приведенном в предыдущем пункте рисунке. Шестиугольное основание является одной гранью. Оставшиеся 6 сторон представляют собой треугольники, опирающиеся на стороны основания и пересекающиеся в вершине пирамиды.
Ребра представляют собой совокупность точек пересечения соседних граней. Фигура имеет два типа этих элементов:
- ребра основания;
- боковые ребра пирамиды.
Их количества, независимо от числа сторон n основания, всегда равны друг другу, то есть фигура имеет 2 × n ребер. Если с ребрами основания все понятно (они являются сторонами n-угольника), то для боковых ребер следует уточнить, что они представляют собой отрезки, соединяющие углы основания с высотой рассматриваемой фигуры.
Наконец, третьим типом элементов пирамиды будут вершины. У фигуры имеется n + 1 вершина. Однако n из них образованы основанием и двумя боковыми гранями. Лишь одна единственная вершина не связана с основанием. Она играет важную роль при изучении количественных характеристик пирамиды, например, ее высоты или апофемы.
Правильные пирамиды
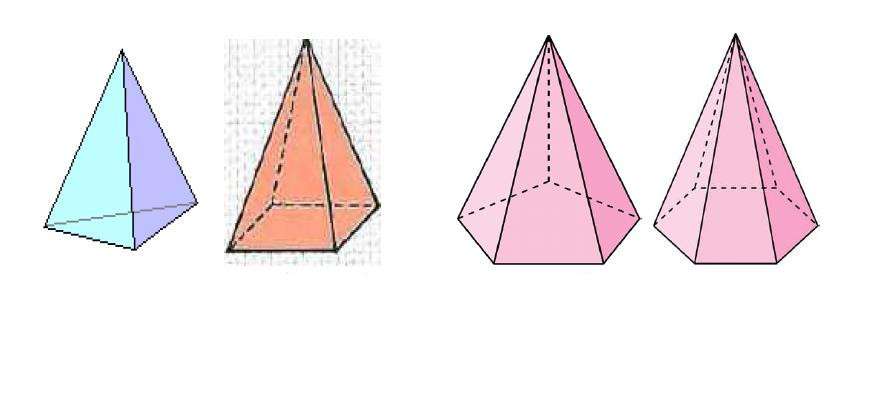
Пирамиды могут быть наклонными и прямыми, правильными и неправильными, выпуклыми и вогнутыми. Все названные типы фигур отличаются друг от друга многоугольным основанием и особенностями поведения высоты.
Предположим, что имеется пирамида, у которой высота (опущенный из вершины к основанию перпендикуляр) падает на многоугольник точно в его геометрическом центре. В этом случая фигура называется прямой. Если же многоугольник является равносторонним, то помимо прямой, пирамида также будет правильной. Напомним, что центр геометрический плоской фигуры аналогичен центру масс в физике. Для квадрата он совпадает с точкой пересечения диагоналей, а для треугольника – с точкой, где медианы пересекаются.
Пирамиды правильные удобно изучать ввиду их симметрии. Так, боковые ребра правильной пирамиды и ее боковые грани равны друг другу. Частным случаем является ситуация, когда боковые грани будут образованы равносторонними треугольниками.
Далее рассмотрим, какими формулами следует пользоваться, чтобы определить размеры боковых ребер пирамид — правильной четырехугольной и треугольной.
Треугольная пирамида
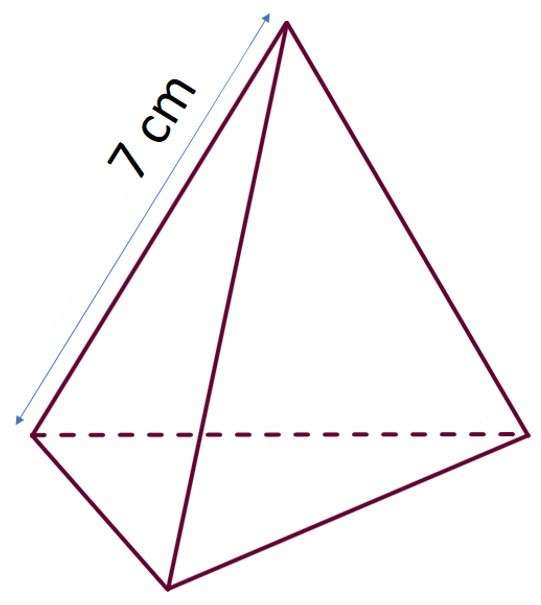
Существуют четыре линейных параметра, которые описывают размеры правильной пирамиды. К ним относятся сторона основания a, боковое ребро b, высота h и апофема hb. Ниже приведем формулы, которые позволяют рассчитать длину бокового ребра для треугольной пирамиды правильной. Основание этой фигуры представляет треугольник с равными сторонами, что позволяет записать следующие равенства:
Обе формулы являются следствием теоремы Пифагора для треугольников, в которых боковое ребро b является гипотенузой.
Четырехугольная пирамида
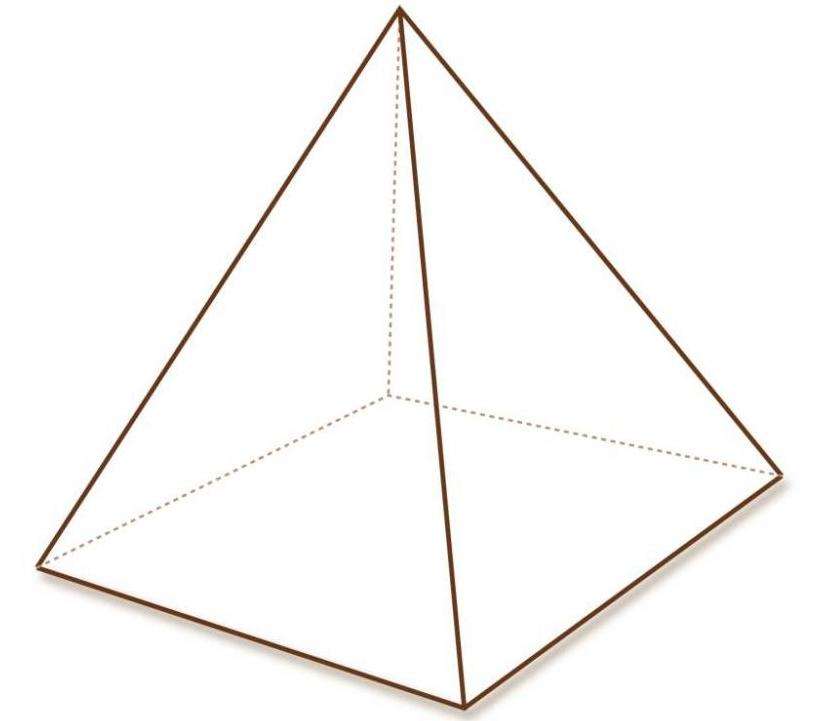
Эта фигура, пожалуй, является самой известной среди остальных пирамид благодаря величественным древним египетским сооружениям. Боковое ребро пирамиды четырехугольной правильной можно определить по таким формулам:
Как и в предыдущем случае, эти выражения являются следствием свойства катетов и гипотенузы прямоугольного треугольника.
Отметим, что формула расчета бокового ребра правильной пирамиды четырехугольной через ее апофему и сторону основания аналогична таковой для треугольной фигуры. Это совпадение не является случайным, поскольку боковые грани обеих пирамид – это равнобедренные треугольники.
Задача на определение бокового ребра пирамиды Хеопса

Каждый человек знает, что первое чудо света – пирамида Хеопса, обладает головокружительными размерами. Она является самой большой из всех пирамид, находящихся в египетской Гизе. Стороны ее основания образуют квадрат с точностью до нескольких десятков сантиметров. Средняя длина стороны пирамиды оценивается в 230,363 метра. Высота пирамиды в настоящее время составляет около 137 метров, однако исходная высота каменного гиганта была 146,50 метров.
Воспользуемся приведенными выше цифрами, чтобы определить, чему равно боковое ребро правильной пирамиды четырехугольной, посвященной фараону Хеопсу.
Поскольку нам известна высота h и длина стороны a монумента, то следует применить такую формулу для b:
Подставляя в нее известные данные, получаем, что боковое ребро правильной четырехугольной пирамиды равно 273 метра, что немногим меньше периметра футбольного поля (300 метров).
[spoiler title=”источники:”]
http://ege.sdamgia.ru/problem?id=27063
http://24simba.ru/zdorove-i-bezopasnost/6790-piramida-i-ee-bokovye-rebra-formuly-bokovoe-rebro-piramidy-heopsa/
[/spoiler]
Когда человек слышит слово “пирамида”, то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .
Что такое пирамида в общем случае?
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.
 Вам будет интересно:Литовские статуты: даты и история изданий, регламент, хронология принятия статутов
Вам будет интересно:Литовские статуты: даты и история изданий, регламент, хронология принятия статутов

Мы видим что первая фигура имеет треугольное основание, вторая – четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.
Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:
- в основании должен находиться правильный многоугольник;
- боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.
Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.
Правильная четырехугольная пирамида
Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).
Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.
Египетские пирамиды в Гизе являются правильными четырехугольными.
Далее приведем формулы, позволяющие определить все характеристики этой фигуры.
Четыре основных линейных параметра
Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.
Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:
b = √(a2 / 2 + h2)
Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):
ab = √(a2 / 4 + h2)
Очевидно, что боковое ребро b всегда больше апофемы ab.
Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.
Площадь и объем фигуры
Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:
So = a2
Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:
Sb = 2 × a × ab
Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.
Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:
S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:
V = 1/3 × h × a2
То есть V равен третьей части произведения высоты фигуры на площадь ее основания.
Свойства правильной усеченной четырехугольной пирамиды
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание – это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.
Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.
Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:
V = 1/3 × h × (So1 + So2 + √(So1 × So2))
Здесь h – расстояние между основаниями фигуры, So1, So2 – площади нижнего и верхнего оснований.
Материал урока.
На прошлых уроках
мы работали с пирамидами. Давайте вспомним, какой многогранник называется
пирамидой, что такое правильная пирамида, вспомним свойства правильной пирамиды.
Многогранник, составленный из -угольника и
треугольников, называется пирамидой.
Пирамида называется правильной,
если ее основание – правильный многоугольник.
Площадь боковой поверхности правильной
пирамиды равна половине произведения периметра основания на апофему.
Все боковые ребра правильной пирамиды
равны, а боковые грани являются равными равнобедренными треугольниками.
Пусть нам дана
пирамида PA1A2…An. Проведем секущую плоскость β,
параллельную плоскости основания пирамиды и пусть эта плоскость пересекает
боковые ребра в точках B1,B2,…,
Bn.
Плоскость β
разбивает пирамиду на две фигуры: пирамиду PB1B2…Bn и многогранник. Многогранник, гранями которого являются n-угольники A1A2…An и B1B2…Bn, расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называется
усеченной пирамидой.
Вокруг нас много
примеров усеченных пирамид. Вытяжка над кухонной плитой имеет форму усеченной
пирамиды.клавиши клавиатуры и другие предметы.
N-угольники
A1A2…An и B1B2…Bn называются соответственно верхним и нижним основанием.
Четырехугольники A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называются боковыми
гранями.
Отрезки A1B1,…, AnBn называются боковыми рёбрами
усеченной пирамиды.
Усеченную пирамиду
обозначают так A1A2…AnB1B2…Bn. Возьмем на верхнем основании произвольную
точку C и из этой точки опустим перпендикуляр на нижнее
основание. Этот перпендикуляр называется высотой усеченной пирамиды.
Теперь давайте
докажем, что боковые грани усеченной пирамиды – это трапеции.
Для доказательства
рассмотрим грань A1A2B2B1. Понятно,
что для других боковых граней доказательство будет проводится аналогично.
Поскольку секущая
плоскость проводилась параллельно плоскости основания, то можно записать, что A1A2
параллельно B1B2.
Очевидно, что две другие стороны четырехугольника A1A2B2B1 не параллельны (они пересекаются в точке P). Получаем, что этот четырехугольник – трапеция. Очевидно,
что все остальные боковые грани тоже будут трапециями.
Как и в случае с
пирамидой, усеченная пирамида тоже может быть правильной.
Усеченная пирамида
называется правильной, если она получена сечением правильной пирамиды
плоскостью, параллельной основанию.
Основаниями
усеченной пирамиды являются правильные многоугольники, а боковые грани –
равнобедренные трапеции.
Высоты этих трапеций
называются апофемами.
Объединение боковых граней называется боковой
поверхностью усеченной пирамиды, а объединение всех граней называется полной
поверхностью усеченной пирамиды. Тогда площадью боковой поверхности
пирамиды называется сумма площадей ее боковых граней.
А площадью полной поверхности пирамиды называется
сумма площадей всех ее граней.
Теперь давайте
сформулируем и докажем теорему о площади боковой поверхности правильной
усеченной пирамиды.
Площадь боковой
поверхности правильной усеченной пирамиды равна произведению полусуммы
периметров основания на апофему.
Доказательство.
Запишем формулу для
нахождения площади боковой поверхности усеченной пирамиды.
Поскольку усеченная
пирамида правильная, значит, ее гранями будут равнобедренные трапеции.
Площадь равнобедренной
трапеции равна произведению полусуммы оснований на высоту. Высота боковой грани
есть ничто иное как апофема усеченной пирамиды.
Подставим все в
исходную формулу, вынесем половину апофемы за скобки, а в скобках сгруппируем
стороны по основаниям. Тогда получим, что площадь боковой поверхности будет
равна произведению полусуммы периметров оснований усеченной пирамиды на
апофему.
Что и
требовалось доказать.
Решим несколько
задач.
Задача. Стороны
оснований правильной усеченной четырехугольной пирамиды равны
и
. Высота пирамиды
равна . Найти площадь
боковой поверхности.
Решение.
Ответ. 120
см2
Решим еще одну
задачу.
Задача. Пирамида
пересечена плоскостью, параллельной основанию. Доказать что боковые ребра и
высота пирамиды делятся этой плоскостью на пропорциональные части.
Решение.
Что и
требовалось доказать.
Решим еще одну
задачу.
Задача. Правильная
треугольная пирамида с высотой
и стороной основания
равной рассечена плоскостью
, проходящей через
середину высоты
параллельно
основанию . Найти площадь
боковой поверхности полученной усеченной пирамиды.
Решение.
Ответ.
135 см2.
Подведем итоги
урока. Сегодня на уроке мы познакомились с такими понятиями как усеченная
пирамида, правильная усеченная пирамида. Рассмотрели свойства правильной
усеченной пирамиды. Решили несколько задач.
