Как посчитать стороны равнобедренного треугольника
- Главная
- /
- Математика
- /
- Геометрия
- /
- Как посчитать стороны равнобедренного треугольника
Чтобы посчитать чему равны стороны равнобедренного треугольника воспользуйтесь нашим удобным онлайн калькулятором:
Онлайн калькулятор
Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
для стороны a:
- длину основания (b) и угол α
- длину основания (b) и угол β
- длину основания (b) и высоту (h)
для стороны b:
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину двух равных сторон (a) и высоту (h)
Введите их в соответствующие поля и получите результат.
Как посчитать сторону a равнобедренного треугольника
Если известна сторона b и угол α
Чему равна сторона a равнобедренного треугольника если длина основания
b =
, а угол
α =?
Ответ:
a =
0
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?
Формула
a = b/2⋅cos α
Пример
Если сторона b = 10 см, а ∠α = 30°, то:
a = 10/2⋅cos 30° = 10/(2⋅0.8660) = 5.77см
Если известна сторона b и угол β
Чему равна сторона a равнобедренного треугольника если длина основания
b =
, а угол
β =?
Ответ:
a =
0
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?
Формула
a = b/2⋅sin β/2
Пример
Если сторона b = 10 см, а ∠β = 30°, то:
a = 10/2⋅sin 15 = 10/(2⋅0.2588) = 19.31см
Если известна сторона b и высота h
Чему равна сторона a равнобедренного треугольника если длина основания
b =
, а высота
h =?
Ответ:
a =
0
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?
Формула
a = √1/b2 + h2
Пример
Если сторона b = 10 см, а высота h = 20 см, то:
a = √1/102 + 202 = √0.01+400 = 20.61см
Как посчитать сторону b (основание) равнобедренного треугольника
Если известна сторона a и угол α
Чему равна сторона b равнобедренного треугольника если длина стороны
a =
, а угол
α =?
Ответ:
b =
0
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
b = 2⋅a⋅cos α
Пример
Если сторона a = 10 см, а ∠α = 30°, то:
b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см
Если известна сторона a и угол β
Чему равна сторона b равнобедренного треугольника если длина стороны
a =
, а угол
β =?
Ответ:
b =
0
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
b = 2⋅a⋅sin β/2
Пример
Если сторона a = 10 см, а ∠β = 40°, то:
b = 2⋅10⋅sin 40/2 = 2⋅10⋅0.342 = 6.84см
Если известна сторона a и высота h
Чему равна сторона b равнобедренного треугольника если длина стороны
a =
, а высота
h =?
Ответ:
b =
0
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?
Формула
b = 2⋅√a2 – h2 , h < a
Пример
Если сторона a = 10 см, а высота h = 5 см, то:
b = 2⋅√102 – 52 = 2⋅√75 = 17.32см
См. также
Стороны равнобедренного треугольника
Свойства
Равнобедренный треугольник имеет две равные по значению боковые стороны a и основание b. Это позволяет рассчитать любые параметры треугольника, необходимые для решения задачи. Периметр равнобедренного треугольника равен удвоенной боковой стороне в сумме с основанием. (рис.88.1) P=2a+b
Высота, проведенная к основанию равнобедренного треугольника, делит его на два конгруэнтных прямоугольных треугольника, с половиной основания в качестве второго катета и боковой стороной как гипотенузой. Такая высота одновременно является и медианой и биссектрисой. Найти ее можно по теореме Пифагора из прямоугольного треугольника. (рис.88.2) h_b=m_b=l_b=√(a^2-(b/2)^2 )=√(4a^2-b^2 )/2
Остальные две высоты равны друг другу и считаются через формулу с произведением разностей полупериметров и сторон, где приравнены боковые стороны. (рис.88.8) h_a=(b√((4a^2-b^2)))/2a
Зная высоту, найти площадь равнобедренного треугольника можно, подставив полученное выражение в формулу, по которой площадь равна половине основания, умноженной на его высоту. S=hb/2=(b√(4a^2-b^2 ))/4
Углы в равнобедренном треугольнике распределяются следующим образом – углы при основании друг другу конгруэнтны, также как и боковые стороны, а в сумме все три угла дают 180 градусов, поэтому найти их можно двумя видами разности. α=(180°-β)/2 β=180°-2α
Если ни один из углов не дан, но есть все стороны, то можно воспользоваться теоремой косинусов, чтобы найти любой угол. cosα=(b^2+c^2-a^2)/2bc=(b^2+a^2-a^2)/2ba=b^2/2ba=b/2a cosβ=(a^2+a^2-b^2)/(2a^2 )=(2a^2-b^2)/(2a^2 )
Медиана и биссектриса, опущенные на основание, вычисляются по формуле высоты, приведенной выше, а оставшиеся две медианы (равно как и две биссектрисы) равны друг другу, поскольку строятся на равных боковых сторонах. Вычислить медиану можно, упростив формулу произвольного треугольника. (рис. 88.3) m_a=√(2a^2+2b^2-a^2 )/2=√(a^2+2b^2 )/2
В формуле биссектрисы аналогично приравниваются боковые стороны, и ее становится возможным вычислить по упрощенной схеме. (рис. 88.4) l_a=√(ab(2a+b)(a+b-a) )/(a+b)=(b√(a(2a+b) ))/(a+b)
Средняя линия равнобедренного треугольника, параллельная основанию, равна его половине, а средние линии, параллельные боковым сторонам, равны между собой и также равны половинам самих боковых сторон. (рис. 88.5) M_b=b/2 M_a=a/2
Радиус окружности, вписанной в равнобедренной треугольник, является производной формулы для произвольного треугольника, и рассчитать его можно, зная боковую сторону и основание. (рис. 88.6) r=b/2 √((2a-b)/(2a+b))
Радиус окружности, описанной вокруг равнобедренного треугольника, также выводится из общей формулы и выглядит упрощенно следующим образом. (рис. 88.7) R=a^2/√(4a^2-b^2 )
Как посчитать стороны равнобедренного треугольника
Онлайн калькулятор
Чтобы вычислить длины сторон равнобедренного треугольника вам нужно знать следующие параметры (либо-либо):
- длину основания (b) и угол α
- длину основания (b) и угол β
- длину основания (b) и высоту (h)
- длину двух равных сторон (a) и угол α
- длину двух равных сторон (a) и угол β
- длину двух равных сторон (a) и высоту (h)
Введите их в соответствующие поля и получите результат.
Как посчитать сторону a равнобедренного треугольника
Если известна сторона b и угол α
Чему равна сторона a равнобедренного треугольника если длина основания , а угол
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол α?
Формула
Пример
Если сторона b = 10 см, а ∠α = 30°, то:
Если известна сторона b и угол β
Чему равна сторона a равнобедренного треугольника если длина основания , а угол
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и угол β?
Формула
Пример
Если сторона b = 10 см, а ∠β = 30°, то:
a = 10 /2⋅sin 15 = 10/(2⋅0.2588) = 19.31см
Если известна сторона b и высота h
Чему равна сторона a равнобедренного треугольника если длина основания , а высота
Чему равна сторона a у равнобедренного треугольника если известны длина основания (сторона b) и высота h?
Формула
Пример
Если сторона b = 10 см, а высота h = 20 см, то:
a = √ 1 /10 2 + 20 2 = √ 0.01+400 = 20.61см
Как посчитать сторону b (основание) равнобедренного треугольника
Если известна сторона a и угол α
Чему равна сторона b равнобедренного треугольника если длина стороны , а угол
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол α?
Формула
Пример
Если сторона a = 10 см, а ∠α = 30°, то:
b = 2⋅10⋅cos 30° = 2⋅10⋅0.8660 = 17.32см
Если известна сторона a и угол β
Чему равна сторона b равнобедренного треугольника если длина стороны , а угол
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и угол β?
Формула
Пример
Если сторона a = 10 см, а ∠β = 40°, то:
Если известна сторона a и высота h
Чему равна сторона b равнобедренного треугольника если длина стороны , а высота
Чему равна сторона b у равнобедренного треугольника если известны длина стороны a и высота h?
Формула
b = 2⋅ √ a 2 – h 2 , h
Пример
Если сторона a = 10 см, а высота h = 5 см, то:
Все формулы для треугольника
1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
a , b , c – стороны произвольного треугольника
α , β , γ – противоположные углы
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b – катеты
c – гипотенуза
α , β – острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b – сторона (основание)
a – равные стороны
α – углы при основании
β – угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
4. Найти длину высоты треугольника
Высота– перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется – ортоцентр.
H – высота треугольника
a – сторона, основание
b, c – стороны
β , γ – углы при основании
p – полупериметр, p=(a+b+c)/2
R – радиус описанной окружности
S – площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
[spoiler title=”источники:”]
http://poschitat.online/storony-ravnobedrennogo-treugolnika
http://www-formula.ru/2011-10-09-11-08-41
[/spoiler]
Калькулятор ребер прямоугольного равнобедренного треугольника через длину основания
При помощи данного калькулятора можно вычислить ребра у равнобедренного прямоугольного треугольника зная длину основания.
Основание треугольника A
У равнобедренного прямоугольного треугольника один из трех углов равен 90°, а два ребра (стороны), которые начинаются с этого угла равны между собой, два оставшихся угла равны 45°.
Для вычисления ребра у прямоугольного равнобедренного треугольника зная длину его основания необходимо воспользоваться следующей формулой:
y = A/√2
где:
y – ребро прямоугольника
A – длина основания равнобедренного прямоугольного треугольника.
Как найти сторону равнобедренного треугольника, если дано основание
Основным свойством равнобедренного треугольника является равенство двух смежных сторон и соответствующих углов. Можно легко найти сторону равнобедренного треугольника, если дано основание и хотя бы один элемент.

Инструкция
В зависимости от условий конкретной задачи, можно найти сторону равнобедренного треугольника, если дано основание и любой дополнительный элемент.
Основание и высота к нему.Перпендикуляр, проведенный к основанию равнобедренного треугольника, является одновременной высотой, медианой и биссектрисой противоположного угла. Этой интересной особенностью можно воспользоваться, применив теорему Пифагора:а = √(h² + (c/2)²), где а – длина равных сторон треугольника, h – высота, проведенная к основанию с.
Основание и высота к одной из боковых сторон.Проведя высоту к боковой стороне, вы получите два прямоугольных треугольника. Гипотенуза одного из них – неизвестная сторона равнобедренного треугольника, катет – заданная высота h. Второй катет неизвестен, обозначьте его х.
Рассмотрите второй прямоугольный треугольник. Его гипотенуза – основание общей фигуры, один из катетов равен h. Другой катет представляет собой разность а – x. По теореме Пифагора запишите два уравнения относительно неизвестных а и х:а² = x² + h²;c² = (а – x)² + h².
Пусть основание равно 10, а высота 8, тогда:а² = x² + 64;100 = (а – x)² + 64.
Выразите искусственно введенную переменную х из второго уравнения и подставьте ее в первое: а – x = 6 → x = а – 6а² = (а – 6)² + 64 → а = 25/3.
Основание и один из равных углов α.Проведите высоту к основанию, рассмотрите один из прямоугольных треугольников. Косинус бокового угла равен отношению прилежащего катета к гипотенузе. В данном случае катет равен половине основания равнобедренного треугольника, а гипотенуза – его боковой стороне:(c/2)/a = cos α → а = c/(2•cos α).
Основание и противоположный угол β.Опустите перпендикуляр на основание. Угол одного из получившихся прямоугольных треугольников равен β/2. Синус этого угла представляет собой отношение противолежащего катета к гипотенузе а, откуда:а = c/(2•sin(β/2))
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Enter any two known values for an isosceles triangle to calculate the edge lengths, altitude, angles, area, perimeter, inradius, and circumradius.
Solution:
| side a: |
3 |
| base b: |
5 |
| angle α: |
33.557° | 0.5857 rad |
| angle β: |
112.89° | 1.97 rad |
| height h: |
1.658 |
| area: |
4.146 |
| perimeter: |
11 |
| inradius: |
0.7538 |
| circumradius: |
2.714 |
Type of Triangle:
obtuse isosceles triangle
Learn how we calculated this below
scroll down
On this page:
-
Calculator
-
What is an Isosceles Triangle?
-
Types of Isosceles Triangles
-
How to Calculate Edge Lengths of an Isosceles Triangle
-
How to Calculate the Angles of an Isosceles Triangle
-
How to Calculate Area and Perimeter
What is an Isosceles Triangle?
An isosceles triangle is a triangle that has two sides of equal length. The third side is often referred to as the base. Isosceles triangles are typically considered to have exactly two sides of equal length.
However, sometimes they are referred to as having at least two sides of equal length. The equilateral triangle, for example, is considered a special case of the isosceles triangle.
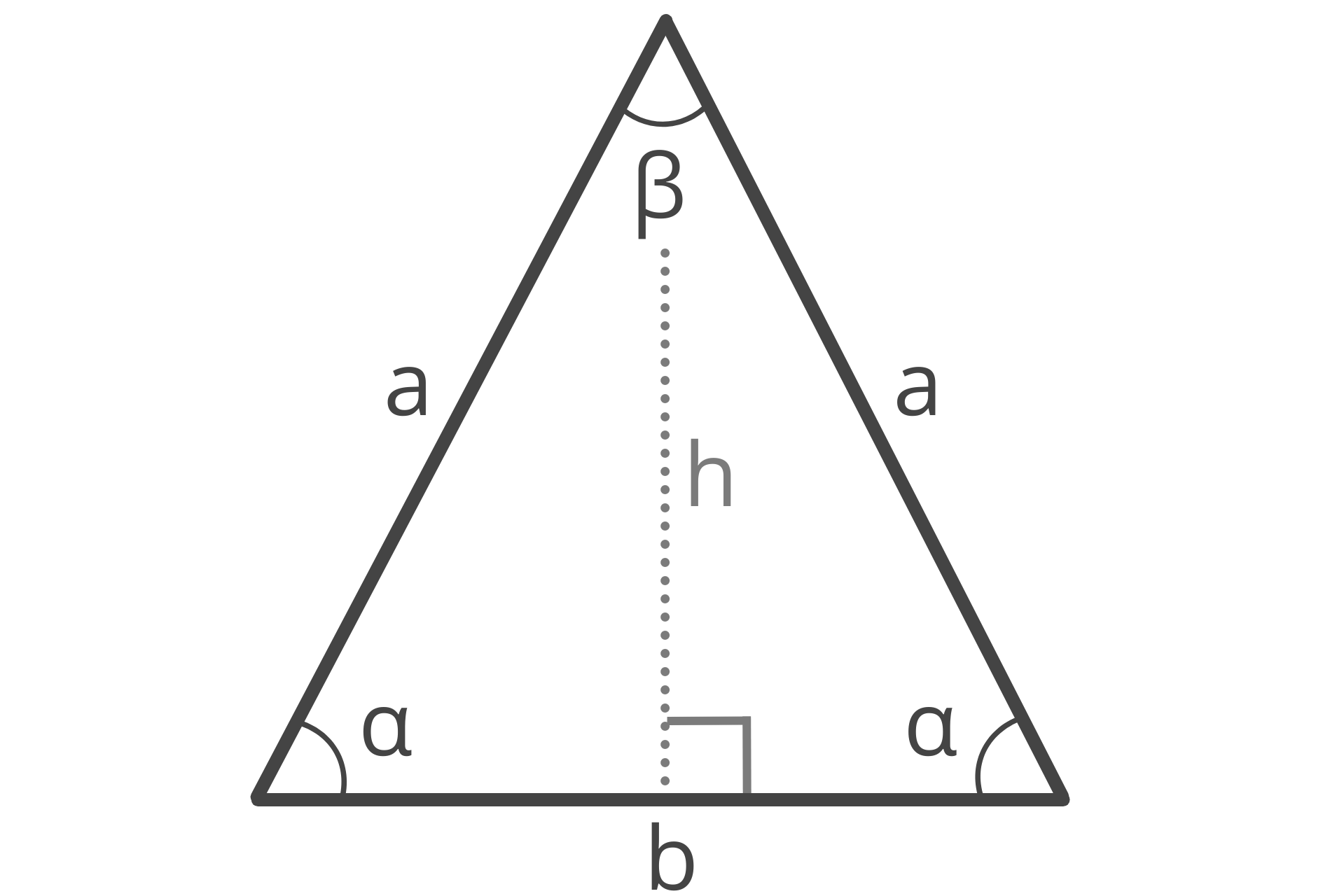
The two interior angles adjacent to the base are called the base angles, while the interior angle opposite the base is called the vertex angle. When references are made to the angles of a triangle, they are most commonly referring to the interior angles.
Because the side lengths opposite the base angles are of equal length, the base angles are also identical. Note, this means that any reference made to side length a applies to either of the identical side lengths as they are equal, and any reference made to base angle α applies to either of the base angles as they are also identical.

Types of Isosceles Triangles
There are four types of isosceles triangles: acute, obtuse, equilateral, and right.
An acute isosceles triangle is an isosceles triangle with a vertex angle less than 90°, but not equal to 60°.
An obtuse isosceles triangle is an isosceles triangle with a vertex angle greater than 90°.
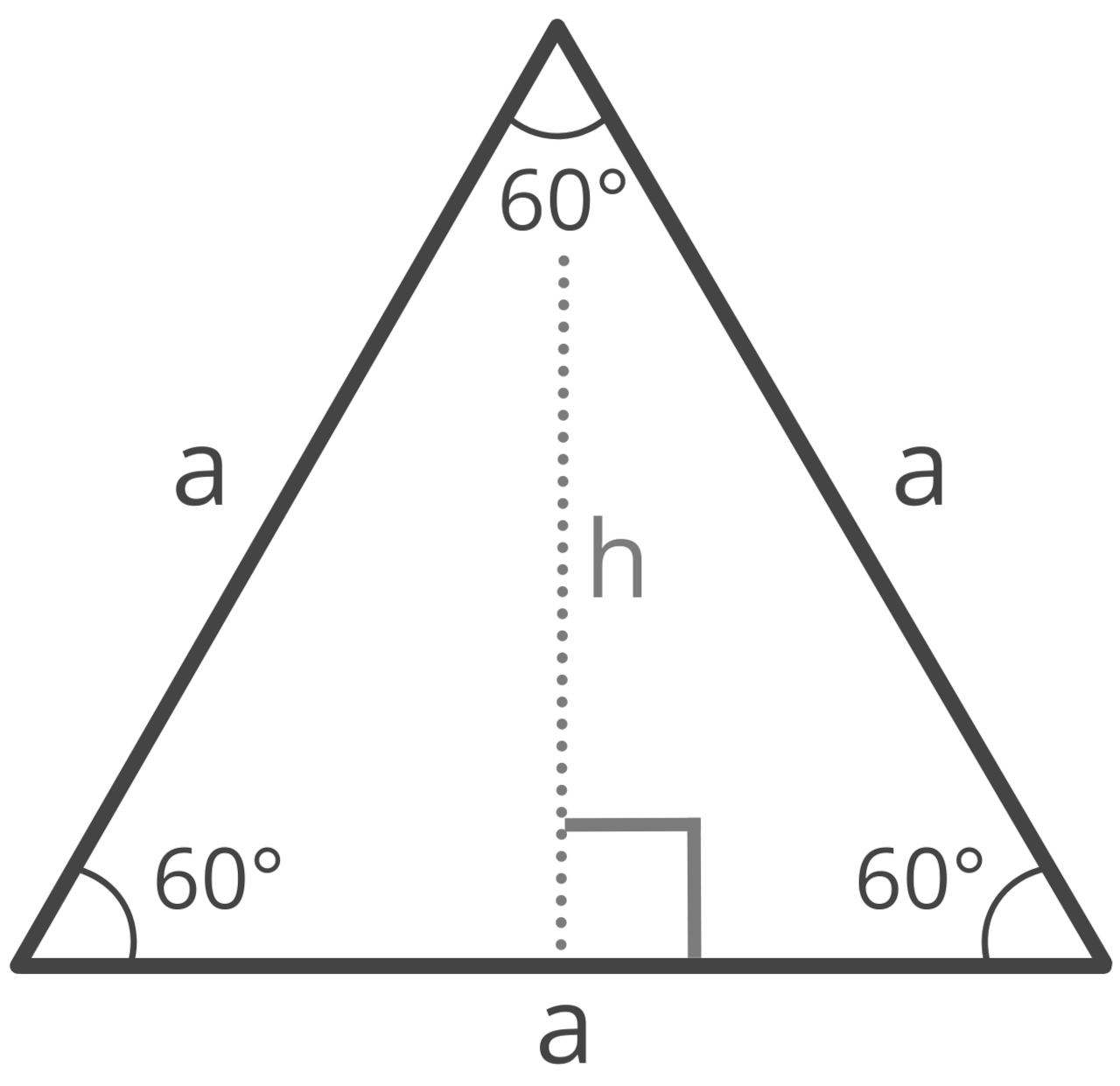
An equilateral triangle is a special case of isosceles triangles. Note, in an equilateral triangle, all three interior angles are identical to one another, and all three side lengths are equal to one another.
Thus, the vertex angle of an equilateral triangle is equal to 60°, as are the base angles. Try our equilateral triangle calculator.
A right isosceles triangle is an isosceles triangle with a vertex angle equal to 90°, and base angles equal to 45°. This is also referred to as a 45 45 90 special right triangle.
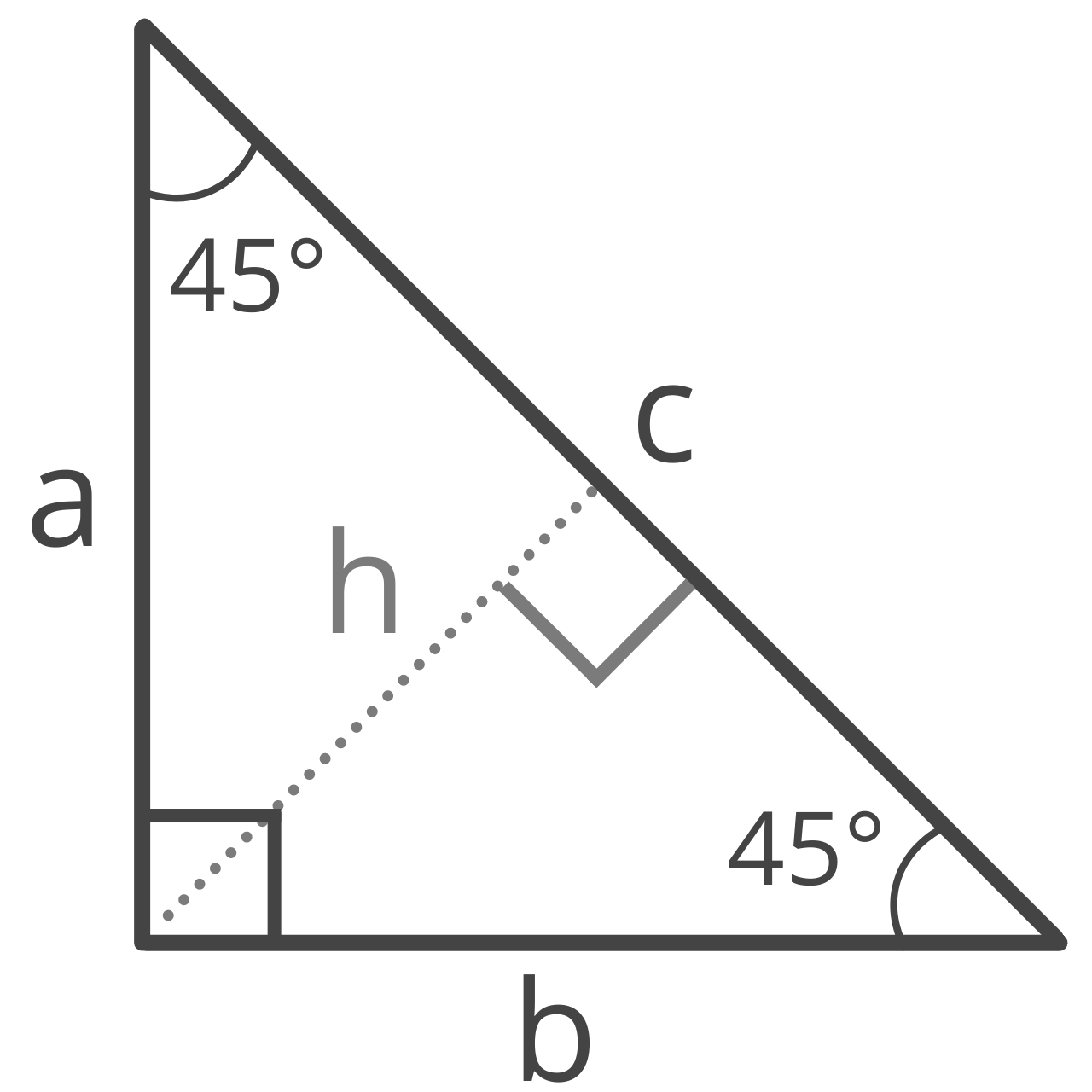
We have a special right triangle calculator to calculate this type of triangle.
How to Calculate Edge Lengths of an Isosceles Triangle
Given the height, or altitude, of an isosceles triangle and the length of one of the sides or the base, it’s possible to calculate the length of the other sides.
Find the Base Length
Use the following formula derived from the Pythagorean theorem to solve the length of the base side:
b = 2a² – h²
The base length b is equal to 2 times the square root of quantity leg a squared minus the height h squared.
Find the Leg Length
Use the following formula also derived from the Pythagorean theorem to solve the length of side a:
a = h² + (b ÷ 2)²
The side length a is equal to the square root of the quantity height h squared plus one-half of base b squared.
How to Calculate the Angles of an Isosceles Triangle
Given any angle in an isosceles triangle, it is possible to solve the other angles.
Find the Base Angle
Use the following formula to solve either of the base angles:
α = 180° – β / 2
The base angle α is equal to quantity 180° minus vertex angle β, divided by 2.
Find the Vertex Angle
Use the following formula to solve the vertex angle:
β = 180° – 2α
The vertex angle β is equal to 180° minus 2 times the base angle α.
How to Calculate Area and Perimeter
Given the side lengths of an isosceles triangle, it is possible to solve the perimeter and area using a few simple formulas.
Find the Perimeter
You can find the perimeter of an isosceles triangle using the following formula:
p = 2a + b
Thus, the perimeter p is equal to 2 times side a plus base b.
Find the Semiperimeter
Given the perimeter, you can find the semiperimeter. The semiperimeter s is equal to half the perimeter.
s = p / 2
Find the Area
You can find the area of an isosceles triangle using the formula:
A = s(s – a)(s – a)(s – b)
The area A is equal to the square root of the semiperimeter s times semiperimeter s minus side a times semiperimeter s minus a times semiperimeter s minus base b.
This is known as Heron’s formula.



