Как найти регрессионную зависимость - Сайт, где вы сможете решить свои вопросы

Регрессио́нный анализ — набор статистических методов исследования влияния одной или нескольких независимых переменных $X_{1},X_{2},...,X_{p}$ на зависимую переменную . Независимые переменные иначе называют регрессорами или предикторами, а зависимые переменные — критериальными или регрессантами. Терминология зависимых и независимых переменных отражает лишь математическую зависимость переменных (см. Корреляция), а не причинно-следственные отношения. Наиболее распространённый вид регрессионного анализа — линейная регрессия, когда находят линейную функцию, которая, согласно определённым математическим критериям, наиболее соответствует данным. Например, в методе наименьших квадратов вычисляется прямая (или гиперплоскость), сумма квадратов между которой и данными минимальна.

Цели регрессионного анализа[править | править код]

Определение степени детерминированности вариации критериальной (зависимой) переменной предикторами (независимыми переменными)
Предсказание значения зависимой переменной с помощью независимой(-ых)
Определение вклада отдельных независимых переменных в вариацию зависимой

Математическое определение регрессии[править | править код]

Строго регрессионную зависимость можно определить следующим образом. Пусть $Y,X_{1},X_{2},ldots ,X_{p}$ — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений $X_{1}=x_{1},X_{2}=x_{2},ldots ,X_{p}=x_{p}$ определено условное математическое ожидание

$y(x_{1},x_{2},ldots ,x_{p})={mathbb {E}}(Ymid X_{1}=x_{1},X_{2}=x_{2},ldots ,X_{p}=x_{p})$

(уравнение регрессии в общем виде),

то функция $y(x_{1},x_{2},ldots ,x_{p})$ называется регрессией величины по величинам $X_{1},X_{2},ldots ,X_{p}$ , а её график — линией регрессии по $X_{1},X_{2},ldots ,X_{p}$ , или уравнением регрессии.

Зависимость от $X_{1},X_{2},ldots ,X_{p}$ проявляется в изменении средних значений при изменении $X_{1},X_{2},ldots ,X_{p}$ . Хотя при каждом фиксированном наборе значений $X_{1}=x_{1},X_{2}=x_{2},ldots ,X_{p}=x_{p}$ величина остаётся случайной величиной с определённым распределением.

Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение при изменении $X_{1},X_{2},...,X_{p}$ , используется средняя величина дисперсии при разных наборах значений $X_{1},X_{2},...,X_{p}$ (фактически речь идёт о мере рассеяния зависимой переменной вокруг линии регрессии).

В матричной форме уравнение регрессии (УР) записывается в виде: Y=BX+U , где — матрица ошибок. При обратимой матрице X◤X получается вектор-столбец коэффициентов B с учётом U◤U=min(B). В частном случае для Х=(±1) матрица X◤X является рототабельной, и УР может быть использовано при анализе временны́х рядов и обработке технических данных.

Метод наименьших квадратов (расчёт коэффициентов)[править | править код]

На практике линия регрессии чаще всего ищется в виде линейной функции ${displaystyle Y=b_{0}+b_{1}X_{1}+b_{2}X_{2}+ldots +b_{N}X_{N}}$ (линейная регрессия), наилучшим образом приближающей искомую кривую. Делается это с помощью метода наименьших квадратов, когда минимизируется сумма квадратов отклонений реально наблюдаемых {Y} от их оценок (имеются в виду оценки с помощью прямой линии, претендующей на то, чтобы представлять искомую регрессионную зависимость):

$sum _{{k=1}}^{{M}}(Y_{k}-{hat {Y_{k}}})^{2}to min$

( — объём выборки). Этот подход основан на том известном факте, что фигурирующая в приведённом выражении сумма принимает минимальное значение именно для того случая, когда $Y=y(x_{1},x_{2},...x_{N})$ .

Для решения задачи регрессионного анализа методом наименьших квадратов вводится понятие функции невязки:

$sigma ({bar {b}})={frac {1}{2}}sum _{{k=1}}^{{M}}{(Y_{k}-{hat {Y}}_{k})^{2}}$

Условие минимума функции невязки:

${displaystyle left{{begin{matrix}{frac {partial sigma ({bar {b}})}{partial b_{i}}}=0\i=0...Nend{matrix}}right.Leftrightarrow {begin{cases}sum limits _{i=1}^{M}{y_{i}}=sum limits _{i=1}^{M}{sum limits _{j=1}^{N}{b_{j}x_{i,j}}}+b_{0}M\sum limits _{i=1}^{M}{y_{i}x_{i,k}}=sum limits _{i=1}^{M}{sum limits _{j=1}^{N}{b_{j}x_{i,j}x_{i,k}}}+b_{0}sum limits _{i=1}^{M}{x_{i,k}}\k=1,ldots ,Nend{cases}}}$

Полученная система является системой N+1 линейных уравнений с N+1 неизвестными $b_{0},ldots ,b_{N}$ .

Если представить свободные члены левой части уравнений матрицей

${displaystyle B=left({begin{matrix}sum limits _{i=1}^{M}{y_{i}}\sum limits _{i=1}^{M}{y_{i}x_{i,1}}\vdots \sum limits _{i=1}^{M}{y_{i}x_{i,N}}end{matrix}}right),}$

а коэффициенты при неизвестных в правой части — матрицей

${displaystyle A=left({begin{matrix}M&sum limits _{i=1}^{M}{x_{i,1}}&sum limits _{i=1}^{M}{x_{i,2}}&...&sum limits _{i=1}^{M}{x_{i,N}}\sum limits _{i=1}^{M}{x_{i,1}}&sum limits _{i=1}^{M}{x_{i,1}x_{i,1}}&sum limits _{i=1}^{M}{x_{i,2}x_{i,1}}&...&sum limits _{i=1}^{M}{x_{i,N}x_{i,1}}\sum limits _{i=1}^{M}{x_{i,2}}&sum limits _{i=1}^{M}{x_{i,1}x_{i,2}}&sum limits _{i=1}^{M}{x_{i,2}x_{i,2}}&...&sum limits _{i=1}^{M}{x_{i,N}x_{i,2}}\vdots &vdots &vdots &ddots &vdots \sum limits _{i=1}^{M}{x_{i,N}}&sum limits _{i=1}^{M}{x_{i,1}x_{i,N}}&sum limits _{i=1}^{M}{x_{i,2}x_{i,N}}&...&sum limits _{i=1}^{M}{x_{i,N}x_{i,N}}end{matrix}}right),}$

то получаем матричное уравнение: , которое легко решается методом Гаусса. Полученная матрица будет матрицей, содержащей коэффициенты уравнения линии регрессии:

$X=left({begin{matrix}b_{0}\b_{1}\vdots \b_{N}end{matrix}}right)$

Для получения наилучших оценок необходимо выполнение предпосылок МНК (условий Гаусса — Маркова). В англоязычной литературе такие оценки называются BLUE (Best Linear Unbiased Estimators — «наилучшие линейные несмещённые оценки»).
Большинство исследуемых зависимостей может быть представлено с помощью МНК нелинейными математическими функциями.

Интерпретация параметров регрессии[править | править код]

Параметры $b_{i}$ являются частными коэффициентами корреляции; $(b_{i})^{2}$ интерпретируется как доля дисперсии Y, объяснённая $X_{i}$ , при закреплении влияния остальных предикторов, то есть измеряет индивидуальный вклад $X_{i}$ в объяснение Y. В случае коррелирующих предикторов возникает проблема неопределённости в оценках, которые становятся зависимыми от порядка включения предикторов в модель. В таких случаях необходимо применение методов анализа корреляционного и пошагового регрессионного анализа.

Говоря о нелинейных моделях регрессионного анализа, важно обращать внимание на то, идёт ли речь о нелинейности по независимым переменным (с формальной точки зрения легко сводящейся к линейной регрессии), или о нелинейности по оцениваемым параметрам (вызывающей серьёзные вычислительные трудности). При нелинейности первого вида с содержательной точки зрения важно выделять появление в модели членов вида $X_{1}X_{2}$ , $X_{1}X_{2}X_{3}$ , свидетельствующее о наличии взаимодействий между признаками $X_{1}$ , $X_{2}$ и т. д. (см. Мультиколлинеарность).

См. также[править | править код]

Корреляция
Мультиколлинеарность
Автокорреляция
Перекрёстная проверка
Линейная регрессия на корреляции

Литература[править | править код]

Дрейпер Н., Смит Г. Прикладной регрессионный анализ. Множественная регрессия = Applied Regression Analysis. — 3-е изд. — М.: «Диалектика», 2007. — 912 с. — ISBN 0-471-17082-8.
Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа = Methoden der Korrelation – und Regressiolynsanalyse. — М.: Финансы и статистика, 1981. — 302 с.
Захаров С. И., Холмская А. Г. Повышение эффективности обработки сигналов вибрации и шума при испытаниях механизмов // Вестник машиностроения : журнал. — М.: Машиностроение, 2001. — № 10. — С. 31—32. — ISSN 0042-4633.
Радченко С. Г. Устойчивые методы оценивания статистических моделей. — К.: ПП «Санспарель», 2005. — 504 с. — ISBN 966-96574-0-7, УДК: 519.237.5:515.126.2, ББК 22.172+22.152.
Радченко С. Г. Методология регрессионного анализа. — К.: «Корнийчук», 2011. — 376 с. — ISBN 978-966-7599-72-0.

Источник

217

5.1. Общие положения

Регрессия
– это зависимость среднего значения
какой-либо величины от некоторой другой
величины или от нескольких других
величин. В отличие от чисто функциональной
зависимости y=f(x),
когда каждому
значению независимой переменной х
соответствует одно определённое значение
зависимой переменной у,
при
регрессионной связи одному и тому же
значению независимой переменной
(фактору) х
могут
соответствовать в зависимости от
конкретного случая различные значения
зависимой переменной (отклика)
у. Если при
каждом значении х=х_iнаблюдается
n_i
значений y_ij;
то
зависимость средних арифметических
значений:отx_i
и является регрессией в статистическом
понимании этого термина. Изучение
регрессии основано на том, что случайные
величины Х
и Y
связаны
между собой вероятностной зависимостью:
при каждом конкретном значении Х=хвеличинаY
является
случайной величиной с вполне определённым
распределением вероятностей. Зависимость
зависимой переменной – отклика от одной
независимой переменной – фактора или
нескольких факторов называется уравнением
регрессии. По количеству факторов
выделяют парную (однофакторную) и
множественную (многофакторную) регрессию.
Для парной будем рассматривать следующие
методы регрессии: линейную, показательную,
экспоненциальную, гиперболическую и
параболическую.

Регрессионный
анализ –
это раздел математической статистики,
изучающий регрессионную зависимость
между случайными величинами по
статистическим данным. Цель регрессионного
анализа состоит в определении общего
вида уравнения регрессии, вычислении
оценок неизвестных параметров, входящих
в уравнение регрессии проверке
статистических гипотез о регрессионной
связи.

При проведении
экспериментов рекомендуется подбирать
переменные, участвующие в экспериментах
так, чтобы они были случайными,
количественными и непрерывными. В этом
случае для обработки результатов
рекомендуется применять регрессионный
анализ, обладающий свойствами сравнительной
простоты и конструктивности, которые
заключаются в возможности использования
регрессионных уравнений для генерации
эффективных решений на основе
оптимизационных методов. Отметим, что
если переменные не количественные, а
качественные, то рекомендуется
использовать дисперсионный анализ.
Если же часть переменных количественная,
а часть качественная, то рекомендуется
корреляционный анализ.

Регрессионный
анализ основан на методе наименьших
квадратов, который требует, чтобы сумма
квадратов отклонений экспериментальных
значений от вычисленных по аппроксимирующей
зависимости была минимальной. Запишем
это условие для однофакторной зависимости:

(5.1.1)

где x_i^*
– i–ое
экспериментальное значение фактора;

y_i^*
– i–ое
экспериментальное значение отклика;

f(x_i^*)
– i–ое
вычисленное значение отклика;

n
– общее
количество экспериментальных значений.

Запишем то же
условие для многофакторной зависимости:

(5.1.2)

где x_ij^*
– i–ое
экспериментальное значение j-го
фактора;

y_i^*
– i–ое
экспериментальное значение отклика;

f(x_i₁^*,x_i₂,…x_im^*)
– i–ое
вычисленное значение отклика;

m
– количество
факторов;

n
– общее количество экспериментальных
значений.

В лучшем случае
при обработке результатов экспериментов
нам известен вид математической
зависимости между переменными и тогда
следует вычислить только неизвестные
коэффициенты. Чаще всего вид математической
зависимости неизвестен. В этом случае
рекомендуется использовать степенные
полиномы, которые при повышении степени
полинома позволяют получать аппроксимирующие
зависимости с любой заданной точностью.
Запишем степенной полином для однофакторной
зависимости:

(5.1.3)

Запишем
полином второго порядка для двухфакторной
зависимости:

y
= b₀х₀+b₁x₁+b₂x₂+b₁₂x₁x₂+b₁₁x₁²+b₂₂x₂²^.(5.1.4)

Технология
регрессионного анализа

Для проведения
регрессионного анализа предлагается
технология, состоящая из следующих
четырёх этапов.

Для однофакторных
зависимостей строится система координат,
по оси

абсцисс делается
масштабирование для фактора x,
по оси ординат – для отклика y.
В принятой системе координат размещаются
экспериментальные точки, по характеру
размещения которых делается предположение
о виде зависимости y=f(x).
Для многофакторных зависимостей этот
пункт не выполняется.

Проводится
корреляционный анализ. Если предполагается
наличие ли-

нейной зависимости
и нормальность распределения фактора
и отклика то для оценки тесноты связи
между переменными рекомендуется
использовать коэффициент
линейной корреляции,
вычисляемый по формуле:

(5.1.5)

В формуле
(5.1.5) оценки математических ожиданий
переменных х,
у
и их произведения
вычисляются
по формулам:

(5.1.6)

Оценки вторых
начальных моментов требуются для
вычисления средних квадратических
отклонений. Для этого используются
следующие формулы:

(5.1.7)

(5.1.8)

Если коэффициент
линейной корреляции близок к 1,
то корреляционная связь между переменными
положительная, близкая к линейной. Если
коэффициент линейной корреляции близок
к -1,
то корреляционная связь между переменными
отрицательная, близкая к линейной. Если
коэффициент линейной корреляции близок
к 0,
то между переменными имеется слабая
корреляционная связь. Для независимых
переменных коэффициент линейной
корреляции равен нулю.

Оценить
существенность коэффициента линейной
корреляции между случайными переменными
по критерию Стьюдента можно при условии,
что распределения этих случайных величин
подчиняется нормальному закону и что
они имеют совместное двумерное нормальное
распределение.

В случае, если
значение коэффициента линейной
корреляции, вычисленное по (5.1.5), по
абсолютной величине не меньше 0,8, то
можно ожидать наличие между переменными
линейной зависимости. Если значение
коэффициента линейной корреляции по
абсолютной величине меньше 0.8 то
рекомендуется в качестве факторов
попробовать использовать сравнительно
несложные функции от факторов.
Рекомендуется использовать следующие
функции от факторов x_i;
:
для увеличения масштаба факторах
относительно
результативного показателя эффективности
у;
–
для уменьшения масштаба факторах
относительно
результативного показателя эффективности
у;
–
для отображения обратной связи между
фактором х
и результативным
показателем эффективности
у. Естественно,
что после вычисления коэффициента
линейной корреляции для простых функций
от факторов, для регрессионного анализа
выбираются функции, коэффициент линейной
корреляции которых с откликом имеет
наибольшее значение.
Таким
образом, и выбирается вид регрессионной
зависимости между переменными.

Эмпирическое
корреляционное отношение
может использоваться для любых
распределений случайных величин без
введения каких-либо ограничений. Оно
вычисляется по формуле

(5.1.9)

где δ^*
– оценка
межгруппового среднего квадратического
отклонения;

σ_у^*
– оценка
среднего квадратического отклонения
результативного

признака.

Оценка
межгруппового среднего квадратического
отклонения вычисляется по формуле:

.
(5.1.10)

Построение
уравнения регрессии, т.е. фактически
вычисление значений

коэффициентов
равнения регрессии.

Для построения
регрессионной зависимости применяется
метод наименьших квадратов (МНК),
требующий, чтобы сумма квадратов
отклонений экспериментальных значений
от вычисленных по аппроксимирующей
зависимости была минимальной. Так как
нам требуется найти некоторое количество
коэффициентов, значения которых на
данном этапе неизвестно, то по (5.1.3)
запишем требование МНК в более общем
виде с вводом в неё и искомых коэффициентов

(5.1.11)

Найдём значения
коэффициентов
обеспечивающих минимальное значение
левой части (5.1.11). Для этого продифференцируем
её пои приравняем производные нулю. Получим
систему уравнений, получивших название
нормальных:

(5.1.12)

Составленная
система нормальных уравнений (5.1.12) не
решается в общем виде, далее по тексту
лекций она будет решена для нескольких
частных случаев.

Найти значения
коэффициентов можно и другим наиболее
часто используемым на практике методом
решением системы уравнений в матричном
виде.

(5.1.13)

Оценка качества
полученных уравнений регрессии.

Главный показатель
качества аппроксимации – стандартная
ошибка и

ещё более сильный
показатель отношение стандартной ошибки
к среднему значению. Стандартная ошибка
для множественной регрессии вычисляется
по формуле:

(5.1.14)

где x_ij^*
– i–ое
экспериментальное значение j-го
фактора;

y_i^*
– i–ое
экспериментальное значение отклика;

f(x_i₁^*,x_i₂,…x_im^*)
– i–ое
вычисленное значение отклика;

m
– количество
факторов;

q
– количество
переменных в уравнении регрессии;

n
– общее количество экспериментальных
значений.

Отношение
стандартной ошибки к среднему значению
должно не превышать рекомендуемый
уровень 0.05 (5 процентов)

(5.1.15)

Отметим, что
воспользоваться рекомендацией (5.1.15)
можно только в случаях, если

Применение
дисперсионного анализа
для оценки
качества уравнений регрессии.
Дисперсионный анализ основан на
разложении общей изменчивости
результативного показателя (общей
дисперсии) на объяснённую дисперсию,
которую удалось объяснить изменением
переменных, вошедших в уравнение
регрессии, и остаточную регрессию,
которую объяснить не удалось. Для
проведения дисперсионного анализа
вычисляются.

Объяснённая сумма
квадратов:

(5.1.16)

с количеством
степеней свободы:

среднее значение
суммы квадратов:

(5.1.17)

Остаточная сумма
квадратов:

(5.1.18)

с количеством
степеней свободы:

среднее значение
суммы квадратов:

(5.1.19)

Общая сумма
квадратов:

(5.1.20)

с количеством
степеней свободы:

Должно выполняться
равенство:

Критерий Фишера

(5.1.21)

с количеством
степеней свободы:

Коэффициент
множественной детерминации, который
показывает, какую

часть изменения
результативного показателя удалось
объяснить изменением переменных,
вошедших в уравнение регрессии.

(5.1.22)

с количеством
степеней свободы:

По статистическим
таблицам для критерия Фишера и коэффициента
множественной детерминации с
вышеприведёнными количествами степеней
свободы и рекомендуемого уровня
значимости 0.05 находят их критические
значения. Если вычисленные значения
критерия Фишера и коэффициента
множественной детерминации не меньше
критических значений, то результаты
аппроксимации признаются удовлетворительными.

Ввиду того, что
коэффициенты уравнения регрессии
вычисляются по

случайным величинам,
то они и сами являются случайными
величинами. Поэтому можно вычислить их
стандартные ошибки и по ним определить
критерий Стьюдента и уровни их значимости.

(5.1.23)

где

– диагональный
элемент матрицы

(5.1.24)

чем больше величина
,
тем лучше.

По статистическим
таблицам для вычисления
,
дляn-1
степеней свободы, для рекомендованного
уровня значимости
вычисляем критическое значение критерия
Стьюдента.
Если вычисленное значениепревышает критическое, то считаем, что
уровень значимостине превышает рекомендуемого значения,
и поэтому вычисленные значения
коэффициентов приемлемы для отображения
экспериментальных данных. В противном
случае рекомендуется подобрать другие
значения переменных в аппроксимирующее
уравнение регрессии, в виде каких-либо
функций от аргументов.

Источник

Простая линейная регрессия — это статистический метод, который можно использовать для понимания связи между двумя переменными, x и y.

Одна переменная x известна как предикторная переменная .

Другая переменная, y , известна как переменная ответа .

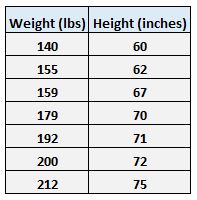
Например, предположим, что у нас есть следующий набор данных с весом и ростом семи человек:

Пусть вес будет предикторной переменной, а рост — переменной отклика.

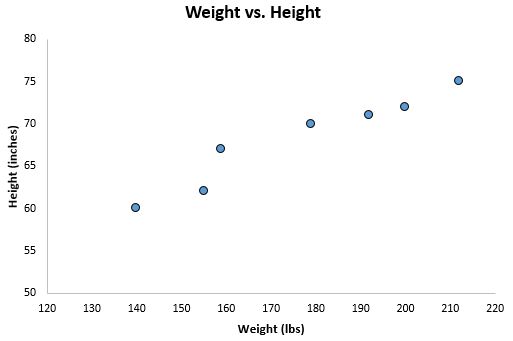
Если мы изобразим эти две переменные с помощью диаграммы рассеяния с весом по оси x и высотой по оси y, вот как это будет выглядеть:

Предположим, нам интересно понять взаимосвязь между весом и ростом. На диаграмме рассеяния мы ясно видим, что по мере увеличения веса рост также имеет тенденцию к увеличению, но для фактической количественной оценки этой взаимосвязи между весом и ростом нам нужно использовать линейную регрессию.

Используя линейную регрессию, мы можем найти линию, которая лучше всего «соответствует» нашим данным. Эта линия известна как линия регрессии наименьших квадратов, и ее можно использовать, чтобы помочь нам понять взаимосвязь между весом и ростом. Обычно вы должны использовать программное обеспечение, такое как Microsoft Excel, SPSS или графический калькулятор, чтобы найти уравнение для этой линии.

Формула линии наилучшего соответствия записывается так:

ŷ = б 0 + б 1 х

где ŷ — прогнозируемое значение переменной отклика, b 0 — точка пересечения с осью y, b 1 — коэффициент регрессии, а x — значение переменной-предиктора.

Связанный: 4 примера использования линейной регрессии в реальной жизни

Поиск «Линии наилучшего соответствия»

Для этого примера мы можем просто подключить наши данные к калькулятору линейной регрессии Statology и нажать « Рассчитать »:

Калькулятор автоматически находит линию регрессии методом наименьших квадратов :

ŷ = 32,7830 + 0,2001x

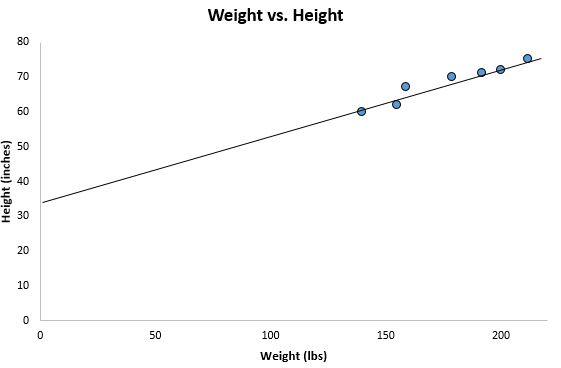
Если мы уменьшим масштаб нашей диаграммы рассеяния и добавим эту линию на диаграмму, вот как это будет выглядеть:

Обратите внимание, как наши точки данных близко разбросаны вокруг этой линии. Это потому, что эта линия регрессии методом наименьших квадратов лучше всего подходит для наших данных из всех возможных линий, которые мы могли бы нарисовать.

Как интерпретировать линию регрессии методом наименьших квадратов

Вот как интерпретировать эту линию регрессии наименьших квадратов: ŷ = 32,7830 + 0,2001x

б0 = 32,7830.Это означает, что когда предикторная переменная веса равна нулю фунтов, прогнозируемый рост составляет 32,7830 дюйма. Иногда может быть полезно знать значение b 0 , но в этом конкретном примере на самом деле нет смысла интерпретировать b 0 , поскольку человек не может весить ноль фунтов.

б 1 = 0,2001.Это означает, что увеличение x на одну единицу связано с увеличением y на 0,2001 единицы. В этом случае увеличение веса на один фунт связано с увеличением роста на 0,2001 дюйма.

Как использовать линию регрессии наименьших квадратов

Используя эту линию регрессии наименьших квадратов, мы можем ответить на такие вопросы, как:

Какого роста мы ожидаем от человека, который весит 170 фунтов?

Чтобы ответить на этот вопрос, мы можем просто подставить 170 в нашу линию регрессии для x и найти y:

ŷ = 32,7830 + 0,2001 (170) = 66,8 дюйма

Какого роста мы ожидаем от человека, который весит 150 фунтов?

Чтобы ответить на этот вопрос, мы можем подставить 150 в нашу линию регрессии для x и найти y:

ŷ = 32,7830 + 0,2001 (150) = 62,798 дюйма

Предупреждение. При использовании уравнения регрессии для ответа на подобные вопросы убедитесь, что вы используете только те значения переменной-предиктора, которые находятся в пределах диапазона переменной-предиктора в исходном наборе данных, который мы использовали для создания линии регрессии методом наименьших квадратов. Например, вес в нашем наборе данных варьировался от 140 до 212 фунтов, поэтому имеет смысл отвечать на вопросы о прогнозируемом росте только тогда, когда вес составляет от 140 до 212 фунтов.

Коэффициент детерминации

Одним из способов измерения того, насколько хорошо линия регрессии наименьших квадратов «соответствует» данным, является использование коэффициента детерминации , обозначаемого как R 2 .

Коэффициент детерминации — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной.

Коэффициент детерминации может варьироваться от 0 до 1. Значение 0 указывает на то, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.

R 2 между 0 и 1 указывает, насколько хорошо переменная отклика может быть объяснена переменной-предиктором. Например, R 2 , равный 0,2, указывает, что 20% дисперсии переменной отклика можно объяснить переменной-предиктором; R 2 , равное 0,77, указывает, что 77% дисперсии переменной отклика можно объяснить переменной-предиктором.

Обратите внимание, что в нашем предыдущем выводе мы получили значение R2, равное 0,9311 , что указывает на то, что 93,11% изменчивости роста можно объяснить предикторной переменной веса:

Это говорит нам о том, что вес является очень хорошим предиктором роста.

Предположения линейной регрессии

Чтобы результаты модели линейной регрессии были достоверными и надежными, нам необходимо проверить выполнение следующих четырех допущений:

1. Линейная зависимость. Существует линейная зависимость между независимой переменной x и зависимой переменной y.

2. Независимость: Остатки независимы. В частности, нет корреляции между последовательными остатками в данных временных рядов.

3. Гомоскедастичность: остатки имеют постоянную дисперсию на каждом уровне x.

4. Нормальность: остатки модели нормально распределены.

Если одно или несколько из этих предположений нарушаются, то результаты нашей линейной регрессии могут быть ненадежными или даже вводящими в заблуждение.

Обратитесь к этому сообщению для объяснения каждого предположения, как определить, выполняется ли предположение, и что делать, если предположение нарушается.

Источник

Цели регрессионного анализа[править | править код]

Математическое определение регрессии[править | править код]

Метод наименьших квадратов (расчёт коэффициентов)[править | править код]

Интерпретация параметров регрессии[править | править код]

См. также[править | править код]

Литература[править | править код]

5.1. Общие положения

Поиск «Линии наилучшего соответствия»

Как интерпретировать линию регрессии методом наименьших квадратов

Как использовать линию регрессии наименьших квадратов

Коэффициент детерминации

Предположения линейной регрессии

Вам также может понравиться

Жирные макароны по флотски как исправить

Как найти дело в апелляции мосгорсуд

Как найти доход на собственный капитал

Добавить комментарий Отменить ответ